王洋洋,蒋兴良
(输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆 400044)
摘要:
为了提高二维瞬态涡流场的计算精度与速度,结合边光滑有限元法计算精度高和边界元法占用计算机内存少的优点,提出一种基于边光滑有限元法——边界元法相结合的混合算法（ES-FEM-BEM）来计算二维瞬态涡流场. 在相同网格划分密度下,相较于传统的有限元-边界元耦合算法(FEM-BEM)而言,该混合算法具有明显提高计算精度的优点. 同时建立了二维脉冲线圈-铝板模型,并对铝板表面的磁场强度进行计算. 结果表明:在网格划分密度相同的情况,ES-FEM-BEM的计算结果与测量结果的最大相对误差只有3.4%,而FEM-BEM的计算结果与测量结果的最大相对误差达到31.8%. 基于边光滑有限元法和边界元法耦合的混合算法,可为瞬态开域涡流场分析提供重要的参考依据.
关键词: 边光滑有限元法 边界元法 瞬态涡流场 二维磁场计算
DOI：10.11918/202001049
分类号:TM723
文献标识码:A
基金项目:国家自然科学基金(51637002)
Calculation of 2D transient eddy current field by ES-FEM-BEM coupling method
WANG Yangyang,JIANG Xingliang
(State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China)
Abstract:
To improve the calculation accuracy and speed for 2D transient eddy current field, a method (ES-FEM-BEM) combining edge smoothed finite element method (ES-FEM) and boundary element method (BEM) is proposed in this paper. The method integrates the advantages of ES-FEM and BEM, which has high calculation accuracy and uses less memory. Compared with the traditional FEM-BEM coupling algorithm, ES-FEM-BEM has obvious advantages in improving calculation accuracy with the same meshing density. A 2D impulse coil-aluminum plate model was established, and the magnetic field strength of the aluminum plate surface was calculated. Results show that the maximum relative error between the calculated results obtained by ES-FEM-BEM and the measured results was only 3.4%, whereas the maximum relative error between the calculated results obtained by FEM-BEM and the measured results was up to 31.8%. The proposed method can provide reference for the analysis of transient open boundary eddy current field.
Key words: edge smoothed finite element method boundary element method transient eddy current field 2D magnetic field calculation
王洋洋, 蒋兴良. 边光滑有限元-边界元耦合法计算二维瞬态涡流场[J]. 哈尔滨工业大学学报, 2021, 53(3): 137-141, 151. DOI: 10.11918/202001049.
WANG Yangyang, JIANG Xingliang. Calculation of 2D transient eddy current field by ES-FEM-BEM coupling method[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 137-141, 151. DOI: 10.11918/202001049.
基金项目 国家自然科学基金(51637002) 作者简介 王洋洋(1990—)，女，博士研究生;
蒋兴良(1961—)，男，教授，博士生导师 通信作者 王洋洋，wangyangyangabc888@163.com 文章历史 收稿日期: 2020-01-10
Abstract Full text Figures/Tables PDF
边光滑有限元-边界元耦合法计算二维瞬态涡流场
王洋洋
, 蒋兴良 输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044
收稿日期: 2020-01-10
基金项目: 国家自然科学基金(51637002)
作者简介: 王洋洋(1990—)，女，博士研究生; 蒋兴良(1961—)，男，教授，博士生导师
通信作者: 王洋洋，wangyangyangabc888@163.com
摘要: 为了提高二维瞬态涡流场的计算精度与速度，结合边光滑有限元法计算精度高和边界元法占用计算机内存少的优点，提出一种基于边光滑有限元法——边界元法相结合的混合算法(ES-FEM-BEM)来计算二维瞬态涡流场. 在相同网格划分密度下，相较于传统的有限元-边界元耦合算法(FEM-BEM)而言，该混合算法具有明显提高计算精度的优点. 同时建立了二维脉冲线圈-铝板模型，并对铝板表面的磁场强度进行计算. 结果表明：在网格划分密度相同的情况，ES-FEM-BEM的计算结果与测量结果的最大相对误差只有3.4%，而FEM-BEM的计算结果与测量结果的最大相对误差达到31.8%. 基于边光滑有限元法和边界元法耦合的混合算法，可为瞬态开域涡流场分析提供重要的参考依据.
关键词: 边光滑有限元法 边界元法 瞬态涡流场 二维磁场计算
Calculation of 2D transient eddy current field by ES-FEM-BEM coupling method
WANG Yangyang
, JIANG Xingliang State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China
Abstract: To improve the calculation accuracy and speed for 2D transient eddy current field, a method (ES-FEM-BEM) combining edge smoothed finite element method (ES-FEM) and boundary element method (BEM) is proposed in this paper. The method integrates the advantages of ES-FEM and BEM, which has high calculation accuracy and uses less memory. Compared with the traditional FEM-BEM coupling algorithm, ES-FEM-BEM has obvious advantages in improving calculation accuracy with the same meshing density. A 2D impulse coil-aluminum plate model was established, and the magnetic field strength of the aluminum plate surface was calculated. Results show that the maximum relative error between the calculated results obtained by ES-FEM-BEM and the measured results was only 3.4%, whereas the maximum relative error between the calculated results obtained by FEM-BEM and the measured results was up to 31.8%. The proposed method can provide reference for the analysis of transient open boundary eddy current field.
Keywords: edge smoothed finite element method boundary element method transient eddy current field 2D magnetic field calculation
在瞬态涡流场研究中，常用的数值计算方法有积分法[1-2]、有限元法[3]、边界元法以及有限元边界元耦合法[4-7]. 虽然传统有限元法(FEM)[8]作为最成功的数值方法之一，已被广泛用于解决工程和科学的各种实际问题，但是因为其有固有的缺点，如剖分网格密度以及计算阶数的复杂程度都对有限元计算精度影响非常大. 单元数量的增加，及其插值函数精度的提高，才能得到更精确的数值解. 特别是在某些复杂的设计优化实例中，有限元法需要重复多次进行网格剖分以及重要部分网格加密操作，这不仅增加了设计的难度，而且还降低了设计计算的效率. 因此国内外学者一直致力于研究如何克服传统有限元法的缺点.
近年来，在努力开发先进数值方法时，文献[9]将无网格中的应变光滑技术与传统有限元法相结合，引入梯度光滑的操作概念，提出一系列广义梯度光滑有限元法. 其包括用梯度光滑技术分别对构造的节点光滑域、边光滑域以及面光滑域进行光滑操作而形成的点光滑有限元法(NS-FEM)[10]、边光滑有限元法(ES-FEM)[11]以及面光滑有限元法(FS-FEM)[12]. 3种方法各有优缺点. 相对于传统有限元法，NS-FEM在精度和效率方面有所提高. 但是NS-FEM在空间上是稳定的在时间上可能是不稳定的，并且由于“过软”特性而不能直接应用于解决动态问题[13]. 然而，ES-FEM可以克服时间不稳定性[14]，由于本文研究的是时变涡流场，因此克服时间不稳定性对于时变涡流场分析尤其重要. 此外，对于固体力学问题，具有线性积分的ES-FEM比线性有限元法更加准确和有效[15]. 至此，ES-FEM近年来得到了广泛的应用. 对于FS-FEM更适用于三维问题.
本文提出一种用ES-FEM与边界元耦合法计算二维瞬态涡流场. 该耦合法同时具有ES-FEM计算精度高以及边界元法占用计算机内存少等优点. 首先将问题域离散化为一组三角形单元，然后进一步构造与三角形单元边相关的积分域，采用伽辽金加权余量法，推导出基于边光滑有限元-边界元耦合算法的离散公式，在导体区域内采用ES-FEM，非导体区域内采用边界元法. 研究导体区域的磁场分布，并与测量结果和有限元-边界元耦合法计算结果进行对比. 计算结果表明，在相同网格密度条件下，基于ES-FEM边界元耦合法计算精度更高，该方法具有更好的应用前景.
1 电磁场的分析模型电磁分析的问题实际上是在给定边界条件下求解一组麦克斯韦方程组的问题. 如图 1所示，为开域涡流场求解区域示意图. 整个电磁场求解域分为涡流区V1和非涡流区V2，Γ1是V1和V2的内部边界，非涡流区V2包括无源电流的非涡流区和有源电流的非涡流区. V1区域内采用ES-FEM，V2区域内采用BEM, 在内部边界上满足的边界条件为
$\vec{A}^{\mathrm{ES}-\mathrm{FEM}} =\vec{A}^{\mathrm{BEM}}, $ (1)
$\nabla \cdot \vec{A}^{\mathrm{ES}-\mathrm{FEM}} =\nabla \cdot \vec{A}^{\mathrm{BEM}} ,$ (2)
$\nu \nabla \times \vec{A}^{\mathrm{ES}-\mathrm{FEM}} \times \vec{n} =\nu \nabla \times \vec{A}^{\mathrm{BEM}} \times \vec{n} .$ (3)
Fig. 1
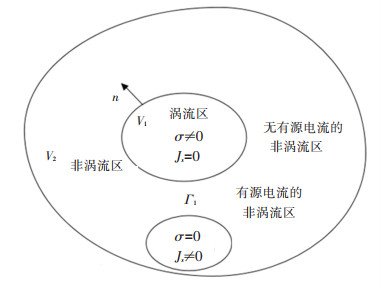图 1 开域涡流场求解示意图 Fig. 1 Diagram of the open boundary eddy current field 式中：
2 边光滑有限元-边界元耦合法介绍 2.1 边光滑有限元法边光滑有限元法是在求解有限元的基础上对其求解域进一步光滑，形成多个光滑子单元，然后在新形成的光滑子单元内引入梯度光滑操作，梯度光滑操作是指在新形成的光滑域上对有限元求解的系数矩阵进行光滑平均运算，其数学表达式为
$\overline{\left(\frac{\partial w_{l}(x)}{\partial x_{i}}\right)}=\int\limits_{\varOmega_{x}} \frac{\partial w_{l}(\zeta)}{\partial x_{i}} \hat{W}(x-\zeta) \mathrm{d} \zeta,$
式中：Ωx为构造的光滑域;
$\hat{W}(x-\zeta)=\bar{W}(x-\zeta)=\left\{\begin{array}{cl}1 / A_{x}, & x \in \varOmega_{x}; \\0, & x \notin \varOmega_{x}.\end{array}\right.$
其中Ax为光滑域的面积. 图 2为边光滑有限元法的计算流程图.
Fig. 2
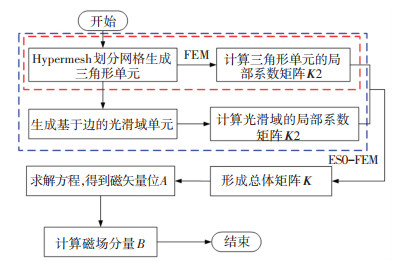图 2 计算流程图 Fig. 2 Calculation flow chart 对于二维求解域，先用划分软件Hypermesh对其进行三角形划分，其中生成N个节点和p条边. 传统有限元的离散矩阵[16]为
$L \frac{\partial \vec{A}}{\partial t}+K_{1} \vec{A}=-M \frac{\partial \vec{A}}{\partial \vec{n}},$ (4)
其中单元系数矩阵分别为
如图 3所示，黑色实线表示三角形单元的边，那么某边L的光滑子域是由边L对应的三角形单元的中心依次与边L两个端点相连接形成，域内光滑域ΓL的个数等于单元边L的边数，其中每个光滑域ΩL都由n个子域组成ΩLi(i=1, 2, …, n).
Fig. 3
图 3 基于边的光滑域 Fig. 3 Edge-based smoothing domain 在磁场中，磁矢量位
$\overline{\nabla A\left(x_{L}\right)}=\frac{1}{A_{L}} \int\limits_{\varOmega_{L}} \nabla A\left(x_{L}\right) \mathrm{d} \varOmega,$ (5)
式中AL为光滑域的面积，在二维求解域单元内，AL的表达式可根据参考文献[9]计算得到.
对式(7)进行格林公式换算，那么对光滑域内位函数的面积分可以转化为光滑域边界上的线积分，即
$\overline{\nabla A\left(x_{L}\right)}=\frac{1}{A_{L}} \int\limits_{\varOmega_{L}} \nabla A\left(x_{L}\right) \mathrm{d} \varOmega=\frac{1}{A_{L}} \int\limits_{\varGamma_{L}} A \cdot n \mathrm{~d} \varGamma,$ (6)
将式(6)代入式(5)中，可得
$\overline{\nabla A\left(x_{L}\right)}=\sum\limits_{i=1}^{m} \overline{B_{i}\left(x_{L}\right)} A_{i},$ (7)
其中：
$\overline{B_{i}\left(x_{L}\right)}=\left[d_{i x}, d_{i y}\right]^{\mathrm{T}},$ (8)
$d_{i j}=\frac{1}{A_{L}} \int\limits_{\varGamma_{L}} N_{i}(x) n_{j}(x) \mathrm{d} \varGamma, j=x, y .$ (9)
对光滑域ΩL采用高斯积分，式(12)的光滑域边界积分形式为
$d_{i j}=\frac{1}{A_{L}} \sum\limits_{K=1}^{N_{A}}\left[\sum\limits_{q=1}^{N_{B}} \delta_{q} N_{i}\left(x_{k, q}\right) n_{j}\left(x_{p}\right)\right].$ (10)
式中：NA为电磁场求解域边界L的个数，NB为高斯点的个数，δq为高斯点积分的权函数.
由式(10)可知，dij是由光滑域各个边中点处的形函数求得，而各个中点处的形函数可通过场节点插值得到，如图 4所示，点1、2、3、4分别为场节点，A、B分别为中心节点，g1、g2、g3、g4分别为高斯积分点[17].
Fig. 4
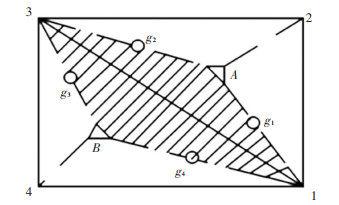图 4 ES-FEM形函数分布 Fig. 4 Shape function distribution of ES-FEM 基于边L的光滑有限元系统的局部光滑域的系数矩阵可以写成：
$\overline{K_{2}}^{(L)}=\overline{\boldsymbol{B}}^{\mathrm{T}} \overline{\boldsymbol{B}} \boldsymbol{A}_{L}.$ (11)
对上述局部系数矩阵进行整体组装，得到域内整体系数矩阵为
$\overline{K_{2}}=\sum\limits_{L=1}^{p} \overline{K_{2}}^{(L)}.$ (12)
2.2 边界元法对于非涡流区应用格林公式，可得对应边界积分方程[5]为
$\vec{A}=\int\limits_{l}\left(G \frac{\partial \vec{A}}{\partial \vec{n}}-\vec{A} \frac{\partial G}{\partial \vec{n}}\right) \mathrm{d} \vec{l}+\int\limits_{S} \mu_{0} G \vec{J}_{s} \mathrm{~d} \vec{s}.$ (13)
式中：μ0为真空磁导率；Js为源电流密度；S为源电流区域面积；G为二维自由空间格林函数，
采用伽辽金余量法对式(13)离散，得
$H\overrightarrow{ A}-G \frac{\partial \vec{A}}{\partial \vec{n}}=\vec{F}.$ (14)
2.3 基于边光滑有限元边界元耦合算法将式(4)和式(14)联立，可得
$\boldsymbol{L} \frac{\partial \vec{A}}{\partial t}+\left(\boldsymbol{K}-\boldsymbol{M} \boldsymbol{G}^{-1} \boldsymbol{H}\right) \vec{A}=\boldsymbol{M} \boldsymbol{G}^{-1} \overrightarrow{\boldsymbol{F}},$ (15)
对式(15)中的导数项，采用向后差分，即
$\left(\frac{1}{\Delta t} \boldsymbol{L}+\boldsymbol{K}\right) \vec{A}_{t+\Delta t}=\frac{1}{\Delta t} \boldsymbol{L} \vec{A}_{t}+\boldsymbol{M} \boldsymbol{G}^{-1} \vec{F}.$ (16)
由2.1节和2.2节可知，系数矩阵L、K、M以及H、G可计算得到，将其代入式(16)中，通过编程求解，可得磁矢量位
$\vec{B}_{t+\Delta t}=\nabla \times \vec{A}_{Z_{t+\Delta t}}=\frac{\partial \vec{A}_{Z_{t+\Delta t}} }{\partial y}\vec{i}-\frac{\partial \vec{A}_{Z_{t+\Delta t}}}{\partial x} \vec{j},$ (17)
导体域的涡流密度
$\vec{J}_{t+\Delta t}=-\sigma \frac{\partial A_{Z}}{\partial t} \vec{k}=-\sigma\left(\frac{A_{Z_{t+\Delta t}}-A_{Z_{t}}}{\Delta t}\right) \vec{k}.$ (18)
3 计算算例与分析 3.1 脉冲线圈-铝板表面磁场分布脉冲线圈-铝板的结构参数：矩形截面为0.6 mm× 4.8 mm的铜丝缠绕成内径、外径分别为3.2、25.5 mm, 匝数为30的圆柱形线圈[19]. 脉冲线圈流过的瞬时电流波形，如图 5所示. 在线圈正上方放置0.8 mm厚的铝板，电导率δ=3.48×107 s/m. 线圈与铝板的间隙为2 mm. 采用本文所提的基于边有限元边界元耦合法求得铝板表面的磁感应强度，其结果分别与测量值以及有限元-边界元法的计算结果进行对比，如图 6~8所示.
Fig. 5
图 5 脉冲电流随时间变化 Fig. 5 Impulse current varying with time Fig. 6
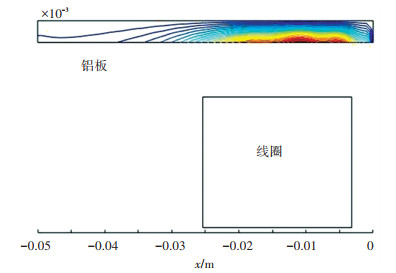图 6 磁矢量位A线的分布云图 Fig. 6 Distribution pattern of magnetic vector potential A Fig. 7
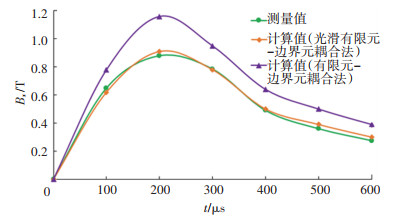图 7 切向磁感应强度随时间的变化(r=10 mm) Fig. 7 Tangential magnetic induction intensity varying with time (r=10 mm) Fig. 8
图 8 垂直磁感应强度随时间的变化(r=7.6 mm) Fig. 8 Vertical magnetic induction intensity varying with time (r=7.6 mm) 由图 6可知，离线圈越近，磁矢量位A值越大，与实际情况一致，说明本文的计算方法合理. 为了验证本文所提方法的计算精度，设相对误差Bi为
${B_i} = \left| {\frac{{{B_0} - {B_1}}}{{{B_0}}}} \right|.$ (19)
式中：B0为测量值，B1是计算值，i=x、y分别代表磁场沿切向、垂直方向的磁场分量.
由图 7、8可知，基于边光滑有限元边界元耦合法与测量结果一致，因此可用本文所提的方法计算涡流场. 在网格单元划分密度相同的条件下，运行两种方法效率对比见表 1，虽然本文所提方法的运行时间稍长于有限元边界元耦合法，但其计算精度远远高于有限元边界元耦合法，另外，对于目前计算机的计算能力而言，本文通过改变模型的大小，对比两种方法的运行时间. 由表 2可知，两种方法运行时间的差别可以忽略. 由此可知，在计算涡流场时基于边光滑有限元边界元法能大大提高计算精度.
表 1
表 1 效率对比 Tab. 1 Comparison of efficiency 方法 Br相对误差/% Bz相对误差/% 运行时间t FEM-BEM 31.8 29.8 0.73
ES-FEM-BEM 3.4 2.5 1.03
表 1 效率对比 Tab. 1 Comparison of efficiency
表 2
表 2 运行时间对比 Tab. 2 Comparison of running time 模型 时间/s 有限元边界元耦合法 基于边光滑有限元边界元耦合法
1/4模型 0.20 0.32
1/2模型 0.36 0.54
3/4模型 0.52 0.79
表 2 运行时间对比 Tab. 2 Comparison of running time
综上所述，在进行涡流场分析时，应优先考虑基于边光滑有限元边界元耦合法.
3.2 铝板表面磁场分布的影响因素 3.2.1 电流密度变化的影响脉冲电流-铝板模型参数如上所述，在进行电流密度对其磁场影响分析时，保持模型的其他参数不变，改变流过脉冲线圈的电流密度Js从10× 106 A/m2到180×106 A/m2变化，间隔为30×106 A/m2. 则上述电流密度变化的情况下铝板表面磁场分量分布如图 9所示.
Fig. 9
图 9 磁场强度随涡流密度的变化 Fig. 9 Magnetic field strength varying with eddy current density 如图 9所示，磁场强度随涡流密度的增大而增大，这是因为涡流密度Js与系数矩阵F成正相关，即当Js增大时，F增大. 由式(20)可知, 随着F增大，所求磁矢量位A增大，因此磁场强度增大.
3.2.2 脉冲线圈-铝板间隙变化的影响脉冲电流-铝板模型参数如上所述，在进行脉冲线圈-铝板间隙对其磁场影响分析时，保持模型的其他参数不变，改变间隙h从2 mm到8 mm之间变化，间隔为1 mm. 则上述间隙变化的情况下铝板表面磁场分量分布如图 10所示.
Fig. 10
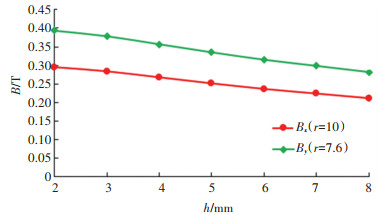图 10 磁场强度随间隙的变化 Fig. 10 Magnetic field strength varying with gap 由图 10可知，随着脉冲线圈与铝板之间间隙h的增大，磁场强度逐渐减小. 这说明如果为了增大铝板中的涡流作用，即产生大的脉冲力，那么脉冲线圈需尽可能近的接近铝板.
4 结论1) 提出了一种计算涡流场分布的基于边光滑有限元边界元耦合法，该方法即具有ES-FEM计算精度高和边界元法占用内存少的优点，并详细给出了该方法的推导过程. 同时，利用本文所提的基于边光滑有限元边界元耦合法计算分析脉冲线圈上方铝板表面的磁场分布，与测量结果对比表明，该方法是正确合理的.
2) 在单元网格密度划分相同的条件下，将本文得到的计算结果与传统有限元边界元耦合法计算得到的结果对比，虽然本文所提方法的运行时间稍长于有限元边界元耦合法，但其计算精度远远高于有限元边界元耦合法，另外，对于目前计算机的计算能力而言，两种方法运行时间的差别可以忽略.
3) 在计算模型的其他参数保持不变，只改变涡流密度的情况下，磁场强度随涡流密度的增大而增大且曲线增大率几乎保持不变，同理，磁感应强度随着脉冲线圈与铝板之间间隙h的增大而减小，且其曲线降低率也几乎保持不变.
参考文献
[1] 幸玲玲, 盛剑霓. 涡检测中平板导体的理想裂缝模型[J]. 中国电机工程学报, 2002, 22(2): 41.
XING Lingling, SHENG Jianni. The ideal crack model of a conducting plate in eddy current nondestructive testing[J]. Proceedings of the CSEE, 2002, 22(2): 41. DOI:10.3321/j.issn:0258-8013.2002.02.009
[2] 刘守豹, 阮江军, 彭迎, 等. 非重叠Mortar有限单元法在运动导体涡流场计算中的应用[J]. 中国电机工程学报, 2012, 32(3): 157.
LIU Shoubao, RUAN Jiangjun, PENG Ying, et al. Application of non-overlapping mortar finite element method in moving conductor eddy current problem[J]. Proceedings of the CSEE, 2012, 32(3): 157.
[3] KOLMBAUER M. A robust FEM-BEM minres solver for distributed multi-harmonic eddy current optimal control problems in unbounded domains[J]. Electronic Transactions on Numerical Analysis, 2012, 39(1): 231.
[4] FEISCHL M, TRAN T. The eddy current LLG equations: FEM-BEM coupling and a priori error estimates[J]. SIAM Journal on Numerical Analysis, 2017, 55(4): 1786. DOI:10.1137/16M1065161
[5] 王泽忠, 王炳革, 卢斌先, 等. 三维开域涡流场A-V位有限元与边界元耦合分析方法[J]. 中国电机工程学报, 2000, 20(5): 1.
WANG Zezhong, WANG Bingge, LU Binxian, et al. FE-BE coupling method of 3D open boundary eddy current fields in potential A-V[J]. Proceedings of the CSEE, 2000, 20(5): 1. DOI:10.3321/j.issn:0258-8013.2000.05.001
[6] 幸玲玲. 用时域有限元边界元藕合法计算三维瞬态涡流场[J]. 中国电机工程学报, 2005, 25(19): 131.
XING Lingling. Computation of 3D transient eddy current by time-stepping finite element boundary element coupling method[J]. Proceedings of the CSEE, 2005, 25(19): 131. DOI:10.3321/j.issn:0258-8013.2005.19.025
[7] LAYTH Q, RAZZAK M. Hybrid finite-element-boundary element analysis of a single-sided sheet rotor linear induction motor[J]. IEEE Transactions on Energy Conversion, 2014, 29(1): 188. DOI:10.1109/TEC.2013.2292057
[8] RODRíGUEZ A A, BERTOLAZZI E, GHILONI R. Finite element simulation of eddy current problems using magnetic scalar potentials[J]. Journal of Computational Physics, 2015, 294: 503. DOI:10.1016/j.jcp.2015.03.060
[9] LIU G R, NGUYEN T. Smoothed finite element methods[M]. Boca Raton: CRC Press, 2010.
[10] MINH T, CHAU N A, NGUYEN M T. A node-based smoothed finite-element method for stability analysis of dual square tunnels in cohesive-frictional soils[J]. Scientia Iranica, 2018, 25(1): 1105.
[11] LI S, CUI X Y. An edge-based smoothed finite element method for nonlinear magnetistatic and eddy current analysis[J]. Applied Mathematical Modelling, 2018, 62(1): 287.
[12] NGUYEN T, LIU G R, LAN K M. A face-based smoothed finite element method (FS-FEM) for 3D linear and nonlinear solid mechanics problems using 4-node tetrahedral elements[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 78(1): 324.
[13] YANG Y T, ZHENG H, DU X L. An enriched edge-based smoothed FEM for linear elastic fracture problems[J]. International Journal of Computational Methods, 2017, 14(5): 23.
[14] NGUYEN X H, WU C T, LIU G R. An adaptive selective ES-FEM for plastic collapse analysis[J]. European Journal of Mechanics A-Solid, 2016, 58(1): 278.
[15] CHEN L, NGUYEN H, NGUYEN T T. Assessment of smoothed point interpolation methods for elastic mechanics[J]. International Journal for Numerical Methods in Biomedical Engineering, 2010, 26(12): 1635. DOI:10.1002/cnm.1251
[16] 邵可然, 周克定. 用有限元- 边界元耦合法解轴对称涡流问题[J]. 华中理工大学学报, 1989, 17(1): 9.
SHAO Keran, ZHOU Keding. The axi-symmetric eddy current problem solved by the hybrid FE-BE method[J]. Journal of Huazhong University of Science and Technology, 1989, 17(1): 9.
[17] 李永利, 边光滑有限元法在汽车电磁兼容计算中的研究及应用[D]. 长沙: 湖南大学, 2016
LI Yongli. Research and application on numerical calculation of auto electromagnetic compatibility based on edge-based smoothed finite element method[D]. Changsha: Hunan University, 2016
[18] 谢德馨, 姚缨英, 白保东, 等. 三维涡流场的有限元分析[M]. 北京: 机械工业出版社, 2001.
XIE Dexin, YAO Yingying, BAI Baodong, et al. Finite element analysis of three-dimensional transient eddy current field[M]. Beijing: China Machine Press, 2001.
[19] ZUMWALT G W, SCHRAG R L, BERNHART W D, et al. Electro-impulse de-icing testing analysis and design[R]. Washington DC: NASA, 1988: 43
