李银通,韩统,聂光戍,周欢,赵辉
(空军工程大学 航空工程学院,西安 710038)
摘要:
为提高无人作战飞机(Unmanned combat aerial vehicle, UCAV)协同实时航迹规划的实时性和可操作性,针对多架UCAV协同执行对地作战任务过程中的协同实时航迹规划问题,提出一种基于自学习策略和Lévy飞行的正弦余弦优化算法(Sine cosine optimization algorithm with self-learning strategy and Lévy flight,SCASL)的多UCAV协同打击多目标实时三维航迹规划方法.首先,构建三维任务空间模型并根据UCAV平台性能设计了飞行速度、飞行高度、相对距离以及威胁规避等约束条件；其次,基于UCAV的三自由度运动学和动力学质点模型设计了协同实时航迹规划的决策变量；最后,根据UCAV作战使用战术原则构建了目标函数将协同实时航迹规划问题转化为优化问题,采用所提出的自学习策略和Lévy飞行的正弦余弦优化算法对模型进行求解,并采用病毒搜索算法（Virus colony search, VCS）求解模型作为对比实验. 仿真结果表明, 同等条件下,VCS求解模型得到的仿真结果满足协同性要求但不满足实时性要求,SCASL求解模型得到的仿真结果满足实时性与协同性要求,验证了本文所提出的基于SCASL的多UCAV协同实时航迹规划方法的有效性与优越性.
关键词: 无人作战飞机 协同航迹规划 实时三维航迹规划 正弦余弦优化算法 优化问题
DOI：10.11918/202006107
分类号:V279;TP311
文献标识码:A
基金项目:航空科学基金(9,2)；陕西省自然科学基金(2020JQ-481)
Real-time 3D trajectory planning of multi-UCAV for cooperative multi-target attacking
LI Yintong,HAN Tong,NIE Guangshu,ZHOU Huan,ZHAO Hui
(College of Aeronautics Engineering, Air Force Engineering University, Xi’an 710038,China)
Abstract:
In view of the problem of collaborative real-time trajectory planning during the execution of ground combat missions by multiple unmanned combat aerial vehicles (UCAV), a real-time 3D trajectory planning method based on the sine cosine optimization algorithm with self-learning strategy and Lévy flight (SCASL) for multi-UCAV cooperatively attacking multi-targets was proposed to improve the real-time performance and operability of UCAV collaborative real-time trajectory planning. Firstly, the model of 3D mission space was constructed, and the constraints of flight speed, flight altitude, relative distance, and threat avoidance were designed according to the performance of UCAV. Secondly, the decision variables of collaborative real-time trajectory planning were designed based on the three-degree-of-freedom kinematics and dynamic particle model of UCAV. Finally, the objective function was constructed by transforming the collaborative real-time trajectory planning problem into an optimization problem according to the tactical principle of UCAV operations. The proposed SCASL was applied to solve the model, and the virus search algorithm (VCS) was adopted for comparison. Simulation results show that under the same conditions, the results obtained by VCS met the requirement of collaboration but not real-time, while the results obtained by SCASL met the requirements of both real-time and collaboration, which verifies the validity and superiority of the SCASL-based multi-UCAV collaborative real-time 3D trajectory planning method proposed in this paper.
Key words: UCAV cooperative trajectory planning real-time 3D trajectory planning sine and cosine optimization algorithm optimization
李银通, 韩统, 聂光戍, 周欢, 赵辉. 多UCAV协同打击多目标实时三维航迹规划[J]. 哈尔滨工业大学学报, 2021, 53(6): 128-137. DOI: 10.11918/202006107.
LI Yintong, HAN Tong, NIE Guangshu, ZHOU Huan, ZHAO Hui. Real-time 3 D trajectory planning of multi-UCAV for cooperative multi-target attacking[J]. Journal of Harbin Institute of Technology, 2021, 53(6): 128-137. DOI: 10.11918/202006107.
基金项目 航空科学基金(20175196019, 201951096002)；陕西省自然科学基金(2020JQ-481) 作者简介 李银通(1995—)，男，博士研究生;
赵辉(1973—)，男，教授，博士生导师 通信作者 赵辉，kgy_zhao@163.com 文章历史 收稿日期: 2020-06-19
Abstract Full text Figures/Tables PDF
多UCAV协同打击多目标实时三维航迹规划
李银通, 韩统, 聂光戍, 周欢, 赵辉
空军工程大学 航空工程学院，西安 710038
收稿日期: 2020-06-19
基金项目: 航空科学基金(20175196019, 201951096002)；陕西省自然科学基金(2020JQ-481)
作者简介: 李银通(1995—)，男，博士研究生; 赵辉(1973—)，男，教授，博士生导师
通信作者: 赵辉，kgy_zhao@163.com
摘要: 为提高无人作战飞机(Unmanned combat aerial vehicle, UCAV)协同实时航迹规划的实时性和可操作性，针对多架UCAV协同执行对地作战任务过程中的协同实时航迹规划问题，提出一种基于自学习策略和Lévy飞行的正弦余弦优化算法(Sine cosine optimization algorithm with self-learning strategy and Lévy flight，SCASL)的多UCAV协同打击多目标实时三维航迹规划方法.首先，构建三维任务空间模型并根据UCAV平台性能设计了飞行速度、飞行高度、相对距离以及威胁规避等约束条件；其次，基于UCAV的三自由度运动学和动力学质点模型设计了协同实时航迹规划的决策变量；最后，根据UCAV作战使用战术原则构建了目标函数将协同实时航迹规划问题转化为优化问题，采用所提出的自学习策略和Lévy飞行的正弦余弦优化算法对模型进行求解，并采用病毒搜索算法(Virus colony search, VCS)求解模型作为对比实验. 仿真结果表明, 同等条件下，VCS求解模型得到的仿真结果满足协同性要求但不满足实时性要求，SCASL求解模型得到的仿真结果满足实时性与协同性要求，验证了本文所提出的基于SCASL的多UCAV协同实时航迹规划方法的有效性与优越性.
关键词: 无人作战飞机 协同航迹规划 实时三维航迹规划 正弦余弦优化算法 优化问题
Real-time 3 D trajectory planning of multi-UCAV for cooperative multi-target attacking
LI Yintong, HAN Tong, NIE Guangshu, ZHOU Huan, ZHAO Hui
College of Aeronautics Engineering, Air Force Engineering University, Xi'an 710038, China
Abstract: In view of the problem of collaborative real-time trajectory planning during the execution of ground combat missions by multiple unmanned combat aerial vehicles (UCAV), a real-time 3D trajectory planning method based on the sine cosine optimization algorithm with self-learning strategy and Lévy flight (SCASL) for multi-UCAV cooperatively attacking multi-targets was proposed to improve the real-time performance and operability of UCAV collaborative real-time trajectory planning. Firstly, the model of 3D mission space was constructed, and the constraints of flight speed, flight altitude, relative distance, and threat avoidance were designed according to the performance of UCAV. Secondly, the decision variables of collaborative real-time trajectory planning were designed based on the three-degree-of-freedom kinematics and dynamic particle model of UCAV. Finally, the objective function was constructed by transforming the collaborative real-time trajectory planning problem into an optimization problem according to the tactical principle of UCAV operations. The proposed SCASL was applied to solve the model, and the virus search algorithm (VCS) was adopted for comparison. Simulation results show that under the same conditions, the results obtained by VCS met the requirement of collaboration but not real-time, while the results obtained by SCASL met the requirements of both real-time and collaboration, which verifies the validity and superiority of the SCASL-based multi-UCAV collaborative real-time 3D trajectory planning method proposed in this paper.
Keywords: UCAV cooperative trajectory planning real-time 3D trajectory planning sine and cosine optimization algorithm optimization
无人作战飞机(Unmanned combat aerial vehicles，UCAV)是目前世界各军事强国争相发展的空中无人作战系统，能实施防空压制、对地打击、对空作战以及情报侦察等多种作战任务[1].UCAV协同航迹规划作为发挥协同作战效能的关键技术，目前已经成为无人作战系统领域的热点问题.
当前，无人机/无人作战飞机离线单/协同航迹规划的研究成果丰富[2-10]，但实时航迹规划研究成果匮乏.江泽强等[11]在考虑无人机的机载探测范围条件下，采用滚动规划策略，提出一种基于RRT算法的单无人机实时二维航迹规划方法，解决了突发威胁条件下的单无人机实时二维航迹规划问题.范伟伦等[12]考虑无人机动力学约束，提出了一种基于RRT算法的单无人机实时二维航迹规划方法，使规划出的航迹满足无人机的实际性能要求.Zhang等[13]提出一种单无人机三维实时航迹规划方法，并采用改进RRT算法求解，结果显示满足实时性要求与误差要求.Cai等[14]提出一种基于三层决策规划模型(Tri-level programing，TLP)的UAV实时航迹规划方法，解决了单UAV突发威胁下的实时航迹规划问题.You等[15]提出一种基于情境空间的UCAV三维路径规划方法，根据战术要求，为单架UCAV规划跟踪目标并避免碰撞的实时航迹.
上述有关UAV/UCAV实时航迹规划的成果大多以单UAV航迹规划为研究对象，其中二维航迹规划成果与UCAV作战实际应用情况不符，三维实时航迹规划考虑地形因素和战术因素较少.在多UCAV协同作战成为研究热点的背景下，单机实时航迹规划已不能满足需求，实时协同航迹规划已成为研究热点问题[16].因此，为满足多UCAV协同作战任务需求，本文以多UCAV协同执行对地作战任务为背景，考虑战术要求，提出一种多UCAV协同打击多目标实时三维航迹规划模型，将多UCAV协同实时航迹规划问题转化为优化问题，在此基础上，采用李银通等[17]提出的自学习策略和Lévy飞行的正弦余弦优化算法(Sine cosine optimization algorithm with self-learning strategy and Lévy flight，SCASL)对模型进行求解.通过仿真实验验证本文所提出方法的有效性.
1 实时协同三维航迹规划模型用于航迹规划的战场信息通常是不完备的，部分敌方威胁只有UCAV抵达其附近一定范围内才可能探测到，这些威胁称为突发威胁.因此，UCAV在按离线航迹飞行过程中需要利用机载设备进行实时探测，一旦发现离线航迹穿过威胁区就需要进行航迹实时重规划以规避威胁.如图 1所示，本文研究内容为实时协同航迹规划的方法，因此仅考虑探测到新威胁源进行实时航迹规划直到抵达目标点的过程，而不考虑UCAV在探测到新威胁之前的飞行状态.
Fig. 1
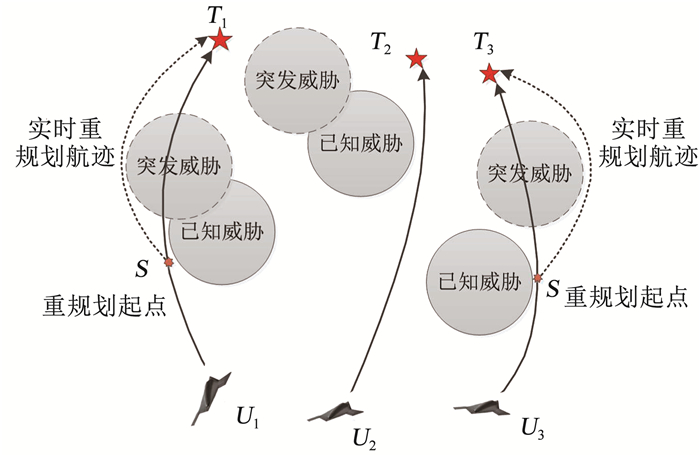图 1 实时航迹重规划示意图 Fig. 1 Schematic diagram of real-time trajectory replanning 本文受滚动时域控制思想的启发，将规划过程进行分割，对多UCAV协同打击多目标实时航迹进行滚动迭代规划.从严格意义上说，每次滚动迭代规划只是对一个时间窗口内的航迹进行寻优规划，是一种局部航迹规划，目的是安全抵达任务目标区域，通常来说实时规划的航迹在局部是最优的，但从全局角度来看整条航迹是非最优的.由于实时航迹规划严格来说是动态的局部规划过程，并且对实时性有严格要求，航迹规划耗时必须小于UCAV的滚动时域的时间窗口，因此必须在求解的耗时与最优性之间进行折中，在满足实时性要求的前提下获得相对较优的安全可飞航迹.
1.1 战场环境构建战场环境构建主要分为地形构建和威胁构建两部分.本文以三维山地地形为战场环境，作战任务空间Φ可表示为
$\boldsymbol{\varPhi}=\left\{(x, y, h) \mid 0 \leqslant x \leqslant x_{\max }, 0 \leqslant y \leqslant y_{\max }, 0 \leqslant h \leqslant h_{\max }\right\}.$ (1)
式中：x、y、h分别为战场空间中的任意一点的横坐标、纵坐标以及高度；xmax、ymax、hmax分别为作战任务空间的边界值.本文采用航天飞机雷达地形测绘任务(shuttle radar topography mission，SRTM)数据来模拟实际的战场环境地形信息.SRTM所包含的地形数据仅为节点处的高度信息，并不包含地形范围内任意位置点地形高度信息，因此，本文在规划过程中采用“二维三次卷积插值法”确定战场空间中任意位置处的地形高度[18].
作战任务空间，尤其是敌方重要目标附近通常部署有敌方的防空系统，主要包括探测雷达、导弹阵地以及防空高炮等.在实际作战过程中，我方通常难以获得准确的敌方防空武器性能参数，只能通过各种探测方式获得部署的大概方位和类型，以此估计相应雷达的探测半径和相关武器的作战半径，所以难以精确建模.此外，低空突防是目前有效的突防手段，在遇到敌方防空火力或雷达时，通常情况下采用转弯来规避而非爬升高度.基于上述两点因素，为保证UCAV在飞行过程中的存活率以及航迹规划模型的简洁性，本文将威胁源的威胁范围和由天气原因形成的禁飞区均简化等效为具有一定高度的障碍模型.
1.2 UCAV运动学模型本文采用UCAV运动学三自由度质点模型对实时航迹规划过程中UCAV的动态特性进行描述(如图 2所示)，三维空间内UCAV在t时刻的运动状态可描述为
$\boldsymbol{\varPsi}(t)=[x(t), y(t), h(t), v(t), \psi(t), {\vartheta}(t), \gamma(t), \alpha(t)].$ (2)
Fig. 2
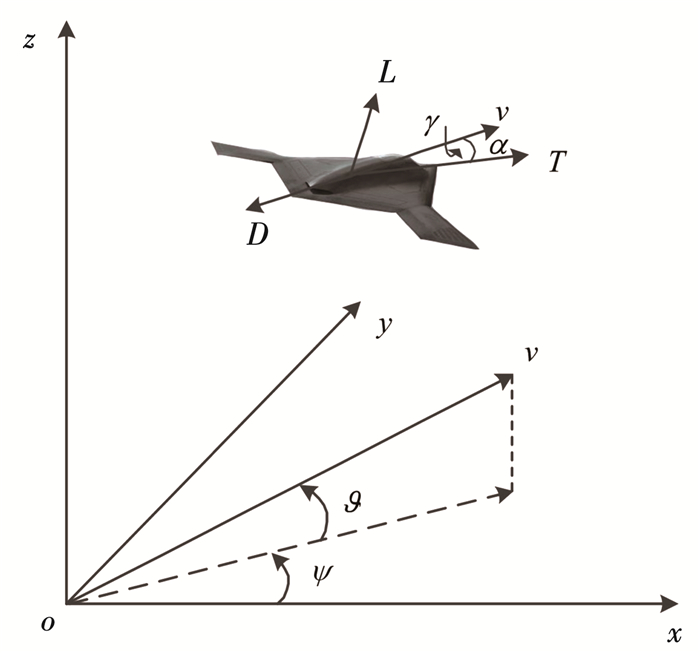图 2 质点运动模型示意图 Fig. 2 Schematic diagram of particle motion model 式中：x(t)、y(t)、h(t)为t时刻UCAV在战场中的位置; v(t)、ψ(t)、υ(t)、γ(t)、α(t)分别为t时刻UCAV的速度、偏航角、航迹倾角、滚转角以及攻角.
UCAV基于惯性坐标系的质点运动学模型可描述为
$\left\{\begin{array}{l}\dot{x}(t)=v(t) \cdot \cos \vartheta(t) \cdot \cos \psi(t), \\\dot{y}(t)=v(t) \cdot \cos \vartheta(t) \cdot \sin \psi(t), \\\dot{h}(t)=v(t) \cdot \sin \vartheta(t).\end{array}\right.$ (3)
UCAV基于航迹坐标系的质点动力学模型可描述为
$\left\{\begin{array}{l}\dot{v}(t)=\frac{T \cdot \cos \alpha(t)-D}{m}-g \cdot \sin \vartheta(t), \\\dot{\psi}(t)=\frac{(L+T \cdot \sin \alpha(t)) \cdot \sin \gamma(t)}{m \cdot v(t) \cdot \cos \vartheta(t)}, \\\dot{{\vartheta}}(t)=\frac{(L+T \cdot \sin \alpha(t)) \cdot \cos \gamma(t)}{m \cdot v(t)}-\frac{g \cos {\vartheta}(t)}{v(t)}.\end{array}\right.$ (4)
式中：g为重力加速度; m为UCAV质量; T为发动机推力; D为空气气动阻力; L为空气气动升力.
UCAV在飞行过程中的阻力和升力模型如下：
$\left\{\begin{array}{l}D(t)=0.5 \cdot \rho \cdot v(t)^{2} \cdot S \cdot C_{D}(t) ,\\L(t)=0.5 \cdot \rho \cdot v(t)^{2} \cdot S \cdot C_{L}(t).\end{array}\right.$ (5)
式中：ρ为空气密度; S为UCAV等效横截面面积; CL(t)为t时刻的气动升力系数; CD(t)为t时刻的气动阻力系数. CL(t)与CD(t)计算公式采用文献[19]拟合出的F-4在攻角α＜15°时的气动力系数模型：
$\left\{\begin{aligned}C_{D}(t)=&(0.043\ 4-0.136\ 9 \cdot \alpha(t)) \cdot \cos \alpha(t)+\\&(0.131+3.082\ 5 \cdot \alpha(t)) \cdot \sin \alpha(t), \\C_{L}(t)=&(-0.043\ 4+0.136\ 9 \cdot \alpha(t)) \cdot \sin \alpha(t)+\\&(0.131+3.082\ 5 \cdot \alpha(t)) \cdot \cos \alpha(t)\end{aligned}\right.$ (6)
发动机推力计算模型为
$T(t)=\zeta(t) T_{\max }(t).$ (7)
式中：Tmax(t)为文献[19]依据F-4发动机数据拟合出的t时刻UCAV以1 000 lb(4 436.26 N)为单位的最大推力，ζ(t)为t时刻UCAV油门的位置.本文在实时航迹规划中使用u(t)=[ζ(t), γ(t), α(t)]作为UCAV在t时刻的控制量.
1.3 约束条件UCAV在进行实时航迹规划时，除了考虑地形条件约束和威胁规避，还要考虑飞行性能约束，使规划出的航迹可以直接供UCAV飞行.
1.3.1 飞行速度约束由于UCAV本身性能的限制，其在飞行过程中存在最大飞行速度vmax，同时由于本文以固定翼UCAV为研究对象，其不可能在空中悬停并且由于战术原因，存在最小飞行速度vmin.因此，飞行速度约束可描述为
${g_1} = \mathop {\max }\limits_{i \in K} \left\{ {{v_{i\min }} - {v_i},{v_i} - {v_{i\max }}} \right\} \le 0.$ (8)
式中：vi为第i架UCAV当前时刻的速度; [vimin, vimax]为第i架UCAV的速度范围; K={1, 2, …, NU}, 其中NU为UCAV的架数.
1.3.2 飞行高度约束由于UCAV本身平台性能的限制，其在飞行过程中存在最大升限，即最高飞行高度hmax，通常为相对海平面的高度；为了减少与地面的碰撞概率，需要限制UCAV的最低飞行高度hmin，通常为相对地形的高度.因此，飞行高度约束可描述为
${{g_2} = \mathop {\max }\limits_{i \in K} \left\{ {{h_{i\min }} - {h_i},{h_i} - {h_{i\max }}} \right\} \le 0,}$ (9)
${{h_{i\min }} = {H_i} + {d_{{\rm{safe }}}}.}$ (10)
式中：hi为第i架UCAV当前时刻的高度; Hi为候选航迹点hi对应的地形高度; [himin, himax]为第i架UCAV的高度范围.
1.3.3 UCAV相对距离约束由于本文研究的为实时航迹规划问题，各UCAV之间的距离大于安全飞行距离dsafe即可避免UCAV之间发生碰撞；同时，在执行作战任务期间，UCAV之间需要进行信息共享，存在最大有效通信距离dmax.该约束可描述为
${{g_3} = \mathop {\max }\limits_{i,j \in K} \left( {{d_{{\rm{safe }}}} - {{\left\| {{\mathit{\boldsymbol{P}}_{i,t}} - {\mathit{\boldsymbol{P}}_{j,t}}} \right\|}_2}} \right) \le 0,}$ (11)
${{g_4} = \mathop {\max }\limits_{i,j \in K} \left( {{{\left\| {{\mathit{\boldsymbol{P}}_{i,t}} - {\mathit{\boldsymbol{P}}_{j,t}}} \right\|}_2} - {d_{\max }}} \right) \le 0,}$ (12)
式中Pi, t、Pj, t分别为t时刻第i架和第j架UCAV的位置.
1.3.4 威胁规避约束障碍物规避约束除了判断当前时刻t规划出的一个时间窗口[t, t+Δt]内的备选航迹是否经过威胁区外，还需要预测t+Δt时刻的位置能否在满足UCAV性能约束的条件下在下一个时间窗口有效规避威胁，其中Δt为时间窗口.当前备选航迹段的威胁源规避约束采用最小距离判断法：
$g_{5}=\max \left(R_{j}+d_{\text {safe }}-d_{i j}\right) \leqslant 0.$ (13)
式中：dij为第i架UCAV当前备选航迹段与威胁源j之间的最短距离; Rj为威胁源j的威胁半径.由于障碍物为具有一定高度的圆柱区域且本文假设的威胁规避策略为转弯规避，因此威胁规避预测模型可以直接在二维平面内考虑，图 3通过UCAV与障碍物在水平面的投影描述了转弯规避障碍物的过程.
Fig. 3
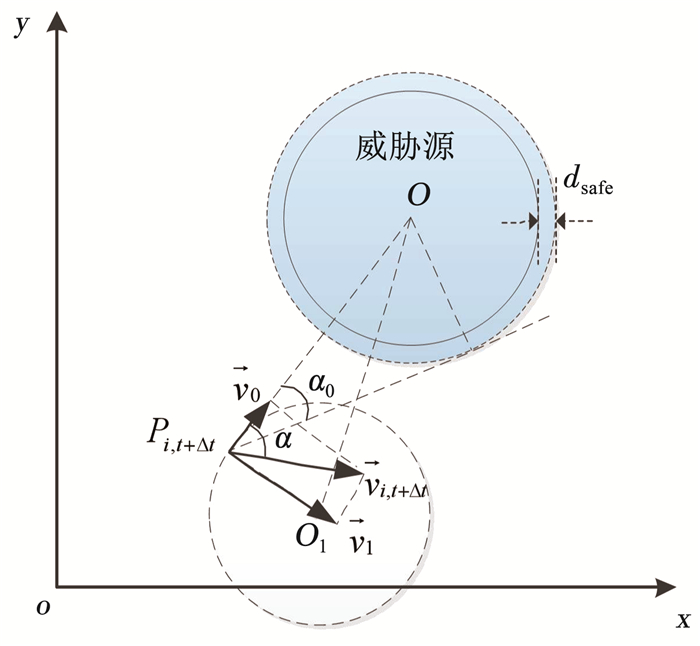图 3 威胁规避预测模型示意 Fig. 3 Schematic diagram of threat avoidance prediction model 图中
$D_{t, i j}=\sqrt{\left(R_{j}+R_{t+\Delta t}+d_{\text {safe }}\right)^{2}-R_{t+\Delta t}^{2}}-\left\|\overrightarrow{\boldsymbol{P}_{i, t+\Delta t} \boldsymbol{O}}\right\| \leqslant 0.$ (14)
则可以规避威胁，否则在UCAV性能约束条件下必然会经过威胁区，无法规避威胁.综上所述，t+Δt时刻的候选航迹点Pi, t+Δt在下一时间窗口无法规避威胁应满足：
$\left\{\begin{array}{l}\angle \alpha<\angle \alpha_{0}, \\D_{t, i j}>0,\end{array}\right.$ (15)
因此，约束条件可描述为：
${{g_6} = \mathop {\max }\limits_{i \in K,j \in O} \left\{ {{D_{t,ij}} \cdot \Delta {\alpha _{ij}}} \right\} \le 0,}$ (16)
${\Delta {\alpha _{ij}} = \left\{ {\begin{array}{*{20}{l}}{0,\angle \alpha \ge \angle {\alpha _0};}\\{1,\angle \alpha < \angle {\alpha _0},}\end{array}} \right.}$ (17)
式中：O={1, 2, …, NO}，其中NO为实时探测到的威胁的总数量.
1.4 目标函数设计本文设计的实时协同三维航迹规划的目标函数包括：航迹长度代价CostL、高度代价Costh以及时间协同代价Costt.空间协同问题已通过式(11)~(13)、(16)进行约束，此处不再赘述.
采用候选航迹点距目标点的欧式距离作为航迹长度代价CostL用以引导UCAV向目标飞行；采用候选航迹点高度为UCAV的高度代价Costh用以引导UCAV选择地势低洼处利用地形遮蔽实现低空突防；时间协同代价Costt是为引导多架UCAV同时到达各自目标点，对各自目标进行同时打击，做到攻其不备，实现闪电式快速多目标打击，提高整体任务成功率.由于实时航迹规划过程中剩余航迹的总长度无法精确获得，无法精确控制同时到达，本文使用基于估计距离差的时间协同控制方法，该方法采用当前位置与目标点的欧式距离来估计剩余航迹长度，以此调节速度使各UCAV之间的估计航迹长度差值最小化，采用该方法时，UCAV越接近目标点估计值越精确.综上所述，各子目标函数可描述为：
${{{{\mathop{\rm Cost}\nolimits} }_L} = \sum\limits_{i = 1}^{{N_U}} {\left\| {{\mathit{\boldsymbol{P}}_{i,t + \Delta t}} - {\mathit{\boldsymbol{T}}_i}} \right\|} ,}$ (18)
${{{{\mathop{\rm Cost}\nolimits} }_h} = \sum\limits_{i = 1}^{{N_U}} {\left| {{h_i}} \right|} ,}$ (19)
${{{{\mathop{\rm Cost}\nolimits} }_t} = \mathop {\max }\limits_{i,j \in K} \left\{ {\left| {{L_{i,t + \Delta t}} - {L_{j,t + \Delta t}}} \right|} \right\}.}$ (20)
式中：Pi, t+Δt为第i架UCAV在t+Δt时刻的候选位置; Ti为第i架UCAV的任务目标位置; hi为第i架UCAV在t+Δt时刻候选位置的飞行高度; Li, t+Δt、Lj, t+Δt分别为t+Δt时刻第i架和第j架UCAV距离各自目标点的估计距离.当Costt=0时，即表示t+Δt在各UCAV候选位置到目标点的估计距离相等，可同时抵达目标点.综上所述，本文提出的实时航迹规划的代价函数可描述为：
$\begin{aligned}\min f=& \delta_{1} \cdot \text { Cost}_{L}+\delta_{2} \cdot \operatorname{Cost}_{h}+\\& \delta_{3} \cdot \operatorname{Cost}_{t}+\delta_{4} \cdot|\Delta h| ,\end{aligned}$ (21)
$\text { s. t. }\ g_{i} \leqslant 0(i=1,2,3,4,5,6).$ (22)
式中：|Δh|=|himin－hi|为高度引导代价，引导UCAV在地面上方安全高度飞行，减少撞地概率；δ1、δ2、δ3、δ4分别为距离代价、高度代价、时间协同代价和高度引导代价的权重因子.
2 求解算法正弦余弦优化算法(sine cosine algorithm，SCA)是澳大利亚学者Mirjalili[20]于2016年提出的一种基于种群的启发式优化算法.与大多数智能优化算法相比，SCA具有架构简单，控制参数少，计算效率高等优点.文献[20]已经验证SCA在整体优化性能上优于萤火虫算法、花朵授粉算法、粒子群算法以及遗传算法等，因此，SCA已经被广泛应用于求解工程实际问题.
通过对SCA的研究，李银通等[17]发现SCA主要依赖正弦函数和余弦函数的震荡特性进行寻优，由于种群更新对当前最优解的依赖过强，算法迭代后期种群多样性迅速降低，导致算法易于陷入局部最优.基于此，为提高算法的收敛精度和局部最优规避能力，李银通等[17]提出了一种自学习策略和Lévy飞行的正弦余弦优化算法(SCASL)，并通过测试函数验证了SCASL的综合性能优于标准SCA和以及SSA[21]，VCS[22]，WOA[23]和GSA[24].由于SCASL的时间复杂度较低，因此本文采用SCASL求解本文提出的多UCAV协同实时航迹规划模型，以期满足实时性要求.
3 仿真实验与分析采用SCASL求解本文所构建协同实时航迹规划问题模型以验证模型的有效性，同时采用文献[17]实验结果中综合寻优性能仅次于SCASL的VCS[22]做对比实验，以对比分析SCASL在求解本模型时的性能.
3.1 条件设置本文以3架UCAV协同执行3个任务目标条件下的实时协同航迹规划为研究对象，设定战场环境与敌方威胁源分布情况是未知的，假定我方掌握的某不完备信息的山地区域作为战场环境，UCAV位置和待执行任务目标位置(已知)以及威胁源分布信息(UCAV起飞前未知，需要飞行过程中利用机载探测装备进行实时探测)见表 1、2.
表 1
表 1 UCAV及任务目标位置 Tab. 1 Locations of UCAV and mission targets UCAV编号 位置/km 任务目标T 位置/km UCAV1 (5, 12) T1 (85, 90)
UCAV2 (7, 9) T2 (88, 85)
UCAV3 (9, 5) T3 (90, 81)
表 1 UCAV及任务目标位置 Tab. 1 Locations of UCAV and mission targets
表 2
表 2 威胁源参数 Tab. 2 Threat parameters 威胁源 威胁类型 位置/km 作用半径/km 高度/km TS1 导弹阵地 (25, 25) 8.0 1.5
TS2 高炮阵地 (35, 48) 7.0 1.5
TS3 禁飞区域 (38, 66) 8.4 1.5
TS4 高炮阵地 (50, 33) 7.5 1.5
TS5 导弹阵地 (63, 56) 7.0 1.5
TS6 雷达阵地 (65, 82) 12.0 1.5
TS7 导弹阵地 (85, 65) 9.0 1.5
表 2 威胁源参数 Tab. 2 Threat parameters
本文以固定翼重型UCAV为研究对象，UCAV等效横截面面积S和质量m参考文献[25]，分别为S=49.24 m2，质量m=14 680 kg.UCAV攻角变化范围为[-αmax, αmax]，αmax=π×15/180，滚转角变化范围为[-γmax, γmax]，γmax=π/3；UCAV之间最小安全飞行距离dsafe=0.1 km，最大有效通信距离dmax=30 km；UCAV实时探测半径为30 km，最高飞行高度hmax=5 km，每架UCAV的vmin=0.3 Ma，vmax=0.8 Ma，重力加速度g=9.8 m/s2.
实时航迹规划模型参数如下：战场任务空间为xmax=100 km，ymax=100 km, zmax=3 km；UCAV控制量油门ζ的变化范围为[0, 1]，空气密度ρ=1.225 kg/m3，代价函数权重因子δ1=0.7，δ2=0.1，δ3=0.1，δ4=0.1，时间协同误差小于20 s，滚动时域时间窗口Δt=1 s(每次迭代规划耗时超过1 s则认为不满足实时性要求).各架UCAV初始航迹倾角与偏航角均指向各自目标.
采用SCASL和VCS在每个时间窗口对模型进行求解，参数设置见表 3，其中VCS参数设置与原文献保持一致.寻优变量X=(ζ1, γ1, α1, ζ2, γ2, α2, ζ3, γ3, α3)，问题维度dim=9，其中(ζ1, γ1, α1)为UCAV1的控制量，(ζ2, γ2, α2)为UCAV2的控制量，(ζ3, γ3, α3)为UCAV3的控制量.基于对算法寻优性能的分析[17]并考虑到机载系统运算能力的限制，为实现实时性和解的质量的折中，算法最大评价次数FEmax=3 000，SCASL中种群搜索个体数设为20，由于VCS每次迭代对种群进行3次评价，在评价次数相同的基础上，为保证两种算法最大迭代次数相近，保证对比结果的公平性，VCS搜索个体数设为7.
表 3
表 3 算法参数设置 Tab. 3 Algorithm parameters setting 算法 参数设置 SCASL α=0.05, β=0.5, a=2
VCS λ=N/2, σ=0.3
表 3 算法参数设置 Tab. 3 Algorithm parameters setting
3.2 结果与分析本文所提出的实时协同航迹规划的原则是在满足实时性要求和协同要求的前提下为多架UCAV规划出可行的协同实时航迹，图 4为飞行过程中SCASL和VCS在各个时间窗口内求解模型，规划下一时间窗口航迹所耗费的时间(规划耗时超过时间窗口Δt=1 s, 则认为不满足实时性要求).
Fig. 4
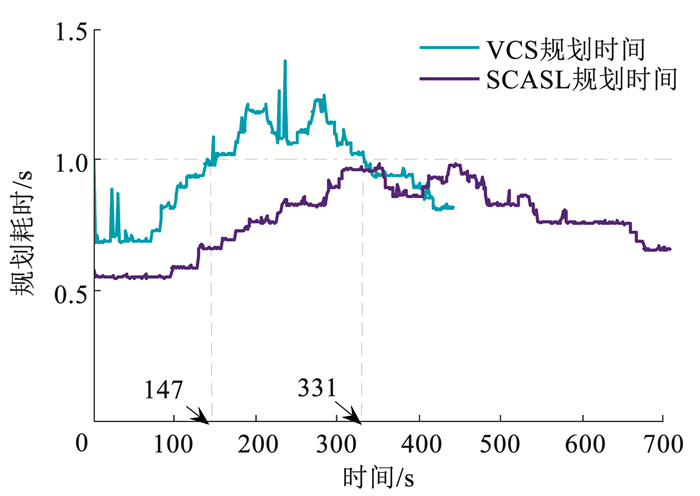图 4 航迹规划耗时 Fig. 4 Time consumption of real-time trajectory planning 由图 4可知，在整个飞行过程中，SCASL航迹规划耗时均小于时间窗口Δt，证明采用改进后的SCASL求解该模型时满足实时性要求；而VCS在第147~331 s的时间段内的规划耗时均超过时间窗口Δt，即不满足实时性要求.因此，SCASL更具有实际应用价值和意义.
SCASL和VCS求解实时协同航迹规划结果见表 4，两种算法所得3架UCAV的航迹总长度近似相等，就航程代价来讲无明显差别；SCASL所得结果中3架UCAV到达各自任务目标的时刻分别为707, 706, 708 s，到达时间仅仅相差2 s，完全满足时间协同的要求；VCS所得结果中3架UCAV到达各自任务目标的时刻分别为432，437, 443 s，到达时间差最大为11 s，同样满足时间协同的要求，但时间协同效果相比SCASL的结果较差.验证了本文所提出的基于估计距离差控制的时间协同航迹规划方法的有效性.
表 4
表 4 航迹规划结果 Tab. 4 Trajectory planning results 算法 UCAV编号 航迹总长度/km 到达时刻/s UCAV1 115.226 6 707
SCASL UCAV2 115.926 2 706
UCAV3 118.082 5 708
UCAV1 115.057 0 432
VCS UCAV2 115.054 7 437
UCAV3 116.985 4 443
表 4 航迹规划结果 Tab. 4 Trajectory planning results
图 5、6分别为3架UCAV在t=200 s和t=400 s时的实时等高线航迹图，图中展示了3架UCAV在200、400 s时处于的位置和已探测到的威胁分布，图中虚线圆覆盖区域为3架UCAV实时探测范围.
Fig. 5
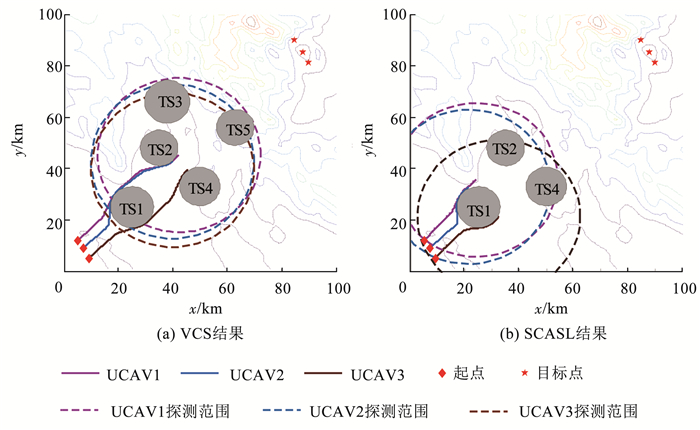图 5 t=200 s时协同实时等高线航迹 Fig. 5 Collaborative real-time trajectory contour when t=200 s Fig. 6
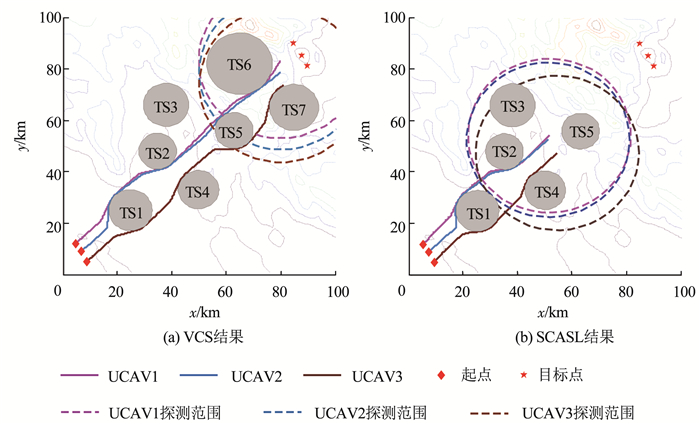图 6 t=400 s时协同实时等高线航迹 Fig. 6 Collaborative real-time trajectory contour when t=400 s 图 7、8分别为两种算法所得结果中3架UCAV均到达目标位置时的协同实时等高线航迹和协同实时三维航迹.由图 7、8可知，两种算法所得到的结果中，3架UCAV均能安全抵达各自任务目标区域附近，在飞行过程中未出现穿过威胁区的情况，有效规避了威胁.此外，可直观的发现，在规避实时探测到的障碍过程中，航迹比较平滑，能做到提前规避，验证本文提出的多UCAV实时协同航迹规划模型的有效性以及威胁预测规避方法的可靠性.
Fig. 7
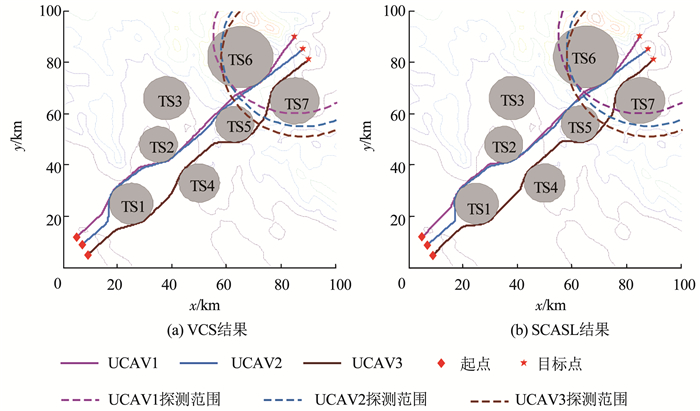图 7 整体协同实时等高线航迹 Fig. 7 Overall collaborative real-time trajectory contour Fig. 8
图 8 整体协同实时三维航迹 Fig. 8 Overall collaborative real-time 3D trajectory 图 9、10分别为两种算法所得结果中各架UCAV在飞行过程中的航迹倾角和偏航角的变化情况.由图 9可知，VCS所得结果中航迹倾角变化范围在[-π/9.49, π/10.94]，SCASL所得结果中航迹倾角变化范围在[-π/9.31, π/9.95]，整体上航迹倾角变化范围相对较小.由于地形微小起伏较为频繁，为进行地形跟随实现低空突防，所以航迹倾角出现较为频繁的微调.由图 10可知，VCS所得结果中偏航角的变化范围为[π/237.93, π/2.06]，SCASL所得结果中偏航角的变化范围为[-π/24.13, π/1.84]，由于任务目标位置固定，在代价函数的引导作用下，未探测到威胁源时UCAV始终指向目标飞行，因此偏航角在飞行过程中整体上相对稳定，由于本文提出的实时航迹规划模型对于威胁源的规避只能提前预测一个时间窗口，因此在探测到需要规避威胁源时，UCAV往往已经距离威胁源较近，此时规避威胁时偏航角会出现相对较大变化.由于本模型中UCAV的机动性能是由控制量的变化范围决定的，所以规划出的航迹均满足UCAV机动性能约束.
Fig. 9
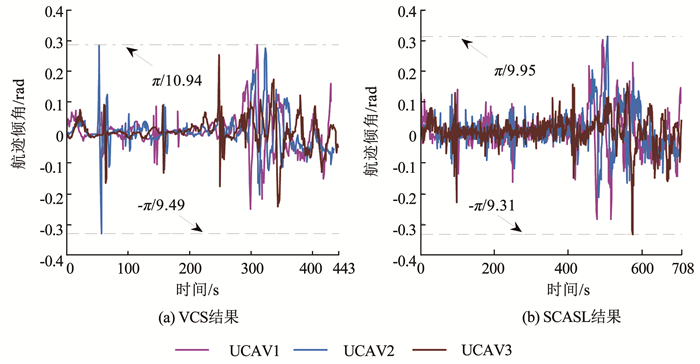图 9 协同实时航迹倾角 Fig. 9 Collaborative real-time trajectory inclination Fig. 10
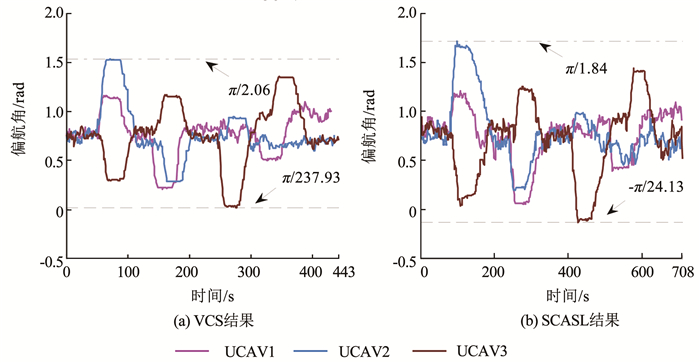图 10 协同实时航迹偏航角 Fig. 10 Collaborative real-time trajectory yaw angle 图 11为3架UCAV在飞行过程中的飞行速度变化情况.VCS所得结果中，3架UCAV在飞行过程中速度大部分时间均接近于速度上限0.8 Ma，因此其到达任务目标区域的飞行时间相对较短，SCASL所得结果中3架UCAV速度变化范围在[0.3 Ma, 0.8 Ma]，符合UCAV的飞行速度约束，速度的变化是为了满足编队在飞行过程中的时间协同，以期同时达到各自任务目标点执行相应任务，3架UCAV到达时间偏差仅为2 s，相比VCS结果中到达时间偏差为11 s，时间协同效果较好，但增加了飞行时间.
Fig. 11
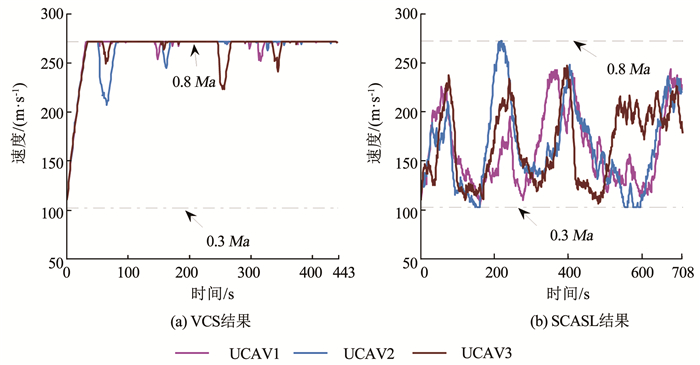图 11 UCAV速度变化 Fig. 11 UCAV speed change 图 12为在飞行过程中3架UCAV之间的相互距离.由图 12可知，两种算法所得结果中3架UCAV整个飞行过程中的距离均大于最小安全距离dsafe，小于最大通信距离dmax，确保各UCAV之间不会发生碰撞并能保持实时通信.
Fig. 12
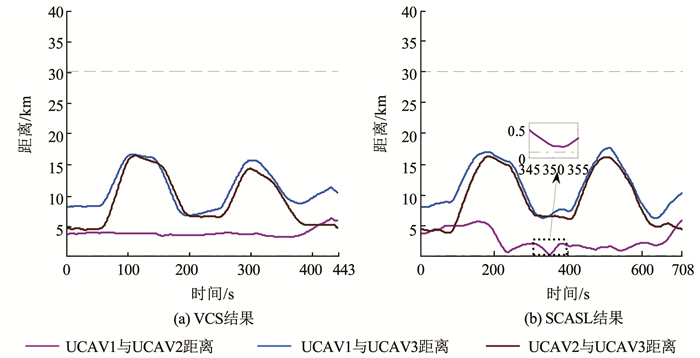图 12 UCAV之间距离 Fig. 12 Distance between UCAVs 图 13为在飞行过程中UCAV的飞行高度以及相应位置的地形高度，两种算法所得结果中，3架UCAV在飞行过程中UCAV实现了相对较好的地形跟随，满足低空突防的要求，再次验证了本文提出的实时协同航迹规划模型的有效性.
Fig. 13
图 13 UCAV地形跟随效果 Fig. 13 Terrain-following effect of UCAV 4 结论1) 以3架UCAV协同执行对地打击任务为背景，根据UCAV平台性能设计了飞行速度、飞行高度、相对距离以及威胁规避等约束条件，基于UCAV的三自由度运动学和动力学质点模型建立了多UCAV协同实时航迹规划模型.VCS求解模型所得结果满足协同性要求，但不满足实时性要求，航迹规划结果整体上劣于SCASL所得结果，证明本文提出的基于SCASL的协同实时航迹规划方法的有效性与优越性.
2) 借鉴滚动时域控制思想，以1 s为时间窗口，采用SCASL反复滚动迭代优化为3架UCAV规划出了满足实时性要求和协同要求的安全可飞的实时航迹，有效提高了UCAV协同实时航迹规划的实时性和可操作性.
3) 本文提出的航迹规划方法在每次滚动迭代优化过程中只考虑下一时间窗口内的一段航迹，得到的是局部最优航迹，如何优化改进模型得到近似全局最优的实时协同航迹是下一步的研究重点.
参考文献
[1] 王群. 无人作战飞机的特点和未来发展[J]. 国防科技, 2011, 32(1): 23.
WANG Qun. Characteristic and future development of UCAV[J]. National Defense Science and Technology, 2011, 32(1): 23. DOI:10.3969/j.issn.1671-4547.2011.01.006
[2] DEWANGAN R K, SHUKLA A, GODFREY W W. Three dimensional path planning using Grey wolf optimizer for UAVs[J]. Applied Intelligence, 2019, 49(6): 2201. DOI:10.1007/s10489-018-1384-y
[3] 赵明, 赵玲玲, 苏小红, 等. 一种三维多UAV协同航迹规划的空间模糊文化算法[J]. 哈尔滨工业大学学报, 2015, 47(10): 29.
ZHAO Ming, ZHAO Lingling, SU Xiaohong, et al. A cultural algorithm with spatial fuzzy set to solve multi-UAVs cooperative path planning in a three dimensional environment[J]. Journal of Harbin Institute of Technology, 2015, 47(10): 29. DOI:10.11918/j.issn.0367-6234.2015.10.007
[4] PAN J S, LIU N X, CHU S C, et al. A hybrid differential evolution algorithm and its application in unmanned combat aerial vehicle path planning[J]. IEEE Access, 2020, 8: 17691. DOI:10.1109/access.2020.2968119
[5] 钱洲元, 雷明. 面向无人机航迹规划的自适应乌贼算法[J]. 哈尔滨工业大学学报, 2019, 51(10): 37.
QIAN Zhouyuan, LEI Ming. Adaptive cuttlefish algorithm for UAV path planning[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 37. DOI:10.11918/j.issn.0367-6234.201805004
[6] QU Chengzhi, GAI Wendong, ZHANG Jing, et al. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning[J]. Knowledge-Based Systems, 2020, 194: 105530. DOI:10.1016/j.knosys.2020.105530
[7] 单文昭, 崔乃刚, 黄蓓, 等. 基于PSO-HJ算法的多无人机协同航迹规划方法[J]. 中国惯性技术学报, 2020, 28(1): 122.
SHAN Wenzhao, CUI Naigang, HUANG Bei, et al. Multiple UAV cooperative path planning based on PSO-HJ method[J]. Journal of Chinese Inertial Technology, 2020, 28(1): 122. DOI:10.13695/j.cnki.12-1222/o3.2020.01.019
[8] XU Chunfang, DUAN Haibin, LIU Fang, et al. Chaotic artificial bee colony approach to Uninhabited Combat Air Vehicle (UCAV) path planning[J]. Aerospace Science and Technology, 2010, 14(8): 535. DOI:10.1016/j.ast.2010.04.008
[9] THARWAT A, ELHOSENY M, HASSANIEN A E, et al. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm[J]. Cluster Computing, 2019, 22: 4745. DOI:10.1007/s10586-018-2360-3
[10] 孙小雷, 齐乃明, 董程, 等. 无人机任务分配与航迹规划协同控制方法[J]. 系统工程与电子技术, 2015, 37(12): 2772.
SUN Xiaolei, QI Naiming, DONG Cheng, et al. Cooperative control algorithm of task assignment and path planning for multiple UAVs[J]. Systems Engineering and Electronics, 2015, 37(12): 2772. DOI:10.3969/j.issn.1001-506X.2015.12.17
[11] 江泽强, 朱旋, 李琪. 突发威胁下的无人机实时航迹规划[J]. 指挥与控制学报, 2017, 3(3): 240.
JIANG Zeqiang, ZHU Xuan, LI Qi. Real time path planning of UAV for pop-up threat[J]. Journal of Command and Control, 2017, 3(3): 240. DOI:10.3969/j.issn.2096-0204.2017.03.0240
[12] 范伟伦, 李薇, 冯杭. 基于改进RRT算法的无人机实时航迹规划[J]. 舰船电子工程, 2019, 39(2): 56.
FAN Weilun, LI Wei, FENG Hang. UAV trajectory planning based on an improved RRT algorithm[J]. Ship Electronic Engineering, 2019, 39(2): 56. DOI:10.3969/j.issn.1672-9730.2019.02.015
[13] ZHANG Shaoqing, LV Mingwei, YANG Chen. Real-time 3D route planning based on modified rapidly exploring random-tree algorithm[C]//Proceedings of the 2nd International Conference on Electronic Information and Communication Technology (ICEICT). Harbin: IEEE, 2019: 147. DOI: 10.1109/ICEICT.2019.8846357
[14] CAI Yawei, ZHAO Hui, LI Mudong, et al. 3D real-time path planning based on cognitive behavior optimization algorithm for UAV with TLP model[J]. Cluster Computing, 2019, 22(2): 5089. DOI:10.1007/s10586-017-1432-0
[15] YOU Shixun, GAO Lipeng, DIAO Ming, et al. Real-time path planning based on the situation space of UCAVs in a dynamic environment[J]. Microgravity Science and Technology, 2018, 30(6): 899. DOI:10.1007/s12217-018-9650-5
[16] 宗群, 王丹丹, 邵士凯, 等. 多无人机协同编队飞行控制研究现状及发展[J]. 哈尔滨工业大学学报, 2017, 49(3): 1.
ZONG Qun, WANG Dandan, SHAO Shikai, et al. Research status and development of multi UAV coordinated formation flight control[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 1. DOI:10.11918/j.issn.0367-6234.2017.03.001
[17] 李银通, 韩统, 赵辉, 等. 自学习策略和Lévy飞行的正弦余弦优化算法[J]. 重庆大学学报, 2019, 42(9): 55.
LI Yintong, HAN Tong, ZHAO Hui, et al. An improved sine cosine optimization algorithm with self-learning strategy and Lévy flight[J]. Journal of Chongqing University, 2019, 42(9): 55. DOI:10.11835/j.issn.1000-582X.2019.09.007
[18] 李清, 侯永军, 沈春林. 数字地形数据的二维三次卷积插值[J]. 南京航空航天大学学报, 1997, 29(4): 378.
LI Qing, HOU Yongjun, SHEN Chunlin. Two-dimensional cubic convolution interpolation for digital map data[J]. Journal of Nanjing University of Aeronautics & Astronautics, 1997, 29(4): 378.
[19] WILLIAMS P. Three-dimensional aircraft terrain-following via real-time optimal control[J]. Journal of Guidance Control and Dynamics, 2007, 30(4): 1201. DOI:10.2514/1.29145
[20] MIRJALILI S. SCA: A Sine Cosine Algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120. DOI:10.1016/j.knosys.2015.12.022
[21] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp Swarm Slgorithm: A bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163. DOI:10.1016/j.advengsoft.2017.07.002
[22] LI Mudong, ZHAO Hui, WENG Xingwei, et al. A novel nature-inspired algorithm for optimization: Virus colony search[J]. Advances in Engineering Software, 2016, 92: 65. DOI:10.1016/j.advengsoft.2015.11.004
[23] MIRJALILI S, LEWIS A. The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95: 51. DOI:10.1016/j.advengsoft.2016.01.008
[24] RASHEDI E, NEZAMABADIPOUR H, SARYAZDI S. GSA: A gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232. DOI:10.1016/j.ins.2009.03.004
[25] 黄长强, 丁达理, 黄汉桥, 等. 无人作战飞机自主攻击技术[M]. 北京: 国防工业出版社, 2014.
HUANG Changqiang, DING Dali, HUANG Hanqiao, et al. Autonomous attack technology for UCAV[M]. Beijing: National Defense Industry Press, 2014.
