郭一竹1,杨皓宇2,郭宏伟3,刘荣强3,罗阿妮2
(1.中国空间技术研究院总体部,北京,100094;2.哈尔滨工程大学 机电学院,哈尔滨,150001; 3.哈尔滨工业大学 机器人与系统国家重点实验室,哈尔滨,150000)
摘要:
为研究弹性伸杆的力学性能,对其压平、拉平过程中的能量与外载荷的变化以及刚度进行了分析. 首先对弹性伸杆的刚度进行了理论分析,找出了影响弹性伸杆刚度的参数. 之后通过ABAQUS对弹性伸杆的拉平与压平的过程进行了仿真分析,并运用控制变量法分析了各项参数对刚度的影响. 仿真结果表明,拉平与压平过程中的能量变化基本一致,而压平所需要的外载荷较小. 增大弹性伸杆的弧段半径、铺层数量和中心距,相同载荷下的弹性伸杆的变形量会逐渐降低. 通过对仿真结果的分析可知,在拉平与压平的开始阶段外载荷较小,外载荷的峰值出现在拉平与压平的最终阶段,增大弹性伸杆的弧段半径、中心距和铺层数量能够有效提高弹性伸杆的刚度.
关键词: 弹性伸杆,力学性能,刚度,弧段半径,仿真分析
DOI：10.11918/201809017
分类号:TU375.2
文献标识码:A
基金项目:航天五院"大变形豆荚杆高精度展开技术研究"预研项目
Analysis of mechanical properties of spatial thin-walled elastic extension bar
GUO Yizhu1,YANG Haoyu2,GUO Hongwei3,LIU Rongqiang3,LUO Ani2
(1. Beijing Institute of Spacecraft System Engineering, China Academy of Space Technology, Beijing 100094, China; 2. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China; 3. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150000, China)
Abstract:
To study the mechanical properties of spatial thin-walled elastic extension bar, the change of energy, external load during leveling and flattening and stiffness are analyzed. Firstly, the stiffness of elastic extension bar is theoretically analyzed, and the parameters that affect the stiffness of elastic extension bar are found out. Then, the process of flattening and leveling the elastic extension bar is simulated by ABAQUS, and the influence of various parameters on the stiffness is analyzed by using the control variable method. The simulation results show that the energy variation in the leveling process is basically consistent with that in the flattening process, but the external load required for the flattening is relatively small. With the increase of the radius of arc section, the number of layers and the center distance, the deformation of the elastic extension bar will gradually decrease under the same load. By the analysis of the simulation results, it can be seen that the external load is smaller in the initial stage of flattening and leveling, and the peak value of the external load appears in the final stage of flattening and leveling, and the stiffness of elastic extension bar can be improved effectively by increasing the radius, center distance and the number of layers.
Key words: spatial thin-walled elastic extension bar mechanical property stiffness arc radius simulation analysis
郭一竹, 杨皓宇, 郭宏伟, 刘荣强, 罗阿妮. 空间薄壁弹性伸杆力学特性分析[J]. 哈尔滨工业大学学报, 2020, 52(1): 107-112. DOI: 10.11918/201809017.
GUO Yizhu, YANG Haoyu, GUO Hongwei, LIU Rongqiang, LUO Ani. Analysis of mechanical properties of spatial thin-walled elastic extension bar[J]. Journal of Harbin Institute of Technology, 2020, 52(1): 107-112. DOI: 10.11918/201809017.
基金项目 航天五院"大变形豆荚杆高精度展开技术研究"预研项目 作者简介 郭一竹(1986—)，男，硕士，工程师;
郭宏伟(1980—)，男，副教授，博士生导师;
刘荣强(1965—)，男，教授，博士生导师 通信作者 郭宏伟，guohw@hit.edu.cn 文章历史 收稿日期: 2018-09-03
Abstract Full text Figures/Tables PDF
空间薄壁弹性伸杆力学特性分析
郭一竹1, 杨皓宇2, 郭宏伟3
, 刘荣强3, 罗阿妮2 1. 中国空间技术研究院总体部，北京，100094;
2. 哈尔滨工程大学 机电学院，哈尔滨，150001;
3. 哈尔滨工业大学 机器人与系统国家重点实验室，哈尔滨，150000
收稿日期: 2018-09-03
基金项目: 航天五院"大变形豆荚杆高精度展开技术研究"预研项目
作者简介: 郭一竹(1986—)，男，硕士，工程师; 郭宏伟(1980—)，男，副教授，博士生导师; 刘荣强(1965—)，男，教授，博士生导师
通信作者: 郭宏伟，guohw@hit.edu.cn
摘要: 为研究弹性伸杆的力学性能，对其压平、拉平过程中的能量与外载荷的变化以及刚度进行了分析.首先对弹性伸杆的刚度进行了理论分析，找出了影响弹性伸杆刚度的参数.之后通过ABAQUS对弹性伸杆的拉平与压平的过程进行了仿真分析，并运用控制变量法分析了各项参数对刚度的影响.仿真结果表明，拉平与压平过程中的能量变化基本一致，而压平所需要的外载荷较小.增大弹性伸杆的弧段半径、铺层数量和中心距，相同载荷下的弹性伸杆的变形量会逐渐降低.通过对仿真结果的分析可知, 在拉平与压平的开始阶段外载荷较小，外载荷的峰值出现在拉平与压平的最终阶段，增大弹性伸杆的弧段半径、中心距和铺层数量能够有效提高弹性伸杆的刚度.
关键词: 弹性伸杆 力学性能 刚度 弧段半径 仿真分析
Analysis of mechanical properties of spatial thin-walled elastic extension bar
GUO Yizhu1, YANG Haoyu2, GUO Hongwei3
, LIU Rongqiang3, LUO Ani2 1. Beijing Institute of Spacecraft System Engineering, China Academy of Space Technology, Beijing 100094, China;
2. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China;
3. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150000, China
Abstract: To study the mechanical properties of spatial thin-walled elastic extension bar, the change of energy, external load during leveling and flattening and stiffness are analyzed. Firstly, the stiffness of elastic extension bar is theoretically analyzed, and the parameters that affect the stiffness of elastic extension bar are found out. Then, the process of flattening and leveling the elastic extension bar is simulated by ABAQUS, and the influence of various parameters on the stiffness is analyzed by using the control variable method. The simulation results show that the energy variation in the leveling process is basically consistent with that in the flattening process, but the external load required for the flattening is relatively small. With the increase of the radius of arc section, the number of layers and the center distance, the deformation of the elastic extension bar will gradually decrease under the same load. By the analysis of the simulation results, it can be seen that the external load is smaller in the initial stage of flattening and leveling, and the peak value of the external load appears in the final stage of flattening and leveling, and the stiffness of elastic extension bar can be improved effectively by increasing the radius, center distance and the number of layers.
Keywords: spatial thin-walled elastic extension bar mechanical property stiffness arc radius simulation analysis
空间薄壁弹性伸杆具有轻质、收展原理简单、收纳率高、可重复性强和精度高等特点，常用作太阳帆、空间薄膜天线阵面等可收展的航天器的支撑体系构件[1-7].
国内外大批学者就其结构受力特性等性能进行了大量研究.康雄建等[8]对长度为10m的弹性伸杆进行了模态试验，得到了其模态和频率，之后运用有限元软件ADINA对试验模型分别在考虑空气和不考虑空气的条件下进行了仿真分析，从而分析出了空气对弹性伸杆模态造成的偏差.蔡祈耀等[9]对弹性伸杆进行了悬臂屈曲分析及试验，并运用有限元软件ABAQUS进行了线性特征值屈曲分析，基于试验和模拟分析，进一步对弹性伸杆壁厚、铺层和杆件长细比进行参数分析，得到了各参数对弹性伸杆悬臂梁屈曲临界载荷的影响.李瑞雄等[10-13]运用ABAQUS分别采用静力法和显式动力法对薄壁弹性伸杆的拉扁、压扁、缠绕和展开过程进行了深入系统地研究，得到了弹性伸杆在缠绕过程中的应力、应变变化规律.刘锦贤等[14-15]对弹性伸杆在空间热辐射环境下的温度场和热变形进行数值模拟，验证了采用层合板整体正交异性热参数和等效壳单元进行计算的适用性，同时也证明了薄壁构件的在轨温度场下的热变形水平满足空间可展天线的形面精度要求.
Sickinger C等[16]利用显式分析软件对弹性伸杆本身的刚度以及弹性伸杆在轴向压缩、组合弯矩作用下的屈曲稳定性进行了仿真分析.欧洲航天局(ESA)和德国宇航中心(DLR)[17]利用电机辅助设备，对弹性伸杆在失重状态下的展开进行了试验，展开效果非常理想，证明弹性伸杆可用做薄膜天线和太阳帆等空间结构的展开支撑件. Irwin等[18]对弹性伸杆的设计、制造、评估进行了研究，并通过四点纯弯试验分析了弹性伸杆纯弯结构响应. Chu等[19]对复合材料薄壁弹性伸杆的设计理论和展开后的结构动态响应进行了研究.
弹性伸杆在展开后需要具备一定的刚度以保持对薄膜的张力，从而达到平面薄膜的展开精度，弹性伸杆的刚度主要与其几何参数有关，关于几何参数对弹性伸杆刚度的影响未见报道，弹性伸杆收缩与展开所需要的驱动载荷也未见分析，因此本文就弹性伸杆的几何参数对其拉伸刚度、弯曲刚度以及扭转刚度的影响以及收缩和展开所需要的驱动载荷进行了分析.
1 弹性伸杆刚度理论分析弹性伸杆由上下两片近似“Ω”型的薄壳肋片粘合而成，横截面呈中空、薄壁、对称透镜状，其外形如图 1所示，工作原理如图 2所示，弹性伸杆的初始态如图 2(a)所示，收起时拉紧块将弹性伸杆根部拉平(图 2(b))，然后滚子将弹性伸杆的过渡段压平，最后将弹性伸杆缠绕在滚筒上(图 2(c))，展开过程是收起的逆过程.
Fig. 1
图 1 弹性伸杆外形图 Fig. 1 The shape of elastic extension bar Fig. 2
图 2 弹性伸杆的工作原理 Fig. 2 Working principle of elastic extension bar 弹性伸杆的截面如图 3所示，其中，α为弧段2的弧度，β为其余弧段的弧度，R为弧段的半径，l为侧边宽度，L为截面宽度.
Fig. 3
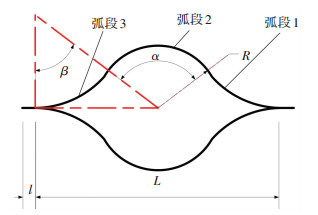图 3 弹性伸杆截面图 Fig. 3 Section of elastic extension bar 弹性伸杆鼓起时的宽度为
${L_1} = L + 2l = \frac{{2R}}{{\tan (\pi - \beta )}} + 2l, $ (1)
压平时的宽度为
${L_2} = (\alpha + 2\beta )R + 2l, $ (2)
截面积为
$A = 2t{L_2} = 2t((\alpha + 2\beta )R + 2l), $ (3)
轴向刚度为
$EA = \frac{F}{\delta }.$ (4)
式中:E为弹性模量，A为弹性伸杆的截面积，F为轴向载荷，δ为轴向变形量，t为弹性伸杆的厚度.通过(4)式可知，弹性伸杆的刚度与截面面积有关，而截面面积主要与弧段半径和壁厚有关，因此增加弧段半径和壁厚可以提高弹性伸杆的轴向刚度.
弹性伸杆在工作时处于完全展开状态，充当结构件，因此不需要考虑大变形的因素，可视为一端固定、一端自由的悬臂梁，受力与变形如图 4所示，受力与变形的关系如式(5)所示.
Fig. 4
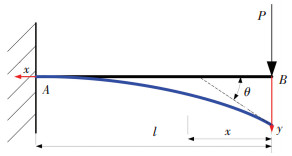图 4 弹性伸杆弯曲变形图 Fig. 4 Bending deformation of elastic extension bar $\left\{ {\begin{array}{*{20}{l}}{M(x) = - Px, }\\{EI{y^{\prime \prime }} = - Px, }\\{EI{y^\prime } = - \frac{P}{2}{x^2} + C, }\\{EIy = - \frac{P}{6}{x^3} + Cx + D.}\end{array}} \right.$ (5)
代入边界条件，求得最大转角和挠度为
$\left\{ {\begin{array}{*{20}{l}}{{\theta _{\max }} = {\theta _B} = - \frac{{P{l^2}}}{{2EI}}, }\\{{y_{\max }} = {y_B} = - \frac{{P{l^3}}}{{3EI}}.}\end{array}} \right.$ (6)
弹性伸杆的弯曲刚度为
$\left\{ {\begin{array}{*{20}{l}}{EI = - \frac{{P{l^2}}}{{2{\theta _B}}}, }\\{EI = - \frac{{P{l^3}}}{{3{y_B}}}.}\end{array}} \right.$ (7)
由(7)式可知，弹性伸杆的弯曲刚度与惯性矩有关，经推导得到弹性伸杆的惯性矩为
$\begin{array}{*{20}{c}}{{I_z} = C\left[ {{R^4} - {{(R - t)}^4}} \right], }\\{C = 4\left[ {\frac{{2{\rm{ \mathit{ π} }} - \alpha }}{8} + 2\sin \beta \cos \frac{\alpha }{2} - ({\rm{ \mathit{ π} }} - \alpha ){{\sin }^2}\beta } \right].}\end{array}$ (8)
因为α和β均是定值，因此惯性矩只与弧段半径R和弹性伸杆的壁厚t有关.
图 5表示为弹性伸杆的自由端在扭矩T下产生的扭转变形，扭转角为φ，则弹性伸杆的扭转刚度可表示为
Fig. 5
图 5 弹性伸杆的扭转变形 Fig. 5 Torsional deformation of elastic extension bar $\varphi = \frac{{Tl}}{{GI}}$ (9)
其中GI为扭转刚度，l为弹性伸杆的长度.由此可知，弹性伸杆的扭转刚度也与惯性矩有关.
2 弹性伸杆拉压仿真分析 2.1 弹性伸杆拉平分析弹性伸杆由碳纤维复合材料制成，材料性能参数如表 1所示.选用铺层厚度为0.1 mm，4层铺层，弧段半径80 mm，长度2 000 mm，铺层角度为[0 45-45 90]的弹性伸杆进行仿真分析，弹性伸杆的两端均处于自由状态，整体添加自接触约束，在弹性伸杆两侧的连接件上施加位移载荷，如图 6所示.
表 1
表 1 碳纤维复合材料的材料属性 Tab. 1 Material properties of carbon fiber composites 参数 E1(0°) E1(90°) ν G 拉伸模量 80.8 GPa 6.17 GPa 0.344 2.93 GPa
压缩模量 60.26 GPa
密度 1 600 kg·m-3
表 1 碳纤维复合材料的材料属性 Tab. 1 Material properties of carbon fiber composites
Fig. 6
图 6 拉平载荷 Fig. 6 Leveling load 仿真过程如图 7所示.
Fig. 7
图 7 拉平过程 Fig. 7 Leveling process 通过仿真可知，可以通过拉平的方式将弹性伸杆由鼓起状态变为扁平状态.其中弧段上的应力值较大，弧段与弧段的连接处应力较小，弹性伸杆从拉平状态到完全鼓起状态的过渡段长1.5m左右.
运用MATLAB对弹性伸杆的内能随时间的变化数据进行拟合，得到的函数关系及拟合曲线如图 8(a)所示.由图可知，随着弹性伸杆逐渐被拉平，弹性伸杆的内能呈指数增加，这说明拉平过程中需要的外力越来越大.通过式(10)可求得拉力与时间的变化关系，关系如图 8(b)所示.由图 8(b)可知，最少需要F=118.475 N的力能将弹性伸杆拉平.
Fig. 8
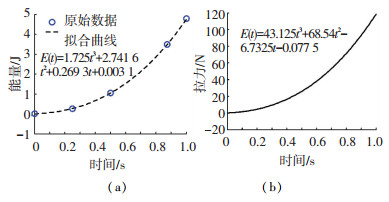图 8 拉平过程的能量及外载荷的变化 Fig. 8 Variation of energy and external load in leveling process $F(t) = \frac{{E(t)}}{{s(t)}}.$ (10)
2.2 弹性伸杆压平分析对同一段弹性伸杆进行压平仿真，将弹性伸杆的一端置于两段压板之间，对上下压板分别施加一对方向相反的位移载荷，使压板对向移动，如图 9所示.
Fig. 9
图 9 压平载荷 Fig. 9 Flattening load 仿真过程如图 10所示.
Fig. 10
图 10 压平过程 Fig. 10 Flattening process 由图 11可知，通过压平的方式也可以将弹性伸杆由鼓起状态变为扁平状态.其应力分布与拉平过程相似，压平后的过渡段长度也在1.5m左右.
运用同样的方法对压平过程进行分析，发现压平过程中能量与外载荷随时间的变化与拉平相似，最后通过式(10)求出压平所需的最小载荷为F=73.235 N.
Fig. 11
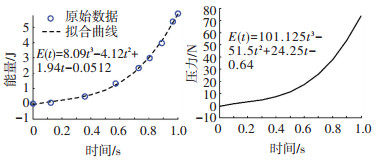图 11 压平过程的能量及外载荷的变化 Fig. 11 Variation of energy and external load in flattening process 对比拉平与压平过程，弹性伸杆由鼓起状态变为扁平状态的内能变化关系相似，内能也基本相等，但是压平需要的外力较小，因此利用压平的方式更容易将弹性伸杆从鼓起状态变为扁平状态.
3 几何参数对弹性伸杆刚度的影响通过前面的分析可知，影响弹性伸杆刚度的几何参数包括弧段半径R，壁厚t和中心距d，而壁厚与铺层数量n有关.下面针对这三项参数对弹性伸杆刚度的影响进行仿真分析.
3.1 弧段半径对刚度的影响运用ABAQUS对长度为2 m，铺层数量4层，铺层厚度0.1 mm，中心距为0，铺层角度为[0 45-45 90]，弧段半径分别为R=60，R=70，R=80，R=90和R=100的弹性伸杆进行仿真分析，仿真模型及加载情况如图 12所示，固定板与弹性伸杆采用绑定连接以便于对弹性伸杆均匀加载，对弹性伸杆整体添加自接触约束，在根部添加固定约束.
Fig. 12
图 12 弹性伸杆有限元模型 Fig. 12 Finite element model of elastic extension bar 因仿真模型较多且仿真结果相似，此处只列出R=80的仿真结果，载荷及变形量如表 2所示，变形云图如图 13所示.
表 2
表 2 弹性伸杆的载荷及变形量 Tab. 2 Load and deformation of elastic extension bar 载荷 变形 轴向载荷100 N 4.55×10－7 m
径向载荷100 N 2.86×10－4 m
扭矩5 Nm 1.56×10－4 rad
表 2 弹性伸杆的载荷及变形量 Tab. 2 Load and deformation of elastic extension bar
Fig. 13
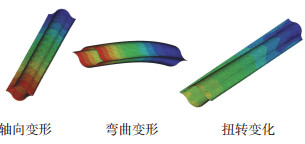图 13 弹性伸杆变形云图 Fig. 13 Deformation nephogram of elastic extension bar 通过仿真可知，随着弧段半径的增加，弹性伸杆的变形量逐渐减小，说明弹性伸杆的轴向刚度随着弧段半径的增加而增加，轴向刚度与弧段半径的关系如图 14(a)所示.同样，弯曲刚度与扭转刚度随弧段半径的变化关系如图 14(b)和14(c)所示.
Fig. 14
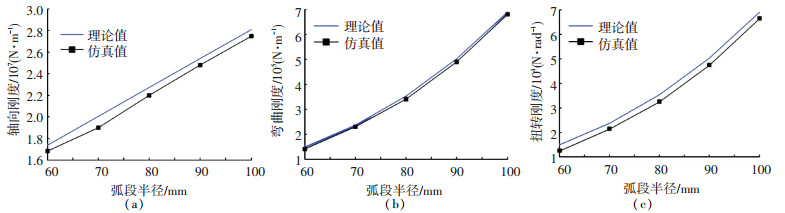图 14 弹性伸杆刚度与弧段半径的关系 Fig. 14 Relationship between stiffness of elastic extension bar and radius of arc segment 由图 14可知，当弧段半径增加20%时，弯曲刚度增大66.7%，扭转刚度增大53.3%，轴向刚度增大25.7%.其中轴向刚度随弧段半径的增长基本呈线性关系，而弯曲刚度和扭转刚度随弧段半径的增长呈指数关系，因此增大弧段半径可以显著提高弹性伸杆的弯曲刚度和扭转刚度.除此之外，发现理论值略大于仿真值，原因是为了便于计算，理论模型忽略了各向异性对材料刚度的影响.
3.2 铺层数量对刚度的影响分别对铺层数量为4层，6层，8层，10层和12层，铺层厚度为0.1 mm，铺层角度分别为[0 45-45 90]，[0 45-45 90 45-45]，[0 45-45 90 0 45-45 90]，[0 45-45 90 0 45-45 90 45-45]，[0 45-45 90 0 45-45 90 0 45-45 90]的弹性伸杆进行仿真分析.
通过仿真可知，随着铺层数量的增加，弹性伸杆的变形量逐渐减小，说明弹性伸杆的轴向刚度随着铺层数量的增加而增加，轴向刚度与铺层数量的关系如图 15(a)所示.同样，弯曲刚度与扭转刚度随铺层数量的变化关系如图 15(b)和15(c)所示.
Fig. 15
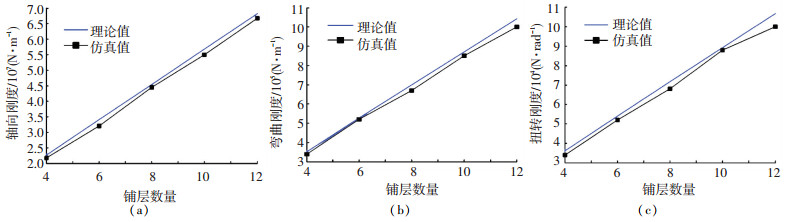图 15 弹性伸杆刚度与铺层数量的关系 Fig. 15 Relationship between the stiffness of elastic extension bar and layering quantity 由图 15可知，当铺层数量每增加2层，弯曲刚度增大60.6%，轴向刚度增加50%，扭转刚度增加48.6%，因此通过增加铺层数量也能够大幅增加弹性伸杆的刚度.
3.3 中心距对刚度的影响前面分析的弹性伸杆属于上下两片肋片同心的情况，除此之外，还有一类上下肋片不同心的弹性伸杆，即肋片之间存在中心距d，如图 16所示.下面将对d=0，d=10，d=20，d=30和d=40五种弹性伸杆的刚度进行仿真分析.
Fig. 16
图 16 不同中心距的弹性伸杆示意图 Fig. 16 Schematic diagram of elastic extension bar with different center distances 仿真结果如图 17所示，弹性伸杆的轴向刚度、弯曲刚度和扭转刚度均随着中心距d的增大而增大，当中心距d增加了40 mm时，弯曲刚度增加了13.9%，扭转刚度增加了13.3%，轴向刚度增加了5.5%.但与弧段半径和铺层数量对弹性伸杆刚度的影响相比，中心距对弹性伸杆刚度的影响较小.
Fig. 17
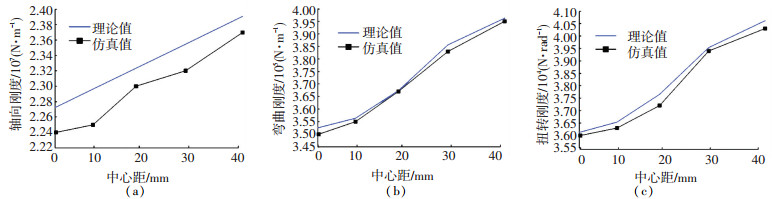图 17 弹性伸杆刚度与中心距的关系 Fig. 17 Relationship between stiffness of elastic extension bar and center distance 4 结论1) 通过拉平与压平两种方式都能够使弹性伸杆从鼓起状态平整地变为扁平状态，两个过程中所需要的能量都在5J左右且变化趋势基本一致，外载荷均是越来越大，拉平与压平过程中的最大载荷分别为118.5 N和73.2 N，因此压平更容易.
2) 弧段半径对弹性伸杆的刚度影响较大.当弧段半径增加20%时，弯曲刚度增大66.7%，扭转刚度增大53.3%，轴向刚度增大25.7%.
3) 铺层数量对弹性伸杆的刚度影响也较大.铺层数量每增加2层，弯曲刚度增大60.6%，轴向刚度增加50%，扭转刚度增加48.6%.
4) 中心距对弹性伸杆的刚度影响较小.当中心距增加了40 mm时，弯曲刚度增加了13.9%，扭转刚度增加了13.3%，轴向刚度增加了5.5%.
参考文献
[1] 陈务军. 空间可展结构体系与分析导论[M]. 北京: 中国宇航出版社, 2006: 1.
CHEN Wujun. Introduction to the system and analysis of spatial developable structures[M]. Beijing: China Aerospace Press, 2006: 1.
[2] WOODS A JR, WADE W. An approach toward design of large diameter offset-fed antennas[C]. //The 20th AIAA Structures Conference. Chicago: AIAA, 1979
[3] LEMAK M E, BANERJEE A K. Comparison of simulation with test of deployment of a wrapped-rib antenna[C]//The 35th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Orlando: AIAA, 1994
[4] WILLIAMS R B, AGNES G S. Lightweight deployable sunshade concepts for passive cooling for space-based telescopes[C]//The 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Schaumburg: AIAA, 2008
[5] 谢超, 严飙, 刘钰, 等. 大型星载薄膜天线高精度制造技术研究[J]. 载人航天, 2018, 24(1): 79.
XIE Chao, YAN Biao, LIU Yu, et al. Research on high-precision manufacturing technology of large space-borne thin film antenna[J]. Manned Spaceflight, 2018, 24(1): 79. DOI: 10.3969/j.issn.1674-5825.2018.01.013
[6] THOMAS W M. Historical perspectives on the development of deployable reflectors[C]//The 50th AIAA /ASME /ASCE /AHS/ASC Structures, Structural Dynamics, and Materials Conference. Palm Springs: AIAA, 2009
[7] LIU R, GUO H, LIU R, et al. Shape accuracy optimization for cablerib tension deployable antenna structure with tensioned cables[J]. Acta Astronautica, 2017, 140: 6.
[8] 康雄建, 陈务军, 邱振宇, 等. 空间薄壁CFRP弹性伸杆模态试验及分析[J]. 振动与冲击, 2017, 36(15): 215.
[9] 蔡祈耀, 陈务军, 张大旭, 等. 空间薄壁CFRP弹性伸杆悬臂屈曲分析及试验[J]. 上海交通大学学报, 2017, 36(1): 145.
KANG Xiongjian, CHEN Wujun, QIU Zhenyu, et al. Modal test and analysis of space thin-walled CFRP pods[J]. Vibration and Shock, 2017, 36(15): 215.
[10] 李瑞雄, 陈务军, 付功义. 缠绕肋缠绕过程试验及力学行为分析[J]. 工程力学, 2016, 50(11): 332.
CAI Jingyao, CHEN Wujun, ZHANG Daxu, et al. Buckling analysis and test of space thin-walled CFRP pods[J]. Journal of Shanghai Jiaotong University, 2016, 50(1): 145.
[11] 李瑞雄, 陈务军, 付功义. 透镜式薄壁CFRP管空间伸展臂轴压屈曲分析及试验[J]. 宇航学报, 2012, 29(08): 1164.
LI Ruixiong, CHEN Wujun, FU Gongyi. Experimental and mechanical behavior analysis of wound[J]. Engineering Mechanics, 2012, 29(11): 332.
[12] 李瑞雄, 陈务军, 付功义, 等. 透镜式缠绕肋压扁缠绕过程数值模拟及参数研究[J]. 工程力学, 2012, 33(11): 244.
LI Ruixiong, CHEN Wujun, FU Gongyi. Axial compression buckling analysis and test of lens thin-walled CFRP tubes with spatial extension[J]. Journal of Aeronautics and Astronautics, 2012, 33(08): 1164.
[13] 李瑞雄, 陈务军, 付功义, 等. 透镜式缠绕肋压扁缠绕过程数值模拟分析[J]. 宇航学报, 2011, 28(01): 224.
LI Ruixiong, CHEN Wujun, FU Gongyi, et al. Numerical simulation and parameter study of filament-wound flattened winding process[J]. Engineering Mechanics, 2011, 28(11): 244.
[14] LI Ruixiong, CHEN Wujun, FU Gongyi, et al. Numerical simulation and analysis of flattened winding process in lens-wound[J]. Acta Astronautica Sinica, 2011, 32(01): 224.
[15] 刘锦贤, 陈务军, 房光强, 等. 碳纤维薄壁杆件空间热辐射分析[J]. 四川兵工学报, 2012, 33(11): 124.
[16] LIU Jinxian, CHEN Wujun, FANG Guangqiang, et al. Analysis of space thermal radiation of carbon fiber thin-walled members[J]. Journal of military Science and Technology of Sichuan, 2012, 33(11): 124.
[17] LEIPOLD M, RUINGE H, SICKINGER C. Large SAR membrane antennas with light weight deployable booms[C]// 28th ESA Antenna Workshop on Space Antenna Systems and Technologies. Noordwijk: ESA/ESTEC, 2005
[18] IRWIN R J, VEEN J A V, BUCHNER-SANTOS E, et al. Low-mass deployable spacecraft booms[J]. AIAA Paper, 2010, 8926: 2010.
[19] CHU Z Y, LEI Y A. Design theory and dynamic analysis of a deployable boom[J]. Mechanism and Machine Theory, 2014, 71: 126-141. DOI:10.1016/j.mechmachtheory.2013.09.009
