刘海波1,王和平1,2,孙俊磊1
(1.西北工业大学 航空学院,西安 710072; 2.西北工业大学 深圳研究院,广东 深圳 518057)
摘要:
为研究存在复合干扰的非常规布局菱形翼长航时侦察无人机姿态控制问题,针对系统存在强耦合、非线性、多输入多输出等特点,结合滑模变结构控制理论、分数阶微积分理论、自适应控制理论、新型基于非线性fal函数的快速趋近律及扩张状态干扰观测器,提出了一种包含干扰观测器的自适应分数阶微积分滑模控制方法.首先,为降低控制器的超调现象,结合分数阶微积分理论,利用分数阶微积分算子信息记忆和遗忘的特性,设计了分数阶微积分滑模面,以柔化控制器的输出,使得控制器超调现象得到良好的控制. 其次,为改善传统趋近律收敛时间长,抖震严重等弱点,利用fal函数“小误差大增益,大误差小增益”良好的特性,将非线性fal函数引入到趋近律的设计中,提出了一种可以快速收敛的新型趋近律,平滑无抖震地加快了系统收敛速度. 最后,由于建模误差和外部干扰的存在,使用扩张状态干扰观测器观测出等效干扰并在控制器中引入等效的补偿. 数值仿真结果表明,所提控制方法具有很强的鲁棒性,达到了理想的控制效果.
关键词: 菱形翼 自适应 分数阶 滑模控制 趋近律 fal函数 干扰观测器
DOI：10.11918/201901087
分类号:V249.122+
文献标识码:A
基金项目:民机专项(MIZ-2015-F-009); 陕西省科技统筹(2015KTCQ01-78)
Attitude control for diamond joined-wing unmanned aerial vehicle based on adaptive fractional sliding mode control
LIU Haibo1,WANG Heping1,2,SUN Junlei1
(1.College of Aeronautics, Northwestern Polytechnical University, Xian 710072, China; 2.Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen 518057, Guangdong, China)
Abstract:
For the attitude control of diamond joined-wing unmanned aerial vehicle (UAV) with unknown external disturbances, the system has the characteristics of strong coupling, non-linearity, multi-input, and multi-output. Combining with sliding mode variable structure control theory, fractional calculus theory, adaptive control theory, new reaching law based on Fal function, and extended state disturbance observer, an adaptive fractional sliding mode control method was proposed. First, by introducing the fractional calculus theory and utilizing the genetic and memory characteristics of fractional calculus operators, the sliding surface of fractional calculus was designed to soften the controller output and control the overshoot of the controller. Then, in order to improve the weaknesses of traditional reaching law such as long convergence time and serious chattering, a new reaching law was proposed based on the Fal function, which could realize fast convergence without chattering. Finally, since there were modeling errors and external disturbances in the control system, the extended state observer was used to estimate and compensate the combined disturbance online. Simulation results show that the proposed control method had strong robustness and achieved ideal control effect.
Key words: diamond joined-wing adaptive fractional sliding mode control reaching law Fal function disturbance observer
刘海波, 王和平, 孙俊磊. 菱形翼布局无人机自适应分数阶滑模姿态控制[J]. 哈尔滨工业大学学报, 2020, 52(4): 84-91. DOI: 10.11918/201901087.
LIU Haibo, WANG Heping, SUN Junlei. Attitude control for diamond joined-wing unmanned aerial vehicle based on adaptive fractional sliding mode control[J]. Journal of Harbin Institute of Technology, 2020, 52(4): 84-91. DOI: 10.11918/201901087.
基金项目 民机专项(MIZ-2015-F-009);陕西省科技统筹(2015KTCQ01-78) 作者简介 刘海波(1981—), 男, 博士研究生;
王和平(1955—), 男, 教授, 博士生导师 通信作者 王和平, flight_control@qq.com 文章历史 收稿日期: 2019-01-14
Abstract Full text Figures/Tables PDF
菱形翼布局无人机自适应分数阶滑模姿态控制
刘海波1, 王和平1,2
, 孙俊磊1 1. 西北工业大学 航空学院, 西安 710072;
2. 西北工业大学 深圳研究院, 广东 深圳 518057
收稿日期: 2019-01-14
基金项目: 民机专项(MIZ-2015-F-009);陕西省科技统筹(2015KTCQ01-78)
作者简介: 刘海波(1981—), 男, 博士研究生; 王和平(1955—), 男, 教授, 博士生导师
通信作者: 王和平, flight_control@qq.com
摘要: 为研究存在复合干扰的非常规布局菱形翼长航时侦察无人机姿态控制问题, 针对系统存在强耦合、非线性、多输入多输出等特点, 结合滑模变结构控制理论、分数阶微积分理论、自适应控制理论、新型基于非线性fal函数的快速趋近律及扩张状态干扰观测器, 提出了一种包含干扰观测器的自适应分数阶微积分滑模控制方法.首先, 为降低控制器的超调现象, 结合分数阶微积分理论, 利用分数阶微积分算子信息记忆和遗忘的特性, 设计了分数阶微积分滑模面, 以柔化控制器的输出, 使得控制器超调现象得到良好的控制.其次, 为改善传统趋近律收敛时间长, 抖震严重等弱点, 利用fal函数“小误差大增益, 大误差小增益”良好的特性, 将非线性fal函数引入到趋近律的设计中, 提出了一种可以快速收敛的新型趋近律, 平滑无抖震地加快了系统收敛速度.最后, 由于建模误差和外部干扰的存在, 使用扩张状态干扰观测器观测出等效干扰并在控制器中引入等效的补偿.数值仿真结果表明, 所提控制方法具有很强的鲁棒性, 达到了理想的控制效果.
关键词: 菱形翼 自适应 分数阶 滑模控制 趋近律 fal函数 干扰观测器
Attitude control for diamond joined-wing unmanned aerial vehicle based on adaptive fractional sliding mode control
LIU Haibo1, WANG Heping1,2
, SUN Junlei1 1. College of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China;
2. Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen 518057, Guangdong, China
Abstract: For the attitude control of diamond joined-wing unmanned aerial vehicle (UAV) with unknown external disturbances, the system has the characteristics of strong coupling, non-linearity, multi-input, and multi-output. Combining with sliding mode variable structure control theory, fractional calculus theory, adaptive control theory, new reaching law based on Fal function, and extended state disturbance observer, an adaptive fractional sliding mode control method was proposed. First, by introducing the fractional calculus theory and utilizing the genetic and memory characteristics of fractional calculus operators, the sliding surface of fractional calculus was designed to soften the controller output and control the overshoot of the controller. Then, in order to improve the weaknesses of traditional reaching law such as long convergence time and serious chattering, a new reaching law was proposed based on the Fal function, which could realize fast convergence without chattering. Finally, since there were modeling errors and external disturbances in the control system, the extended state observer was used to estimate and compensate the combined disturbance online. Simulation results show that the proposed control method had strong robustness and achieved ideal control effect.
Keywords: diamond joined-wing adaptive fractional sliding mode control reaching law Fal function disturbance observer
菱形翼布局无人机的结构特点是前翼后掠后翼前掠, 后翼的翼稍与前翼的翼稍或者翼中相连接, 俯视来看, 前翼与后翼联结形成的框架构成了一个菱形, 所以命名为菱形翼布局飞行器, 一些文献将其称为盒式翼或者联翼布局飞机.菱形翼布局飞行器, 由于其特有的后翼对前翼的支撑特点, 使飞行器机翼的结构刚度更大, 可以显著减少前翼的弯曲变形, 在不增加机翼结构强度的前提下, 有效增加升阻比, 减轻了结构质量, 通过合理布置, 飞行器的前翼附面层可以通过后翼向后输送, 有效降低了前翼翼尖涡强度.菱形翼由于具有4副机翼, 可以提供360°传感器探测覆盖, 将探测传感器天线安装在菱形布局的机翼内, 探测能力将得到大幅提升, 而飞机气动特性几乎没有受到任何影响, 因而菱形翼布局飞行器在侦察传感器飞行器的候选布局中具有得天独厚的优势.这种菱形翼无人机具有升阻比高、结构质量轻、隐身性能好等特点, 非常适用于高空长航时侦察飞行器, 但是由于采用了非常规气动布局, 它的气动特性要比常规布局飞行器复杂的多, 飞行控制难度也相应增加了许多.其姿态控制系统具有多输入多输出、非线性、强耦合等特点.在气动分析方面, 文献[1]通过数值模拟和理论分析, 研究了菱形翼布局无人机的气动特性和操纵面性能, 文献[2]针对菱形连翼布局飞行器的俯仰力矩非线性特性的产生机理进行了深入的研究.然而, 菱形连翼飞行器作为新型的非常规布局无人机, 相关飞行控制系统的研究非常稀少, 文献[3]针对菱形翼布局无人机按照小扰动假设采用线性化模型设计的PID控制器, 姿态指令跟踪也取得了良好的效果, 但是在存在建模误差以及外界复合干扰的情况下, 线性PID控制器的鲁棒性和指令跟踪精度是很难得到保证的.所以, 设计具有强鲁棒性的非线性控制器以克服不确定系统以及外部复合干扰对控制器性能的不利影响, 在菱形翼布局飞行器的理论研究和工程实践上都具有重要意义.
滑模变结构控制本质就是一种非线性控制方法, 通过设计滑模面, 强迫系统状态向滑模面趋近运动, 当系统状态进入滑动模态, 系统将与对象参数和外部扰动无关, 这就使得滑模控制器具有物理实现简单、响应迅速、对干扰不敏感等优良特点.近年来, 飞控系统设计中广泛地应用滑模变结构控制[4-9].滑模面函数通常由误差信号及其微积分的线性组合而成, 由于滑动面初始误差的积分往往会延长系统的调整时间, 甚至恶化系统的暂态性能, 因此采用分数阶微积分算子的记忆及遗传特性来衰减作用于被控系统的能量, 以降低整数阶微积分滑模面超调现象.近年来, 分数阶微积分理论在滑模控制中的应用得到了广泛的研究.文献[10]设计了一种新型分数阶滑模控制器, 用于永磁同步电动机的高精度速度控制; 文献[11]通过分数阶滑模控制器实现柔性机器人与未知环境相互作用的鲁棒阻抗控制; 文献[12]基于滑模控制和分数阶理论, 提出了一种适用于变速风力机的新型控制策略; 文献[13-14]以混沌系统和超混沌系统的同步问题作为研究对象, 应用分数阶滑模控制做了大量研究; 文献[15]针对水下液压机械手多自由度控制问题, 提出一种实用的连续分数阶非奇异端滑模控制方法; 文献[16]针对一类具有不匹配扰动的前馈非线性系统, 提出了一种新的分数阶反演滑模控制方法; 文献[17]提出了一种基于分数阶微积分滑模面的双油箱混合动力系统液位滑模控制器; 文献[18]使用分数阶自适应积分滑模控制方案, 进行了六自由度机器人的轨迹跟踪控制.滑动模态运动涉及两个过程:趋近运动和滑模运动.为了改善趋近运动的动态品质高为炳[19]提出趋近律的概念, 为了进一步加快传统的趋近律的收敛速度和消弱抖震, 本文将非线性fal函数引入到趋近律的设计中, 使新型趋近律提高了系统状态的收敛速度, 抖震也得到了有效抑制.
由于菱形翼长航时侦察无人机姿态模型存在建模不确定项和外界干扰项存在, 当系统的复合干扰比较大时, 其控制精度及控制器鲁棒性并不理想, 本文采用自抗扰控制技术[20]的核心部分, 扩张状态观测器对系统中的复合干扰进行实时的估计, 它的主要思想是将控制系统的输入输出选取为简单的积分串联标准型, 将建模中的不确定项和外界复合干扰与精确建模相异的部分视为系统的“总和扰动”, 采用扩张状态干扰观测器对总和扰动进行估计, 并将估计值对控制系统进行补偿, 从而抑制了复合干扰对控制系统的影响, 提高了控制系统的鲁棒性.综合上述分析, 本文设计了含扩张状态干扰观测器的自适应分数阶微积分滑模控制器, 并给出了相关稳定性证明, 通过数值仿真, 所提控制方案能够有效抑制复合干扰对系统的不利影响, 使得飞行器可以精确, 迅速地跟踪上控制指令.
1 菱形翼长航时侦察无人机姿态模型本文研究的菱形翼长航时侦察无人机如图 1所示, 该无人机的俯仰控制通道、滚转控制通道与偏航控制通道分别通过相应的控制舵面偏转来实现.
Fig. 1
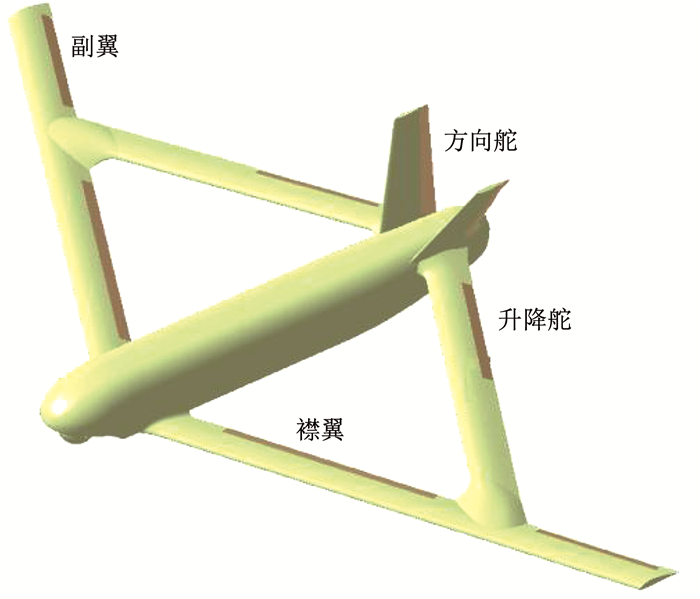图 1 菱形翼无人机结构示意 Fig. 1 Schematic of the diamond joined-wing UAV configuration 考虑到菱形翼长航时侦察无人机建模不确定部分和外部干扰, 得到如下的多输入多输出菱形翼长航时无人机姿态动力学模型:
$\left\{ {\begin{array}{*{20}{l}}{\mathit{\boldsymbol{W}} = {\mathit{\boldsymbol{F}}_1}(\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}) + {\mathit{\boldsymbol{G}}_1}(\mathit{\boldsymbol{ \boldsymbol{\varOmega} }})\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{T}}_{d\mathit{\Omega }}},}\\{\mathit{\boldsymbol{\dot \omega }} = {\mathit{\boldsymbol{F}}_2}(\mathit{\boldsymbol{\omega }}) + {\mathit{\boldsymbol{G}}_2}(\mathit{\boldsymbol{\omega }}){\mathit{\boldsymbol{M}}_c} + {\mathit{\boldsymbol{T}}_{d\omega }},}\\{y = \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}.}\end{array}} \right.$
式中:Ω为姿态角向量, 包含迎角α、侧滑角β和滚转角μ; ω为姿态角速度向量, 包含滚转角速率p、俯仰角速率q和偏航角速率r; MC为控制力矩向量, 包含滚转力矩lc、俯仰mc和偏航力矩nc.F1=[fα fβ fμ]T、F2=[fp fq fr]T分别为系统状态函数; G1∈R3×3、G2∈R3×3分别为系统控制矩阵, 其中:
${f_\alpha } = \frac{1}{{M{V_\alpha }\cos \beta }}\left[ { - L + Mg\cos {\gamma _\alpha }\cos \mu - T\sin \alpha } \right],$
${f_\beta } = \frac{1}{{M{V_\alpha }}}\left[ {Y + Mg\cos {\gamma _\alpha }\sin \mu - T\sin \beta \cos \alpha } \right],$
$\begin{array}{l}{f_\mu } = \frac{1}{{M{V_\alpha }}}\left[ {L\left( {\tan {\gamma _\alpha }\sin \mu + \tan \beta } \right) - } \right.\\\;\;\;\;\;\;\;\;Mg\cos {\gamma _\alpha }\cos \mu \tan \beta + \\\;\;\;\;\;\;\;\;\;T\sin \alpha \left( {\tan {\gamma _\alpha }\sin \mu + \tan \beta } \right) - \\\;\;\;\;\;\;\;\;\;T\cos \alpha \tan {\gamma _\alpha }\cos \mu \sin \beta + \\\;\;\;\;\;\;\;\;\;\left. {Y\tan {\gamma _\alpha }\cos \mu \cos \beta } \right],\end{array}$
${f_p} = \frac{{\left( {{I_{xx}} - {I_y} + {I_z}} \right)pq + \left[ {{I_{xz}}\left( {{I_y} - {I_{xx}}} \right) - I_{xz}^2} \right]qr}}{{{I_{xx}}{I_{xz}} - I_{xz}^2}},$
${f_q} = \frac{{\left( {{I_{xz}} - {I_{xx}}} \right)pr + {I_{xz}}\left( {{r^2} - {p^2}} \right)}}{{{I_{yy}}}},$
${f_r} = \frac{{\left[ {{I_{xx}}\left( {{I_{xx}} - {I_y}} \right) + I_{xz}^2} \right]pq - {I_{xz}}\left( {{I_{xx}} - {I_{yy}} + {I_{xz}}} \right)pr}}{{{I_{xx}}{I_{xz}} - I_{xz}^2}},$
${\mathit{\boldsymbol{G}}_1} = \left[ {\begin{array}{*{20}{c}}{ - \tan \beta \cos \alpha }&1&{ - \tan \beta \sin \alpha }\\{\sin \alpha }&0&{ - \cos \alpha }\\{\sec \beta }&0&{\sec \beta \sin \alpha }\end{array}} \right],$
${\mathit{\boldsymbol{G}}_2} = \left[ {\begin{array}{*{20}{c}}{\frac{{{I_{zz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}&0&{\frac{{{I_{xz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}\\0&{\frac{1}{{{I_{yy}}}}}&0\\{\frac{{{I_{xz}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}&0&{\frac{{{I_{xx}}}}{{{I_{xx}}{I_{zz}} - I_{xz}^2}}}\end{array}} \right].$
TdΩ、Tdω为建模误差及外部干扰等姿态控制系统的复合干扰, 具体表达式为:
${\mathit{\boldsymbol{T}}_{d\mathit{\Omega }}} = \Delta {\mathit{\boldsymbol{F}}_1} + \Delta {\mathit{\boldsymbol{G}}_1}\mathit{\boldsymbol{\omega }} + {\mathit{\boldsymbol{d}}_1},$
${\mathit{\boldsymbol{T}}_{d\omega }} = \Delta {\mathit{\boldsymbol{F}}_2} + \Delta {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{M}}_c} + {\mathit{\boldsymbol{d}}_2}.$
式中:ΔF1、ΔF2、ΔG1、ΔG2分别为建模误差; d1、d2分别为外部干扰.
因为系统中存在复合干扰, 控制系统的设计目的是通过调整舵面偏角使菱形翼布局无人机跟踪上姿态角指令.利用backstepping控制的思想, 首先设计姿态角控制器, 以姿态角控制环的输出作为角速率的虚拟控制量, 然后设计姿态角速率控制器产生舵面控制力矩.
2 新型快速趋近律设计为了加快趋近运动的收敛速度和消弱抖震, 本文提出一种基于非线性fal函数设计的新型滑模变结构控制趋近律, 有如下形式:
${{\dot S}_i} = - {k_1}{\rm{fal}}\left( {{S_i},a,b} \right) - {k_2}{\rm{\cosh}} \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right).$ (1)
式中:k1、k2分别为待设计增益参数且均大于0;cosh|Si|sgn(Si)为双曲余弦函数; Si为滑模面函数, fal函数是自抗扰控制提出的一种非线性函数, 具体表达式如下:
${\rm{fal}}\left( {{S_i},a,b} \right) = \left\{ {\begin{array}{*{20}{l}}{{{\left| {{S_i}} \right|}^a}{\rm{sgn}}\left( {{S_i}} \right),\left| {{S_i}} \right| > b;}\\{\frac{{{S_i}}}{{{b^{1 - a}}}},\left| {{S_i}} \right| \le b.}\end{array}} \right.$ (2)
fal函数具有“小误差大增益, 大误差小增益”的良好品质, 将fal函数引入到趋近律的设计中, 可以消除传统趋近律带来的抖震, 提高趋近运动品质.式(2)中, 当|Si|≤b时, 系统状态与滑模面距离较近, 新型趋近律中－k1fal(Si, a, b)为光滑连续函数, 可以有效地降低控制输入的抖震现象, 保证了系统平滑地进入滑动模态, 当|Si|>b时, 系统状态与滑模面距离较远k2cosh|Si|sgn(Si)项可以加大趋近滑模面的速度.利用fal非线性函数项与双曲余弦函数的优点, 保证了趋近运动的品质, 采用基于非线性函数fal函数的快速趋近律, 有如下定理成立.
定理1??对于新型包含非线性fal函数的快速趋近律, 滑模面Si及其导数
证明??由式(1)可得:
$\begin{array}{l}{{\dot S}_i} = - {k_1}{\rm{fal}}\left( {{S_i},a,b} \right) - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right) = \\\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{l}}{ - {k_1}{{\left| {{S_i}} \right|}^a}{\rm{sgn}}\left( {{S_i}} \right) - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right),\left| {{S_i}} \right| > b;}\\{ - \frac{{{k_1}{S_i}}}{{{b^{1 - a}}}} - {k_2}\cosh \left| {{S_i}} \right| {\rm{sgn}} \left( {{S_i}} \right),\left| {{S_i}} \right| \le b.}\end{array}} \right.\end{array}$
当|Si|>b时, 有
${{\dot S}_i} = - {k_1}{\left| {{S_i}} \right|^a}{\rm{sgn}}\left( {{S_i}} \right) - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right),$
可得:
${\rm{d}}{t_i} = \frac{{{\rm{d}}{S_i}}}{{ - {k_1}{{\left| {{S_i}} \right|}^a}{\rm{sgn}}\left( {{S_i}} \right) - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right)}}.$ (3)
对式(3)两边积分, 上、下限分别为Si(0)和bsgn(Si(0)), 即
$\begin{array}{l}{t_i} = \int\limits_{{S_i}\left( 0 \right)}^{b{\mathop{\rm sgn}} \left( {{S_i}\left( 0 \right)} \right)} {\frac{1}{{ - {k_1}{{\left| {{S_i}} \right|}^a}{\rm{sgn}}\left( {{S_i}} \right) - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right)}}{\rm{d}}{S_i}} = \\\;\;\;\;\;\int\limits_b^{\left| {{S_i}\left( 0 \right)} \right|} {\frac{1}{{{k_1}S_i^a + {k_2}\cosh {S_i}}}{\rm{d}}{S_i}} \le \\\;\;\;\;\;\int\limits_b^{\left| {{S_i}\left( 0 \right)} \right|} {\frac{1}{{{k_1}S_i^a}}{\rm{d}}{S_i}} = \frac{{\left| {{S_i}\left( 0 \right)} \right| - {b^{1 - a}}}}{{{k_1}\left( {1 - a} \right)S_i^a}}.\end{array}$
结果表明, 系统状态在有限时间内收敛到|Si|=b.
当滑模面继续由|Si|=b趋近到滑模面Si=0的过程中, 下式成立:
${{\dot S}_i} = - \frac{{{k_1}{S_i}}}{{{b^{1 - a}}}} - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right),$
可得:
${\rm{d}}{t_i} = \frac{{{\rm{d}}{S_i}}}{{ - \frac{{{k_1}{S_i}}}{{{b^{1 - a}}}} - {k_2}\cosh \left| {{S_i}} \right|{\rm{sgn}}\left( {{S_i}} \right)}}.$ (4)
对式(4)从Si(0)到0进行积分, 可得:
$\begin{array}{l}{t_i} = \int\limits_{{S_i}\left( 0 \right)}^0 {\frac{1}{{ - \frac{{{k_1}{S_i}}}{{{b^{1 - a}}}} - {k_2}\cosh \left| {{S_i}} \right| {\rm{sgn}} \left( {{S_i}} \right)}}{\rm{d}}{S_i}} = \\\;\;\;\;\;\;\int\limits_0^{\left| {{S_i}\left( 0 \right)} \right|} {\frac{1}{{\frac{{{k_1}{S_i}}}{{{b^{1 - a}}}} + {k_2}\cosh {S_i}}}{\rm{d}}{S_i}} \le \\\;\;\;\;\;\;\int\limits_0^{\left| {{S_i}\left( 0 \right)} \right|} {\frac{1}{{{k_2}\cosh {S_i}}}{\rm{d}}{S_i}} = \\\;\;\;\;\;\;\int\limits_0^{\left| {{S_i}\left( 0 \right)} \right|} {\frac{2}{{{k_2}\left( {{{\rm{e}}^{{S_i}}} + {{\rm{e}}^{ - {S_i}}}} \right)}}{\rm{d}}{S_i}} = \\\;\;\;\;\;\;\frac{2}{{{k_2}}}\left[ {\arctan \left( {{{\rm{e}}^{\left| {{S_i}\left( 0 \right)} \right|}}} \right) - \arctan \left( {{{\rm{e}}^0}} \right)} \right] \le \frac{\pi }{{{k_2}}},\end{array}$
即k2>π时, 在有限时间内, 系统进入滑模模态, 当Si=0时
3 含扩张状态干扰观测器的姿态角回路分数阶滑模控制律设计 3.1 自适应分数阶微积分滑模控制器设计传统整数阶微积分型滑模面设计为
$\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{S}}_\mathit{\Omega }} = {e_\mathit{\Omega }} + {\lambda _1}{{\dot e}_\mathit{\Omega }} + {\lambda _2}\int\limits_0^t {{e_\mathit{\Omega }}\left( \tau \right){\rm{d}}\tau } ,}\\{{\lambda _1},{\lambda _2} > 0.}\end{array}$ (5)
由式(5)可以看出, 当使用传统整数阶微积分滑模面时, 在所有时刻对系统误差的积分权重是固定的, 当系统误差比较大时, 过大初始误差的积分会导致控制系统超调比较大, 为了能够有效提高控制精度, 减小超调, 本文将分数阶微积分算子引入到整数阶微积分滑模面的设计中, 依据Caputo型分数阶微积分定义:
$_{{t_0}}\mathit{\boldsymbol{D}}_t^{ - \eta }{e_\mathit{\Omega }}\left( \tau \right) = \frac{1}{{\mathit{\Gamma }\left( \eta \right)}}\int\limits_{{t_0}}^t {\mathit{\Xi }\left( {t - \tau } \right){e_\mathit{\Omega }}(\tau ){\rm{d}}\tau } .$
$\left\{ {\begin{array}{*{20}{l}}{{\mathit{\boldsymbol{S}}_\mathit{\Omega }} = {\mathit{\boldsymbol{e}}_\mathit{\Omega }} + {\lambda _1}{D^{{\eta _1}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }} + {\lambda _2}{D^{ - {\eta _2}}}{e_\mathit{\Omega }},}\\{{\mathit{\boldsymbol{q}}_\mathit{\Omega }} = \frac{1}{{{\vartheta _\mathit{\Omega }}}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{c}}} - {\lambda _1}{D^{{\eta _1}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }} - {\lambda _2}{D^{ - {\eta _2}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }}} \right),}\end{array}} \right.$
则
自适应分数阶微积分滑模控制律设计为
$\begin{array}{l}{\mathit{\boldsymbol{\omega }}_{\rm{c}}} = - \mathit{\boldsymbol{G}}_1^{ - 1}\left( {{\mathit{\boldsymbol{F}}_1} + {\mathit{\boldsymbol{T}}_{d\mathit{\Omega }}} - {{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_{\rm{c}}} + {\lambda _1}{D^{1 + {\eta _1}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }} + } \right.\\\;\;\;\;\;\;\;{\lambda _2}{D^{1 - {\eta _2}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }} + {k_1}{\rm{fal}}\left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }},a,b} \right) + \\\;\;\;\;\;\;\;\left. {{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) + {{\hat \vartheta }_\mathit{\Omega }}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}} \right).\end{array}$
式中:λΩ, 1, λΩ, 2, kΩ, 1, kΩ, 2∈R+; TdΩ为待估计的复合干扰.
3.2 扩张状态干扰观测器建模误差和外界干扰对于菱形翼高空长航时侦察无人机姿态角控制回路系统的影响非常大, 本文在控制器中使用扩张状态干扰观测器对系统中的复合干扰进行实时估计, 观测器设计如下:
$\left\{ \begin{array}{l}\mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }} = \mathit{\boldsymbol{ \boldsymbol{\hat \varOmega} }} - \mathit{\boldsymbol{ \boldsymbol{\varOmega} }},\\\mathit{\boldsymbol{ \boldsymbol{\dot {\hat \varOmega}} }} = {\mathit{\boldsymbol{F}}_1}\left( \mathit{\Omega } \right) + {\mathit{\boldsymbol{G}}_1}\left( \mathit{\Omega } \right)\mathit{\boldsymbol{\omega }} + {{\mathit{\boldsymbol{\hat T}}}_{d\mathit{\Omega }}} - {\mathit{\boldsymbol{\varepsilon }}_1}\mathit{\boldsymbol{ \boldsymbol{\tilde \varOmega} }},\\{{\mathit{\boldsymbol{\dot {\hat T}}}}_{d\mathit{\Omega }}}{\rm{ = }}{\varepsilon _2}{\rm{fal}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }},\sigma ,l} \right).\end{array} \right.$
式中:
综上所述, 含扩张状态干扰观测器的自适应分数阶微积分滑模控制律设计为
$\begin{array}{l}{\mathit{\boldsymbol{\omega }}_{\rm{c}}} = - \mathit{\boldsymbol{G}}_1^{ - 1}\left( {{\mathit{\boldsymbol{F}}_1} + {{\mathit{\boldsymbol{\hat T}}}_{d\mathit{\Omega }}} - {{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_{\rm{c}}} + {\lambda _1}{D^{1 + {\eta _1}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }} + } \right.\\\;\;\;\;\;\;{\lambda _2}{D^{1 - {\eta _2}}}{\mathit{\boldsymbol{e}}_\mathit{\Omega }} + {k_1}{\rm{fal}}\left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }},a,b} \right) + \\\left. {\;\;\;\;\;\;{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) + {{\hat \vartheta }_\mathit{\Omega }}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}} \right).\end{array}$ (6)
定理2??针对菱形翼高空长航时传感器无人机姿态控制系统, 选取分数阶微积分滑模面, 使用控制律式(6), 则有闭环控制系统的状态渐进稳定在滑模面上.
证明??定义姿态角控制回路Lyapunov函数为
${\mathit{\boldsymbol{V}}_1} = \frac{1}{2}\mathit{\boldsymbol{S}}_\mathit{\Omega }^2 + \frac{1}{{2\mathit{\pmb{\varpi}}}}{\mathit{\pmb{\tilde \vartheta}}} _\mathit{\Omega }^2,$
其中:
对V1求一阶导数为
$\begin{array}{l}{{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{S}}_\mathit{\Omega }}{{\mathit{\boldsymbol{\dot S}}}_\mathit{\Omega }} + \frac{1}{\mathit{\pmb{\varpi}}}{{\tilde {\mathit{\pmb{\vartheta}}} }_\mathit{\Omega }}{{\dot {\tilde {\mathit{\pmb{\vartheta}}}} }_\mathit{\Omega }} = \\\;\;\;\;\;\;{\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( {\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }} - {{\mathit{\pmb{\vartheta}}} _\mathit{\Omega }}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}} \right) + \frac{1}{\mathit{\pmb{\varpi}}}{{\tilde {\mathit{\pmb{\vartheta}}} }_\mathit{\Omega }}{{\dot {\tilde {\mathit{\pmb{\vartheta}}}} }_\mathit{\Omega }},\end{array}$
取自适应律为
${{\dot {\hat {\mathit{\pmb{\vartheta}}}} }_\mathit{\Omega }} = - \mathit{\pmb{\varpi}}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}{\mathit{\boldsymbol{S}}_\mathit{\Omega }},$
定义估计误差
$\begin{array}{l}{{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( {\mathit{\dot \Omega } - {\vartheta _\mathit{\Omega }}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}} \right) + \frac{1}{\mathit{\pmb{\varpi}}}{{\tilde {\mathit{\pmb{\vartheta}}} }_\mathit{\Omega }}\left( { - \mathit{\pmb{\varpi}}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) = \\\;\;\;\;\;\;{\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( {{{\mathit{\boldsymbol{\tilde T}}}_{d\mathit{\Omega }}} - {k_1}{\rm{fal}}\left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }},a,b} \right) - } \right.\\\;\;\;\;\;\;{k_2}\cosh \left| {{S_\mathit{\Omega }}} \right|{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) + \\\;\;\;\;\;\;\left. {{{\widehat {\mathit{\pmb{\vartheta}}} }_\mathit{\Omega }}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }} - {{\mathit{\pmb{\vartheta}}} _\mathit{\Omega }}{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}} \right) - {{\tilde {\mathit{\pmb{\vartheta}}} }_\mathit{\Omega }}\left( {{{\mathit{\boldsymbol{\dot q}}}_\mathit{\Omega }}{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right).\end{array}$
1) 当|SΩ|>b时,
$\begin{array}{*{20}{c}}{{{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( {{{\mathit{\boldsymbol{\tilde T}}}_{d\mathit{\Omega }}} - {k_1}{{\left| {{S_\mathit{\Omega }}} \right|}^a}{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) - } \right.}\\{\left. {{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right)} \right).}\end{array}$ (7)
由于有限时间内, 扩张状态观测器实现对干扰TdΩ的估计, 即在有限时间内有
$\begin{array}{l}{{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( { - {k_1}{{\left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|}^a}{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) - {k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right)} \right) = \\\;\;\;\;\;\;\; - {k_1}{\left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|^{1 + a}} - {k_2}\left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right| \le 0.\end{array}$
2) 当|SΩ|≤b时,
${{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( {{{\mathit{\boldsymbol{\tilde T}}}_{d\mathit{\Omega }}} - {k_1}\frac{{{\mathit{\boldsymbol{S}}_\mathit{\Omega }}}}{{{b^{1 - a}}}} - {k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right)} \right).$ (8)
由于有限时间内, 扩张状态观测器实现对干扰TdΩ的估计, 即在有限时间内有
$\begin{array}{*{20}{c}}{{{\mathit{\boldsymbol{\dot V}}}_1} = {\mathit{\boldsymbol{S}}_\mathit{\Omega }}\left( { - {k_1}\frac{{{\mathit{\boldsymbol{S}}_\mathit{\Omega }}}}{{{b^{1 - a}}}} - {k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right)} \right) = }\\{ - {k_1}\frac{{\mathit{\boldsymbol{S}}_\mathit{\Omega }^2}}{{{b^{1 - a}}}} - {k_2}\left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right| \le 0.}\end{array}$
综上所述, 采用自适应分数阶滑模控制律式(6), 姿态角闭环控制回路是稳定的.证毕.
4 姿态角速率回路自适应分数阶微积分自适应滑模控制律设计姿态角速率回路的控制器设计方法与姿态角回路类似, 直接给出设计结果, 对姿态角速率回路滑模面设计为
$\left\{ \begin{array}{l}{\mathit{\boldsymbol{S}}_\omega } = {\mathit{\boldsymbol{e}}_\omega } + {\lambda _1}{D^{{\eta _1}}}{\mathit{\boldsymbol{e}}_\omega } + {\lambda _2}{D^{ - {\eta _2}}}{\mathit{\boldsymbol{e}}_\omega },\\{\mathit{\boldsymbol{q}}_\omega } = \frac{1}{{{\vartheta _\omega }}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{c}}} - {\lambda _1}{D^{{\eta _1}}}{\mathit{\boldsymbol{e}}_\omega } - {\lambda _2}{D^{ - {\eta _2}}}{\mathit{\boldsymbol{e}}_\omega }} \right),\end{array} \right.$
则
自适应分数阶微积分滑模控制律设计为
$\begin{array}{l}{\mathit{\boldsymbol{M}}_{\rm{c}}} = - \mathit{\boldsymbol{G}}_2^{ - 1}\left( {{\mathit{\boldsymbol{F}}_2} + {{\mathit{\boldsymbol{\hat T}}}_{d\omega }} - {{\mathit{\boldsymbol{\dot w}}}_c} + {\lambda _1}{D^{1 + {\eta _1}}}{\mathit{\boldsymbol{e}}_\Omega } + } \right.\\\;\;\;\;\;\;\;\;{\lambda _2}{D^{1 - {\eta _2}}}{\mathit{\boldsymbol{e}}_\omega } + {k_1}{\rm{fal}}\left( {{\mathit{\boldsymbol{S}}_\omega },a,b} \right) + \\\;\;\;\;\;\;\;\;\left. {{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\omega }} \right|{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\omega }} \right) + {{\hat {\mathit{\pmb{\vartheta}}} }_\omega }{{\mathit{\boldsymbol{\dot q}}}_\omega }} \right),\end{array}$ (9)
式中各变量的定义与姿态角回路类似, 整体闭环系统稳定性分析如下.
定理3??针对无人机姿态控制系统, 使用控制律式(6)、式(9), 则有闭环控制系统的状态渐进稳定.
证明??定义姿态控制回路Lyapunov函数为
${\mathit{\boldsymbol{V}}_2} = {\mathit{\boldsymbol{V}}_1} + \frac{1}{2}\mathit{\boldsymbol{S}}_\omega ^2 + \frac{1}{{2\mathit{\pmb{\varpi}}}}\tilde {\mathit{\pmb{\vartheta}}} _\omega ^2.$
式中:
$\begin{array}{l}{{\mathit{\boldsymbol{\dot V}}}_2} = {{\dot V}_1} + {\mathit{\boldsymbol{S}}_\omega }{{\mathit{\boldsymbol{\dot S}}}_\omega } + \frac{1}{\mathit{\pmb{\varpi}}}{{\tilde {\mathit{\pmb{\vartheta}}} }_\omega }{{\dot {\tilde {\mathit{\pmb{\vartheta}}}} }_\omega },\\{{\mathit{\boldsymbol{\dot V}}}_2} = {{\mathit{\boldsymbol{\dot V}}}_1} + {\mathit{\boldsymbol{S}}_\omega }\left( {\mathit{\boldsymbol{\dot \omega }} - {{\mathit{\pmb{\vartheta}}} _\omega }{{\dot q}_\mathit{\boldsymbol{\omega }}}} \right) + \frac{1}{\mathit{\pmb{\varpi}}}{{\tilde {\mathit{\pmb{\vartheta}}} }_\omega }\left( { - \mathit{\pmb{\varpi}}{{\mathit{\boldsymbol{\dot q}}}_\omega }{\mathit{\boldsymbol{S}}_\omega }} \right) = \\\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\dot V}}}_1} + {\mathit{\boldsymbol{S}}_\omega }\left( {{{\mathit{\boldsymbol{\tilde T}}}_{d\omega }} - {k_1}{\rm{fal}}\left( {{\mathit{\boldsymbol{S}}_\omega },a,b} \right) - } \right.\\\;\;\;\;\;\;\;{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\omega }} \right|{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\omega }} \right) + \\\;\;\;\;\;\;\;\left( {{{\hat {\mathit{\pmb{\vartheta}}} }_\omega }{{\mathit{\boldsymbol{\dot q}}}_\omega } - {{\mathit{\pmb{\vartheta}}} _\omega }{{\mathit{\boldsymbol{\dot q}}}_\omega }} \right) - {{\tilde {\mathit{\pmb{\vartheta}}} }_\omega }\left( {{{\mathit{\boldsymbol{\dot q}}}_\omega }{\mathit{\boldsymbol{S}}_\omega }} \right).\end{array}$ (10)
由于扩张状态观测器在有限时间内实现对干扰Tdω的估计, 有
1) 当|Sω|>b时,
$\begin{array}{l}{{\mathit{\boldsymbol{\dot V}}}_2} = {{\mathit{\boldsymbol{\dot V}}}_1} + {\mathit{\boldsymbol{S}}_\omega }\left( {{{\mathit{\boldsymbol{\tilde T}}}_{d\omega }} - {k_1}{{\left| {{\mathit{\boldsymbol{S}}_\omega }} \right|}^a}{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\omega }} \right) - } \right.\\\;\;\;\;\;\;\left. {{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\omega }} \right|{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\omega }} \right)} \right) = {{\mathit{\boldsymbol{\dot V}}}_1} - {k_1}{\left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|^{1 + a}} - \\\;\;\;\;\;\;{k_2}\left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right|\cosh \left| {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right| \le 0.\end{array}$
2) 当|Sω|≤b时,
$\begin{array}{l}{{\mathit{\boldsymbol{\dot V}}}_2} = {{\mathit{\boldsymbol{\dot V}}}_1} + {\mathit{\boldsymbol{S}}_\omega }\left( {{{\mathit{\boldsymbol{\tilde T}}}_{d\omega }} - {k_1}\frac{{{\mathit{\boldsymbol{S}}_\omega }}}{{{b^{1 - a}}}} - } \right.\\\;\;\;\;\;\;\left. {{k_2}\cosh \left| {{\mathit{\boldsymbol{S}}_\omega }} \right|{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\omega }} \right)} \right) = \\\;\;\;\;\;\; - {k_1}\frac{{\mathit{\boldsymbol{S}}_\omega ^2}}{{{b^{1 - a}}}} - {k_2}\left| {{\mathit{\boldsymbol{S}}_\omega }} \right|\cosh \left| {{\mathit{\boldsymbol{S}}_\omega }} \right| \le 0.\end{array}$
综上所述, 通过设计自适应分数阶滑模控制律式(6)、式(9), 使得无人机的姿态控制系统满足了李雅普诺夫稳定性理论条件, 从而保证了系统具有全局意义下的渐进稳定性.证毕.
5 仿真与结果分析 5.1 仿真参数菱形翼长航时侦察无人机质量为25.8 kg, 机翼参考面积为1.63 m2, 平均气动弦长0.28 m, 转动惯量Ixx=8.227 kg·m2, Iyy=5.627 kg·m2, Izz=18.285 kg·m2, 惯性积Ixz=0.082 9 kg·m2, 空速Vα=25 m/s, 姿态角初始状态为α0=β0=μ0=0°, 姿态角速率p0=q0=r0=0 rad/s, 目标指令为αc=4°, μc=5°, βc=3°, 姿态角与姿态角速率分别施加幅值为0.05的高斯白噪声, 转动惯量施加10%不确定量, 设在仿真零时刻开始, 施加时变干扰力矩为
$\Delta M = \left[ \begin{array}{l}40\sin \left( {2t} \right) + 20\cos \left( {0.5t} \right)\\25\sin \left( {0.6t} \right) + 5\cos \left( {1.5t} \right)\\8\sin \left( {3t} \right) + 7\cos \left( t \right)\end{array} \right].$
为了验证本文的研究结论, 以菱形翼长航时侦察无人机作为被控对象, 分别采用以下两种控制方案对其姿态系统控制.
控制方案1??结合分数阶微积分滑模面, 基于非线性fal函数设计的新型趋近律, 扩张状态观测器设计的自适应分数阶微积分滑模控制器.
控制方案2??结合整数阶微积分滑模面, 传统指数趋近律, 扩张状态干扰观测器设计的整数阶微积分滑模控制器, 控制律设计如下:
$\begin{array}{*{20}{c}}{{\omega _{\rm{c}}} = - \mathit{\boldsymbol{G}}_1^{ - 1}\left( {{\lambda _1}{{\mathit{\boldsymbol{\dot e}}}_\mathit{\Omega }} + {\lambda _2}\int\limits_0^t {{\mathit{\boldsymbol{e}}_\mathit{\Omega }}(\tau ){\rm{d}}t} + {k_1}{\mathit{\boldsymbol{S}}_\mathit{\Omega }} + } \right.}\\{\left. {{k_2}sgn\left( {{\mathit{\boldsymbol{S}}_\mathit{\Omega }}} \right) + {\mathit{\boldsymbol{F}}_1} + {{\mathit{\boldsymbol{\hat T}}}_{d\mathit{\Omega }}} - {{\mathit{\boldsymbol{ \boldsymbol{\dot \varOmega} }}}_{\rm{c}}}} \right),}\end{array}$
$\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{M}}_{\rm{c}}} = - \mathit{\boldsymbol{G}}_2^{ - 1}\left( {{\lambda _1}{{\mathit{\boldsymbol{\dot e}}}_\omega } + {\lambda _2}\int\limits_0^t {{\mathit{\boldsymbol{e}}_\omega }(\tau ){\rm{d}}t} + {k_1}{\mathit{\boldsymbol{S}}_\omega } + } \right.}\\{\left. {{k_2}{\rm{sgn}}\left( {{\mathit{\boldsymbol{S}}_\omega }} \right) + {\mathit{\boldsymbol{F}}_2} + {{\mathit{\boldsymbol{\hat T}}}_{d\omega }} - {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{c}}}} \right).}\end{array}$
两种滑模控制方案所选取的控制器参数:控制方案1中λ1=diag{15, 15, 25}, λ2=diag{0.5, 0.5, 2.0}, k1=diag{10, 10, 10}, k2=diag{5, 5, 5}, a=0.6, b=0.02, η1=η2=0.2,
5.2 仿真结果分析针对存在复合干扰的菱形翼长航时侦察无人机姿态控制系统, 分别采用了自适应分数阶微积分滑模控制方法和整数阶微积分滑模控制方法两种控制方案进行了仿真, 仿真结果如图 2~4所示, 图 2为两种控制方案姿态角的响应曲线, 从图 2中可知, 迎角、侧滑角、滚转角控制系统存在建模误差和外加时变力矩干扰的情况下, 控制方案1自适应分数阶微积分滑模控制律的姿态角跟踪稳态精度比较高, 无超调, 收敛速度快, 鲁棒性较强.控制方案2整数阶微积分滑模控制律虽然跟踪上姿态角指令, 但是稳态精度不高, 姿态角震荡收敛, 这是由于常规整数阶微积分滑模的积分项是一阶整数积分, 这样就导致在整个控制过程中, 对误差的积分权重不变, 当存在较大初始误差时, 超调现象将不可避免.而控制方案1设计的自适应分数阶微积分滑模控制律, 由于引入了分数阶微积分算子, 其积分权重随着时间的推移而逐渐变小, 有效地抑制了积分饱和, 提高了控制系统的稳态性能.
Fig. 2
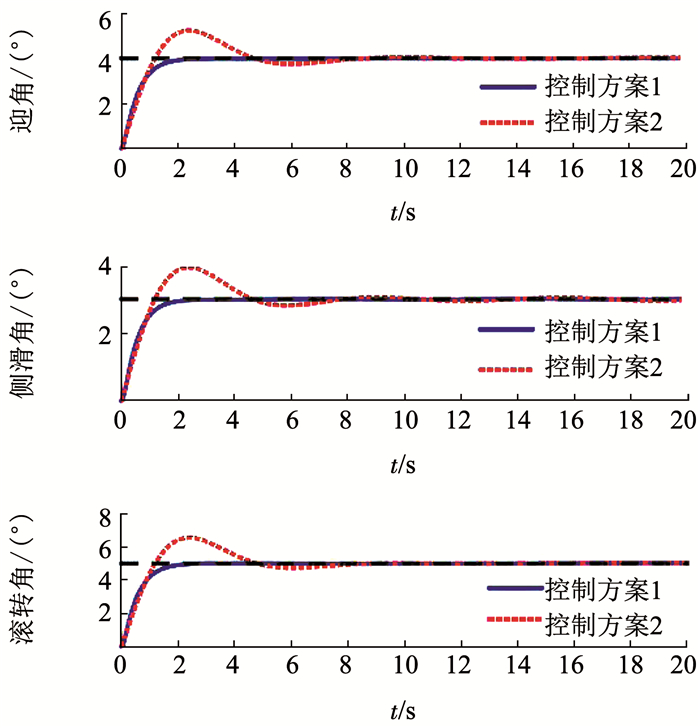图 2 两种控制方案姿态角响应曲线 Fig. 2 Attitude angle response curves of two control schemes Fig. 3
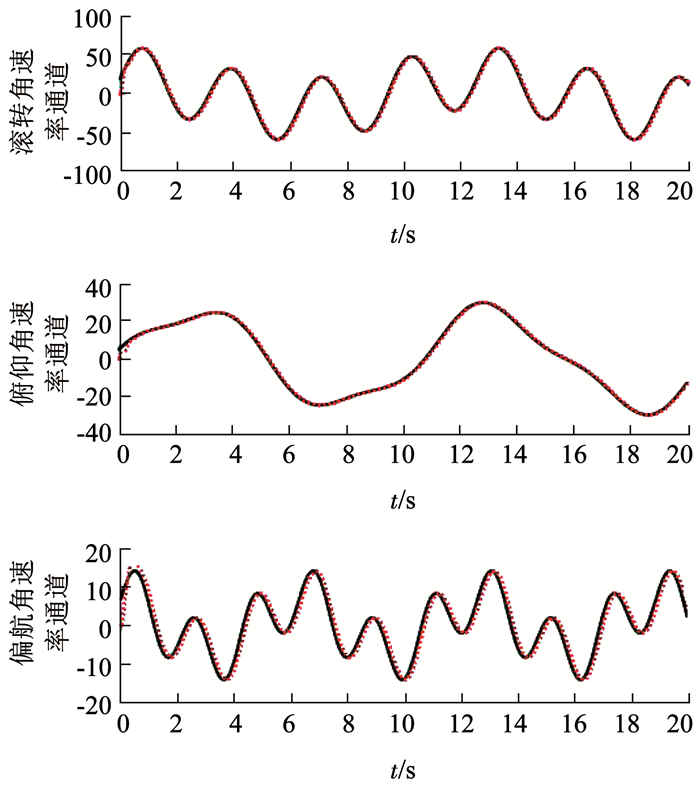图 3 控制方案1姿态角速率控制各通道实际干扰与估计 Fig. 3 Disturbance and disturbance estimate of each channel in attitude angular rate control(scheme 1) Fig. 4
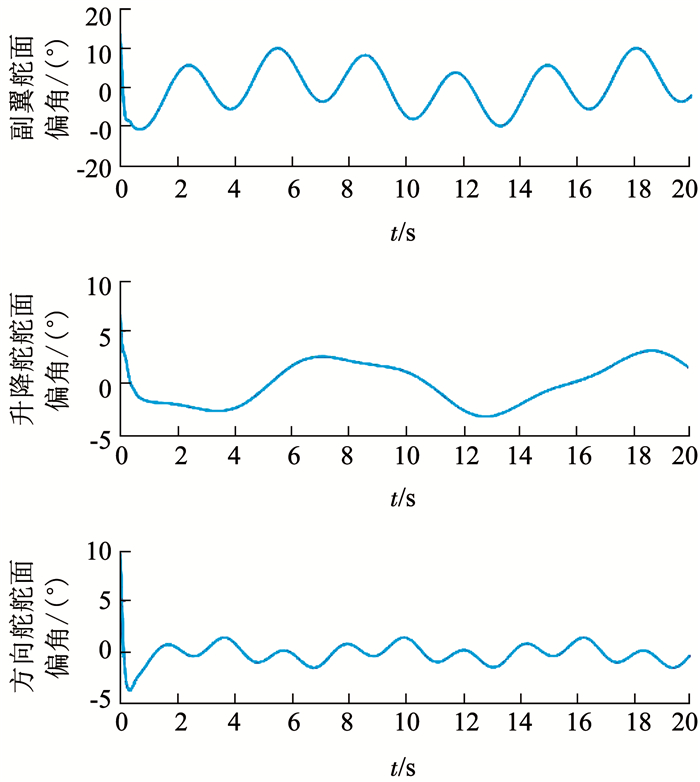图 4 控制方案1各通道控制舵面偏角变化曲线 Fig. 4 Variation curves of rudder deflection in each channel(scheme 1) 图 3中的干扰观测器对复合干扰的估计曲线表明, 虽然起始阶段没有精确逼近时变干扰, 但是经过短时的波动, 很快就精确跟踪上了复合干扰, 干扰估计的波动也非常小, 抑制了复合干扰对控制系统的影响.
由图 4采用控制方案1各控制通道的舵面偏角曲线可以看出, 由于控制方案1采用了基于非线性fal函数设计的新型滑模变结构控制趋近律, 充分发挥fal函数具有“小误差大增益, 大误差小增益”的良好品质, 有效地抑制了控制器的抖震, 达到了控制系统的设计目的.
6 结论1) 本文提出了基于非线性fal函数的趋近律的自适应分数阶微积分滑模控制方法, 控制器在系统的收敛速度、稳态精度、鲁棒性等方面都表现出了优良的效果, 由于滑模面引入了分数阶微积分算子, 与传统整数阶微积分滑模面相比, 超调现象得到有效抑制, 为了抑制复合干扰对控制效果的影响, 使用扩张状态观测器估计出复合干扰并在控制器加入等效补偿, 显著增强了控制系统的鲁棒性.
2) 为了改善传统趋近律的趋近运动品质, 提出了新型包含fal函数的快速趋近律, 平滑无抖震地加快了系统收敛速度, 仿真结果表明, 所提自适应分数阶微积分滑模控制方案具有良好的控制性能.
3) 此外, 文中所提自适应分数阶微积分滑模控制方法本质是一种非线性控制系统, 由于具有鲁棒性强, 控制器易于物理实现等优良特点, 可应用领域非常广泛, 适用于多种类型系统的控制, 如时滞、不确定性、非线性、线性等系统的控制.除了可以应用于飞行控制系统设计以外, 还可以应用于存在非线性因素、外部干扰、参数摄动的电机控制、船舶控制、机器人控制、航天器姿态控制等.
参考文献
[1] SUN Junlei, WANG Heping, ZHOU Zhou, et al. Aerodynamic numerical analysis of the low Reynolds number diamond joined-wing configuration unmanned aerial vehicle[J]. International Journal of Aeronautical and Space Sciences, 2018, 19(3): 544. DOI:10.1007/s42405-018-0072-9
[2] 孙俊磊, 王和平, 周洲, 等. 菱形连翼布局俯仰力矩非线性特性数值分析[J]. 北京航空航天大学学报, 2017, 43(8): 1567.
SUN Junlei, WANG Heping, ZHOU Zhou, et al. Numerical analysis of pitching moment non-linear characteristics of diamond joined-wing configuration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(8): 1567. DOI:10.13700/j.bh.1001-5965.2016.0584
[3] 王亚龙, 祝小平, 周洲, 等. 菱形翼布局无人机多舵面控制特性研究[J]. 飞行力学, 2016, 34(2): 5.
WANG Yalong, ZHU Xiaoping, ZHOU Zhou. Research on control characteristics of diamond-wing UAV with multiple control surfaces[J]. Flight Dynamics, 2016, 34(2): 5. DOI:10.13645/j.cnki.f.d.20160110.016
[4] SEYEDTABAⅡ S, DELAVARI M. The choice of sliding surface for robust roll control: Better suppression of high angle of attack/sideslip perturbations[J]. International Journal of Micro Air Vehicles, 2018, 10(4): 330. DOI:10.1177/1756829318771059
[5] DASMAHAPATRA S, SAHA R, MOOKHERJEE S, et al. Designing an input-linearized adaptive sliding mode coupled nonlinear integral controller[J]. IEEE-ASME Transactions on Mechatronics, 2018, 23(6): 2888. DOI:10.1109/TMECH.2018.2870911
[6] MUKHERJEE B K, SINHA M. Nonlinear dynamics and control of a laterally mass varying fighter aircraft[J]. Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering, 2018, 232(16): 3118. DOI:10.1177/0954410017723360
[7] RAJ K, MUTHUKUMAR V, SINGH S, et al. Finite-time sliding mode and super-twisting control of fighter aircraft[J]. Aerospace Science and Technology, 2018, 82/83: 487. DOI:10.1016/j.ast.2018.09.028
[8] PANATHULA C B, ROSALES A, SHTESSEL Y B, et al. Closing gaps for aircraft attitude higher order sliding mode control certification via practical stability margins identification[J]. IEEE Transactions on Control Systems Technology, 2018, 26(6): 2020. DOI:10.1109/TCST.2017.2753162
[9] WANG Yuhui, CHEN Mou, WU Qingxian, et al. Fuzzy adaptive non-affine attitude tracking control for a generic hypersonic flight vehicle[J]. Aerospace Science and Technology, 2018, 80: 56. DOI:10.1016/j.ast.2018.06.033
[10] RUI Xiaoming, YIN Wenliang, DONG Yongxing, et al. Fractional-order sliding mode control for hybrid drive wind power generation system with disturbances in the grid[J]. Wind Energy, 2019, 22(1): 49. DOI:10.1002/we.2269
[11] FAYAZI A, PARIZ N, KARIMPOUR A, et al. Robust position-based impedance control of lightweight single-link flexible robots interacting with the unknown environment via a fractional-order sliding mode controller[J]. Robotica, 2018, 36(12): 1920. DOI:10.1017/S0263574718000802
[12] TALEBI J, GANJEFAR S. Fractional order sliding mode controller design for large scale variable speed wind turbine for power optimization[J]. Environmental Progress & Sustainable Energy, 2018, 37(6): 2124. DOI:10.1002/ep.12878
[13] NIAN Fuzhong, LIU Xinmeng, ZHANG Yaqiong. Sliding mode synchronization of fractional-order complex chaotic system with parametric and external disturbances[J]. Chaos Solitons & Fractals, 2018, 116: 22. DOI:10.1016/j.chaos.2018.09.017
[14] DEEPIKA D, KAUR S, NARAYAN S. Uncertainty and disturbance estimator based robust synchronization for a class of uncertain fractional chaotic system via fractional order sliding mode control[J]. Chaos Solitons & Fractals, 2018, 115: 196. DOI:10.1016/j.chaos.2018.07.028
[15] WANG Yaoyao, CHEN Bai, WU Hongtao. Practical continuous fractional-order nonsingular terminal sliding mode control of underwater hydraulic manipulators with valve deadband compensators[J]. Proceedings of the Institution of Mechanical Engineers Part M-Journal of Engineering for the Maritime Environment, 2018, 232(4): 459. DOI:10.1177/1475090217753900
[16] DELAVARI H, HEYDARINEJAD H. Fractional-order backstepping sliding-mode control based on fractional-order nonlinear disturbance observer[J]. Journal of Computational and Nonlinear Dynamics, 2018, 13(11): 111009-1. DOI:10.1115/1.4041322
[17] KUMAR E G, ARUNSHANKAR J. Control of nonlinear two-tank hybrid system using sliding mode controller with fractional-order PI-D sliding surface[J]. Computers & Electrical Engineering, 2018, 71: 953. DOI:10.1016/j.compeleceng.2017.10.005
[18] DUMLU A. Design of a fractional-order adaptive integral sliding mode controller for the trajectory tracking control of robot manipulators[J]. Proceedings of the Institution of Mechanical Engineers Part I-Journal of Systems and Control Engineering, 2018, 232(5): 1212. DOI:10.1177/0959651818778218
[19] 高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1996: 241.
GAO Weibing. Theory and design method for variable sliding mode control[M]. Beijing: Science Press, 1996: 241.
[20] 韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 183.
HAN Jingqing. Active disturbance rejection control technique——The technique for estimating and compensating the uncertainties[M]. Beijing: National Defense Industry Press, 2008: 183.
[21] HUANG Yi, HAN Jingqing. Analysis and design for the second order nonlinear continuous extended states observer[J]. Chinese Science Bulletin, 2000, 45(21): 1938. DOI:10.1007/BF02909682
