陈松1,乔春生1,叶青1,冀少鹏2
(1.北京交通大学 土木建筑工程学院,北京 100044; 2.北京安捷工程咨询有限公司,北京 100037)
摘要:
针对工程实际中的冻融受荷岩体,以岩石初始损伤状态为参考状态,将冻融与荷载作用引起的损伤视为细观损伤,节理引起的损伤视为宏观损伤,根据Lemaitre应变等效性假设,推导建立考虑宏细观缺陷的节理岩体复合损伤模型.应用该模型分析贯通率和冻融次数分别对岩体力学性质劣化的影响,结果表明:在贯通率一定时,损伤演化曲线随冻融次数的增加而增加,试验与理论峰值强度(或弹性模量)曲线随冻融循环次数增加而降低;在冻融次数一定时,损伤演化曲线与贯通率呈正相关关系,试验与理论峰值强度(或弹性模量)与贯通率呈负相关关系.说明贯通率与冻融次数对岩体的劣化产生一定影响,且饱和试验组受冻融效应较天然试验组力学性能劣化严重.将所建模型计算结果与试验值进行比较,理论曲线与试验曲线吻合良好,验证了所建模型的合理性与有效性.
关键词: 岩石力学 节理岩体 冻融循环 宏细观缺陷 损伤模型
DOI:10.11918/j.issn.03676234.201711056
分类号:TU45
文献标识码:A
基金项目:中央高校基本科研业务专项资金(2018YJS127); 国家自然科学基金(51278046)
Compositedamage model of jointed rock mass under freezing and thawing load
CHEN Song1,QIAO Chunsheng1,YE Qing1,JI Shaopeng2
(1.School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China; 2.Beijing Anjie Engineering Consulting Corporation, Beijing 100037, China)
Abstract:
For the frozen thawing rock mass in the engineering practice, taking the initial damage state of rock as the baseline state, the damage caused by freezing thawing and loading is considered as meso damage, and the damage caused by joints is regarded as macroscopic damage. According to the hypothesis of Lemaitre strain equivalence, a composite damage model of jointed rock mass considering macro and micro defects was derived. The effect of the penetration rate and the number of freezing and thawing on the deterioration of mechanical properties of rock mass was analyzed by this model. The results show that when the penetration rate was constant, the damage evolution curve increased with the increase of freeze-thaw times, and the experimental and theoretical peak strength (or modulus of elasticity) curves decreased with the increase of freeze-thaw times. When the freeze-thaw times were constant, the damage evolution curve was positively correlated with the penetration rate, and the experimental and theoretical peak strength (or modulus of elasticity) were negatively correlated with the penetration rate. It indicates that the penetration rate and the freezing thawing times have a certain effect on the deterioration of the rock mass, and the freezing thawing effect of the saturated test group is worse than the natural test group. The calculated results of the model were compared with the experimental values, and the theoretical curves are in good agreement with the experimental curves, which verified the rationality and validity of the model.
Key words: rock mechanics jointed rock mass freeze-thaw cycles macro meso defects damage model
陈松, 乔春生, 叶青, 冀少鹏. 冻融荷载下节理岩体的复合损伤模型[J]. 哈尔滨工业大学学报, 2019, 51(2): 100-108. DOI: 10.11918/j.issn.0367-6234.201711056.

CHEN Song, QIAO Chunsheng, YE Qing, JI Shaopeng. Compositedamage model of jointed rock mass under freezing and thawing load[J]. Journal of Harbin Institute of Technology, 2019, 51(2): 100-108. DOI: 10.11918/j.issn.0367-6234.201711056.

基金项目 中央高校基本科研业务专项资金(2018YJS127);国家自然科学基金(51278046) 作者简介 陈松(1989—),男,博士研究生;
乔春生(1958—),男,教授,博士生导师 通信作者 乔春生, qiaocs@163.com 文章历史 收稿日期: 2017-11-13
Contents -->Abstract Full text Figures/Tables PDF
冻融荷载下节理岩体的复合损伤模型
陈松1, 乔春生1

 , 叶青1, 冀少鹏2
, 叶青1, 冀少鹏2 1. 北京交通大学 土木建筑工程学院,北京 100044;
2. 北京安捷工程咨询有限公司,北京 100037
收稿日期: 2017-11-13
基金项目: 中央高校基本科研业务专项资金(2018YJS127);国家自然科学基金(51278046)
作者简介: 陈松(1989—),男,博士研究生;
乔春生(1958—),男,教授,博士生导师
通信作者: 乔春生, qiaocs@163.com
摘要: 针对工程实际中的冻融受荷岩体,以岩石初始损伤状态为参考状态,将冻融与荷载作用引起的损伤视为细观损伤,节理引起的损伤视为宏观损伤,根据Lemaitre应变等效性假设,推导建立考虑宏细观缺陷的节理岩体复合损伤模型.应用该模型分析贯通率和冻融次数分别对岩体力学性质劣化的影响,结果表明:在贯通率一定时,损伤演化曲线随冻融次数的增加而增加,试验与理论峰值强度(或弹性模量)曲线随冻融循环次数增加而降低;在冻融次数一定时,损伤演化曲线与贯通率呈正相关关系,试验与理论峰值强度(或弹性模量)与贯通率呈负相关关系.说明贯通率与冻融次数对岩体的劣化产生一定影响,且饱和试验组受冻融效应较天然试验组力学性能劣化严重.将所建模型计算结果与试验值进行比较,理论曲线与试验曲线吻合良好,验证了所建模型的合理性与有效性.
关键词: 岩石力学 节理岩体 冻融循环 宏细观缺陷 损伤模型
Compositedamage model of jointed rock mass under freezing and thawing load
CHEN Song1, QIAO Chunsheng1

 , YE Qing1, JI Shaopeng2
, YE Qing1, JI Shaopeng2 1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;
2. Beijing Anjie Engineering Consulting Corporation, Beijing 100037, China
Abstract: For the frozen thawing rock mass in the engineering practice, taking the initial damage state of rock as the baseline state, the damage caused by freezing thawing and loading is considered as meso damage, and the damage caused by joints is regarded as macroscopic damage. According to the hypothesis of Lemaitre strain equivalence, a composite damage model of jointed rock mass considering macro and micro defects was derived. The effect of the penetration rate and the number of freezing and thawing on the deterioration of mechanical properties of rock mass was analyzed by this model. The results show that when the penetration rate was constant, the damage evolution curve increased with the increase of freeze-thaw times, and the experimental and theoretical peak strength (or modulus of elasticity) curves decreased with the increase of freeze-thaw times. When the freeze-thaw times were constant, the damage evolution curve was positively correlated with the penetration rate, and the experimental and theoretical peak strength (or modulus of elasticity) were negatively correlated with the penetration rate. It indicates that the penetration rate and the freezing thawing times have a certain effect on the deterioration of the rock mass, and the freezing thawing effect of the saturated test group is worse than the natural test group. The calculated results of the model were compared with the experimental values, and the theoretical curves are in good agreement with the experimental curves, which verified the rationality and validity of the model.
Keywords: rock mechanics jointed rock mass freeze-thaw cycles macro meso defects damage model
工程地质体在冻融、荷载等多种环境因素下的力学特性研究已成为冻融灾变防治与冻融岩体稳定性急需解决的关键性科学问题,这对于指导工程实践具有重要的理论意义[1-2].天然岩体是由许多矿物经长期的地质作用而形成的集合体,内部存在天然形成的结构面以及经过地应力作用形成的后期结构裂隙等,这些宏微观缺陷在冻融作用下势必会导致岩体的损伤破坏等劣化现象[3].
目前,国内外学者在岩石冻融损伤方面的研究已经取得一些成果,如Papk等[4]通过对玄武岩、闪长岩进行饱水冻融循环试验,并结合CT与SEM等技术观察岩石在冻融过程中内部微缺陷的结构变化,来研究冻融条件下岩石的物理力学性能;Chen等[5-6]研究了水的饱和度对岩石在冻融作用下劣化性能的影响;Yamabe等[7-8]研究了温度在岩石冻融循环试验中的影响;Khanlari等[9-10]通过冻融循环和将液氮作为冻融条件研究砂岩和煤岩的物理性质;Matsuoka[11]通过试验方法研究了冻结作用下岩石破裂力学机制;Nicholson等[12]对含有宏观裂隙的沉积岩在冻融风化作用下岩石物理性能的劣化进行了研究;Prick[13]通过冻融循环作用对多孔石灰岩样品的体积膨胀行为进行了研究;Ruiz等[14]通过冻融循环试验利用X射线扫描对白云岩孔隙结构的演变特征进行了研究;Bayram[15]通过冻融循环与单轴抗压试验对土耳其寒区的天然石灰岩进行了力学强度损失研究,建立了预测强度劣化统计模型;Huang等[16]考虑热应力和水在椭圆腔(裂缝)中的流动影响,提出了一种预测岩石椭圆腔中冻胀压力的数学模型.徐光苗等[17-18]通过对岩石进行冻融试验,分析了岩石损伤劣化破坏的机理及其引起岩石内部微缺陷发生变化的影响因素;文献[19-21]采用CT扫描试验,建立以CT数为变量的损伤函数,分析岩石的细观损伤扩展规律,以及建立CT数、岩石强度与冻融循环次数的联系;张慧梅等[22-23]通过冻融单轴抗压试验,建立了单向应力状态下冻融岩石损伤模型;刘红岩等[24-25]以相似材料预制的节理岩体进行了冻融试验,结果发现,冻融对节理岩体力学性能及其损伤破坏程度有很大影响;陈有亮等[26-27]通过在不同环境条件下进行冻融单轴压缩试验,分析了岩石的初始损伤对冻融破坏的影响;李新平等[28]对寒区裂隙岩体在冻融单轴荷载作用下建立了损伤劣化模型并对其损伤劣化机理进行了讨论.
从已有研究成果来看,以往主要是针对完整岩石的冻融试验研究,而对于具有不同几何特征的裂隙岩体冻融试验的研究甚少,已有研究主要停留在试验层面上,且主要是以单向受力状态为主[22-28].对于在不同冻融循环次数下的三向受力状态的岩体冻融损伤模型少有报道,且建立冻融荷载下的损伤模型主要是完整岩石微细观损伤模型,未能将工程实际中岩体内部宏观尺度的缺陷所引起的损伤考虑进来.后来刘红岩等[24-25]只是在试验的层面对预制的节理岩体做了冻融试验研究,发现这种宏、微观尺度的缺陷对岩体的力学性能影响较大.鉴于此,为更好地反映工程实际中岩体的受力情况,在前人研究的基础上,根据Lemaitre应变等效性假设,将宏观节理引起的损伤考虑进来,建立宏细观缺陷的冻融受荷节理岩体三向应力状态下的复合损伤模型,并通过现有的试验资料对模型进行合理性验证.
1 节理裂隙岩体冻融受荷损伤演化方程 1.1 岩石受荷作用下细观损伤从统计损伤的角度考虑,因岩石内部各种缺陷的随机性,考虑到岩石材料在加载过程中的损伤是一个连续的过程,且在缺陷尺度很小的情况下,假设[29-30]:1)岩石材料在宏细观上为各向同性;2)岩石微元破坏前服从虎克定律, 即微元具有线弹性性质.因此,采用Weibull概率分布,密度函数为
$P\left( \varepsilon \right) = \frac{m}{{{F_0}}}{\left( {\frac{\varepsilon }{{{F_0}}}} \right)^{m - 1}}\exp \left[ { - {{\left( {\frac{\varepsilon }{{{F_0}}}} \right)}^m}} \right].$ (1)
式中:P(ε)为岩石在微应变下对应的强度分布概率,ε为岩石在力作用下的微应变,m和F0为Weibull分布参数.其中m反映的是岩石的脆性参数,F0代表了岩石的宏观平均强度[29].
随荷载不断增加,当加载到一定的应变水平时,岩石内部微元数目的破坏数量为
${N_{\rm{s}}} = \int_0^\varepsilon {NP\left( x \right){\rm{d}}x} = N\left[ {1 - {{\rm{e}}^{ - \left( {\frac{\varepsilon }{{{F_0}}}} \right)m}}} \right].$ (2)
定义岩石损伤变量D为岩石在荷载作用下岩石微元的破坏数n与无损伤时总微元数目N的比值,其取值范围为0~1,即
$D = \frac{{{N_{\rm{s}}}}}{N}.$ (3)
将式(2)代入式(3)即可得到岩石在受力状态下的损伤演化方程:
$D = 1 - {{\rm{e}}^{ - \left( {\frac{\varepsilon }{{{F_0}}}} \right)m}}.$ (4)
1.2 物理参数的求解依据岩石的的本构关系曲线,采用具有普遍明确物理意义的几何关键点求导法.首先,在峰荷前(包括峰荷点)建立本构曲线关系图上的几何约束条件:
${\varepsilon _1} = 0,{\sigma _1} = 0;$
${\varepsilon _1} = 0,\frac{{{\rm{d}}{\sigma _1}}}{{{\rm{d}}{\varepsilon _1}}} = E;$
${\varepsilon _1} = {\varepsilon _{\rm{f}}},{\sigma _1} = {\sigma _{\rm{f}}};$
${\varepsilon _1} = {\varepsilon _{\rm{f}}},\frac{{{\rm{d}}{\sigma _1}}}{{{\rm{d}}{\varepsilon _1}}} = 0.$
εf,σf分别为完整岩石的峰值应变、峰值应力.具体推导过程见文献[31].两参数的表达式如下:
$\left\{ \begin{array}{l}m = \frac{{{\varepsilon _{\rm{f}}} - \left( {1 - 2\mu } \right){\sigma _3}/E}}{{{\varepsilon _{\rm{f}}}\ln \frac{{E{\varepsilon _{\rm{f}}}}}{{{\sigma _{\rm{f}}} - 2\mu {\sigma _3}}}}},\\{F_0} = \left[ {{\varepsilon _{\rm{f}}} - \left( {1 - 2\mu } \right){\sigma _3}/E} \right]{\left[ {\frac{{m{\varepsilon _{\rm{f}}}}}{{{\varepsilon _{\rm{f}}} - \frac{{\left( {1 - 2\mu } \right){\sigma _3}}}{E}}}} \right]^{1/m}}.\end{array} \right.$ (5)
1.3 岩石冻融作用下细观损伤岩石在冻融循环作用下,其内部结构会受到损伤劣化,最终导致岩石力学性能弱化.岩石在冻融循环过程中内部微细观缺陷发生着非常复杂的损伤演化过程,损伤劣化的程度可以通过岩石外在的宏观物理量来反映,因此,可以采用宏观唯象损伤力学方法[28].以岩石的弹性模量作为内部损伤度量的基准来描述岩石的冻融损伤变量,即
${D_n} = 1 - \frac{{{E_n}}}{{{E_0}}}.$ (6)
式中:E0和En分别为冻融前和n次冻融循环后的岩石弹性模量.
1.4 岩石冻融荷载下细观损伤根据Lemaitre的应变等价性假设,文献[28, 32]将岩石的初始损伤状态作为岩石的基准损伤状态,然后提出了推广后的应变等价原理.将岩石冻融后的损伤状态视为第一种损伤状态,冻融受荷造成的损伤视为第二种损伤状态,如下为两种损伤状态的本构关系:
${\sigma _n} = {E_0}\left( {1 - {D_n}} \right){\varepsilon _n},$ (7)
$\sigma = {E_n}\left( {1 - D} \right)\varepsilon .$ (8)
式中En为冻融后的弹性模量.
将式(6)代入式(8)可得到如下本构关系:
$\sigma = {E_0}\left( {1 - {D_{\rm{t}}}} \right)\varepsilon ,$ (9)
其中
${D_{\rm{t}}} = {D_n} + D - {D_n}D.$ (10)
式中:Dt为岩石冻融荷载耦合后的损伤,D为岩石受荷后引起的细观损伤,DnD为两种损伤的耦合项.式(10)表明,岩石在冻融与荷载耦合作用下加剧了损伤的进行,表现出非线性特征的性质.分析认为,岩石在冻融过程中使得岩石内部的微观缺陷增强,相对密度提高,因此,岩石在受力的作用下,内部晶粒间的滑移与错动受到阻碍.相反,在岩石受力过程中,内部微缺陷闭合压密,导致冻融时液体的存在方式发生了变化,对液体产生的冻胀力和渗透力起到了一定的限制作用.由两种方式引起的损伤相互作用,相互影响,最终导致岩石的力学性质发生了变化.因此,两种作用形式下引起的损伤不能简单地理解为叠加,耦合项前的“-”号代表由于耦合作用使得总损伤有所弱化[28, 32].
由式(4)、(6)及(10)可得由于岩石的冻融受荷引起的损伤演化关系为
${D_{\rm{t}}} = 1 - \frac{{{E_n}}}{{{E_0}}}{{\rm{e}}^{ - \left( {\frac{\varepsilon }{{{F_0}}}} \right)m}}.$ (11)
由式(11)考虑两种极端情况:当岩石仅受到荷载损伤时,En=E0,此时Dt=D;当岩石仅受到冻融作用时,ε=0,此时Dt=Dn.
1.5 冻融荷载下节理岩体宏细观缺陷耦合损伤基于文献[33-34]中两种损伤变量耦合的基本条件假设:1)采用人的视力能不能看见宏细观缺陷作为区分的标准,假设宏细观两种损伤具有均匀一致的各向同性.2)采用不同的描述方法来分别表述宏细观缺陷.3)依据损伤力学中Lemaitre提出的基本假设,利用应变等效原理进行耦合,而不是两种损伤变量简单的叠加.如图 1所示,假设图 1(a)~(d)分别代表同时含有宏细观缺陷岩体、仅含宏观缺陷岩体、仅含细观缺陷岩体以及完全不含缺陷岩体,对应的弹模分别为E12、E1、E2、E0,在外载作用下对应的应变量分别为ε12、ε1、ε2、ε0,基于Lemaitre应变等效假设,则有
${\varepsilon _{12}} = {\varepsilon _1} + {\varepsilon _2} - {\varepsilon _0}.$ (12)
Fig. 1
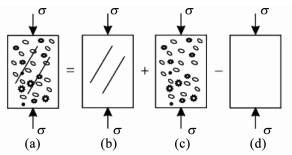 图 1 应变等效计算示意 Fig. 1 Schematic diagram of calculated equivalence strain
图 1 应变等效计算示意 Fig. 1 Schematic diagram of calculated equivalence strain 假设在外载作用方向上造成的宏、细观损伤变量分别为D1和D2,耦合后的损伤变量为D12,则有
$\frac{\sigma }{{{E_{12}}}} = \frac{\sigma }{{{E_1}}} + \frac{\sigma }{{{E_2}}} - \frac{\sigma }{{{E_0}}}.$ (13)
根据Lemaitre假设可得
$\left\{ \begin{array}{l}{E_{12}} = {E_0}\left( {1 - {D_{12}}} \right),\\{E_1} = {E_0}\left( {1 - {D_1}} \right),\\{E_2} = {E_0}\left( {1 - {D_2}} \right),\end{array} \right.$ (14)
将式(14)代入式(13)可得
${D_{12}} = 1 - \frac{{\left( {1 - {D_1}} \right)\left( {1 - {D_2}} \right)}}{{1 - {D_1}{D_2}}}.$ (15)
对于式(15)中两种极端情况为:1)当D2=0,将其代入式(15)可得:D12=D1,此时岩体的耦合损伤变量就等于岩体的宏观损伤变量;2)当D1=0,将其代入式(15)得:D12=D2,即此时岩体的耦合损伤变量等于岩体的细观损伤变量.
根据上面推导出的宏细观损伤耦合公式(15),将完整岩石初始损伤状态视为岩石的基准状态,将预制节理引起的损伤视为宏观损伤D0,岩石在冻融与荷载耦合作用引起的损伤视为细观损伤Dt,将预制节理岩体在冻融与荷载共同作用下引起的总损伤视为Dm,则式(15)变为
${D_{\rm{m}}} = 1 - \frac{{\left( {1 - {D_0}} \right)\left( {1 - {D_{\rm{t}}}} \right)}}{{1 - {D_0}{D_{\rm{t}}}}},$ (16)
其中
${D_0} = 1 - \frac{{{E_{\rm{j}}}}}{{{E_0}}}.$ (17)
式中:Ej为节理岩体的弹性模量,E0为完整岩石在基准损伤状态下的弹性模量.Dt的含义及计算同前.
2 模型实例验证与分析为进一步验证模型的有效性及合理性,引用文献[35]中的试验数据,文献中试验采用三峡库区石英白砂岩的三轴压缩,围压恒定设为10 MPa,预制节理倾角设定为30°,泊松比μ=0.11,将各贯通率的试验组岩样分别进行0,40,80,120,160次的循环冻融试验,结果表明,冻融循环次数越大,含水率越高,贯通率越大,试件损伤破坏越严重.根据文献[35]中试验数据,如表 1所示,依据本文所建立的损伤模型,分别讨论岩样贯通率(K=0(完整),0.25,0.5,0.75)与冻融循环荷载次数(0,40,80,120,160次)在模型应用中的效果.岩样受力后经历裂隙压密、弹性、屈服、破坏、残余应力等阶段,在加载过程中,裂隙压密及线弹性阶段微缺陷损伤不会发生,进入非线性弹性阶段微缺陷开始萌生,数量开始增多,到达屈服时,内部微裂隙发展迅速加快,直到承载力峰值点.此后随着变形的不断增大,承载力下降,表现出应变软化的特征,此时微裂纹逐渐贯通,形成宏观节理.在工程实际中最关心的是岩石的最大承载力即应力峰值点,因此,可以将峰值点处的损伤值作为衡量岩石破坏损伤程度的一个基准值.利用式(4)计算完整岩石受荷作用下的细观损伤D,这里应变ε取峰值应变,峰值应变可通过文献[35]中试验得出的已知峰值强度与弹性模量计算得出,当ε=εf峰值应变时,天然状态下的损伤D=0.066,饱和状态下的损伤D=0.079.岩石冻融损伤(Dn)由式(6)计算得出,由式(10)计算得出冻融与荷载耦合作用下的损伤Dt,由式(16)、(17)计算考虑宏细观损伤耦合作用引起的损伤Dm.
表 1
完整 K=0.25 K=0.5 K=0.75 完整 K=0.25 K=0.5 K=0.75
0 171.80 152.35 135.46 114.00 26.80 24.47 20.25 18.19
40 161.76 138.21 125.50 104.90 24.22 22.74 18.55 13.24
天然 80 153.97 134.42 109.34 90.54 21.09 17.87 15.58 12.69
120 146.93 124.81 103.88 82.07 20.66 15.90 13.22 11.59
160 144.23 120.00 98.62 76.39 18.81 14.58 12.43 10.41
0 141.21 129.33 114.13 100.36 22.67 18.61 16.91 13.44
40 120.33 113.10 97.84 83.67 20.43 16.03 12.13 8.24
饱和 80 110.34 102.10 74.63 59.97 17.54 10.27 7.30 4.52
120 102.35 90.26 58.42 53.74 9.07 7.15 3.60 1.72
160 99.11 80.00 55.80 44.09 7.24 5.23 2.95 1.61
表 1 三轴压缩下的物理力学参数[35] Tab. 1 Physical mechanics parameters under three axis compression[35]
图 2为天然与饱和状态下总损伤随冻融循环次数的变化, 可以看出,各贯通率的损伤曲线随冻融次数的增加呈递增的变化规律.饱和状态下各贯通率的损伤严重程度明显大于天然状态,在贯通率K=0的情况下,冻融循环次数在80次内,两种状态下的损伤变化差异并不明显.80次之后,两者出现明显的差别,损伤值大概最大相差0.4.随贯通率不断增大,两种状态下的损伤随冻融次数的变化曲线出现明显差异,且冻融次数越多,差异性越明显.在冻融120次之前(包括120次)损伤曲线增长速率较快,超过120次后,曲线变化速率放缓,且两种状态下损伤最为严重的曲线随着冻融次数的增加均未趋向于1,两种状态下K=0.75对应的曲线损伤最为严重,极限值分别趋向于0.55与0.91.分析表明,由于水的冻融作用,饱和试验组的损伤随冻融次数增加变化效果较为敏感,且含水率越高,损伤越严重,刚度弱化越大,抗冻性能就弱.而损伤未趋向于1,表明岩体的承载能力未完全丧失,因围压的存在,对提高岩体的强度有一定的优化作用.
Fig. 2
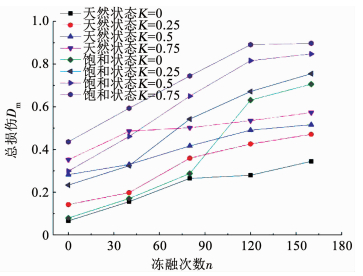 图 2 两种状态下各贯通率的总损伤随冻融次数的变化 Fig. 2 Total damage of each connectivity rate varies with the freeze-thaw times under the two conditions
图 2 两种状态下各贯通率的总损伤随冻融次数的变化 Fig. 2 Total damage of each connectivity rate varies with the freeze-thaw times under the two conditions 图 3为天然与饱和状态下各冻融次数的损伤随贯通率大小变化规律.可以看出,各冻融循环次数的损伤随贯通率的不断增大呈递增的趋势.天然状态下,在较低的冻融循环次数下,如40次,总损伤随贯通率的增加变化率较快,曲线变化呈下凹型增长,当冻融循环达80次之后,曲线随贯通率的增大变化率变缓,曲线变化呈上凹型增长.饱和状态下,各冻融次数下的总损伤随贯通率的增加一直处于迅速增长的状态,较天然状态更为敏感.对比两种状态下的损伤曲线发现,饱和状态下,各冻融次数间的总损伤变化曲线幅差值较天然状态大,尤其在80次冻融循环之后,两种状态下总损伤随贯通率的变化差异更大,但极限值都未趋向于1.在120次冻融循环后,两种状态下的试件在K=0.5和0.75情况下,天然状态下损伤变量超过0.5,饱和状态下损伤变量超过0.8,饱和状态的损伤程度更严重,损伤也未达到1.说明在饱和状态下岩体经过数次的冻融循环完全可以丧失承载能力,因围压的存在导致存在部分残余应力.天然试样组的损伤变量随贯通率的增加变化不太明显,而饱和试验组的损伤变量随贯通率的增加变化较大,损伤严重,说明贯通率的增加对饱和试验组中损伤变量的影响较天然试验组强烈.
Fig. 3
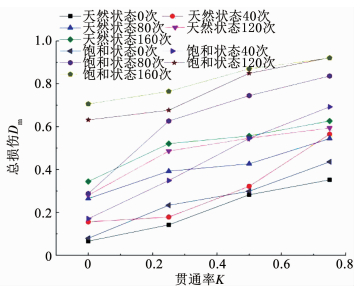 图 3 两种状态下各冻融次数的总损伤随贯通率的变化 Fig. 3 Total damage of each freeze-thaw cycle varies with the connectivity rate under the two conditions
图 3 两种状态下各冻融次数的总损伤随贯通率的变化 Fig. 3 Total damage of each freeze-thaw cycle varies with the connectivity rate under the two conditions 图 4为两种状态下各贯通率试验峰值强度与理论峰值强度随冻融循环次数变化.由式(9)及式(16)可知,考虑宏细观耦合作用引起总损伤岩样的峰值强度计算公式为:σp=E0(1-Dm)εf+2μσ3,其中,εf为峰值应变,σp为峰值应力,μ=0.11为泊松比,天然状态E0=26.8 GPa,饱和状态E0=22.67 GPa,其他参数意义同前.由图 4可知,随冻融循环次数增加,理论曲线与试验曲线都近似呈线性化逐渐降低,理论值与试验值总体上吻合良好.图 4各贯通率下的岩样,经过160次冻融循环后,天然状态下的峰值强度分别为σp=116.62, 102.87, 83.92 MPa,与未冻融前相比,强度分别降低18.5%, 20%, 22.9%;饱和状态下的峰值强度σp=84.93, 65.3, 63.65 MPa,与未冻融前相比,强度分别降低29.7%, 39.1%, 36.7%.其中饱和状态下贯通率K=0.75时,理论值与试验值较前两种贯通率下的误差大些.造成这种误差大的内因可能是贯通率越来越大,岩体的冻融损伤占据主导作用,大大弱化了节理引起的损伤作用,外因可能是含水率较高受外界温度等影响较敏感.从以上数据分析可知,岩体在长期循环冻融下,随冻融次数增加,饱和试验组的强度衰减较大,抗冻融破坏能力下降较快.
Fig. 4
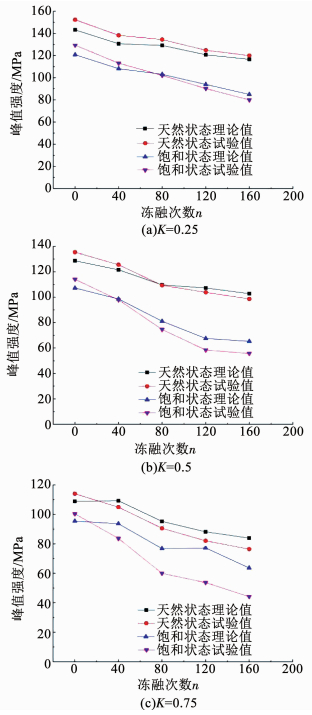 图 4 两种状态下各贯通率的峰值强度随冻融次数的变化 Fig. 4 Peak strength of each connectivity rate varies with the frequency of freeze-thaw cycles under the two conditions
图 4 两种状态下各贯通率的峰值强度随冻融次数的变化 Fig. 4 Peak strength of each connectivity rate varies with the frequency of freeze-thaw cycles under the two conditions 对比图 4(a)、(b)、(c)发现,各贯通率下的曲线变化趋势基本一致.从以上数据分析可知,两种理论峰值强度与试验值峰值强度经过160次冻融循环后分别在降低,与实际相符,但各贯通率下峰值强度降低的程度不同,贯通率越大,峰值强度衰减越严重.分析认为,贯通率越大,水的贯通性比较好,集水能力较强,在冻融往复循环中,水的冻胀力与渗透力前后应力差大,造成强度衰减程度就大.饱和状态下的理论峰值强度与试验值都低于天然状态下的峰值强度,在前120次冻融循环中天然试验组的峰值强度变化曲线斜率较小,峰值强度衰减较慢,而饱和试验组峰值强度曲线斜率较陡,峰值强度衰减较快.分析表明,贯通率、冻融循环次数以及含水率的高低对岩体强度劣化有一定影响.
图 5为两种状态下各冻融次数的峰值强度理论与试验值随贯通率变化规律.可以看出,各冻融循环次数下,理论与试验峰值强度都随着贯通率的增大呈近似线性递减的趋势,各冻融次数下,天然与饱和状态下的峰值强度曲线近似平行,斜率相当,反映出两种状态下峰值强度衰减的速率基本相同.对比图 5中各图发现,随着冻融循环次数的增加,天然与饱和状态峰值强度曲线间的幅值差在增大,冻融循环达到一定次数(120次)时这种间距差变化不再明显,说明贯通率的大小对峰值强度衰减的速率影响较小,而冻融循环次数对峰值强度的衰减影响较大.
Fig. 5
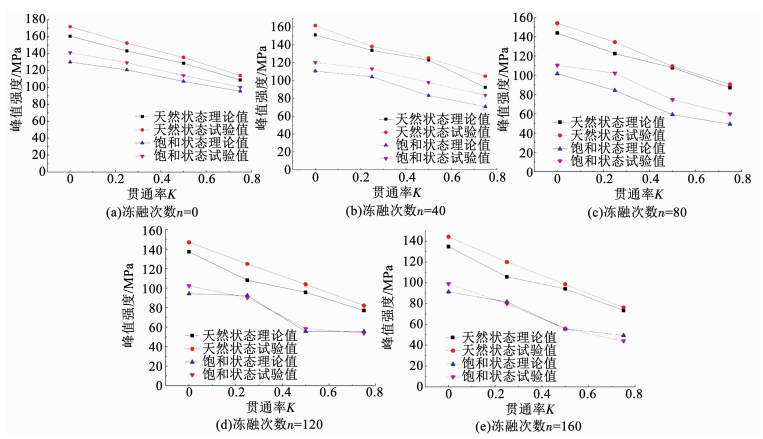 图 5 两种状态下各冻融次数的峰值强度随贯通率变化 Fig. 5 Peak strength of freeze-thaw cycles varies with connectivity rate under two conditions
图 5 两种状态下各冻融次数的峰值强度随贯通率变化 Fig. 5 Peak strength of freeze-thaw cycles varies with connectivity rate under two conditions 图 6为两种状态下各贯通率的弹性模量理论与试验值随冻融次数变化规律.弹性模量的理论计算公式可表示为E=E0(1-Dm),天然状态弹性模量E0=26.8 GPa,饱和状态弹性模量E0=22.67 GPa.从图 6可以看出,理论值与试验值随冻融次数的变化趋势基本一致,且理论曲线与试验曲线吻合良好.天然与饱和状态的弹性模量随着冻融次数的增加呈现递减的趋势,说明在发生冻融循环时,由于冻胀力与渗透力的往复循环作用,导致内部微缺陷结构发生变化,加之节理裂隙等宏观缺陷的耦合作用,最终导致弹性模量弱化,岩体抗变形性能得到劣化,饱和试验组的衰减程度更大.随着贯通率的不断增大,天然与饱和状态曲线间的幅值差在随着冻融循环次数的增大而增大,说明不但贯通率与冻融次数对弹性模量有劣化影响,且含水率越高越加速这种劣化效果.
Fig. 6
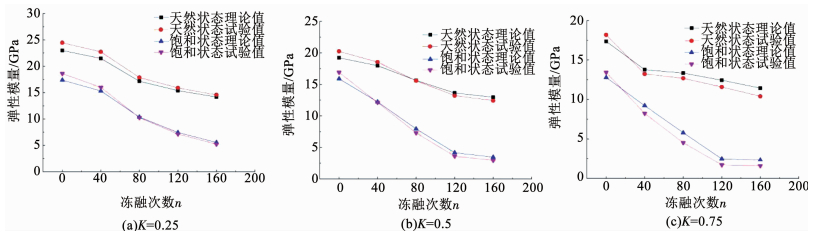 图 6 两种状态下各贯通率弹性模量随冻融次数变化 Fig. 6 Elastic modulus of the connectivity rate varies with the freeze-thaw cycles under two conditions
图 6 两种状态下各贯通率弹性模量随冻融次数变化 Fig. 6 Elastic modulus of the connectivity rate varies with the freeze-thaw cycles under two conditions 图 7为两种状态下各冻融次数的弹性模量理论与试验值随贯通率变化规律.可以看出,理论弹性模量与试验值随贯通率的变化基本一致,理论曲线与试验曲线吻合良好.各冻融次数下弹性模量随贯通率增加呈递减的变化趋势,说明节理贯通率大小对岩体物理力学性能有很大影响,且饱和组试样较天然组变化衰减较为敏感.随冻融循环次数的增加,两种状态下的弹性模量曲线间的幅值差在不断增大,天然组试件弹性模量曲线的斜率变化不明显,饱和组试件的弹性模量曲线斜率变化比较显著,说明饱和试验组弹性模量弱化比较严重,抗冻能力差.当达到一定冻融次数后,弹性模量衰减变化的程度也在变缓.
Fig. 7
 图 7 两种状态下各冻融次数的弹性模量随贯通率变化 Fig. 7 Elastic modulus of freeze-thaw cycles varies with connectivity rate under two conditions
图 7 两种状态下各冻融次数的弹性模量随贯通率变化 Fig. 7 Elastic modulus of freeze-thaw cycles varies with connectivity rate under two conditions 3 结论1) 天然与饱和状态下各贯通率的损伤演化曲线随冻融次数的增加而增大,各冻融循环次数的损伤演化曲线随贯通率的增大而增加,且饱和试验组受冻融效应较天然组增加敏感.冻融次数较多,贯通率较大,损伤越严重,岩体刚度衰减越大,抗冻性能越差.
2) 天然与饱和状态下各贯通率的试验峰值强度与理论峰值强度随冻融循环次数增加而降低,各冻融次数的试验峰值强度与理论峰值强度随贯通率增加而降低.随冻融次数增加,饱和试验组的峰值强度曲线斜率较大,衰减较快;随贯通率增加,两种状态下的理论与试验峰值强度曲线斜率近似平行,衰减的速率基本相同,说明峰值强度衰减受冻融次数的影响较大.
3) 天然与饱和状态下各贯通率的弹性模量理论值与试验值随冻融次数增加而递减,各冻融次数的弹性模量理论值与试验值随贯通率增加而递减.无论是贯通率还是冻融循环次数的增大,天然与饱和状态曲线间的幅值差都在增大,且饱和试验组反映更加敏感,说明贯通率与冻融次数对弹性模量具有一定的劣化影响,
4) 所建模型计算结果的理论曲线与试验曲线吻合良好,验证了所建模型的可行性与有效性.
参考文献
[1] 刘泉声, 黄诗冰, 康永水, 等. 裂隙岩体冻融损伤研究进展与思考[J]. 岩石力学与工程学报, 2015, 34(3): 452.
LIU Quansheng, HUANG Shibing, KANG Yongshui, et al. Advance and review on freezing-thawing damage of fractured rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 452. DOI:10.13722/j.cnki.jrme.2015.03.003
[2] LAI Y, XU X, DONG Y, et al. Present situation and prospect of mechanical research on frozen soils in China[J]. Cold Regions Science and Technology, 2013, 87(1): 6. DOI:10.1016/j.coldregions.2012.12.001
[3] 申艳军, 杨更社, 荣腾龙, 等. 冻融循环作用下单裂隙类砂岩局部化损伤效应及端部断裂特性分析[J]. 岩石力学与工程学报, 2017, 36(3): 562.
SHEN Yanjun, YANG Gengshe, RONG Tenglong, et al. Localized damage effects of quasi-sandstone with single fracture and fracture behaviors of joint end under cyclic freezing and thawing[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 562. DOI:10.13722/j.cnki.jrme.2016.0122
[4] PARK J, HYUN C U, PARK H D. Changes in microstructure and physical properties of rocks caused by artificial freeze-thaw action[J]. Bulletin of Engineering Geology and the Environment, 2015, 74(2): 555. DOI:10.1007/s10064-014-0630-8
[5] CHEN T C, YEUNG M R, MORIC N. Effect of water saturation on deterioration of welded tuff due to freeze-thaw action[J]. Cold Regions Science and Technology, 2004, 38(1): 127. DOI:10.1016/j.coldregions.2003.10.001
[6] LUO X, JIANG N, ZUO C, et al. Damage characteristics of altered and unaltered diabases subjected to extremely cold freeze-thaw cycles[J]. Rock Mechanics & Rock Engineering, 2014, 47(6): 1997. DOI:10.1007/s00603-013-0516-2
[7] YAMABE T, NEAUPANE K M. Determination of some thermomechanical properties of Sirahama sandstone under subzero temperature condition[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(7): 1209. DOI:10.1016/S1365-1609(1)00067-3
[8] KANG Y, LIU Q, HUANG S. A fully coupled thermo-hydro-mechanical model for rock mass under freezing/thawing condition[J]. Cold Regions Science & Technology, 2013, 95(11): 19. DOI:10.1016/j.coldregions.2013.08.002
[9] KHANLARI G, SAHAMIEH R Z, ABDILOR Y. The effect of freeze-thaw cycles on physical and mechanical properties of upper red formation sandstones, central part of Iran[J]. Arabian Journal of Geosciences, 2014, 1. DOI:10.1007/s12517-014-1653-y
[10] QIN L, ZHAI C, LIU S, et al. Changes in the petrophysical properties of coal subjected to liquid nitrogen freeze-thaw-A nuclear magnetic resonance investigation[J]. Fuel, 2017, 194: 102. DOI:10.1016/j.fuel.2017.01.005
[11] MATSUOKA N. Mechanics of rock breakdown by frost action: An experimental approach[J]. Cold Regions Science and Technology, 1990, 17(3): 253. DOI:10.1016/S0165-232X(05)80005-9
[12] NICHOLSON D T, NICHOLSON F H. Physical deterioration of sedimentary rocks subjected to experimental freeze-thaw weathering[J]. Earth Surface Processes and Landforms, 2015, 25(12): 1295.
[13] PRICK A. Dilatometrical behaviour of porous calcareous rock samples subjected to freeze-thaw cycles[J]. Catena, 1995, 25(1-4): 7. DOI:10.1016/0341-8162(94)00038-G
[14] RUIZ V G, REY R A, CELORIO C, et al. Characterization by computed X-ray tomography of the evolution of the pore structure of a dolomite rock during freeze-thaw cyclic tests[J]. Physics and Chemistry of the Earth, 1999, 24(7): 633. DOI:10.1016/S1464-1895(99)00092-7
[15] BAYRAM F. Predicting mechanical strength loss of natural stones after freeze-thaw in cold regions[J]. Cold Regions Science and Technology, 2012, 83/84(12): 98. DOI:10.1016/j.coldregions.2012.07.003
[16] HUANG S, LIU Q, LIU Y, et al. Frost heaving and frost cracking of elliptical cavities (fractures) in low-permeability rock[J]. Engineering Geology, 2018, 1. DOI:10.1016/j.enggeo.2017.12.024
[17] 徐光苗, 刘泉声. 岩石冻融破坏机理分析及冻融力学试验研究[J]. 岩石力学与工程学报, 2005, 24(17): 3076.
XU Guangmiao, LIU Quansheng. Analysis of mechanism of rock failure due to freezing-thawing cycling and mechanical testing study on frozenthawed rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3076. DOI:10.3321/j.issn:1000-6915.2005.17.012
[18] 张继周, 缪林昌, 杨振峰. 冻融条件下岩石损伤劣化机制和力学特性研究[J]. 岩石力学与工程学报, 2008, 27(8): 1688.
ZHANG Jizhou, MIAO Linchang, YANG Zhenfeng. Research on rock degradation and deterioration mechanisms and mechanical characteristics under cyclic freezing-thawing[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(8): 1688. DOI:10.3321/j.issn:1000-6915.2008.08.020
[19] 刘慧, 杨更社, 叶万军, 等. 基于CT图像的冻结岩石冰含量及损伤特性分析[J]. 地下空间与工程学报, 2016, 12(4): 912.
LIU Hui, YANG Gengshe, YE Wanjun, et al. Analysis of ice content and damage characteristics of frozen rock based on pseudo-color enhanced CT image[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(4): 912.
[20] 葛修润, 任建喜, 蒲毅彬, 等. 岩石细观损伤扩展规律的CT实时试验[J]. 中国科学, 2000, 30(2): 104.
GE Xiurun, REN Jianxi, PU Yibin, et al. Primary study of CT real-time testing of fatigue meso-damage propagation law of rock[J]. Chinese Journal of Geotechnical Engineering, 2000, 30(2): 104. DOI:10.3321/j.issn:1006-9275.2000.02.002
[21] 赖远明, 吴紫汪, 朱元林, 等. 大坂山隧道围岩冻融损伤的CT分析[J]. 冰川冻土, 2000, 22(3): 206.
LAI Yuanming, WU Ziwang, ZHU Yuanlin, et al. CT analysis of frost damage of the surrounding rocks of a tunnel in the Daban Mountain[J]. Journal of Glaciology and Geocryology, 2000, 22(3): 206. DOI:10.3969/j.issn.1000-0240.2000.03.003
[22] 张慧梅, 杨更社. 冻融与荷载耦合作用下岩石损伤模型的研究[J]. 岩石力学与工程学报, 2010, 29(3): 471.
ZHANG Huimei, YANG Gengshe. Research on damage model of rock under coupling action of freeze-thaw and load[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 471.
[23] 袁小清, 刘红岩, 刘京平. 冻融荷载耦合作用下节理岩体损伤本构模型[J]. 岩石力学与工程学报, 2015, 34(8): 1602.
YUAN Xiaoqing, LIU Hongyan, LIU Jingping. A damaging model of jointed rock under coupled action of freezing and thawing[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(8): 1602. DOI:10.13722/j.cnki.jrme.2014.1342
[24] 刘红岩, 刘冶, 邢闯锋, 等. 循环冻融条件下节理岩体损伤破坏试验研究[J]. 岩土力学, 2014, 35(6): 1547.
LIU Hongyan, LIU Ye, XING Chuangfeng, et al. Test study of damage failure of jointed rock mass under freezing-thawing cycles[J]. Rock and Soil Mechanics, 2014, 35(6): 1547.
[25] 路亚妮, 李新平, 肖家双. 单裂隙岩体冻融力学特性试验分析[J]. 地下空间与工程学报, 2014, 10(3): 594.
LU Yani, LI Xinping, XIAO Jiashuang. Experimental analysis on mechanical characteristic of single cracked rock mass under freeze-thaw condition[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(3): 594.
[26] 陈有亮, 代明星, 刘明亮, 等. 含初始损伤岩石的冻融损伤试验研究[J]. 力学季刊, 2013, 34(1): 74.
CHEN Youliang, DAI Mingxing, LIU Mingliang, et al. Experimental investigation on freezing damage characteristics of granite with initial damage[J]. Chinese Quarterly of Mechanics, 2013, 34(1): 74. DOI:10.3969/j.issn.0254-0053.2013.01.010
[27] 刘松明, 陈有亮, 杜曦, 等. 酸侵蚀区白砂岩冻融损伤的影响因素研究[J]. 水资源与水工程学报, 2014, 25(5): 127.
LIU Songming, CHEN Youliang, DU Xi, et al. Study on influences factor of freezing-thawing damage of white sandstone in acid erosion area[J]. Journal of Water Resources and Water Engineering, 2014, 25(5): 127. DOI:10.11705/j.issn.1672-643X.2014.05.028
[28] 李新平, 路亚妮, 王仰君. 冻融荷载耦合作用下单裂隙岩体损伤模型研究[J]. 岩石力学与工程学报, 2013, 32(11): 2307.
LI Xinping, LU Yani, WANG Yangjun. Research on damage model of single jointed rock masses under coupling action of freeze-thaw and loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2307.
[29] 曹文贵, 方祖烈, 唐学军. 岩石损伤软化统计本构模型之研究[J]. 岩石力学与工程学报, 1998, 17(6): 628.
CAO Wengui, FANG Zulie, TANG Xuejun. A study of statistical constitutive model for soft and damage rock[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(6): 628. DOI:10.3321/j.issn:1000-6915.1998.06.004
[30] KRAJCINOVIC D, SILVA M A G. Statistical aspects of the continuous damage theory[J]. International Journal of Solids and Structures, 1982, 18(7): 551. DOI:10.1016/0020-7683(82)90039-7
[31] 张慧梅, 雷利娜, 杨更社. 温度与荷载作用下岩石损伤模型[J]. 岩石力学与工程学报, 2014(s2): 3391.
ZHANG Huimei, LEI Lina, YANG Gengshe. Damage model of rock under temperature and load[J]. Chinese Journal of Rock Mechanics and Engineering, 2014(s2): 3391. DOI:10.13722/j.cnki.jrme.2014.s2.001
[32] 张全胜, 杨更社, 任建喜. 岩石损伤变量及本构方程的新探讨[J]. 岩石力学与工程学报, 2003, 22(1): 30.
ZHANG Quansheng, YANG Gengshe, REN Jianxi. New study of damage variable and constitutive equation of rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 30. DOI:10.3321/j.issn:1000-6915.2003.01.005
[33] 杨更社, 谢定义.岩体宏观细观损伤的耦合计算分析[C]//第六次全国岩石力学与工程学术大会论文集.武汉: [s.n.], 2000: 327
YANG Gengshe, XIE Dingyi. Coupling analysis on the macro-damage and meso-damage of rock masses[C]// Symposium on the Sixth National Rock Mechanics and Engineering Academic Conference. Wuhan: [s.n.], 2000: 327
[34] 张力民, 吕淑然, 刘红岩. 综合考虑宏细观缺陷的岩体动态损伤本构模型[J]. 爆炸与冲击, 2015, 35(3): 428.
ZHANG Limin, LV Shuran, LIU Hongyan. A dynamic damage constitutive model of rock mass by comprehensively considering macroscopic and mesoscopic flaws[J]. Explosion and Shock Waves, 2015, 35(3): 428.
[35] 王乐华, 陈招军, 金晶, 等. 节理岩体冻融力学特性试验研究[J]. 水利水电技术, 2016(5): 149.
WANG Lehua, CHEN Zhaojun, JIN Jing, et al. Experimental study on mechanic characteristics of jointed rock under freeze-thaw condition[J]. Water Resources and Hydropower Engineering, 2016(5): 149. DOI:10.13928/j.cnki.wrahe.2016.05.035
