石建平1,2,李培生1,刘国平1,刘鹏3
(1.南昌大学 机电工程学院,南昌 330031; 2.贵阳学院 电子与通信工程学院,贵阳 550005; 3.河北地质大学 宝石与材料工艺学院,石家庄 050031)
摘要:
为解决克隆选择算法收敛速度慢、收敛精度低等问题,提出了双层协同进化克隆选择算法,该算法的每一层使用不同的进化方案进行寻优搜索,并通过信息共享实现了层间的协同进化,形成层内竞争与层间协作的进化模式.通过构建基于多种进化策略的混合协同进化机制,实现了不同进化策略在优化过程中的优势互补与信息增值,达到有效平衡算法的全局探索与局部开发的目的,同时也较好避免了算法的早熟收敛问题.用10个标准测试函数来验证所提出算法的可行性与有效性,仿真实验结果表明:相比克隆选择算法及其两个改进的算法,本文提出的优化算法具有全局搜索能力强、稳定性好、收敛速度快、收敛精度高等优势,且测试函数维度的增加对本文算法的收敛性能影响不大,其优势更加凸显.针对混沌系统控制与同步中的系统参数估计问题,以Lorenz混沌系统的参数估计为例,进行了未知参数估计的数值仿真,结果显示本文算法实现了混沌系统参数的高精度估计,是一种有效的混沌系统参数估计方法.
关键词: 克隆选择算法 协同进化 多策略 混沌系统 参数估计
DOI：10.11918/j.issn.0367-6234.201812176
分类号:TP301.6
文献标识码:A
基金项目:国家自然科学基金(51566012)；贵州省联合基金资助项目(黔科合LH字[2015]7302号)
Bilevel coevolutionary clonal selection algorithm and its application
SHI Jianping1,2,LI Peisheng1,LIU Guoping1,LIU Peng3
(1.School of Mechanical & Electrical Engineering, Nanchang University, Nanchang 330031,China; 2.School of Electronic & Communication Engineering, Guiyang University, Guiyang 550005, China; 3.School of Gems and Materials Technology, Hebei GEO University, Shijiazhuang 050031, China）
Abstract:
In order to solve the problem of slow convergence speed and low convergence precision inherent in the clone selection algorithm, a bilevel coevolutionary clonal selection algorithm is proposed. The algorithm used different evolutionary schemes for each level of evolution to search for optimization. Through information sharing, co-evolution between levels was realized. Moreover, an evolutionary model of intra-level competition and inter-level cooperation was formed. By constructing a hybrid co-evolution mechanism of multi-evolutionary strategies, it could realize the complementary advantages and information increment of different evolutionary strategies in the optimization process. Thus, the purpose of effectively balancing the global exploration and local exploitation of the algorithm was achieved. Simultaneously, the premature convergence problem of the algorithm could also be better avoided. The feasibility and effectiveness of the proposed algorithm were verified by 10 benchmarks. Experimental results show that the proposed algorithm had obvious advantages such as stronger global search ability, better stability, faster convergence speed, higher convergence accuracy, and so on. Furthermore, these advantages became more prominent with the increase of testing dimensions. Lorenz chaotic system was taken as an example to test the algorithm in estimating the parameters. Simulation results confirmed that the proposed algorithm can be used for high-precision estimation of system parameters, and it is an effective parameter estimation method for chaotic systems.
Key words: clonal selection algorithm co-evolution multi-strategy chaotic system parameter estimation
石建平, 李培生, 刘国平, 刘鹏. 双层协同进化克隆选择算法及其应用[J]. 哈尔滨工业大学学报, 2019, 51(11): 174-182. DOI: 10.11918/j.issn.0367-6234.201812176.
SHI Jianping, LI Peisheng, LIU Guoping, LIU Peng. Bilevel coevolutionary clonal selection algorithm and its application[J]. Journal of Harbin Institute of Technology, 2019, 51(11): 174-182. DOI: 10.11918/j.issn.0367-6234.201812176.
基金项目 国家自然科学基金(51566012)；贵州省联合基金资助项目(黔科合LH字[2015]7302号) 作者简介 石建平(1981—)，男，博士研究生;
李培生(1969—)，男，教授，博士生导师 通信作者 李培生，lps20150331@163.com 文章历史 收稿日期: 2018-12-28
Contents -->Abstract Full text Figures/Tables PDF
双层协同进化克隆选择算法及其应用
石建平1,2, 李培生1
, 刘国平1, 刘鹏3 1. 南昌大学 机电工程学院，南昌 330031;
2. 贵阳学院 电子与通信工程学院，贵阳 550005;
3. 河北地质大学 宝石与材料工艺学院，石家庄 050031
收稿日期: 2018-12-28
基金项目: 国家自然科学基金(51566012)；贵州省联合基金资助项目(黔科合LH字[2015]7302号)
作者简介: 石建平(1981—)，男，博士研究生;
李培生(1969—)，男，教授，博士生导师
通信作者: 李培生，lps20150331@163.com
摘要: 为解决克隆选择算法收敛速度慢、收敛精度低等问题，提出了双层协同进化克隆选择算法，该算法的每一层使用不同的进化方案进行寻优搜索，并通过信息共享实现了层间的协同进化，形成层内竞争与层间协作的进化模式.通过构建基于多种进化策略的混合协同进化机制，实现了不同进化策略在优化过程中的优势互补与信息增值，达到有效平衡算法的全局探索与局部开发的目的，同时也较好避免了算法的早熟收敛问题.用10个标准测试函数来验证所提出算法的可行性与有效性，仿真实验结果表明：相比克隆选择算法及其两个改进的算法，本文提出的优化算法具有全局搜索能力强、稳定性好、收敛速度快、收敛精度高等优势，且测试函数维度的增加对本文算法的收敛性能影响不大，其优势更加凸显.针对混沌系统控制与同步中的系统参数估计问题，以Lorenz混沌系统的参数估计为例，进行了未知参数估计的数值仿真，结果显示本文算法实现了混沌系统参数的高精度估计，是一种有效的混沌系统参数估计方法.
关键词: 克隆选择算法 协同进化 多策略 混沌系统 参数估计
Bilevel coevolutionary clonal selection algorithm and its application
SHI Jianping1,2, LI Peisheng1
, LIU Guoping1, LIU Peng3 1. School of Mechanical & Electrical Engineering, Nanchang University, Nanchang 330031, China;
2. School of Electronic & Communication Engineering, Guiyang University, Guiyang 550005, China;
3. School of Gems and Materials Technology, Hebei GEO University, Shijiazhuang 050031, China
Abstract: In order to solve the problem of slow convergence speed and low convergence precision inherent in the clone selection algorithm, a bilevel coevolutionary clonal selection algorithm is proposed. The algorithm used different evolutionary schemes for each level of evolution to search for optimization. Through information sharing, co-evolution between levels was realized. Moreover, an evolutionary model of intra-level competition and inter-level cooperation was formed. By constructing a hybrid co-evolution mechanism of multi-evolutionary strategies, it could realize the complementary advantages and information increment of different evolutionary strategies in the optimization process. Thus, the purpose of effectively balancing the global exploration and local exploitation of the algorithm was achieved. Simultaneously, the premature convergence problem of the algorithm could also be better avoided. The feasibility and effectiveness of the proposed algorithm were verified by 10 benchmarks. Experimental results show that the proposed algorithm had obvious advantages such as stronger global search ability, better stability, faster convergence speed, higher convergence accuracy, and so on. Furthermore, these advantages became more prominent with the increase of testing dimensions. Lorenz chaotic system was taken as an example to test the algorithm in estimating the parameters. Simulation results confirmed that the proposed algorithm can be used for high-precision estimation of system parameters, and it is an effective parameter estimation method for chaotic systems.
Keywords: clonal selection algorithm co-evolution multi-strategy chaotic system parameter estimation
受生物免疫系统对外界入侵病原体产生免疫应答中的克隆选择原理的启发，De Castro等提出了克隆选择算法(Clonal Selection Algorithm, CSA)[1].克隆选择算法及其相关改进算法通过对免疫系统执行免疫应答过程中的克隆选择、克隆扩增、高频变异和受体编辑等免疫机理的模拟，使其具有良好的自学习和自适应能力，成为智能信息处理的有效工具并在诸多工程领域得到了很好的应用[2-11].克隆选择算法是一种确定性和随机性相结合的启发式群智能随机搜索算法，同其它群智能优化算法一样，克隆选择算法在解决复杂优化问题时同样存在易于陷入早熟收敛的不足.为了提高克隆选择算法的收敛速度与收敛精度，国内外广大专家学者对其进行了深入的研究，提出了很多新的改进方案.张英杰等[12]采用混沌技术对种群进行初始化以及利用正态云发生器实现抗体的变异操作，进而提出了混沌云克隆选择算法，并将该算法应用于自抗扰控制器的参数优化整定；Peng等[13]通过引入Baldwinian学习和正交学习两种机制来引导免疫应答过程，提出了基于混合学习机制的克隆选择算法；Zhang等[14]提出一种具有重组算子和超变异算子的混合克隆选择算法，该算法利用重组算子来增强算法的搜索能力，并利用超变异算子获得高质量的候选解；针对一般群智能优化算法中虚拟碰撞而导致的全局搜索效率降低的问题，宋丹等[15]将基于模糊非基因信息的搜索与克隆选择原理相结合，提出了一种模糊非基因信息记忆的双克隆选择算法；Xu等[16]提出了一种退化识别的克隆选择算法，该算法通过挖掘和利用非最优区域的信息来识别新种群的退化现象并避免由此带来的计算成本，从而提高了算法的计算效率；Zhang等[17]提出一种混合克隆选择算法，该算法利用改进的组合重组方法改善种群的多样性，并引入基于成功历史信息的自适应变异策略来提高算法的搜索能力.
根据No free Lunch定理，不存在一种方法对所有的问题都是有效的，每种方法都有其相应的优势，也有其相应的劣势.针对复杂优化问题的求解，单一进化模式的优化算法难以获得问题的最优解或满意解.而混合协同进化利用各种进化模式独特的优点和机制来相互取长补短，实现优化过程的信息增值，有助于提高算法的全局搜索能力.受文献[18]中阶层型进化算法的启发，本文将双层协同进化思想应用于克隆选择算法的改进研究，提出了改进的克隆选择算法，即双层协同进化克隆选择算法(Bilevel Coevolutionary Clonal Selection Algorithm, BCECSA).该算法通过底层和顶层分别采用不同的进化方案，并利用信息共享机制促进两者的协同进化，有效提高了算法的综合收敛性能.最后，以典型的Lorenz混沌系统为例，将算法应用于解决混沌系统的参数估计问题，拓展了算法的工程应用范围.
1 算法原理 1.1 算法进化模型算法采用两层协同进化机制，其进化模型如图 1所示.其中，底层进化和顶层进化分别采用了不同的进化方案.将底层进化得到的更新后的历史最优抗体集作为每一代顶层进化寻优搜索的初始种群，经过顶层进化更新后的最优抗体通过信息共享机制用于参与引导底层的进化操作.底层和顶程两层进化之间通过最优信息的传递形成相互促进的协同进化机制，蕴含了在同一进化环境中个体间的竞争与协作思想，有助于克服单一进化机制容易陷入局部极值的早熟收敛等缺陷，有效改善了算法的优化性能.
Fig. 1
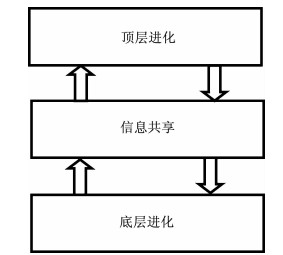图 1 算法进化模型 Fig. 1 Algorithmic evolution model 1.2 底层进化设D维搜索空间的抗体种群由m个抗体组成，第i个抗体用向量Xi=[xi1, xi2, …, xiD, ](i=1, 2, …, m)表示，每个抗体对应了问题的潜在解.本文将目标函数视为抗原，目标函数值对应抗体和抗原的亲和度.亲和度的大小反映了解的质量，针对最小优化问题，亲和度越小则表明解的质量越高.本文采用如下的方案进行底层进化操作：
$\begin{aligned} X_{i}(t+1) &=r \times X_{\mathrm{r} 1}(t)+(1-r) \times G_{\mathrm{best}}+\\ F_{1} & \times\left(X_{\mathrm{r} 2}(t)-X_{\mathrm{r} 3}(t)\right) , \end{aligned}$ (1)
$F_{1}=f_{\min }+\left(f_{\max }-f_{\min }\right) \times \frac{t}{t_{\max }}.$ (2)
式中：Gbest为种群迄今为止的全局最佳历史抗体；r1、r2和r3为从集合(1, 2，…，m)中随机选取的互不相同且与索引i不同的整数，即满足r1≠r2≠r3≠i；F1为扰动缩放因子，用于控制扰动差分向量的大小，缩放因子采用式(2)的线性递增的更新方式，其最大值fmax与最小值fmin分别为0.9、0.4；r为[0, 1]区间内均匀分布的随机数；t为当前进化代数；tmax为最大进化代数.
上述进化思想是以随机选择的第r1个抗体和全局最优抗体Gbest的加权和为基向量，利用随机差分向量F1×(Xr2(t)－Xr3(t))对基向量进行扰动而得到下一代抗体Xi，该进化策略兼顾了种群的多样性与算法的收敛性.在算法进化的初期阶段，由于种群的多样性较好，为避免扰动过大而导致抗体出界现象的发生，缩放因子F1应该取值较小；在算法进化的后期阶段，随着种群多样性的降低，为避免扰动量过于偏小而导致算法陷入停滞现象，缩放因子F1应该取值较大.因此，缩放因子F1采用随迭代次数线性递增的更新方式.
每一次进化操作后，立即评估得到的下一代抗体Xi，如果Xi的适应值优于其对应的历史最佳抗体Pi，则实时更新历史最佳抗体Pi；如果Xi的适应值优于种群迄今为止的全局最佳历史抗体Gbest，则实时更新全局最佳历史抗体Gbest.
1.3 顶层进化顶层进化采用克隆选择进化方案.克隆选择的基本思想是：只有能够识别抗原的抗体将被免疫系统选择保留下来，并对其进行克隆扩增；而不能识别抗原的抗体不被选择，也不进行扩增.本文利用底层进化的历史最优抗体群P作为顶层进化的初始种群.将抗体群P按亲和度从小到大进行排序，得到排序后的临时抗体群P′，选取抗体群P′中前20%的优质抗体进行克隆扩增，克隆规模为
$m_{\mathrm{c}}=\sum\limits_{l=1}^{0.2 m} \mathrm{R}\left(\left(\frac{\beta m}{l}\right)^{2}\right).$ (3)
式中：β为放大系数；l为被选抗体的排序序号；R(·)为取整算子；m为抗体群的抗体总数(即种群的规模)；mc为所有被选择抗体所产生的克隆体的总数.可见，抗体的亲和度越小，对应的克隆规模越大.
在免疫算法中，抗体的高频变异能够在局部邻域内开发出质量更高的候选解，即对应局部精细搜索；受体编辑则允许算法在更为广阔的空间进行全局搜索，即赋予算法逃离局部极值束缚的能力.为了有效保持抗体群的多样性，同时促进克隆体的亲和度成熟，本文采用了多策略混合进化的方案，即在式(4)~(6)中任选其中一方程对当前克隆体进行免疫进化操作.
$ P_{\mathrm{lk}}^{*}=P_{1}^{\prime}+F_{2} \times\left(P_{\mathrm{r} 4}^{\prime}-P_{\mathrm{r5}}^{\prime}\right), $ (4)
$ P_{\mathrm{lk}}^{*}=P_{1}^{\prime} \times \mathrm{rand}_{1}+P_{1}^{\prime} \times\left(0.5-\mathrm{rand}_{2}\right), $ (5)
$P_{\mathrm{lk}}^{*}=X_{\mathrm{min}}+\left(X_{\mathrm{max}}-X_{\mathrm{min}}\right) \times \mathrm{rand}_{3}, $ (6)
$F_{2}=f_{\min }+\left(f_{\max }-f_{\min }\right) \times \frac{k}{k_{\max }}.$ (7)
式中：Plk*为经过高频变异或受体编辑后得到的成熟抗体，l=1, 2, …, 0.2m，k=1, 2, …, kmax，kmax=
设A(·)为亲和度大小，则按式(8)、(9)对临时抗体P′l和全局最优抗体Gbest进行更新.所有克隆体完成高频变异或受体编辑免疫操作后，得到了亲和度成熟的抗体群P*.为了提高算法的收敛速度并兼顾抗体群的多样性，将部分成熟抗体替换原抗体群中亲和度较差的抗体.经过大量的数值仿真实验，本文选择抗体群P*中最优秀的前0.2m个成熟抗体用于替换原抗体群P中亲和度最差的0.2m个抗体.
$P_\text{l}^{\prime}=\left\{\begin{array}{l}{P_{ \mathrm{lk}}^{*}, A\left(P_{\mathrm{lk}}^{*}\right) \leqslant A\left(P_\text{l}^{\prime}\right)}; \\ {P_\text{l}^{\prime}, \text { others. }}\end{array}\right.$ (8)
$G_{\mathrm{best}}=\left\{\begin{array}{l}{P_{ \mathrm{lk}}^{*}, A\left(P_{\mathrm{lk}}^{*}\right) \leqslant A\left(G_{\mathrm{best}}\right)}; \\ {G_{\mathrm{best}}, \text { others. }}\end{array}\right.$ (9)
为进一步提升算法的收敛质量，将临时抗体群P′中排序位于中间的60%个临时抗体(目前为止，该部分抗体未进行任何免疫操作)按式(10)向全局最优抗体Gbest学习.
$P_{1}^{\prime \prime}=G_{\mathrm{best}}+G_{\mathrm{best}} \times\left(0.5-\mathrm{rand}_{4}\right).$ (10)
式中:l=0.2m+1, 0.2m+2, …, 0.8m.由于临时抗体P′l与抗体群P中的第i个抗体Pi本质上是同一抗体，于是按贪婪选择机制在P″l和Pi中选择较优者作为下一代抗体，确保寻优过程不出现退化现象.具体按式(11)、(12)进行抗体更新.
$P_{i}=\left\{\begin{array}{l}{P_\text{l}^{\prime \prime}, A\left(P_\text{l}^{\prime \prime}\right) \leqslant A\left(P_{i}\right)}; \\ {P_{i}, \text { others. }}\end{array}\right.$ (11)
$G_{\mathrm{best}}=\left\{\begin{array}{l}{P_\text{l}^{\prime \prime}, A\left(P_\text{l}^{\prime \prime}\right) \leqslant A\left(G_{\mathrm{best}}\right)}; \\ {G_{\mathrm{best}}, \text { others. }}\end{array}\right.$ (12)
1.4 越界处理在底层进化和顶层进化的过程中，会出现抗体超出搜索空间范围的现象.对于越界现象，通常的做法是将其设置为边界值.为较好保持种群的多样性，本文将越界分量设置为rand×(Xmax, j－Xmin, j)+Xmin, j.其中，rand为[0, 1]区间内均匀分布的随机数，Xmax, j为Xmax的第j维分量，Xmin, j为Xmin的第j维分量.
1.5 算法步骤综上所述，本文提出算法的具体步骤如下：
步骤1??参数设置与初始化，设置抗体的搜索范围、种群规模、缩放因子的最大值与最小值，进化迭代次数，在搜索空间内对抗体进行随机初始化.
步骤2??计算每个抗体的适应值，抗体Xi即为历史最佳抗体Pi，抗体群P的全局最佳抗体即为全局历史最佳抗体Gbest.
步骤3??按式(1)、(2)更新抗体Xi，并进行越界处理.计算抗体Xi的适应值，若A(Xi)≤A(Pi)，则Pi=Xi；若A(Xi)≤A(Gbest)，则Gbest=Xi.
步骤4??所有抗体更新完毕，则执行步骤5，否则返回步骤3继续更新下一个抗体.
步骤5??按亲和度从小到大对抗体群P中的抗体进行排序，得到临时抗体群P′.
步骤6 ??选择临时抗体群P′的前20%个优质抗体，按式(3)~(9)进行免疫进化操作并进行越界处理，得到成熟的抗体群P*.
步骤7??将抗体群P*中优秀的前0.2m个成熟抗体用于替换抗体群P中0.2m个亲和度最差的抗体.
步骤8??对临时抗体群P′排序为中间的60%个抗体按式(10)向全局最优抗体Gbest学习，按式(11)实时更新原抗体群P中的对应抗体，按式(12)实时更新全局最优抗体；
步骤9??若当前迭代次数小于最大迭代数，则返回步骤3开始下一轮迭代，否则寻优过程结束并输出寻优结果.
2 数值实验与结果分析 2.1 测试函数与参数设置采用表 1中的10个标准测试函数来验证本文提出算法的可行性和有效性.
表 1
表 1 用于测试算法性能的基准函数 Tab. 1 Benchmark functions used to test the performances 函数 搜索范围 最优值 表 1 用于测试算法性能的基准函数 Tab. 1 Benchmark functions used to test the performances
其中，前5个函数为单峰函数，用于检验算法的收敛速度与收敛精度；后5个函数为多峰函数，用于检验算法的全局搜索能力.除了函数f10的全局最小值为-78.332 33之外，其余函数的全局最小值均为0.
本文提出算法所涉及的主要参数有放大系数β.下面以函数f3、f8为例，讨论放大系数β对算法收敛性能的影响.
固定种群规模为30，最大迭代次数tmax=100，函数维数D=30，放大系数β分别设置为0.1、0.2、0.3、0.4、0.5及0.6，各测试函数独立重复实验30次，放大系数β取不同值时算法寻优的最优值Best、最差值Worst、平均值Mean、标准差Std.及平均有效总评估次数TNE(Total Number of Evaluations)分别如表 2所示.其中，平均有效总评估次数是指算法收敛于全局最优值时的最小评估次数的平均值(对于未能收敛于函数全局最优的情形，则按照实际最大评估次数统计).
表 2
表 2 不同放大系数的实验结果 Tab. 2 Experimental results of different amplification factors β Mean Best Worst Std. TNE/次 f3 0.1 4.05×10-245 3.21×10-276 7.99×10-244 ≈0 6 100
0.2 0 0 0 0 5 128.20
0.3 0 0 0 0 4 286.23
0.4 0 0 0 0 3 931.33
0.5 0 0 0 0 3 676.37
0.6 0 0 0 0 3 646.20
f8 0.1 2.49×10-4 9.09×10-12 6.95×10-3 1.25×10-3 6 100
0.2 7.28×10-12 7.28×10-12 7.28×10-12 0 10 100
0.3 7.28×10-12 7.28×10-12 7.28×10-12 0 16 800
0.4 7.28×10-12 7.28×10-12 7.28×10-12 0 26 300
0.5 7.28×10-12 7.28×10-12 7.28×10-12 0 38 300
0.6 7.28×10-12 7.28×10-12 7.28×10-12 0 53 100
表 2 不同放大系数的实验结果 Tab. 2 Experimental results of different amplification factors
根据表 2的实验结果可知：当放大系数为0.2、0.3、0.4、0.5及0.6时，算法都能够收敛于函数f3的全局最优值，且随着放大系数的增加，算法的平均有效评价次数逐渐降低，这是由于尽管较大的放大系数对应了较大的克隆规模，而较大的克隆规模大大提升了算法的收敛速度，反而导致平均有效评价次数的降低；当放大系数≥0.2时，算法对函数f8获得了较高的收敛精度且最好的标准差，继续增大放大系数，算法的收敛精度难以提高，但计算成本却明显增加.综上，放大系数β过小，导致算法的收敛质量难以得到保障；增大放大系数β对进一步提高算法的收敛精度并不明显.为了兼顾算法的收敛质量和计算成本，本文将放大系数β设置为0.5.
2.2 仿真实验与结果分析为全面检测算法的寻优能力，考虑基准测试函数维数分别为30维、100维的情形.本文算法的种群规模m=30，大系数β为0.5，最大迭代次数tmax=100，各测试函数独立重复实验30次.将BCECSA算法的实验结果与CSA、FDCSA[15]及MSHCSA[17]算法的寻优结果进行对比，实验数据如表 3所示.其中，CSA和FDCSA算法的数据来源于文献[15]；MSHCSA算法的种群规模为m=6*D，最大迭代次数tmax=800，其余参数设置与参考文献[17]相同.BCECSA算法的部分函数平均寻优收敛曲线如图 2所示(为了便于收敛曲线的显示和观察, 将f10以外的其余函数平均适应值取以10为底的对数).
表 3
表 3 实验结果对比 Tab. 3 Comparison of simulation results 算法 D=30 D=100 Mean Best Worst Std. TNE/次 Mean Best Worst Std. TNE/次
f1 CSA 1.20×10-5 5.52×10-6 5.52×10-5 5.65×10-6 150 000 2.49×10-5 1.33×10-5 3.94×10-5 7.89×10-6 500 000
FDCSA 0 0 0 0 150 000 0 0 0 0 500 000
MSHCSA 2.59×10-19 7.76×10-23 2.24×10-18 5.13×10-19 145 881.53 1.74×10-8 2.72×10-10 7.46×10-8 1.93×10-8 482 484.53
BCECSA 0 0 0 0 1 880.70 0 0 0 0 1 844.43
f2 CSA 2.62×10+2 2.12×10+2 3.31×10+2 1.42×10+2 150 000 1.12×10+4 1.06×10+4 1.24×10+4 1.68×10+3 500 000
FDCSA 3.16×10-1 1.78×10-1 4.97×10-1 1.23×10-1 150 000 9.87×10+2 7.44×10+2 1.18×10+3 1.47×10+2 500 000
MSHCSA 7.64×10-4 1.17×10-5 7.05×10-3 1.34×10-3 146 622.40 8.89×10+1 2.05×10+1 3.68×10+2 7.82×10+1 485 333.57
BCECSA 0 0 0 0 1 894.67 0 0 0 0 1 834.87
f3 CSA 1.48×10-3 8.39×10-4 1.96×10-3 4.22×10-4 150 000 3.93×10-3 3.52×10-3 5.13×10-3 6.04×10-4 600 000
FDCSA 3.91×10-15 0 2.11×10-14 3.57×10-15 150 000 2.40×10-12 1.69×10-13 9.77×10-12 3.69×10-12 600 000
MSHCSA 1.75×10-7 7.44×10-10 1.77×10-6 3.98×10-7 148 135.53 4.90×10-5 3.75×10-6 2.34×10-4 4.92×10-5 482 485.37
BCECSA 0 0 0 0 3 676.37 0 0 0 0 3 686.57
f4 CSA 5.71×10-2 4.33×10-2 7.27×10-2 1.04×10-2 300 000 4.09×10-1 3.39×10-1 6.21×10-1 5.68×10-2 900 000
FDCSA 5.90×10-4 4.06×10-7 2.50×10-3 9.71×10-4 300 000 7.88×10+1 5.67×10+1 9.94×10+1 1.88×10+1 900 000
MSHCSA 2.55×10-3 3.98×10-4 9.24×10-3 2.03×10-3 153 285.17 1.14×10+1 5.77×100 1.68×10+1 2.65×100 537 207.10
BCECSA 0 0 0 0 3 783.27 0 0 0 0 3 728.90
f5 CSA 0 0 0 0 150 000 0 0 0 0 500 000
FDCSA 0 0 0 0 150 000 0 0 0 0 500 000
MSHCSA 0 0 0 0 22 561.83 0 0 0 0 126 194.20
BCECSA 0 0 0 0 43.87 0 0 0 0 44.47
f6 CSA 3.65×10-3 1.17×10-3 7.84×10-3 2.41×10-3 150 000 7.23×10-3 4.67×10-3 9.39×10-3 1.57×10-3 500 000
FDCSA 0 0 0 0 150 000 0 0 0 0 500 000
MSHCSA 1.12×10+2 9.76×10+1 1.27×10+2 7.65×10+1 159 602.57 5.63×10+2 5.26×10+2 5.92×10+2 1.51×10+1 529 268.57
BCECSA 0 0 0 0 94.900 0 0 0 0 99.17
f7 CSA 5.04×10-3 2.22×10-3 1.06×10-2 2.96×10-3 150 000 2.08×10-3 9.45×10-4 3.49×10-3 8.85×10-4 500 000
FDCSA 3.33×10-17 0 3.34×10-16 9.99×10-17 150 000 5.55×10-17 0 2.22×10-16 8.95×10-17 500 000
MSHCSA 2.70×10-3 1.11×10-16 3.44×10-2 6.57×10-3 146 848.90 9.48×10-4 1.01×10-9 1.97×10-2 3.73×10-3 482 547.43
BCECSA 0 0 0 0 105.63 0 0 0 0 104.77
f8 CSA 5.52×10-5 2.01×10-5 9.69×10-5 2.59×10-5 150 000 2.13×10-4 1.44×10-4 2.52×10-4 3.93×10-5 500 000
FDCSA 1.09×10-12 0 2.34×10-12 1.20×10-12 150 000 1.00×10-10 7.46×10-11 2.12×10-10 5.92×10-11 500 000
MSHCSA 1.19×10+3 9.11×10+2 1.49×10+3 1.35×10+2 163 288.67 1.99×10+4 1.83×10+4 2.06×10+4 4.62×10+2 537 872.13
BCECSA 7.28×10-12 7.28×10-12 7.28×10-12 0 38 300 9.46×10-11 9.46×10-11 9.46×10-11 0 38 300
f9 CSA 8.85×10-4 5.61×10-4 1.16×10-3 2.21×10-4 150 000 7.18×10-4 6.41×10-4 9.26×10-4 1.06×10-4 500 000
FDCSA 5.44×10-14 2.31×10-14 9.82×10-14 1.27×10-14 150 000 2.21×10-13 1.02×10-13 3.58×10-13 2.87×10-14 500 000
MSHCSA 4.70×10-10 5.83×10-11 2.12×10-9 5.28×10-10 146 456.90 9.31×10-5 4.02×10-6 2.94×10-4 7.49×10-5 483 642.20
BCECSA 8.88×10-16 8.88×10-16 8.88×10-16 0 38 300 8.88×10-16 8.88×10-16 8.88×10-16 0 38 300
f10 CSA -78.332 331
351 836 7 -78.332 331
382 061 7 -78.332 331
323 715 9 1.87×10-8 150 000 -78.332 331
364 515 6 -78.332 331
383 502 9 -78.332 331
337 295 7 1.51×10-8 500 000
FDCSA -78.332 331
407 542 8 -78.332 331
407 542 8 -78.332 331
407 542 8 1.10×10-14 150 000 -78.332 331
407 542 8 -78.332 331
407 542 8 -78.332 331
407 542 8 2.21×10-14 500 000
MSHCSA -78.307 444
149 226 9 -78.331 955
094 679 3 -77.631 664
180 020 5 1.25×10-1 151 570.47 -69.254 564
863 120 2 -70.524 009
236 668 8 -68.505 449
466 460 0 5.52×10-1 509 809.63
BCECSA -78.332 331
407 543 1 -78.332 331
407 543 1 -78.332 331
407 543 0 2.73×10-14 38 300 -78.332 331
407 543 1 -78.332 331
407 543 5 -78.332 331
407 542 9 2.22×10-13 38 300
表 3 实验结果对比 Tab. 3 Comparison of simulation results
Fig. 2
图 2 部分函数的收敛曲线 Fig. 2 Convergence graphs on some functions 根据表 3的实验结果可知：对于5个单峰函数，BCECSA算法都能够以较快的收敛速度收敛于全局最优值，且算法的稳定性好；对于多峰函数而言，BCECSA算法能够快速收敛于函数f6、f7的全局最优值，函数f8、f9及f10也获得了较高的收敛精度，且算法寻优稳定性好；函数维数的改变对BCECSA算法的收敛精度等性能指标影响不大，不管是低维函数还是高维函数，算法都获得相近的收敛质量.
在文献[15]中，CSA和FDCSA算法的种群规模为m=3(f7: m=40)，大部分远小于本文算法的种群规模.但是文献[15]中算法的总评估次数最大达900 000次，而本文算法的最大平均评估次数为38 300次，前者是后者的大约23.50倍.显然，本文算法的计算成本以及收敛速度比CSA和FDCSA算法更具优势，如果按照有效评估次数来计算，则本文算法的优越性更加明显(如对于函数f5，当函数维数为30维时，BCECSA算法评估只需评估43.87次即可收敛于函数的全局最优值；当函数维数为100维时，BCECSA算法平均只需评估44.47次即可收敛于函数的全局最优值).对于MSHCSA算法有相同的结论，即本文算法的函数评估次数明显小于MSHCSA算法，本文算法的收敛精度也比MSHCSA算法的收敛精度高.具体从算法的收敛精度来看，CSA算法只有一个函数(f5)能够收敛于全局最优，对于其余函数都不能收敛于全局最优；FDCSA算法有3个函数(f1、f5、f6)能够收敛于全局最优，其余函数都不能收敛于全局最优，但大部分获得了比CSA算法更好的收敛质量(函数f4除外)；MSHCSA算法只有一个函数(f5)能够收敛于全局最优，对于其余函数都不能收敛于全局最优，随着函数规模的增加，MSHCSA算法收敛质量的降低较为明显；BCECSA算法有7个函数(f1- f7)能够收敛于全局最优；对于函数f8和f9，BCECSA算法的收敛精度同样远高于CSA、FDCSA和MSHCSA，且算法稳定性最好；对于函数f10，本文算法和FDCSA算法获得相近的收敛性能，其收敛质量和算法稳定性都比CSA和MSHCSA好.总体而言，BCECSA算法在10函数中的9个函数上的平均值、最好值、最差值和标准差4项指标均优于CSA和MSHCSA算法，1个函数(f5)的上述指标与CSA和MSHCSA算法相当；BCECSA算法在10函数中的6个函数上的平均值、最好值、最差值和标准差4项指标均优于FDCSA算法，4个函数(f1、f5、f6、f10)的上述指标与FDCSA算法相当；在所有10个函数中，本文算法的总评价次数最少，收敛速度最快.图 2的平均收敛曲线图进一步验证了BCECSA算法具有收敛速度快、收敛精度高以及稳定性好的优点.
3 算法应用研究 3.1 问题描述本文以混沌系统的参数估计问题来讨论算法的应用.考虑如下混沌系统
$\dot{X}=f\left(X, X_{0}, \theta_{0}\right).$ (13)
式中：X=[x1, x2, …, xn]T为系统状态变量，X0为系统状态变量初值，θ0=[θ10, θ20, …, θd0]T为系统参数的实际值.
混沌系统的参数估计一般以系统结构已知为前提，则估计系统为
$\dot{Y}=f\left(Y, X_{0}, \theta\right).$ (14)
式中:Y=[y1, y2, …, yn]T为估计系统的状态变量，θ为系统参数θ0的估计值.
定义估计系统与原系统的状态误差向量为E=[e1, e2, …, en]T，其中，e1=y1－x1，e2=y2－x2，…，en=yn－xn.参数估计问题本质上是以式(15)为优化目标的寻优问题.混沌系统参数估计的原理如图 3所示.
$\min J=\min \int\limits_{0}^{\tau} f\left(\left|e_{1}\right|+\left|e_{2}\right|+, \cdots, +\left|e_\mathrm{n}\right|\right) \mathrm{d} t.$ (15)
Fig. 3
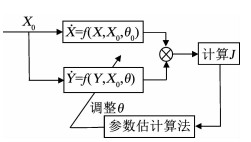图 3 混沌系统参数估计原理 Fig. 3 Parameter estimation model for chaotic systems 3.2 仿真及分析以典型的Lorenz混沌系统为实验对象，考虑最为复杂的3个系统参数都未知的情形.Lorenz系统的数学模型如下
$\left\{\begin{array}{l}{\dot{x}=-a(x-y)}; \\ {\dot{y}=b x-x z-y}; \\ {\dot{z}=-c z+x y}.\end{array}\right.$ (16)
当系统参数取值为a=10、b=28、
则估计系统为
$\left\{\begin{array}{l}{\dot{x}_{1}=-a_{1}\left(x_{1}-y_{1}\right)}; \\ {\dot{y}_{1}=b_{1} x_{1}-x_{1} z_{1}-y_{1}}; \\ {\dot{z}_{1}=-c_{1} z_{1}+x_{1} y_{1}}.\end{array}\right.$ (17)
式中:a1、b1、c1为参数真值a、b、c的估计值.定义估计系统与原系统的状态误差为e1=x1－x、e2=y1－y、e3=z1－z，则优化目标函数为
$\min J=\min \int\limits_{0}^{\tau} t\left(\left|e_{1}\right|+\left|e_{2}\right|+\left|e_{3}\right|\right) \mathrm{d} t.$ (18)
设Lorenz系统估计参数(a1, b1, c1)的搜索空间分别为a1∈[9, 11]、b1∈[20, 30]、c1∈[2, 3]，系统的初始状态为(0.5, 0.1, 0.3)，Lorenz系统方程采用步长为0.001 s的四阶Runge-Kutta方法进行求解，方程的仿真时间为0.1 s.对系统连续进行10次仿真实验，取其平均值为最后的参数辨识值，并与CSA算法、粒子群优化算法(PSO, Particle Swarm Optimization)[19]进行对比.各算法的种群规模都为30，最大迭代次数为200；BCECSA算法的其余参数设置与前述相同；PSO算法的惯性权重采用线性递减的方式，其最大值和最小值分别为0.9、0.4，学习因子c1＝c2＝2；CSA算法的参数β=1，n等于种群规模m的20%，d=0.各算法的仿真实验结果如表 4和图 4所示.(为便于收敛曲线的显示和观察, 将平均适应值取以10为底的对数)
表 4
表 4 各算法的参数估计结果 Tab. 4 Parameter estimation results of different algorithms 算法 平均值 J a1 b1 c1
CSA 10.008 820 756 473 263 27.991 349 005 723 190 2.666 575 503 777 088 9.870 351 107 134 217×10-8
PSO 10.000 000 001 436 115 28.000 000 000 410 190 2.666 666 666 528 075 3.441 130 203 881 102×10-14
BCECSA 10 28 2.666 666 666 666 667 0
表 4 各算法的参数估计结果 Tab. 4 Parameter estimation results of different algorithms
Fig. 4
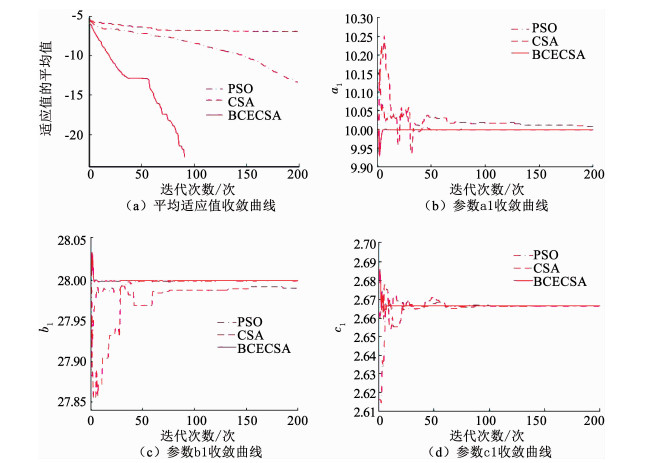图 4 Lorenz系统参数估计优化曲线 Fig. 4 Parameter estimation optimization curvesof Lorenz system 由表 4的仿真实验结果可知：BCECSA算法实现了对3个系统参数的精确估计，是一种有效的混沌系统参数估计方法；PSO算法的参数估计精度仅次于BCECSA算法，其目标函数值可达10-14数量级；CSA算法的参数估计精度最差，其目标函数值为10-8数量级.图 4的参数估计图进一步验证了表 4的结果.
4 结论本文针对一般克隆选择算法收敛速度慢和收敛精度不高的不足，引入双层进化机制，提出了双层协同进化克隆选择算法.用标准测试函数验证了本文提出算法的可行性与有效性，并与CSA、MSHCSA及FDCSA算法进行对比分析，实验结果表明本文算法具有收敛速度快、收敛精度高及稳定性强的优点.以Lorenz混沌系统为例，将BCECSA算法用于解决混沌系统的参数估计问题，并与CSA和PSO算法进行仿真比较，仿真实验表明CSA和PSO算法的参数估计精度不高，而本文算法实现了对三个系统参数的精确估计，拓展了BCECSA算法的应用范围.
参考文献
[1] DE CASTRO L N, VON ZUBEN F J. Learning and optimization using the clonal selection principle[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(3): 239. DOI:10.1109/TEVC.2002.1011539
[2] CHITSAZ H, AMJADY N, ZAREIPOUR H. Wind power forecast using wavelet neural network trained by improved clonal selection algorithm[J]. Energy Conversion and Management, 2015, 89: 588. DOI:10.1016/j.enconman.2014.10.001
[3] SHUI Xinguo, ZUO Xingquan, CHEN Cheng, et al. A clonal selection algorithm for urban bus vehicle scheduling[J]. Applied Soft Computing, 2015, 36: 36. DOI:10.1016/j.asoc.2015.07.001
[4] CAI Qing, GONG Maoguo, MA Lijia, et al. A novel clonal selection algorithm for community detection in complex networks[J]. Computational Intelligence, 2015, 31(3): 442. DOI:10.1111/coin.12031
[5] MARINAKI M, MARINAKIS Y. A hybridization of clonal selection algorithm with iterated local search and variable neighborhood search for the feature selection problem[J]. Memetic Computing, 2015, 7(3): 181. DOI:10.1007/s12293-015-0161-2
[6] YIN Chunyong, MA Luyu, FENG Lu. A feature selection method for improved clonal algorithm towards intrusion detection[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2016, 30(5): 1659013. DOI:10.1142/S0218001416590138
[7] LIANG Hongtao, KANG Fengju. Adaptive chaos parallel clonal selection algorithm for objective optimization in WTA application[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(6): 3459. DOI:10.1016/j.ijleo.2015.12.122
[8] 武健, 舒健生, 李亚雄, 等. 基于人工免疫克隆选择算法的无人机三维航迹规划[J]. 系统工程与电子技术, 2018, 40(1): 86.
WU Jian, SHU Jiansheng, LI Yaxiong, et al. Three-dimensional planning of unmanned aerial vehicle based on AICS[J]. Systems Engineering and Electronics, 2018, 40(1): 86. DOI:10.3969/j.issn.1001-506X.2018.01.13
[9] 周炳海, 谭芬. 基于循环配送策略的汽车装配线物料配送调度方法[J]. 东北大学学报(自然科学版), 2018, 39(3): 389.
ZHOU Binghai, TAN Fen. Scheduling method of material delivery for automotive assembly lines based on milk-run delivery[J]. Journal of Northeastern University (Natural Science), 2018, 39(3): 389. DOI:10.12068/j.issn.1005-3026.2018.03.017
[10] BURCU C Y, NILUFER Y, OZHAN O. Prediction of protein secondary structure with clonal selection algorithm and multilayer perceptron[J]. IEEE Access, 2018, 6: 45256. DOI:10.1109/ACCESS.2018.2864665
[11] AVATEFIPOUR O, NAFISIAN A. A novel electric load consumption prediction and feature selection model based on modified clonal selection algorithm[J]. Journal of Intelligent and Fuzzy Systems, 2018, 34(4): 2261. DOI:10.3233/JIFS-171292
[12] 张英杰, 赵芳芳. 混沌云克隆选择算法及其应用[J]. 湖南大学学报:自然科学版, 2014, 41(3): 101.
ZHANG Yingjie, ZHAO Fangfang. Chaos cloud clonal selection algorithm and its application[J]. Journal of Hunan University (Natural Sciences), 2014, 41(3): 101. DOI:10.3969/j.issn.1674-2974.2014.03.018
[13] PENG Yong, LU Baoliang. Hybrid learning clonal selection algorithm[J]. Information Sciences, 2015, 296(1): 128. DOI:10.1016/j.ins.2014.10.056
[14] ZHANG Weiwei, LIN Jingjing, JING Honglei, et al. A novel hybrid clonal selection algorithm with combinatorial recombination and modified hypermutation operators for global optimization[J]. Computational Intelligence & Neuroscience, 2016, 2016: 1. DOI:10.1155/2016/6204728
[15] 宋丹, 樊晓平, 文中华, 等. 模糊非基因信息记忆的双克隆选择算法[J]. 电子与信息学报, 2017, 39(2): 255.
SONG Dan, FAN Xiaoping, WEN Zhonghua, et al. Double clonal selection algorithm based on fuzzy non-genetic information memory[J]. Journal of Electronics & Information Technology, 2017, 39(2): 255. DOI:10.11999/JEIT160359
[16] XU Nan, DING Yongsheng, REN Lihong, et al. Degeneration recognizing clonal selection algorithm for multimodal optimization[J]. IEEE Transactions on Cybernetics, 2018, 48(3): 848. DOI:10.1109/TCYB.2017.2657797
[17] ZHANG Weiwei, GAO Kui, ZHANG Weizheng, et al. A hybrid clonal selection algorithm with modified combinatorial recombination and success-history based adaptive mutation for numerical optimization[J]. Applied Intelligence, 2019, 49(2): 819. DOI:10.1007/s10489-018-1291-2
[18] ARAKAWA T, FUKUDA T. Natural motion generation of biped locomotion robot using hierarchical trajectory generation method consisting of GA, EP layers[C]//International Conference on Robotics and Automation, 1997: 211. DOI: 10.1109/robot.1997.620040
[19] SHI Yuhui, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceeding of Congress on Evolutionary Computation. Piscataway: IEEE Service Center, 1999: 1945. DOI: 10.1109/CEC.1999.785511
