轻集料混凝土局部受压试验及动力本构分析

余振鹏,黄侨,任政

(东南大学 交通学院,南京 210096)



摘要:

为探究轻集料混凝土单轴局部受压动力特性，采用试验机对轻集料混凝土单轴局部受压本构关系进行相关试验研究.考虑了5种不同加载应变率和4种不同加载面积，在位移控制下，得到轻集料混凝土单轴局部受压应力-应变曲线.根据应力-应变曲线特征点的峰值应力、峰值应变和弹性模量，分析不同加载应变率与加载面积对特征点的影响.同时根据混凝土黏弹塑性损伤本构模型，考虑不同加载应变率和加载面积的影响修正模型参数，并通过试验数据验证理论模型的合理性.研究结果表明：加载应变率和加载面积对轻集料混凝土应力-应变曲线影响明显；不同加载面积对轻集料混凝土弹性模量、峰值应力及峰值应变有较大影响；所提出的理论模型能够准确描述轻集料混凝土材料局部动力荷载作用下的应变率效应和非线性行为.

关键词:  轻集料混凝土  加载应变率  承压面积  损伤本构  试验力学性能

DOI：10.11918/j.issn.0367-6234.201707013

分类号:U441.4

文献标识码:A

基金项目:中央高校基本科研业务费专项资金；江苏省研究生科研与实践创新计划项目(KYCX_170132)



Experiment and dynamic constitutive analysis of lightweight aggregate concrete under local compression

YU Zhenpeng,HUANG Qiao,REN Zheng

(School of Transportation, Southeast University, Nanjing 210096, China)

Abstract:

To investigate the dynamic behavior of lightweight aggregate concrete under uniaxial compression, the displacement controlled uniaxial compression experiments were carried out together by considering five loading rates and four loading areas, and the stress-strain curves of lightweight aggregate concrete were obtained. The effects of loading rates and loading areas on the peak stress, peak strain and elastic modulus were analyzed and discussed. The constitutive model of viscoelastic and plastic damage of concrete was developed by correcting the model parameters, and the rationality of proposed model was verified through experimental data. Results show that loading rates and loading areas have a significant effect on stress-strain curves of the concrete. Loading areas exhibit greater effects on elastic modulus, peak stress and peak strain of the lightweight aggregate concrete. The proposed model can accurately describe the strain rate effect and nonlinear behavior of the lightweight aggregate concrete under dynamic loading.

Key words:  lightweight aggregate concrete  loading strain rate  loading area  damage constitutive relation  mechanical properties


余振鹏, 黄侨, 任政. 轻集料混凝土局部受压试验及动力本构分析[J]. 哈尔滨工业大学学报, 2018, 50(3): 18-25. DOI: 10.11918/j.issn.0367-6234.201707013.
YU Zhenpeng, HUANG Qiao, REN Zheng. Experiment and dynamic constitutive analysis of lightweight aggregate concrete under local compression[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 18-25. DOI: 10.11918/j.issn.0367-6234.201707013.
基金项目 中央高校基本科研业务费专项资金；江苏省研究生科研与实践创新计划项目(KYCX_170132) 作者简介 余振鹏(1990—)，男，博士研究生;
黄侨(1958—)，男，教授，博士生导师 通信作者 黄侨，qhuanghit@126.com 文章历史 收稿日期: 2017-07-03



Contents            -->Abstract            Full text            Figures/Tables            PDF


轻集料混凝土局部受压试验及动力本构分析
余振鹏, 黄侨, 任政    
东南大学 交通学院，南京 210096

收稿日期: 2017-07-03
基金项目: 中央高校基本科研业务费专项资金；江苏省研究生科研与实践创新计划项目(KYCX_170132)
作者简介: 余振鹏(1990—)，男，博士研究生;
黄侨(1958—)，男，教授，博士生导师
通信作者: 黄侨，qhuanghit@126.com


摘要: 为探究轻集料混凝土单轴局部受压动力特性，采用试验机对轻集料混凝土单轴局部受压本构关系进行相关试验研究.考虑了5种不同加载应变率和4种不同加载面积，在位移控制下，得到轻集料混凝土单轴局部受压应力-应变曲线.根据应力-应变曲线特征点的峰值应力、峰值应变和弹性模量，分析不同加载应变率与加载面积对特征点的影响.同时根据混凝土黏弹塑性损伤本构模型，考虑不同加载应变率和加载面积的影响修正模型参数，并通过试验数据验证理论模型的合理性.研究结果表明：加载应变率和加载面积对轻集料混凝土应力-应变曲线影响明显；不同加载面积对轻集料混凝土弹性模量、峰值应力及峰值应变有较大影响；所提出的理论模型能够准确描述轻集料混凝土材料局部动力荷载作用下的应变率效应和非线性行为.
关键词: 轻集料混凝土    加载应变率    承压面积    损伤本构    试验力学性能    
Experiment and dynamic constitutive analysis of lightweight aggregate concrete under local compression
YU Zhenpeng, HUANG Qiao, REN Zheng    
School of Transportation, Southeast University, Nanjing 210096, China


Abstract: To investigate the dynamic behavior of lightweight aggregate concrete under uniaxial compression, the displacement controlled uniaxial compression experiments were carried out together by considering five loading rates and four loading areas, and the stress-strain curves of lightweight aggregate concrete were obtained. The effects of loading rates and loading areas on the peak stress, peak strain and elastic modulus were analyzed and discussed. The constitutive model of viscoelastic and plastic damage of concrete was developed by correcting the model parameters, and the rationality of proposed model was verified through experimental data. Results show that loading rates and loading areas have a significant effect on stress-strain curves of the concrete. Loading areas exhibit greater effects on elastic modulus, peak stress and peak strain of the lightweight aggregate concrete. The proposed model can accurately describe the strain rate effect and nonlinear behavior of the lightweight aggregate concrete under dynamic loading.
Key words: lightweight aggregate concrete    loading strain rate    loading area    damage constitutive relation    mechanical properties    
轻集料混凝土有着较高的强重比，轻质、高强、高耐久性等优点，它的导热性能只相当于普通混凝土的12%~33%，具有良好的防火性能^[1-3].在相同的强度等级下，其质量比普通混凝土低15%~25%，轻质高强便于结构设计的优化，受到国内外研究者的广泛关注，成为国内外混凝土衍生研究的重要方向之一，近年来轻集料高强混凝土也逐步成为研究热点，其具有更高的比强度，拓宽了轻集料混凝土的应用范围^[4].

轻集料混凝土与普通混凝土特性类似，属于多相复合性材料，其力学性能具有普通混凝土非线性、随机性和动力率相关效应的特征^[5].混凝土应用在结构中不仅受到静荷载作用同时也会受到地震、风等动荷载作用. 1953年，文献[6]总结大量实验数据，提出了普通混凝土单轴受压全过程的经验表达式，此后国外大量学者对普通混凝土动力性能展开试验与理论研究^[7-9].此外文献[10-11]详细总结了普通混凝土单轴受压全过程基本特征，提出了混凝土本构关系和破坏准则.文献[5、12-13]在普通混凝土随机动力学和损伤力学方面做出了创新性研究.文献[14]对高应变率下的混凝土力学行为影响因素展开了研究.然而针对轻集料混凝土局部受压动力性能的研究尚未受到国内外研究者的关注.

本文通过对轻集料混凝土设计4个不同加载面积和5种不同加载应变率，对轻集料混凝土局部受压动力性能进行试验研究，通过轻集料混凝土应力-应变曲线，提取峰值应力、峰值应变和弹性模量，分析不同加载应变率和加载面积对轻集料混凝土影响规律.同时在混凝土单标量弹塑性损伤本构模型的基础上, 对其进行动力扩展, 并在模型中同时考虑不同加载应变率以及不同加载面积的影响，修正模型参数.给出在不同加载应变率和不同加载面积情况下混凝土材料的数值模拟结果，并与轻集料混凝土试验结果对比分析, 验证所提出理论模型的合理性和有效性.

1 试验 1.1 材料性能及混凝土配合比本文试验根据文献[15]确定轻集料混凝土各组成材料比例关系，计算各组成材料的数量.本次试验选取了LC30轻集料混凝土，轻集料混凝土采用32.5级普通硅酸盐水泥，细骨料采用最大粒径为5 mm河砂，水为城市自来水，粗骨料采用5~15 mm页岩陶粒，每立方米轻集料混凝土需要水泥460 kg、水200 kg、砂650 kg和页岩陶粒670 kg.

1.2 试件设计与制作以不同的加载应变率、承压面积为变化参数，设计20组不同工况混凝土试件，每组工况制作3个试件，试件尺寸为100 mm×100 mm×100 mm.采用机械搅拌，振动台振捣密实，24 h后拆模并将试件放入20 ℃±3 ℃、湿度为95%以上标准养护室养护，养护时间为28 d，在28 d后即开展试验.根据相关文献普通混凝土的密度约在2 400 kg/m³，本文所浇筑混凝土容重均值在1 896 kg/m³，相比于普通混凝土容重降低了21%，轻集料混凝土容重降低明显^[1].为便于后期数据对比分析，制定试件工况编号见表 1.

表 1
表 1 不同工况轻集料混凝土编号 Table 1 Test conditions and numbers of lightweight aggregate concrete samples 加载应
变率/s^-1编号

100 mm×100 mm60 mm×60 mm20 mm×20 mm15 mm×15 mm

1.0×10^-5LC30-A-1LC30-A-2LC30-A-3LC30-A-4

5.0×10^-5LC30-B-1LC30-B-2LC30-B-3LC30-B-4

1.0×10^-4LC30-C-1LC30-C-2LC30-C-3LC30-C-4

5.0×10^-4LC30-D-1LC30-D-2LC30-D-3LC30-D-4

1.0×10^-3LC30-E-1LC30-E-2LC30-E-3LC30-E-4

注：根据文献[12]定义1.0×10^-5 s^-1为静态加载应变率${{\dot \varepsilon }_{\rm{s}}}$，5.0×10^-5 s^-1、1.0×10^-4 s^-1、5.0×10^-4 s^-1和1.0×10^-3 s^-1为动态加载应变率${{\dot \varepsilon }_{\rm{d}}}$.



表 1 不同工况轻集料混凝土编号 Table 1 Test conditions and numbers of lightweight aggregate concrete samples


1.3 加载装置及加载制度采用岩体裂隙渗流试验机，该设备内设精密力和位移传感器，3个相互垂直的加载作动头，每个加载作动头的加载量程为100 t，液压油泵通过一根特制油管与加载作动头连接提供压力，轴向变形与荷载由内置测试系统同步记录及显示在测试仪上，变形精度为0.000 5 mm，为获取混凝土应力-应变曲线，该设备装备刚架，使其具有足够的刚度，以获取得到应力-应变曲线下降段部分，试验加载装置如图 1(a)所示.

Figure 1
图 1 试件加载装置与试件 Figure 1 Test equipment and samples


局部荷载加载方式通过在试件加载面中心位置放置正方形钢块，厚度均为30 mm，并在钢块上放置100 mm×100 mm×5 mm钢板，对试件进行局部加载，钢块平面尺寸分别为60 mm×60 mm、20 mm×20 mm和15 mm×15 mm，钢块如图 1(b)所示.

试验采用位移控制加载制度.先将试件放置于加载台上，对试件进行预加载到2 kN，稳压0.5 min消除试件与加载台的间隙，将荷载降至0 kN，而后采用位移控制加载方式对试件进行加载.考虑动力加载主要考虑地震作用量级的加载应变率，即应变率范围为(1.0×10^-5~1.0×10^-3)s^-1并根据加载应变率将试验分为5组见表 1，加载直至试件破坏为止，测试仪记录的轴向荷载和变形曲线上出现的荷载峰值点定义为峰值应力，峰值应力对应的应变值定义为峰值应变.试件如图 1所示.

2 试验结果及其分析 2.1 试验现象及破坏形态设计强度等级为LC30轻集料混凝土，在不同加载应变率下混凝土破坏形态类似，其破坏过程的主要区别在于：高应变率加载等级下混凝土破坏所需要时间较短，混凝土裂缝发展以斜裂缝为主.而对于不同受压面积时，破坏过程及形态差异性较大，取部分图进行说明，如图 2所示.

Figure 2
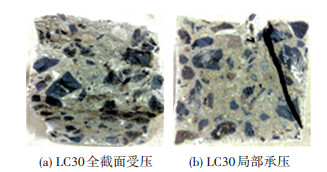图 2 轻集料混凝土破坏形态 Figure 2 Failure modes of lightweight aggregate concrete


在轻集料混凝土轴向加载中，轻集料混凝土的破坏是页岩陶粒的受剪破坏，该破坏形态与承压面积和加载应变率无关.根据相关文献普通混凝土静动载作用下的破坏形态均是普通混凝土粘结材料的破坏，与轻集料混凝土破坏形态存在明显的差异性^[6].

不同受压面积下，混凝土的破坏过程及形态差异性较大，取部分图加载应变率为1.0×10^-5s^-1轻集料混凝土破坏形态，如图 3所示.

Figure 3
图 3 不同承压面积下轻集料混凝土破坏形态 Figure 3 Failure modes of lightweight aggregate concrete under different loading areas


在轻集料混凝土全截面加载时，其加载面与自由面均形成多条裂纹，最终导致构件破坏.在局部加载面积为60 mm×60 mm，在钢块与混凝土接触面上形成贯穿破坏裂缝，自由面裂纹数量少于全截面加载工况.当局部加载面积为20 mm×20 mm和15 mm×15 mm时，在钢块与混凝土接触的4个顶点处形成4条主裂纹，裂纹由此发展至自由面上，自由面裂纹数量相对较少，深度较浅.

2.2 混凝土试件应力-应变曲线通过三轴岩石渗流应力耦合试验机在不同加载应变率与受压面积作用下，得到轻集料混凝土应力-应变曲线如图 4所示，相关工况应力-应变曲线是均值应力-应变曲线.其中应力是通过试验设备的压力传感器实时获得荷载数据与加载面积的比值，应变是加载作动头即局部变形的位移与试件高度的比值.试件受压作用下峰值应力、峰值应变及其弹性模量三项特征值来自于应力-应变曲线.

Figure 4
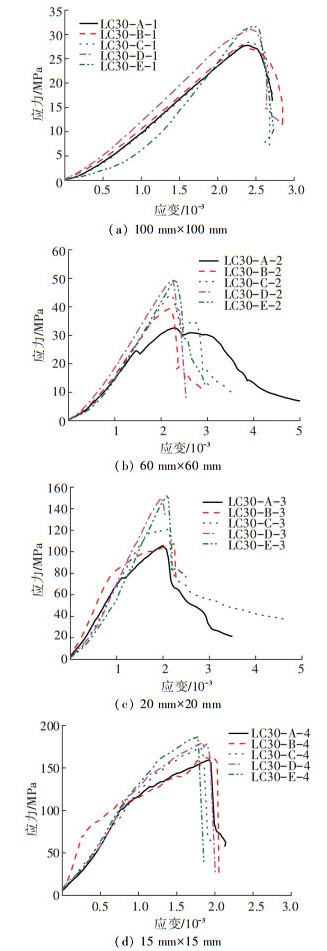图 4 LC30混凝土不同加载面积时应力-应变均值曲线 Figure 4 Stress-strain curves of LC30 concrete under uniaxial compression


如图 4(a)~4(d)所示为轻集料混凝土应力-应变曲线，当加载面积为全截面和60 mm×60 mm，应力达到峰值应力后，应力-应变曲线下降较为缓慢，形成一定弧形下降趋势；当加载面积为20 mm×20 mm和15 mm×15 mm，应力达到峰值应力后，应力-应变曲线突变成折线状下降趋势.该变化趋势与混凝土的加载应变率无关.究其原因，轻集料混凝土局部加载时，当加载面积较小(20 mm×20 mm和15 mm×15 mm时)，其应力值较全截面峰值应力提高4.3~6.8倍，混凝土试件局部应力集中，钢与混凝土加载面角点处裂纹发展贯穿，局部加载区域与周边混凝土发生剥离，应力瞬间释放在混凝土局部加载区域，导致该工况混凝土应力-应变曲线发生折线突变下降现象.

2.3 峰值应力根据图 4轻集料混凝土应力-应变曲线，提取各个工况混凝土应力峰值点，研究不同加载应变率和加载面积对轻集料混凝土峰值应力影响.为便于研究将加载应变率进行对数无量纲化，相同加载面积，用(5.0×10^-5~1.0×10^-3)s^-1峰值应力分别除以1.0×10^-5s^-1峰值应力如图 5(a)所示；相同加载应变率，用加载面积60 mm×60 mm、20 mm×20 mm和15 mm×15 mm混凝土的峰值应力分别除以全截面加载工况的峰值应力如图 5(b)所示.

Figure 5
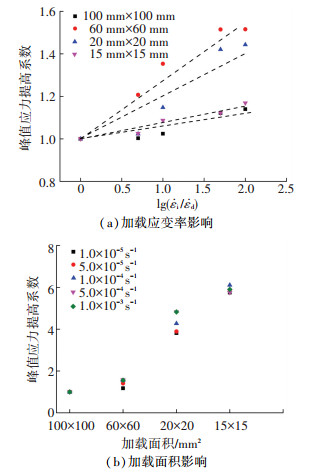图 5 L30混凝土峰值应力提高系数 Figure 5 Effect of loading rates on the peak stress of LC30 concrete


如图 5(a)所示，当混凝土加载应变率从(1.0×10^-5~1.0×^-3)s^-1时，其峰值应力呈上升趋势，轻集料混凝土强度有所提高，提高倍数在1.1~1.6倍之间，在局部受压60 mm×60 mm轻集料混凝土工况，提高强度倍数最高达1.52倍.加载应变率增大混凝土峰值应力明显提高，这与其他研究者对普通混凝土受应变率影响峰值应力提高系数变化范围基本相同，由于混凝土材料存在随机性的特点其应变率效应或强或弱.该结论符合混凝土损伤力学的观点，高应变率对混凝土的损伤演化产生迟滞作用，因此混凝土动力强度随着应变率增加而提高^[5].

如图 5(b)所示，将相同加载面积不同加载应变率混凝土4组峰值应力值取平均值，加载面积从60 mm×60 mm、20 mm×20 mm和15 mm×15 mm，轻集料混凝土相对全截面加载强度分别提高了1.46、4.35、5.88倍.由于局部加载混凝土中心部位，周围未受力混凝土部分对受力加载区域形成约束作用，延缓核心混凝土的变形，最终导致局部加载区域混凝土峰值应力有较大提高.

2.4 峰值应变为研究加载应变率和加载面积对轻集料混凝土峰值应变影响，根据图 4轻集料混凝土应力-应变曲线，提取各个工况混凝土峰值应变数据，为便于研究将数据无量纲化，如图 6所示.

Figure 6
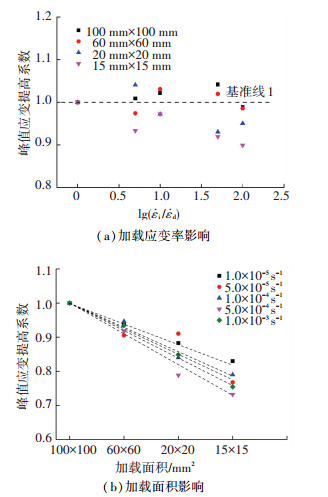图 6 LC30混凝土峰值应变提高系数 Figure 6 Effect of loading rates on the peak strain of LC30 concrete


根据图 6(a)所示，不同加载应变率对轻集料混凝土峰值应变影响，混凝土在相同加载面积，从加载应变率为(1.0×10^-5~1.0×10^-3) s^-1时，其应变整体变化较小，轻集料混凝土应变变化率基本均在8%之内，由于混凝土加载的随机性特点，存在有个别数据略超出变化范围.说明相同加载面积，加载应变率对混凝土的峰值应变影响较小，可忽略不计.根据相关文献研究，针对普通混凝土受压试验，加载应变率对于峰值应变影响并未得到确定结论，文献[13]对此进行总结，主要存在3种观点：1)混凝土峰值应变随着加载应变率增大而增大；2)混凝土峰值应变随着加载应变率增大而减小；3)混凝土峰值应变不随加载应变率的增大而变化.本文轻集料混凝土研究结果与上述观点3基本吻合.

根据图 6(b)，可见不同加载面积对轻集料混凝土峰值应变影响，混凝土在相同应变率，加载面积有全截面60 mm×60 mm、20 mm×20 mm和15 mm×15 mm，轻集料混凝土峰值应变逐步减小，呈线性变化态势.究其原因，混凝土加载面积减小，在加载过程中周围混凝土的约束作用越强，加载区域混凝土刚度逐步提高，导致其峰值应变逐步降低.

2.5 弹性模量弹性模量作为混凝土材料本构关系重要特征值之一，为研究加载应变率和加载面积对轻集料混凝土弹性模量影响，根据图 4轻集料混凝土应力-应变曲线，提取各个工况混凝土弹性模量，为便于对比研究将数据无量纲化，如图 7所示为不同加载应变率和加载面积对轻集料混凝土弹性模量影响.

Figure 7
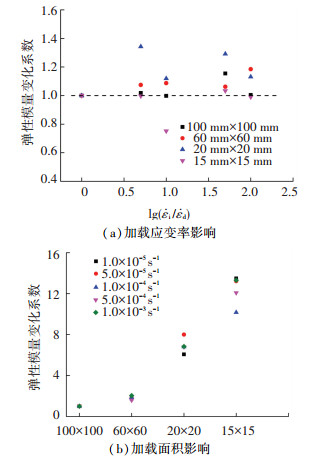图 7 LC30混凝土弹性模量提高系数 Figure 7 Effect of loading rates on the elastic modulus of LC30 concrete


根据图 7(a)所示，不同加载应变率率对轻集料混凝土弹性模量影响，混凝土试块在相同加载面积时，从加载应变率为(1.0×10^-5~1.0×10^-3) s^-1，其弹性模量整体变化较不规律，当加载面积为全截面加载时，轻集料混凝土弹性模量变化较小，基本控制在2%左右.根据相关文献研究结论，随着加载应变率增加弹性模量值也随之增加，文献[12]中普通混凝土加载应变率为(1.0×10^-5~1.0×10^-1)s^-1，其弹性模量相对增量最大为11.1%.本研究弹性模量变化范围与此不相违背.

在局部加载面积60 mm×60 mm、20 mm×20 mm和15 mm×15 mm的轻集料混凝土，加载应变率为(1.0×10^-5~1.0×10^-3) s^-1时，轻集料混凝土变化波动较大，但一般变化在20%以内，由于混凝土离散性与随机性特点导致个别数据弹性模量发生异常.究其原因由于局部加载和不同加载应变率下轻集料混凝土的耦合作用，导致弹性模量出现相对较大的波动.

如图 7(b)所示，加载面积为60 mm×60 mm, 20 mm×20 mm和15 mm×15 mm，为便于试验对比分析研究，将相同加载面积不同加载应变率混凝土4组弹性模量值取平均值，轻集料混凝土弹性模量相对于全截面加载弹性模量分别提高约1.81、6.90、12.44倍.

2.6 局部加载模型分析为便于更深入分析研究局部加载工况混凝土试件受力机理，根据加载工况将其简化成局部加载约束模型进行分析.

当混凝土试件全截面加载时，试件不受周围混凝土约束作用，轻集料混凝土4个自由面受到约束应力作用为0，由破坏形态图 3(a)所示，该工况4个自由面发生了明显的剥落和破坏；当混凝土试件受局部加载影响时，此时仅加载区域核心混凝土受到荷载作用，受力过程中，周围混凝土对其有一定的约束作用，核心混凝土受到三向作用，其作用随着加载面积的减小而增大.由破坏形态图 3(b)~3(d)所示，有约束作用的混凝土4个自由面没有发生明显的剥落和破坏，仅每个自由面出现1、2条明显开展裂缝，约束作用越大，自由面裂缝越不明显.核心混凝土面积部分越小，约束面积越大，核心混凝土的弹性模量值也会随之增大.

3 动力黏弹塑性损伤本构理论模型与试验验证 3.1 单标量弹塑性损伤本构模型在文献中，建议了基于能量的静力弹塑性损伤本构模型.一般认为，当描述均质材料的各向同性损伤时，若不关心反复荷载作用下的刚度恢复等效应，单标量弹塑性损伤本构模型已经能够满足要求.

对于弹塑性损伤材料，在有效应力空间中的无损材料符合经典弹塑性模型.根据应变等效原理，有

$\bar \sigma = {E_0}:{\varepsilon ^{\rm{e}}} = {E_0}:\left( {\varepsilon - {\varepsilon ^{\rm{p}}}} \right).$ (1)

式中:σ为有效应力，E₀为弹性刚度张量，ε^e为弹性应变张量，ε^p为塑性应变张量，ε为总应变张量.

从而得到混凝土弹塑性损伤本构关系为

$\sigma = \left( {1 - d} \right)\bar \sigma = \left( {1 - d} \right){E_0}:\left( {\varepsilon - {\varepsilon ^{\rm{p}}}} \right).$ (2)

式中d为损伤变量, 损伤会导致材料的卸载刚度退化，即0≤d≤1.

3.2 内变量演化法则 3.2.1 塑性流动法则假设混凝土损伤材料的塑性流动发生在混凝土材料的无损伤部分，则塑性流动法则的确定应在有效应力空间内进行.由于在有效应力空间考虑塑性变形，所以考察其物理意义，是混凝土材料损伤的发展影响混凝土塑性变形的发展，这符合实际情况.

对于塑性应变演化法则，在不影响计算精度的前提下，可采用简化公式

${{\dot \varepsilon }^{\rm{p}}} = {b^{\rm{p}}}\bar \sigma , $ (3)

${b^{\rm{p}}} = {E_0}\xi H\left( {\dot d} \right)\frac{{\left\langle {{\varepsilon ^{\rm{e}}}:\dot \varepsilon } \right\rangle }}{{\bar \sigma :\bar \sigma }} \ge 0.$ (4)

式中:ξ为描述混凝土受压塑性变形的模型参数，0≤ξ≤1，ξ=0、1分别对应于有效应力空间的线弹性和理想弹塑性.根据相关文献及数据分析在此令ξ=0.2^[5].

H(·)为Heaviside函数，定义为

$H\left( x \right) = \left\{ \begin{array}{l}1, x > 0;\\0, x \le 0.\end{array} \right.$

〈·〉为Macaulay括号，定义为$\left\langle x \right\rangle = \frac{{x + \left| x \right|}}{2}$.

3.2.2 损伤演化法则混凝土材料的率相关效应，与塑性变形发展和损伤演化均有关系，但损伤演化在率相关效应中占主导地位.对于损伤内变量d，在确定性损伤力学框架内，可通过对损伤流动因子${{\dot \lambda }^d}$进行动力扩展，用来反映混凝土在动力加载时损伤演化的滞后效应.

在经典损伤力学中，通过引入损伤势函数来确定材料的损伤状态，损伤势函数G(Y, r)可定义为

$G\left( {Y, r} \right) = g\left( Y \right) - g\left( r \right).$ (5)

式中：G=0确定的曲面为损伤面；g(·)为单调递增函数；Y为混凝土在某一时刻t的损伤能释放率；r为时刻t的损伤能释放率阈值，$r = \max \left\{ {{r_0}, \mathop {\max }\limits_{\tau = \left[ {0, t} \right]} {Y_\tau }} \right\}$，其中r₀为材料初始损伤能释放率阈值.

考虑损伤准则的确立，只有当材料损伤能释放率Y超过材料初始损伤能释放率阈值r₀时，损伤才发生.在材料加载过程中任一时刻t，若材料损伤能释放率Y_t超过历史最大损伤能释放率r_t时，材料损伤将进一步发展，即处于损伤加载状态，否则处于损伤卸载或中性变载阶段.

根据文献，令混凝土材料的损伤能释放率为

$Y = \alpha {{\bar I}_1} + \sqrt {3{{\bar J}_2}} .$ (6)

式中:I₁、J₂分别为有效应力张量σ的第一不变量和有效偏应力张量s的第二不变量；α为常数，$\alpha = \left( {\frac{{{f_{{\rm{by}}}}}}{{{f_{\rm{y}}}}} - 1} \right)/\left( {2\frac{{{f_{{\rm{by}}}}}}{f} - 1} \right)$，其中f_by为双轴等压峰值强度，f_y为单轴受压峰值强度.根据文献[5]，建议模型中双轴等压和单轴受压强度之比取为1.16，则有α=0.121 2.

则可得到混凝土的初始弹塑性损伤能阈值为

${r_0} = \left( {1 - \alpha } \right){f_0}.$ (7)

式中:f₀对应于单轴受压状态下的线弹性极限强度，一般取为(0.3~0.5)f_c，其中f_c为混凝土单轴抗压强度.

直接对损伤能释放率进行动力扩展，即

${{\dot r}_t} = \mu {\left\langle {\frac{{{Y_t}}}{{{r_t}}} - 1} \right\rangle ^n}.$ (8)

式中:Y_t为动力损伤能释放率；r₀为初始损伤能释放率阈值；r_t为历史最大损伤能释放率；μ、n为动力效应经验参数.

根据上述损伤准则以及损伤变量演化法则，给出动力受压损伤演化的表达式为

$d = 1 - \frac{{{r_0}}}{{{r_t}}}\left( {1 - A} \right) - A\exp \left[ {B\left( {1 - \frac{{{r_{\rm{t}}}}}{{{r_{\rm{0}}}}}} \right)} \right].$ (9)

式中:A、B分别为模型参数，可根据试验得到的应力应变曲线加以标定.

3.3 模型的修正及数值实现考虑混凝土单轴受压时加载面积对轻集料混凝土强度的影响，根据试验结果可初步推断，混凝土加载面积越小，周围混凝土对加载区域的核心混凝土约束作用越强，从而导致混凝土整体刚度增大.为了反映混凝土刚度随着加载面积减小而增大的效应，可通过对混凝土初始弹性模量乘一个放大系数α来近似考虑.

根据试验数据拟合结果，在横纵坐标轴均取对数坐标的前提下，放大系数α与混凝土加载面积S近似成线性关系，拟合函数表达式为

$\ln \alpha = 4.900 - 0.532\ln S.$ (10)

根据该拟合函数表达式，可对混凝土弹塑性损伤本构模型进行修正, 即

$\begin{array}{l}\sigma = \left( {1 - d} \right)\alpha {E_0}:\left( {\varepsilon - {\varepsilon ^{\rm{p}}}} \right) = \\\;\;\;\;\;\;\left( {1 - d} \right){{\rm{e}}^{4.900 - 0.532\ln S}}{E_0}:\left( {\varepsilon - {\varepsilon ^{\rm{p}}}} \right).\end{array}$ (11)

相关参数意义如上各式所示.

3.4 理论结果分析根据式(3)~(11)，用MATLAB编程实现混凝土弹塑性损伤本构模型的数值算法.混凝土材料的力学性能参数如下：初始弹性模量、泊松比和单轴抗压强度.根据混凝土在不同应变率作用下的单轴试验，可确定模型参数f₀、μ和n.模型中的其他参数引用文献[5], 有A=1.0，B=0.213.

由上述计算参数和计算模型，利用MATLAB编程实现得到轻集料混凝土不同加载应变率和加载面积下应力-应变曲线，其计算工况与上述试验工况一致对应，如图 8所示为轻集料混凝土试件应力-应变曲线.

Figure 8
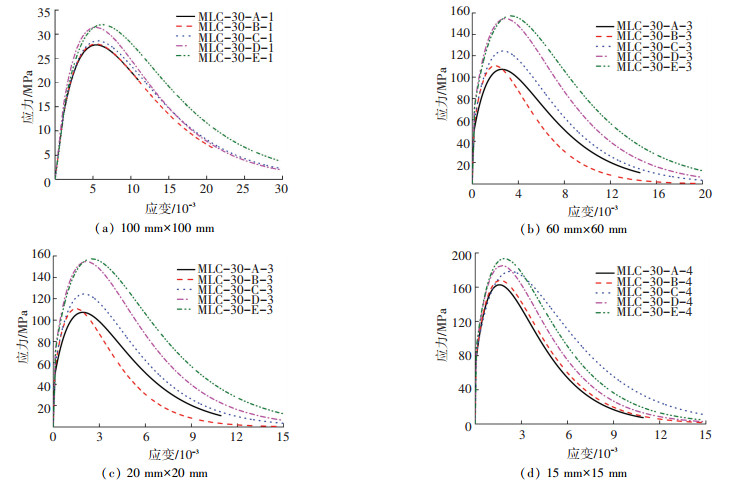图 8 LC30混凝土应力-应变均值理论曲线 Figure 8 Stress-strain theoretical curves of LC30 concrete under uniaxial compression


如图 8(a)~8(d)所示，当加载面积相同时，随着加载应变率的增加，轻集料混凝土试件材料非线性也会随之降低，其轴向抗压强度有一定程度的提高；当加载应变率相同时，随着加载面积减小，轻集料混凝土轴向抗压强度提高幅度较高；这与试验结果相一致.在峰值应力与峰值应变比较中，所提出的模型与试验数据吻合较好；应力-应变曲线下降段部分，模型所得到应力-应变曲线与试验曲线存在较为明显差异性，其主要原因在于混凝土受压面积与应变率的耦合作用导致在应力-应变曲线后阶段发展的复杂性使其具有明显差异性，但不影响对轻集料混凝土局部受压动力性能应力-应变曲线特征值的分析比较.

3.5 试验与理论结果对比分析将轻集料混凝土试件各个工况试验所得到峰值应力值与计算模型得到对应工况峰值应力值对比分析，如图 9所示.

Figure 9
图 9 LC30混凝土试验峰值应力与理论计算峰值应力对比 Figure 9 Comparison of test value and theoretical value about peak stress of LC30 concrete


如图 9所示，轻集料混凝土理论模型计算所得到的峰值应力值与试验所得到的峰值应力值吻合度高，理论计算模型所得到峰值应力值均略高于试验所得到的峰值应力值，最大误差在3.01%.当加应变率率相同，加载面积越小，其理论值与试验值误差相对越大；当加载面积相同，加载应变率越大，其理论值与试验值误差相对越大.所提出理论计算模型在单轴受压并考虑不同加载面积的情况下，能够很好地描述混凝土在动力作用下的应变率效应和非线性行为.

4 结论1) 轻集料混凝土破坏是页岩陶粒剪切破坏，破坏形态均与承压面积和加载应变率无关.轻集料混凝土加载面积为全截面和60 mm×60 mm，应力-应变曲线到峰值点后下降趋势形成一定弧形；当加载面积为20 mm×20 mm和15 mm×15 mm，曲线突变折线状下降趋势.

2) 当加载应变率从1.0×10^-5s^-1到1.0×10^-3 s^-1时，轻集料混凝土峰值应力均有所提高，提高倍数在1.1~1.6倍之间，最高达1.52倍.加载面积减小，轻集料混凝土峰值应变呈线性减小趋势，轻集料混凝土峰值应力和弹性模量均有明显提高，本试验弹性模量最大提高到10倍左右.

3) 所提出考虑加载面积影响的混凝土动力黏弹塑性损伤本构模型应用于轻集料混凝土材料非线性数值模拟中，理论模型能够准确描述轻集料混凝土材料动力荷载作用下的应变率效应和非线性行为.


参考文献
[1] 过镇海. 混凝土的强度和变形-实验基础和本构关系[M]. 北京: 清华大学出版社, 1997.
GUO Zhenhai. Concrete strength and deformation of a test basis and constitutive relation[M]. Beijing: Tsinghua University Press, 1997.


[2] 吉伯海, 胡正清, 陈甲树, 等. 圆钢管轻集料混凝土构件抗弯性能的试验研究[J]. 土木工程学报, 2007, 40(8): 35-40.
JI Bohai, HU Zhengqing, CHEN Jiashu, et al. An experimental study on the behavior of lightweight aggregate concrete filled circular steel tubes under pure bending load[J]. China Civil Engineering Journal, 2007, 40(8): 35-40.


[3] 程从密, 苏达根, 焦楚杰, 等. 有机轻集料混凝土的单轴受压试验研究[J]. 华南理工大学学报(自然科学版), 2011, 39(11): 114-119.
CHENG Congmi, SU Dagen, JIAO Chujie, et al. Experimental investigation into compression property of organic lightweight aggregate concrete under uniaxial loading[J]. Journal of South China University of Technology (Natural Science), 2011, 39(11): 114-119. DOI:10.3969/j.issn.1000-565X.2011.11.021


[4] 李文斌. 陶粒轻集料高性能混凝土的试验研究[D]. 西安: 西安建筑科技大学, 2012.
LI Wenbin. Research on the light-weight haydite aggregate concrete[D]. Xi'an: Xi'an University of Architecture and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10703-1012045275.htm


[5] 李杰, 吴建营, 陈建兵. 混凝土随机损伤力学[M]. 北京: 科学出版社, 2014.
LI Jie, WU Jianying, CHEN Jianbing. Stochastic damage mechanics of concrete structures[M]. Beijing: Science Press, 2014.


[6] BISCHOFF P H, PERRY S H. Compressive behaviour of concrete at high strain rates[J]. Materials & Structures, 1991, 24(6): 425-450.


[7] MANDER J B, PRIESTLEY M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804)


[8] DILGER W H, KOCH R, KOWALCZYK R. Ductility of plain and confined concrete under different strain rates[J]. Journal of the American Concrete Institute, 1984, 81(1): 73-81.


[9] ALDUAIJ J, ALSHALEH K, HAQUE M N, et al. Structural beha-vior of selected lightweight concrete beams[J]. Kuwait Journal of Science & Engineering, 2003, 30(2): 139-152.


[10] 过镇海, 张秀琴, 张达成, 等. 混凝土应力-应变全曲线的试验研究[J]. 建筑结构学报, 1982, 3(1): 1-12.
GUO Zhenhai, ZHANG Xiuqin, ZHANG Dacheng, et al. Experimental investigation of the complete stress-strain curve of concrete[J]. Journal of Building Structures, 1982, 3(1): 1-12.


[11] 施林林, 宋玉普, 沈璐. 不同应变率下大骨料及湿筛混凝土单轴受压试验研究[J]. 世界地震工程, 2016, 32(2): 270-276.
SHI Linlin, SONG Yupu, SHEN Lu. Experimental study on uniaxial compression properties of large aggregate and wet-screened concrete at different strain rates[J]. World Earthquake Engineering, 2016, 32(2): 270-276.


[12] 李杰, 晏小欢, 任晓丹. 不同加载速率下混凝土单轴受压性能大样本试验研究[J]. 建筑结构学报, 2016, 37(8): 66-75.
LI Jie, YAN Xiaohuan, REN Xiaodan. Large-sample experimental study on uniaxial compressive behavior of concrete under different loading rates[J]. Journal of Building Structures, 2016, 37(8): 66-75.


[13] 曾莎洁, 李杰. 混凝土单轴受压动力全曲线试验研究[J]. 同济大学学报(自然科学版), 2013, 41(1): 7-10.
ZENG Shajie, LI Jie. Experimental study on uniaxail compression behavior of concrete under dynamic loading[J]. Journal of Tongji University (Natural Science), 2013, 41(1): 7-10.


[14] LU D, WANG G, Du X, et al. A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete[J]. International Journal of Impact Engineering, 2017, 103(4): 124-137.


[15] 轻骨料混凝土技术规程: JGJ51-2002[S]. 北京: 中国建筑工业出版社, 2002.
Light aggregate concrete technology discipline: JGJ51-2002[S]. Beijing: China Architecture & Building Press, 2002.