田秀娟1,于德新1,2,邢雪3,商强1,王树兴4
(1.吉林大学 交通学院,长春 130022; 2. 吉林省道路交通重点实验室,长春 130022; 3.吉林化工学院 信息与控制工程学院,吉林 吉林132022; 4. 山东高速股份有限公司,济南 250000)
摘要:
为提高交叉口短时交通流预测精度，以历史交通流量数据为基础，提出一种基于自适应噪声完整集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)-排列熵(permutation entropy，PE)-在线序贯极限学习机(online sequential extreme learning machine，OSELM)组合预测模型(CEEMDAN-PE-OSELM).首先对交通流历史时间序列数据进行CEEMDAN分解，得到多个本征模态函数(intrinsic mode function，IMF)分量；通过PE算法对IMF分量进行重组，形成具有复杂度差异的重组子序列.然后，分别构建重组子序列OSELM预测模型，将预测结果相加得到最终预测流量.最后选取一实际交叉口，进行模型验证分析.结果表明：CEEMDAN-PE-OSELM模型的MAE、MAPE和MSE的值均低于其他模型，预测误差最小；EC值为0.963，高于ARIMA模型的EC值(0.898)，最接近于1，预测精度最高，稳定性最好.就同一预测模型而言，经过CEEMDAN-PE处理的模型的各项误差明显降低，预测精度有所提高.
关键词: 时间序列 短时流量预测 组合预测 经验模态分解 极限学习机
DOI：10.11918/j.issn.0367-6234.201703102
分类号:U491
文献标识码:A
基金项目:国家科技支撑计划项目(2014BAG03B03)； 山东省省管企业科技创新项目(20122150251-1)
Prediction model of CEEMDAN PE OSELM for intersections short term traffic flow
TIAN Xiujuan1,YU Dexin1,2,XING Xue3,SHANG Qiang1,WANG Shuxing4
(1. College of Transportation, Jilin University, Changchun 130022, China; 2. Jilin Province Key Laboratory of Road Traffic, Changchun 130022, China; 3. College of Information and Control Engineering, Jilin Institute of Chemical Technology, Jilin 132022, Jilin, China;4. Shandong High-Speed Company Limited, Jinan 250000, China)
Abstract:
To improve the prediction accuracy of intersection short-term traffic flow, a new CEEMDAN-PE-OSELM model is developed based on the complete ensemble empirical mode decomposition with adaptive noise(CEEMDAN), permutation entropy(PE) and online sequential extreme learning machine(OSELM). Firstly, traffic flow historical time series are decomposed by CEEMDAN algorithm. Secondly, PE algorithm is used to recombine the IMF components obtained by CEEMDAN, and a series of restructured subsequences can be obtained, which have a significant difference in terms of complexity. Then, the OSELM prediction models are proposed for each restructured subsequence respectively, and the final results are got by adding the prediction results. Finally, a typical intersection is verified the effect and performance of the hybrid prediction model. Results show that the values of MAE, MAPE and MSE of CEEMDAN-PE-OSELM prediction model are lower than other models, and get a minimal error. The EC value of the improved model is 0.963, which is higher than that of ARIMA model (0.898) and the most close to 1. The CEEMDAN-PE-OSELM prediction model has the highest precision and best stability, and the errors decrease obviously.
Key words: time series short-term traffic prediction hybrid prediction empirical mode decomposition extreme learning machine
田秀娟, 于德新, 邢雪, 商强, 王树兴. 交叉口短时流量CEEMDAN-PE-OSELM预测模型[J]. 哈尔滨工业大学学报, 2018, 50(3): 83-89. DOI: 10.11918/j.issn.0367-6234.201703102.
TIAN Xiujuan, YU Dexin, XING Xue, SHANG Qiang, WANG Shuxing. Prediction model of CEEMDAN-PE-OSELM for intersections short-term traffic flow[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 83-89. DOI: 10.11918/j.issn.0367-6234.201703102.
基金项目 国家科技支撑计划项目(2014BAG03B03)；山东省省管企业科技创新项目(20122150251-1) 作者简介 田秀娟(1990—)，女，博士研究生;
于德新(1972—)，男，教授，博士生导师 通信作者 于德新，yudx@jlu.edu.cn 文章历史 收稿日期: 2017-03-21
Contents -->Abstract Full text Figures/Tables PDF
交叉口短时流量CEEMDAN-PE-OSELM预测模型
田秀娟1, 于德新1,2
, 邢雪3, 商强1, 王树兴4 1. 吉林大学 交通学院，长春 130022;
2. 吉林省道路交通重点实验室，长春 130022;
3. 吉林化工学院 信息与控制工程学院，吉林 吉林132022;
4. 山东高速股份有限公司，济南 250000
收稿日期: 2017-03-21
基金项目: 国家科技支撑计划项目(2014BAG03B03)；山东省省管企业科技创新项目(20122150251-1)
作者简介: 田秀娟(1990—)，女，博士研究生;
于德新(1972—)，男，教授，博士生导师
通信作者: 于德新，yudx@jlu.edu.cn
摘要: 为提高交叉口短时交通流预测精度，以历史交通流量数据为基础，提出一种基于自适应噪声完整集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise，CEEMDAN)-排列熵(permutation entropy，PE)-在线序贯极限学习机(online sequential extreme learning machine，OSELM)组合预测模型(CEEMDAN-PE-OSELM).首先对交通流历史时间序列数据进行CEEMDAN分解，得到多个本征模态函数(intrinsic mode function，IMF)分量；通过PE算法对IMF分量进行重组，形成具有复杂度差异的重组子序列.然后，分别构建重组子序列OSELM预测模型，将预测结果相加得到最终预测流量.最后选取一实际交叉口，进行模型验证分析.结果表明：CEEMDAN-PE-OSELM模型的MAE、MAPE和MSE的值均低于其他模型，预测误差最小；EC值为0.963，高于ARIMA模型的EC值(0.898)，最接近于1，预测精度最高，稳定性最好.就同一预测模型而言，经过CEEMDAN-PE处理的模型的各项误差明显降低，预测精度有所提高.
关键词: 时间序列 短时流量预测 组合预测 经验模态分解 极限学习机
Prediction model of CEEMDAN-PE-OSELM for intersections short-term traffic flow
TIAN Xiujuan1, YU Dexin1,2
, XING Xue3, SHANG Qiang1, WANG Shuxing4 1. College of Transportation, Jilin University, Changchun 130022, China;
2. Jilin Province Key Laboratory of Road Traffic, Changchun 130022, China;
3. College of Information and Control Engineering, Jilin Institute of Chemical Technology, Jilin 132022, Jilin, China;
4. Shandong High-Speed Company Limited, Jinan 250000, China
Abstract: To improve the prediction accuracy of intersection short-term traffic flow, a new CEEMDAN-PE-OSELM model is developed based on the complete ensemble empirical mode decomposition with adaptive noise(CEEMDAN), permutation entropy(PE) and online sequential extreme learning machine(OSELM). Firstly, traffic flow historical time series are decomposed by CEEMDAN algorithm. Secondly, PE algorithm is used to recombine the IMF components obtained by CEEMDAN, and a series of restructured subsequences can be obtained, which have a significant difference in terms of complexity. Then, the OSELM prediction models are proposed for each restructured subsequence respectively, and the final results are got by adding the prediction results. Finally, a typical intersection is verified the effect and performance of the hybrid prediction model. Results show that the values of MAE, MAPE and MSE of CEEMDAN-PE-OSELM prediction model are lower than other models, and get a minimal error. The EC value of the improved model is 0.963, which is higher than that of ARIMA model (0.898) and the most close to 1. The CEEMDAN-PE-OSELM prediction model has the highest precision and best stability, and the errors decrease obviously.
Key words: time series short-term traffic prediction hybrid prediction empirical mode decomposition extreme learning machine
作为智能交通系统(intelligent transportation systems, ITS)重要子系统，交通控制和诱导系统皆以交通状态预测为前提，而短时交通流量预测是交通状态预测的基础.通常，信号控制周期小于3 min，诱导周期为5 min.虽然采集设备日趋完善，但对于高效的控制和诱导系统而言，检测设备采集的信息仍具有一定的滞后性.此外，ITS快速发展对交通流预测提出了更高的要求.因此，研究高效准确的短时(通常为5 min)交通流预测方法具有重要意义.针对短时交通流预测，国内外进行了大量研究，建立了多种模型，大体分为4类：1)统计模型，如时间序列[1]、Klaman模型[2]等. 2)非线性模型，如混沌理论[3]、小波理论模型[4]等. 3)智能模型，如神经网络[5]、支持向量机模型[6]等. 4)组合预测模型，如AFSA-LSSVM[7]、PSR-RELM模型[8]等.混沌理论、神经网络及支持向量机在分析复杂非线性不确定系统方面具有明显优势.但传统神经网络多采用梯度下降法，易陷入局部最优，且学习速度慢.极限学习机(extreme learning machine，ELM)[9]学习速度快，泛化性能好，广泛应用于工程问题. OSELM算法[10]是对ELM的改进，分批训练历史数据，支持可变样本数.交通流量数据在实际采集和传输中，缺失与错误不可避免，应根据情况分批训练，因此，OSELM算法能满足交通流量预测要求.此外，交叉口交通流数据具有非平稳性，进行先验分析有助于提高预测精度. CEEMDAN[11]是对EEMD[12]的改进，提高分解效率同时重构误差几乎为零.基于现有研究，本文提出一种基于CEEMDAN-PE-OSELM的组合预测模型，以提高交叉口短时流量预测精度.
1 CEEMDAN-PE数据分解与重组对交叉口流量时间序列进行CEEMDAN分解；然后利用PE算法计算IMF分量的排列熵值，对序列重组.
1.1 CEEMDAN方法EMD方法是按照不同波动尺度对原始序列进行分解，得到不同幅值的IMF分量[13]. CEEMDAN方法则通过在每一分解阶段添加自适应白噪声，计算唯一余量以获取IMF分量，分解过程完整[11].
记原始交通流量时间序列为s(n)，第i(1, 2, ..., I)次添加的标准正态分布白噪声序列为vi(n)，则第i次分解交通流量序列可以表示为si(n)=s(n)+vi(n).定义Ek(·)和FIM, k分别为第k个由EMD和CEEMDAN产生的模态分量. CEEMDAN步骤如下.
步骤1?与EEMD方法[12]相同，CEEMDAN也是针对交通流时间序列s(n)+ε0vi(n)进行I次分解.因此，可以通过EMD方法获取第1个模态分量为
${F_{{\rm{IM}},1}}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {F_{{\rm{IM}},1}^i\left( n \right)} = \overline {{F_{{\rm{IM}},1}}} \left( n \right).$ (1)
步骤2 ?在第1阶段(k=1)，计算第1个唯一的余量流量序列为
${r_1}\left( n \right) = s\left( n \right) - {F_{{\rm{IM}},1}}\left( n \right).$ (2)
步骤3 ?对流量序列r1(n)+ε1E1(vi(n))进行i(1, 2, ..., I)次分解，直到得到第1个EMD流量模态分量为止.同理，可得到第2个模态分量为
${F_{{\rm{IM}},2}}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}\left( {{r_1}\left( n \right)} \right)} + {\varepsilon _1}{E_1}\left( {{v^i}\left( n \right)} \right).$ (3)
步骤4 ?类似地，计算其他阶段的第k(2, 3, ..., K)个余量序列；然后依据步骤3，得到第k+1个模态分量，即
${r_k}\left( n \right) = {r_{k - 1}}\left( n \right) - {F_{{\rm{IM}},k}}\left( n \right),$ (4)
${F_{{\rm{IM}},k + 1}}\left( n \right) = \frac{1}{I}\sum\limits_{i = 1}^I {{E_1}\left( {{r_k}\left( n \right)} \right)} + {\varepsilon _k}{E_k}\left( {{v^i}\left( n \right)} \right).$ (5)
步骤5 ?当余量序列不能继续分解时，即余量信号的极值点个数至多不超过两个，算法结束.此时，共得到K个模态分量，余量序列的最终结果为
$R\left( n \right) = s\left( n \right) - \sum\limits_{k = 1}^K {{F_{{\rm{IM}},k}}} .$ (6)
则原始交通流量时间序列s(n)最终被分解为
综上，CEEMDAN分解过程完整，能够对原始交通流量时间序列精确分解.
1.2 PE算法PE算法[14]可以衡量系统复杂度，表征时间序列的随机性和动力学突变特性.概念简单，计算速度快，抗干扰能力强，特别适用于非线性数据，对时间序列变化的敏感性很高，并且具有很好的鲁棒性[15]，已广泛应用于各种时间序列.
交叉口流量数据具有一定的随机性和非平稳性，使得CEEMDAN分解得到的交通流IMF分量较多.因此，为了减小计算规模，本文采用PE算法进行IMF重组，步骤如下.
步骤1 ?首先对CEEMDAN得到的各IMF流量序列{X(i), i=1, 2, ..., N}进行相空间重构[16]，得到相空间矩阵
$Y = \left[ {\begin{array}{*{20}{c}}{x\left( 1 \right)}&{x\left( {1 + \tau } \right)}& \cdots &{x\left( {1 + \left( {m - 1} \right)\tau } \right)}\\ \vdots&\vdots&\vdots&\vdots \\{x\left( j \right)}&{x\left( {j + \tau } \right)}& \cdots &{x\left( {j + \left( {m - 1} \right)\tau } \right)}\\ \vdots&\vdots&\vdots&\vdots \\{x\left( K \right)}&{x\left( {K + \tau } \right)}& \cdots &{x\left( {K + \left( {m - 1} \right)\tau } \right)}\end{array}} \right].$ (7)
式中m和τ分别表示嵌入维数和延迟时间; j=1, 2, …, K.
步骤2?将上述矩阵的每行作为一个分量，则共有K个分量，存在关系K=n－(m－1)τ.以第j个分量(x(j), x(j+τ), …, x(j+(m－1)τ))为例，按照各元素数值大小，进行升序排列，即
$\begin{array}{*{20}{c}}{x\left( {i + \left( {{j_1} - 1} \right)\tau } \right) \le x\left( {i + \left( {{j_2} - 1} \right)\tau } \right) \le }\\{ \cdots \le x\left( {i + \left( {{j_m} - 1} \right)\tau } \right).}\end{array}$ (8)
式中j1, j2, …, jm表示各分量元素所在列序号.如存在x(i+(j1－1)τ)=x(i+(j2－1)τ)，则按照j1和j2值大小排序.综上，对于任意流量时间序列X(i)的相空间重构矩阵的每一行向量都可以得到一组序列S(l)为
$S\left( l \right) = \left\{ {{j_1},{j_2}, \cdots ,{j_m}} \right\}.$ (9)
式中l=1, 2, …, k，且存在k≤m!, m维相空间共有m!种不同的映射符号序列.
步骤3 ?计算每种符号序列S(l)出现的概率P1，P2，…，Pk.按照Shannon熵的形式，可以将流量时间序列X(i)的第k种不同符号序列的排列熵Hp(m)定义为
${H_{\rm{p}}}\left( m \right) = - \sum\limits_{j = 1}^k {{P_j}\ln {P_j}} .$ (10)
由上式可知，当Pj=1/m!时，Hp(m)达到最大值ln(m)!.为了方便，将Hp(m)进行标准化处理
${H_{{\rm{PE}}}}\left( m \right) = {H_{\rm{p}}}\left( m \right)/\ln \left( {m!} \right),$ (11)
式中0≤HPE(m)≤1，大小表示时间序列的随机程度.值越大，随机性越强；反之，随机性越弱.嵌入维数m和延迟时间τ是PE算法两个重要参数.研究表明，当样本量较小时，嵌入维数m通常较小；对于样本量大于1 024的时间序列来说，当m=6时，即可获得稳定的排列熵值；而延迟时间τ对于排列熵的影响较小[17].
通过以上步骤，计算各IMF排列熵.依据排列熵值接近程度，对IMF分量合并，得到重组子序列.
2 CEEMDAN-PE-OSELM组合预测模型构建将重组子序列作为输入数据构建OSELM预测模型，将多个预测结果相加得到最终预测流量.
2.1 OSELM算法在OSELM算法训练中，仅需输入当前批次数据更新网络权值，无需重复扫描历史数据，泛化能力强.分为初始化和序贯学习两个阶段，步骤如下.
步骤1?从给定的交叉口交通流量训练集D={(xi, ti)|xi∈Rn, ti∈Rm, i=1, L, N)}中选取少量的流量数据D0={(xi, ti)}i=1N0，初始化，其中L为隐含层节点数，N0满足N0≥L.
步骤2 ?随机生成隐含层节点参数(ai, bi), i=1, 2, ..., L；计算得到初始隐含层输出矩阵为
${\mathit{\boldsymbol{H}}_0} = {\left[ {\begin{array}{*{20}{c}}{G\left( {{a_1},{b_1},{x_1}} \right)}& \cdots &{G\left( {{a_L},{b_L},{x_1}} \right)}\\ \vdots&\cdots&\vdots \\{G\left( {{a_1},{b_1},{x_{{N_0}}}} \right)}& \cdots &{G\left( {{a_L},{b_L},{x_{{N_0}}}} \right)}\end{array}} \right]_{{N_0} \times L}}.$ (12)
步骤3 ?计算初始输出权重β(0)=P0H0TT0，其中P0=(H0TT0)－1，T0=[t1, ..., tN0]T.
步骤4?初始化加入网络的样本批次k=0.
步骤5?计算新加入的第k+1批训练数据
$\begin{array}{l}{\mathit{\boldsymbol{H}}_{k + 1}} = \\{\left[ {\begin{array}{*{20}{c}}{G\left( {{a_1},{b_1},{x_{\left( {\sum\nolimits_{j = 0}^k {{N_j}} } \right) + 1}}} \right)}& \cdots &{G\left( {{a_L},{b_L},{x_{\left( {\sum\nolimits_{j = 0}^k {{N_j}} } \right) + 1}}} \right)}\\ \vdots&\cdots&\vdots \\{G\left( {{a_1},{b_1},{x_{\sum\nolimits_{j = 0}^{k + 1} {{N_j}} }}} \right)}& \cdots &{G\left( {{a_L},{b_L},{x_{\sum\nolimits_{j = 0}^{k + 1} {{N_j}} }}} \right)}\end{array}} \right]_{{N_{k + 1}} \times L}}.\end{array}$ (13)
步骤6?计算更新输出权重β(k+1)和Pk+1.
${\mathit{\boldsymbol{P}}_{k + 1}} = {\mathit{\boldsymbol{P}}_k} - {\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\left( {\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{H}}_{k + 1}}{\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}_{k + 1}}{\mathit{\boldsymbol{P}}_k},$ (14)
${\beta ^{\left( {k + 1} \right)}} = {\beta ^{\left( k \right)}} + {\mathit{\boldsymbol{P}}_{k + 1}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}\left( {{\mathit{\boldsymbol{T}}_{k + 1}} - {\mathit{\boldsymbol{H}}_{k + 1}}{\beta ^{\left( k \right)}}} \right).$ (15)
其中
${\mathit{\boldsymbol{P}}_{k + 1}} = {\mathit{\boldsymbol{P}}_k} - \frac{{{\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{h}}\left( {{x_{k + 1}}} \right){\mathit{\boldsymbol{h}}^{\rm{T}}}\left( {{x_{k + 1}}} \right){\mathit{\boldsymbol{P}}_k}}}{{1 + {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( {{x_{k + 1}}} \right){\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{h}}\left( {{x_{k + 1}}} \right)}},$ (16)
${\beta ^{\left( {k + 1} \right)}} = {\beta ^{\left( k \right)}} + {\mathit{\boldsymbol{P}}_{k + 1}}\mathit{\boldsymbol{h}}\left( {{x_{k + 1}}} \right)\left( {\mathit{\boldsymbol{t}}_{k + 1}^{\rm{T}} - {\mathit{\boldsymbol{h}}^{\rm{T}}}\left( {{x_{k + 1}}} \right){\beta ^{\left( k \right)}}} \right).$ (17)
式中h(xk+1)=[G(a1, b1, xk+1)…G(aL, bL, xk+1)].
步骤7 ?令k=k+1，返回步骤5继续执行，直至算法结束.
其中，步骤1至步骤4为初始化阶段，步骤5至步骤7为序贯学习阶段.当rank(H0)=L时，OSELM和ELM算法学习能力相同.
2.2 组合预测模型构建构建交叉口短时流量CEEMDAN-PE-OSELM组合预测模型，流程如图 1所示.
Figure 1
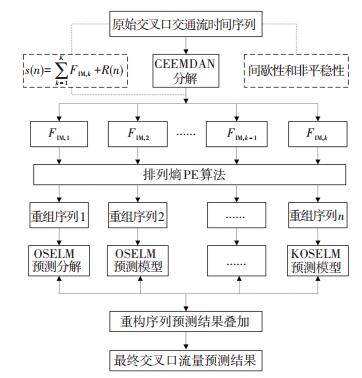图 1 CEEMDAN-PE-OSELM交叉口流量预测流程 Figure 1 Flowchart of intersection traffic flow prediction model based on CEEMDAN-PE-OSELM 为提高预测精度，在建立预测模型之前将流量重组序列进行归一化处理，即
$X'\left( i \right) = \frac{{\left( {X\left( i \right) - \min \left\{ {X\left( i \right)} \right\}} \right)}}{{\left( {\max \left\{ {X\left( i \right)} \right\} - \min \left\{ {X\left( i \right)} \right\}} \right)}}.$ (18)
反之，可以反归一化处理，即
$\begin{array}{l}X\left( i \right) = X'\left( i \right) \cdot \left( {\max \left\{ {X\left( i \right)} \right\} - \min \left\{ {X\left( i \right)} \right\}} \right) + \\\min \left\{ {X\left( i \right)} \right\}.\end{array}$ (19)
式中X′(i)为归一化流量数据，X(i)为重组流量序列数据.
3 实例验证选取一典型十字交叉口，进行短时流量预测.该交叉口几何特性如图 2所示.
Figure 2
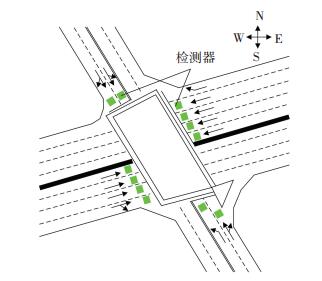图 2 交叉口几何特性 Figure 2 Geometry characteristics of the intersection 采集东进口连续5个工作日的5 min流量数据，如图 3所示.经过预处理，得到1 440个可用数据点.前4个工作日的1 152个数据点用于预测模型建立，第5个工作日的数据用于模型验证.
Figure 3
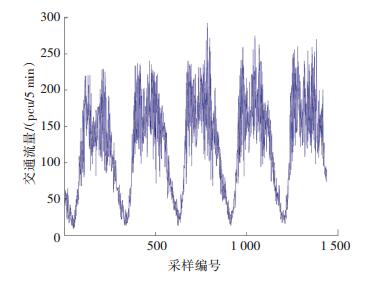图 3 交叉口东进口5 min流量分布 Figure 3 Traffic flow distribution of the eastern approach at the interval of 5 min 3.1 交通流量序列CEEMDAN-PE分解重组通过MATLAB软件编程，对原始交叉口流量序列进行CEEMDAN分解，分解时添加I=500组标准差为0.2的白噪声信号，结果如图 4所示. 图 4中交叉口流量原始时间序列被分解为10个随机性不同的IMF分量，相邻IMF分量波动程度相似.
Figure 4
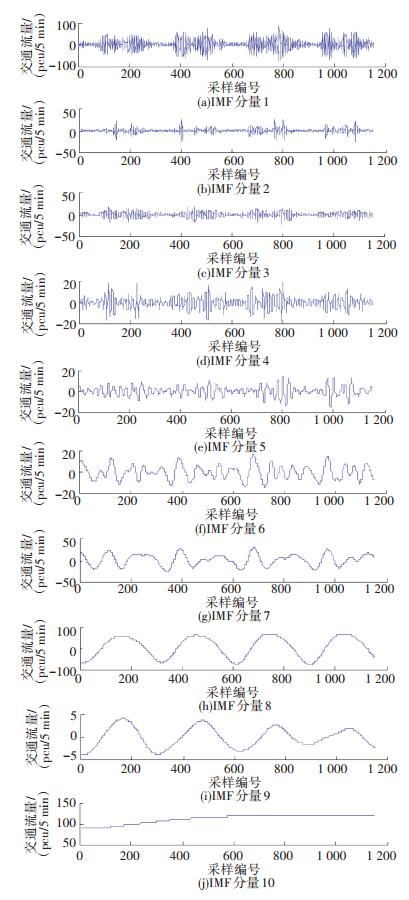图 4 交叉口流量数据CEEMDAN分解结果 Figure 4 Intersection traffic data decomposition results by CEEMDAN algorithm 图 5为流量序列CEEMDAN分解百分比误差图示.由图 5可知，该流量时间序列的分解误差非常小，达到了10-14级；说明了交叉口流量序列得到了完全分解，证明了该方法的有效性.
Figure 5
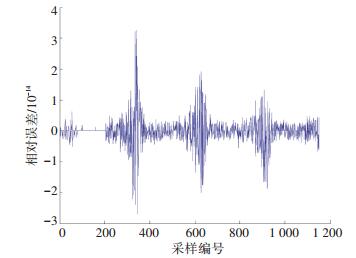图 5 CEEMDAN分解相对误差 Figure 5 Relative percentage error of CEEMDAN 根据前文，取嵌入维数m=6，延迟时间τ=3，计算FIM, k排列熵值，结果见表 1. Hp(m)为FIM, k排列熵值，HPE(m)为标准化排列熵值，ΔHPE(m)为相邻分量标准排列熵值之差.各IMF分量标准化排列熵值分布如图 6所示.
表 1
表 1 各IMF分量的排列熵值 Table 1 Permutation entropy values of each IMF component FIM, k Hp(m) HPE(m) ΔHPE(m) FIM, 1 5.509 0.837 0.015
FIM, 2 5.410 0.822 0.043
FIM, 3 5.123 0.779 0.128
FIM, 4 4.280 0.651 0.154
FIM, 5 3.271 0.497 0.101
FIM, 6 2.605 0.396 0.077
FIM, 7 2.099 0.319 0.065
FIM, 8 1.670 0.254 0.018
FIM, 9 1.551 0.236 0.131
FIM, 10 0.693 0.105 —
表 1 各IMF分量的排列熵值 Table 1 Permutation entropy values of each IMF component
Figure 6
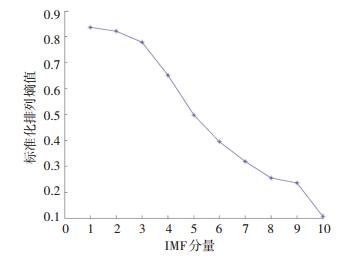图 6 各IMF分量标准化排列熵值 Figure 6 Standardized permutation entropy values of each IMF component 将ΔHPE(m)值小于0.1的相邻FIM, k合并，且综合比较同一FIM, k与前后FIM, k之间的差值，保证运行效率和结果精确度.由表 1和图 6可知，随机性最强的3个分量为FIM, 1、FIM, 2和FIM, 3，对预测结果影响最大，且标准化PE值相差甚小，因此将FIM, 1、FIM, 2和FIM, 3合并；FIM, 4和FIM, 5虽然相邻，但标准化PE值与相邻的其他分量相差较大，因此作为单独分量；FIM, 6和FIM, 7相邻且标准化PE值相差较小，可合并；FIM, 8和FIM, 9的标准化PE值差异为0.018，将其合并.由于FIM, 9与FIM, 10的标准化PE值之差和FIM, 8与FIM, 9的标准化PE值之差相差较大，为了保证精确性，不进行合并.综上，可以得到6组重组序列：FIM, 1+FIM, 2+FIM, 3，FIM, 4，FIM, 5，FIM, 6+FIM, 7，FIM, 8+FIM, 9，FIM, 10.重组序列分布如图 7所示.
Figure 7
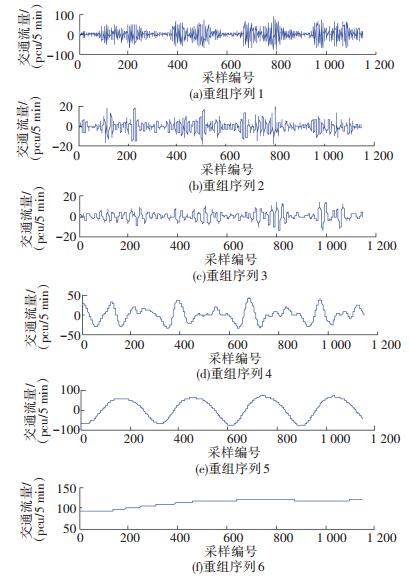图 7 经CEEMDAN-PE处理的交叉口流量重组序列 Figure 7 Restructured intersection traffic flow subsequences obtained by CEEMDAN-PE 3.2 预测结果分析采用滚动单步预测，模型输入为预测点前两个小时的流量序列，输出为预测值序列.则1 152个数据可构建1 128组输入-输出数据，组成训练集.分别构建ARIMA、BP、ELM、OSELM、CEEMDAN-PE-BP、CEEMDAN-PE-ELM和CEEMDAN-PE-OSELM，对比预测效果.
OSELM与ELM需要提前确定隐含层节点数L；选取N0=L个样本数据作为初始化阶段训练样本，用于增量学习的样本数据量为1 128-N0.经过交叉验证试验，得到最优L为30.
预测评价指标选取平均绝对误差EMA、平均相对误差PMAE、均方误差SME和均等系数CE分别为
${E_{{\rm{MA}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{y_i} - {{\hat y}_i}} \right|} ,$ (20)
${P_{{\rm{MAE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{y_i} - {{\hat y}_i}}}{{{y_i}}}} \right|} ,$ (21)
${S_{{\rm{ME}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} ,$ (22)
${C_{\rm{E}}} = 1 - \frac{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_i}} \right)}^2}} } + \sqrt {\sum\limits_{i = 1}^n {{{\left( {{{\hat y}_i}} \right)}^2}} } }}.$ (23)
其中
各模型的预测效果曲线如图 8所示，预测性能评价指标见表 2.
Figure 8
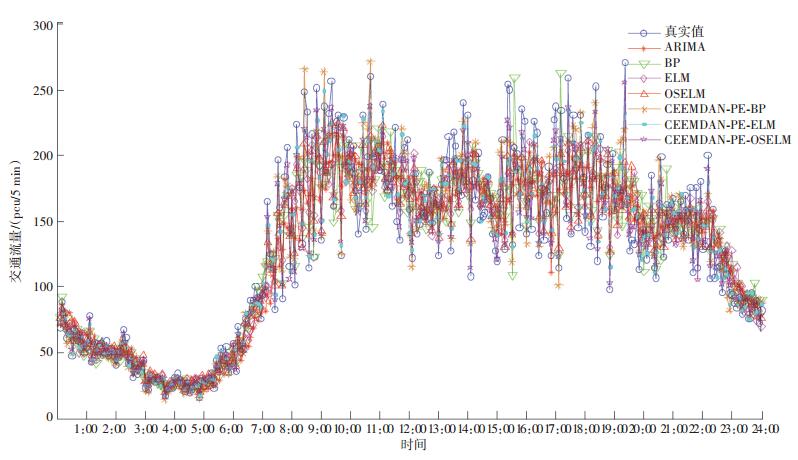图 8 各模型预测结果 Figure 8 Prediction results of each model 表 2
表 2 各预测模型性能指标对比 Table 2 Comparisons of prediction performance indexes for each prediction model 模型 EMA PMAE/% SME CE ARIMA 22.09 17.13 872.59 0.898
BP 20.39 15.50 723.37 0.907
ELM 17.75 13.88 576.71 0.917
OSELM 14.68 11.73 386.34 0.932
CEEMDAN-PE-BP 13.52 9.97 311.91 0.940
CEEMDAN-PE-ELM 11.25 8.44 223.65 0.949
CEEMDAN-PE-OSELM 8.65 6.51 114.33 0.963
表 2 各预测模型性能指标对比 Table 2 Comparisons of prediction performance indexes for each prediction model
由图 8可知，与其他预测模型相比，本文CEEMDAN-PE-OSELM模型流量预测值与真实值最为接近. ARIMA模型与真实值的拟合程度最低，与真实值的偏离程度最大；BP模型、ELM模型和OSELM模型的预测值与真实值的拟合程度逐渐提高，但是相比于经过序列分解与重组的CEEMDAN-PE-BP模型、CEEMDAN-PE-ELM模型及CEEMDAN-PE-OSELM模型，与真实值的偏离程度仍然很大.
由表 2可知，CEEMDAN-PE-OSELM模型的EMA、PMAE和SME的值均低于其他模型，说明其预测误差最小，预测精度最高；且CE值为0.963，高于ARIMA模型的CE值(0.898)，相比于其他方法，CE值最接近于1，说明其预测值与真实值的偏离程度最小，预测效果最好，模型的稳定性最好.就同一预测模型而言，经过CEEMDAN-PE处理的模型的各项误差明显降低，预测精度有所提高.
综上，基于CEEMDAN-PE-OSELM的交叉口短时交通流预测模型性能较好，能够满足预测要求.
4 结论1) 基于交叉口历史流量时间序列，提出了一种基于CEEMDAN-PE-OSELM的交叉口短时交通流量预测方法，该方法与其他经典预测模型相比，模型流量预测值与真实值最为接近，平均绝对误差、平均相对误差、均方误差均最小.
2) 预测模型的均等系数为0.963，高于ARIMA模型的均等系数0.898；且与其他模型相比，均等系数最接近1，与真实值的偏离程度最小，预测效果最好.
3) 经过CEEMDAN-PE分解与重组的模型的各项误差明显降低，预测精度有所提高.
参考文献
[1] LINGRAS P, SHARMA S C, OSBORNE P, et al. Traffic volume time-series analysis according to the type of road use[J]. Computer-Aided Civil and Infrastructure Engineering, 2000, 15(5): 365-373. DOI:10.1111/mice.2000.15.issue-5
[2] GAO Junwei, LENG Ziwen, ZHANG Bin, et al. The application of adaptive Kalman filter in traffic flow forecasting[J]. Advanced Materials Research, 2013, 680: 495-500. DOI:10.4028/www.scientific.net/AMR.680
[3] 张玉梅, 曲仕茹, 温凯歌. 交通流量的混沌特性分析及预测模型研究[J]. 土木工程学报, 2009, 42(1): 119-123.
ZHANG Yumei, QU Shiru, WEN Kaige. Chaotic property analysis and prediction model study for traffic flow time series[J]. China Civil Engineering Journal, 2009, 42(1): 119-123.
[4] 丁恒, 郑小燕, 刘燕, 等. 基于小波分析的随机交通流组合预测方法研究[J]. 系统仿真学报, 2012, 24(2): 377-381.
DING Heng, ZHENG Xiaoyan, LIU Yan, et al. Stochastic traffic series time combination forecasting based on wavelet analysis[J]. Journal of System Simulation, 2012, 24(2): 377-381.
[5] JIANG X, ADELI H. Dynamic wavelet neural network model for traffic flow forecasting[J]. Journal of Transportation Engineering, 2005, 131(10): 771-779. DOI:10.1061/(ASCE)0733-947X(2005)131:10(771)
[6] 杨兆升, 王媛, 管青. 基于支持向量机方法的短时交通流量预测方法[J]. 吉林大学学报(工学版), 2006, 36(6): 881-884.
YANG Zhaosheng, WANG Yuan, GUAN Qing. Short-time traffic prediction method based on SVM[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(6): 881-884.
[7] 刘静. 基于AFSA-LSSVM的短时交通流量预测[J]. 计算机工程与应用, 2013, 49(17): 226-229.
LIU Jing. Short-time traffic prediction model based on LSSVM optimized by artificial fish swarm algorithm[J]. Computer Engineering and Applications, 2013, 49(17): 226-229. DOI:10.3778/j.issn.1002-8331.1211-0182
[8] 商强, 杨兆升, 李志林, 等. 基于相空间重构和RELM的短时交通流量预测[J]. 华南理工大学学报(自然科学版), 2016, 44(4): 109-114.
SHANG Qiang, YANG Zhaosheng, LI Zhilin, et al. Short-term traffic flow prediction based on phase space reconstruction and RELM[J]. Journal of South China University of Technology (Natural Science Edition), 2016, 44(4): 109-114.
[9] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications[J]. Neuro Computing, 2006, 70(1/2/3): 489-501.
[10] LIANG N Y, HUANG G B, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423. DOI:10.1109/TNN.2006.880583
[11] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]//2011 IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2011: 4144-4147.
[12] WU Z H, HUANG N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
[13] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A—Mathematical Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193
[14] BANDT C, POMPE B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, The American Physiological Society, 2002, 88(17): 174102. DOI:10.1103/PhysRevLett.88.174102
[15] ZUNINO L, ROSSO O A, SORIANO M C. Characterizing the hyper chaotic dynamics of a semiconductor laser subject to optical feedback via permutation entropy[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2011, 17(5): 1250-1257. DOI:10.1109/JSTQE.2011.2145359
[16] 吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002.
LV Jinhu, LU Jun'an, CHEN Shihua. Chaotic time series analysis and application[M]. Wuhan: Wuhan University Press, 2002.
[17] YAN R, LIU Y, GAO R X. Permutation entropy: a nonlinear statistical measure for status characterization of rotary machines[J]. Mechanical Systems and Signal Processing, 2012, 29(1): 474-484.
