改进模糊聚类方法的物流园交通小区划分

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编哈尔滨工业大学/2019-10-24

改进模糊聚类方法的物流园交通小区划分

温惠英,卢德佑,吴亚平,曾强

(华南理工大学土木与交通学院, 广州 510641)

摘要:

为获取物流园交通小区的最佳分类结果，首先对物流园进行定性划分，然后构造加权模糊相似矩阵，再利用邻接矩阵对加权模糊相似矩阵进行修正，采用改进的模糊聚类方法对小区进行聚类合并，并且基于类内距离和类间距离构造F指标以确定最佳分类数.实验结果表明，基于改进的模糊聚类方法能够较大程度地减少物流园交通小区数量，并且能够快速得到较好的小区分类，还能避免将地理位置不相邻的小区划分为同一类.

关键词: 物流园交通小区邻接矩阵模糊聚类类内距离类间距离

DOI：10.11918/j.issn.0367-6234.201612076

分类号:U491

文献标识码:A

基金项目:国家自然科学基金(2,7)；广东省自然科学资金资助项目(2016A030310427)

Division of logistics park traffic zones based on the improved fuzzy clustering method

WEN Huiying,LU Deyou,WU Yaping,ZENG Qiang

(School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China)

Abstract:

To obtain the best classification results of logistics park, the qualitative division of logistics park traffic zones is carried out, then the weighted fuzzy similar matrix is constructed, and the adjacency matrix is used to amend the weighted fuzzy similar matrix. The improved fuzzy clustering method is employed to the clustering of merger of logistics park traffic zones. In addition, the F index is constructed to determine the optimal number of class based on the distance in the class and the distance between the class. The results show that the improved fuzzy clustering method could greatly reduce the amount of logistics park traffic zones, and it can quickly get the better logistics park traffic zones classification and avoid dividing logistics park traffic zones which are in the non-adjacent geographical position into the same class.

Key words: logistics park traffic zones adjacency matrix fuzzy clustering distance in the class distance between the class

温惠英, 卢德佑, 吴亚平, 曾强. 改进模糊聚类方法的物流园交通小区划分[J]. 哈尔滨工业大学学报, 2018, 50(3): 103-108. DOI: 10.11918/j.issn.0367-6234.201612076. 复制到剪切板

WEN Huiying, LU Deyou, WU Yaping, ZENG Qiang. Division of logistics park traffic zones based on the improved fuzzy clustering method[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 103-108. DOI: 10.11918/j.issn.0367-6234.201612076. 复制到剪切板

基金项目国家自然科学基金(51378222，51578247)；广东省自然科学资金资助项目(2016A030310427) 作者简介温惠英(1965—)，女，教授，博士生导师通信作者卢德佑，2504314984@qq.com 文章历史收稿日期: 2016-12-14

Contents            -->Abstract            Full text            Figures/Tables            PDF

改进模糊聚类方法的物流园交通小区划分
温惠英, 卢德佑, 吴亚平, 曾强
华南理工大学土木与交通学院，广州 510641

收稿日期: 2016-12-14
基金项目: 国家自然科学基金(51378222，51578247)；广东省自然科学资金资助项目(2016A030310427)
作者简介: 温惠英(1965—)，女，教授，博士生导师
通信作者: 卢德佑，2504314984@qq.com

摘要: 为获取物流园交通小区的最佳分类结果，首先对物流园进行定性划分，然后构造加权模糊相似矩阵，再利用邻接矩阵对加权模糊相似矩阵进行修正，采用改进的模糊聚类方法对小区进行聚类合并，并且基于类内距离和类间距离构造F指标以确定最佳分类数.实验结果表明，基于改进的模糊聚类方法能够较大程度地减少物流园交通小区数量，并且能够快速得到较好的小区分类，还能避免将地理位置不相邻的小区划分为同一类.
关键词: 物流园交通小区    邻接矩阵    模糊聚类    类内距离    类间距离
Division of logistics park traffic zones based on the improved fuzzy clustering method
WEN Huiying, LU Deyou, WU Yaping, ZENG Qiang
School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China

Abstract: To obtain the best classification results of logistics park, the qualitative division of logistics park traffic zones is carried out, then the weighted fuzzy similar matrix is constructed, and the adjacency matrix is used to amend the weighted fuzzy similar matrix. The improved fuzzy clustering method is employed to the clustering of merger of logistics park traffic zones. In addition, the F index is constructed to determine the optimal number of class based on the distance in the class and the distance between the class. The results show that the improved fuzzy clustering method could greatly reduce the amount of logistics park traffic zones, and it can quickly get the better logistics park traffic zones classification and avoid dividing logistics park traffic zones which are in the non-adjacent geographical position into the same class.
Key words: logistics park traffic zones    adjacency matrix    fuzzy clustering    distance in the class    distance between the class
随着区域联系的不断加强，区域之间的贸易更加频繁，物流活动也不断增加，从而使得物流业的发展进一步加快，物流园作为物流业的重要组成部分，其规划设计的合理性对于提高物流生产运作效率、节约社会资源、降低企业成本具有重大的作用.将交通小区划分理论应用于城市道路中，有博弈论的动态交通小区划分方法^[1]、基于谱图理论的交通小区划分方法^[2]、过饱和状态下交通控制小区动态划分方法^[3]等，为研究城市道路提供了新的思路.在物流配送方面，建立了物流配送中心选址的双层规划模型^[4]、整型线性规划模型^[5]、单物流配送点选址模型^[6].但是由于物流需求点较多，部分模型计算过程比较复杂.在物流园功能区布局方面，文献[7]在获取各个物流园功能区相互关系的基础上用遗传算法求解各个功能区布局的最优位置.文献[8]提出了将功能区基于划分线进行配置和切割结构技术确定功能区最终布局两种模型.文献[9]利用物流园位置和规模作为决策变量建立区域物流网络模型，最终利用启发式隐枚举算法进行模型求解.

目前国内外关于物流园区的探讨主要是集中在物流配送中心选址、功能区布局等方面.传统交通工程中的交通小区划分理论主要是应用于城市路网、交通信号控制等领域，对物流园进行交通小区划分以及将模糊聚类分析法应用于物流园交通小区划分的探讨也相对比较少，在探讨物流配送的过程中往往选择多个物流需求点进行研究.本文提出基于改进的模糊聚类方法进行物流园交通小区划分，旨在有效减少物流园交通小区数量，从而减少物流园规划设计中的调查研究对象，并且能够避免将地理位置不相邻的物流园交通小区划分为同一类，降低了人工修正分类结果的工作量以及误差.将物流园交通小区划分理论应用于实际当中，能够较好地实现物流园的分区配送和分区经营管理，提高物流效率，可进行物流规划和物流预测.

1 物流园交通小区 1.1 物流园交通小区的概念在研究交通源与交通源之间的交通流时，为了降低研究的复杂性，需要将交通源合并成若干个小区，这些小区称为交通小区，这是传统交通工程中交通小区的一般定义.目前还没有关于物流园交通小区的统一定义，本文结合物流园交通小区划分的意义及物流相关理论给出了物流园交通小区的一般定义.物流园交通小区是在研究物流源和物流源之间的物流量时，由于物流源太多不能够很好地掌握源流特性而将各个物流源进行合并成为的多个小区.

1.2 物流园交通小区的划分原则通过借鉴交通小区的划分原则^[10]并且结合物流配送实际情况提出物流园交通小区的划分原则如下：1)尽量以道路、铁路线等作为划分物流园交通小区的界线；2)物流园交通小区在地理空间位置上应该是相邻的；3)尽量不打破行政区域，方便利用现有资料以及后期规划管理；4)根据物流园规模科学合理确定分区数量和面积；5)被合并的物流园交通小区的物流货量等属性和特征应该尽量一致.

2 模糊聚类的物流园交通小区划分方法在完成物流园交通小区的定性划分之后，一般情况下小区数量仍然很多，为降低研究的复杂难度，采用模糊聚类的方法对物流园交通小区进行合并.本文通过定性和定量的方法进行物流园交通小区的划分，首先依据物流园交通小区划分原则定性地对物流园进行区域分割，然后利用模糊聚类分析方法定量地对小区进行合并^[11]，最后结合物流配送实际情况以及物流园规模对交通小区划分进行结果修正.物流园交通小区划分流程如下图 1所示.

Figure 1
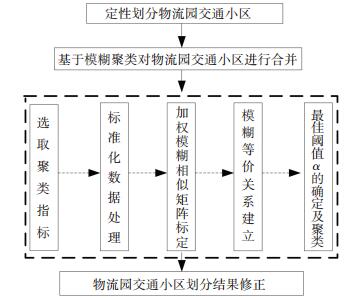点击查看原图

图 1 物流园交通小区划分流程 Figure 1 The division process of logistics park traffic zones

2.1 定性划分物流园交通小区定性划分物流园交通小区就是根据交通小区所属的行政区域、道路铁路等界限、交通小区的土地利用性质等定性指标对区域进行分割，使得性质相近的物流点能够被划分到同一个小区之内.

对物流园进行定性的区域分割之后，虽然能够使得研究对象有所减少，但是基于主观的划分方法仍然会有一定的误差存在，并没有得到小区的最佳分类数，因此有必要应用一定的数学模型对定性划分之后的小区开展合并，将定性方法和定量方法结合起来，使得物流园交通小区的划分更科学.

2.2 基于模糊聚类分析的区域合并在完成物流园交通小区的定性划分之后，采用模糊聚类的方法分析小区之间的相似性和紧密程度^[12]，将类似的在地理位置上相邻的小区合并为一个比较大的小区，从而缩减研究对象.如果比较相似的小区集里面有个别小区在地理位置上与其他小区不相邻，则要根据实际情况将其单独作为一个物流园交通小区.具体步骤如下.

2.2.1 选取聚类指标物流园各个物流园交通小区的进出货量、商户数、营业面积、营业额、营业成本等会对物流量有着很大的影响.因此可以考虑将进出货量、商户数、营业面积、营业额、营业成本等作为聚类分析的指标，将进出货量等相似的小区合并成为更大的物流园交通小区，以达到分区配送、分区规划、分区管理的目的.聚类指标的选取除了要考虑对物流量的影响程度之外，还要考虑数据的可得性和准确性.

2.2.2 标准化数据处理由于各聚类指标具有不同的量纲，需要对原始数据进行标准化处理.设L={l₁, l₂, …, l_f}为物流园交通小区集，f为物流园交通小区的数量，其中，L物流园交通小区集中的每个对象l_k用p个参数值进行表征，每个参数值描述某个小区的某个特征.则每个小区l_k会衍生一向量(l_k1, l_k2, …, l_kp)，即原始矩阵中的每一行，因此矩阵中的某一行对应某一个小区的属性数据，而每个一维特征l_v的f个原始数据为(l_1v, l_2v, …, l_fv)，即矩阵中的每一列，因此矩阵中的每一列对应着一个聚类指标.因此可以得到原始矩阵

$\left[ {\begin{array}{*{20}{c}}{{l_{11}}}&{{l_{12}}}& \cdots &{{l_{1p}}}\\{{l_{21}}}&{{l_{22}}}& \cdots &{{l_{2p}}}\\ \vdots&\vdots&\cdots&\vdots \\{{l_{f1}}}&{{l_{f2}}}& \cdots &{{l_{fp}}}\end{array}} \right].$

而对每个原始数据进行标准化处理的目的就是为了使得数据处理之后能够属于[0, 1]，以方便后面模糊矩阵的建立.标准化数据处理算法为

${{l'}_{kv}} = \frac{{{l_{kv}} - \overline {{l_v}} }}{{{S_v}}},k = 1,2, \cdots ,f.$ (1)

$\overline {{l_v}} = \frac{1}{f}\sum\limits_{k = 1}^f {{l_{kv}}} ,v = 1,2, \cdots ,p;$ (2)

${S_v} = \sqrt {\frac{1}{f}\sum\limits_k^f {{{\left( {{l_{kv}} - \overline {{l_v}} } \right)}^2}} } .$ (3)

其中：$\overline {{l_v}} $为各个物流园交通小区某一个聚类指标的平均值，S_v为各个物流园交通小区某一个聚类指标的标准差.但是经过处理之后的l′_kv并不一定属于[0, 1]，因此需要进行极值标准化变换，即

${l_{kv}} = \frac{{{{l'}_{kv}} - {{l'}_{v\min }}}}{{{{l'}_{v\max }} - {{l'}_{v\min }}}},$ (4)

式中l′_vmax、l′_vmin分别为(l′_1v, l′_2v, …, l′_fv)中的最大值和最小值.

2.2.3 加权模糊相似矩阵标定模糊矩阵标定即计算衡量被分类物流园交通小区之间近似程度的统计量θ_kh(k, h=1, 2, …, f)，θ_kh为小区l_k和l_h之间的近似程度.设物流园交通小区集L={l₁, l₂, …, l_f}，则可以建立关于L的相似矩阵M′(l_k, l_h)=θ_kh，0≤θ_kh≤1.每个小区对象的维度为p，l_k=(l_k1, l_k2, …, l_kp).这里将会选用绝对值减数法构建模糊相似矩阵，从而获取各个小区之间的物流特性的近似程度.由于各个聚类指标对聚类结果的影响是不同的，因此对各个聚类指标赋予一定的权重w_v.权重w_v可以根据专家评价法和AHP法(层次分析法)进行确定.首先由专家根据1-9标度法对各个聚类指标之间的相对重要程度进行判断，从而得到判断矩阵.当一个指标和另外一个指标进行比较时，若两个指标同样重要，判断矩阵元素取值为1，若前者比后者稍微重要，元素取值为3，若前者比后者明显重要，元素取值为5，若前者比后者重要得多，元素取值为7，若前者比后者极端重要，元素取值为9，若重要程度介于以上相邻两种情况之间，元素取值分别为2，4，6，8.设指标s和指标t的重要程度之比为b_st，那么指标t和指标s的重要程度之比b_ts=1/b_st.设判断矩阵为

$\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}}{{b_{11}}}&{{b_{12}}}& \cdots &{{b_{1p}}}\\{{b_{21}}}&{{b_{22}}}& \cdots &{{b_{2p}}}\\ \vdots&\vdots&\vdots&\vdots \\{{b_{p1}}}&{{b_{p2}}}& \cdots &{{b_{pp}}}\end{array}} \right].$

1) 将判断矩阵每一列归一化：

${{\bar b}_{st}} = {b_{st}}/\sum\limits_{m = 1}^p {{b_{mt}}} ,s,t = 1,2, \cdots ,p.$ (5)

2) 将每一列归一化后的矩阵按行相加：

${C_s} = \sum\limits_{t = 1}^p {{{\bar b}_{st}}} ,\;\;\;\;s = 1,2, \cdots ,p.$ (6)

3) 将向量C=(C₁, C₂, …, C_P)^T归一化：

${w_s} = {C_s}/\sum\limits_{t = 1}^p {{C_t}} ,\;\;s = 1,2, \cdots ,p.$ (7)

所求的w=(w₁, w₂, …, w_p)即为对应的聚类指标的权重.计算各物流园交通小区间相似系数θ_kh的公式为

${\theta _{kh}} = \left\{ \begin{array}{l}1,k = h;\\1 - N\sum\limits_{v = 1}^p {{w_v}\left| {{l_{kv}} - {l_{hv}}} \right|} ,k \ne h.\end{array} \right.$ (8)

式中N为一个使得0≤θ_kh≤1的数，从而可以得到加权模糊相似矩阵

$\mathit{\boldsymbol{M'}} = \left[ {\begin{array}{*{20}{c}}1&{{\theta _{12}}}& \cdots &{{\theta _{1f}}}\\{{\theta _{21}}}&1& \cdots &{{\theta _{2f}}}\\ \vdots&\vdots&\vdots&\vdots \\{{\theta _{f1}}}&{{\theta _{f2}}}& \cdots &1\end{array}} \right].$

其中0≤θ_kh≤1，k, h=1, 2, …, f.

2.2.4 加权模糊相似矩阵的修正在以往的研究当中，在建立模糊相似矩阵的时候没有考虑小区在地理位置上的相邻关系，从而将地理位置不相邻的物流园交通小区划分为一个类，需要进一步确认小区之间的相邻关系并将地理位置互不相邻的小区分离出去，从而完成小区分类结果的人工修正.在小区数量比较多的情况下，这个工作量是比较庞大的，容易造成不必要的误差.因此本文提出将邻接矩阵应用于模糊相似矩阵当中，从而快速得到比较正确的分区结果.

所谓的邻接矩阵是表示物流园交通小区之间相邻关系的一个矩阵，邻接关系如图 2所示.定义邻接矩阵为

Figure 2
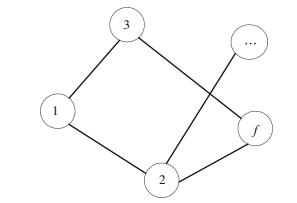点击查看原图

图 2 邻接关系图 Figure 2 Adjacency relations figure

$\mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}}1&1&1& \cdots &0\\1&1&0& \cdots &1\\1&0&1& \cdots &1\\ \vdots&\vdots&\vdots&\vdots&\vdots \\0&1&1& \cdots &1\end{array}} \right].$

$定义\;G\left( {k,h} \right) = \left\{ \begin{array}{l}1,\;表示物流小区\;k\;和\;h\;相邻;\\0,表示物流小区\;k\;和\;h\;不相邻.\end{array} \right.$

将邻接矩阵应用于原来的模糊相似矩阵计算公式中，可以得到

${{\theta '}_{kh}} = \left\{ \begin{array}{l}1,k = h;\\G\left( {k,h} \right) \cdot \left( {1 - N\sum\limits_{v = 1}^p {{w_v}\left| {{l_{kv}} - {l_{hv}}} \right|} } \right),k \ne h.\end{array} \right.$

其中0≤θ′_kh≤1，k, h=1, 2, …, f.

则可以得到修正的模糊相似矩阵为

$\mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}}1&{{{\theta '}_{12}}}& \cdots &{{{\theta '}_{1f}}}\\{{{\theta '}_{21}}}&1& \cdots &{{{\theta '}_{2f}}}\\ \vdots&\vdots&\vdots&\vdots \\{{{\theta '}_{f1}}}&{{{\theta '}_{f2}}}& \cdots &1\end{array}} \right].$

2.2.5 模糊等价关系建立通过绝对值减数法得到模糊相似矩阵M之后，如果M满足以下条件：1)自反性(θ_kk=1, k=1, 2, …, f)，2)对称性(θ_kh=θ_hk k, h=1, 2，…, f)，3)传递性(M·M?M)，则M(θ_kh)_f×f是一个模糊等价矩阵，只有M满足模糊等价关系的时候才能对物流园交通小区进行聚类合并，如果M不满足以上条件，则需要通过其他计算方法将非模糊等价矩阵构建成为模糊等价矩阵，使其满足模糊等价关系.

进行合成运算M²=M·M, M⁴=M²·M², 当首次出现M^2t=M^t·M^t时，表明传递包矩阵已经建立，模糊等价关系矩阵也得以建立起来^[13-14].

2.2.6 最佳阈值α的确定及聚类计算得到模糊等价矩阵之后，将矩阵中互不相同的元素从大到小进行排列，对应的元素即为所有阈值α的取值.固定阈值α，将模糊等价关系矩阵中所有θ_kh≥α的元素改为1，其余为0，之后将矩阵中完全相同的行对应的小区合并成为一个类，其他行对应的小区独自成为一个类.

由于阈值α的不同取值对应着不同的物流园交通小区的分类，因此聚类分析结果是动态的，具有不确定性.但是在实际的物流园交通小区分区过程中一般都是需要确定一个分类，以此剔除不符合条件的分类，最终得到小区最佳分类结果，从而更好地满足研究需求.为了确定最佳阈值，这里引入类间距离和类内距离，类间距离大并且类内距离小，则这个分类的效果是比较好的.

设L={l₁, l₂, …, l_f}为一个样本空间，L样本空间中的每个指标l_k用p个参数值进行表征，则每个聚类指标l_k会衍生一向量(l_k1, l_k2, …, l_kp)，假设对应某个阈值α的物流园交通小区分类数为c，第e类的样本量为f_e，其样本记做l^e₁, l^e₂, …, l_fe^e，那么$\overline {{l^e}} = \left( {\overline {l_1^e}, \overline {l_2^e}, \cdots, \overline {l_v^e}, \cdots, \overline {l_p^e} } \right)$为第e类聚类中心向量，其中$\overline {l_v^e} = \frac{1}{{{f_e}}}\sum\limits_{k = 1}^{{f_e}} {l_{kv}^e}, v = 1, 2, \cdots, p$.由此式可以构造类间距离D^B和类内距离D^I分别为

${D^B} = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^c {{{\left\| {\overline {{l^i}} - \overline {{l^j}} } \right\|}^2}/\left[ {2c\left( {c - 1} \right)} \right]} } ,$

$\begin{array}{l}{D^I} = \sum\limits_{e = 1}^c {\sum\limits_{k = 1}^{{f_e}} {{{\left\| {l_k^e - \overline {{l^e}} } \right\|}^2}/\left( {f - c} \right)} } ,\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;F = {D^B} - {D^I}.\end{array}$

式中$\left\| {\overline {{l^i}}-\overline {{l^j}} } \right\|$为第i类聚类中心向量和第j类聚类中心向量的欧式距离，定义为

$\left\| {\overline {{l^i}} - \overline {{l^j}} } \right\| = \sqrt {\sum\limits_{v = 1}^p {{{\left( {\overline {l_v^i} - \overline {l_v^j} } \right)}^2}} } .$

式中$\left\| {l_k^e-\overline {{l^e}} } \right\|$为第e类中${\overline {{l^e}} }$和l_k^e的欧式距离，f为聚类前物流园交通小区的数量.

将所有F值计算出来之后，F最大值所对应的阈值即为最佳阈值，对应的分类数即为最佳分类数.

2.2.7 物流园交通小区划分结果修正物流园交通小区聚类合并完成之后，有时候会出现小区面积过大、物流园规模和和分区数量不匹配或者其他严重不符合小区划分原则的情况出现，这时就需要对小区的划分结果进行修正，从而使得小区的划分结果更加准确，更加符合实际.

3 实例分析下面将以广州市沙河物流园作为实例研究的对象.沙河物流园位于广州市天河区，是国内外比较大型的服装批发市场之一，目前有21个比较大型的服装批发市场.对沙河物流园进行物流园交通小区划分，对未来实现沙河物流园的分区配送和分区经营管理有着重要的指导意义.

3.1 定性划分物流园交通小区定性区域分割主要是依据物流园交通小区划分原则对沙河物流园进行分割，使得属性相近的物流点尽量被划分到同一个小区之内，同时尽量不要打破原有行政区域规划和跨越道路、铁路干线.

目前沙河街道办和沙东街道办大致以铁路线为界，因此小区不应该跨越这两个行政区域，以方便后期的规划和管理，为了减少物流配送对交通的影响，小区应该尽量不要跨越濂泉路、梅东北延长线和先烈东路等主要交通干道.沙河服装批发市场目前主要是分为女装市场和男装市场两个大类，基于商品的种类的考虑，男装市场和女装市场应该尽量不要划分到同一个小区内.综合考虑以上因素将沙河地区物流园划分为8个物流园交通小区，见图 3和表 1.

Figure 3
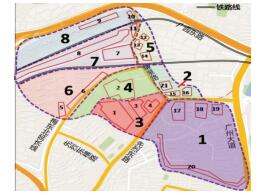点击查看原图

图 3 物流园交通小区初步分区图 Figure 3 Preliminary partition map of logistics park traffic zones

表 1

表 1 物流园交通小区初步分区结果 Table 1 Preliminary partition results of logistics park traffic zones 小区编号市场编号

1 17，18，19，20

2 15，16，21

3 1，3，4

4 2

5 12，13，14

6 5，6

7 7，8，11

8 9，10

表 1 物流园交通小区初步分区结果 Table 1 Preliminary partition results of logistics park traffic zones

3.2 模糊聚类分析法对物流园交通小区进行合并根据调查可以得知，沙河地区各个物流园交通小区的进出货量、物流点商户数、物流点营业面积对物流量有着较大的影响，因此将这4个因素作为聚类合并的指标.各个小区的基础资料见表 2.

表 2

表 2 各物流园交通小区基础资料 Table 2 Basic information of the logistics park traffic zones 小区编号进货量/t 出货量/t 商户数营业面积/m²

1 392 368 3 054 37 294

2 251 235 1 953 23 632

3 924 868 7 290 73 520

4 85 80 600 17 460

5 42 39 323 4 079

6 96 91 744 10 256

7 531 499 3 608 131 220

8 74 69 552 10 438

表 2 各物流园交通小区基础资料 Table 2 Basic information of the logistics park traffic zones

对上面数据进行标准化处理之后，得到新矩阵

$\left[ {\begin{array}{*{20}{c}}{0.323}&{0.322}&{0.355}&{ - 0.029}\\{ - 0.169}&{ - 0.171}&{ - 0.141}&{ - 0.365}\\{2.176}&{2.176}&{2.259}&{0.861}\\{ - .747}&{ - 0.746}&{ - 0.749}&{ - 0.517}\\{ - 0.879}&{ - 0.898}&{ - 0.873}&{ - 0.845}\\{ - 0.709}&{ - 0.705}&{ - 0.684}&{ - 0.693}\\{0.807}&{0.808}&{0.604}&{2.278}\\{ - 0.785}&{ - 0.787}&{ - 0.770}&{ - 0.689}\end{array}} \right].$

根据专家评价法和AHP法^[15]确定进货量、出货量、商户数和营业面积的权重分别为0.394，0.394，0.141，0.071.

物流园交通小区之间的相邻关系可以用邻接矩阵表示为

$\left[ {\begin{array}{*{20}{c}}1&1&1&0&0&0&0&0\\1&1&1&1&1&0&0&0\\1&1&1&1&0&0&0&0\\0&1&1&1&0&1&0&0\\0&1&0&0&1&0&1&0\\0&0&0&1&0&1&1&0\\0&0&0&0&1&1&1&1\\0&0&0&0&0&0&1&1\end{array}} \right].$

经过相关计算得到模糊等价矩阵为

$\left[ {\begin{array}{*{20}{c}}{1.000}&{0.921}&{0.705}&{0.909}&{0.883}&{0.909}&{0.739}&{0.727}\\{0.921}&{1.000}&{0.705}&{0.909}&{0.883}&{0.909}&{0.739}&{0.727}\\{0.705}&{0.707}&{1.000}&{0.705}&{0.705}&{0.705}&{0.705}&{0.705}\\{0.909}&{0.909}&{0.705}&{1.000}&{0.883}&{0.991}&{0.739}&{0.727}\\{0.883}&{0.883}&{0.705}&{0.883}&{1.000}&{0.883}&{0.739}&{0.727}\\{0.909}&{0.909}&{0.705}&{0.991}&{0.883}&{1.000}&{0.739}&{0.727}\\{0.739}&{0.739}&{0.705}&{0.739}&{0.739}&{0.739}&{1.000}&{0.727}\\{0.727}&{0.727}&{0.705}&{0.727}&{0.727}&{0.727}&{0.727}&{1.000}\end{array}} \right].$

各个分类数对应的物流园交通小区见表 3.由表 3可知，当α=0.909时，F值最大，所以将沙河物流园分为(1，2，4，6)，3，5，7，8一共5个物流园交通小区.但是将小区1，2，4，6合并成为一个小区之后，小区面积过于庞大，因此需要将其拆分为(1，2)，(4，6)两个小区，则最终将沙河物流园划分为(1，2)，(4，6)，3，5，7，8一共6个物流园交通小区.

表 3

表 3 物流园交通小区聚类合并结果 Table 3 The cluster merging results of logistics park traffic zones α 分类数合并后的物流园交通小区 F

1 8 1，2，3，4，5，6，7，8

0.991 7 (4，6)，1，2，3，5，7，8 4.942

0.921 6 (1，2)，(4，6)，3，5，7，8 5.630

0.909 5 (1，2，4，6)，3，5，7，8 6.512

0.883 4 (1，2，4，5，6)，3，7，8 6.479

0.739 3 (1，2，4，5，6，8)，3，7 5.515

0.727 2 (1，2，4，5，6，7，8)，3 4.587

0.705 1 (1，2，3，4，5，6，7，8)

表 3 物流园交通小区聚类合并结果 Table 3 The cluster merging results of logistics park traffic zones

在未对模糊相似矩阵进行修正时，物流园交通小区的分类数为4，合并后的物流园交通小区为3，7，(1，2)，(4，5，6，8).分区结果中出现了地理位置不相邻的小区，需要进行人工修正，修正后分为(1，2)，(4，6)，3，7，5，8共6个小区.在对模糊相似矩阵进行修正后，物流园交通小区的分类数为6，合并后的物流园交通小区为(1，2)，(4，6)，3，5，7，8.分区结果中没有出现地理位置不相邻的小区，可以直接得到正确的分区结果, 如图 4所示.

Figure 4
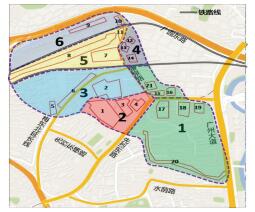点击查看原图

图 4 物流园交通小区最终分区图 Figure 4 Final partition map of logistics park traffic zones

由此可知，将邻接矩阵应用于模糊相似矩阵中对模糊矩阵进行修正后，分区结果不会出现地理位置不相邻的小区，可以直接得到正确的分区结果.

4 结论1) 通过实例验证，发现将模糊聚类方法应用于物流园交通小区划分当中能够减少小区的数量，聚类合并效果比较明显.

2) 将邻接矩阵应用到模糊相似矩阵后，分区结果不会出现地理位置不相邻的小区，可以直接得到正确的分区结果.

3) 根据类内距离和类间距离构造的F指标确定的最佳阈值能够得到较好的分类数，F指标值随着阈值的减小没有呈现明显的变化规律，而物流园交通小区分类数随着阈值的减小而减少.

4) 在物流园交通小区聚类合并完成之后，应该根据物流园规模对物流园分区结果进行修正，因此具体用哪些指标衡量物流园规模以及物流园规模对应的物流园交通小区数量是今后的研究方向之一.

参考文献
[1] LIU H. A dynamic traffic zone division scheme based on game theory[J]. Journal of Information & Computational Science, 2013, 10(10): 2961-2969. DOI:10.12733/jics20101878

[2] WU S M, PEI Y L, CHENG G Z. Method of traffic zone division based on spectral graph theory[J]. Computer Modeling & New Technology, 2014, 18(2): 186-191.

[3] 杨晓光, 黄玮, 马万经. 过饱和状态下交通控制小区动态划分方法[J]. 同济大学学报(自然科学版), 2010, 38(10): 1450-1457.
YANG Xiaoguang, HUANG Wei, MA Wanjing. Method of delimiting urban traffic signal coordinate control subarea under oversaturated condition[J]. Journal of Tongji University(Natural Science), 2010, 38(10): 1450-1457. DOI:10.3969/j.issn.0253-374x.2010.10.009

[4] SUN H J, GAO Z Y, WU J J. A bi-level programming model and solution algorithm for the location of logistics distribution centers[J]. Applied Mathematical Modeling, 2008, 32(4): 610-616. DOI:10.1016/j.apm.2007.02.007

[5] TANG J X, TANG L X, WANG X P. Solution method for the location planning problem logistics park with variable capacity[J]. Computers Operations & Operations Research, 2013, 10(1): 406-417.

[6] 龚延成, 郭晓汾, 蔡团结, 等. 物流配送点选址模型及其算法研究[J]. 中国公路学报, 2003, 16(2): 123-126.
GONG Yancheng, GUO Xiaofen, CAI Tuanjie, et al. Research on the choosing model of physical distribution[J]. China Journal of Highway and Transport, 2003, 16(2): 123-126.

[7] ZHANG Q, JIANG C S. Application of genetic algorithm in functional area layout of railway logistics park[J]. Procedia-Social and Behavioral Sciences, 2014, 7(204): 269-278.

[8] CHEN Y R, JIANG Y S, WAHAB M I M, et al. The facility layout problem in non-rectangular logistics parks with split lines[J]. Expert Systems with Applications, 2015, 42(21): 7768-7780. DOI:10.1016/j.eswa.2015.06.009

[9] ZHANG D Z, EGLESS R, LI S Y. Optimal location and size of logistics parks in a regional logistics network with economies of scale and CO emission taxes[J]. Transport, 2015, 33(1): 1-17. DOI:10.3846/16484142.2015.1004644

[10] 马超群, 王瑞. 基于区内出行比例的城市交通小区半径计算方法[J]. 交通运输工程学报, 2007, 7(1): 68-72.
MA Chaoqun, WANG Rui. Calculating method of traffic zone radius in city based on inner trip proportion[J]. Journal of Traffic and Transportation Engineering, 2007, 7(1): 68-72.

[11] 张敏, 于剑. 基于划分的模糊聚类算法[J]. 软件学报, 2004, 15(6): 858-868.
ZHANG Min, YU Jian. Fuzzy partitional clustering algorithms[J]. Journal of Software, 2004, 15(6): 858-868. DOI:10.13328/j.cnki.jos.2004.06.008

[12] 李晓丹, 杨晓光, 陈华杰. 城市道路网络交通小区划分方法研究[J]. 计算机工程与应用, 2009, 45(5): 19-22.
LI Xiaodan, YANG Xiaoguang, CHEN Huajie. Study on traffic zone division based on spatial clustering analysis[J]. Computer Enginee-ring and Applications, 2009, 45(5): 19-22. DOI:10.3778/j.issn.1002-8331.2009.05.006

[13] 谭庆, 何清, 赵卫中, 等. 基于进化规划的FCMBP模糊聚类改进方法[J]. 系统工程理论与实践, 2011, 31(7): 1363-1371.
TAN Qing, HE Qing, ZHAO Weizhong, et al. Evolutionary programming based FCMBP fuzzy clustering method[J]. Systems Engineering—Theory & Practice, 2011, 31(7): 1363-1371. DOI:10.12011/1000-6788(2011)7-1363

[14] 雷英杰, 王宝树, 胡军红. 直觉模糊等价矩阵构造方法[J]. 系统工程理论与实践, 2007, 27(7): 127-131.
LEI Yingjie, WANG Baoshu, HU Junhong. Method for constructing intuitionistic fuzzy equivalent matrixes[J]. Systems Engineering—Theory & Practice, 2007, 27(7): 127-131.

[15] 邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7): 93-100.
DENG Xue, LI Jiaming, ZENG Haojian, et al. The analysis and application research of analytic hierarchy process(AHP) weight calculation method[J]. Mathematics in Practice and Theory, 2012, 42(7): 93-100.