Xiaoye Zhao, Xunsheng Ji, Yuanxiang Li,Li Peng
(Engineering Research Center of Internet of Things Technology Applications of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, Jiangsu, China )
Abstract:
Recognition of the human actions by computer vision has become an active research area in recent years. Due to the speed and the high similarity of the actions, the current algorithms cannot get high recognition rate. A new recognition method of the human action is proposed with the multi-scale directed depth motion maps (MsdDMMs) and Log-Gabor filters. According to the difference between the speed and time order of an action, MsdDMMs is proposed under the energy framework. Meanwhile, Log-Gabor is utilized to describe the texture details of MsdDMMs for the motion characteristics. It can easily satisfy both the texture characterization and the visual features of human eye. Furthermore, the collaborative representation is employed as action recognition by the classification. Experimental results show that the proposed algorithm, which is applied in the MSRAction3D dataset and MSRGesture3D dataset, can achieve the accuracy of 95.79% and 96.43% respectively. It also has higher accuracy than the existing algorithms, such as super normal vector(SNV), hierarchical recurrent neural network (Hierarchical RNN).
Key words: human action recognition depth motion maps Log-Gabor filters collaborative representation based classifier
DOI:10.11916/j.issn.1005-9113.17090
Clc Number:TP391.4
Fund:
Xiaoye Zhao, Xunsheng Ji, Yuanxiang Li, Li Peng. Combining Multi-scale Directed Depth Motion Maps and Log-Gabor Filters for Human Action Recognition[J]. Journal of Harbin Institute of Technology (New Series), 2019, 26(4): 89-96. DOI: 10.11916/j.issn.1005-9113.17090.

Fund Sponsored by the Jiangsu Prospective Joint Research Project (Grant No. BY2016022-28) Corresponding author Xiaoye Zhao, E-mail: jndx_zxy@126.com Article history Received: 2017-07-21
Contents Abstract Full text Figures/Tables PDF
Combining Multi-scale Directed Depth Motion Maps and Log-Gabor Filters for Human Action Recognition
Xiaoye Zhao

 , Xunsheng Ji, Yuanxiang Li, Li Peng
, Xunsheng Ji, Yuanxiang Li, Li Peng Engineering Research Center of Internet of Things Technology Applications of the Ministry of Education, School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, Jiangsu, China
Received: 2017-07-21
Sponsored by the Jiangsu Prospective Joint Research Project (Grant No. BY2016022-28)
Corresponding author: Xiaoye Zhao, E-mail: jndx_zxy@126.com
Abstract: Recognition of the human actions by computer vision has become an active research area in recent years. Due to the speed and the high similarity of the actions, the current algorithms cannot get high recognition rate. A new recognition method of the human action is proposed with the multi-scale directed depth motion maps (MsdDMMs) and Log-Gabor filters. According to the difference between the speed and time order of an action, MsdDMMs is proposed under the energy framework. Meanwhile, Log-Gabor is utilized to describe the texture details of MsdDMMs for the motion characteristics. It can easily satisfy both the texture characterization and the visual features of human eye. Furthermore, the collaborative representation is employed as action recognition by the classification. Experimental results show that the proposed algorithm, which is applied in the MSRAction3D dataset and MSRGesture3D dataset, can achieve the accuracy of 95.79% and 96.43% respectively. It also has higher accuracy than the existing algorithms, such as super normal vector(SNV), hierarchical recurrent neural network (Hierarchical RNN).
Keywords: human action recognition depth motion maps Log-Gabor filters collaborative representation based classifier
1 Introduction Currently, human action recognition has become a hot topic in machine vision and pattern recognition. It has been widely used in human computer interaction applications, including video retrieval, video surveillance, medical and health care[1-2]. Human action recognition is still facing with enormous challenges, because of scene changes, occlusion and noise interference etc. The depth images are not sensitive to lighting condition and background clutter, which limit the robustness of action recognition[3-4]. Compared with RGB images, the depth images can also provide more three dimensional information.Based on the depth images, research on human action recognition, has got great concern in the past years[5-7].
Inspired by the high recognition rate of motion history image, based on RGB video in human action recognition[8], a method, called depth motion maps (DMMs) was proposed by Yang, et al.[9], to capture the motion energy in the time dimension. Based on Ref.[9], the calculation method of DMMs, eliminating the threshold of motion energy expression, was improved by Chen, et al[10]. At the same time, the local binary model (LBP) was also introduced to describe the detailed information in DMMs. Liang, et al.[11], put forward the horizontal stratification optimization to DMMs. Multi-layer DMMs was obtained, where the nth layer of DMMs was used to calculate the difference energy sum of the whole video. The video was got by sampling the original depth video every interval n frames. Finally, the human action recognition can be achieved by combining the LBP features with collaborative representation classification (CRC)[9]. Recently, Wang, et al.[12], attempted to put the DMMs directly into the depth convolution neural network for the behavior classification. However, DMMs, based on the entire depth sequences, will lose time information and detail information of human behavior. Therefore, it is difficult to distinguish between two similar human actions, such as 'sitting down' and 'standing up'. Such actions are mainly different in time order. In addition, the DMMs do not consider the intra-class error, caused by the different execution speed of the action, which reduces the recognition rate.
This paper presents a method of human action recognition, based on multi-scale directed depth motion maps (MsdDMMs) and Log-Gabor filter. Firstly, considering the different execution speed of the action, a video segmentation method, based on energy uniformization, is used to divide an action video into several sub-video sequences. In order to make the different layers of the time pyramid contain more details, the nth pyramid divides the entire video into 2n-1, not 2n-1, where n is 3. Secondly, in order to distinguish two similar actions with different time order, this paper presents a new method, called as improved MsdDMMs, where the details and time information of the actions can be captured simultaneously. Then, in order to describe the texture details of MsdDMMs, the Log-Gabor filter[13] is used as the action characteristic descriptor. Finally, the CRC is used to identify the action. The flow of the algorithm is shown in Fig. 1.
Fig.1
 Fig.1 Flow of this algorithm
Fig.1 Flow of this algorithm 2 Multi-scale Directional DMMs In order to recognize human action, the depth images firstly are projected into three orthogonal Cartesian planes. DMMs and the improved MsdDMMs, proposed in this paper, will be introduced in detail.
2.1 DMMs DMMs[9] can fully capture the body shape and motion information, reflected by each depth image in the video. The original depth images will be projected into three orthogonal planes (front, side, top) to calculate the inter frame difference energy over the entire video sequence and to get DMMs. Assuming that the original depth video sequence has N frames, DMMs can be calculated as follows:
${\rm{DM}}{{\rm{M}}_{\left\{ {f, s, t} \right\}}} = \sum\limits_{i = 2}^N {\left| {I_{\left\{ {f, s, t} \right\}}^i - I_{\left\{ {f, s, t} \right\}}^{i - 1}} \right|} $ (1)
whereI{f, s, t}i is the corresponding projection in front, side and top of the ith image.
2.2 Directed DMMs For human action recognition, the direction of movement is also crucial besides body shape and movement information. Given two similar actions, shown in Fig. 2(a) and (b), the corresponding DMM is shown in Fig. 2(c). The DMM are the same and easily misclassified as one action obviously. Inspired by GTI with positive value and negative value to overcome the lack of direction in GBI[14], this paper presents the directed DMMs.
Fig.2
 Fig.2 Action #1 and Action #2 represent 'raising hands' and 'laying hands' and the corresponding DMM, PDMM and NDMM
Fig.2 Action #1 and Action #2 represent 'raising hands' and 'laying hands' and the corresponding DMM, PDMM and NDMM Directed DMMs include positive DMM (PDMM) and negative DMM (NDMM). The PDMM reflects the shape and motion information of the positive depth value, while the NDMM reflects that of negative depth value. PDMM{f, s, t} and NDMM{f, s, t} are the corresponding PDMM and NDMM in front, side, top of ith projection image. They can be calculated as follows:
${\rm{PDM}}{{\rm{M}}_{\left\{ {f, s, t} \right\}}} = \sum\limits_{i = 2}^N {\left( {I_{\left\{ {f, s, t} \right\}}^i - I_{\left\{ {f, s, t} \right\}}^{i - 1}} \right)} , I_{\left\{ {f, s, t} \right\}}^i \ge I_{\left\{ {f, s, t} \right\}}^{i - 1}$ (2)
${\rm{NDM}}{{\rm{M}}_{\left\{ {f, s, t} \right\}}} = \sum\limits_{i = 2}^N {\left( {I_{\left\{ {f, s, t} \right\}}^i - I_{\left\{ {f, s, t} \right\}}^{i - 1}} \right)} , I_{\left\{ {f, s, t} \right\}}^i \le I_{\left\{ {f, s, t} \right\}}^{i - 1}$ (3)
where I{f, s, t}i is the corresponding projection in front, side and top of the ith image. When the body moves forward or backward, it will be seen that PDMM{f, s, t} and NDMM{f, s, t} gather the energy of body rather than the absolute sum of the body movement energy as the traditional methods. The motion depth images, based on the entire video and regardless of the direction of motion, ignore the direction information of the action itself. The two human movements, which are basically similar, but opposite in direction, cannot be separated, such as 'raising hands' and 'laying hands'. Otherwise, the directed DMMs, proposed in the algorithm, can fully carry the direction of information and can distinguish them well.
Fig. 2(d) and (e) show the PDMM and NDMM corresponding to the front projection image of two similar actions in Fig. 2(a) and (b). It can be easily seen that the PDMM and NDMM are reversed and can be distinguished between two actions.
2.3 Multi-scale Directed DMMs The motion direction of DMMs with the whole video, can reflect the whole motion information of the video, but neglects the time information of the action, where the details in the time dimension are lost. Therefore, it can be considered to divide the whole video sequence into multiple sub-video sequences. The classic video segmentation method is able to use a time-separated pyramid method and segmented uniformly in the time dimensions. However, amplitude and speed will change even if different people complete the same action several times. Bigger amplitude and faster speed of the action contains not only greater energy, but also more details. In contrast, smaller amplitude and slower speed of the motion has the opposite result. So, a video segmentation method, based on energy uniformity[15], is used to divide an action video into multiple sub-video sequences.
In Ref. [15], the normalized energy was divided into four equal parts and obtains 5 moments t1, t2, t3, t4, t5. Then, a three-layer time pyramid was constructed by the corresponding seven subsequences including [t1, t5], [t1, t3], [t3, t5], [t1, t2], [t2, t3], [t3, t4], [t4, t5]. The higher layer contained all the details of the lower layer. Different from the nth floor pyramid being divided into 2n-1 parts equally[8], this paper divides into 2n-1 and can contain more details in different layers. {f, s, t} were front, side, top respectively. The energy of ith image could be calculated as follows:
$\varepsilon \left( i \right) = \left\{ \begin{array}{l}0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1\\\sum\limits_{v \in \{ f, s, t\} } {\sum\limits_{j = 1}^{i - 1} {\left| {I_v^{j + 1} - I_v^j} \right|, i > 1} } \end{array} \right.$ (4)
The moving image sequences, obtained by the inter-frame difference method, are respectively divided by different energy divisions to obtain multiple sub-video sequences, and to construct different layers of the time pyramid. As shown in Fig. 3(a), the energy is evenly divided to construct a 3-layer time pyramid. The pyramid is shown in Fig. 3(b). Corresponding to the three orthogonal planes of all the subsequences, the PDMMs and NDMMs can be calculated by the Eq.(2) and Eq.(3) respectively. By constructing the time pyramid, we can get sub-video sequences with different particle sizes. The PDMMs and NDMMs are different scales. Large scale embodies the global profile information. The small scale contains a lot of local details.
Fig.3
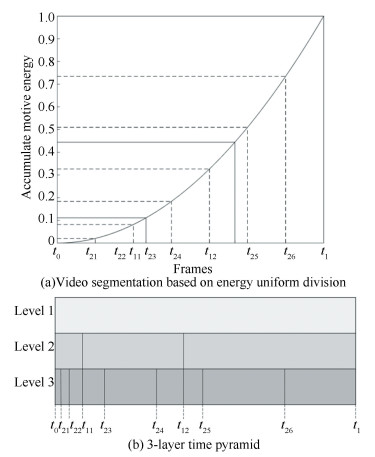 Fig.3 The video segmentation and the corresponding construction of 3-layer time pyramid
Fig.3 The video segmentation and the corresponding construction of 3-layer time pyramid 3 Feature Representation and Classification 3.1 Log-Gabor Feature Representation Studies have shown that Gabor wavelet can simulate the human eye photosensitive properties. It can be characterized that the corresponding visual characteristics of the human eye by building multi-scale, multi-directional Gabor filter. In addition, Field[13] proposed the Log-Gabor wavelet on the basis of Gabor wavelet in 1987, whose frequency performance was more superior and more consistent with the non-linearity of human vision.
In order to describe the local texture and shape information of PDMMs and NDMMs, the amplitude characteristics of 24 Log-Gabor filters[11] are used. The 24 filters are made up of 4-scale and 6-direction 6 Log-Gabor feature vectors. The 6 Log-Gabor feature vectors, corresponding to PDMMs and NDMMs of three planar (front, side, top), is as follows:
${\mathit{\boldsymbol{\vec g}}} = \left[ {{{{\mathit{\boldsymbol{\vec g}}} }_{{\rm{PDM}}{{\rm{M}}_f}}}, {{{\mathit{\boldsymbol{\vec g}}} }_{{\rm{NDM}}{{\rm{M}}_f}}}, {{{\mathit{\boldsymbol{\vec g}}} }_{{\rm{PDM}}{{\rm{M}}_s}}}, {{{\mathit{\boldsymbol{\vec g}}} }_{{\rm{NDM}}{{\rm{M}}_s}}}, {{{\mathit{\boldsymbol{\vec g}}} }_{{\rm{PDM}}{{\rm{M}}_t}}}, {{{\mathit{\boldsymbol{\vec g}}} }_{{\rm{NDM}}{{\rm{M}}_t}}}} \right]$ (5)
Concatenated feature representation has a very high dimension. The principal component analysis (PCA) is used to reduce the feature dimension before classification. As a result, it still can retain 95% of the original characteristic energy.
3.2 Collaborative Representation Classification Collaborative representation classification (CRC) has a good classification performance and computational efficiency in face recognition, image classification and action recognition[10]. The collaborative representation is a linear combination of training samples to represent the test samples. Theoretically, the classifier assumes that each test sample is reconstructed by all trained samples. The trained samples, which belong to the same class with the test sample, account for the largest proportion in the linear reconstruction. Hence, the test sample can be classified into the corresponding class, which contributes the most to the reconstruction. Collaboration representation is used to determine whether the test sample belongs to a class or not. It is necessary to judge whether the difference between the test sample and the class is small or not. And it is also necessary to judge the difference between the test sample and other class is large. The 'double check' makes the identification more efficient and robust.
In this paper, the Log-Gabor feature is put forward to the CRC to achieve human action recognition. Supposing that there are M trained samples, coming from C classes of actions, a feature vector g with d dimensions, is made up by such action sequence generates. The trained set can be denoted as
$\begin{array}{l}\mathit{\boldsymbol{\vec G = }}\left[ {{{\mathit{\boldsymbol{\vec G}}}_1}, {{\mathit{\boldsymbol{\vec G}}}_2}, \cdots , {{\mathit{\boldsymbol{\vec G}}}_\mathit{\boldsymbol{c}}}} \right] \in {R^{d \times M}}, {\rm{where}}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\vec G}}}_\mathit{\boldsymbol{j}}} = \left[ {{g_1}, {g_2}, \cdots , {g_{mj}}} \right]\end{array}$
denotes mj trained samples from the jth class, j=1, 2, ..., C. Let y∈Rd denotes the feature representation of a test sample, the collaborative representation can be mathematically represented as follows:
$\overrightarrow {\hat a} = \arg \;\mathop {\min }\limits_a \left\{ {\left\| {y - {\mathit{\boldsymbol{\vec G}}} {\mathit{\boldsymbol{\vec \alpha}}} } \right\|_2^2 + \lambda \left\| {{\mathit{\boldsymbol{\vec \alpha}}} } \right\|_2^2} \right\}$ (6)
where λ is the regularization parameter to achieve the stabilization of the reconstruction error and sparseness, α is a coefficient vector corresponding to all the trained samples.
Finally, the class label of y can be obtained as follows:
${\rm{class}}(y) = \arg \;\mathop {\min }\limits_{j = 1, \ldots , c} {\left\| {y - \overrightarrow {{\mathit{\boldsymbol{G}}_j}} {{\overrightarrow {\mathit{\boldsymbol{\hat \alpha }}} }_j}} \right\|_2}$ (7)
where
4 Experiment In order to demonstrate the recognition performance of the algorithm, the following experiments and analysis are carried out on two public datasets.
4.1 MSRAction3D Dataset The MSRAction3D dataset is a public database of human action collection, consisting of 20 actions. Each action is repeated 2-3 times by 10 performers. 20 kinds of actions include 'high arm wave', 'horizontal arm wave', 'hammer', 'hand catch', 'forward punch', 'high throw', 'draw x', 'draw tick', 'draw circle', 'hand clap', 'two hand wave', 'side boxing', 'bend', 'forward kick', 'side kick', 'jogging', 'tennis swing', 'tennis serve', 'golf swing', 'pick up and throw'. The database has a total of 557 video sequences. Size of each frame is 240×320. Although the background of this database has been processed, but it's identification is still quite challenging due to the high similarity between many actions.
In order to ensure a fair comparison, the experimental setup of this paper is exactly the same as Refs. [9-10]. 20 actions are selected as one set. The odd order subjects are selected as trained subjects. The even subjects are selected as the test subjects. In the experiment, the size of MsdDMMs of front, side and top, are normalized to 102×54, 102×75 and 75×54 respectively. Size of the Log-Gabor filter is set to 10×11.
λ in CRC generally ranges from 0.0001 to 1. In the experiment, different values of λ is taken for experiment. The results are shown in Table 1. When λ is set as 0.001, the highest recognition accuracy is got.
表 1
Accuracy (%)95.4195.7995.0595.0594.34
Table 1 MSRAction3D dataset: comparison of the recognition rate for different λ
Performance from the different operators of Log-Gabor, HOG, LBP, Gabor, is also compared and shown in Table 2. Seen from the Table 2, the Log-Gabor operator has the best performance.
表 2
Accuracy (%)92.2294.3594.7095.79
Table 2 MSRAction3D dataset: comparison of the recognition rate for different feature operators
In Table 3, our proposed algorithm is compared with the other excellent recognition methods in recent years. It can be seen that the algorithm can achieve a high recognition rate of 95.79%. In addition, Fig. 4 also shows the corresponding confusion matrix, where the horizontal and vertical coordinates represent identified and marked types of actions respectively. The experimental results can show that most of the movements have been correctly identified, except for the special similar movements such as 'hand catch' and 'high throwing'.
表 3
Depth Motion Maps[10]201288.73
HON4D[16]201388.89
Actionlet-Ensemble[17]201488.20
SNV[18]201493.09
DMM-LBP-DF[11]201593.00
Hierarchical RNN[19]201594.49
Hierarchical 3D Kernel Descriptors[20]201693.99
MsdDMMs+Log-Gabor (Ours)-95.79
Table 3 MSRAction3D dataset: comparison of the recognition rate between the algorithm and the existing method
Fig.4
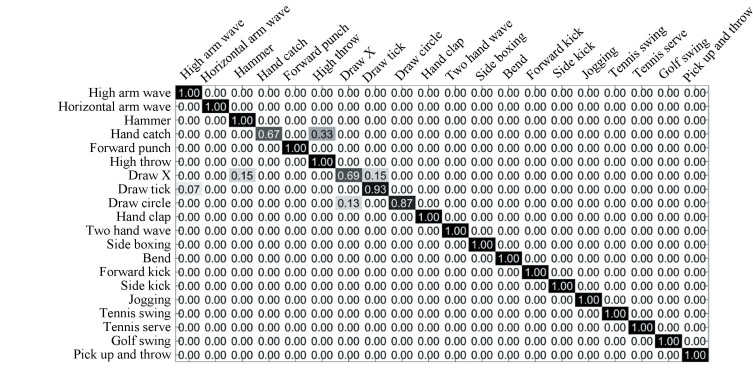 Fig.4 MSRAction3D dataset: confusion matrix
Fig.4 MSRAction3D dataset: confusion matrix 4.2 MSRGesture3D Dataset MSRGesture3D dataset is a hand gesture dataset consisting of 333 video sequences and contains 12 standard gestures. The 12 standard gesture include 'z', 'j', 'where', 'store', 'pig', 'past', 'hungry', 'green', 'finish', 'blue', 'bathroom', 'milk'. Each action was repeated 2~3 times by the 10 performers. The database is challenging due to self-occlusion problem. In this paper, the leave-one-out cross-validation method[9-10] is used. The first experiment uses all the data of the first performer as the test set, the rest as the trained set. The second experiment uses all the data of the second performer as the test set, the remaining as the train set, and so on. Finally, 10 experiments are carried out. Average of the 10 experimental results is as the final recognition rate. In the experiment, the size of MsdDMMs of front, side and top, are normalized to 118×133, 118×29 and 29×133, respectively. Size of the Log-Gabor filter is set to 10×11. λ in CRC generally ranges from 0.0001 to 1. In the experiment, different λ is used to finish the test. The results are shown in Table 4. When λ is set as 0.01, the highest recognition accuracy can be achieved via this experiment.
表 4
Accuracy (%)94.6096.3296.4395.8893.98
Table 4 MSRGesture3D dataset: comparison of the recognition rate for different λ
Performance from the different operators of Log-Gabor, HOG, LBP, Gabor, is also compared and shown in Table 5. Seen from the Table 5, the Log-Gabor operator has the best performance. The confusion matrix on this database is shown in Fig. 5.
表 5
Accuracy (%)93.6094.7095.4496.43
Table 5 MSRGesture3D dataset: comparison of the recognition rate for different feature operators
Fig.5
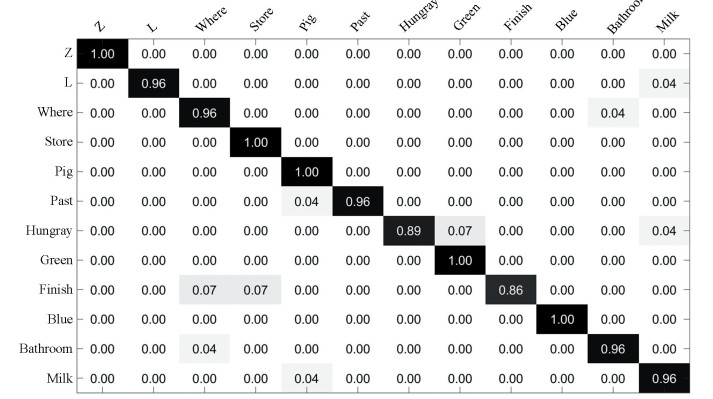 Fig.5 MSRGesture3D dataset: confusion matrix
Fig.5 MSRGesture3D dataset: confusion matrix It can be easily shown that the algorithm has excellent performance in many gestures. In Table 6, the performance of this algorithm is compared with other excellent methods in recent years. It can be seen that the algorithm can achieve a recognition rate of 96.43%.
表 6
Random Occupancy Pattern[21]201288.50
HON4D[16]201392.45
Edge enhanced DMM[22]201489.20
3D-CNN+DMM-Paramid[23]201494.35
SNV[18]201494.47
HOG3D+LLC[24]201594.10
DMM-LBP-DF[11]201594.60
MsdDMMs+Log-Gabor (Ours)-96.43
Table 6 MSRGesture3D dataset: comparison of the recognition rate between the algorithm and the existing method
4.3 Real-time Analysis Real-time, based on MSRAction3D dataset, is analyzed. The average time for extracting MsdDMMs is 1.69 s per sequence on 3.2 GHz machine with 4 GB RAM, using Matlab R2012. The average time for calculating Log-Gabor is 0.89 s per sequence. The average time of PCA to reduce dimension and CRC classification is 0.51 ms per sequence and 1.43 ms per sequence respectively.
5 Conclusions The problem of a human action recognition method together with multi-scale directed depth motion maps (MsdDMMs) and Log-Gabor filters is addressed in this paper, where a new MsdDMMs based on the energy framework is designed. The texture details of MsdDMMs as well action recognition are described via the Log-Gabor filter and CRC, respectively. Subsequently, MsdDMMs with Log-Gabor filters is designed so as to achieve the high recognition rate. According to the new interval values, the velocity variation is applied by MsdDMMs by means of energy uniformity method. The PDMMs and NDMMs are first described as the action direction. Compared with many existing algorithms including super normal vector (SNV), hierarchical recurrent neural network (Hierarchical RNN), etc, the proposed algorithm has high recognition rate and robustness. However, the proposed algorithm is not suitable for the complex behavior of camera perspective changes in the real applications.
References
[1] Chen C, Kehtarnavaz N, Jafari R. A medication adherence monitoring system for pill bottles based on a wearable inertial sensor. Proceedings of Engineering in Medicine and Biology Society. New York: Kwang Suk Park, 2014: 4983-4986. DOI:10.1109/EMBC.2014.6944743 (
 0)
0)[2] Yussiff A L, Yong S P, Baharudin B B. Human action recognition in surveillance video of computer laboratory. 2016 3rd International Conference on Computer and Information Sciences (ICCOINS). Bangkok: Robert J. Taormina, 2016. 418-423. DOI: 10.1109/ICCOINS.2016.7783252. (
 0)
0)[3] Chao Shen, Chen Yufei, Yang Gengshan. On motion-sensor behavior analysis for human-activity recognition via smartphones. IEEE International Conference on Identity, Security and Behavior Analysis. Sendai: Adams Kong, 2016. 1-6. DOI: 10.1109/ISBA.2016.7477231. (
 0)
0)[4] Ke S R, Thuc H L, Lee Y J, et al. A review on video-based human activity recognition. Computers, 2013, 2(2): 88-131. DOI:10.3390/computers2020088 (
 0)
0)[5] Lei Qing, Li Shaozi, Chen Duansheng. Using poselet and scene information for action recognition in still images. Journal of Chinese Computer Systems, 2015, 41(5): 259-263. (in Chinese) (
 0)
0)[6] Li Ruifeng, Wang Liangliang, Wang Ke. A survey of human body action recognition. Pattern Recognition and Artificial Intelligence (PR&AI), 2014, 1(1): 35-48. (in Chinese) DOI:10.16451/j.cnki.issn1003-6059.2014.01.005 (
 0)
0)[7] Liang Bin, Zheng Lihong. A survey on human action recognition using depth sensors. International Conference on Digital Image Computing: Techniques and Applications. Adelaide: Jamie Sherrah, 2015: 1-8. DOI:10.1109/DICTA.2015.7371223 (
 0)
0)[8] Tian Yingli, Cao Liangliang, Liu Zicheng, et al. Hierarchical filtered motion for action recognition in crowded videos. IEEE Transactions on Systems Man & Cybernetics Part C, 2012, 42(3): 313-323. DOI:10.1109/TSMCC.2011.2149519 (
 0)
0)[9] Yang Xiaodong, Zhang Chenyang, Tian Yingli. Recognizing actions using depth motion maps-based histograms of oriented gradients. Association for Computing Machinery (ACM) International Conference on Multimedia. New York: Kien A. Hua, 2012: 1057-1060. DOI:10.1145/2393347.2396382 (
 0)
0)[10] Chen Chen, Jafari Roozbeh, Kehtarnavaz Nasser. Action recognition from depth sequences using depth motion maps-based local binary patterns. IEEE Winter Conference on Applications of Computer Vision. Hawaii: Bir-Bhanu, 2015. 1092-1099. DOI: 10.1109/WACV.2015.150. (
 0)
0)[11] Liang Chengwu, Chen Enqing, et al. Improving action recognition using collaborative representation of local depth maps feature. IEEE Signal Processing Letters, 2016, 23(9): 1241-1245. DOI:10.1109/LSP.2016.2592419 (
 0)
0)[12] Wang Pichao, Li Wanqing, Gao Zhimin, et al. Convnets-based action recognition from depth maps through virtual cameras and pseudocoloring. ACM Mm ACM. Brisbane: Alberto Del Bimbo, 2015: 1119-1122. DOI:10.1145/2733373.2806296 (
 0)
0)[13] Field David J. Relations between the statistics of natural images and the response properties of cortical cells. Journal of the Optical Society of America A Optics & Image Science, 1987, 4(12): 2379. DOI:10.1145/2733373.2806296 (
 0)
0)[14] Liu Mengyuan, Hong Liu, Chen Chen. 3D Action Recognition Using Multi-scale Energy-based Global Ternary Image. IEEE Transactions on Circuits & Systems for Video Technology, 2017, 1(99): 1-1. DOI:10.1109/TCSVT.2017.2655521 (
 0)
0)[15] Wang Jiang, Liu Zicheng, Chorowski Jan, et al. Robust 3d action recognition with random occupancy patterns. European Conference on Computer Vision (ECCV). Firenze: Roberto Cipolla, 2012. 872-885. (
 0)
0)[16] Oreifej Omar, Liu Zicheng. HON4D: Histogram of oriented 4d normals for activity recognition from depth sequences. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Portland: Gerard Medioni, 2013. 716-723. DOI: 10.1109/CVPR.2013.98. (
 0)
0)[17] Wang Jiang, Liu Zicheng, Wu Ying, et al. Learning actionlet ensemble for 3d human Action recognition. IEEE Transactions on Software Engineering, 2013, 36(5): 914-927. DOI:10.1109/TPAMI.2013.198 (
 0)
0)[18] Yang Xiaodong, Tian Yingli.Super normal vector for activity recognition using depth sequences. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Columbus: Sven Dickinson, 2014. 804-811. DOI: 10.1109/CVPR.2014.108. (
 0)
0)[19] Yong D, Wang W, Wang L. Hierarchical recurrent neural network for skeleton based action recognition. Intelligent Perception and Computing Research Center, 2015(CVPR): 1110-1118. DOI:10.1109/CVPR.2015.7298714 (
 0)
0)[20] Kong Yu, Satarboroujeni Behnam, Fu Yun. Learning hierarchical 3D kernel descriptors for RGB-D action recognition. Computer Vision & Image Understanding, 2016, 144(C): 14-23. DOI:10.1109/FG.2015.7163084 (
 0)
0)[21] He Weihua. Human Action Recognition Key Technology Research. Chongqing: Chongqing University, 2012. (
 0)
0)[22] Zhang Chenyang, Tian Yingli. Edge enhanced depth motion map for dynamic hand gesture recognition. 2013 IEEE Conference on Computer Vision and Pattern Recognition Workshop (CVPRW). Piscataway: IEEE, 2013. 500-505. DOI: 10.1109/CVPRW.2013.80. (
 0)
0)[23] Yang R, Yang R. DMM-Pyramid Based Deep Architectures for Action Recognition with Depth Cameras. The 12th Asian Conference on Computer Vision (ACCV). Singapore: Michael S. Brown, 2014. 37-49. (
 0)
0)[24] Rahmani Hossein, Du Huynh, Mahmood Arif, et al. Discriminative human action classification using locality-constrained linear coding. Pattern Recognition Letters, 2015, 72: 62-71. DOI:10.1109/ICPR.2014.604 (
 0)
0)