Xin Sun1, Di Huang2,Qixiu Cheng2
(1. Nanjing Institute of City & Transport Planning Co., Ltd., Nanjing 210008, China; 2. Jiangsu Key Laboratory of Urban ITS, Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Southeast University, Nanjing 210096, China)
Abstract:
In order to address the optimal distance toll design problem for cordon-based congestion pricing incorporating the issue of equity, this paper presents a toll user equilibrium (TUE) model based on a transformed network with elastic demand, to evaluate any given toll charge function. A bi-level programming model is developed for determining the optimal toll levels, with the TUE being represented at the lower level. The upper level optimizes the total equity level over the transport network, represented by the Gini coefficient, where a constraint is imposed to the total travel impedance of each OD pair after the levy. A genetic algorithm (GA) is implemented to solve the bi-level model, which is verified by a numerical example.
Key words: congestion pricing optimal tolls equity issue bi-level model distance-based pricing
DOI：10.11916/j.issn.1005-9113.2016.06.011
Clc Number:U491.13
Fund:
Xin Sun, Di Huang, Qixiu Cheng. Optimal Nonlinear Distance Toll for Cordon-Based Congestion Pricing Considering Equity Issue[J]. Journal of Harbin Institute of Technology, 2016, 23(6): 73-79. DOI: 10.11916/j.issn.1005-9113.2016.06.011.
Fund Sponsored by the National Natural Science Foundation of China(Grant No.61374195 and 71501038), the Fundamental Research Funds for the Central Universities(Grant No.2242015R30036) and the Natural Science Foundation of Jiangsu Province in China(Grant No.BK20150603) Corresponding author E-mail: vic_dhuang@163.com Article history Received: 2015-07-29
Contents Abstract Full text Figures/Tables PDF
Optimal Nonlinear Distance Toll for Cordon-Based Congestion Pricing Considering Equity Issue
Xin Sun1, Di Huang2
, Qixiu Cheng2 1. Nanjing Institute of City & Transport Planning Co., Ltd., Nanjing 210008, China;
2. Jiangsu Key Laboratory of Urban ITS, Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Southeast University, Nanjing 210096, China
Received: 2015-07-29
fund: Sponsored by the National Natural Science Foundation of China(Grant No.61374195 and 71501038), the Fundamental Research Funds for the Central Universities(Grant No.2242015R30036) and the Natural Science Foundation of Jiangsu Province in China(Grant No.BK20150603)
Corresponding author: E-mail: vic_dhuang@163.com
Abstract: In order to address the optimal distance toll design problem for cordon-based congestion pricing incorporating the issue of equity, this paper presents a toll user equilibrium (TUE) model based on a transformed network with elastic demand, to evaluate any given toll charge function. A bi-level programming model is developed for determining the optimal toll levels, with the TUE being represented at the lower level. The upper level optimizes the total equity level over the transport network, represented by the Gini coefficient, where a constraint is imposed to the total travel impedance of each OD pair after the levy. A genetic algorithm (GA) is implemented to solve the bi-level model, which is verified by a numerical example.
Key words: congestion pricing optimal tolls equity issue bi-level model distance-based pricing
1 IntroductionTraffic congestion is a severe problem confronted with in many large urban areas, which leads to high levels of fuel consumption, air pollution, economic loss and crashes. Cordon-based congestion pricing has been widely recognized as an efficient way to ameliorate urban traffic congestion[1-5]. Currently most countries have implemented daily license[6] or entry-based congestion pricing schemes[3], which are not equitable because drivers have different levels of usage of toll roads. Hence, May and Milne[7] proposed and explored three alternative toll charge schemes: time-based, congestion-based and distance-based schemes to replace the current congestion pricing schemes. The first two schemes may have negative impacts on drivers because they can encourage aggressive driving behavior drivers leading to the increased safety problems. Compared to time and congestion based schemes, distance-based toll charging schemes are linked with the distance travelled inside a pricing cordon and thus are more reasonable and practical than the first two schemes in the real world.
The issue of equity is quite crucial for public acceptance of congestion pricing schemes[8]. Although the theoretical soundness of congestion pricing has been well recognized by researchers[9-10], political and public resistance are still major hurdles for its practical implementation, due to concerns that congestion pricing is not equitable, resulting in fears that car travel will become a privilege only for the rich. Therefore, it is of considerable importance to perform in-depth research on the equity of distance tolls. The aim of this paper is to present a methodology for addressing the optimal nonlinear distance toll that can optimize the level of equity over an entire traffic network.
2 Distance-Based Toll Design Problem2.1 Problem DescriptionA strongly connected urban transportation network is denoted by G=(N, A), where N and A are the sets of nodes and links, respectively. Cordon-based congestion pricing divides the network G=(N, A) into two parts: an external network
${{\tau }_{wk}}\left( \varphi \right)=\varphi ({{d}_{k}}^{w})$ (1)
Different toll charge functions φ(d) yield different impacts on the network. Thus, how to determine the optimal function that can improve the equity level of the transport network is a critical issue. The nonlinear function has no specific functional form, and there is also no practical data to calibrate this function, making the toll design problem for distance tolls a challenging one. Following the ideas from previous studies by Meng[11] and Lawphongpanich and Yin[12], a piecewise linear function is adopted to approximate a nonlinear function form. Specific details of the piecewise linear approximation method are illustrated in Fig. 1.
Figure 1
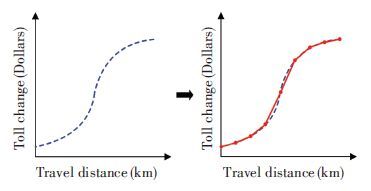Figure 1 An illustration for the piecewise linear approximation function As claimed by Lawphongpanich and Yin[12], compared with a highly nonlinear function, such a piecewise linear function is easier to understand by users and is more practical for implementation whilst having most of the advantages of a general nonlinear pricing function. It starts with defining the minimum and maximum length on the path in the pricing cordon and then the nonlinear toll charge function is evenly divided into n intervals, using a linear function within each interval as an approximation.
$[{{d}_{min}},\text{ }{{d}_{2}}\left] ,\text{ } \right[{{d}_{2}},\text{ }{{d}_{3}}\left] ,\text{ }\ldots ,\text{ } \right[{{d}_{i}},\text{ }{{d}_{i+1}}\left] ,\text{ }\ldots ,\text{ } \right[{{d}_{n}},\text{ }{{d}_{max}}]$
Secondly, based on the principle of piecewise linear approximation method, tolls on any path can be uniquely determined. It is noted that if the interval is set to be n, then there are n+1 vertex values in the piecewise linear approximation function. Thus the piecewise linear approximation function is defined accordingly as follows:
$\begin{align} & {{{\bar{\varphi }}}_{n}}\left( d,\text{ }y \right)={{y}_{i}}+\frac{{{y}_{i+1}}-{{y}_{i}}}{{{d}_{i+1}}-{{d}_{i}}}(d-{{d}_{i}}),{{d}_{i}}\le d ＜{{d}_{i+1}} \\ & i=1,\text{ }2,\text{ }\ldots ,\text{ }n \\ \end{align}$ (2)
where d1=dmin and dn+1=dmax. The column vector of vertex values y is defined as y=(y1, y2, …, yn+1)T. Therefore, tolls on any paths k∈Rw can be calculated using Eq.(2) , as an approximation of Eq.(1) .
2.2 User Equilibrium Traffic Assignment with Distance TollsBefore introducing the UE traffic assignment model with distance tolls, we define the generalized travel time and the corresponding user equilibrium condition after imposing the distance tolls. For any given toll charge function, the overall travel impedance on each path k∈Rw consists of the path travel time cwk(v) and the distance tolls τwk(φ). Thus the generalized travel time along the path k∈Rw between OD pair w∈W is defined as:
${{C}_{wk}}(v,\text{ }{{\tau }_{wk}}\left( \varphi \right))={{c}_{wk}}\left( v \right)+{{\tau }_{wk}}\left( \varphi \right)/\alpha $ (3)
where α is the drivers’ value of time, used to convert the toll charge into time-units. The principle of assigning the link flow to the network follows the user equilibrium, which has been explained in Sheffi[13].
Let the number of users traveling between each OD pair or the demand function be qw=Dw(uw). This demand function is assumed to be a strictly decreasing function of the minimum generalized OD travel time uw and nonnegative for all OD pairs. The travel time on link a∈A is defined as ta(va). va denotes the flow on link a and fww denotes the flow on path k between OD pair w∈W. The following conditions should be satisfied by the equilibrium flows:
$\left\{ \begin{align} & {{c}_{wk}}\left( v \right)+{{\tau }_{wk}}\left( \varphi \right)/\alpha ={{u}_{w}},~if~{{f}_{w}}^{w}>0,\text{ }\forall k\in {{R}_{w}},\text{ }w\in W \\ & {{c}_{wk}}\left( v \right)+{{\tau }_{wk}}\left( \varphi \right)/\alpha \ge {{u}_{w}},~if~{{f}_{w}}^{w}=0,\text{ }\forall k\in {{R}_{w}},\text{ }w\in W \\ & {{u}_{w}}={{D}_{1}}^{-1}\left( {{q}_{w}} \right),~if~{{q}_{w}}>0,\text{ }\forall k\in {{R}_{w}},\text{ }w\in W \\ & {{u}_{w}}\ge {{D}_{1}}^{-1}\left( {{q}_{w}} \right),~if~{{q}_{w}}=0,\text{ }\forall k\in {{R}_{w}},\text{ }w\in W \\ \end{align} \right.$ (4)
We propose an optimization model for the toll user equilibrium (TUE) problem with elastic demand, based on a given toll charge τwk, r∈Rw, w∈W, which is formulated as follows:
TUE:
$\begin{align} & \text{min }\!\!~\!\!\text{ }Z=\sum\limits_{a\in A}^{{}}{\int_{0}^{{{v}_{a}}}{{{t}_{a}}}}\left( v \right)dv+\sum\limits_{w\in W}{\sum\limits_{k\in {{R}_{w}}}{{{\tau }_{wk}}{{f}_{k}}^{w}}}- \\ & \sum\limits_{w\in W}{\int_{0}^{{{q}_{w}}}{{{D}_{w}}^{-1}\left( x \right)dx}} \\ \end{align}$ (5)
s.t.
$\sum\limits_{k\in {{R}_{w}}}{{{f}_{k}}^{w}}={{q}_{w}},\text{ }\forall w\in W$ (6)
${{v}_{a}}=\sum\limits_{w\in W}{\sum\limits_{k\in {{R}_{w}}}{{}}}{{f}_{k}}^{w}{{\delta }_{ak}}^{w},\text{ }\forall a\in A$ (7)
${{f}_{k}}^{w}\ge 0,\text{ }\forall k\in {{R}_{w}},\text{ }w\in W$ (8)
${{q}_{w}}\le {{{\bar{q}}}_{w}}$ (9)
where qw represents the upper bound of demand. Eq.(6) represents the set flow conservation constraints, which state that the flow on all paths connecting each O-D pair has to equal the O-D trip rate. Eq.(7) indicates that the flow on each link is the sum of the flows on all paths going through that link, known as the path-link incidence relationships, which can convert path flows into aggregate link flows. The nonnegative condition in Eq.(8) is required to ensure that the solution of the program will be physically meaningful.
This optimization model is an extension of model used by Sheffi[13] for un-tolled UE with elastic demand. This model is evidently convex in terms of the link flows and OD demands. Its KKT (Karush-Kuhn-Tucker) conditions show that the optimal solution can fulfill the equilibrium conditions in Eq.(4) . Thus, solving this model gives the equilibrium flows associated with any given toll charge function φ(d), and these equilibrium flows are used to assess the impacts of φ(d) on the network flows and its equity level.
3 Equity Impact Evaluation3.1 Specification of Equity ConstraintYang and Zhang[14] used an example to explain the inequity problems with a simple network. This shows the travel costs for several OD pairs increasing and their percentage increase are different. In order to ensure the relative equity of all network users, a simple practicable method is used to prevent the percentage increase of travel cost of critical network users from exceeding a pre-specified threshold in determining the distance tolls. As a consequence of the complexity of the problem, it is not possible to design a completely equitable toll charge scheme, but the inequity impacts from the toll charge scheme can be limited to a certain level set by the authority or government. Therefore, these kinds of equity issues considering changes in the OD travel costs can be incorporated into the upper level as a constraint. The change of the generalized OD travel time is termed as the OD travel cost ratio and is defined as:
${{r}_{w}}\left( s \right)=\frac{{{\mu }_{w}}\left( s \right)}{{{{\tilde{\mu }}}_{w}}},\text{ }w\in W$
where rw(s) represents the OD travel cost ratio under a toll charge scheme s; μw(s), w∈W is the equilibrium generalized OD travel time for given scenario s and correspondingly,
In order to find the critical network users who suffer the most additional costs, the critical OD travel cost ratio is defined as the maximum among all OD pairs:
$r\left( s \right)=\underset{w\in W}{\mathop{\text{max}}}\,\left\{ {{r}_{w}}\left( s \right) \right\}$
where r(s) is the critical ratio of OD travel cost.
Based on those specifications above, the equity constraint is defined as:
$r\left( s \right)\le \beta $
where β is a predetermined threshold. When β is set as β＜1.0, then each road user will have access to the benefits from the toll charging scheme; however, if β is set to be β>1.0, it means that users from some OD pairs may incur the increased travel costs induced by the toll charging scheme.
3.2 Lorenz Curve and Gini CoefficientAlthough there are some literatures using different equity indicator to study the equity issue[15-18], these methods cannot capture the loss in consumer surplus from the depressed demand and do not provide a measurable index for estimating the network level of the equity impacts. Hence, Lorenz curve and the Gini coefficient are adopted to evaluate the spatial equity at a network level[19-22]. Firstly, a Lorenz curve is developed to represent the cumulative distribution function of wealth across a population as shown in Fig. 2. The area between the straight line and curve represents the skew of the actual income distribution from the ideal equitable distribution. The Gini coefficient (G) is defined as the ratio of this area between the curves divided by the total area under the line of equality to measure the degree of equity. In this way, the distribution of two different curves can be mathematically compared and thus the Gini function is formulated as[23]:
$G=\frac{\sum\limits_{i}{\sum\limits_{j}{\left| {{x}_{i}}-{{x}_{j}} \right|}}}{2{{n}^{2}}\mu }$ (10)
where xi and xj are the income level of individual i and j, respectively; n is the total number of individuals in the population and μ is the mean of the income in the population.
In order to estimate the Gini coefficient to be used in the distance-based toll design model, the variable of interest regarding equity, namely xi, needs to be defined. The aggregate total user benefit for each OD pair w∈W can be defined as:
$U{{B}_{w}}=\int_{0}^{{{q}_{w}}}{{{D}_{w}}^{-1}}\left( x \right)dx-\sum\limits_{k}{{{C}_{wk}}{{f}_{k}}^{w}}$
where Cwk is the generalized travel cost for path k shown by Eq.(3) (consisting of travel time and toll fare). Then, the income level of individual in the original Gini coefficient xi, can be replaced by the disaggregate average user benefit for each traveler belonging to the OD pair w∈W as follows:
$u{{b}_{w}}=\frac{1}{{{q}_{w}}}\int_{0}^{{{q}_{w}}}{{}}{{D}_{w}}^{-1}\left( x \right)dx-\sum\limits_{k}{{{C}_{wk}}{{f}_{k}}^{w}}$ (11)
Finally, based on Eqs.(10) and (11) , the modified Gini coefficient for the distribution of user benefits can be expressed as:
$G=\frac{\sum\limits_{w}{\sum\limits_{{{w}^{\prime }}}{{{q}_{w}}{{q}_{{{w}^{\prime }}}}\left| u{{b}_{w}}-u{{b}_{{{w}^{\prime }}}} \right|}}}{2{{(\sum\limits_{w}{{{q}_{w}}})}^{2}}\overline{ub}}$
Figure 2
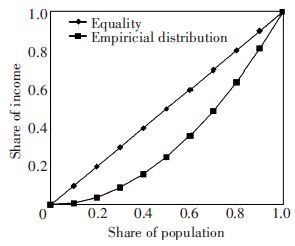Figure 2 Lorenz curve 4 Bi-level Programming for the Optimal Distance-Based Toll DesignFor the optimal toll charge design, we want to obtain the optimal distance-based toll charging scheme with the best Gini coefficient at a network level and restrict the critical OD travel cost ratio to be less than a given positive value, the aim of which is to make users of most OD pairs enjoy more benefits from the optimal toll charge scheme. This kind of toll charge design can be formulated by the following bi-level programming model:
Upper level
$\text{min}~G({{{\bar{\varphi }}}_{n}}\left( d,\text{ }y \right))=\frac{\sum\limits_{w}{\sum\limits_{w}{{{q}_{w}}{{q}_{w'}}\left| u{{b}_{w}}-u{{b}_{w'}} \right|}}}{2{{(\sum\limits_{w}{{{q}_{w}}})}^{2}}\overline{ub}}$
s.t.
$\begin{align} & r\left( s \right)\le \beta \\ & {{y}_{\text{min}}}\le {{y}_{1}} \\ & {{y}_{i-1}}\le {{y}_{i}}\le {{y}_{i+1}},\text{ }\forall i=2,\text{ }3,\text{ }\ldots ,\text{ }n-1 \\ & {{y}_{n}}\le {{y}_{\text{max}}} \\ & n\text{ }~is\text{ }a\text{ }constant \\ \end{align}$
Lower level
Equations(5)-(9)
It is noted that a toll charge scheme is regarded as optimum if it can give rise to the minimum Gini coefficient under the constraint of equity measured by the critical OD travel cost ratio.
5 Solution Method5.1 Solution Algorithm for Traffic Assignment with Distance TollsAs previously mentioned, the distance-based toll charge method is non-additive. Hence, the link-based algorithms cannot be used to solve this traffic assignment model independently. In order to use the link-based Frank-Wolfe algorithm to solve this non-additive problem, a new network transformation technique is adopted by replacing the paths in the cordon by dummy links[11, 24]. In this way, the non-additive path-based toll charges are converted into link-based ones in the transformed network. Details of the network transformation method can be found in Meng et al.[11]. The Frank-Wolfe method for solving user equilibrium problems in the transformed network is summarized as follows:
Step 1 (Initialization). Assuming that the traffic flow on the original network G=(N, A) is zero. Based on the link travel time function ta=ta(0) , the free flow travel time can be obtained. Then the travel time on the dummy link is sum of the travel time on the corresponding links. Thus the generalized travel time on the dummy link is defined as the sum of the travel time on the dummy link and toll. Based on that, to perform the all-or-nothing loading and obtain the link flows on the composite network {x′a1}.
Step 2 (Link flow conversion). To assign the link flows on the composite network to the corresponding links on the original network and obtain the link flows on the original network {xa1}. Set counter n=1.
Step 3 (Updating). According to the link flow on the original network as shown by Step 2, update the link travel time based on the tan=ta(van). Then the travel time on the dummy link is sum of the travel time on the corresponding links. Thus the generalized travel time on the dummy link is defined as the sum of the travel time on the dummy link and toll.
Step 4 (Direction finding). On the composite network G′=(N′, A′), to conduct an all-or-nothing loading and obtain the auxiliary traffic flow on each link {y′an}. After that, to perform Step 2 again to obtain the auxiliary link flows on the original network {yan}.
Step 5 (Line search). To find αn that solves
$\begin{align} & \underset{0\le \alpha \le 1}{\mathop{\text{min}}}\,\sum\limits_{a\in A}{{{\int }_{0}}^{{{x}^{n}}+\alpha ({{y}_{a}}^{n}-{{x}_{a}}^{n})}}{{t}_{a}}\left( w \right)dw+\sum\limits_{w\in W}{\sum\limits_{k\in {{R}_{w}}}{{{\tau }_{wk}}}} \\ & [x{{\prime }_{a}}^{n}+\alpha \left( y{{\prime }_{a}}^{n}-x{{\prime }_{a}}^{n} \right)] \\ \end{align}$
Step 6 (Move). Set
$\left\{ \begin{array}{*{35}{l}} {{x}_{a}}^{n+1}={{x}_{a}}^{n}+{{\alpha }_{n}}\left( {{y}_{a}}^{n}-{{x}_{a}}^{n} \right)\text{ }\forall a\in A \\ x{{\prime }_{a}}^{n+1}=x{{\prime }_{a}}^{n}+{{\alpha }_{n}}\left( y{{\prime }_{a}}^{n}-x{{\prime }_{a}}^{n} \right)\forall a\in A \\\end{array} \right.$
Step 7 (Convergence test). If a criterion that is based on the change in flows is met, stop; otherwise, go to the Step 3.
$\frac{\sum\limits_{a}{{{x}_{a}}^{n}}{{({{x}_{1}}^{n+1}-{{x}_{a}}^{n})}^{2}}}{\sum\limits_{a}{{{x}_{a}}^{n}}}\le \varepsilon $
where ε is the predetermined precision parameter.
5.2 Solution Algorithm for the Bi-level ModelDue to the complexity of the proposed bi-level model, it is difficult to adopt any gradient-based algorithm[25]. Thus a heuristic Genetic Algorithm (GA) is used as solution method for this model.
The chromosome for the GA is developed as follows. Firstly, each feasible chromosome represents the piecewise-linear toll charge function φn(d, y). A feasible chromosome is given as (y1, y2, …, yi, yi+1, …, yn+1), where yi represents the boundary value in the piecewise-linear toll charge function and is defined as a gene of one chromosome.
For each chromosome, tolls on the different paths inside the pricing cordon can be obtained and thus lead to different values of the critical OD travel cost ratio r(s) and the Gini coefficient. If the value of the critical OD travel cost ratio, as the constraint of the Gini coefficient, exceeds the predetermined value β, the corresponding value of the Gini coefficient and the chromosome will be deleted (the Gini coefficient can be set to 1 in the coding if the constraint r(s)≤β, is not satisfied). Calculation of the Gini coefficient is a TUE problem, which can be solved by the network transformation and Frank-Wolfe method outlined in Section 5.1.
6 Numerical Example6.1 Data DescriptionTo numerically validate the proposed methodology, one example network (as shown in Fig. 3) from Yang et al.[24] and Meng et al.[11] is adopted. The travel demand function between each OD pair w∈W and link travel time function on link a∈A are identical to those in Yang et al.[24] The length of each link in the pricing cordon is shown in Table 1 that can be used to measure the drivers’ total travel distance in the pricing cordon. It is noted that the minimum and maximum of path lengths are 480 and 2 563, respectively. The lower and upper bound value of toll charges are set to be ymin=1 and ymax=20. The number of intervals is set to be n=8. The parameters used in the GA for the numerical test are shown in Table 2.
Figure 3
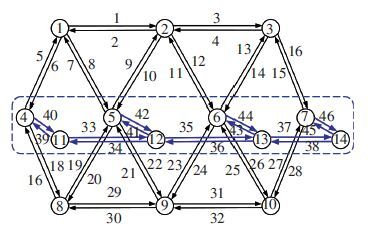Figure 3 Structure of the example network 表 1
Table 1 Length of links in the pricing cordon Link No.Length (m)33930
341 050
35320
36510
37640
38892
3985
4038
4135
4278
4382
4450
4585
4626
Table 1 Length of links in the pricing cordon
表 2
Table 2 Set of the GA parameters used in the tests ParametersGenerationnumberPopulationnumberProb. ofcrossoverProb. of mutationValue used501000.80.15
Table 2 Set of the GA parameters used in the tests
In order to test and validate the proposed model and algorithm, the experiment was run on the Intel Core i7-3770/3.4 GHz, 8 GB Ram the computer, using C programming language in Visual Studio 2012.
6.2 Result AnalysisAccording to the different value of β, the corresponding value of minimum Gini coefficient and toll charge function can be obtained, as shown in Table 3.
表 3
Table 3 Computational results for different value β βGNon-tollImprovement(%)Toll charge functiony1y2y3y4y5y6y7y8y9
1.010.322 70.338 74.722.885.948.169.1411.7613.4015.1416.7618.05
1.020.318 60.338 75.932.944.586.829.1011.2112.6714.3016.4117.75
1.030.319 40.338 75.702.354.045.998.299.6011.8413.5816.1617.20
1.040.320 50.338 75.372.395.516.008.079.6813.2714.0015.9817.66
1.050.318 40.338 75.994.545.627.6710.0611.5112.5814.1116.8718.36
1.100.318 90.338 75.854.145.937.2510.3613.0214.0215.6217.7619.20
1.150.320 70.338 75.312.313.605.077.4210.5012.0913.9916.0118.47
1.200.320 50.338 75.373.554.607.0810.3011.5913.0214.8816.0717.65
1.250.320 50.338 75.372.615.147.689.8912.1813.0514.4916.4718.21
1.300.320 50.338 75.372.615.147.689.8912.1813.0514.4916.4718.21
Table 3 Computational results for different value β
The Gini coefficient at the network with non-toll is calculated to be 0.338 7 in advance. It is evident based on Table 3 that when β is set to be 1.05, the minimum Gini coefficient can be reached to be 0.318 4 and the inequity level is decreased by 5.99%. Accordingly, the toll charge function is shown in Fig. 4(a). It is straightforward to see from Fig. 4(a) that the optimal distance-based toll charge function is displayed to be highly nonlinear. Compared with the optimal uniform toll function based on Maruyama and Sumalee[19-22], the improvement of equity level with nonlinear distance-based toll function is more obvious and effective. In addition, by comparing the corresponding shape of toll charge function with different Gini coefficient based on Fig. 4, it can be concluded that as Gini coefficient is increased, namely inequity level is increased, and the optimal toll charge function is approximate to linear function although it still displays nonlinear form.
Figure 4
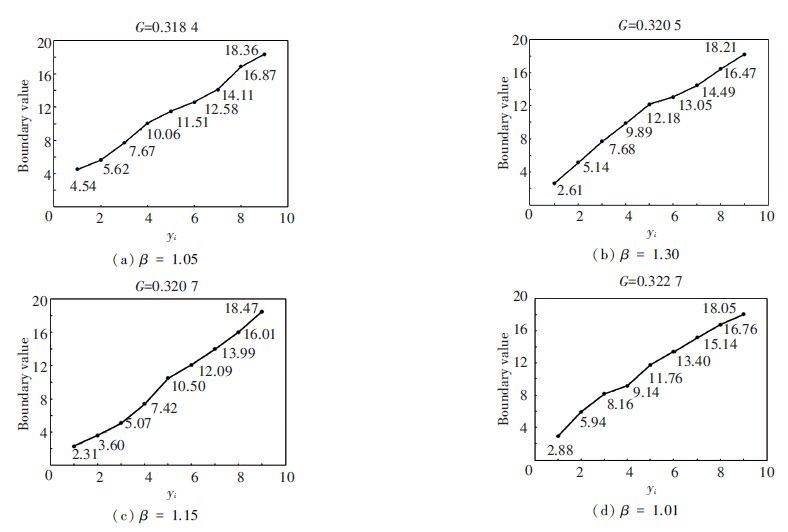Figure 4 Form of toll charge function with different Gini coefficient 7 Conclusions and Future WorkThis paper addresses how to optimize equity within the toll charge design problem for a cordon-based congestion pricing scheme with distance toll. A bi-level model is developed for solving the optimal toll charge design problem. The upper level of bi-level model is associated with equity issues, the aim of which is to obtain the optimal toll charge function with the best Gini coefficient under the constraint of the spatial equity. Previous researches investigating the impacts from congestion pricing have not fully incorporated equity impacts for travelers. This paper presents a measureable index at the network level of the equity impact and combines it with spatial equity. In the upper level, the OD travel cost ratio is used as the constraint to ensure all road users experience a travel cost reduction. Under this condition, the Gini coefficient is used to identify the optimal charging scheme.
The results show that the proposed model and algorithm can be demonstrated to be efficient by the numerical example. The optimal distance-based toll charge function is highly nonlinear when the minimum Gini coefficient is reached. By comparing the toll charge function with different Gini coefficient, it is evident that the toll charge function is approximate to linear form as the inequity level increases.
Distance-based congestion pricing has various impacts on many considerations, which is a complicated and difficult problem. This paper, just only from theoretical perspective, presents some initial steps towards incorporating equity issues in determining nonlinear distance tolls. Further work is required to further extend these models to consider more practical issues such as multi-objective problem, dynamic traffic networks, heterogeneous or continuous values-of-time and multi-vehicle types. In addition, regarding the final solution in the conclusion part, we present the optimal distance-based congestion pricing scheme only considering the equity issues. Although this final result cannot be applied in the real world immediately, it indeed provides a method, idea and direction for further research in the future.
References
[1]Liu Z, Meng Q, Wang S. Speed-based toll design for cordon-based congestion pricing scheme.Transportation Research Part C: Emerging Technologies, 2013, 31(2): 83-98.(
0)[2]Liu Z, Wang S, Meng Q. Toll pricing framework under logit-based stochastic user equilibrium constraints.Journal of Advanced Transportation, 2014, 48(8): 1121-1137.DOI:10.1002/atr.v48.8(
0)[3]Liu Z, Wang S, Meng Q. Optimal joint distance and time toll for cordon-based congestion pricing.Transportation Research Part B: Methodological, 2014, 69: 81-97.DOI:10.1016/j.trb.2014.08.005(
0)[4]Li Z C. Design of sustainable cordon toll pricing schemes in a monocentric city.Networks and Spatial Economics, 2014, 14(2): 133-158.DOI:10.1007/s11067-013-9209-3(
0)[5]Xiao F, Zhang H. Pareto-improving toll and subsidy scheme on transportation networks.EJTIR, 2014, 14(1): 46-65.(
0)[6]Metz D. Demographic determinants of daily travel demand.Transport Policy, 2012, 21: 20-25.DOI:10.1016/j.tranpol.2012.01.007(
0)[7]May A D, Milne D S. Effects of alternative road pricing systems on network.Transportation Research Part A Policy & Practice, 2000, 34(6): 407-436.(
0)[8]Taylor B, Kalauskas R. Addressing equity in political debates over road pricing: Lessons from recent projects.Transportation Research Record: Journal of the Transportation Research Board, 2010(2187): 44-52.(
0)[9]May A D. The impact of cordon design on the performance of road pricing schemes.Transport Policy, 2002, 9(3): 209-220.DOI:10.1016/S0967-070X(02)00031-8(
0)[10]Ho H. Cordon-based congestion pricing in a continuum traffic equilibrium system.Transportation Research Part A: Policy and Practice, 2005, 39(7): 813-834.(
0)[11]Meng Q, Liu Z, Wang S. Optimal distance tolls under congestion pricing and continuously distributed value of time.Transportation Research Part E: Logistics and Transportation Review, 2012, 48(5): 937-957.DOI:10.1016/j.tre.2012.04.004(
0)[12]Lawphongpanich S, Yin Y. Nonlinear pricing on transportation networks.Transportation Research Part C: Emerging Technologies, 2012, 20(1): 218-235.DOI:10.1016/j.trc.2011.05.010(
0)[13]Sheffi Y. Urban Transportation Networks.Englewood Cliffs: Prentice-Hall, 1985.(
0)[14]Yang H, Zhang X. Multiclass network toll design problem with social and spatial equity constraints.Journal of Transportation Engineering, 2002, 128(5): 420-428.DOI:10.1061/(ASCE)0733-947X(2002)128:5(420)(
0)[15]Altshuler A. Equity, pricing, and surface transportation politics.Urban Affairs Review, 2010.(
0)[16]Cools M. The socio-cognitive links between road pricing acceptability and changes in travel-behavior.Transportation Research Part A: Policy and Practice, 2011, 45(8): 779-788.DOI:10.1016/j.tra.2011.06.006(
0)[17]Bills T, Sall E, Walker J. Activity-based travel models and transportation equity analysis: Research directions and exploration of model performance.Transportation Research Record: Journal of the Transportation Research Board, 2012(2320): 18-27.(
0)[18]Wang S. Efficiency and equity of speed limits in transportation networks.Transportation Research Part C: Emerging Technologies, 2013, 32: 61-75.DOI:10.1016/j.trc.2013.04.003(
0)[19]Sumalee A. Optimal toll ring design with spatial equity impact constraint: An evolutionary approach.Journal of Eastern Asia Society for Transportation Studies, 2003, 5: 1813-1828.(
0)[20]Vold A. Optimal land use and transport planning for the Greater Oslo area.Transportation Research Part A: Policy and Practice, 2005, 39(6): 548-565.DOI:10.1016/j.tra.2005.02.007(
0)[21]Maruyama T, Sumalee A. Efficiency and equity comparison of cordon- and area-based road pricing schemes using a trip-chain equilibrium model.Transportation Research Part A: Policy and Practice, 2007, 41(7): 655-671.DOI:10.1016/j.tra.2006.06.002(
0)[22]Delbosc A, Currie G. Using Lorenz curves to assess public transport equity.Journal of Transport Geography, 2011, 19(6): 1252-1259.DOI:10.1016/j.jtrangeo.2011.02.008(
0)[23]Gini C. Variability and mutability, contribution to the study of statistical distribution and relaitons.Studi Economico-Giuricici della R, 1912.(
0)[24]Yang H, Zhang X, Meng Q. Modeling private highways in networks with entry-exit based toll charges.Transportation Research Part B: Methodological, 2004, 38(3): 191-213.DOI:10.1016/S0191-2615(03)00050-X(
0)[25]Wang S, Meng Q, Yang H. Global optimization methods for the discrete network design problem.Transportation Research Part B: Methodological, 2013, 50: 42-60.DOI:10.1016/j.trb.2013.01.006(
0)