 , 靳全锋1,2
, 靳全锋1,2
 , 柴红玲1, 郭福涛2
, 柴红玲1, 郭福涛21. 丽水职业技术学院, 丽水 323000;
2. 福建农林大学林学院, 福州 350002
收稿日期: 2020-04-29; 修回日期: 2020-07-28; 录用日期: 2020-07-28
基金项目: 国家自然科学基金(No.31770697);2017年浙江省访问工程师项目(No.FG2017240);浙江省教育厅一般项目(No.Y201840513)
作者简介: 陈兵红(1974-), 男, E-mail: 443684825@qq.com
通讯作者(责任作者): 靳全锋, E-mail: jinquanfeng2006@126.com
摘要:该研究以浙江省2014-2019年PM2.5浓度数据为研究对象,应用多元线性回归和随机森林方法结合气象、植被、地形、经济、人口和基础设施等因子进行分析.研究结果表明PM2.5浓度时空分布不均匀,时间上季节变化差异显著,总体呈冬季>春季>秋季>夏季分布规律,每年呈下降趋势;空间上呈西北多东南少的分布特征.多元线性回归和随机森林模型显示日最低地表气温(MI-GST)、日最低气压(MI-PRS)、日蒸发量(EVP)、日最小相对湿度(MI-RHU)、月植被覆盖度(FVC)、日降水量(PRE)、日极大风速(MM-WIN)、日平均相对湿度(AV-RHU)、铁路密度(Railway)、日最大风速(MA-WIN)、日照时长(SSD)、海拔(DEM)、日平均风速(AV-WIN)和河流密度(River)等15个因子对PM2.5浓度影响显著;随机森林模型均方根误差(RMSE)、均方绝对百分比误差(MAPE)和变异解释量(R2)分别为0.133、17.83%和0.834,明显优于多元线性回归(0.278、40.48%和0.575),表明随机森林更适合浙江省PM2.5浓度估测,该研究揭示PM2.5时空分布及相关因子分析,为限制空气污染提供有效策略.
关键词:浙江省PM2.5时空分布相关因子随机森林模型多元线性回归
Spatiotemporal distribution and correlation factors of PM2.5 concentrations in Zhejiang Province
CHEN Binghong1
 , JIN Quanfeng1,2
, JIN Quanfeng1,2
 , CHAI Hongling1, GUO Futao2
, CHAI Hongling1, GUO Futao21. Lishui Vocational and Technical College, Lishui 323000;
2. Forestry College, Fujian Agriculture and Forestry University, Fuzhou 350002
Received 29 April 2020; received in revised from 28 July 2020; accepted 28 July 2020
Abstract: The multiple linear regression and random forest methods,which combine factors including meteorology,vegetation,terrain,economy,population and infrastructure,were applied to analyze the data of PM2.5 concentrations in the Zhejiang region from 2014 to 2019. Results show that the spatial and temporal distribution of PM2.5 concentrations varied,with a significant seasonal order of winter > spring > autumn > summer,and the trend of annual PM2.5 concentrations gradually decreased over the study period. The spatial concentration distribution of PM2.5 in northwest part of the province is much higher in the northeast part of the province. Results of the multiple linear regression and random forest models show that PM2.5 concentrations were significantly impacted by a variety of 15 factors,such as the daily minimum surface temperature (MI-GST),daily minimum pressure (MI-PRS),daily evaporation (EVP),daily minimum relative humidity (MI-RHU),monthly vegetation coverage (FVC),daily precipitation (PRE),daily maximum wind speed (MM-WIN),daily average relative humidity (AV-RHU),railway density (Railway),daily maximum wind speed (MA-WIN),sunshine duration (SSD),digital elevation model (DEM),wind speed (AV-WIN) and river density (River). The root mean square error (RMSE),absolute mean square error (MAPE) and variance interpretation (R2) of the random forest model were 0.133,17.83% and 0.834,respectively,which were substantially better than the multiple linear regression analysis of 0.278,40.48% and 0.575. This indicates that the random forest model is better for the estimation of Zhejiang data of PM2.5 concentrations. Overall this study characterized the spatiotemporal distribution and correlation factors for PM2.5 concentrations,which can provide important information on which to base an effective strategy for controlling air pollution.
Keywords: Zhejiang ProvincePM2.5spatiotemporal distributioncorrelation factorsrandom forest modelmultiple linear regression
1 引言(Introduction)空气细小颗粒物(PM2.5)污染是政府和科学界一直关注的科学问题(Wang et al., 2018;Zhan et al., 2018), 随着经济增长、城市化进程加快、工业、交通运输和能源发电等领域不断扩大, 排放大量细小颗粒物(Huang et al., 2014;Xu et al., 2019), 其污染面积占地球面积的0.5%(United Nations, 2014), 对大气环境、人类健康和生态系统健康威胁日益加剧(Guerreiro et al., 2016;Popek et al., 2018;Yuan et al., 2018;Jin et al., 2018). 研究显示PM2.5大量排放可以影响地球太阳辐射, 促进光化学反应和阴霾形成, 降低大气能见度(Schiferl et al., 2018), 改变土壤pH, 直接或间接影响全球气候变化(Kok et al., 2018;靳全锋等, 2019);研究显示PM2.5与人类健康之间存在相关关系(Lelieveld et al., 2015;Liu et al., 2016), 细小颗粒物可以直接进入人类呼吸系统, 导致支气管炎、心血管疾病、哮喘和其他疾病(Chen et al., 2013;Hofman et al., 2013, 靳全锋等, 2017), 显著增加妊娠期孕妇产后狂躁和抑郁风险几率(Qiu et al., 2018;Zeng et al., 2019;Niedzwiecki et al., 2020), 大量文献研究显示长期暴露于PM2.5环境下, PM2.5与非偶然性和特定病引起死亡率增加相关(Brook et al., 2010;Pope et al., 2011;Burnett et al., 2014), 卫生计量评估研究所(IHME)全球疾病负担项目研究显示2016年PM2.5导致全球410万人过早死亡(Cohen et al., 2017), 2013年中国因PM2.5过早死亡达763595人(Song et al., 2016), 其中北京每年约9000人过早死亡(Liu et al., 2016), 因此, 解决PM2.5问题对大气环境、生态系统、人类健康和社会共同利益至关重要.
中国正处于经济和城市化大发展时期, 长三角为密集型工业排放区, 大量PM2.5排放到大气中, 加剧了空气质量恶化(Li et al., 2019). 浙江省位于长三角经济核心位置, 因此探索浙江省PM2.5时空分布及相关因子对于中国东部环境问题至关重要. 目前国内已开展PM2.5浓度研究, 并取得一定进展(Jiang et al., 2018;Du et al., 2018;Gui et al., 2019), 以往以研究PM2.5时空格局(Fan et al., 2020;Li et al., 2020)和影响因素(Yang et al., 2018;Chen et al., 2018)为主, 目前尚未有效降低PM2.5浓度和危害的方法(Liacos et al., 2012;Solazzo et al., 2012).
目前国内关于大气污染物影响因素的研究主要采用源解析方法(Cai et al., 2019), 利用地面数据与遥感影像结合探索城市空气质量(Zhang et al., 2019), 利用气溶胶(AOD)反演PM2.5时空格局(Ma et al., 2016)等方法探索空气污染物时空变化及影响因素, 发现这些方法仅能解释变量53%~75%(Li et al., 2019), 无法准确探索影响因素, 因此, 本研究基于前人研究基础运用多元线性回归和随机森林方法来解决环境问题, 多元线性回归方法是普遍适用的方法. 随机森林(Random Forest)是一种非参数模型(Breiman, 2001), 可以用来解决分类和回归问题. 随机森林算法不需要考虑变量之间相互关系且不受线性回归模型的假设条件限制, 具有预测精度高及不易过渡拟合等优点(Svetnik et al., 2003). 近年来, 随机森林方法在生物学、地理学、生态学和环境污染等领域得到广泛应用.鉴于此, 本研究以浙江省2014—2019年PM2.5浓度数据为研究对象, 应用多元线性回归和随机森林方法结合气象、植被、地形、经济、人口和基础设施等因子探索PM2.5时空分布及相关因子以及为相关模型研究和政府大气环境污染防控提供科学依据.
2 资料来源与方法(Data and methods)本研究以浙江省2014—2019年PM2.5数据为研究对象, 应用多元线性回归和随机森林方法结合气象、植被、地形、经济、人口和基础设施等因子探索PM2.5时空分布及相关因子.
2.1 研究区概况浙江省位于中国东部, 区域范围是北纬27°06′~31°11′, 东经118°01′~123°10′, 面积为1.02×105 km2(图 1). 全省地貌类型复杂多样, 总体呈西南向东北倾斜趋势, 南部多丘陵地带;该区域地处亚热带季风气候区, 夏季雨热同期、冬季寒冷干燥, 年平均气温为15~18 ℃, 年平均雨量为980~2000 mm, 年均日照时长为1710~2100 h, 人口约为5737万人, 地区生产总值(GDP)为56197亿元人民币, 其中工业产值超过总产值41%(靳全锋等, 2019).
图 1(Fig. 1)
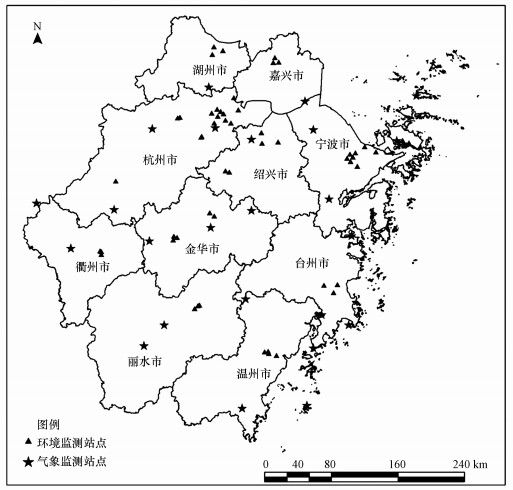 |
| 图 1 浙江省分布 Fig. 1The spatial distribution of area in Zhejiang |
2.2 数据来源与处理本研究数据由环境监测、地形、气象、植被和人类活动数据等5部分组成.
2.2.1 环境监测数据2014—2019年PM2.5实时监测站数据来源于中国环境监测总站(http://www.cnemc.cn/). 对位于浙江省城市及周边56个国控监测站点进行PM2.5监测, 并每小时进行一次采样. 计算每天、每月和每年各污染物平均值. 然后与地形、气象、植被和人类活动数据等数据进行叠加分析.
2.2.2 地形数据地形数据包括高程、坡向、坡度. 其中DEM数据来源于地理空间数据云(http://www.gsclo-ud.cn/sources/?cdataid=265&pdataid=10), 运用ArcGIS对DEM数据进行3D分析获得坡向和坡度等数据, 坡向指数是目前地形研究的主要数据(Zhang et al., 2014), 该研究基于坡向计算坡向指数为:
 | (1) |
2.2.3 气象数据气象数据来源于中国气象数据共享网络(http://cdc.cma.gov.cn/), 浙江省及周边42个国家级气象站每日气象数据. 每日气象数据共包含蒸发、降水、湿度、温度、风速、光照和地表温度等22个气象因子, 本研究对气象数据进行预处理, 去除由于仪器设备损坏缺失的数据, 剩余气象因子包括蒸发量(mm)、日平均地表气温(℃)、日最高地表气温(℃)、日最低地表气温(℃)、日平均风速(m·s-1)、日最大风速(m·s-1)、日最大风速的风向(°)、日极大风速(m·s-1)、日极大风速的风向(°)、日降水量(mm)、日平均气压(hPa)、日最高气压(hPa)、日最低气压(hPa)、日照时数(h)、日平均气温(℃)、日最高气温(℃)、日最低气温(℃)、日平均相对湿度和日最小相对湿度共19个气象因子.
2.2.4 植被数据植被覆盖数据根据地理空间数据云(http://www.gscloud.cn)Landsat影像经过拼接、校正、投影等变换合成归一化植被指数(NDVI), 根据前人研究成果, 以NDVI为基础采用像元二分模型求取植被覆盖(Zhang et al., 2013), 计算方法见式(2).
 | (2) |
2.2.5 人类活动数据人类活动数据主要由基础设施(铁路密度、道路密度和河网密度)、经济数据和人口数据组成. 基础设施数据来源于国家地球系统科学数据共享平台(http://www.geodata.cn/Portal/index.jsp), 分辨率为1 km×1 km的栅格数据. 经济和人口数据来源于浙江省统计局(http://tjj.zj.gov.cn/col/col1525563/index.html).
2.3 数据处理2.3.1 多重共线性诊断多重共线性是自变量间相关关系的重要表现, 如果模型存在较高共线性, 会导致显著性检验失去意义及模型的预测功能失效. 因此, 在模型建模前应对自变量进行多重共线性诊断, 剔除有显著共线性的自变量. 本研究运用方差膨胀因子(VIF)对因子进行多重共线性检验, 以VIF=10为标准, 当VIF>10表明自变量间存在多重共线性, 将其剔除并以逐步回归法得到最优结果;当VIF < 10表明自变量间不存在多重共线性.
2.3.2 多元线性回归模型多元线性回归模型是用多个自变量解释因变量的变化的一种常用统计模型, 其公式见式(3).
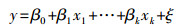 | (3) |
2.3.3 随机森林模型随机森林是一种非参数算法可用于回归和分类(Breiman, 2001), 在数据集上表现良好, 对数据具有极强的适应和抗噪能力, 对于大样本运算速度较快, 实现比较简单. 本研究运用回归的方法研究PM2.5浓度影响变量, 利用bootstrap抽样思想, 有放回的抽取a个自助样本并构建a棵回归树, 从全部属性中等概率随机抽取一个最优属性, 然后对a棵回归树的节点分裂, 一般每个节点分裂mtry次, 并通过a个袋外误差(out-of-bag error, OOBE)来估测森林的强度. 其中袋外误差的个数a与节点分裂的次数mtry (mtry<m)是重要的自定义参数. 李欣海的研究表明, 随机森林用于回归模型中每个节点分裂的次数mtry最适取值为m/3, 研究表明在随机森林回归过程中参数a的值应尽量大, 保证袋外误差的稳定性, 本研究中自变量的个数m等于28, 取mtry的值为9, 参数a的取值为10000.
2.3.4 模型变量的选择及运算本研究根据前人研究成果, 将总样本数据随机分成60%的训练样本和40%测试样本(Rodrigues et al., 2014), 有放回随机抽样, 重复5次, 分别得到5组样本, 对5组样本进行多元线性回归和随机森林运算, 建立5个中间模型. 以得到各自的显著变量大于3次为基准, 确定最终变量, 从而进行最终样本的运算. 研究通过对观测值和预测值进行相关系数的计算来分析其是否有显著相关性, 验证中间模型得出模型的预测能力. 在选择好变量后, 应用完整的数据集构建最终模型并进行分析. 应用计算包Relaimpo R软件(Gromping, 2006)来计算每个变量的贡献度, 用“lmg”指标测定评估每个变量的相对重要性(Lindeman et al., 1980).
2.4 浙江省PM2.5浓度精度评价本研究在浙江省PM2.5浓度精度验证过程中分别对PM2.5浓度实测数据与多元线性回归和随机森林模型预测值进比较分析. 精度验证通过分别计算均方根误差(RMSE)、均方绝对百分比误差(MAPE)以及变异解释量(R2)来评估PM2.5浓度精度. RMSE、MAPE和R2计算公式见式(4)~(7).
 | (4) |
 | (5) |
 | (6) |
 | (7) |
3 结果与分析(Results and analysis)3.1 浙江省PM2.5浓度时空分布图 2a显示浙江省平均PM2.5浓度月变化存在差异, 总体呈“V”分布, 其中极大值多集中在1—2月, 最低值多集中在7—8月, 1—12月PM2.5平均浓度分别为64.36、49.01、45.15、40.85、37.90、30.57、24.58、25.44、29.43、35.45、42.39和55.82 μg·m-3. PM2.5浓度具有明显季节性差异, PM2.5平均浓度高低顺序为冬季>春季>秋季>夏季, 春、夏、秋和冬季PM2.5平均浓度分别为41.30、26.82、35.75和56.14 μg·m-3. 研究显示夏季空气质量最优, 冬季最差, 一方面夏季植被生长旺盛、降水充沛有利于降低空气PM2.5湿沉降及盛行东风和海洋清洁空气对浙江空气污染稀释作用, 从而降低空气中PM2.5浓度. 另一方面, 因为冬季PM2.5浓度偏高的主要原因一是排放较高, 二是不利的气象条件, 受干湿沉降的影响与这两个主要原因相比应该是较小.
图 2(Fig. 2)
 |
| 图 2 2014—2019年浙江省PM2.5浓度时间变化(a)及年变化(b) Fig. 2Time variation(a) and annual variation(b) of PM2.5 concentration in Zhejiang in from 2014 to 2019 |
图 2b为2014—2019年浙江省空气PM2.5平均浓度总体呈下降趋势, 2014—2019年PM2.5平均浓度分别为54.04、45.77、39.89、37.56、32.64和30.56 μg·m-3, 年平均减少11.8%. 研究显示工业排放是造成空气污染的主要原因(Krotkov et al., 2016;Zhao et al., 2019), 为了控制空气PM2.5浓度, 2013年政府出台《中国国家环境空气质量标准》;政府加大工业排放控制力度, 工业排放限值和空气质量控制措施甚至更加严格, 政府不仅相继出台了多项排放控制政策, 而且还根据近年来的实际情况来确定了减排目标(Guan et al., 2014;Silver et al., 2018). 特别是政府为减少工业和汽车尾气排放以及使用清洁能源做出了许多努力, 所有现有的燃煤电厂都达到了2014年发布的新排放标准(GB13223—2011)要求(Karplus et al., 2018), 因此, PM2.5显著下降可能归因于中央和地方政府实施的有效控制措施.
3.2 浙江省PM2.5浓度空间分布根据浙江省各站点PM2.5实时监测数据, 运用ArcGIS10.4在UTM-48投影坐标系统下运用普通克里金差值方法, 绘制2014—2019年污染物时空分布图(图 3), PM2.5浓度空间上不均衡, 呈西北多东南少的分布特征. 杭州、湖州、嘉兴、金华、丽水、宁波、衢州、绍兴、台州、温州和舟山区域PM2.5年均浓度分别为47.18、46.18、44.89、45.41、34.76、38.91、41.74、48.21、36.31和38.07 μg·m-3. 浙江省北部PM2.5浓度较高, 其浓度远超过中国环境空气质量标准(GB3095—2012), 尽管区域PM2.5总体呈下降趋势, 但PM2.5浓度水平仍然高于中国环境空气质量标准确定水平. 研究表明浙江北部区域空气质量改善相对较小, 主要由于浙北地区是浙江重工业分布区, 区域城市化水平、人口密度、民用汽车拥有量及交通设施导致生产生活中颗粒物排放增加以及冬季该区域受到来自内蒙古以及山西、河北、河南、安徽和山东等省的西北污染空气团的影响, 有效促进区域空间PM2.5浓度增加(Wang et al., 2014;Sun et al., 2019).
图 3(Fig. 3)
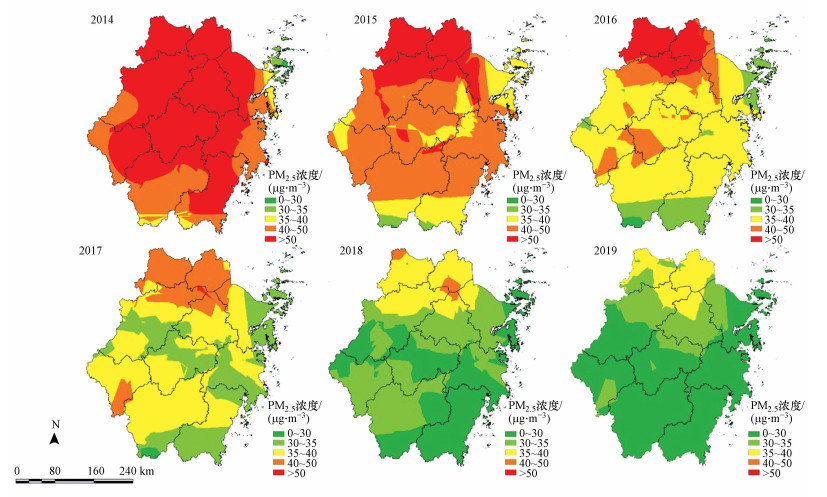 |
| 图 3 2014—2019年浙江省PM2.5浓度空间分布 Fig. 3Spatial distributions of PM2.5 concentration in Zhejiang in from 2014 to 2019 |
3.3 浙江省PM2.5浓度变化相关因子分析3.3.1 多元线性回归模型(MLR)分析结果本研究运用方差膨胀因子对模型自变量进行多重共线性诊断, 其中日平均气压(AV-PRS)、日平均气温(AV-TEM)、日最低气温(MI-TEM)、日平均地表气温(AV-GST)、日最高气压(MA-PRS)、道路密度(Road)和日最大气温(MA-TEM)等方差膨胀因子(VIF)分别为443.92、305.97、89.93、88.80、41.76、42.89和19.86, 运用逐步剔除方法, 剔除具有显著共线性7个自变量;进一步运用变量解释度剔除极大风速的风向(DMM-WIN)、日最大风速的风向(DMA-WIN)、人均国内生产总值(GDP)、坡向指数(Aspect index)和坡度(Slope)等贡献度小的因子详见表 1.
表 1(Table 1)
| 表 1 多元线性回归模型因子筛选 Table 1 Factor screening for multiple linear regression models | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 多元线性回归模型因子筛选 Table 1 Factor screening for multiple linear regression models
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
研究显示多元线性回归模型最终由16个变量构成, 变量对PM2.5浓度影响大小顺序见表 2, 其中日最低地表气温(MI-GST)、日蒸发量(EVP)、日最小相对湿度(MI-RHU)、日极大风速(MM-WIN)、日降水量(PRE)、日照时长(SSD)、海拔(DEM)、日平均风速(AV-WIN)和人口密度(POP)等8个因子与PM2.5浓度呈负相关关系, 其余10个因子对PM2.5浓度有促进作用.
表 2(Table 2)
| 表 2 最终多元线性回归模型 Table 2 The final Multiple Linear Regression model | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 最终多元线性回归模型 Table 2 The final Multiple Linear Regression model
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.3.2 随机森林模型分析结果随机森林模型的平均准确率降低度(Mean Decrease Accuracy)是衡量把一个变量的取值变为随机数, 预测准确性降低程度的一个参数, 其值越大说明变量重要性越强. 基于随机森林方法对模型变量筛选, 本文基于平均准确率降低度值50%作为阈值, 逐步剔除平均准确率降低度小于50%的变量, 其余变量进入模型进行拟合. 各变量因子对PM2.5影响程度如图 4所示, 各样本组中变量的重要性顺序基本一致, 经筛选, 确定17个变量进行构建随机森林的回归模型, 最终模型中变量重要性顺序见表 3.
图 4(Fig. 4)
 |
| 图 4 随机森林运算对PM2.5浓度影响的自变量的重要性排序 (X1为日蒸发量, X2为月植被覆盖度, X3为日照时长, X4为日降水量, X5为日极大风速, X6为日最大风速风向积, X7为日最小相对湿度, X8为日平均相对湿度, X9为日平均风速, X10为日极大风向, X11为日最大风速, X12为铁路密度, X13为日最小气压, X14为河流密度, X15为海拔, X16为道路密度, X17为日最低地表气温, X18为日最低气温, X19为日最高气温, X20为日平均气温, X21为国内生产总值, X22为坡度, X23为日平均气压, X24为日最高气压, X25为人口密度, X26为日平均地表气温, X27为日最高地表气温, X28为坡向指数) Fig. 4Random forests affecting PM2.5 concentration sort the importance of independent variables |
表 3(Table 3)
| 表 3 最终随机森林模型变量的重要性排序 Table 3 The importance of variables included in the final model using Random Forest | ||||||||||||||||||||||||||||||||||||||||||
表 3 最终随机森林模型变量的重要性排序 Table 3 The importance of variables included in the final model using Random Forest
| ||||||||||||||||||||||||||||||||||||||||||
经筛选, 确定17个变量进行构建随机森林的回归模型(表 3).在最终模型中变量重要性顺序见表 3.
3.4 模型拟合能力比较多元线性回归模型中每个训练样本的调整R2为0.32~0.33, 变量解释度为31%~34%, 观测值与预测值的相关性都在0.56~0.58(表 4), 结果表明多元线性回归模型拟合效果不佳, 但依然能解释PM2.5浓度与因子间相关关系.
表 4(Table 4)
| 表 4 多元线性回归模型中的调整R2和观测值与预测值之间的相关性值 Table 4 Adjust R2 and correlation values between observed and predicted values in the Multiple Linear Regression model | ||||||||||||||||||||||||||||||||
表 4 多元线性回归模型中的调整R2和观测值与预测值之间的相关性值 Table 4 Adjust R2 and correlation values between observed and predicted values in the Multiple Linear Regression model
| ||||||||||||||||||||||||||||||||
随机森林模型中训练样本与测试样本的解释度都在77.4%~78.8%之间, 均方残差在128.564~ 139.265之间, 且观测值与预测值的相关性在0.88之上(表 5), 其解释度和相关性分别高于多元线性回归模型40%和30%左右. 结果表明PM2.5浓度影响因子分析上, 其模型因子差异不大, 随机森林模型拟合度更高, 其模型显著优于多元线性回归模型(图 5). 此外, 随机森林模型和多元线性回归模型皆高估PM2.5浓度情况, 其中多元线性回归模型预测值高于随机森林模型结果, 随着PM2.5浓度增加多元线性回归模型预测值偏离远大于随机森林模型结果, 预测值偏差较大是由于较高PM2.5浓度数据密度不高的情况下, 训练样本没有足够信息, 容易造成高PM2.5浓度边缘错失现象, 导致PM2.5浓度被估测误差较大.
表 5(Table 5)
| 表 5 随机森林模型的结果, 包括观测值与预测值之间的相关性 Table 5 The result of Random Forest, including the correlation values between observed (obs) and predicted (pred) values | ||||||||||||||||||||||||||||||||
表 5 随机森林模型的结果, 包括观测值与预测值之间的相关性 Table 5 The result of Random Forest, including the correlation values between observed (obs) and predicted (pred) values
| ||||||||||||||||||||||||||||||||
图 5(Fig. 5)
 |
| 图 5 多元线性回归(MLR)与随机森林(RF)模型观测值和预测值线性拟合图 Fig. 5Plots of the observed and the predicted values calculated by MLR and RF model for the final model |
3.5 拟合精度评价图 6显示基于全样本模型预测PM2.5浓度与实测值进行拟合精度比较, 其中随机森林模型均方根误差(RMSE)、均方绝对百分比误差(MAPE)和变异解释量(R2)分别为0.133、17.83%和0.834, 明显优于多元线性回归模型, 所以随机森林回归模型更适合浙江省PM2.5浓度预测评估.
图 6(Fig. 6)
 |
| 图 6 PM2.5浓度精度验证 Fig. 6Accuracy validations of PM2.5 concentration |
3.6 重要变量依赖性为了更好揭示各因子对PM2.5浓度影响, 运用随机森林算法中partialPlot函数绘制16个重要影响因子各自对PM2.5浓度影响区间. 日最低地表气温(MI-GST)、日蒸发量(EVP)、日照时长(SSD)、日降水量(PRE)、日平均风速(AV-WIN)、日极大风速(MM-WIN)和海拔(DEM)对PM2.5浓度影响呈下降趋势, 当日最低地表气温(MI-GST)、日蒸发量(EVP)、日平均风速(AV-WIN)分别达到25 ℃、9.0 mm和3.5 m·s-1时, PM2.5浓度影响最小, 当日降水量(PRE)、日照时长(SSD)、日极大风速(MM-WIN)和海拔(DEM)分别超过40 mm、12 h、10 m·s-1和100 m时, PM2.5浓度影响基本稳定;月植被覆盖度(FVC)、铁路密度(Railway)、河流密度(River)、日最高气压(MA-PRS)和日最低气压(MI-PRS)对PM2.5浓度影响总体呈上升趋势;日最大风速风向(DMA-WIN)、日平均相对湿度(AV-RHU)、日极大风速风向(DMM-WIN)和日最大风速(MA-WIN)对PM2.5浓度影响呈先降低后增加变化, 其极小值分别是0.6 m·s-1、95%、5°和4.5 m·s-1;河流密度(River)对PM2.5浓度影响总体呈先增加后降低变化趋势.
4 讨论(Discussion)研究表明2014—2019年浙江省PM2.5浓度时空分布不均匀, 每年呈下降趋势, 而季节变化差异显著, 总体呈冬季>春季>秋季>夏季规律;空间上呈西北多东南少的分布特征. 该研究结果与Wang等(2018)研究结果一致. 利用传统多元线性回归与随机森林方法探究浙江省PM2.5浓度与影响因子之间关系, 研究结果表明:随机森林模型比多元线性回归模型具有更优的均方根误差(RMSE)、均方绝对百分比误差(MAPE)、变异解释量(R2)和更好拟合效果, 能够充分体现出各因子对PM2.5浓度影响.
运用多元线性回归与随机森林模型研究显示日最低地表气温(MI-GST)、日最低气压(MI-PRS)、日蒸发量(EVP)、日最小相对湿度(MI-RHU)、月植被覆盖度(FVC)、日降水量(PRE)、日极大风速(MM-WIN)、日平均相对湿度(AV-RHU)、铁路密度(Railway)日最大风速(MA-WIN)、日照时长(SSD)、海拔(DEM)、日平均风速(AV-WIN)和河流密度(River)等15个因子对PM2.5浓度的影响较为显著. 日最低地表气温(MI-GST)、日蒸发量(EVP)、日最小相对湿度(MI-RHU)、日降水量(PRE)、日极大风速(MM-WIN)、日照时长(SSD)、海拔(DEM)和日平均风速(AV-WIN)等因子与PM2.5浓度呈显著负相关, 研究显示当日照时长变长增加最低地表气温, 日蒸发量增强, 空气中相对湿度接近或达到饱和时, 会增加降水量降低PM2.5浓度(He et al., 2019);PM2.5浓度随着海拔增加而降低, PM2.5在对流层底部分布较多, 该污染源受到风速影响较大, 风速增强有利于PM2.5扩散(He et al., 2019), 此外, 风速逐步增加有利于高污染区域PM2.5向浙江省输送, 增加区域PM2.5浓度. 日最低气压(MI-PRS)、日最高地表气温(MA-GST)、月植被覆盖度(FVC)、日平均相对湿度(AV-RHU)、铁路密度(Railway)、日最大风速(MA-WIN)和河流密度(River)与PM2.5浓度呈显著正相关关系, 当日最高地表气温, 相对湿度极大地促进了干燥条件下的二次反应, 这导致PM 2.5浓度增加(Liu et al., 2016), 铁路密度(Railway)和河流密度(River)有效激活人类活动, 增加区域PM2.5排放, 增加区域PM2.5浓度.
图 7(Fig. 7)
 |
| 图 7 主要因子对PM2.5浓度影响 Fig. 7Partial plots show the effect of each variable on PM2.5 concentration |
因此, 政府应采取有效措施减少大气PM2.5浓度, 第一, 结果表明降水和空气相对湿度与空气中PM2.5浓度呈负相关, 政府可以从10月—次年3月适当增加浙江省北部区域人工降水量及空气相对湿度, 能够有效降低空气PM2.5浓度. 第二, 人口密度有效增加空气PM2.5浓度, 人口密度越大民用车辆越多, 适当减少私家车出行数量, 提倡绿色出行, 在一定程度上减少空气PM2.5浓度;第三, Fausto等(2014)研究指出每公顷植被每年能有效清除16~149 kg颗粒物, 浙江省北部区域森林覆盖率较低, 政府可以适当增加高吸纳植被种植, 有效降低区域PM2.5干沉降;最后, 大气环境是人类赖以生存的物质基础, 大气环境易受到人类活动影响, 建议保护大气环境从生活点滴做起.
5 结论(Conclusions)1) 浙江省PM2.5浓度时间分布不均匀, 时间上每年呈下降趋势, 季节变化差异显著, 总体呈冬季>春季>秋季>夏季的规律.
2) 浙江省PM2.5浓度空间上不均衡, 呈西北多东南少分布特征, 北部PM2.5浓度局部较高, 其浓度远超过中国环境空气质量标准.
3) 回归模型结果表明日最低地表气温、日最低气压、日蒸发量、日最小相对湿度、月植被覆盖度、日降水量、日极大风速、日平均相对湿度、铁路密度、日最大风速、日照时长、海拔、日平均风速和河流密度等15个因子对PM2.5浓度影响显著.
4) 随机森林模型均方根误差(RMSE)、均方绝对百分比误差(MAPE)和变异解释量(R2)分别为0.133、17.83%和0.834明显优于多元线性回归(0.278、40.48%和0.575), 表明随机森林更适合浙江省PM2.5浓度估测.
参考文献
| Breiman Leo. 2001. Random forests[J]. Machine Learning, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| Brook R D, Rajagopalan S, Pope III C A, et al. 2010. Particulate matter air pollution and cardiovascular disease: an update to the scientific statement from the American Heart Association[J]. Circulation, 121(21): 2331-2378. DOI:10.1161/CIR.0b013e3181dbece1 |
| Burnett R T, Pope III C A, Ezzati M, et al. 2014. An integrated risk function for estimating the global burden of disease attributable to ambient fine particulate matter exposure[J]. Environmental Health Perspectives, 122(4): 397-403. DOI:10.1289/ehp.1307049 |
| Cai Q L, Tong L, Zhang J J, et al. 2019. Characteristics of long-range transported PM2.5 at a coastal city using the single particle aerosol mass spectrometry[J]. Environmental Engineering Research, 24(4): 690-698. DOI:10.4491/eer.2018.354 |
| Chen J, Zhou C, Wang S, et al. 2018. Identifying the socioeconomic determinants of population exposure to particulate matter (PM2.5) in China using geographically weighted regression modeling[J]. Environmental Pollution, 241: 494-503. DOI:10.1016/j.envpol.2018.05.083 |
| Chen Y, Ebenstein A, Greenstone M, et al. 2013. Evidence on the impact of sustained exposure to air pollution on life expectancy from China's Huai River policy[J]. Proceedings of the National Academy of Sciences, 110(32): 12936-12941. DOI:10.1073/pnas.1300018110 |
| Cohen A J, Brauer M, Burnett R, et al. 2017. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015[J]. The Lancet, 389(10082): 1907-1918. DOI:10.1016/S0140-6736(17)30505-6 |
| Du Y, Sun T, Peng J, et al. 2018. Direct and spillover effects of urbanization on PM2.5 concentrations in China's top three urban agglomerations[J]. Journal of Cleaner Production, 190: 72-83. DOI:10.1016/j.jclepro.2018.03.290 |
| Fan H, Zhao C, Yang Y. 2020. A comprehensive analysis of the spatio-temporal variation of urban air pollution in China during 2014-2018[J]. Atmospheric Environment, 220: 117066. DOI:10.1016/j.atmosenv.2019.117066 |
| Fausto M, Valerio S, Elisabetta S, et al. 2014. Urban ecosystem services: tree diversity and stability of PM10 removal in the metropolitan area of rome[J]. Gastroenterologia Japonica, 4(1): 19-26. |
| Guan D, Su X, Zhang Q, et al. 2014. The socioeconomic drivers of China's primary PM2.5 emissions[J]. Environmental Research Letters, 9(2): 024010. DOI:10.1088/1748-9326/9/2/024010 |
| Guerreiro C, Ortiz A G, de Leeuw F, et al. 2016. Air quality in Europe 2016 report[M]. Publications Office of the European Union |
| Gui K, Che H, Wang Y, et al. 2019. Satellite-derived PM2.5 concentration trends over Eastern China from 1998 to 2016:Relationships to emissions and meteorological parameters[J]. Environmental pollution, 247: 1125-1133. DOI:10.1016/j.envpol.2019.01.056 |
| He J, Ding S, Liu D. 2019. Exploring the spatiotemporal pattern of PM2.5 distribution and its determinants in Chinese cities based on a multilevel analysis approach[J]. Science of the Total Environment, 659: 1513-1525. DOI:10.1016/j.scitotenv.2018.12.402 |
| Hofman J, Stokkaer I, Snauwaert L, et al. 2013. Spatial distribution assessment of particulate matter in an urban street canyon using biomagnetic leaf monitoring of tree crown deposited particles[J]. Environmental Pollution, 183: 123-132. DOI:10.1016/j.envpol.2012.09.015 |
| Huang R J, Zhang Y, Bozzetti C, et al. 2014. High secondary aerosol contribution to particulate pollution during haze events in China[J]. Nature, 514(7521): 218-222. DOI:10.1038/nature13774 |
| Jiang P, Yang J, Huang C, et al. 2018. The contribution of socioeconomic factors to PM2.5 pollution in urban China[J]. Environmental Pollution, 233: 977-985. DOI:10.1016/j.envpol.2017.09.090 |
| Jin Q, Ma X Q, Wang G Y, et al. 2018. Dynamics of major air pollutants from crop residue burning in mainland China, 2000-2014[J]. Journal of Environmental Sciences, 70(8): 190-205. |
| 靳全锋, 马祥庆, 王文辉, 等. 2017. 中国亚热带地区2000-2014年林火排放颗粒物时空动态变化[J]. 环境科学学报, 37(6): 2238-2247. |
| 靳全锋, 沈培福, 黄海松, 等. 2019. 基于MODIS影像估算中国大陆区域草地火污染物时空格局[J]. 环境科学学报, 39(5): 1412-1424. |
| 靳全锋, 叶文晶, 沈培福, 等. 2019. 浙江2001-2016年露天生物质燃烧排放污染物时空格局[J]. 环境科学学报, 39(1): 259-269. |
| Karplus V J, Zhang S, Almond D. 2018. Quantifying coal power plant responses to tighter SO2 emissions standards in China[J]. Proceedings of the National Academy of Sciences, 115(27): 7004-7009. DOI:10.1073/pnas.1800605115 |
| Kok J F, Ward D S, Mahowald N M, et al. 2018. Global and regional importance of the direct dust-climate feedback[J]. Nature Communications, https://doi:10.1038/s41467-017-02620-y |
| Krotkov N A, McLinden C A, Li C, et al. 2016. Aura OMI observations of regional SO2 and NO2 pollution changes from 2005 to 2015[J]. Atmospheric Chemistry and Physics, 16(7): 4605-4629. DOI:10.5194/acp-16-4605-2016 |
| Li L, Lu C, Chan P W, et al. 2020. Tower observed vertical distribution of PM2.5, O3 and NOx in the Pearl River Delta[J]. Atmospheric Environment, 220: 117083. DOI:10.1016/j.atmosenv.2019.117083 |
| Li R, Wang Z, Cui L, et al. 2019. Air pollution characteristics in China during 2015-2016: Spatiotemporal variations and key meteorological factors[J]. Science of the Total Environment, 648: 902-915. DOI:10.1016/j.scitotenv.2018.08.181 |
| Liacos J W, Kam W, Delfino R J, et al. 2012. Characterization of organic, metal and trace element PM2.5 species and derivation of freeway-based emission rates in Los Angeles, CA[J]. Science of the Total Environment, 435: 159-166. |
| Lindeman R H, Merenda P F, Gold R Z. 1980. Introduction to Bivariate and Multivariate Analysis[M]. Glenview: Scott Foresman, 752. |
| Liu J, Han Y, Tang X, et al. 2016. Estimating adult mortality attributable to PM2.5 exposure in China with assimilated PM2.5 concentrations based on a ground monitoring network[J]. Science of the Total Environment, 568: 1253-1262. DOI:10.1016/j.scitotenv.2016.05.165 |
| Ma X, Wang J, Yu F, et al. 2016. Can MODIS AOD be employed to derive PM2.5 in Beijing-Tianjin-Hebei over China[J]. Atmospheric Research, 2016: 250-256. |
| Niedzwiecki M M, Rosa M J, Solano-González M, et al. 2020. Particulate air pollution exposure during pregnancy and postpartum depression symptoms in women in Mexico City[J]. Environment International, 134: 105325. DOI:10.1016/j.envint.2019.105325 |
| Olson K C, Sindelar B W. 1985. Response of vegetation of the northern great plains to precipitation amount and grazing intensity[J]. Journal of Range Management, 38(4): 357-361. DOI:10.2307/3899422 |
| Pope III C A, Burnett R T, Turner M C, et al. 2011. Lung cancer and cardiovascular disease mortality associated with ambient air pollution and cigarette smoke: shape of the exposure-response relationships[J]. Environmental Health Perspectives, 119(11): 1616-1621. DOI:10.1289/ehp.1103639 |
| Popek R, Przybysz A, Gawrońska H, et al. 2018. Impact of particulate matter accumulation on the photosynthetic apparatus of roadside woody plants growing in the urban conditions[J]. Ecotoxicology and Environmental Safety, 163: 56-62. DOI:10.1016/j.ecoenv.2018.07.051 |
| Qiu H, Zhu X, Wang L, et al. 2019. Attributable risk of hospital admissions for overall and specific mental disorders due to particulate matter pollution: A time-series study in Chengdu, China[J]. Environmental Research, 170: 230-237. DOI:10.1016/j.envres.2018.12.019 |
| Rodrigues M, Riva J D L. 2014. An insight into machine-learning algorithms to model human-caused wildfire occurrence[J]. Environmental Modelling & Software, 57: 192-201. |
| Schiferl L D, Heald C L. 2018. Particulate matter air pollution may offset ozone damage to global crop production[J]. Atmospheric Chemistry and Physics, 18(8): 5953-5966. DOI:10.5194/acp-18-5953-2018 |
| Shen Y, Zhang L, Fang X, et al. 2019. Spatiotemporal patterns of recent PM2.5 concentrations over typical urban agglomerations in China[J]. Science of the Total Environment, 655: 13-26. DOI:10.1016/j.scitotenv.2018.11.105 |
| Silver B, Reddington C L, Arnold S R, et al. 2018. Substantial changes in air pollution across China during 2015-2017[J]. Environmental Research Letters, 13(11): 104-112. DOI:10.1088/1748-9326/aae718 |
| Solazzo E, Bianconi R, Pirovano G, et al. 2012. Operational model evaluation for particulate matter in Europe and North America in the context of AQMEII[J]. Atmospheric Environment, 53: 75-92. DOI:10.1016/j.atmosenv.2012.02.045 |
| Song Y, Maher B A, Li F, et al. 2015. Particulate matter deposited on leaf of five evergreen species in Beijing, China: Source identification and size distribution[J]. Atmospheric Environment, 105: 53-60. DOI:10.1016/j.atmosenv.2015.01.032 |
| Sun X, Luo X S, Xu J, et al. 2019. Spatio-temporal variations and factors of a provincial PM2.5 pollution in eastern China during 2013-2017 by geostatistics[J]. Scientific Reports, 9(1). DOI:10.1038/s41598-019-40426-8 |
| Svetnik V, Liaw A, Tong C, et al. 2003. Random forest: a classification and regression tool for compound classification and QSAR modeling[J]. Journal of Chemical Information & Computer Sciences, 43(6): 1947-1958. |
| United Nations, Department of Economic and Social Affairs, Population Division, 2014. World Urbanization Prospects: The 2014 Revision, Highlights (ST/ESA/SER.A/352) |
| Wang L T, Wei Z, Yang J, et al. 2014. The 2013 severe haze over southern Hebei, China: model evaluation, source apportionment, and policy implications[J]. Atmospheric Chemistry and Physics, 14(6). DOI:10.5194/acp-14-3151-2014 |
| Wang S, Liu X, Yang X, et al. 2018. Spatial variations of PM2.5 in Chinese cities for the joint impacts of human activities and natural conditions: A global and local regression perspective[J]. Journal of Cleaner Production, 203: 143-152. DOI:10.1016/j.jclepro.2018.08.249 |
| Xu H, Xiao Z, Chen K, et al. 2019. Spatial and temporal distribution, chemical characteristics, and sources of ambient particulate matter in the Beijing-Tianjin-Hebei region[J]. Science of the Total Environment, 658: 280-293. DOI:10.1016/j.scitotenv.2018.12.164 |
| Yang D, Wang X, Xu J, et al. 2018. Quantifying the influence of natural and socioeconomic factors and their interactive impact on PM2.5 pollution in China[J]. Environmental Pollution, 241: 475-483. DOI:10.1016/j.envpol.2018.05.043 |
| Yuan M, Huang Y, Shen H, et al. 2018. Effects of urban form on haze pollution in China: Spatial regression analysis based on PM2.5 remote sensing data[J]. Applied Geography, 98: 215-223. DOI:10.1016/j.apgeog.2018.07.018 |
| Zeng Y, Lin R, Liu L, et al. 2019. Ambient air pollution exposure and risk of depression: A systematic review and meta-analysis of observational studies[J]. Psychiatry Research, 276: 69-78. DOI:10.1016/j.psychres.2019.04.019 |
| Zhan D, Kwan M P, Zhang W, et al. 2018. The driving factors of air quality index in China[J]. Journal of Cleaner Production, 197: 1342-1351. DOI:10.1016/j.jclepro.2018.06.108 |
| Zhang H, Qi P, Guo G. 2014. Improvement of fire danger modelling with geographically weighted logistic model[J]. International Journal of Wildland Fire, 23(8): 1130-1146. DOI:10.1071/WF13195 |
| Zhang K, Zhao C, Fan H, et al. 2019. Toward Understanding the Differences of PM2.5 Characteristics Among Five China Urban Cities[J]. Asia Pacific Journal of the Atmospheric Sciences, (5043).https://doi.org/10.1016/j.atmosenv.2019.117066 |
| Zhang X F, Liao C H, Li J, et al. 2013. Fractional vegetation cover estimation in arid and semi-arid environments using hj-1 satellite hyperspectral data[J]. International Journal of applied Earth Observation & Geoinformation, 21(4): 506-512. |
| Zhao C, Wang Y, Shi X, et al. 2019. Estimating the contribution of local primary emissions to particulate pollution using high-density station observations[J]. Journal of Geophysical Research: Atmospheres, 124(3): 1648-1661. DOI:10.1029/2018JD028888 |
