 ,1,2
,1,2Using Bayesian tip-dating method to estimate divergence times and evolutionary rates
ZHANG Chi ,1,2
,1,2通讯作者: zhangchi@ivpp.ac.cn
收稿日期:2021-01-18
| 基金资助: |
Corresponding authors: zhangchi@ivpp.ac.cn
Received:2021-01-18

摘要
贝叶斯支端定年法是近些年开发的推断类群分异时间和演化速率的方法。它克服了传统分步计算的缺陷,但涉及的统计学知识也更多。本文从贝叶斯统计计算的角度分层剖析了支端定年法的原理和计算过程,按照分异时间的先验分布、演化速率的先验分布、特征状态变化的模型和马氏链蒙特卡罗算法几个部分,叙述并讨论了定年计算中的主要模型和算法。旨在一定程度上为古生物学家分析实际数据提供参考。
关键词:
Abstract
Bayesian tip dating is a recently developed method to estimate divergence times and evolutionary rates. It overcomes several drawbacks in traditional stepwise approach. However, it also requires more knowledge about statistics. This paper hierarchically explains the theory and computation in the Bayesian tip-dating approach, and divides the whole process into prior for the divergence times, prior for the evolutionary rates, model for the character changes and Markov chain Monte Carlo algorithm, which are key components in this method. The aim is to provide a general guidance for paleontologists in empirical data analyses.
Keywords:
PDF (829KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张驰. 贝叶斯支端定年法推断分异时间和演化速率. 古脊椎动物学报[J], 2021, 59(4): 333-341 DOI:10.19615/j.cnki.2096-9899.210516
ZHANG Chi.
1 简介
推断类群的系统关系和分异时间是分支系统学分析的基础。如何合理利用化石的形态和地质年代的数据来完成此类推断一直是一个棘手的问题。传统的推断过程往往采用分步的策略。首先单独从形态数据出发,利用简约法构建类群的系统关系。这个关系只有拓扑结构而没有时间的信息,而且只代表给定时间和搜索条件下最优的结果(即最简约的树或其合意树)。然后固定这个拓扑结构,从化石年代出发,利用最小枝长法(Laurin, 2004)或等距枝长法(Brusatte et al., 2008)确定树中内部节点的分异时间。最小枝长法是把当前节点的时间往前推一个百万年作为祖先节点的时间;而等距枝长法则是把祖先节点到后代节点的时间的中点最为当前节点的时间。至于演化速率,可以通过祖先状态重建和每个树枝上特征变化的次数,结合上一步推断的时间来估计。这种分步计算的方式比较直观,因此被用于实际数据分析(Wang and Lloyd, 2016)。然而,该策略存在诸多缺陷。首先,它每一步都忽略了推断中的不确定性,包括树的拓扑结构、分异时间和祖先特征状态;其次,每一步都只利用了一部分数据信息,如建树时只用到形态特征,定年时只用到化石年代;再次,定年的方式很主观,对化石数量的增减很敏感,且不适用于现生类群;最后,整个过程缺乏一个严谨的统计学框架,无法对不同的模型假设进行检验。近些年开发的贝叶斯支端定年法(Bayesian tip dating) (Ronquist et al., 2012; Gavryushkina et al., 2014; Zhang et al., 2016)很好地克服了上述问题。贝叶斯支端定年法把化石形态和年代数据整合在一次完整的计算过程中,能够尽可能地利用数据信息,同时考虑了树的拓扑结构、分异时间、演化速率以及化石年代的不确定性。该方法通过统计模型来描述特征的演化、类群的生灭以及化石的采样等过程,并借助相对成熟的贝叶斯统计框架和计算方法来进行参数估计和模型选择。但该方法相对来说比较复杂,需要较多的统计学知识,对古生物学家来说往往难于理解和上手,而且鲜有系统阐述支端定年法计算过程和参数意义的文献(Gavryushkina and Zhang, 2020)。本文逐层剖析支端定年法的计算过程,解释其中用到的重要模型和参数意义,旨在一定程度上为古生物学家分析实际数据提供参考。
本文首先介绍描述时间树的石化生灭过程(fossilized birth-death process)模型(Stadler, 2010), 然后介绍描述特征演化速率的宽松形态钟(relaxed clock)模型,接着介绍描述特征状态变化的Mk模型(Lewis, 2001), 再通过贝叶斯公式把上述模型联系起来,最后介绍估计参数后验分布的马氏链蒙特卡罗(Markov chain Monte Carlo, MCMC)算法。附录提供了计算中生代鸟类数据(Zhang and Wang, 2019)的MrBayes命令。
2 分异时间
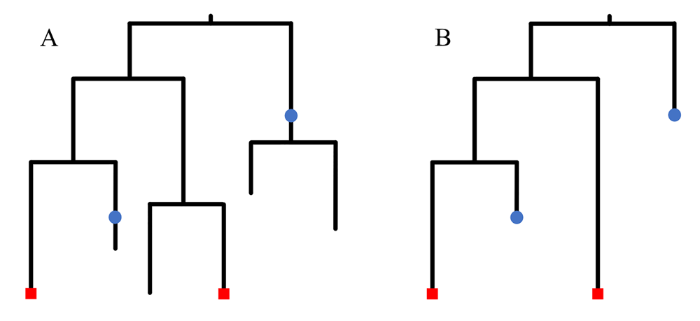
时间树(timetree)代表类群的系统关系和分异时间,它的概率分布可以通过石化生灭过程(Stadler, 2010)来给出。该过程描述了从这些类群的最近共同祖先(树根)开始,分异、灭绝、采集化石和采样现生类群这一系列事件的发生,并对应于一棵完整树(图1A)。但是实际数据分析中无法推断这个完整树,只能推断和样本相关的部分,即样本树(图1B)。记每个树枝的分异速率(或叫成种率)为λ, 灭绝速率为μ, 沿每个树枝的化石采样速率为ψ, 现生类群的采样概率(或采样比例)为ρ, 通过建立并求解一系列常微分方程,可以得到给定λ, μ, ψ, ρ时,样本时间树T = {τ, t}的概率分布,记为P(T | λ, μ, ψ, ρ), 其中τ代表拓扑结构,t代表以百万年为单位的分异时间。图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1石化生灭过程可能得到的时间树
A. 生灭过程对应的完整树; B. 只保留和样本相关的分支得到的样本树,包含两个现生类群(红点)和两个化石(蓝点)
Fig. 1Example timetree generated from the fossilized birth-death process
A. compete tree by keeping all branches; B. sampled tree by only keeping branches leading to two extant taxa (red dots) and two fossils (blue dots)
在MrBayes软件中,该生灭过程以树根时间t1为起始条件(图2), 计算时要指定t1的先验分布。通常这个先验比较宽泛(最大范围从0到无穷), 不过一般能从研究的类群预估一个更精确的范围,例如,其下界不会早于最古老化石的年代。化石的时间可以固定为具体的数值(百万年前), 也可以用一个均匀分布给出时间的上下界。在计算时还需要提供现生类群大致的采样比例(ρ)。现生类群可以有两种采样策略,一种是均匀随机采样(random), 另一种是多样化采样(diversity) (Zhang et al., 2016), 可以根据实际数据的情况自行选择,后者可能更符合高阶元类群的采样模式(如每个科只取一个代表的属或者每个属取一个代表物种)。对于分异、灭绝和化石采样速率,程序为了设置先验方便,重新参数化为d = λ - μ, v= μ / λ, s = ψ / (μ+ψ)。d的默认先验为指数分布(范围从0到无穷), v和s的默认先验为均匀分布(范围从0到1, 更一般地为贝塔分布)。这样,时间树包括分异时间等参数的先验分布基本就确定了。
图2
 新窗口打开|下载原图ZIP|生成PPT
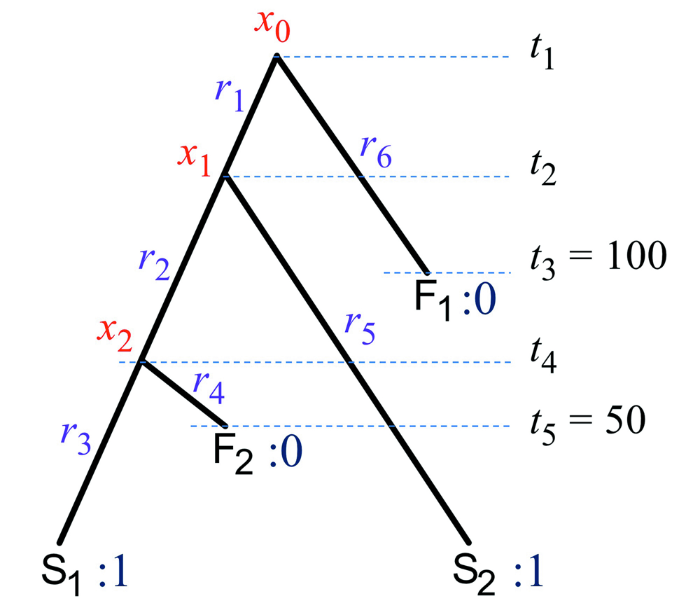
新窗口打开|下载原图ZIP|生成PPT图2用于各个概率分布公式中参数的示例
树上化石F1和F2的特征状态为0,现生类群S1和S2的特征状态为1,内部节点的特征状态用x0, x1, x2表示化石的年代分别为t3 = 100 Ma, t5 = 50 Ma, 树根的时间为t1, 其他分异时间为t2和t4记t = {t1, t2, t3, t4, t5}。各个枝上的特征演化速率为r = {r1, r2, r3, r4, r5}
Fig. 2Example parameters and symbols used in the probability distributions
The character states for fossils F1 and F2 are 0, for extant taxa S1 and S2 are 1, for internal nodes are x0, x1, x2. The ages of fossils F1 and F2 are t3 = 100 Ma and t5 = 50 Ma
The root age is t1 and the remaining divergence times are t2 and t4. Denote t = {t1, t2, t3, t4, t5}. The evolutionary rates on the branches are r = {r1, r2, r3, r4, r5}
需特别提到的是,有些数据只包含了化石而没有现生类群。这时一般假设生灭过程在未到达现今时间点所有类群就都灭绝了。因此现生类群不论采用何种采样策略和比例(程序默认为1.0), 都没有样本被采集到。不过由于MrBayes软件的限制,最年轻的样本总被显示为现生类群(时间为0), 因此需要把整棵树的时间轴进行相应的平移,或者说分异时间要加上年代最近的化石的年代。这只是结果显示的问题而不是程序计算的错误(后续版本将修复这个问题)。
除了石化生灭过程之外,MrBayes还为时间树提供了一个均匀分布的先验(Ronquist et al., 2012)。它没有生灭和采样这些参数,只依赖于树根时间t1, 因此只需设置t1的先验分布。均匀分布时常被认为是没有信息的先验,但它实际上往往带有很强的信息,在定年这个问题上,会影响对分异时间的估计。而石化生灭过程看似参数很多,但实际上其设置可以很灵活。例如,分异、灭绝和化石采样速率都可以随时间变化,在不同的时间段内各自独立(Gavryushkina et al., 2014; Zhang et al., 2016)。这可能更符合实际生物学过程,同时还能推测净成种速率和化石采样速率随时间的变化。
3 演化速率
形态特征的演化速率是指每百万年每个特征期望的变化次数。对于给定的一段时间,演化速率越快,则特征最终期望的变化次数越多。一般给每个树枝一个演化速率参数,记为r (图2)。时钟模型应用于形态数据时被称为形态钟模型,类比于用在分子数据时的分子钟模型。严格钟(strict clock)模型假设演化速率在各个树枝上都相同,这通常不适用于形态数据,实际分析时往往需使用宽松钟(relaxed clock)模型。宽松钟模型可以分为两类,一类为独立速率,另一类为自相关(autocorrelated)速率,区别在于r的概率分布P(r)不同。独立速率模型假设枝上的演化速率彼此独立,它们都服从均值相同的某个概率分布。常用的概率分布包括伽马分布(Lepage et al., 2007)和对数正态分布(Drummond et al., 2006)。分布的均值也被称为基准速率(base rate), 反映平均的演化速率大小。分布的方差则反映演化速率在树枝之间变化的剧烈程度:方差较小时各个速率相差不大,这意味着演化速率在整棵树上没有明显的差异;而方差越大,不同树枝上速率的差异越明显。
自相关速率模型假设后代树枝上的演化速率依赖于临近祖先那枝上的速率(例如r2和r5都依赖r1, r3和r4都依赖r2)。当前树枝上的速率一般假设服从对数正态分布(Kishino et al., 2001; Thorne and Kishino, 2002), 其均值为临近祖先节点的速率。同理,分布的方差也反映演化速率在树枝之间变化的剧烈程度。
这两类速率模型往往对分异时间的估计也有影响,这主要是因为自相关速率模型会倾向于速率的变化是渐进的,而独立速率模型没有这种限制,会更适应临近树枝间速率变化比较剧烈的情况。对化石形态数据来说,独立速率模型可能更适用。
默认的情况下,形态数据矩阵中所有特征都共享每个枝上的演化速率,因此,这个速率代表的是所有特征的平均情况。如果需要考虑不同特征演化速率的异质性,就需要对特征进行分区。一般可以按照不同特征类型或不同身体部位或功能来分,每个分区内的特征共享一组演化速率,而分区之间特征演化速率的模式是独立的,这样就可以推断不同部位或功能相关特征随时间会发生怎样的变化(Lee, 2016; Zhang and Wang, 2019)。需注意的是,分区越多,每个分区内的特征数量就越少,因此能够估计演化速率参数的信息就越少,会造成方差很大甚至参数个数超过特征数量导致无法进行参数估计。因此,要在考虑演化速率异质性和分区数量之间做一个权衡。
4 特征状态变化
有了分异时间和演化速率,就可以计算在给定时间段t和演化速率r的情况下,形态特征从一个状态变为另一个状态的概率(称为转移概率)。这个概率由Mk模型(Lewis, 2001)给出。Mk模型是描述特征状态变化最简单的模型,它假设状态之间转换的速率是相等的。这里只以两个状态的特征为例,用P00(r, t)表示状态0保持不变的概率,P01(r, t)表示从0变到1的概率,P10(r, t)表示从1变到0的概率,P11(r, t)表示状态1保持不变的概率,则P00(r, t) = P11(r, t) = 1/2 + 1/2 × exp(-2rt), P01(r, t) = P10(r, t) = 1/2 - 1/2 × exp(-2rt)。从公式中可以发现,时间t和速率r总是以乘积的形式出现,因此,在没有化石年代信息时,两者是不可识别的。换句话说,单单依靠形态数据来建树,树的枝长为时间和速率的乘积,即距离,以每个特征期望的变化次数为单位。只有同时利用化石形态和年代数据才能将分异时间和演化速率单独估计出来。以图2为例,化石F1和F2的特征状态为0, 现生类群S1和S2的特征状态为1, 内部节点的特征状态未知用x0, x1, x2表示。F1和F2的时间分别为100和50 Ma。那么根据Mk模型,给定时间树T = {τ, t}和速率r时,特征状态列0011的概率为
P(0011|T, r) = ∑x0∑x1∑x2Px0x1(t1-t2, r1)Px1x2(t2-t4, r2)Px21(t4, r3) Px20 (t4-t5, r4)Px11(t2, r5)Px00 (t1-t3, r6)。
其中西格玛符号代表对特征在内部节点所有可能状态的求和。由于形态特征矩阵往往只包含可变的特征,因此这个概率还要除以所有可变状态的概率,即P(0011 | T, r)/ [1 - P(0000 | T, r) - P(1111 | T, r)]。带有这一校正的Mk模型称为Mkv模型(Lewis, 2001)。
假设形态矩阵中的特征都彼此独立,那么就可以计算每一列特征在树上的概率,再把这些概率乘起来。这个概率被称为似然函数,表示为P(D| T, r), 其中D代表形态特征矩阵数据。
5 贝叶斯公式
在统计推断时,参数都是未知的随机变量,需要根据数据来估计它们的分布,即计算P(T, r, θ | D), 该分布称为后验分布,其中T = {τ, t}为时间树,r为演化速率,θ代表其它参数(包括λ, μ, ψ等)。根据分层贝叶斯公式,可得P(T, r, θ | D) = P(D | T, r) P(r) P(T| θ) P(θ)/P(D)。等号右侧分子中,第一项似然函数在第四节给出,第二项演化速率的先验分布在第三节给出,第三项和第四项为时间树及其参数的先验分布在第二节给出。这样公式分子中各项都可以计算了。分母P(D)是特征数据的概率,这需要计算对所有参数的多重积分,实际上基本无法给出解析表达式,只能通过数值算法进行近似。所以贝叶斯计算在绝大多数情况下会使用马氏链蒙特卡罗算法。6 马氏链蒙特卡罗算法
马氏链蒙特卡罗(MCMC)算法通过构造马尔可夫链,使其平稳分布为要估计的后验分布。这里为了简化,只以一维参数的情形为示例(图3)。实际分析中,参数一般是多维的(如τ, t, r, θ), 不过算法的思想是类似的。图3
 新窗口打开|下载原图ZIP|生成PPT
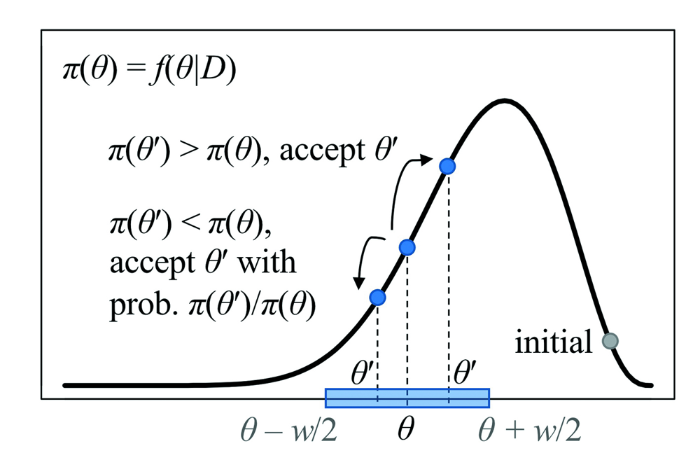
新窗口打开|下载原图ZIP|生成PPT图3马氏链蒙特卡罗算法在一维情形的示例参数θ的后验分布π(θ)为估计的目标(曲线)
Fig. 3Illustration of the MCMC algorithm for one dimensional parameter
The posterior distribution π(θ) of parameter θ is the target distribution to be estimated (curve)
MCMC采用的Metropolis-Hastings算法(Metropolis et al., 1953; Hastings, 1970)可分为如下几步:
(1) 为θ设定任意初始值;
(2) 基于θ当前的值,建议一个新的值θ’, 例如θ’ ~ uniform(θ - w/2, θ + w/2);
(3) 如果π(θ’) > π(θ), 就接受θ’; 否则,以概率α= π(θ’) / π(θ) 接受θ’;
(4) 如果θ’被接受,就更新θ = θ’; 否则,保持θ不变;
(5) 记录θ的值,回到步骤(2)。
注意到,在计算概率α的时候,会计算后验分布的比,这样后验分布分母的部分就约掉了,只剩分子部分的比。也就是说,只要能够把分子部分写出解析表达式,MCMC算法就可以使用来估计参数的后验分布了。
计算结束后,就收集到一些θ的样本。由于参数的初始状态往往比较差,MCMC需要经过很多代才收敛到后验概率密度比较高的地方,因此在估计后验分布的时候会舍弃初始的一些样本(burn-in), 只用MCMC链收敛后记录的样本来估计后验分布。MrBayes默认舍弃前25%的样本。同时,MCMC链还要迭代足够多次,以保证有足够多的有效样本来估计参数的后验分布。一般需要有效样本大小(ESS)大于100。
实际运算中,最好独立运行至少两次MCMC, 以确保两次的结果是一致的。有时链长不够,或者不同的运算卡在不同的后验分布区域,都会导致估计的结果不一致。这时调整MCMC的设置或者改善模型都可能帮助MCMC算法发挥更好的效能。使用Metropolis-coupled MCMC也是有效跨越多峰分布的手段(Lakner et al., 2008)。该算法同时运行多条MCMC链,一条为冷链(cold chain), 其余为热链(hot chains), 热链和冷链之间可以相互交换。当然MCMC样本只从冷链中采集,热链只是用来帮助跨越多峰的。MrBayes默认同时独立运行两次,每次运算使用四条链,其中一条为冷链,其余三条为热链。
7 讨论
本文从贝叶斯统计计算的角度分层剖析了支端定年法的原理和计算过程。贝叶斯后验分布包含先验分布和似然函数,其中先验分布的两个重要组成部分:分异时间和演化速率模型,在定年分析中尤为关键,是影响定年准确性的主要因素。石化生灭过程作为描述类群分异、灭绝和采样的随机过程,具有较大的灵活性。不过该模型还有待完善之处。现生类群的采样方式可以是随机的或多样化的,这两种情形可能都是极端,真实的采样模式可能介于两者之间,或者有的支系是随机采样,有的支系是多样化采样,但目前还没有模型能够支持这种情况。在更好的模型被开发出来之前,可能只能调整数据来尽量符合其中一种采样策略。这种处理方式在现生类群比较少或根本没有时一般问题不大。另外,分异速率、灭绝速率和化石采样速率可以按分段的方式随时间变化,不过在同一时间段内,所有树枝都共享同一速率。对于不同支系明显受到的选择压力不同或化石保存的完整性明显不同等情况,按支系分段而非时间分段的模型(Barido-Sottani et al., 2020)可能更合适,虽然这一类模型本身也有其他限制。不论怎样,石化生灭过程只是作为时间的先验分布,当数据量比较大时(包括化石在树上的分布程度和数量以及形态特征的数量和完整度), 数据在推断中会起主导作用而先验的影响减少。但是实际情况往往比较复杂,数据量也不尽如人意,这时考察不同先验的影响就尤为重要。
演化速率的先验,即形态钟模型,也会和时间相互作用,从而影响对最终分异时间的估计。这种影响在化石较少或化石在树上分布很不均时尤为明显。这主要是因为化石形态数据只提供了距离的信息(每个特征期望的变化次数), 其为时间和速率的乘积(见第四节)。当缺少化石时,就没办法准确提供时间的信息,那么对于同样的距离,可以是很长时间速率很慢,也可以是很短时间但速率很快,具体是怎样就只能取决于时间和演化速率的先验了。对于某些支系时间估计得明显偏大或偏小,但又没有化石来校正的情况,可以通过添加内部节点的校正分布来得到更合理的时间估计(O’Reilly and Donoghue, 2016)。在完全没有化石只有现生类群时,节点定年法(另一类型定年方法) (Yang and Rannala, 2006)就是通过使用内部节点的校正分布来完成的。
描述形态特征状态变化的模型也有很大的改进空间,其中涉及更多的建模和随机模拟等工作,不是本研究的重点,这里只简单讨论一下Mk模型对定年可能的影响。Mk模型假设特征各个状态间转变的速率都是相等的。这种转变有无序和有序之分(只对三个及以上状态的特征)。无序是指特征可以直接从一个状态变为任意其他状态(如从0直接变为3), 而有序是指特征只能在临近状态间直接变化(如从0到1, 从1到2, 再从2到3)。显然,有序需要更多次变化(也就是更长的距离)才能从当前状态变为不相邻的状态,因此对有序的特征假设无序的变化会低估距离。更复杂的情况是,各个状态间转变的速率未必相等甚至相差很多,极端情况像Dollo特征甚至是不可逆的。这时使用Mk模型也会造成距离估计的偏差。在计算时还假设不同特征之间都是独立的,如果有些特征有较强的相关性,则会导致演化距离的高估。前面提到,距离是时间和速率的乘积,因此在化石(时间信息)很丰富的理想情况下,距离的偏差会主要体现到演化速率上而对分异时间影响较小。但是分析实际数据时会更复杂一些,要具体问题具体分析。相关的工作还较少(Klopfstein et al., 2019), 需要更多后续研究来更详细地考察。
最后提到贝叶斯计算使用的MCMC算法。该算法的策略与简约法和似然法有明显不同。简约法寻找的是简约树长最小的树,似然法寻求的是似然值最大时参数的估计(即最大似然树)。因此在设计树的搜索方法时,只要尽可能快速地找到最优的树就可以了。MCMC算法是为了估计参数的后验分布,这不仅仅是一个点,而是参数的空间。因此MCMC算法的效率涉及收敛(convergence)和混合(mixing)两部分。收敛是指MCMC达到分布概率密度高的区域,混合是指MCMC能够按概率分布进行取样。提高收敛速度相对容易,可以通过如简约树长向导的方式来快速找到概率大的树(Zhang et al., 2020)。提高混合则更困难,需要设计更好的建议(proposal)方法,这是贝叶斯计算的重点也是难点。
总之,贝叶斯支端定年法作为整合的分析方法,能够结合化石形态和年代数据以及现生类群的形态和分子数据来推断类群的系统关系,分异时间和演化速率,同时考虑了树的拓扑结构、分异时间、演化速率以及化石年代的不确定性。但该方法仍处于发展初期,模型和算法的诸多方面还亟待完善,因此还有很多工作需要做。
Supplementary material can be found on the website of Vertebrata PalAsiatica (
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOIPMID [本文引用: 1]

Heterogeneous populations can lead to important differences in birth and death rates across a phylogeny. Taking this heterogeneity into account is necessary to obtain accurate estimates of the underlying population dynamics. We present a new multitype birth-death model (MTBD) that can estimate lineage-specific birth and death rates. This corresponds to estimating lineage-dependent speciation and extinction rates for species phylogenies, and lineage-dependent transmission and recovery rates for pathogen transmission trees. In contrast with previous models, we do not presume to know the trait driving the rate differences, nor do we prohibit the same rates from appearing in different parts of the phylogeny. Using simulated data sets, we show that the MTBD model can reliably infer the presence of multiple evolutionary regimes, their positions in the tree, and the birth and death rates associated with each. We also present a reanalysis of two empirical data sets and compare the results obtained by MTBD and by the existing software BAMM. We compare two implementations of the model, one exact and one approximate (assuming that no rate changes occur in the extinct parts of the tree), and show that the approximation only slightly affects results. The MTBD model is implemented as a package in the Bayesian inference software BEAST 2 and allows joint inference of the phylogeny and the model parameters.[Birth-death; lineage specific rates, multi-type model.].© The Author(s) 2020. Published by Oxford University Press, on behalf of the Society of Systematic Biologists.
DOIPMID [本文引用: 1]

The rise and diversification of the dinosaurs in the Late Triassic, from 230 to 200 million years ago, is a classic example of an evolutionary radiation with supposed competitive replacement. A comparison of evolutionary rates and morphological disparity of basal dinosaurs and their chief "competitors," the crurotarsan archosaurs, shows that dinosaurs exhibited lower disparity and an indistinguishable rate of character evolution. The radiation of Triassic archosaurs as a whole is characterized by declining evolutionary rates and increasing disparity, suggesting a decoupling of character evolution from body plan variety. The results strongly suggest that historical contingency, rather than prolonged competition or general "superiority," was the primary factor in the rise of dinosaurs.
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 2]
DOIURL [本文引用: 1]
PMID [本文引用: 1]

Rates of molecular evolution vary over time and, hence, among lineages. In contrast, widely used methods for estimating divergence times from molecular sequence data assume constancy of rates. Therefore, methods for estimation of divergence times that incorporate rate variation are attractive. Improvements on a previously proposed Bayesian technique for divergence time estimation are described. New parameterization more effectively captures the phylogenetic structure of rate evolution on a tree. Fossil information and other evidence can now be included in Bayesian analyses in the form of constraints on divergence times. Simulation results demonstrate that the accuracy of divergence time estimation is substantially enhanced when constraints are included.
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
PMID [本文引用: 3]

Evolutionary biologists have adopted simple likelihood models for purposes of estimating ancestral states and evaluating character independence on specified phylogenies; however, for purposes of estimating phylogenies by using discrete morphological data, maximum parsimony remains the only option. This paper explores the possibility of using standard, well-behaved Markov models for estimating morphological phylogenies (including branch lengths) under the likelihood criterion. An important modification of standard Markov models involves making the likelihood conditional on characters being variable, because constant characters are absent in morphological data sets. Without this modification, branch lengths are often overestimated, resulting in potentially serious biases in tree topology selection. Several new avenues of research are opened by an explicitly model-based approach to phylogenetic analysis of discrete morphological data, including combined-data likelihood analyses (morphology + sequence data), likelihood ratio tests, and Bayesian analyses.
DOIURL [本文引用: 1]
[本文引用: 1]
DOIPMID [本文引用: 2]

Phylogenies are usually dated by calibrating interior nodes against the fossil record. This relies on indirect methods that, in the worst case, misrepresent the fossil information. Here, we contrast such node dating with an approach that includes fossils along with the extant taxa in a Bayesian total-evidence analysis. As a test case, we focus on the early radiation of the Hymenoptera, mostly documented by poorly preserved impression fossils that are difficult to place phylogenetically. Specifically, we compare node dating using nine calibration points derived from the fossil record with total-evidence dating based on 343 morphological characters scored for 45 fossil (4--20 complete) and 68 extant taxa. In both cases we use molecular data from seven markers (~5 kb) for the extant taxa. Because it is difficult to model speciation, extinction, sampling, and fossil preservation realistically, we develop a simple uniform prior for clock trees with fossils, and we use relaxed clock models to accommodate rate variation across the tree. Despite considerable uncertainty in the placement of most fossils, we find that they contribute significantly to the estimation of divergence times in the total-evidence analysis. In particular, the posterior distributions on divergence times are less sensitive to prior assumptions and tend to be more precise than in node dating. The total-evidence analysis also shows that four of the seven Hymenoptera calibration points used in node dating are likely to be based on erroneous or doubtful assumptions about the fossil placement. With respect to the early radiation of Hymenoptera, our results suggest that the crown group dates back to the Carboniferous, ~309 Ma (95% interval: 291--347 Ma), and diversified into major extant lineages much earlier than previously thought, well before the Triassic. [Bayesian inference; fossil dating; morphological evolution; relaxed clock; statistical phylogenetics.].
DOIPMID [本文引用: 2]

I consider the constant rate birth-death process with incomplete sampling. I calculate the density of a given tree with sampled extant and extinct individuals. This density is essential for analyzing datasets which are sampled through time. Such datasets are common in virus epidemiology as viruses in infected individuals are sampled through time. Further, such datasets appear in phylogenetics when extant and extinct species data is available. I show how the derived tree density can be used (i) as a tree prior in a Bayesian method to reconstruct the evolutionary past of the sequence data on a calender-timescale, (ii) to infer the birth- and death-rates for a reconstructed evolutionary tree, and (iii) for simulating trees with a given number of sampled extant and extinct individuals which is essential for testing evolutionary hypotheses for the considered datasets.Copyright © 2010 Elsevier Ltd. All rights reserved.
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIPMID [本文引用: 2]

Recently, comprehensive morphological datasets including nearly all the well-recognized Mesozoic birds became available, making it feasible for statistically rigorous methods to unveil finer evolutionary patterns during early avian evolution. Here, we exploited the advantage of Bayesian tip dating under relaxed morphological clocks to estimate both the divergence times and evolutionary rates while accounting for their uncertainties. We further subdivided the characters into six body regions (i.e. skull, axial skeleton, pectoral girdle and sternum, forelimb, pelvic girdle and hindlimb) to assess evolutionary rate heterogeneity both along the lineages and across partitions. We observed extremely high rates of morphological character changes during early avian evolution, and the clock rates are quite heterogeneous among the six regions. The branch subtending Pygostylia shows an extremely high rate in the axial skeleton, while the branches subtending Ornithothoraces and Enantiornithes show notably high rates in the pectoral girdle and sternum and moderately high rates in the forelimb. The extensive modifications in these body regions largely correspond to refinement of the flight capability. This study reveals the power and flexibility of Bayesian tip dating implemented in MrBayes to investigate evolutionary dynamics in deep time.
DOIPMID [本文引用: 3]

Bayesian total-evidence dating involves the simultaneous analysis of morphological data from the fossil record and morphological and sequence data from recent organisms, and it accommodates the uncertainty in the placement of fossils while dating the phylogenetic tree. Due to the flexibility of the Bayesian approach, total-evidence dating can also incorporate additional sources of information. Here, we take advantage of this and expand the analysis to include information about fossilization and sampling processes. Our work is based on the recently described fossilized birth-death (FBD) process, which has been used to model speciation, extinction, and fossilization rates that can vary over time in a piecewise manner. So far, sampling of extant and fossil taxa has been assumed to be either complete or uniformly at random, an assumption which is only valid for a minority of data sets. We therefore extend the FBD process to accommodate diversified sampling of extant taxa, which is standard practice in studies of higher-level taxa. We verify the implementation using simulations and apply it to the early radiation of Hymenoptera (wasps, ants, and bees). Previous total-evidence dating analyses of this data set were based on a simple uniform tree prior and dated the initial radiation of extant Hymenoptera to the late Carboniferous (309 Ma). The analyses using the FBD prior under diversified sampling, however, date the radiation to the Triassic and Permian (252 Ma), slightly older than the age of the oldest hymenopteran fossils. By exploring a variety of FBD model assumptions, we show that it is mainly the accommodation of diversified sampling that causes the push toward more recent divergence times. Accounting for diversified sampling thus has the potential to close the long-discussed gap between rocks and clocks. We conclude that the explicit modeling of fossilization and sampling processes can improve divergence time estimates, but only if all important model aspects, including sampling biases, are adequately addressed.©The Author(s) 2015. Published by Oxford University Press, on behalf of the Society of Systematic Biologists.
DOIPMID [本文引用: 1]

Sampling across tree space is one of the major challenges in Bayesian phylogenetic inference using Markov chain Monte Carlo (MCMC) algorithms. Standard MCMC tree moves consider small random perturbations of the topology, and select from candidate trees at random or based on the distance between the old and new topologies. MCMC algorithms using such moves tend to get trapped in tree space, making them slow in finding the globally most probable trees (known as "convergence") and in estimating the correct proportions of the different types of them (known as "mixing"). Here, we introduce a new class of moves, which propose trees based on their parsimony scores. The proposal distribution derived from the parsimony scores is a quickly computable albeit rough approximation of the conditional posterior distribution over candidate trees. We demonstrate with simulations that parsimony-guided moves correctly sample the uniform distribution of topologies from the prior. We then evaluate their performance against standard moves using six challenging empirical data sets, for which we were able to obtain accurate reference estimates of the posterior using long MCMC runs, a mix of topology proposals, and Metropolis coupling. On these data sets, ranging in size from 357 to 934 taxa and from 1740 to 5681 sites, we find that single chains using parsimony-guided moves usually converge an order of magnitude faster than chains using standard moves. They also exhibit better mixing, that is, they cover the most probable trees more quickly. Our results show that tree moves based on quick and dirty estimates of the posterior probability can significantly outperform standard moves. Future research will have to show to what extent the performance of such moves can be improved further by finding better ways of approximating the posterior probability, taking the trade-off between accuracy and speed into account. [Bayesian phylogenetic inference; MCMC; parsimony; tree proposal.].© The Author(s) 2020. Published by Oxford University Press, on behalf of the Society of Systematic Biologists.
