Yuan-Zhang Cui^,*, Wei Xu^,*School of Mathematics and Physics, China University of Geosciences, Wuhan 430074, China

First author contact: ^*Authors to whom any correspondence should be addressed.
Received:2021-05-26Revised:2021-06-16Accepted:2021-06-26Online:2021-08-16


Abstract
We present an exact three-dimensional massive Kiselev AdS black hole solution. This Kiselev black hole is neither perfectly fluid, nor is it the quintessential solution, but the BTZ black hole modified by the anisotropic matter. This black hole possesses an essential singularity at its radial origin and a single horizon whose radius will increase monotonically when the parameter of the anisotropic matter field ω decreases. We calculate all thermodynamic quantities and find that the first law of thermodynamics of this massive Kiselev AdS black hole can be protected, while the consistent Smarr formula is only held in the extended thermodynamic phase space. After examining the sign of free energy, we conclude that there is no Hawking-Page transition since the massive Kiselev AdS black hole phase is always thermodynamically favored. Moreover, we study the phase transition between the Kiselev AdS black hole and BTZ black hole by considering the matchings for their temperature. We find that the Kiselev AdS black hole is still a thermodynamically more preferred phase, because it always has a smaller amount of free energy than the BTZ black hole, which seems to indicate that the anisotropic matter field may emerge naturally in BTZ black hole spacetime under some thermal fluctuations. We also show a first order phase transition between the Kiselev AdS black hole phase with $-1\lt \omega \lt -\tfrac{1}{2}$ and the black hole phase with $-\tfrac{1}{2}\lt \omega \lt 0$. As the Kiselev AdS black hole has some notable features on the phase transition of black holes in three dimensions, it provides important clues to further investigate these both surprising and similar behaviors in four and higher dimensions.
Keywords： Kiselev black hole;black hole thermodynamics;three dimensions


PDF (415KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Yuan-Zhang Cui, Wei Xu. Three-dimensional massive Kiselev AdS black hole and its thermodynamics. Communications in Theoretical Physics, 2021, 73(10): 105401- doi:10.1088/1572-9494/ac0ed8

1. Introduction

In the present day, it is a well-established fact that black hole thermodynamics could connect gravity and quantum mechanics closely. This has been a fascinating area of theoretical investigation in recent decades, in order to explore more clues on quantum gravity and its property. In particular, black hole thermodynamics continues to be a focus area for researchers, inspired by the previous prominent discoveries, i.e. the Hawking-Page transition between thermal AdS vacuum and Schwarzschild AdS black hole in four-dimensional Einstein gravity [1]. This famous phase transition is interpreted as the confinement/deconfinement phase transition in gauge theory [2] inspired by the AdS/CFT correspondence [3–5]. The research of black hole thermodynamics has been greatly improved because of this pioneering work by Hawking-Page.

This paper will focus on the Kiselev black hole solution and its thermodynamics. The Kiselev black hole is an extremely popular toy model [6], which has accumulated over 300 citations, with most of the citing articles being published. Originally, the Kiselev black hole solution was used to explain the spacetime surrounded by quintessence dark energy [7]. The matter field of the Kiselev black hole has an equation of state $\bar{p}=\omega \rho $, where $\bar{p}$ is the average pressure, ρ is the energy density and ω is the state parameter, hence it seems that the Kiselev black hole reflects some features about the spacetime surrounded by quintessence dark energy, in a sense. Recently Matt Visser pointed out that, the Kiselev black hole is neither perfect fluid, nor is it quintessence [8], while it is actually a spacetime surrounded by anisotropic matter field. The anisotropy of the stress-energy supporting the Kiselev black hole is discussed in detail in [9]. Despite this terminological issue, the Kiselev black hole does have some interesting physical and mathematical properties. Besides, the Kiselev black hole has a great generality, since the w=0 limit of former corresponds to the Schwarzschild black hole, its $w=\tfrac{1}{3}$ limit reduces to the Reissner-Nordstrom black hole, and its w=−1 limit corresponds to the Schwarzschild-(A)dS black hole. Therefore the Kiselev black hole could be used as a useful theoretical laboratory for studying black hole physics. Recently, it was found that, the anisotropic matter field in the Kiselev black hole spacetime changes no matter the spacetime structure of black hole [6, 10–17], but also black hole thermodynamics [17–26], which has consequently attracted considerable interest [6, 10–29].

The main purpose of this paper is generalizing the discussion to three dimensions, studying the Kiselev black hole solution and thermodynamics in (2+1) dimensions. It is often much easier to obtain black hole solutions and analyze their thermodynamics in three dimensions than in four and other dimensions. Initiated in the early 1980s, gravity in (2+1)-dimensional spacetime has been a stirring topics of gravitational physics. Especially the discovery of the Banados-Teitelboim-Zanelli (BTZ) black hole [30] led to an increased interest in three-dimensional gravity, not only because black hole solutions exist, but also because such theories are ideal theoretical laboratories for studying AdS/CFT [31–35]. Besides, the study of the three-dimensional massive Kiselev AdS black hole solution and its thermodynamics, is also expected to shed some lights on the understanding of more realistic or complicated cases of four-dimensional gravities, and a further understanding of the relationship between anisotropic matter and black holes. Moreover, considering black hole thermodynamics and phase transitions of the BTZ black hole modified by anisotropic matter, could also improve the understanding of the quantum and holographic properties of gravity, and induce many applications about the mutual study on particle physics [31, 32] and the condensed-matter theory [33–35] in the spirit of the AdS/CFT correspondence.

Actually, three-dimensional massive Kiselev AdS black hole solution is neither perfect fluid, nor is it quintessence, which is consistent with the case in four dimensions. It just corresponds to the BTZ black hole surrounded by an anisotropic matter field. On the other hand, it is shown that, the parameter ω of anisotropic matter field brings a notable effect on the spacetime structure and black hole thermodynamics in three dimensions, especially for the phase transitions. It is found that the spacetime of BTZ solution is greatly modified by anisotropic matter, where an essential singularity at r=0 emerges and there is a single horizon with its radius increasing monotonically when ω decreases from 0 to −1. There is no Hawking-Page transition, since the free energy of BTZ black hole modified by anisotropic matter is negative, which indicates that the Kiselev black hole phase is always thermodynamically favored. Beside, a possible phase transition between the massive Kiselev AdS black hole and BTZ black hole could be arisen under some thermal fluctuations. After considering the matchings for black hole temperature, we show that the massive Kiselev AdS black hole is a thermodynamically more preferred phase, since it always has smaller free energy than the BTZ black hole. We also find an unexpected first order phase transition between the Kiselev AdS black hole phase with $-1\lt \omega \lt -\tfrac{1}{2}$ and the Kiselev AdS black hole phase with $-\tfrac{1}{2}\lt \omega \lt 0$. One can expect that a natural generalization for these phase transitions between the four-dimensional Kiselev AdS black hole and Schwarzschild AdS black hole may exist.

The paper is organized as follows. In section 2, we will present the three-dimensional massive Kiselev AdS black hole solution. In section 3, we obtain thermodynamics of this black hole, including the thermodynamical quantities and laws. In section 4, we discuss the phase transitions between this three-dimensional Kiselev AdS black hole and BTZ black hole. Finally some concluding remarks are given in section 5.

2. Three-dimensional massive Kiselev AdS black hole solution

We begin with the metric ansatz for a black hole solution in three dimensions(1)$\begin{eqnarray}{\rm{d}}{s}^{2}=-f(r){\rm{d}}{t}^{2}+\displaystyle \frac{1}{f(r)}{\rm{d}}{r}^{2}+{r}^{2}{\rm{d}}{\psi }^{2}.\end{eqnarray}$Einstein's field equations in three-dimensional AdS spacetime with non-vanishing matter field should be(2)$\begin{eqnarray}{R}_{\mu \nu }-\displaystyle \frac{1}{2}{g}_{\mu \nu }R+{\rm{\Lambda }}{g}_{\mu \nu }=8\pi {T}_{\mu \nu },\end{eqnarray}$where ${\rm{\Lambda }}=-\tfrac{1}{{{\ell }}^{2}}$ is the cosmological constant. T_μν is the energy-momentum tensor for the matter field. The massless Kiselev AdS black hole in three dimensions was presented in [11, 27], for which the metric function takes the form $f(r)=\tfrac{{r}^{2}}{{{\ell }}^{2}}-\tfrac{a}{{r}^{2\omega }}$. Here a is related to the energy density ρ for the matter field, which can be described by $\rho =-\tfrac{a\omega }{{r}^{2(\omega +1)}}$. It is well known that the black hole mass in three dimensions corresponds to the constant term of f(r) in the above metric ansatz equation (1) (See it in next section.). Hence, we can directly obtain the metric function for the three-dimensional massive Kiselev AdS solution, i.e.(3)$\begin{eqnarray}f(r)=-M+\displaystyle \frac{{r}^{2}}{{{\ell }}^{2}}-\displaystyle \frac{a}{{r}^{2\omega }},\end{eqnarray}$where M is the black hole mass as calculated in next section.

Then substituting the above equation into Einstein's field equations, it is easy to derive(4)$\begin{eqnarray}{T}_{t}{}^{t}=-{T}_{r}{}^{r}=\rho =-{p}_{r},\quad {T}_{\psi }{}^{\psi }=(2\omega +1)\rho ={p}_{t}.\end{eqnarray}$For the average pressure, one can obtain $\bar{p}=\tfrac{{p}_{t}+{p}_{r}}{2}=\omega \rho $. However, such an average pressure can always be defined, other than refer in particular to the spacetime surrounded by quintessence. Indeed, for the pressure ratio and relative pressure anisotropy, we have(5)$\begin{eqnarray}\displaystyle \frac{{p}_{t}}{{p}_{r}}=-(2\omega +1),{\rm{\Delta }}=\displaystyle \frac{{\rm{\Delta }}p}{\bar{p}}=\displaystyle \frac{{p}_{r}-{p}_{t}}{\bar{p}}=-\displaystyle \frac{2(\omega +1)}{\omega }.\end{eqnarray}$The matter field is distinctly not isotropic when $\omega \ne -1$¹(¹The case with ω=−1 is just the BTZ black hole with an un-renormalized cosmological constant.), so it is not a perfect fluid. Therefore the three-dimensional massive Kiselev black hole does characterize the BTZ black hole surrounded by anisotropic matter. This is consistent with the case of the Kiselev black hole in four dimensions [8, 9].

Since the energy density should be positive, it results in aω<0. Without loss of generality, we choose a>0. Then the parameter ω<0 is needed. As shown later, the solution equations (1), (3) describes the three-dimensional massive Kiselev AdS black hole solution. In particular, this solution with a=0 reduces to the well known BTZ black hole [30]. For the parameter ω, since the asymptotic AdS solution requires that $\tfrac{{r}^{2}}{{{\ell }}^{2}}$ should be the leading term of f(r) at the $r\to +\infty $ limit, there exists an additional constraint −2ω<2, namely, −1<ω<0. Noting that the limit ω=0 corresponds to the BTZ black hole with an un-renormalized black hole mass, and the limit ω=−1 corresponds to the BTZ black hole with an un-renormalized cosmological constant. This is consistent with the discussion about the energy conditions. One can get that(6)$\begin{eqnarray}\begin{array}{rcl}\rho +{p}_{r} & = & 0,\quad \rho +{p}_{t}=2(\omega +1)\rho ,\\ \rho +{p}_{t}+{p}_{r} & = & {p}_{t}=(2\omega +1)\rho .\end{array}\end{eqnarray}$For the case discussed in this paper, i.e.(7)$\begin{eqnarray}a\gt 0,-1\lt \omega \lt 0,\end{eqnarray}$the null energy condition and the weak energy condition are both satisfied, while the strong energy condition leads to a stronger constraint $-\tfrac{1}{2}\lt \omega \lt 0$.

Now we present the Ricci scalar as an example of the geometric quantities of this solution(8)$\begin{eqnarray}R=-\displaystyle \frac{6}{{{\ell }}^{2}}+\displaystyle \frac{2a\omega (2\omega -1)}{{r}^{2(1+\omega )}},\end{eqnarray}$which shows that the solution under the condition equation (7) has an essential singularity at r=0 whenever $a\ne 0$. As we are interested in black hole solutions, this solution needs to contain one event horizon to surround the singularity. We consider the metric function equation (3) to study the horizon structure. After a little calculation, one can find that there is a zero point for f′(r), which corresponds to a minimum of f(r). This indicates that f(r) will decrease from f(0)=−M to a minimum, and then increase to $f(+\infty )=+\infty $ in the region r>0, which replies that the curve for f(r) will cross the horizontal axes one time, corresponding to a single horizon, i.e. the event horizon r=r₊. One can see figure 1 for a clear understanding about the horizon structure. From figure 1, one can also find that the radius of the event horizon r₊ will increase monotonically when ω decreases from 0 to −1.

Figure 1.

New window|Download| PPT slide
Figure 1.Horizon structure for the three-dimensional massive Kiselev AdS black holes with different ω. The solid curve denotes the BTZ black hole case with ω=0. The values of ω for the curves decrease from left to right in the first quadrant.

3. Thermodynamics of three-dimensional massive Kiselev AdS black hole

For this Kiselev AdS black hole, the mass can be calculated by adopting the Brown-York method [36]. One can find the quasilocal mass m(r) at r taking the form [36–38] $m(r)=\sqrt{f(r)}E(r),$ where $E(r)=2(\sqrt{{f}_{0}(r)}-\sqrt{f(r)})$ is the quasilocal energy at r, and ${f}_{0}(r)=\tfrac{{r}^{2}}{{{\ell }}^{2}}$ corresponds to a background metric function (i.e. the massless BTZ spacetime) that determines the zero of the energy. As a result, one can take the following limit to obtain the black hole mass: ${\mathrm{lim}}_{r\to \infty }m(r)=M$. Since f(r₊)=0, from equation (3) we can derive another form of the black hole mass, i.e.(9)$\begin{eqnarray}M=\displaystyle \frac{{r}_{+}^{2}}{{{\ell }}^{2}}-\displaystyle \frac{a}{{r}_{+}^{2\omega }}.\end{eqnarray}$

The black hole entropy follows the area law and should be(10)$\begin{eqnarray}S=\displaystyle \frac{{A}_{H}}{4G}=4\pi {r}_{+},\end{eqnarray}$where A_H is the area of the event horizon. The temperature of this three-dimensional massive Kiselev AdS black hole can be derived as(11)$\begin{eqnarray}T=\displaystyle \frac{{f}^{{\prime} }({r}_{+})}{4\pi }=\displaystyle \frac{{r}_{+}}{2\pi }\left(\displaystyle \frac{1}{{{\ell }}^{2}}+\displaystyle \frac{a\omega }{{r}_{+}^{2(\omega +1)}}\right).\end{eqnarray}$For $T\geqslant 0$, we can obtain a lower bound for the radius of the Kiselev AdS black hole(12)$\begin{eqnarray}{r}_{+}\geqslant {r}_{{\rm{ex}}},\quad {r}_{{\rm{ex}}}^{2(\omega +1)}=-a\omega {{\ell }}^{2},\end{eqnarray}$where r_ex denotes the horizon of the extremal black hole. After combining these quantities, M, T, and S, we can verify that the first law of thermodynamics(13)$\begin{eqnarray}{\rm{d}}M=T{\rm{d}}S,\end{eqnarray}$holds. For the Smarr formula, we give an additional discussion in the appendix since the main aim of this paper is the thermodynamics and phase transitions of the massive Kiselev AdS black hole in the non-extended thermodynamic phase space.

In the rest of this paper, in order to study the global thermodynamic stability and phase transitions of the three-dimensional massive Kiselev AdS black hole, it is necessary to work with the free energy(14)$\begin{eqnarray}F=M-{TS}=-\displaystyle \frac{{r}_{+}^{2}}{{{\ell }}^{2}}-\displaystyle \frac{(2\omega +1)a}{{r}_{+}^{2\omega }}.\end{eqnarray}$Then we focus on the existence of the Hawking-Page transition, which means that the case with a negative F should be regarded as the Kiselev AdS black hole solution being thermodynamically favored over the background spacetime; and the case with vanishing F just corresponds to the famous Hawking-Page transition point, which characterizes the phase transition between the Kiselev AdS black hole phase and the background spacetime phase.

From equation (14), it is clear that for black holes with $-\tfrac{1}{2}\lt \omega \lt 0$, the free energies are always negative; while the free energies have zero for black holes with $-1\lt \omega \lt -\tfrac{1}{2}$. This seems to suggest the existence of the Hawking-Page transition of three-dimensional massive Kiselev AdS black hole. However, we depict the free energies for the Kiselev AdS black holes with different ω in figure 2, which always shows some negative free energies. In fact, this can be understood naturally as the zero free energy phase for black holes with $-1\lt \omega \lt -\tfrac{1}{2}$ corresponds to a negative temperature which is unacceptable physically. Now we derive directly the sign of free energies for massive Kiselev AdS black holes with different ω∈(−1, 0). The free energy can be rewritten as $F=-{r}_{+}^{-2\omega }\left(\tfrac{{r}_{+}^{2(\omega +1)}}{{{\ell }}^{2}}+(2\omega +1)a\right).$ From equation (12), we can obtain $\left(\tfrac{{r}_{+}^{2(\omega +1)}}{{{\ell }}^{2}}+(2\omega +1)a\right)$ $\gt \tfrac{-a\omega {{\ell }}^{2}}{{{\ell }}^{2}}$ + $(2\omega +1)a=a(\omega +1)\gt 0$, hence F<0 for Kiselev black holes with ω∈(−1, 0). Finally, we can conclude that the free energy of three-dimensional massive Kiselev AdS black hole is always negative; this Kiselev AdS black hole is thermodynamically favored over the background spacetime and there is no Hawking-Page transition.

Figure 2.

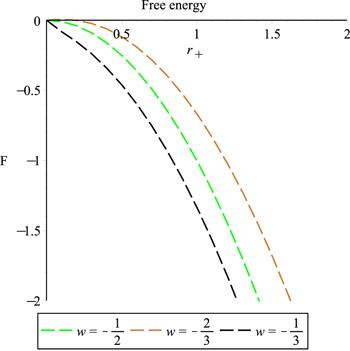New window|Download| PPT slide
Figure 2.Free energies for three-dimensional Kiselev AdS black holes with different ω. For the curves of free energy, the values of ω decrease from left to right.

4. Phase transitions between three-dimensional Kiselev AdS black hole and BTZ black hole

In this section, we compare the free energies for a three-dimensional Kiselev AdS black hole and the BTZ black hole, in order to find the more stable one. In the vanishing-matter limit, i.e. $a\to 0$, the Einstein equations equation (2) admit the BTZ black hole [30]$\begin{eqnarray*}{\rm{d}}{s}^{2}=-\left(-\hat{M}+\displaystyle \frac{{\hat{r}}^{2}}{{{\ell }}^{2}}\right){\rm{d}}{t}^{2}+\displaystyle \frac{1}{\left(-\hat{M}+\tfrac{{\hat{r}}^{2}}{{{\ell }}^{2}}\right)}{\rm{d}}{\hat{r}}^{2}+{\hat{r}}^{2}{\rm{d}}{\psi }^{2}.\end{eqnarray*}$Then the thermodynamic quantities of the BTZ black hole are given by(15)$\begin{eqnarray}\hat{M}=\displaystyle \frac{{\hat{r}}_{+}^{2}}{{{\ell }}^{2}},\quad \hat{S}=4\pi {\hat{r}}_{+},\ \ \hat{T}=\displaystyle \frac{{\hat{r}}_{+}}{2\pi {{\ell }}^{2}},\quad \hat{F}=-\displaystyle \frac{{\hat{r}}_{+}^{2}}{{{\ell }}^{2}}.\end{eqnarray}$

To compare the free energies of the BTZ black hole and the Kiselev black hole, we need to match the temperature $\hat{T}=T$ of these two black holes, i.e.(16)$\begin{eqnarray}\displaystyle \frac{{\hat{r}}_{+}}{2\pi {{\ell }}^{2}}=\displaystyle \frac{{r}_{+}}{2\pi }\left(\displaystyle \frac{1}{{{\ell }}^{2}}+\displaystyle \frac{a\omega }{{r}_{+}^{2(\omega +1)}}\right).\end{eqnarray}$In figure 3, we plot the free energies F of BTZ black hole and three-dimensional Kiselev AdS black holes with different values of ω. We find that the free energies F of the three-dimensional Kiselev AdS black holes are always smaller than that of the BTZ black hole when T>0.

Figure 3.

New window|Download| PPT slide
Figure 3.F–T diagram for three-dimensional Kiselev AdS black holes with different ω. The values of ω for the curves decrease from left to right. The red solid curve corresponds to the BTZ case.


Then we derive the above result analytically and directly. It is easy to obtain the free energy $\hat{F}(\hat{T})$ of the BTZ black hole as a function of the temperature $\hat{T}$, i.e.(17)$\begin{eqnarray}\hat{F}=-4{\pi }^{2}{{\ell }}^{2}{\hat{T}}^{2}=-4{\pi }^{2}{{\ell }}^{2}{T}^{2},\end{eqnarray}$where the temperature $\hat{T}=T$ of black holes are matched. After inserting equations (11), (14) and equation (17), we can compare the free energies of the BTZ black hole and Kiselev black hole(18)$\begin{eqnarray}\bigtriangleup F\equiv \hat{F}-F=\displaystyle \frac{a}{{r}_{+}^{2\omega }}-\displaystyle \frac{{a}^{2}{{\ell }}^{2}{\omega }^{2}}{{r}_{+}^{4\omega +2}}.\end{eqnarray}$To find the sign of $\bigtriangleup F$, we introduce its derivative(19)$\begin{eqnarray}\bigtriangleup {F}^{{\prime} }({r}_{+})=\displaystyle \frac{2(2\omega +1){a}^{2}{{\ell }}^{2}{\omega }^{2}}{{r}_{+}^{4\omega +3}}-\displaystyle \frac{2a\omega }{{r}_{+}^{2\omega +1}}.\end{eqnarray}$Hence the discussion is divided into two cases:• When $-\tfrac{1}{2}\leqslant \omega \lt 0$, since $\bigtriangleup {F}^{{\prime} }({r}_{+})\gt 0$, $\bigtriangleup F$ will increase monotonically in the region r₊>r_ex. As a result,(20)$\begin{eqnarray}\bigtriangleup F\gt \bigtriangleup F{| }_{{r}_{+}={r}_{{\rm{ex}}}}=\displaystyle \frac{a({\omega }_{1}+1)}{{r}_{+}^{2\omega }}\gt 0.\end{eqnarray}$Now we can conclude that $\hat{F}\gt F$ for Kiselev AdS black holes with $-\tfrac{1}{2}\leqslant \omega \lt 0$.
• When $-1\lt \omega \lt -\tfrac{1}{2}$, we can find that $\bigtriangleup {F}^{{\prime} }({r}_{+})$ has a single zero point located at ${r}_{+}={r}_{0},{r}_{0}^{2({\omega }_{q}+1)}=(2{\omega }_{q}+1)a{\omega }_{q}{{\ell }}^{2}$, which corresponds to the minimum of $\bigtriangleup F$; and when r₊>r₀, the value of $\bigtriangleup F$ also increases monotonically. Since r₊>r_ex>r₀, one can find again that $\bigtriangleup F\gt \bigtriangleup F{| }_{{r}_{+}={r}_{{\rm{ex}}}}\gt 0$, and $\hat{F}\gt F$ for Kiselev AdS black holes with $-1\lt \omega \lt -\tfrac{1}{2}$.


Now it is clear that $\hat{F}\gt F$ when ω∈(−1, 0), i.e. the free energies of the Kiselev AdS black holes are really always smaller than that of BTZ black hole. The relationship between the free energies of the BTZ black hole and the three-dimensional Kiselev AdS black hole is not affected by the values of the parameter ω∈(−1, 0) of the anisotropic matter. This means that the three-dimensional massive Kiselev AdS black hole is more thermodynamically preferred. A possible thermodynamical phase transition for the BTZ black hole becoming the Kiselev black hole exists, provided that there are some thermal fluctuations. This indicates that, in the thermodynamic frame, the anisotropic matter field seems to emerge naturally in the BTZ black hole spacetime under some thermal fluctuations. This is different from the cases in the BTZ black hole spacetime modified by other matter fields. For example, it is found that the BTZ black hole always has smaller free energy than the three-dimensional scalar black hole, indicating the BTZ black hole is a thermodynamically more preferred phase [39].

Finally, for massive Kiselev AdS black holes with ω∈(−1, 0), it is also interesting to study: which black hole phase with ω is more thermodynamically preferred? We match the temperature of the Kiselev AdS black holes with different ω as well, and plot their F–T diagrams in figure 4. In this figure, ω of curves increase from up to down at low temperature; while ω of curves decrease from up to down at high temperature. One can find that the Kiselev AdS black hole phase with $-\tfrac{1}{2}\lt \omega \lt 0$ has smaller free energy and is more thermodynamic stable globally when the temperature is low, while the Kiselev AdS black hole phase with $-1\lt \omega \lt -\tfrac{1}{2}$ has smaller free energy and is more thermodynamic stable globally when the temperature is high. The Kiselev AdS black hole phase with $\omega =-\tfrac{1}{2}$ always has bigger free energy and is not thermodynamic stable globally no matter whether the temperature is low or high. At the medium temperature, a possible phase transition between the Kiselev AdS black holes with different ω exists. It seems that when the temperature increases, the Kiselev AdS black hole phase with $-\tfrac{1}{2}\lt \omega \lt 0$ changes into the Kiselev AdS black hole phase with $-1\lt \omega \lt -\tfrac{1}{2}$ under a first order phase transition. However, it is difficult to discuss the phase diagram of this first order phase transition, since the function F(T) for Kiselev AdS black holes with different ω have very complicated forms.

Figure 4.

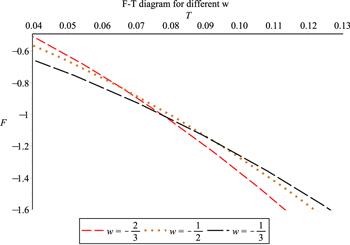New window|Download| PPT slide
Figure 4.Phase transition between three-dimensional massive Kiselev AdS black holes with different ω.

5. Conclusion

In this paper, we present the three-dimensional massive Kiselev AdS black hole solution with the parameter ω∈(−1, 0). It is stated that this black hole is neither perfect fluid, nor is it quintessence, but just the BTZ solution modified by anisotropic matter. After examining the geometric quantities of this solution, it is found that an essential singularity at r=0 exists. We also studied the horizon structure of the Kiselev solution, and found an event horizon whose radius will increase monotonically when ω decreases from 0 to −1. Then we studied the thermodynamics of the massive Kiselev AdS black hole in three dimensions, gave the thermodynamic quantities, including the black hole mass, entropy, temperature and others, and found that the first law of thermodynamics of this massive Kiselev AdS black hole can be protected, while the consistent Smarr formula is only held in the extended thermodynamic phase space. We also disclosed that there is no Hawking-Page transition between the massive Kiselev AdS black hole and the background spacetime. Since the free energy of three-dimensional Kiselev AdS black hole is negative, the black hole phase is always thermodynamically favored.

On the other hand, we found that a possible phase transition between the massive Kiselev AdS black hole and BTZ black hole under some thermal fluctuations exists. Considering the matchings for the temperature, we find that the massive Kiselev AdS black hole is a thermodynamically more preferred phase, since it always has smaller free energy than the BTZ black hole. In this sense, we argued that, in the thermodynamic frame, the anisotropic matter seems to emerge naturally in the BTZ black hole spacetime under some thermal fluctuations. Moreover, we discussed which black hole phase with different ω is more thermodynamically preferred. After comparing their free energies in the F–T diagram, it shows that when the temperature increases, the Kiselev AdS black hole phase with $-\tfrac{1}{2}\lt \omega \lt 0$ changes into the Kiselev AdS black hole phase with $-1\lt \omega \lt -\tfrac{1}{2}$ under a first order phase transition.

In conclusion, the Kiselev black hole contains some notable features on the black hole thermodynamics in three dimensions, especially for the phase transition. Hence it would be of great importance to investigate the theoretical properties and thermodynamics of the Kiselev black holes. Besides, since the properties of three-dimensional black holes are found always to be similar to those of four-dimensional solutions, it is a natural generalization to explore the phase transitions between the four-dimensional Kiselev AdS black hole and the Schwarzschild black hole. This is left to a future task.

Acknowledgments

Wei Xu was supported by the National Natural Science Foundation of China (NSFC) and the Fundamental Research Funds for the Central Universities, China University of Geosciences (Wuhan).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Hawking S W Page D N 1983 Commun. Math. Phys. 87 577
DOI:10.1007/BF01208266 [Cited within: 1]

[2]Witten E 1998 Adv. Theor. Math. Phys. 2 505
DOI:10.4310/ATMP.1998.v2.n3.a3 [Cited within: 1]

[3]Maldacen J M 1998 Adv. Theor. Math. Phys. 2 231
DOI:10.4310/ATMP.1998.v2.n2.a1 [Cited within: 1]

[4]Gubser S S Klebanov I R Polyakov A M 1998 Phys. Lett. B 428 105
DOI:10.1016/S0370-2693(98)00377-3

[5]Witten E 1998 Adv. Theor. Math. Phys. 2 253
DOI:10.4310/ATMP.1998.v2.n2.a2 [Cited within: 1]

[6]Kiselev V V 2003 Class. Quant. Grav. 20 1187
DOI:10.1088/0264-9381/20/6/310 [Cited within: 3]

[7]Copeland E J Sami M Tsujikawa S 2006 Int. J. Mod. Phys. D 15 1753
DOI:10.1142/S021827180600942X [Cited within: 1]

[8]Visser M 2020 Class. Quant. Grav. 37 045001
DOI:10.1088/1361-6382/ab60b8 [Cited within: 2]

[9]Boonserm P Ngampitipan T Simpson A Visser M 2020 Phys. Rev. D 101 024022
DOI:10.1103/PhysRevD.101.024022 [Cited within: 2]

[10]de J Toledo M Bezerra V B 2018 Eur. Phys. J. C 78 534
DOI:10.1140/epjc/s10052-018-6001-z [Cited within: 2]

[11]de Oliveira J Fontana R D B 2018 Phys. Rev. D 98 044005
DOI:10.1103/PhysRevD.98.044005 [Cited within: 1]

[12]Ghosh S G Maharaj S D Baboolal D Lee T H 2018 Eur. Phys. J. C 78 90
DOI:10.1140/epjc/s10052-018-5570-1

[13]Ghosh S G Amir M Maharaj S D 2017 Eur. Phys. J. C 77 530
DOI:10.1140/epjc/s10052-017-5099-8

[14]Xu Z Wang J 2017 Phys. Rev. D 95 064015
DOI:10.1103/PhysRevD.95.064015

[15]Ghosh S G 2016 Eur. Phys. J. C 76 222
DOI:10.1140/epjc/s10052-016-4051-7

[16]Belhaj A El Balali A El Hadri W El Moumni H Sedra M B 2019 Eur. Phys. J. Plus 134 422
DOI:10.1140/epjp/i2019-12803-y

[17]Wang Y Wu C H Yue R H 2019 Sci. China Phys. Mech. Astron. 62 110411
DOI:10.1007/s11433-019-9382-0 [Cited within: 2]

[18]Chen S Wang B Su R 2008 Phys. Rev. D 77 124011
DOI:10.1103/PhysRevD.77.124011

[19]Thomas B B Saleh M Kofane T C 2012 Gen. Rel. Grav. 44 2181
DOI:10.1007/s10714-012-1382-z

[20]Azreg-Aïnou M Rodrigues M E 2013 J. High Energy Phys.JHEP09 (2013) 146


[21]Li G Q 2014 Phys. Lett. B 735 256
DOI:10.1016/j.physletb.2014.06.047

[22]Xu W Wu Y 2018 EPL 121 40001
DOI:10.1209/0295-5075/121/40001

[23]Ghaderi K Malakolkalam B 2016 Astrophys. Space Sci. 361 161
DOI:10.1007/s10509-016-2744-x

[24]Ghaderi K Malakolkalami B 2016 Nucl. Phys. B 903 10
DOI:10.1016/j.nuclphysb.2015.11.019

[25]Liu H Meng X H 2017 Eur. Phys. J. C 77 556
DOI:10.1140/epjc/s10052-017-5134-9

[26]Wu Y Xu W 2020 Phys. Dark Univ. 27 100470
DOI:10.1016/j.dark.2020.100470 [Cited within: 1]

[27]Chen S Pan Q Jing J 2013 Class. Quant. Grav. 30 145001
DOI:10.1088/0264-9381/30/14/145001 [Cited within: 1]

[28]Khan S U Ren J 2020 Phys. Dark Univ. 30 100644
DOI:10.1016/j.dark.2020.100644

[29]Zeng X X Zhang H Q 2020 Eur. Phys. J. C 80 1058
DOI:10.1140/epjc/s10052-020-08656-7 [Cited within: 1]

[30]Banados M Teitelboim C Zanelli J 1992 Phys. Rev. Lett. 69 1849
DOI:10.1103/PhysRevLett.69.1849 [Cited within: 3]

[31]Erlich J Katz E Son D T Stephanov M A 2005 Phys. Rev. Lett. 95 261602
DOI:10.1103/PhysRevLett.95.261602 [Cited within: 2]

[32]Karch A Katz E Son D T Stephanov M A 2006 Phys. Rev. D 74 015005
DOI:10.1103/PhysRevD.74.015005 [Cited within: 1]

[33]Kovtun P Son D T Starinets A O 2005 Phys. Rev. Lett. 94 111601
DOI:10.1103/PhysRevLett.94.111601 [Cited within: 1]

[34]Hartnoll S A Herzog C P Horowitz G T 2008 Phys. Rev. Lett. 101 031601
DOI:10.1103/PhysRevLett.101.031601

[35]Hartnoll S A 2009 Class. Quant. Grav. 26 224002
DOI:10.1088/0264-9381/26/22/224002 [Cited within: 2]

[36]Brown J D York J WJr. 1993 Phys. Rev. D 47 1407
DOI:10.1103/PhysRevD.47.1407 [Cited within: 2]

[37]Brown J D Creighton J Mann R B 1994 Phys. Rev. D 50 6394
DOI:10.1103/PhysRevD.50.6394

[38]Creighton J D E Mann R B 1995 Phys. Rev. D 52 4569
DOI:10.1103/PhysRevD.52.4569 [Cited within: 1]

[39]Zou D C Liu Y Wang B Xu W 2014 Phys. Rev. D 90 104035
DOI:10.1103/PhysRevD.90.104035 [Cited within: 1]

[40]Dolan B P 2011 Class. Quant. Grav. 28 235017
DOI:10.1088/0264-9381/28/23/235017 [Cited within: 1]

[41]Cvetic M Gibbons G W Kubiznak D Pope C N 2011 Phys. Rev. D 84 024037
DOI:10.1103/PhysRevD.84.024037

[42]Dolan B P Kastor D Kubiznak D Mann R B Traschen J 2013 Phys. Rev. D 87 104017
DOI:10.1103/PhysRevD.87.104017

[43]Kastor D Ray S Traschen J 2010 Class. Quant. Grav. 27 235014
DOI:10.1088/0264-9381/27/23/235014 [Cited within: 1]

[44]Castro A Dehmami N Giribet G Kastor D 2013 J. High Energy Phys.JHEP07 (2013) 164


[45]Mahmoud El-Menoufi B Ett B Kastor D Traschen J 2013 Class. Quant. Grav. 30 155003
DOI:10.1088/0264-9381/30/15/155003 [Cited within: 1]

[46]Kastor D Ray S Traschen J 2009 Class. Quant. Grav. 26 195011
DOI:10.1088/0264-9381/26/19/195011 [Cited within: 2]

[47]Altamirano N Kubiznak D Mann R B Sherkatghanad Z 2014 Galaxies 2 89
DOI:10.3390/galaxies2010089 [Cited within: 1]

[48]Kubiznak D Mann R B Teo M 2017 Class. Quant. Grav. 34 063001
DOI:10.1088/1361-6382/aa5c69 [Cited within: 1]

[49]Xu W Wang C Y Zhu B 2019 Phys. Rev. D 99 044010
DOI:10.1103/PhysRevD.99.044010 [Cited within: 1]

[50]Wang Y Y Su B Y Li N 2021 Phys. Dark Univ. 31 100769
DOI:10.1016/j.dark.2020.100769

[51]Su B Y Wang Y Y Li N 2020 Eur. Phys. J. C 80 305
DOI:10.1140/epjc/s10052-020-7870-5 [Cited within: 1]