Hang Zhou, Ning Liu^,Physics Department and Institute of Theoretical Physics, Nanjing Normal University, Nanjing, 210023, China

Received:2020-04-13Revised:2020-05-12Accepted:2020-05-27Online:2020-09-16


Abstract
The standard model is a successful theory but is lacking a mechanism for neutrino mass generation as well as a solution to the naturalness problem. In the models that are proposed to simultaneously solve the two problems, heavy Majorana neutrinos and top partners are usually predicted to lead to a new decay mode of the top partner mediated by the heavy Majorana neutrinos: $T\to b\,{W}^{+}\to b\,{{\ell }}^{+}{{\ell }}^{+}q\bar{q^{\prime} }$. In this paper, we will study the observability of such a new signature via the pair production process of a top partner ${pp}\to T\bar{T}\to 2b+{{\ell }}^{\pm }{{\ell }}^{\pm }+4j$ in a model independent way. By performing Monte Carlo simulations, we present the 2σ exclusion limits of the top partner mass and mixing parameters at the HL-LHC.
Keywords： top quark partner;LHC;same sign leptons


PDF (600KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Hang Zhou, Ning Liu. Probing vector-like top partner from same-sign dilepton events at the LHC. Communications in Theoretical Physics, 2020, 72(10): 105201- doi:10.1088/1572-9494/aba245

1. Introduction

The standard model (SM) has been a successful low-energy effective theory in describing microscopic phenomena and was completed by the discovery of the Higgs boson in 2012 at the LHC. However, a theory beyond the SM (BSM) is necessary from both theoretical and experimental points of view, one of which is the so-called naturalness problem. With the mass of the observed scalar (∼125 GeV) being comparable to the electroweak scale (∼10² GeV), the naturalness arguments require some mechanism or symmetries to suppress or cancel out the large quadratic divergence when considering loop corrections from heavy particles, such as the SM top quark, which can lead the Higgs mass up to the Planck scale (∼10¹⁹ GeV) instead of the electroweak one. Many BSM models, such as the little Higgs models [1, 2] and composite Higgs models [3-6], have been proposed to solve this problem by introducing a spontaneously broken global symmetry, leading the Higgs boson to be a pseudo Goldstone boson. In these BSM models, vector-like top partners (VLTs), usually referred to as T, are predicted. VLTs are color-triplet fermions but with the left- and right-handed components transforming in the same way under the gauge group SU(2)⨂U(1). These new particles have been searched for at hadron colliders, where they can be produced both singly and in pairs, with subsequent decays into an SM quark and a gauge boson or Higgs boson [7-16]. Searches at the LHC for VLTs have been performed and presented by the ATLAS and CMS collaborations with the lower mass bounds on T reaching up to about $740\sim 1370\,\mathrm{GeV}$, depending on the SU(2) multiplets they belong to and different branching fractions assumed [17, 18].

Another motivation for BSM is the observation of neutrino oscillation in solar, atmospheric, reactor and accelerator experiments, which implies that neutrinos of three flavors are mixed and have tiny masses (∼sub-eV) [19]. Various schemes have been proposed to include neutrino masses in the SM, among which the most popular one is the so-called seesaw mechanism [20-30], since it not only generates neutrino mass in an elegant way, but also connects the observed baryon asymmetry in the Universe (BAU) and the origin of neutrino mass through leptogenesis [31-41]. Some variations of the seesaw mechanism can also accommodate dark matter candidates [42-45]. Among several seesaw mechanisms, the type-I seesaw [20-23] in a straightforward way introduces three singlet right-handed (RH) neutrinos (N_Rα), leading to Dirac mass terms as well as the RH Majorana mass terms. Consideration of both mass terms can generate sub-eV Majorana neutrino masses if the RH Majorana mass is set at ∼10¹⁴ GeV. Neutrino mass generation via the seesaw mechanism comes with violation of lepton number (LNV) by Δ L=2, which may be used on experiments as a sign for the Majorana nature of neutrinos. Many experiments and tests on the nature and properties of neutrinos are already in progress, such as the search for neutrinoless double beta decay (0νββ) [46, 47], as well as other LNV processes including rare τ decays, meson decays and hyperon decays [48-53]. However, the Δ L=2 processes are suppressed either by a factor of ${m}_{\nu }^{2}/{m}_{W}^{2}$ due to the smallness of the light neutrino mass m_ν, or by a factor of $| {V}_{\alpha m}{V}_{\beta m}{| }^{2}$ due to the small mixings, depending on whether the exchanged neutrino is light or heavy compared to the scale of the LNV processes [54]. Fortunately, the LNV processes may be enhanced substantially as a result of resonant production of heavy neutrinos, if the heavy neutrino mass can be kinematically accessible (below TeV) as in some low-scale type-I seesaw scenarios [55-64], which may be produced directly at collider experiments and searched for [54, 65-75]. An upper bound has been given by the LEP experiments on the mixings $| {V}_{{eN},\mu N}{| }^{2}\lt { \mathcal O }({10}^{-5})$ for a heavy neutrino mass of (80, 205) GeV [76]. CMS broadened the mass range to (20, 1600) GeV and put a similar limit as $| {V}_{{eN},\mu N}{| }^{2}\lt { \mathcal O }({10}^{-5})$ [77, 78].

To solve the above two problems of naturalness and neutrino oscillation, models have been proposed to incorporate neutrino masses into some scenarios with the VLTs, such as ones that include lepton-number violation between the scalar triplet and lepton doublet within the Littlest Higgs scenario [79], as well as other Little Higgs [80-90], Composite Higgs [91-95], Top Seesaw [96-98], Higgs Inflation models [99], etc [100, 101]. A common feature of these new models is that VLTs and heavy Majorana neutrinos are predicted, which leads to a new decay mode of VLT through the mediation of heavy Majorana neutrinos. Taking into account that VLTs and heavy Majorana neutrinos in low-energy type-I seesaw models are both within the search abilities at the LHC, in a model-independent way, we propose in this paper a search strategy for the above new decay channel of the VLT. There are some traditional ways to search for the vector-like top partner at the LHC, such as $T\to b\,{jj}$. These searches have been performed [17, 18] and exclude the top partner mass up to 740∼1370 GeV. In this work, we will investigate the process $T\to b\,{{\ell }}^{+}{{\ell }}^{+}{jj}$, which can be used to probe the top partner and to test the seesaw mechanism simultaneously at the LHC. In a scenario that incorporates three right-handed Majorana neutrinos and a top partner T (+2/3 electrically charged and SU(2) singlet), we demonstrate that with the heavy Majorana neutrinos at the GeV scale, the new decay mode of T can be probed at the LHC by searching for a signal of same-sign dileptons [102], which has also been utilized in a phenomenological study on a topcolor-assisted technicolor model [103] and rare B decay [104]. In section 2 we will introduce the relative effective Lagrangian of the scenario and then in section 3 we will present our analysis by Monte Carlo simulation of the search at the LHC and show the observability for the mixing V_Tb between the top partner and the SM quark, as well as the light-heavy neutrino mixing ${V}_{\mu N}$. Section 4 is the conclusion.

2. Effective Lagrangian and the new decay mode of top partner

Without losing generality, we will adopt the effective interaction method to perform a phenomenological study in the following sections. The relevant interaction between a singlet top partner and W boson is given by,(1)$\begin{eqnarray}{{ \mathcal L }}_{T}=-\displaystyle \frac{g}{\sqrt{2}}{\bar{u}}_{\alpha L}{\gamma }^{\mu }{V}_{\alpha i}{d}_{{iL}}{W}_{\mu }^{+}+{\rm{H.c.}},\end{eqnarray}$where V is the CKM matrix but generalized to 4×3 dimensionally to include the additional VLT. Note that α=1∼4 runs over all generations of quarks including the VLT (here for brevity we label the singlet top partner T as the 4th generation), while i=1∼3 is the index for three generations of the SM fermions. g is the weak coupling. As for the type-I seesaw, for simplicity and without losing the features of a low-scale type-I seesaw, the model is parameterized as a mass scale of the RH Majorana neutrino M_N and a mixing parameter between the light and heavy neutrinos V_ij, then the effective Lagrangian for interactions between the heavy Majorana neutrinos and charged leptons can be written as(2)$\begin{eqnarray}{{ \mathcal L }}_{N}=-\displaystyle \frac{g}{2\sqrt{2}}{V}_{{\ell }N}{W}_{\mu }^{+}{\ell }{\gamma }^{\mu }(1-{\gamma }_{5}){N}^{c}+{\rm{H.c.}},\end{eqnarray}$where ℓ (ℓ=e, μ, τ are charged leptons) and N (N=N_1,2,3 label heavy Majorana neutrinos) are mass eigenstates.

Introduction of interaction terms equations (1) and (2) leads to T decay channel through the heavy Majorana neutrinos into a same-sign dilepton plus jets,(3)$\begin{eqnarray}T\to {{bW}}^{+}\to b\,{{\ell }}^{+}{{\ell }}^{+}q\bar{q^{\prime} },\end{eqnarray}$the Feynman diagram of which is presented in figure 1. The final same-sign dilepton may serve as a distinct signature at the LHC as a probe for this rare decay, as we will show in the next section. The relevant interaction terms for the process can be parameterized and written as an effective Lagrangian(4)$\begin{eqnarray}\begin{array}{rcl}{ \mathcal L } & = & -\displaystyle \frac{g}{2\sqrt{2}}{W}_{\mu }^{+}\left[{V}_{{\ell }N}{\ell }{\gamma }^{\mu }(1-{\gamma }_{5}){N}^{c}\right.\\ & & \left.+{V}_{{Tb}}\bar{T}{\gamma }^{\mu }(1-{\gamma }_{5})b\right]+{\rm{H.c.}},\end{array}\end{eqnarray}$in which the indices are the same as equation (2). Assuming $\mathrm{Br}(T\to {{bW}}^{+})=50 \% $, the branching ratio of the rare decay of T is shown in figure 2, with respect to mass of the heavy Majorana neutrino. In the calculation we set m_T=2 TeV, V_Tb=0.1 and ${V}_{{\ell }N}=0.004$ which are not excluded by current experiments (note that ${V}_{\mu N}=0.004$ survives [76] in the mass range of figure 2 while V_eN does not [105]). As can be seen, the branching ratio of the rare decay decreases as m_N grows in the kinematically accessible range (15∼75GeV). For a larger m_N from 10² GeV to TeV scale, the rare decay can be enhanced a bit due to on-shell W boson from N decay, but the branching ratio of T rare decay is still lower (∼10⁻⁸) than that in a light mass region. Therefore in section 3 we will focus on the relatively small mass range of the heavy Majorana neutrino with ${m}_{N}\lesssim {m}_{W}$ and explore the possibilities for a probe of the top partner's new decay channel.

Figure 1.

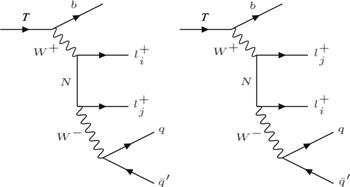New window|Download| PPT slide
Figure 1.Feynman diagrams of the top partner decay $T\to b\,{{\ell }}^{+}{{\ell }}^{+}q\bar{q^{\prime} }$ including t- and u-channels.

Figure 2.

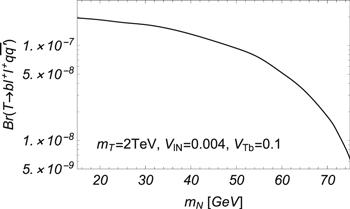New window|Download| PPT slide
Figure 2.Branching ratio of the top partner decay $T\to b\,{{\ell }}^{+}{{\ell }}^{+}q\bar{q^{\prime} }$, with respect to the heavy Majorana neutrino mass. $\mathrm{Br}(T\to {{bW}}^{+})=50 \% $ is assumed.

3. Search at the LHC

In the scenario we introduced in the last section, the SU(2) singlet top partner can be produced in pairs via QCD processes at the LHC, and then goes through a rare decay mediated by the heavy Majorana neutrino. If one of the paired VLTs goes through the rare decay $T\to b\,{{\ell }}^{+}{{\ell }}^{+}{jj}$ and the other decays into hadrons $\bar{T}\to \bar{b}\,{W}^{-}\to b\,{jj}$, then we have the distinct signal at the hadronic environment of the LHC as a same-sign dilepton with multi-jets including two b-tagged ones:(5)$\begin{eqnarray}{pp}\to T\bar{T}\to {{\ell }}^{+}{{\ell }}^{+}+b\,\bar{b}+\,{j}_{1}{j}_{2}{j}_{3}{j}_{4}.\end{eqnarray}$However, the GERDA experiments [105] already put a very stringent limit on the e-flavor mixing $| {V}_{{eN}}{| }^{2}$ to about 10⁻⁸ in the GeV∼100 GeV mass range of the heavy Majorana neutrino. Besides, probing for τ-flavor mixing ${V}_{\tau N}$ requires accurate tagging of final τ's, which is not realized with high efficiency in the current collider simulation. Given these facts, we expect an improvement of sensitivity for the μ-flavor mixing ${V}_{\mu N}$ in the kinematically accessible mass range of heavy neutrino (${m}_{N}\lesssim {m}_{W}$ in our case), which can lead to its resonant production as we discussed in section 1. The contribution of CP-conjugate process of (5),(6)$\begin{eqnarray}{pp}\to T\bar{T}\to {{\ell }}^{-}{{\ell }}^{-}+b\,\bar{b}+\,{j}_{1}{j}_{2}{j}_{3}{j}_{4},\end{eqnarray}$is also included in the following simulations. Note that the top partner can also be produced singly via electroweak processes. The cross section of the singly production is smaller than that of the pair production in a small mass range of VLT. As the VLT mass increases (≳1.1 TeV), the singly production cross section will surpass that of pair production and lead to a better sensitivity for the new decay mode.

For the signal processes (5) and (6) whose final states contain a same-sign dilepton and jets, major SM backgrounds at the LHC come from prompt multi-leptons (mainly from events with $t\bar{t}\,{W}^{\pm }$ and ${W}^{\pm }{W}^{\pm }$+jets) and fake leptons (mainly from events with jets of heavy flavor, such as $t\bar{t}$). To be exact, opposite-sign dileptons with one of which mismeasured should also constitute our backgrounds, but as the rate of mismeasurement for muons is generally low enough that we ignore its effects, then the SM backgrounds we consider are(7)$\begin{eqnarray}\begin{array}{rcl}{pp} & \to & t\bar{t}\,{W}^{\pm },\\ {pp} & \to & {W}^{\pm }{W}^{\pm }+\mathrm{jets},\\ {pp} & \to & t\bar{t}.\end{array}\end{eqnarray}$

Monte Carlo simulations are performed for both the signal (5), (6) and backgrounds (7) at the LHC with the center-of-mass energy of 14 TeV. For the signal we specify the N₂-mediated decay processes for the probing of ${V}_{\mu N}$. As we adopt a diagonalized mixing matrix ${V}_{{\ell }N}$, thus N₂ couples only to the μ-flavor. In the simulation, we use the benchmark point as follows,(8)$\begin{eqnarray}{m}_{N}=50\,\mathrm{GeV},\quad {m}_{T}=2\,\mathrm{TeV},\quad {V}_{{Tb}}=0.1,\quad {V}_{\mu N}=1.0,\end{eqnarray}$whereby m_N means the mass of N₂ for simplicity, while for N₁ (N₃) that couples to e (τ), we assume a kinematically inaccessible mass 300 GeV (1 TeV). Hence the processes mediated by N_1,3 are not included in the simulation of the search for the VLT new decay, due to their inaccessible large masses. Parton-level events of signal and backgrounds are generated through MadGraph5_aMC@NLO [106] with the NN23LO1 PDF [107], then go through parton showering and hadronization by Pythia-8.2 [108]. The renormalization and factorization scales are set at the value of VLT mass, that is, 2000 GeV. Detector simulations are carried out by tuned Delphes3 [109] within the framework of CheckMATE2 [110]. Jet-clustering is done using FastJet [111] with an anti-k_t algorithm [112]. We assume b-tagging efficiency to be 70% in our simulation. In addition, contributions from higher order QCD corrections are taken into account by normalizing the leading-order cross sections of $t\bar{t}$ and $t\bar{t}\,{W}^{\pm }$ to NNLO and NLO, respectively [113, 114].

We present the distributions of kinematic variables for signal and the SM background processes at the 14 TeV LHC in figure 3, including the product of charges of the final dimuon (figure 3(a)), missing transverse energy ${{/}\!\!\!\!{E}}_{T}$ (figure 3(b)), the relative distance between the final dimuon ${\rm{\Delta }}{R}_{\mu \mu }$ (figure 3(c)) and the transverse momentum of the leading b-jet (figure 3(d)). Figure 3(e) is the distribution of ${m}_{b2\mu 2j}$, the invariant mass reconstructed from the final two muons, a leading b-jet and two jets. It can be seen from figure 3(a) that the charges of final dimuon for the backgrounds $t\bar{t}$ and $t\bar{t}\,{W}^{\pm }$ tend to be opposite, compared with the signal. The distribution of missing transverse energy for the signal is more flat than that for the backgrounds and more signal events are found in the range of a large ${{/}\!\!\!\!{E}}_{T}$ (100 GeV∼900 GeV). Intuitively there are no neutrinos present in the final states of signal and hence signal events tend to have smaller ${{/}\!\!\!\!{E}}_{T}$ compared with the backgrounds, in which neutrinos from W decay constitute much of the missing transverse energy. However, note that it is the jets after parton-showering that arrive at the detectors, rather than the partonic final states. b\$\bar{b}$ quarks from the signal (5) and (6) are highly energetic as they are decay products of T with mass of 2 TeV and by parton-showering, these b\$\bar{b}$ quarks decay to neutrinos that are highly energetic as well, leading to the ${{/}\!\!\!\!{E}}_{T}$ distribution shown in figure 3(b). The dimuon in the signal comes from decay of the same top partner (equations (5) and (6)) while in the SM backgrounds, the final leptons come from decays of different parent particles, that is, ${W}^{+}{W}^{-}$ in the $t\bar{t}$, $t\bar{t}\,{W}^{\pm }$ and ${W}^{\pm }{W}^{\pm }$+jets events. The final two muons thus tend to be closer in the signal than in the backgrounds, which is reflected in the distributions of the relative distance between them (figure 3(c)). Moreover, we set m_T in the benchmark point to be 2 TeV, which is much more massive than the SM top quark and whose decay product b quark tends to be much harder than that from top decay in the backgrounds event (figure 3(d)). Furthermore, to distinguish the signal and backgrounds more efficiently, we reconstruct the parent T by the invariant mass ${m}_{b2\mu 2j}$ clustering the decay products from the VLT rare decay, in which we use the leading b-jet and two soft jets, since the jets come from the secondary decay of the mediating Majorana neutrino and hence tend to be softer than ones in the SM backgrounds. As can be seen from figure 3(e), more events of the signal distribute around the range $800\,\mathrm{GeV}\lesssim {m}_{b2\mu 2j}\lesssim 2000\,\mathrm{GeV}$, while for the three backgrounds the peaks of the distributions are all below 800 GeV.

Figure 3.

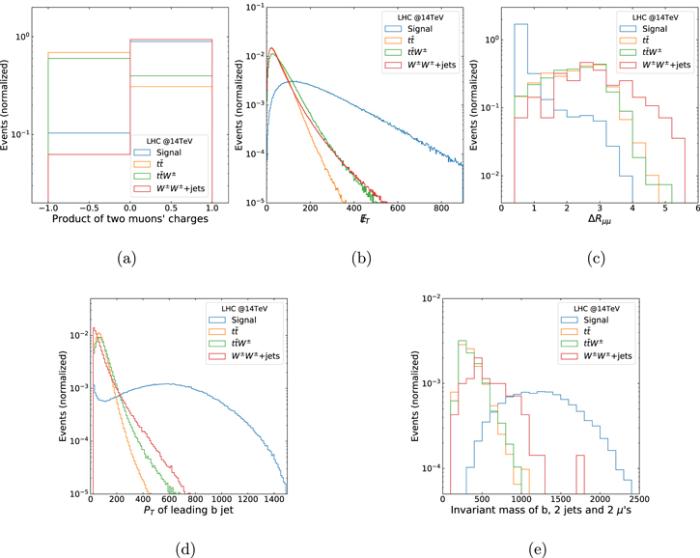New window|Download| PPT slide
Figure 3.Kinematic distributions of the signal ${pp}\to {\mu }^{\pm }{\mu }^{\pm }+2b+4j$ and the SM backgrounds $t\bar{t}$, $t\bar{t}{W}^{\pm }$, ${W}^{\pm }{W}^{\pm }$+jets at the 14 TeV LHC. The benchmark point is chosen as m_T=2 TeV, m_N=50 GeV, V_Tb=0.1, ${V}_{\mu N}=1.0$.


Based on the above analysis, we apply the following kinematic cuts to the events to distinguish a signal from the SM backgrounds.• Cut 1: a same-sign muons is required with each of them satisfying ${p}_{T}(\mu )\gt 10\,\mathrm{GeV}$ and $| \eta (\mu )| \lt 2.8$.
• Cut 2: we demand at least 6 jets in the final states with each of them having p_T(j)>15 GeV and $| \eta (j)| \lt 3.0$.
• Cut 3: a large missing transverse energy is required as ${{/}\!\!\!\!{E}}_{T}\gt 180\,\mathrm{GeV}$.
• Cut 4: the relative distance is also required for the dilepton separation as $0.4\lt {\rm{\Delta }}{R}_{\mu \mu }\lt 1.2$, for jets separation as ${\rm{\Delta }}{R}_{{jj}}\gt 0.4$ and for jet-lepton separation as ${\rm{\Delta }}{R}_{\mu j}\gt 0.4$.
• Cut 5: among the final jets, at least one of them is required to be a b-jet. And the leading b-jet should have p_T>280 GeV.
• Cut 6: the invariant mass ${m}_{b2\mu 2j}$ clustering the decay products of T rare decay is required to be larger than 800 GeV.


With the above cuts applied, we present in table 1 the cutflow of cross sections for signal and the SM backgrounds at the 14 TeV LHC. Among the three kinds of SM backgrounds, we can see from table 1 that the dominant one are the $t\bar{t}$ events. The first two cuts on numbers of final same-sign muons and jets can suppress the main backgrounds to the same order as the signal. Then the large ${{/}\!\!\!\!{E}}_{T}$ requirement can cut about 95% SM backgrounds while keeping 40% signal events that have survived from the first two steps of cuts. The final three cuts can effectively remove the $t\bar{t}$ and WW+jets events while leaving the $t\bar{t}{W}^{\pm }$ to an almost negligible level (about 4 orders smaller than the signal). Through the above event selection, we can reach an effective probe towards the parameter space in the present scenario.


Table 1.
Table 1.Cutflow of cross sections for the signal process ${pp}\to {\mu }^{\pm }{\mu }^{\pm }+2b+4j$ and the SM background processes ${pp}\to t\bar{t},t\bar{t}{W}^{\pm },{WW}$+jets at the 14 TeV LHC. The cross sections are in the unit of pb. The benchmark point is the same as in figure 3.

	$t\bar{t}$	$t\bar{t}\,{W}^{\pm }$	WW+jets	signal
Cut 1: same-sign dimuon	8.24	2.00×10−2	1.77×10−3	0.590
Cut 2: at least 6 jets	0.832	3.55×10−3	1.10×10−4	0.268
Cut 3: ${{/}\!\!\!\!{E}}_{T}\gt 180\,\mathrm{GeV}$	3.88×10−2	3.19×10−4	2.24×10−5	0.116
Cut 4: on relative distance	9.00×10−3	6.31×10−5	1.74×10−6	9.22×10−2
Cut 5: at least 1 b-jet(pT>280 GeV)	4.91×10−4	7.24×10−6	0	4.87×10−2
Cut 6: mb2μ2j>800 GeV	0	4.13×10−6	0	3.95×10−2

New window|CSV

We present in figure 4 the exclusion bounds at 2σ on the signal ${pp}\to T\bar{T}\to {\mu }^{\pm }{\mu }^{\pm }+b\bar{b}+4j$, where the statistical significance is calculated using the formula(9)$\begin{eqnarray}\alpha =\displaystyle \frac{S}{\sqrt{B+{\left(\beta B\right)}^{2}}},\end{eqnarray}$where S(B) is the event number after the above cuts for signal(background). β denotes the systematic uncertainty, which in our case mainly comes from the background with misidentified leptons and is assumed to be 5% in the following discussion. The integrated luminosity at the 14 TeV LHC is set to be $3\,{\mathrm{ab}}^{-1}$. Figure 4(a) shows the 2σ limits on the parameter plane of $| {V}_{\mu N}{| }^{2}$ versus m_T, in which three colored lines correspond to V_Tb=0.1, 0.5, 1.0, respectively. It can be seen that for a relatively low mass range of m_T ≲ 1.4 TeV and V_Tb ≳ 0.5, the heavy-light Majorana neutrino mixing $| {V}_{\mu N}{| }^{2}$ can be probed to orders of 10⁻⁵ and below, which surpasses the current bounds on $| {V}_{\mu N}{| }^{2}\sim {10}^{-5}$ for m_N∼50 GeV given by the DELPHI Collaboration [76], as well as the LHC search for same-sign dileptons [77] and trileptons events [78]. For example, we can read from figure 4(a) that, at the point of m_T=1.3 TeV and V_Tb=1.0, the exclusion limit on $| {V}_{\mu N}{| }^{2}$ reaches 7.6×10⁻⁶. Figure 4(b) is plotted on the plane of V_Tb versus m_T, in which three colored lines correspond to ${V}_{\mu N}=0.002,0.004,0.01$, respectively. Within the mass range of m_T below 1.8 TeV, the upper bound on the coupling of the top partner with the SM b quark can be given at V_Tb ≲ 1.0 with ${V}_{\mu N}\sim {10}^{-3}$. For instance, at ${V}_{\mu N}=0.004$ and m_T=1.3 TeV, V_Tb>0.35 can be excluded at 2σ. Finally in figure 5 we present the 2σ exclusion limit on the cross sections of the signal process ${pp}\to T\bar{T}\to {\mu }^{\pm }{\mu }^{\pm }+b\bar{b}+4j$ with respect to the top partner mass at the 14 TeV LHC, with V_Tb=0.1, ${V}_{\mu N}=0.004$ and m_N=50 GeV. Furthermore, it can be inferred from figure 2 that with a less massive heavy Majorana neutrino, the branching ratio of the top partner's rare decay will increase and may lead to a better sensitivity.

Figure 4.

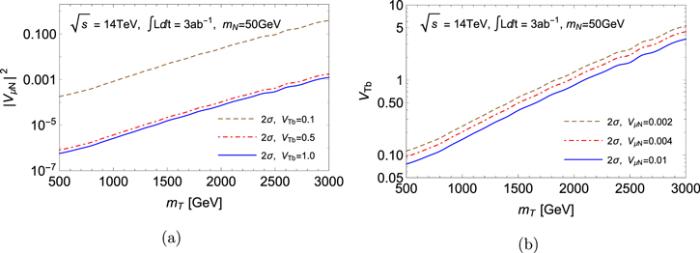New window|Download| PPT slide
Figure 4.Contours of 2σ exclusion limits on the signal ${pp}\to T\bar{T}\to {\mu }^{\pm }{\mu }^{\pm }+b\bar{b}+4j$ at the 14 TeV LHC, with integrated luminosity of 3 ab⁻¹. Systematic uncertainty β is taken as 5%. (a) Plotted on the plane of $| {V}_{\mu N}{| }^{2}$ versus m_T and (b) on the plane of V_Tb versus m_T.

Figure 5.

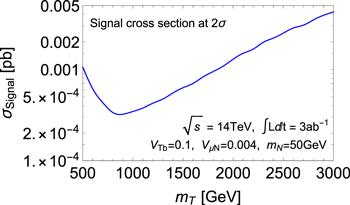New window|Download| PPT slide
Figure 5.2σ exclusion on the cross sections of signal ${pp}\to T\bar{T}\to {\mu }^{\pm }{\mu }^{\pm }+b\bar{b}+4j$ with respect to the top partner mass at the 14 TeV LHC.


It should be noted that we have not considered pileup effects in our discussion, which is important for a fully realistic simulation and needs proper removal techniques [115-117]. However, the pileup effects can be limited on our results since the event-selection is based on a pair of hard same-sign leptons.

4. Conclusion

In this paper, we investigate the observability for the rare decay of a singlet top partner in a model-independent scenario that combines the low-energy type-I seesaw and a vector-like singlet top partner. We present a search strategy at the 14 TeV LHC for a distinguishable signal with a same-sign dilepton plus multiple jets. In a kinematically accessible mass range of the heavy Majorana neutrino (we choose m_N=50 GeV as a benchmark point), the detector-level simulation at the 14 TeV LHC with integrated luminosity of 3 ab⁻¹ shows that, the μ-flavor mixing with the heavy Majorana neutrino $| {V}_{\mu N}{| }^{2}\gt 7.6\times {10}^{-6}$ can be excluded at 2σ for V_Tb ≲ 1.0 and m_T∼1.3 TeV. The coupling between the singlet top partner and the SM b quark V_Tb>0.35 can be excluded at 2σ for ${V}_{\mu N}=0.004$ and m_T∼1.3 TeV. It is then concluded that in a kinematically accessible mass range of the heavy Majorana neutrino, searching at the LHC for the rare decay of a singlet top partner mediated by the heavy Majorana neutrino can be promising through the same-sign dilepton signal.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (NNSFC) under grant Nos. 11847208 and 11705093, as well as the Jiangsu Planned Projects for Postdoctoral Research Funds under grant No. 2019K197.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Perelstein M Peskin M E Pierce A 2004 Phys. Rev. D 69 075002
DOI:10.1103/PhysRevD.69.075002 [Cited within: 1]

[2]Matsedonskyi O Panico G Wulzer A 2013 J. High Energy Phys. JHEP01(2013)164
DOI:10.1007/JHEP01(2013)164 [Cited within: 1]

[3]Dugan M J Georgi H Kaplan D B 1985 Nucl. Phys. B 254 299
DOI:10.1016/0550-3213(85)90221-4 [Cited within: 1]

[4]Kaplan D B 1991 Nucl. Phys. B 365 259
DOI:10.1016/S0550-3213(05)80021-5

[5]Contino R Da Rold L Pomarol A 2007 Phys. Rev. D 75 055014
DOI:10.1103/PhysRevD.75.055014

[6]Contino R Kramer T Son M Sundrum R 2007 J. High Energy Phys. JHEP05(2007)074
DOI:10.1088/1126-6708/2007/05/074 [Cited within: 1]

[7]del Aguila F Perez-Victoria M Santiago J 2000 Phys. Lett. B 492 98
DOI:10.1016/S0370-2693(00)01071-6 [Cited within: 1]

[8]del Aguila F Perez-Victoria M Santiago J 2000 J. High Energy Phys. JHEP09(2000)011
DOI:10.1088/1126-6708/2000/09/011

[9]Aguilar-Saavedra J A 2009 J. High Energy Phys. JHEP11(2009)030
DOI:10.1088/1126-6708/2009/11/030

[10]Chala M 2017 Phys. Rev. D 96 015028
DOI:10.1103/PhysRevD.96.015028

[11]Zhou H Liu N 2019 Phys. Lett. B 791 1
DOI:10.1016/j.physletb.2019.02.016

[12]Han C Kobakhidze A Liu N Wu L Yang B 2014 Nucl. Phys. B 890 388
DOI:10.1016/j.nuclphysb.2014.11.021

[13]Liu N Wu L Yang B Zhang M 2016 Phys. Lett. B 753 664
DOI:10.1016/j.physletb.2015.12.066

[14]Yang B Zhang H Hou B Liu N 2018 Chin. Phys. C 42 103102
DOI:10.1088/1674-1137/42/10/103102

[15]Liu Y B Moretti S 2019 Phys. Rev. D 100 015025
DOI:10.1103/PhysRevD.100.015025

[16]Yang S 2010 Commun. Theor. Phys. 53 1133
DOI:10.1088/0253-6102/53/6/28 [Cited within: 1]

[17]Aaboud M et al.(ATLAS Collaboration) 2018 Phys. Rev. Lett. 121 211801
DOI:10.1103/PhysRevLett.121.211801 [Cited within: 2]

[18]Sirunyan A M et al.(CMS Collaboration) 2019 Phys. Rev. D 100 072001
DOI:10.1103/PhysRevD.100.072001 [Cited within: 2]

[19]Tanabashi M et al.(Particle Data Group) 2018 Phys. Rev. D 98 030001
DOI:10.1103/PhysRevD.98.030001 [Cited within: 1]

[20]Minkowski P 1977 Phys. Lett. B 67 421
DOI:10.1016/0370-2693(77)90435-X [Cited within: 2]

[21]Yanagida T 1979 Proc. of the Workshop on Unified Theory and the Baryon Number of the Universe Sawada O Sugamoto A Tsukuba


[22]Mohapatra R N Senjanović G 1980 Phys. Rev. Lett. 44 912
DOI:10.1103/PhysRevLett.44.912

[23]Schechter J Valle J W F 1980 Phys. Rev. D 22 2227
DOI:10.1103/PhysRevD.22.2227 [Cited within: 1]

[24]Weinberg S 1979 Phys. Rev. Lett. 43 1566
DOI:10.1103/PhysRevLett.43.1566

[25]Magg M Wetterich C 1980 Phys. Lett. B 94 61
DOI:10.1016/0370-2693(80)90825-4

[26]Cheng T P Li L F 1980 Phys. Rev. D 22 2860
DOI:10.1103/PhysRevD.22.2860

[27]Lazarides G Shafi Q Wetterich C 1981 Nucl. Phys. B 181 287
DOI:10.1016/0550-3213(81)90354-0

[28]Mohapatra R N Senjanović G 1981 Phys. Rev. D 23 165
DOI:10.1103/PhysRevD.23.165

[29]Foot R Lew H He X G Joshi G C 1989 Z. Phys. C 44 441
DOI:10.1007/BF01415558

[30]Ma E 1998 Phys. Rev. Lett. 81 1171
DOI:10.1103/PhysRevLett.81.1171 [Cited within: 1]

[31]Fukugita M Yanagida T 1986 Phys. Lett. B 174 45
DOI:10.1016/0370-2693(86)91126-3 [Cited within: 1]

[32]Kuzmin V A Rubakov V A Shaposhnikov M E 1985 Phys. Lett. B 155 36
DOI:10.1016/0370-2693(85)91028-7

[33]Langacker P Peccei R D Yanagida T 1986 Mod. Phys. Lett. A 1 541
DOI:10.1142/S0217732386000683

[34]Luty M A 1992 Phys. Rev. D 45 455
DOI:10.1103/PhysRevD.45.455

[35]Mohapatra R N Zhang X 1992 Phys. Rev. D 46 5331
DOI:10.1103/PhysRevD.46.5331

[36]Flanz M Paschos E A Sarkar U 1995 Phys. Lett. B 345 248
DOI:10.1016/0370-2693(94)01555-Q

[37]Covi L Roulet E Vissani F 1996 Phys. Lett. B 384 169
DOI:10.1016/0370-2693(96)00817-9

[38]Pilaftsis A 1997 Phys. Rev. D 56 5431
DOI:10.1103/PhysRevD.56.5431

[39]Ma E Sarkar U 1998 Phys. Rev. Lett. 80 5716
DOI:10.1103/PhysRevLett.80.5716

[40]Hambye T Senjanović G 2004 Phys. Lett. B 582 73
DOI:10.1016/j.physletb.2003.11.061

[41]Gu P H 2020 Phys. Lett. B 800 135118
DOI:10.1016/j.physletb.2019.135118 [Cited within: 1]

[42]Ma E 2006 Phys. Rev. D 73 077301
DOI:10.1103/PhysRevD.73.077301 [Cited within: 1]

[43]Ma E 2015 Phys. Rev. Lett. 115 011801
DOI:10.1103/PhysRevLett.115.011801

[44]Gu P H 2020 Phys. Rev. D 101 015006
DOI:10.1103/PhysRevD.101.015006

[45]Zhou H Gu P H 2017 J. Cosmol. Astropart. Phys. JCAP01(2017)030
DOI:10.1088/1475-7516/2017/01/030 [Cited within: 1]

[46]Furry W H 1939 Phys. Rev. 56 1184
DOI:10.1103/PhysRev.56.1184 [Cited within: 1]

[47]Doi M Kotani T Takasugi E 1985 Prog. Theor. Phys. Suppl. 83 1
DOI:10.1143/PTPS.83.1 [Cited within: 1]

[48]Ng J N Kamal A N 1978 Phys. Rev. D 18 3412
DOI:10.1103/PhysRevD.18.3412 [Cited within: 1]

[49]Abad J Esteve J G Pacheco A F 1984 Phys. Rev. D 30 1488
DOI:10.1103/PhysRevD.30.1488

[50]Dib C Gribanov V Kovalenko S Schmidt I 2000 Phys. Lett. B 493 82
DOI:10.1016/S0370-2693(00)01134-5

[51]Ali A Borisov A V Zamorin N B 2001 Eur. Phys. J. C 21 123
DOI:10.1007/s100520100702

[52]Littenberg L S Shrock R E 1992 Phys. Rev. D 46R892
DOI:10.1103/PhysRevD.46.R892

[53]Barbero C Lopez Castro G Mariano A 2003 Phys. Lett. B 566 98
DOI:10.1016/S0370-2693(03)00773-1 [Cited within: 1]

[54]Atre A Han T Pascoli S Zhang B 2009 J. High Energy Phys. JHEP05(2009)030
DOI:10.1088/1126-6708/2009/05/030 [Cited within: 2]

[55]Asaka T Blanchet S Shaposhnikov M 2005 Phys. Lett. B 631 151
DOI:10.1016/j.physletb.2005.09.070 [Cited within: 1]

[56]Asaka T Shaposhnikov M 2005 Phys. Lett. B 620 17
DOI:10.1016/j.physletb.2005.06.020

[57]Asaka T Laine M Shaposhnikov M 2007 J. High Energy Phys. JHEP01(2007)091
DOI:10.1088/1126-6708/2007/01/091

Asaka T Laine M Shaposhnikov M 2015 J. High Energy Phys. JHEP02(2015)028 Erratum
DOI:10.1088/1126-6708/2007/01/091

[58]Asaka T Shaposhnikov M Kusenko A 2006 Phys. Lett. B 638 401
DOI:10.1016/j.physletb.2006.05.067

[59]Xing Z z 2009 Prog. Theor. Phys. Suppl. 180 112
DOI:10.1143/PTPS.180.112

[60]Ibarra A Molinaro E Petcov S T 2010 J. High Energy Phys. JHEP09(2010)108
DOI:10.1007/JHEP09(2010)108

[61]Adhikari R Raychaudhuri A 2011 Phys. Rev. D 84 033002
DOI:10.1103/PhysRevD.84.033002

[62]Boucenna S M Morisi S Valle J W F 2014 Adv. High Energy Phys. 2014 831598
DOI:10.1155/2014/831598

[63]Zhou H Gu P H 2018 Nucl. Phys. B 927 184
DOI:10.1016/j.nuclphysb.2017.12.016

[64]Gu P H He H J 2019 Phys. Rev. D 99 015025
DOI:10.1103/PhysRevD.99.015025 [Cited within: 1]

[65]de Gouvea A Jenkins J Vasudevan N 2007 Phys. Rev. D 75 013003
DOI:10.1103/PhysRevD.75.013003 [Cited within: 1]

[66]Ibarra A Molinaro E Petcov S T 2011 Phys. Rev. D 84 013005
DOI:10.1103/PhysRevD.84.013005

[67]Bajc B Nemevsek M Senjanovic G 2007 Phys. Rev. D 76 055011
DOI:10.1103/PhysRevD.76.055011

[68]de Gouvea A arXiv:0706.1732[hep-ph]


[69]Kersten J Smirnov A Y 2007 Phys. Rev. D 76 073005
DOI:10.1103/PhysRevD.76.073005

[70]He X G Oh S Tandean J Wen C C 2009 Phys. Rev. D 80 073012
DOI:10.1103/PhysRevD.80.073012

[71]Han T Zhang B 2006 Phys. Rev. Lett. 97 171804
DOI:10.1103/PhysRevLett.97.171804

[72]Dev P S B Pilaftsis A Yang U K 2014 Phys. Rev. Lett. 112 081801
DOI:10.1103/PhysRevLett.112.081801

[73]Deppisch F F Bhupal Dev P S Pilaftsis A 2015 New J. Phys. 17 075019
DOI:10.1088/1367-2630/17/7/075019

[74]Das A 2018 Adv. High Energy Phys. 2018 9785318
DOI:10.1007/JHEP12(2018)096

[75]Liu N Si Z G Wu L Zhou H Zhu B arXiv:1910.00749 [hep-ph]
[Cited within: 1]

[76]Abreu P et al.(DELPHI Collaboration) 1997 Z. Phys. C 74 57
DOI:10.1007/s002880050370 [Cited within: 3]

Abreu P(DELPHI Collaboration) et al. 1997 Z. Phys. C 75 580 Erratum
DOI:10.1007/s002880050370 [Cited within: 3]

[77]Sirunyan A M et al.(CMS Collaboration) 2019 J. High Energy Phys. JHEP01(2019)122
DOI:10.1007/JHEP01(2019)122 [Cited within: 2]

[78]Sirunyan A M et al.(CMS Collaboration) 2018 Phys. Rev. Lett. 120 221801
DOI:10.1103/PhysRevLett.120.221801 [Cited within: 2]

[79]Han T Logan H E Mukhopadhyaya B Srikanth R 2005 Phys. Rev. D 72 053007
DOI:10.1103/PhysRevD.72.053007 [Cited within: 1]

[80]Del Aguila F Illana J I Perez-Poyatos J M Santiago J 2019 J. High Energy Phys. JHEP12(2019)154
DOI:10.1007/JHEP12(2019)154 [Cited within: 1]

[81]Dey P Gupta S K Mukhopadhyaya B 2009 Phys. Lett. B 674 188
DOI:10.1016/j.physletb.2009.03.013

[82]de Almeida F M L Coutinho Y A Martins Simoes J A Ramalho A J Wulck S do Vale M A B arXiv:0707.1105 [hep-ph]


[83]Li N Yue C X Li X X 2011 Chin. Phys. Lett. 28 107305
DOI:10.1088/0256-307X/28/10/107305

[84]Hektor A Kadastik M Muntel M Raidal M Rebane L 2007 Nucl. Phys. B 787 198
DOI:10.1016/j.nuclphysb.2007.07.014

[85]Goyal A 2006 Mod. Phys. Lett. A 21 1931
DOI:10.1142/S0217732306020561

[86]Abada A Bhattacharyya G Losada M 2006 Phys. Rev. D 73 033006
DOI:10.1103/PhysRevD.73.033006

[87]Goyal A 2005 AIP Conf. Proc. 805 302


[88]del Aguila F Masip M Padilla J L 2005 Phys. Lett. B 627 131
DOI:10.1016/j.physletb.2005.08.115

[89]Lee J arXiv:0504136 [hep-ph]


[90]Chang S He H J 2004 Phys. Lett. B 586 95
DOI:10.1016/j.physletb.2004.02.027 [Cited within: 1]

[91]Coito L Faubel C Santamaria A arXiv:1912.10001 [hep-ph]
[Cited within: 1]

[92]Shindou T 2017 Bled Workshops Phys. 18 190


[93]Smetana A 2013 Eur. Phys. J. C 73 2513
DOI:10.1140/epjc/s10052-013-2513-8

[94]del Aguila F Carmona A Santiago J 2010 J. High Energy Phys. JHEP08(2010)127
DOI:10.1007/JHEP08(2010)127

[95]Lee J Y 2005 J. High Energy Phys. JHEP06(2005)060
DOI:10.1088/1126-6708/2005/06/060 [Cited within: 1]

[96]He H J Tait T M P Yuan C P 2000 Phys. Rev. D 62 011702
DOI:10.1103/PhysRevD.62.011702 [Cited within: 1]

[97]He H J Hill C T Tait T M P 2002 Phys. Rev. D 65 055006
DOI:10.1103/PhysRevD.65.055006

[98]Wang X F Du C He H J 2013 Phys. Lett. B 723 314
DOI:10.1016/j.physletb.2013.05.015 [Cited within: 1]

[99]He H J Xianyu Z Z 2014 J. Cosmol. Astropart. Phys. JCAP10(2014)019
DOI:10.1088/1475-7516/2014/10/019 [Cited within: 1]

[100]Dud C He H J Kuang Y P Zhang B Christensen N D Chivukula R S Simmons E H 2012 Phys. Rev. D 86 095011
DOI:10.1103/PhysRevD.86.095011 [Cited within: 1]

[101]Abe T Chen N He H J 2013 J. High Energy Phys. JHEP01(2013)082
DOI:10.1007/JHEP01(2013)082 [Cited within: 1]

[102]Cao J Wang L Wu L Yang J M 2011 Phys. Rev. D 84 074001
DOI:10.1103/PhysRevD.84.074001 [Cited within: 1]

[103]Liu G L 2011 Commun. Theor. Phys. 55 852
DOI:10.1088/0253-6102/55/5/21 [Cited within: 1]

[104]Bao S S Li H L Si Z G Yang Y B 2013 Commun. Theor. Phys. 59 472
DOI:10.1088/0253-6102/59/4/15 [Cited within: 1]

[105]Agostini M et al.(GERDA Collaboration) 2018 Phys. Rev. Lett. 120 132503
DOI:10.1103/PhysRevLett.120.132503 [Cited within: 2]

[106]Alwall J et al. 2014 J. High Energy Phys. JHEP07(2014)079
DOI:10.1007/JHEP07(2014)079 [Cited within: 1]

[107]Ball R D et al. 2013 Nucl. Phys. B 867 244
DOI:10.1016/j.nuclphysb.2012.10.003 [Cited within: 1]

[108]Sjostrand T Mrenna S Skands P Z 2006 J. High Energy Phys. JHEP05(2006)026
DOI:10.1088/1126-6708/2006/05/026 [Cited within: 1]

[109]de Favereau J et al.(DELPHES 3 Collaboration) 2014 J. High Energy Phys. JHEP02(2014)057
DOI:10.1007/JHEP02(2014)057 [Cited within: 1]

[110]Dercks D Desai N Kim J S Rolbiecki K Tattersall J Weber T 2017 Comput. Phys. Commun. 221 383
DOI:10.1016/j.cpc.2017.08.021 [Cited within: 1]

[111]Cacciari M Salam G P Soyez G 2012 Eur. Phys. J. C 72 1896
DOI:10.1140/epjc/s10052-012-1896-2 [Cited within: 1]

[112]Cacciari M Salam G P Soyez G 2008 J. High Energy Phys. JHEP04(2008)063
DOI:10.1088/1126-6708/2008/04/063 [Cited within: 1]

[113]Czakon M Mitov A 2014 Comput. Phys. Commun. 185 2930
DOI:10.1016/j.cpc.2014.06.021 [Cited within: 1]

[114]Frixione S Hirschi V Pagani D Shao H-S Zaro M 2015 J. High Energy Phys. JHEP06(2015)184
DOI:10.1007/JHEP06(2015)184 [Cited within: 1]

[115]Cacciari M Salam G P 2008 Phys. Lett. B 659 119
DOI:10.1016/j.physletb.2007.09.077 [Cited within: 1]

[116]Berta P Spousta M Miller D W Leitner R 2014 J. High Energy Phys. JHEP06(2014)092
DOI:10.1007/JHEP06(2014)092

[117]Krohn D Schwartz M D Low M Wang L T 2014 Phys. Rev. D 90 065020
DOI:10.1103/PhysRevD.90.065020 [Cited within: 1]