Vikas ¹, Keshav Walia², R K Verma^,11Department of Physics, Central University of Rajasthan, NH-8 Bandarsindri, Ajmer-305817, Rajasthan, India
²Department of Physics, DAV University, Jalandhar-144012, Punjab, India

Received:2020-02-28Revised:2020-05-07Accepted:2020-05-25Online:2020-08-05


Abstract
A lossy mode resonance (LMR)-supported fiber optic sensor in which a uniform fiber core is placed among two identical tapered regions, is investigated numerically. Indium tin oxide (ITO) and aluminum-doped zinc oxide (AZO) are considered as LMR active materials used to excite several lossy modes and gold and silver are used as surface plasmon resonance (SPR) active materials. In this probe design, a central uniform core coated with ITO/AZO is the active sensing region, whereas tapered regions are meant for bringing the incident angle close to the critical angle. The sensitivity of the present fiber optic bio-sensor is evaluated for first two LMRs utilizing both ITO and AZO separately, along with its variation with the taper ratio (TR). For ITO, the maximum sensitivity values are observed to be 18.425 μm RIU⁻¹ (refractive index unit) and 0.825 μm RIU⁻¹, corresponding to the first and second LMRs, respectively, at a TR of 1.6 and for AZO, equivalent values are 0.79 μm RIU⁻¹ and 0.35 μm RIU⁻¹, respectively, at a TR of 2.0. The results illustrate that the first LMR is more sensitive than the second LMR and the ITO-coated probe possesses greater sensitivity than the AZO-coated probe for both LMRs. Similarly, for the fiber optic SPR sensor, the maximum value of sensitivity is 5.6425 μm RIU⁻¹, in the case of gold and 5.0615 μm RIU⁻¹ in the case of silver, at a TR of 1.6. Hence, the result shows that the sensor with the present fiber optic probe design has around a 3-fold enhancement in sensitivity compared with conventional SPR sensors. This study will have applications in many sensing schemes where the requirement of large sensitivity is vital.
Keywords： fiber optic sensors;lossy modes;surface plasmons;indium tin oxide;aluminum-doped zinc oxide;sensitivity


PDF (1055KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Vikas , Keshav Walia, R K Verma. Lossy mode resonance-based uniform core tapered fiber optic sensor for sensitivity enhancement. Communications in Theoretical Physics, 2020, 72(9): 095502- doi:10.1088/1572-9494/aba240

1. Introduction

In recent years, lossy mode resonance (LMR) technique has been under ample consideration by researchers as it is more effective and beneficial over the surface plasmon resonance (SPR) technique in many sensing applications [1–3]. The first application of LMR, in the area of sensing, was carried out by Dell Villar et al in 2010 utilizing indium tin oxide (ITO), both experimentally and theoretically [1]. In LMR-based sensors, lossy modes can be excited by using both transverse magnetic (TM) and transverse electric (TE) polarized light unlike SPR-based sensors, in which only TM polarized light can excite surface plasmons. For LMR to occur, the real part of the dielectric constant of a coated lossy material must be a positive value and greater in magnitude than its own imaginary part, as well as the dielectric constant of the surrounding medium. Owing to the capability of exciting several lossy modes, in LMR-based sensors a metal oxide layer of finite thickness is used instead of metals [3, 4]. Additionally, the spectral position of these resonances can be sought just by varying the thickness of the coated lossy material. Also, the sensitivity values can be attuned as a function of the dielectric permittivity and the thickness of the lossy material. The phenomenon of LMR takes place when a waveguide mode is coupled with a lossy mode at a finite value of coated film thickness. The basic need for coupling of these modes is overlying of the mode fields and similar phases. A state of similar phase is attained only if the wave vector (real part) of both the modes, i.e. waveguide mode and lossy mode, exactly matches. As soon as lossy modes cross the cutoff condition, they began to guide in the coated film of metal oxides which leads to multiple LMR generation at specific values of thickness, and a sharp fall in the spectra of transmitted power is detected at these resonance wavelengths. Therefore, unlike SPR, multiple optical resonances can be achieved when the thickness of the coating is increased and all these resonances can be utilized for sensing as well as other applications. In line with the development of sensing devices a lot of research work has been carried out for the enhancement of the sensitivity of the fiber optic sensors, based on the phenomenon of LMR [5–16]. In 2014, Kaur et al studied LMR by using both spectral and angular interrogation methods theoretically and revealed that a dielectric layer having a low refractive index value, placed between a prism and the lossy wave guiding film, enhances the sensitivity of the sensor up to 4000–5000 nm RIU⁻¹ [5]. In the same year, an LMR-supported fiber optic sensor utilizing bilayers of ITO and titanium dioxide (${{\rm{TiO}}}_{2}$) was developed theoretically and revealed that the enhancement of sensitivity can also be done by changing the total bilayer thickness and the ratio of bilayer thickness [6]. In 2016, Zubiate et al developed a highly sensitive pH sensor based on TM and TE LMRs [7]. In the same year, Arregui et al developed LMR-based D-shaped optical fiber sensors [8]. In 2017, Villar et al designed optical sensors based on LMR and discussed the optimization and generation conditions of LMR [9]. In 2018, the effect of graphene oxide was studied on an LMR-based optical fiber ethanol sensor [10]. Wu et al developed an LMR-based sensor by depositing layers of black phosphorus on the base of a prism and an experimental investigation was carried out on both SPR- and LMR-based fiber optic sensors [11, 12]. Recently, an LMR optical sensor based on indium gallium zinc oxide thin film was studied by using both multimode and monomode D-shaped fibers with a sensitivity value of 12 929 nm RIU⁻¹ [14]. In 2019, Wang et al proposed an LMR-based optical fiber sensor fabricated with SnO₂ thin films and SnO₂ nanoparticles deposited over thin film that possessed sensitivity values up to 5334 nm RIU⁻¹ [15].

In the current study, we have developed a numerical analysis of an LMR-supported fiber optic sensor by conceptualizing the deposition of a thin metal oxide film on the uniform fiber core sandwiched between two unclad tapered fiber regions. For ITO and AZO, the real part of the dielectric constant is positive and higher in magnitude than its own imaginary part [8, 17]. Therefore, both these materials satisfy the condition of an LMR as explained above. We have chosen the thicknesses 90 nm and 900 nm, respectively, for ITO and AZO materials such that only the first two LMRs are obtained. To show their comparison with SPR, gold (Au) and silver (Ag) were used as the SPR active materials. We have calculated the sensitivity of the proposed fiber optic sensor with taper ratios (TRs). Additionally, the sensitivity values for the first two LMRs are evaluated for ITO and AZO separately and are compared. The study reveals that the LMR sensor with the present fiber optic probe design shows around 3-fold enhancement in the sensitivity when compared with the conventional SPR-based fiber optic probe.

2. Principle and mathematical considerations

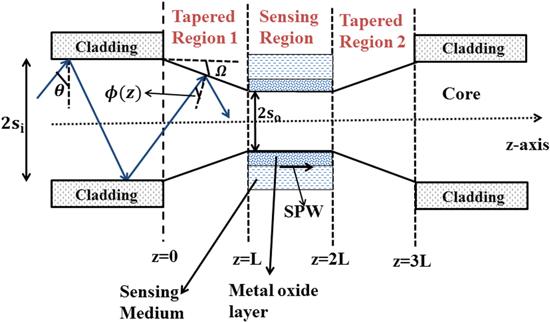
For mathematical modeling, the Kretschmann configuration [18] was realized on a plastic clad silica (PCS) multimode fiber of core diameter 600 μm and numerical aperture 0.22. A very small part of the cladding, about 0.5 cm of length, was removed (usually the central portion) from the optical fiber. The cladding-removed portion around uniform core of the optical fiber can be tapered by using flame brush method [19]. Figure 1 displays a schematic of the proposed fiber optic probe. There are three regions shown in figure 1 viz. sensing region, consisting of a uniform core placed amid two cladding-removed tapered regions 1 and 2. Then, a thin layer of ITO and AZO was deposited over the cladding-removed portion of the uniform fiber core and subsequently the sensing region was kept for the sensitivity measurements [20]. Using a polychromatic source of light (tungsten halogen lamp), light was launched in the fiber core through one end at an angle of incidence ‘θ’, another end of the optical fiber was spectrally interrogated using an Avasoft spectrometer. The spectrometer was further interfaced to a computer to obtain transmission spectrum. Due to the phenomenon of total internal reflection (TIR), light will be propagating inside the fiber core. After this, the guided rays of light propagated through the tapered region and the angle of incidence ‘θ’ gets modified to ‘φ (z)’ which can be calculated as [21](1)$ \begin{eqnarray}\phi (z)\,={\cos }^{-1}\left[\displaystyle \frac{{s}_{i}\,\cos \,\theta }{s(z)}\right]-\,{\rm{\Omega }},\end{eqnarray}$here, ‘${s}_{i}$’ and ‘${s}_{o}$’ denote the radii of the fiber optic core at the input and output ends of the taper, respectively. ‘$s(z)$’ represents the radius of the fiber core at the taper position ‘z’ and ‘${\rm{\Omega }}$’ represents the taper angle which can be written as(2)$ \begin{eqnarray}{\rm{\Omega }}={\tan }^{-1}\left(\displaystyle \frac{{s}_{i}-{s}_{o}}{L}\right),\end{eqnarray}$here ‘L’ represents the length of the sensing layer. If the entire guided rays are launched into the optical fiber, then at the output end of the taper (i.e. $s(z)$ = ${s}_{o}$), angles ${\theta }_{1}\left(={\sin }^{-1}\left(\tfrac{{n}_{2}}{{n}_{1}}\right)\right),$ and ${\theta }_{2}=\tfrac{\pi }{2}$ get converted into ${\phi }_{1}\,\,$and ${\phi }_{2}$ which can be calculated using equation (1) with ${n}_{1},$${n}_{2}$ denoting the refractive indices of the optical fiber core and metal oxide/metal layer, respectively.

Figure 1.

New window|Download| PPT slide
Figure 1.Schematic diagram of proposed fiber optic bio-sensing probe with uniform fiber core placed inbetween two tapered fiber regions 227×137 mm (96×96 DPI).


Further, since we have used the wavelength interrogation method the dispersion relation of each layer has to be taken into consideration. The wavelength-dependent silica core refractive index was calculated using the Sellmeier formula as [22](3)$ \begin{eqnarray}{n}_{1}\left(\lambda \right)=\sqrt{1+\displaystyle \frac{{a}_{1}{\lambda }^{2}}{{\lambda }^{2}-{b}_{1}^{2}}+\displaystyle \frac{{a}_{2}{\lambda }^{2}}{{\lambda }^{2}-{b}_{2}^{2}}+\displaystyle \frac{{a}_{3}{\lambda }^{2}}{{\lambda }^{2}-{b}_{3}^{2}}},\end{eqnarray}$here, ‘$\lambda $’ represents the wavelength measured in μm and ${a}_{1},$${a}_{2},$${a}_{3},$${b}_{1},$${b}_{2}$ and ${b}_{3}$ are Sellmeier coefficients having values as ${a}_{1}$=0.696 1663, ${a}_{2}$=0.407 9426, ${a}_{3}$=0.897 4794, ${b}_{1}$= 0.068 4043, ${b}_{2}$=0.116 2414, and ${b}_{3}$=9.896 161. The dispersion relations of ITO was obtained using the Drude formula and can be written as [23](4)$ \begin{eqnarray}\varepsilon \left(\lambda \right)={\varepsilon }_{r}+{\rm{i}}\,{\varepsilon }_{{\rm{i}}}={\varepsilon }_{\infty }-\displaystyle \frac{{\lambda }^{2}{\lambda }_{c}}{{\lambda }_{p}^{2}\left({\lambda }_{c}+{\rm{i}}\,\lambda \right)},\end{eqnarray}$here, ${\varepsilon }_{\infty }=3.80$ and ${\lambda }_{c},$${\lambda }_{p}$ are the collision and plasma wavelengths, respectively, having values 11.210 76×${10}^{-6}$ m and 5.6497×${10}^{-6}$ m, respectively. Similarly, the dispersion formula for AZO can be written as [17](5)$ \begin{eqnarray}\varepsilon \left(\omega \right)={\varepsilon }_{\infty }-\displaystyle \frac{{\omega }_{p}^{2}}{{\omega }^{2}+{\gamma }^{2}}+\displaystyle \frac{{\rm{i}}\,\gamma }{\omega }\displaystyle \frac{{\omega }_{p}^{2}}{({\omega }^{2}+{\gamma }^{2})},\end{eqnarray}$here, ${\varepsilon }_{\infty }$ denotes the background permittivity, ${\omega }_{p}$ is the plasma frequency and $\gamma $ is the damping frequency and their mathematical values can be expressed as ${\varepsilon }_{\infty }=3.40,$${\omega }_{p}\,=3.22\times {10}^{14}\,{\rm{Hz}}$ and $\gamma =6.86\times {10}^{13}\,{\rm{Hz}}.$ If the whole range of guided rays is launched at the input end of the fiber using a microscopic objective, then the angular power distribution of the guided rays can be calculated as [24](6)$ \begin{eqnarray}{\rm{d}}P\propto \displaystyle \frac{{n}_{1}^{2}\,\sin \,\theta \,\cos \,\theta }{{(1-{n}_{1}^{2}{\cos }^{2}\theta )}^{2}}{\rm{d}}\theta ,\end{eqnarray}$here ‘${n}_{1}$’ denotes the refractive index value of the fiber core and ‘$\theta $’ denotes the incident angle formed between the incident ray of light and the normal drawn on the core cladding interface. The required expression for intensity of reflected light or reflectance $({R}_{p})$ was calculated using the N-layer matrix method. For the present study, N=3 i.e. fiber core/sensing layer/surrounding region. Further, we represent ${t}_{k}$ as the thickness, ${\varepsilon }_{k}$ as the permittivity, ${\mu }_{k}$ as the permeability and ${n}_{k}$ as the refractive index of any random layer. If ${E}_{1}$ and ${B}_{1}$ represent the tangential components of the electric field and magnetic field at the first boundary, respectively then the tangential components of electric field and magnetic field at the Nth layers ${E}_{N-1}\,\,$and ${B}_{N-1}$, respectively can be written as:(7)$ \begin{eqnarray}\left[\begin{array}{c}{E}_{1}\\ {B}_{1}\end{array}\right]=m\left[\begin{array}{c}{E}_{N-1}\\ {B}_{N-1}\end{array}\right],\end{eqnarray}$here ‘m’ represents the characteristic matrix of order 2×2 and thus can be written as(8)$ \begin{eqnarray}m=\displaystyle \prod _{k=2}^{N-1}{m}_{k}=\left[\begin{array}{cc}{m}_{11} & {m}_{12}\\ {m}_{21} & {m}_{22}\end{array}\right],\end{eqnarray}$and(9)$ \begin{eqnarray}{m}_{k}=\left[\begin{array}{cc}\cos \,{\beta }_{k} & (-{\rm{i}}\,\sin \,{\beta }_{k})/{q}_{k}\\ -{\rm{i}}\,{q}_{k}\,\sin \,{\beta }_{k} & \cos \,{\beta }_{k}\end{array}\right],\end{eqnarray}$here,(10)$ \begin{eqnarray}{q}_{k}={\left(\displaystyle \frac{{\mu }_{k}}{{\varepsilon }_{k}}\right)}^{\tfrac{1}{2}}\,\cos \,{\theta }_{k}=\displaystyle \frac{{({\varepsilon }_{k}-{n}_{1}^{2}{\sin }^{2}{\theta }_{1})}^{\tfrac{1}{2}}}{{\varepsilon }_{k}}\,{\rm{and}}\end{eqnarray}$(11)$ \begin{eqnarray}\begin{array}{l}{\beta }_{k}=\displaystyle \frac{2\pi }{\lambda }{n}_{k}\,\cos \,{\theta }_{k}({Z}_{k}-{Z}_{k-1})\\ \,\,=\,\displaystyle \frac{2\pi {t}_{k}}{\lambda }{({\varepsilon }_{k}-{n}_{1}^{2}{\sin }^{2}{\theta }_{1})}^{\tfrac{1}{2}},\end{array}\end{eqnarray}$here, ${\theta }_{1}$ is the angle made by the ray from normal to the kth interface. Thus, the amplitude of reflection coefficient for incident p-polarized light will be written as(12)$ \begin{eqnarray}{r}_{p}=\displaystyle \frac{\left({m}_{11}+{m}_{12}{q}_{N}\right){q}_{1}-\left({m}_{21}+{m}_{22}{q}_{N}\right)}{\left({m}_{11}+{m}_{12}{q}_{N}\right){q}_{1}+\left({m}_{21}+{m}_{22}{q}_{N}\right)}.\end{eqnarray}$

Therefore, the reflectance for a p-polarized light will be(13)$ \begin{eqnarray}{R}_{p}={\left|{r}_{p}\right|}^{2}.\end{eqnarray}$

The required expression for transmitted power in present case of fiber optic probe can be written as(14)$ \begin{eqnarray}{P}_{{\rm{trans}}}=\displaystyle \frac{\displaystyle {\int }_{{\phi }_{1}}^{{\phi }_{2}}{{R}_{p}}^{\left.{N}_{{\rm{ref}}}(\theta \right)}\tfrac{{n}_{1}^{2}\,\sin \,\theta \,\cos \,\theta }{{\left(1-{n}_{1}^{2}{\cos }^{2}\theta \right)}^{2}}{\rm{d}}\theta }{\displaystyle {\int }_{{\phi }_{1}}^{{\phi }_{2}}\tfrac{{n}_{1}^{2}\,\sin \,\theta \,\cos \,\theta }{{\left(1-{n}_{1}^{2}{\cos }^{2}\theta \right)}^{2}}{\rm{d}}\theta },\end{eqnarray}$here, ‘${N}_{{\rm{ref}}}\left(\theta \right)$’ denotes the number of reflections which can be written as(15)$ \begin{eqnarray}{N}_{{\rm{ref}}}\left(\theta \right)=\displaystyle \frac{L}{2{s}_{o}\,\tan (\theta +{\rm{\Omega }})}.\end{eqnarray}$

3. Results and discussion

In our simulation, we have taken ITO and AZO as the LMR active materials coated over a uniform fiber core, sandwiched between two cladding-removed identical tapered fiber regions. All the calculations were done with the help of MATLAB software. It is also to be noted that the first tapered region was used to bring the angle of incidence close to the critical angle and the second tapered region allows the rays to regain their initial values. Since our focus is only on the first two LMRs, therefore we have taken the optimum thicknesses of ITO and AZO as 90 nm and 900 nm, respectively, such that only the first two LMRs are attained [13]. Next, we shall consider the effect of changing the surrounding region refractive indices (SRI) on the LMR wavelength. As a number of biological samples are found to be in aqueous form, we have considered SRI near to the refractive index of distilled water i.e. 1.333.

3.1. Shift in LMR curves

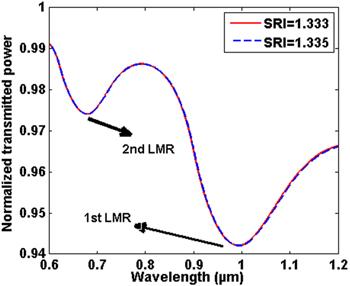
The sensing medium having RI 1.333 was placed around the sensing layer so that the LMR’s spectrum was obtained for ITO and AZO separately. To measure change in the resonance wavelength, the SRI was increased by an amount of 0.002 RIU. The transmission spectra showing the first two LMR curves for ITO and AZO is depicted in figures 2 and 3, respectively. In figure 2, if the SRI is 1.333, then corresponding resonance wavelengths for the first and second LMR were obtained as 2.0818 μm and 0.6319 μm, respectively. But if we increase the SRI to 1.335, then resonance wavelengths shifted to 2.1185 μm and 0.6335 μm, respectively. Similarly, from figure 3, if the SRI is 1.333 then resonance wavelengths corresponding to the first and second LMR are obtained as 0.9927 μm and 0.3500 μm, respectively and shifted to 0.9942 μm and 0.6796 μm if the SRI was increased to 1.335. Thus, it was observed that with an increase in the SRI, the LMR curves show a red shift. This is because if we increase the SRI, the effective index of the multilayer structure also gets changed and hence the resonant excitation of the LMR takes place at some higher value of the wavelength [17]. Also from figures 2 and 3, we inferred that the first LMR for ITO and AZO lies near the IR region whereas the second LMR lies in the visible region. The multiple LMRs can be generated if we further increase the thickness of the coated materials.

Figure 2.

New window|Download| PPT slide
Figure 2.Transmission spectra for ITO deposited over the uniform core of optical fiber at a TR of 1.6.

Figure 3.

New window|Download| PPT slide
Figure 3.Transmission spectra for AZO deposited over the uniform core of optical fiber at a TR of 2.0.

3.2. Effect of tapering

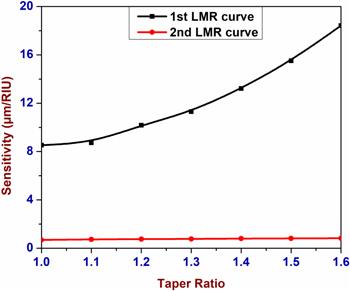
In the case of ITO, if the TR is 1.0 i.e. an untapered fiber core around a uniform core sensing region, sensitivity values of the first and second LMRs are obtained as 8.53 μm RIU⁻¹ and 0.69 μm RIU⁻¹, respectively. It was observed that sensitivity enhances if the TR is increased. Sensitivity values were calculated up to a TR of 1.6 with an increment of 0.1. From table 1, it can be seen that the sensitivity is increased for both the LMRs with an increase in TR. Maximum sensitivity values for the first and second LMRs were obtained as 18.4250 μm RIU⁻¹ and 0.8250 μm RIU⁻¹, respectively at a TR of 1.6 confirming that the first LMR was more sensitive compared to the second LMR. If there is a further increase in the TR, then a distorted LMR spectrum is obtained and sensitivity cannot be calculated. Therefore 1.6 is the optimum value of TR for ITO in sensing applications at this particular thickness. The enhancement in the sensitivity can be explained as follows: using taper region 1, the angle of the incidence of bounded rays into the optical fiber comes closer to the critical angle. This can be obtained by taking the optimum output diameter of taper fiber core due to which entire bounded rays will propagate inside the sensing region. Then, after crossing the sensing area, the rays will enter into tapered region 2, which further converts the angle of bounded rays to their original values in order to get the complete bounded rays at the output end of the optical fiber. If we choose the optimum value of the tapered core diameter, then no ray will escape out and in the sensing region, a major number of rays will propagate with the angle closer to the critical angle. Due to this reason the evanescent wave will penetrate in the sensing layer with a larger penetration depth as a result of which stronger coupling between the evanescent wave and the lossy modes will lead to the higher value of the sensitivity of the proposed fiber optic probe. Figure 4 shows the sensitivity comparison of the first and second LMRs for the present fiber optic probe.


Table 1.
Table 1.Values of sensitivities of the first and second LMRs for ITO coated over uniform fiber core with TRs.

	Sensitivity (μm RIU−1)
TR	1st LMR	2nd LMR
1.0	8.5300	0.6900
1.1	8.7250	0.7300
1.2	10.1750	0.7550
1.3	11.3050	0.7700
1.4	13.2100	0.7950
1.5	15.5100	0.8150
1.6	18.4250	0.8250

New window|CSV

Figure 4.

New window|Download| PPT slide
Figure 4.Sensitivity comparison of the first and second LMRs with TRs for ITO.


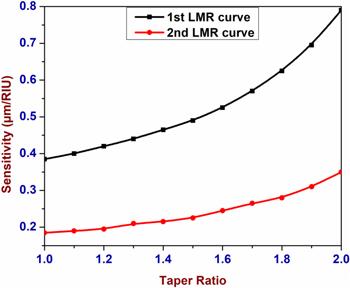
Similarly, for AZO at a TR of 1.0, the sensitivity values for the first and second LMRs are obtained as 0.385 μm RIU⁻¹ and 0.185 μm RIU⁻¹, respectively. The values are increased further by increasing the TR up to 2.0 with an increment of 0.1. From table 2 it can be seen that the maximum values of sensitivity for the first and second LMRs are 0.79 μm RIU⁻¹ and 0.35 μm RIU⁻¹, respectively at a TR of 2.0. Figure 5 shows the sensitivity comparison of the first and second LMRs for the present fiber optic probe with AZO, showing that the first LMR is much more sensitive than the second LMR.


Table 2.
Table 2.Values of sensitivities of the first and second LMRs for AZO coated over uniform fiber core with TRs.

	Sensitivity (μm RIU−1)
TR	1st LMR	2nd LMR
1.0	0.3850	0.1850
1.1	0.4000	0.1900
1.2	0.4200	0.1950
1.3	0.4400	0.2100
1.4	0.4650	0.2150
1.5	0.4900	0.2250
1.6	0.5250	0.2450
1.7	0.5700	0.2650
1.8	0.6250	0.2800
1.9	0.6950	0.3100
2.0	0.7900	0.3500

New window|CSV

Figure 5.

New window|Download| PPT slide
Figure 5.Sensitivity comparison of the first and second LMRs with TRs for AZO.

3.3. Comparison with SPR

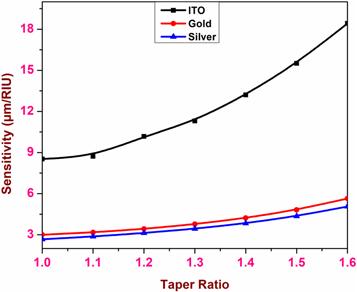
Au and Ag of optimum thicknesses 50 nm have been used here to show the comparison of an LMR sensor with an SPR sensor. Table 3 provides the sensitivity values for Au and Ag when used as the SPR active material in the designed tapered structure. From the results we inferred that with an increase in TR, sensitivity increases up to a TR of 1.6. After this the SPR curves become shallow and its sensitivity value cannot be realized practically. At a TR of 1.6, sensitivity values are 5.6425 μm RIU⁻¹ and 5.0615 μm RIU⁻¹ for Au and Ag, respectively. Figure 6 shows sensitivity comparison of the first LMR of ITO, Au and Ag. From this figure, we can see that the trend of sensitivity is ITO>Au>Ag. Thus, it is established that the LMR sensor with the present fiber optic probe shows a larger value of sensitivity when compared with the conventional fiber optic SPR sensor. Also, the use of a suitable LMR active material with proper thickness is an essential parameter to develop a highly sensitive fiber optic sensing probe.


Table 3.
Table 3.Values of sensitivities for Au and Ag coated over uniform fiber core with TRs.

	Sensitivity (μm RIU−1)
TR	For gold (Au)	For silver (Ag)
1.0	3.0020	2.6725
1.1	3.1730	2.8725
1.2	3.4300	3.1240
1.3	3.7720	3.4395
1.4	4.2195	3.8395
1.5	4.8175	4.3605
1.6	5.6425	5.0615

New window|CSV

Figure 6.

New window|Download| PPT slide
Figure 6.Sensitivity comparison of LMR- and SPR-based optical fiber probes.

4. Conclusion

An LMR-supported tapered fiber optic bio-sensor by depositing a thin layer of metal oxide on a uniform fiber core placed inbetween two unclad tapered fiber regions is modeled and studied theoretically. It is observed that the sensitivity values for both the LMRs increases with an increase in the TR up to a certain value. The results also show that the first LMR is more sensitive than the 2nd LMR for both ITO and AZO and records a 3-fold increment in sensitivity when compared with conventional SPR-based fiber optic sensors. It is therefore concluded that the present probe structure with the given parameters will possess maximum sensitivity and hence is more suitable in bio-sensing applications. Also the study recommends to choose ITO as the LMR active material for making fiber optic sensors with large values of sensitivity.

Acknowledgments

One of the authors, Mr Vikas, gratefully acknowledges the Department of Science and Technology (DST), INDIA for providing the INSPIRE fellowship (Registration No.-IF170543).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Villar I D Zamarreno C R Hernaez M Arregui F J Matias I R 2010 Lossy mode resonance generation with indium-tin-oxide-coated optical fibers for sensing applications
J. Lightwave Technol. 28 111 117
DOI:10.1109/JLT.2009.2036580 [Cited within: 2]

[2]Villar I D Hernaez M Zamarreno C R Sanchez P Fernandez-Valdivielso C Arregui F J Matias I R 2012 Design rules for lossy mode resonance based sensors
Appl. Opt. 51 4298 4307
DOI:10.1364/AO.51.004298

[3]Wang Q Zhao W M 2018 A comprehensive review of lossy mode resonance-based fiber optic sensors
Opt. Lasers Eng. 100 47 60
DOI:10.1016/j.optlaseng.2017.07.009 [Cited within: 2]

[4]Usha S P Shrivastav A M Gupta B D 2018 Semiconductor metal oxide/polymer based fiber optic lossy mode resonance sensors: a contemporary study
Opt. Fiber Technol. 45 146 166
DOI:10.1016/j.yofte.2018.07.003 [Cited within: 1]

[5]Kaur D Sharma V K Kapoor A 2014 High sensitivity lossy mode resonance sensors
Sensors Actuators B 198 366 376
DOI:10.1016/j.snb.2014.03.058 [Cited within: 2]

[6]Paliwal N John J 2014 Theoretical modeling of lossy mode resonance based refractive index sensors with ITO/TiO₂ bilayers
Appl. Opt. 53 3241 3246
DOI:10.1364/AO.53.003241 [Cited within: 1]

[7]Zubiate P Zamarreño C R Del Villar I Matias I R Arregui F J 2016 Tunable optical fiber pH sensors based on TE and TM lossy mode resonances (LMRs)
Sensors Actuators B 231 484 490
DOI:10.1016/j.snb.2016.03.024 [Cited within: 1]

[8]Arregui F J Del Villar I Zamarreño C R Zubiate P Matias I R 2016 Giant sensitivity of optical fiber sensors by means of lossy mode resonance
Sensors Actuators B 232 660 665
DOI:10.1016/j.snb.2016.04.015 [Cited within: 2]

[9]Del Villar I et al. 2017 Optical sensors based on lossy-mode resonances
Sensors Actuators B 240 174 185
DOI:10.1016/j.snb.2016.08.126 [Cited within: 1]

[10]Hernaez M Mayes A G Melendi-Espina S 2018 Graphene oxide in lossy mode resonance-based optical fiber sensors for ethanol detection
Sensors 18 1 10
DOI:10.3390/s18010058 [Cited within: 1]

[11]Wu L Wang Q Ruan B Zhu J You Q Dai X Xiang Y 2018 High-performance lossy-mode resonance sensor based on few-layer black phosphorus
J. Phys. Chem. 122 7368 7373
DOI:10.1021/acs.jpcc.7b12549 [Cited within: 1]

[12]Verma R K Joy A Sharma NVikas 2019 Performance study of surface plasmon resonance and lossy mode resonance based fiber optic sensors utilizing silver and indium oxide layers: an experimental investigation
Opt. Laser Technol. 112 420 425
DOI:10.1016/j.optlastec.2018.11.041 [Cited within: 1]

[13]VikasVerma R K 2018 Sensitivity enhancement of a lossy mode resonance based tapered fiber optic sensor with an optimum taper profile
J. Phys. D: Appl. Phys. 51 415302
DOI:10.1088/1361-6463/aadb0f [Cited within: 1]

[14]Ozcariz A Dominik M Smietana M Zamarreno C R Del Villar I Arregui F J 2019 Lossy mode resonance optical sensors based on Indium-gallium-zinc oxide thin film
Sensors Actuators A 290 20 27
DOI:10.1016/j.sna.2019.03.010 [Cited within: 1]

[15]Wang Q Li X Zhao W Jin S 2019 Lossy mode resonance based fiber optic sensor using layer by layer SnO₂ thin film and SnO₂ nanoparticles
Appl. Surf. Sci. 492 374 381
DOI:10.1016/j.apsusc.2019.06.168 [Cited within: 1]

[16]Smita Singh R KVerma Gupta B D 2009 Surface plasmon resonance based fiber optic sensor with symmetric and asymmetric metallic coatings: a comparative study
Sensors Transducers 100 116 124
[Cited within: 1]

[17]Zhang Y Wei T Dong W Huang C Zhang K Sun Y Chen X Dai N 2013 Near-perfect infrared absorption from dielectric multilayer of plasmonic aluminum-doped zinc oxide
Appl. Phys. Lett. 102
DOI:10.1063/1.4808206 [Cited within: 3]

[18]Kretschmann E Raether H 1968 Radiative decay of non-radiative surface plasmons excited by light
Z. Naturforsch. 23 2135 2136
DOI:10.1515/zna-1968-1247 [Cited within: 1]

[19]Birks T A Li Y W 1992 The Shape of Fiber Tapers
J. Lightwave Technol. 10 432 438
DOI:10.1109/50.134196 [Cited within: 1]

[20]Vikas Verma R K 2019 Design considerations of a surface plasmon resonance (SPR) based tapered fiber optic bio-sensing probe with graphene-MoS₂ over layers
Optik 180 330 343
DOI:10.1016/j.ijleo.2018.11.081 [Cited within: 1]

[21]Snyder A W Love J 1983 Optical Waveguide Theory Berlin Springer
[Cited within: 1]

[22]Ghatak A K Thyagarajan K 1998 Introduction to Fiber Optics Cambridge Cambridge University Press
[Cited within: 1]

[23]Shah K Sharma N K Sajal V 2017 SPR based fiber optic sensor with bi layers of indium tin oxide and platinum: a theoretical evaluation
Optik 135 50 56
DOI:10.1016/j.ijleo.2017.01.055 [Cited within: 1]

[24]Gupta B D Sharma A Singh C D 1993 Evanescent wave absorption sensors based on uniform and tapered fibers: a comparitive study of their sensitivities
Int. J. Optoelectron. 8 409 418
[Cited within: 1]