Feng Huang¹, Han-Shuang Chen^2,?1 School of Mathematics and Physics, Anhui Jianzhu University, Hefei 230601, China
2 School of Physics and Materials Science, Anhui University, Hefei 230601, China

Corresponding authors: ?E-mail: chenhshf@ahu.edu.cn

Received:2019-06-22Online:2019-12-1

Fund supported:

*Supported by the National Natural Science Foundation of China under Grant .Nos. 11875069 Supported by the National Natural Science Foundation of China under Grant .Nos. 11405001 the Key Scientific Research Fund of Anhui Provincial Education Department under Grant.No. KJ2019A0781

Abstract
Heterogeneous mean-field theory is commonly used methodology to study dynamical processes on complex networks, such as epidemic spreading and phase transitions in spin models. In this paper, we propose an improved heterogeneous mean-field theory for studying the Ising model on complex networks. Our method shows a more accurate prediction in the critical temperature of the Ising model than the previous heterogeneous mean-field theory. The theoretical results are validated by extensive Monte Carlo simulations in various types of networks.
Keywords： heterogeneous mean field theory;Ising model;phase transition


PDF (268KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Feng Huang, Han-Shuang Chen. An Improved Heterogeneous Mean-Field Theory for the Ising Model on Complex Networks*. [J], 2019, 71(12): 1475-1479 doi:10.1088/0253-6102/71/12/1475

1 Introduction

Many social, biological, and physical phenomena can be well understood on the top of complex networks.^[1-6] A common topic in the research community is to establish the relationship between the topologies and the dynamics on them. Owing to degree heterogeneity in the interacting patterns, many fascinating phenomena have been revealed, such as the anomalous scaling behavior of Ising model,^[7-11] a vanishing percolation threshold,^[12-13] the absence of epidemic thresholds that separate healthy and endemic phases^[14-16] and explosive emergence of phase transitions.^[17-30]

The heterogeneous mean-field (HMF) theory has been widely used to study dynamical processes on complex networks.^[3,5-6] This theory is based on the assumption that the nodes of the same degree are statistically equivalent. The main purpose of the HMF theory is to derive the dynamical equations for the quantities of interest in different degree classes. In general, the set of dynamical equations are intertwined with each other. However, for degree uncorrelated networks, they can be reduced to a single equation for an order parameter, such as the average magnetization in the Ising model^[8] and the average infection probability in the susceptible-infected-susceptible model.^[14] By linear stability analysis near the phase transition point, the HMF theory can produce an elegant analytical result of the phase transition point. For example, it has been shown that the critical temperature of the Ising model is $T_c=\langle {k^2} \rangle / \langle {k} \rangle $,^[8] where $\langle {k^n} \rangle$ is the $n$th moment of degree distribution $P(k)$. For scale-free networks, $P(k) \sim k ^{-\gamma}$ with the exponent $\gamma<3$, $\langle {k^2} \rangle$ is divergent, and thus $T_c \rightarrow \infty$. The HMF theory has also shown its power in many other models, such as rumor spreading model,^[31-32] metapopulation model,^[33] zero-temperature Ising model,^[34-35] majority-vote model,^[36-37] etc.

In the present work, we propose an improved heterogenous mean-field (IHMF) theory to study the Ising model on complex networks. We derive the mean-field equation and then obtain the critical condition under which the phase transition temperature should be satisfied. Under the approximation of large average degree, the phase transition temperature $T_c$ is given analytically, $T_c = {{\langle {{k^2}} \rangle }}/{{\langle k \rangle }} - {{\langle k \rangle \langle {{k^3}} \rangle }}/{{{{\langle {{k^2}} \rangle }^2}}}$, that is different from the result of the HMF theory, ${{\langle {{k^2}} \rangle }}/{{\langle k \rangle }}$. By extensive Monte Carlo simulations in diverse types of networks, we find that our theoretical result is more successful in predicting $T_c$ than the previous HMF theory.

2 Model and Simulation Details

The Ising model in a network of size $N$ is described by the Hamiltonian,

(1) $$ E = - J\sum\limits_{i < j} {{A_{ij}}{\sigma _i}{\sigma _j}}\,, $$
where spin variable $\sigma_i$ at node $i$ takes either $+1$ (up) or $-1$ (down). $J>0$ is the ferrimagnetic interaction constant. The elements of the adjacency matrix of the network take $A_{ij}=1$ if nodes $i$ and $j$ are connected and $A_{ij}=0$ otherwise.

The Monte Carlo (MC) simulation is performed by the so-called Glauber spin-flip dynamics,^[38] in which one attempts to flip each spin once, on average, during each MC cycle. In each attempt, a randomly chosen spin $i$ is tried to flip with the probability

(2)$$ {w_i}= \frac{1}{2}\Big[ {1 - \tanh \Big( {\frac{{\beta \Delta E}}{2}} \Big)} \Big]\,, $$
where $\beta=1/(k_B T)$ is the inverse temperature, $k_B$ is the Boltzmann constant, and $\Delta E = 2{\sigma _i}\sum\nolimits_j {{A_{ij}}{\sigma _j}}$ is the energy change due to the flipping process.

3 Theoretical Results

Let us define $m_k$ as the average magnetization of a node of degree $k$, i.e., ${m_k} = N_k^{ - 1}\sum\nolimits_{i,{k_i} = k}^{} {{\sigma _i}}$, where $N_k$ is the number of nodes of degree $k$. For a network without degree correlation, the probability of an end node of a randomly chosen edge having connectivity $k$ is $k$P($k$)/${{\langle k \rangle }}$,^[3] where $P(k)=N_k/N$ is the probability of a randomly chosen node having connectivity $k$, and $\langle k \rangle = \sum\nolimits_{k'} {k'} P({k'})$ is the average degree. Thus, the average magnetization of an end node of a randomly chosen edge can be written as,

(3) $$ tilde m = \sum\limits_{k} {\frac{{k P(k)}}{{\langle k\rangle }}} {m_{k}}\,. $$
This implies that the spin orientation of an end node of a randomly chosen edge points up or down with the probability $(1+\tilde m)/2$ or $(1-\tilde m)/2$, respectively. Thus, for a node of degree $k$, the probability that there are $n$ up spins among the neighborhood of the node can be written as a binomial distribution

(4) $$ {p_{k,n}(\tilde m)} = C_k^n {\Big( {\frac{{1 + \tilde m}}{2}}\Big)^n}{\Big( {\frac{{1 - \tilde m}}{2}} \Big)^{k -n}}\,, $$
where $C_k^n = k!/[n!(k-n)!]$ is the binomial coefficient. For an up-spin node of degree $k$ with $n$ up-spin neighbor, the energy change to flip this spin is $4n-2k$. Combining Eqs. (2) and (4), we can write down the probability of flipping an up-spin node of degree $k$,

(5) $$ w_k^ + = \frac{1}{2} - \frac{1}{2}\sum\limits_{n = 0}^k {{p_{k,n}}}\tanh ( {\beta ( {2n - k} )} )\,. $$
Likewise, we can express the probability of flipping a down-spin node of degree $k$ as

(6) $$ w_k^ - = \frac{1}{2} + \frac{1}{2}\sum\limits_{n = 0}^k {{p_{k,n}}}\tanh ( {\beta ( {2n - k} )} )\,. $$
At each spin-flip process, the expectation of the change in $m_k$ can be written as

(7) $$ \Delta {m_k} =\frac{{{N_k}}}{N}\Big( { - \frac{2}{{{N_k}}}}\Big)\Big( {\frac{{1 + {m_k}}}{2}} \Big)w_k^ +\\\ +\frac{{{N_k}}}{N}\Big( { + \frac{2}{{{N_k}}}} \Big)\Big({\frac{{1 - {m_k}}}{2}} \Big)w_k^ -\,, $$
where the factor is $N_k/N$ which is the probability that a class of nodes of degree $k$ are chosen, and $\mp 2/N_k$ is the change in $m_k$ due to the flip of an up (down) spin of degree $k$, and $(1 \pm m_k)/2$ is the probability of an up (down) spin of degree $k$ is chosen. If we set $\Delta t=1/N$, Eq. (7) can be rewritten as

(8) $$ \frac{{d{m_k}}}{{d t}} = - ( {1 + {m_k}} )w_k^ + + ( {1 - {m_k}} )w_k^ - {\frac{{d{m_k}}}{{d t}} }= - {m_k} + \sum\limits_{n = 0}^k {{p_{k,n}(\tilde m)}} \tanh [ {\beta ( {2n - k} )} ]\,. $$
Substituting Eq. ({3}) into Eq. ({8}), we arrive at a self-consistent equation of $\tilde m$,

(9) $$ \frac{{d\tilde m}}{{d t}} = - \tilde m + \sum\limits_k {\frac{{kP(k)}}{{\langle k \rangle }}} \sum\limits_{n = 0}^k{{p_{k,n}(\tilde m)}} \tanh [ {\beta ( {2n - k} )}]\,. $$
In equilibrium, $d \tilde m/d t=0$ and $d m_k/d t=0$, we have

(10) $$ \tilde m = \sum\limits_k{\frac{{k P(k)}}{{\langle k \rangle }}} \sum\limits_{n =0}^k {{p_{k,n}(\tilde m)}} \tanh [ {\beta ( {2n - k})} ]\,, $$
(11) $$ {m_k}= \sum\limits_{n = 0}^k {{p_{k,n}(\tilde m)}} \tanh [ {\beta ( {2n - k} )} ]\,. $$
Considering the fact

$ p_{k,n}(0)= p_{k,k-n}(0)\,, \quad \tanh (-x) = -\tanh (x)\,,$

it is not hard to verify that $\tilde m=0$ is always a solution of Eq. ({10}). Such a trivial solution corresponds to a disordered phase. The other solutions corresponding to $\tilde m\neq 0$ (an ordered phase) exist when the solution of $\tilde m=0$ loses its stability. This requires that the derivative of the right hand side of Eq. ({10}) with respect to $\tilde m$ is larger than one at $\tilde m=0$. The requirement yields the critical temperature of the Ising model that separates the disorder phase and ordered phase. To the end, we expand $p_{k,n}$ around $\tilde m=0$ to the first order, $ {p_{k,n}(\tilde m)} = p_{k,n}(0) + p_{k,n}(0) ( {2n - k} )\tilde m + O(\tilde m^2) $ with ${p_{k,n}}(0) = C_k^n{(1/ 2)^k}$.)^k}$. The critical temperature is determined by

(12) $$ {\sum\limits_k {\frac{{k P(k)}}{{\langle k \rangle }}\sum\limits_{n = 0}^k {{p_{k,n}}(0)(2n - k)\tanh[ {\beta_c(2n - k)} ]} } = 1\,.}$$
Equation (12) is the main result of the present work. For a given degree distribution $P(k)$, the critical temperature $T_c=1/\beta_c$ can be calculated numerically by Eq. ({12}). Moreover, for networks with large average degree, $\beta_c$ approaches to zero. To the end, we expanse

(13) $$ \tanh( {{\beta _c}(2n - k)} ) \approx {\beta _c}(2n - k)- \frac{1}{3}\beta _c^3{(2n - k)^3}\,, $$
and substitute Eq. ({13}) into Eq. ({12}), we have

(14) $$ \sum\limits_k {\frac{{k P(k)}}{{\langle k \rangle }}}\Big[ {\langle {{{(2n - k)}^2}} \rangle {\beta _c} -\frac{1}{3}\langle {{{(2n - k)}^4}} \rangle \beta _c^3}\Big] = 1\,, $$
where

(15) $$ \langle {{{(2n - k)}^2}} \rangle = \sum\limits_{n = 0}^k{{p_{k,n}}(0){{(2n - k)}^2}} = k\,, $$
(16) $$ \langle {{{(2n - k)}^4}} \rangle = \sum\limits_{n = 0}^k{{p_{k,n}}(0){{(2n - k)}^4}} = k(3 k-2)\approx 3k^2\,. $$
Substituting Eqs. ({15}) and ({16}) into Eq. ({14}), we obtain

(17) $$ \frac{{\langle {{k^2}} \rangle }}{{\langle k\rangle }}{\beta _c} - \frac{{\langle {{k^3}}\rangle }}{{\langle k \rangle }}\beta _c^3 =1\,, $$
where $\langle {{k^n}} \rangle = \sum\nolimits_k{{k^n}P(k)}$ is the $n$-th moment of degree distribution.

If we drop out the second term on the left hand side of Eq. (17), we recover to the result of the HMF theory,

(18) $$ T_c^{\rm HMF} = \frac{{\langle {{k^2}} \rangle}}{{\langle k \rangle }}\,. $$
Substituting Eq. (18) into Eq. (17), we arrive at an improved result of the HMF theory,

(19) $$ T_c^{\rm IHMF} = \frac{{\langle {{k^2}} \rangle}}{{\langle k \rangle }} - \frac{{\langle k\rangle \langle {{k^3}} \rangle }}{{{{\langle{{k^2}} \rangle }^2}}}\,. $$

4 Numerical Validation

In order to validate the theoretical result, we need to numerically determine $T_c$, which can be located by calculating the so-called Binder's fourth-order cumulant $U$,^[39] defined as

(20) $$ U = 1 - \frac{{[ {\langle {{m^4}} \rangle }]}}{{3{{[ {\langle {{m^2}} \rangle }]}^2}}}\,, $$
where $m = \sum_{i = 1}^N {{\sigma _i}}/N$ is the average magnetization per node, $\langle \cdot \rangle$ denotes time averages taken at equilibrium, and $[ \cdot ]$ stands for the averages over different network configurations for a given degree distribution. $T_c$ is estimated as the point where the curves $U \sim T$ for different network sizes $N$ intercept each other.

We first show the results in regular random networks (RRNs), in which each node is randomly connected to exactly $k$ neighbors and degree distribution follows the $\delta$-function, and thus $\langle {{k^n}} \rangle = {k^n}$,

(21) $$ T_{c,\rm RRN}^{\rm HMF} = k\,, $$
(22)$$ T_{c,\rm RRN}^{\rm IHMF} = k - 1\,.$$
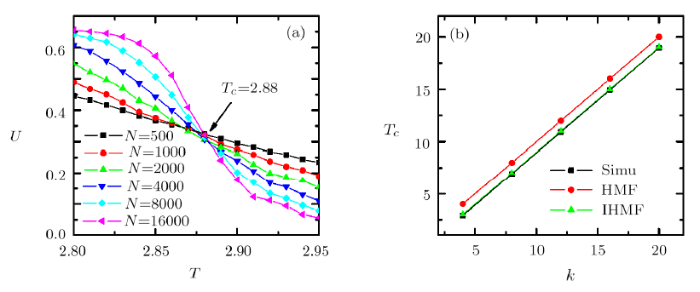
In Fig. 1(a), we show $U$ as a function of $T$ for different network sizes $N$ in RRNs with $k=4$. The intersection point locates the critical temperature $T_c=2.88$, which is closer to our theoretical result $k-1=3$ (Eq. (22)) than the previous one $k=4$ (Eq. (21)). In Fig. 1(b), we compare the numerical results of $T_c$ with the theoretical predictions for different $k$'s in RRNs. It is obvious that our improved theory is superior to the previous HMF theory.

New window|Download| PPT slide
Fig. 1(Color online) (a) The Binder's fourth-order cumulant $U$ as a function of the temperature $T$ for different network sizes $N$ in RRNs with $k=4$. (b) The critical temperature $T_c$ in RRNs as a function of $k$.

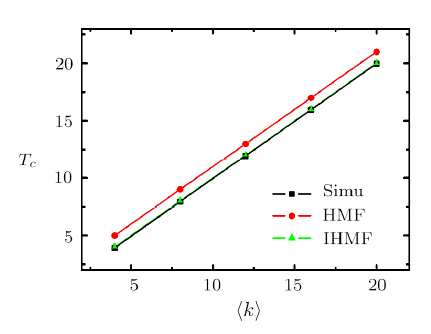
New window|Download| PPT slide
Fig. 2(Color online) The critical temperature $T_c$ in ER random networks as a function of average degree $\langle k\rangle$.



For Erd\"os-Rényi (ER) random networks whose degree distribution follows a Poisson distribution,$P(k) = e^{-\langle k \rangle } {\langle k \rangle }^k/ {k!}$, we have $\langle {{k^2}} \rangle = {\langle k \rangle^2} + \langle k \rangle$ and $\langle {{k^3}}\rangle = {\langle k \rangle ^3} + 3{\langle k \rangle ^2} + \langle k \rangle$,

(23) $$ T_{c,\rm ER}^{\rm HMF} = \langle k \rangle + 1\,, $$
(24) $$ T_{c,\rm ER}^{\rm IHMF} = \langle k \rangle -\frac{{\langle k \rangle }}{{{{( {\langle k \rangle + 1} )}^2}}} \approx \langle k \rangle\,. $$
In Fig. 2, we compare the numerical results of $T_c$ with the theoretical predictions for different average degree $\langle k \rangle$ in ER random networks. As expected, our improved theory is superior to the previous HMF theory.

For scale-free networks (SFNs) whose degree distribution follows a power-law function,

$P(k) = ( {\gamma - 1} )k_0^{\gamma- 1}{k^{ - \gamma }}\,,$

with the minimal degree $k_0$ and the power exponent of degree distribution $\gamma$, we have $\langle k\rangle=( {\gamma - 1} ){k_0}/({\gamma - 2})$,$\langle k^2 \rangle=( {\gamma - 1} ){k_0^2}/({\gamma - 3)}$,$\langle k^3 \rangle=( {\gamma - 1} ){k_0^3}/({\gamma - 4})$

(25) $$ T_{c,\rm SF}^{\rm HMF} = \frac{{\gamma - 2}}{{\gamma -3}}{k_0}\,, $$
(26) $$ T_{c,\rm SF}^{\rm IHMF} = \frac{{\gamma - 2}}{{\gamma - 3}}{k_0} -\frac{{{{( {\gamma - 3} )}^2}}}{{( {\gamma - 2})( {\gamma - 4} )}}\,. $$
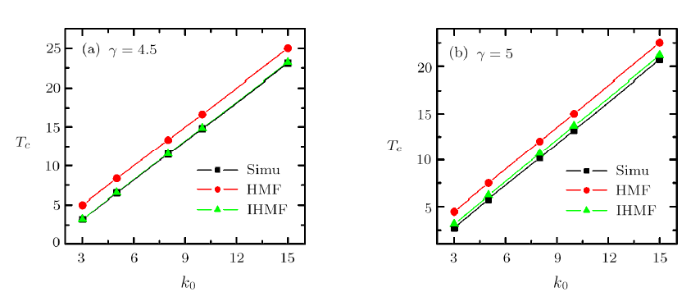
As mentioned before, for SFNs with $\gamma \leq 3$, $\langle k^2 \rangle$ is divergent in the limit of $N \rightarrow \infty$, and thus $T_c \rightarrow \infty$. While for $3<\gamma\leq4$, $\langle k^3 \rangle$ is divergent in the limit of $N \rightarrow \infty$, and therefore Eq. ({26}) is only valid for $\gamma>4$. In Fig. 3(a) and 3(b), we show the results in SFNs with $\gamma=4.5$ and $\gamma=5.0$,respectively. It is obvious that our improved theory is more inagreement with the simulation results than the previous HMF theory.

New window|Download| PPT slide
Fig. 3(Color online) The critical temperature $T_c$ in SF networks as a function of minimal degree $k_0$. (a) $\gamma=4.5$;(b) $\gamma=5$.

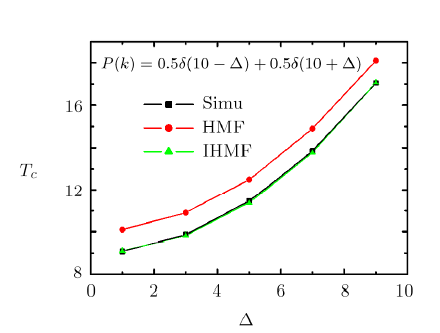
New window|Download| PPT slide
Fig. 4(Color online) The critical temperature $T_c$ in random networks with a bimodal degree distribution $P(k) =({1}/{2})\delta ( {k - \langle k \rangle - \Delta} ) + ({1}/{2})\delta ( {k - \langle k \rangle + \Delta } )$ with $\langle k\rangle=10$.



At last, we construct a network with degree distribution following a bimodal distribution $P(k) = ({1}/{2})\delta ( {k -\langle k \rangle - \Delta } ) + ({1}/{2})\delta( {k - \langle k \rangle + \Delta } )$. We have $\langle k \rangle = \langle k \rangle$,$\langle {{k^2}} \rangle = {\langle k \rangle^2} + {\Delta ^2}$, and $\langle {{k^3}} \rangle = {\langle k \rangle^3} + 3{\Delta^2}\langle k \rangle$. In terms of Eqs. ({18}) and ({19}), we can obtain the results of the HMF and IHMF theories. As shown in Fig. 4, the IHMF theory is more accurate in predicting the critical temperature than the HMF theory.

5 Conclusions

In conclusion, we have proposed an improved heterogeneous mean-field theory to study the Ising model on complex networks. Our theory shows that the critical temperature of the Ising model is $T_c=\langle k^2 \rangle/\langle k \rangle -\langle k \rangle \langle k^3 \rangle/\langle k^2 \rangle ^2$, that is an improvement of the result of the customary heterogeneous mean-field theory, $\langle k^2 \rangle/\langle k \rangle$. By comparing the critical temperature with simulations in various networks, we have shown that our theoretical prediction is more accurate than the previous heterogeneous mean-field one.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] S. Boccaletti, V. Latora, Y. Moreno , et al., Phys. Rep. 424(2006) 175.
DOI:10.1016/j.physrep.2005.10.009URL [Cited within: 1]

[2] A. Arenas , A. Díaz-Guilera, J. Kurths, et al., Phys. Rep. 469(2008) 93.
DOI:10.1016/j.physrep.2008.09.002URL

[3] S. N. Dorogovtsev, A. V. Goltsev, J. F. F . Mendes, Rev. Mod. Phys. 80(2008) 1275.
[Cited within: 2]

[4] S. Boccaletti, G. Bianconi, R. Criado , et al., Phys. Rep. 544(2014) 1.
DOI:10.1016/j.physrep.2014.07.001URL
In the past years, network theory has successfully characterized the interaction among the constituents of a variety of complex systems, ranging from biological to technological, and social systems. However, up until recently, attention was almost exclusively given to networks in which all components were treated on equivalent footing, while neglecting all the extra information about the temporal- or context-related properties of the interactions under study. Only in the last years, taking advantage of the enhanced resolution in real data sets, network scientists have directed their interest to the multiplex character of real-world systems, and explicitly considered the time-varying and multilayer nature of networks. We offer here a comprehensive review on both structural and dynamical organization of graphs made of diverse relationships (layers) between its constituents, and cover several relevant issues, from a full redefinition of the basic structural measures, to understanding how the multilayer nature of the network affects processes and dynamics. (C) 2014 Elsevier B.V.

[5] A. Barrat, M. Barth′elemy, A. Vespignani , Dynamical Processes on Complex Networks, Cambridge University Press, Cambridge( 2008).
[Cited within: 1]

[6] R. Pastor-Satorras, C. Castellano, P. Van Mieghem, A. Vespignani , Rev. Mod. Phys. 87(2015) 925.
DOI:10.1103/RevModPhys.87.925URL [Cited within: 2]

[7] A. Aleksiejuk, J. A. Holysta, D. Stauffer , Physica A 310 ( 2002) 260.
[Cited within: 1]

[8] G. Bianconi , Phys. Lett. A 303 ( 2002) 166.
[Cited within: 2]

[9] S. N. Dorogovtsev, A. V. Goltsev, J. F. F. Mendes , Phys. Rev. E 66 ( 2002) 016104.
DOI:10.1103/PhysRevE.66.016104URLPMID:12241423
We find the exact critical temperature T(c) of the nearest-neighbor ferromagnetic Ising model on an &quot;equilibrium&quot; random graph with an arbitrary degree distribution P(k). We observe an anomalous behavior of the magnetization, magnetic susceptibility and specific heat, when P(k) is fat tailed, or, loosely speaking, when the fourth moment of the distribution diverges in infinite networks. When the second moment becomes divergent, T(c) approaches infinity, the phase transition is of infinite order, and size effect is anomalously strong.

[10] M. Leone, A. Vázquez, A. Vespignani, R. Zecchina , Eur. Phys. J. B 28 ( 2002) 191.


[11] S. Bradde, F. Caccioli, L. Dall’Asta, G. Bianconi , Phys. Rev. Lett. 104(2010) 218701.
DOI:10.1103/PhysRevLett.104.218701URLPMID:20867147 [Cited within: 1]
An anomalous mean-field solution is known to capture the nontrivial phase diagram of the Ising model in annealed complex networks. Nevertheless, the critical fluctuations in random complex networks remain mean field. Here we show that a breakdown of this scenario can be obtained when complex networks are embedded in geometrical spaces. Through the analysis of the Ising model on annealed spatial networks, we reveal, in particular, the spectral properties of networks responsible for critical fluctuations and we generalize the Ginsburg criterion to complex topologies.

[12] R. Cohen, K. Erez , D. ben Avraham, and S. Havlin, Phys. Rev. Lett. 85(2000) 4626.
DOI:10.1103/PhysRevLett.85.4626URLPMID:11082612 [Cited within: 1]
A common property of many large networks, including the Internet, is that the connectivity of the various nodes follows a scale-free power-law distribution, P(k) = ck(-alpha). We study the stability of such networks with respect to crashes, such as random removal of sites. Our approach, based on percolation theory, leads to a general condition for the critical fraction of nodes, p(c), that needs to be removed before the network disintegrates. We show analytically and numerically that for alpha&lt;/=3 the transition never takes place, unless the network is finite. In the special case of the physical structure of the Internet (alpha approximately 2.5), we find that it is impressively robust, with p(c)&gt;0.99.

[13] D. S. Callaway, M. E. J .Newman, S. H. Strogatz, and D.J. Watts, Phys. Rev. Lett. 85(2000) 5468.
DOI:10.1103/PhysRevLett.85.5468URLPMID:11136023 [Cited within: 1]
Recent work on the Internet, social networks, and the power grid has addressed the resilience of these networks to either random or targeted deletion of network nodes or links. Such deletions include, for example, the failure of Internet routers or power transmission lines. Percolation models on random graphs provide a simple representation of this process but have typically been limited to graphs with Poisson degree distribution at their vertices. Such graphs are quite unlike real-world networks, which often possess power-law or other highly skewed degree distributions. In this paper we study percolation on graphs with completely general degree distribution, giving exact solutions for a variety of cases, including site percolation, bond percolation, and models in which occupation probabilities depend on vertex degree. We discuss the application of our theory to the understanding of network resilience.

[14] R. Pastor-Satorras and A. Vespignani, Phys. Rev. Lett. 86(2001) 3200.
DOI:10.1103/PhysRevLett.86.3200URLPMID:11290142 [Cited within: 2]
The Internet has a very complex connectivity recently modeled by the class of scale-free networks. This feature, which appears to be very efficient for a communications network, favors at the same time the spreading of computer viruses. We analyze real data from computer virus infections and find the average lifetime and persistence of viral strains on the Internet. We define a dynamical model for the spreading of infections on scale-free networks, finding the absence of an epidemic threshold and its associated critical behavior. This new epidemiological framework rationalizes data of computer viruses and could help in the understanding of other spreading phenomena on communication and social networks.

[15] M. Bogu?á, R. Pastor-Satorras, and A. Vespignani, Phys. Rev. Lett. 90(2003) 028701.
DOI:10.1103/PhysRevLett.90.028701URLPMID:12570587
Random scale-free networks have the peculiar property of being prone to the spreading of infections. Here we provide for the susceptible-infected-susceptible model an exact result showing that a scale-free degree distribution with diverging second moment is a sufficient condition to have null epidemic threshold in unstructured networks with either assortative or disassortative mixing. Degree correlations result therefore irrelevant for the epidemic spreading picture in these scale-free networks. The present result is related to the divergence of the average nearest neighbor's degree, enforced by the degree detailed balance condition.

[16] M. Bogu?á, C. Castellano, and R. Pastor-Satorras , Phys. Rev. Lett. 111(2013) 068701.
DOI:10.1103/PhysRevLett.111.068701URLPMID:23971619 [Cited within: 1]
We develop an analytical approach to the susceptible-infected-susceptible epidemic model that allows us to unravel the true origin of the absence of an epidemic threshold in heterogeneous networks. We find that a delicate balance between the number of high degree nodes in the network and the topological distance between them dictates the existence or absence of such a threshold. In particular, small-world random networks with a degree distribution decaying slower than an exponential have a vanishing epidemic threshold in the thermodynamic limit.

[17] D. Achlioptas, R. M. D’Souza, J. Spencer , Science 323 ( 2009) 1453.
[Cited within: 1]

[18] E.J. Friedman and A. S. Landsberg, Phys. Rev. Lett. 103(2009) 255701.
DOI:10.1103/PhysRevLett.103.255701URLPMID:20366263
The existence of explosive phase transitions in random (Erd?s Rényi-type) networks has been recently documented by Achlioptas, D'Souza, and Spencer [Science 323, 1453 (2009)] via simulations. In this Letter we describe the underlying mechanism behind these first-order phase transitions and develop tools that allow us to identify (and predict) when a random network will exhibit an explosive transition. Several interesting new models displaying explosive transitions are also presented.

[19] F. Radicchi and S. Fortunato, Phys. Rev. Lett. 103(2009) 168701.
DOI:10.1103/PhysRevLett.103.168701URLPMID:19905730
We study scale-free networks constructed via a cooperative Achlioptas growth process. Links between nodes are introduced in order to produce a scale-free graph with given exponent lambda for the degree distribution, but the choice of each new link depends on the mass of the clusters that this link will merge. Networks constructed via this biased procedure show a percolation transition which strongly differs from the one observed in standard percolation, where links are introduced just randomly. The different growth process leads to a phase transition with a nonvanishing percolation threshold already for lambda&gt;lambda(c) approximately 2.2. More interestingly, the transition is continuous when lambda&lt;or=3 but becomes discontinuous when lambda&gt;3. This may have important consequences for both the structure of networks and for the dynamics of processes taking place on them.

[20] Y. S. Cho, J. S. Kim, J. Park, B. Kahng, D. Kim , Phys. Rev. Lett. 103(2009) 135702.
DOI:10.1103/PhysRevLett.103.135702URLPMID:19905523
It has been recently shown that the percolation transition is discontinuous in Erdos-Rényi networks and square lattices in two dimensions under the Achlioptas process (AP). Here, we show that when the structure is highly heterogeneous as in scale-free networks, a discontinuous transition does not always occur: a continuous transition is also possible depending on the degree distribution of the scale-free network. This originates from the competition between the AP that discourages the formation of a giant component and the existence of hubs that encourages it. We also estimate the value of the characteristic degree exponent that separates the two transition types.

[21] R. A. da Costa, S. N. Dorogovtsev, A. V. Goltsev, and J. F. F. Mendes, Phys. Rev. Lett. 105(2010) 255701.
DOI:10.1103/PhysRevLett.105.255701URLPMID:21231601
Recently a discontinuous percolation transition was reported in a new &quot;explosive percolation&quot; problem for irreversible systems [D. Achlioptas, R. M. D'Souza, and J. Spencer, Science 323, 1453 (2009)] in striking contrast to ordinary percolation. We consider a representative model which shows that the explosive percolation transition is actually a continuous, second order phase transition though with a uniquely small critical exponent of the percolation cluster size. We describe the unusual scaling properties of this transition and find its critical exponents and dimensions.

[22] P. Grassberger, C. Christensen, G. Bizhani, S. W. Son, M. Paczuski , Phys. Rev. Lett. 106(2011) 225701.
DOI:10.1103/PhysRevLett.106.225701URLPMID:21702616
We study four Achlioptas-type processes with &quot;explosive&quot; percolation transitions. All transitions are clearly continuous, but their finite size scaling functions are not entirely holomorphic. The distributions of the order parameter, i.e., the relative size s(max)/N of the largest cluster, are double humped. But-in contrast to first-order phase transitions-the distance between the two peaks decreases with system size N as N(-η) with η&gt;0. We find different positive values of β (defined via (s(max)/N)～(p-p(c))β for infinite systems) for each model, showing that they are all in different universality classes. In contrast, the exponent Θ (defined such that observables are homogeneous functions of (p-p(c))N(Θ)) is close to-or even equal to-1/2 for all models.

[23] O. Riordan and L. Warnke , Science 333 ( 2011) 322.


[24] S. V. Buldyrev, R. Parshani, G. Paul , et al., Nature (London) 464(2010) 1025.
DOI:10.1038/nature08932URLPMID:20393559
Complex networks have been studied intensively for a decade, but research still focuses on the limited case of a single, non-interacting network. Modern systems are coupled together and therefore should be modelled as interdependent networks. A fundamental property of interdependent networks is that failure of nodes in one network may lead to failure of dependent nodes in other networks. This may happen recursively and can lead to a cascade of failures. In fact, a failure of a very small fraction of nodes in one network may lead to the complete fragmentation of a system of several interdependent networks. A dramatic real-world example of a cascade of failures ('concurrent malfunction') is the electrical blackout that affected much of Italy on 28 September 2003: the shutdown of power stations directly led to the failure of nodes in the Internet communication network, which in turn caused further breakdown of power stations. Here we develop a framework for understanding the robustness of interacting networks subject to such cascading failures. We present exact analytical solutions for the critical fraction of nodes that, on removal, will lead to a failure cascade and to a complete fragmentation of two interdependent networks. Surprisingly, a broader degree distribution increases the vulnerability of interdependent networks to random failure, which is opposite to how a single network behaves. Our findings highlight the need to consider interdependent network properties in designing robust networks.

[25] R. Parshani, S. V. Buldyrev, S. Havlin , Phys. Rev. Lett. 105(2010) 048701.
DOI:10.1103/PhysRevLett.105.048701URLPMID:20867893
We study a system composed from two interdependent networks A and B, where a fraction of the nodes in network A depends on nodes of network B and a fraction of the nodes in network B depends on nodes of network A. Because of the coupling between the networks, when nodes in one network fail they cause dependent nodes in the other network to also fail. This invokes an iterative cascade of failures in both networks. When a critical fraction of nodes fail, the iterative process results in a percolation phase transition that completely fragments both networks. We show both analytically and numerically that reducing the coupling between the networks leads to a change from a first order percolation phase transition to a second order percolation transition at a critical point. The scaling of the percolation order parameter near the critical point is characterized by the critical exponent β=1.

[26] J. Gao, S. V. Buldyrev, S. Havlin, H. E. Stanley , Phys. Rev. Lett. 107(2011) 195701.
DOI:10.1103/PhysRevLett.107.195701URLPMID:22181627
Network research has been focused on studying the properties of a single isolated network, which rarely exists. We develop a general analytical framework for studying percolation of n interdependent networks. We illustrate our analytical solutions for three examples: (i) For any tree of n fully dependent Erd?s-Rényi (ER) networks, each of average degree k, we find that the giant component is P∞ =p[1-exp(-kP∞)](n) where 1-p is the initial fraction of removed nodes. This general result coincides for n = 1 with the known second-order phase transition for a single network. For any n&gt;1 cascading failures occur and the percolation becomes an abrupt first-order transition. (ii) For a starlike network of n partially interdependent ER networks, P∞ depends also on the topology-in contrast to case (i). (iii) For a looplike network formed by n partially dependent ER networks, P∞ is independent of n.

[27] J. Gómez-Garde?es, S. Gómez, A. Arenas, and Y. Moreno, Phys. Rev. Lett. 106(2011) 128701.
DOI:10.1103/PhysRevLett.106.128701URLPMID:21517358
Explosive collective phenomena have attracted much attention since the discovery of an explosive percolation transition. In this Letter, we demonstrate how an explosive transition shows up in the synchronization of scale-free networks by incorporating a microscopic correlation between the structural and the dynamical properties of the system. The characteristics of the explosive transition are analytically studied in a star graph reproducing the results obtained in synthetic networks. Our findings represent the first abrupt synchronization transition in complex networks and provide a deeper understanding of the microscopic roots of explosive critical phenomena.

[28] I. Leyva, R. Sevilla-Escoboza, J. M. Buld′u , et al., Phys. Rev.Lett. 108(2012) 168702.
DOI:10.1103/PhysRevLett.108.168702URLPMID:22680761
Critical phenomena in complex networks, and the emergence of dynamical abrupt transitions in the macroscopic state of the system are currently a subject of the outmost interest. We report evidence of an explosive phase synchronization in networks of chaotic units. Namely, by means of both extensive simulations of networks made up of chaotic units, and validation with an experiment of electronic circuits in a star configuration, we demonstrate the existence of a first-order transition towards synchronization of the phases of the networked units. Our findings constitute the first prove of this kind of synchronization in practice, thus opening the path to its use in real-world applications.

[29] A. Majdandzic, B. Podobnik, S. V. Buldyrev , et al., Nat. Phys. 10(2014) 34.
DOI:10.1038/NPHYS2819URL
Much research has been carried out to explore the structural properties(1-10) and vulnerability(11-19) of complex networks. Of particular interest are abrupt dynamic events that cause networks to irreversibly fail(13-17). However, in many real-world phenomena, such as brain seizures in neuroscience or sudden market crashes in finance, after an inactive period of time a significant part of the damaged network is capable of spontaneously becoming active again. The process often occurs repeatedly. To model this marked network recovery, we examine the effect of local node recoveries and stochastic contiguous spreading, and find that they can lead to the spontaneous emergence of macroscopic 'phase-flipping' phenomena. As the network is of finite size and is stochastic, the fraction of active nodes z switches back and forth between the two network collective modes characterized by high network activity and low network activity. Furthermore, the system exhibits a strong hysteresis behaviour analogous to phase transitions near a critical point. We present real-world network data exhibiting phase switching behaviour in accord with the predictions of the model.

[30] H. Chen, C. Shen, H. Zhang , et al., Phys. Rev. E 95 ( 2017) 042304.
DOI:10.1103/PhysRevE.95.042304URLPMID:28505870 [Cited within: 1]
We generalize the original majority-vote model by incorporating inertia into the microscopic dynamics of the spin flipping, where the spin-flip probability of any individual depends not only on the states of its neighbors, but also on its own state. Surprisingly, the order-disorder phase transition is changed from a usual continuous or second-order type to a discontinuous or first-order one when the inertia is above an appropriate level. A central feature of such an explosive transition is a strong hysteresis behavior as noise intensity goes forward and backward. Within the hysteresis region, a disordered phase and two symmetric ordered phases are coexisting and transition rates between these phases are numerically calculated by a rare-event sampling method. A mean-field theory is developed to analytically reveal the property of this phase transition.

[31] M. Nekovee, Y. Moreno, G. Bianconi, M. Marsili , Physica A 374 ( 2007) 457.
DOI:10.1038/374457a0URLPMID:7700355 [Cited within: 1]
The GTPase Rac1 is a key component in the reorganization of the actin cytoskeleton that is induced by growth factors or oncogenic Ras1. Here we investigate the role of Rac1 in cell transformation and show that Rat1 fibroblasts expressing activated Val-12 Rac1 (Rac1 with valine at residue 12) display all the hallmarks of malignant transformation. In a focus-forming assay in NIH3T3 fibroblasts to measure the efficiency of transformation, we found that dominant-negative Asn-17 Rac1 inhibited focus formation by oncogenic Ras, but not by RafCAAX, a Raf kinase targeted to the plasma membrane by virtue of the addition of a carboxyterminal localization signal from K-Ras. This indicates that Rac is essential for transformation by Ras. In addition, Val-12 Rac1 synergizes strongly with RafCAAX in focus-formation assays, indicating that oncogenic Ras drives both the Rac and MAP-kinase pathways, which cooperate to cause transformation.

[32] J. Zhou, Z. Liu, B. Li , Phys. Lett. A 368 ( 2007) 458.
[Cited within: 1]

[33] V. Colizza, R. Pastor-Satorras, A. Vespignani , Nat. Phys. 3(2007) 276.
[Cited within: 1]

[34] H. Zhou and R. Lipowsky , Proc. Natl. Acad. Sci. USA 102 ( 2005) 10052.
DOI:10.1073/pnas.0409296102URLPMID:16006533 [Cited within: 1]
A general class of dynamic models on scale-free networks is studied by analytical methods and computer simulations. Each network consists of N vertices and is characterized by its degree distribution, P(k), which represents the probability that a randomly chosen vertex is connected to k nearest neighbors. Each vertex can attain two internal states described by binary variables or Ising-like spins that evolve in time according to local majority rules. Scale-free networks, for which the degree distribution has a power law tail P(k) approximately k(-gamma), are shown to exhibit qualitatively different dynamic behavior for gamma &lt; 5/2 and gamma &gt; 5/2, shedding light on the empirical observation that many real-world networks are scale-free with 2 &lt; gamma &lt; 5/2. For 2 &lt; gamma &lt; 5/2, strongly disordered patterns decay within a finite decay time even in the limit of infinite networks. For gamma &gt; 5/2, on the other hand, this decay time diverges as ln(N) with the network size N. An analogous distinction is found for a variety of more complex models including Hopfield models for associative memory networks. In the latter case, the storage capacity is found, within mean field theory, to be independent of N in the limit of large N for gamma &gt; 5/2 but to grow as N(alpha) with alpha = (5 - 2gamma)/(gamma - 1) for 2 &lt; gamma &lt; 5/2.

[35] C. Castellano and R. Pastor-Satorras, J. Stat. Mech . ( 2006) P05001.
[Cited within: 1]

[36] H. Chen, C. Shen, G. He , et al., Phys. Rev. E 91 ( 2015) 022816.
DOI:10.1103/PhysRevE.91.022816URLPMID:25768561 [Cited within: 1]
The majority-vote model with noise is one of the simplest nonequilibrium statistical model that has been extensively studied in the context of complex networks. However, the relationship between the critical noise where the order-disorder phase transition takes place and the topology of the underlying networks is still lacking. In this paper, we use the heterogeneous mean-field theory to derive the rate equation for governing the model's dynamics that can analytically determine the critical noise f(c) in the limit of infinite network size N→∞. The result shows that f(c) depends on the ratio of 〈k〉 to 〈k(3/2)〉, where 〈k〉 and 〈k(3/2)〉 are the average degree and the 3/2 order moment of degree distribution, respectively. Furthermore, we consider the finite-size effect where the stochastic fluctuation should be involved. To the end, we derive the Langevin equation and obtain the potential of the corresponding Fokker-Planck equation. This allows us to calculate the effective critical noise f(c)(N) at which the susceptibility is maximal in finite-size networks. We find that the f(c)-f(c)(N) decays with N in a power-law way and vanishes for N→∞. All the theoretical results are confirmed by performing the extensive Monte Carlo simulations in random k-regular networks, Erd?s-Rényi random networks, and scale-free networks.

[37] H. Chen and G. Li , Phys. Rev. E 97 ( 2018) 062304.
DOI:10.1103/PhysRevE.97.062304URLPMID:30011539 [Cited within: 1]
We generalize the original majority-vote (MV) model from two states to arbitrary p states and study the order-disorder phase transitions in such a p-state MV model on complex networks. By extensive Monte Carlo simulations and a mean-field theory, we show that for p≥3 the order of phase transition is essentially different from a continuous second-order phase transition in the original two-state MV model. Instead, for p≥3 the model displays a discontinuous first-order phase transition, which is manifested by the appearance of the hysteresis phenomenon near the phase transition. Within the hysteresis loop, the ordered phase and disordered phase are coexisting, and rare flips between the two phases can be observed due to the finite-size fluctuation. Moreover, we investigate the type of phase transition under a slightly modified dynamics [Melo et?al., J. Stat. Mech. (2010) P110321742-546810.1088/1742-5468/2010/11/P11032]. We find that the order of phase transition in the three-state MV model depends on the degree heterogeneity of networks. For p≥4, both dynamics produce the first-order phase transitions.

[38] R. J. Glauber, J. Math. Phys . 4(1963) 294.
[Cited within: 1]

[39] K. Binder , Z. Phys. B 43 ( 1981) 119.
[Cited within: 1]