 ,1,2,?
,1,2,? Corresponding authors: ? E-mail:mtcheng@ahut.edu.cn
Received:2019-05-1Online:2019-11-1
| Fund supported: |

Abstract
Keywords:
PDF (642KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Wei Hu, Xiao-San Ma, Bing Wang, Xian-Shan Huang, Mu-Tian Cheng. Coherent Controlling Single Photon Asymmetric Transmission in the Atom Chirally Coupled Waveguide System*. [J], 2019, 71(11): 1304-1308 doi:10.1088/0253-6102/71/11/1304
1 Introduction
Single photon diode, which allows the transmission of single photon in only one direction, has important applications in quantum information processing. The realization of single photon diode has been discussed widely in recent years.[1-9] Hafezi and Rabl suggested using an optomechanical resonator to break the parity-time symmetry to realize the nonreciprocal of the single photon transport properties.[1] Later, Xia et al. proposed to realize single photon isolator in the atom-whispering gallery microresonator-waveguide system.[2] Their idea was demonstrated by Scheucher et al.[9] In the atomic system, there are also a lot of advancements in realization of optical diode. For example, Wang et al. reported optical diode based on a moving photonic crystal and experimentally demonstrated in a room temperature Cs vapor cell.[10] Xia, Xu, and Yang proposed optical diode on few-photon level based on asymmetric cavity configuration,[11] which is experimentally demonstrated very recently.[12]Atom-waveguide system with chiral coupling is a good platform to investigate the non-reciprocal quantum phenomena.[13] The chiral coupling between atom (artificial atom) and waveguide has been realized in many configurations, such as atom-nanofiber system,[5, 14] quantum dot-nanobeam waveguide system,[15] and quantum dot-photonic crystal waveguide system.[16-17] Here, the chiral coupling means that the coupling strengths between the atom and photon in the waveguide are propagation-direction dependent. Many quantum devices, such as single photon router,[18-23] frequency converter,[24] $\sqrt{\rm SWAP}$ gate,[25] SWAP gate,[26-27] quantum interface between atom and photon, have been proposed.[15] The single photon diode has also been discussed in such a system. The main idea is that when the single photon incidents from one direction of the waveguide, it is scatted into free space such that there is no transmission in the other end. However, when the photon incidents from the other direction of the waveguide, it can pass through freely due to no interaction between the atom and waveguide. Thus, asymmetric transmission is realized. For the two-level system chiral coupling to the waveguide, the diode can be realized only for the resonant photon.[5] However, one can use an external coherent field to drive $\Lambda$-type system to realize single photon diode with specific frequency points.[28]
Phase difference between two coherent fields can play important roles in manipulating dynamics of quantum systems, such as narrowing down the atomic spectrum of spontaneous emission,[29] controlling the dynamical behaviors of nonclassical correlations,[30] and population swapping.[31] Recently, Yuan and Fan proposed to realize nonreciprocal single photon transmission by using phase difference between two coherent fields in the system composed of waveguide coupling to a pair of $V$-type systems.[32] Yu et al. proposed phase difference controlled single photon switching in the atom-cavity-waveguide system and waveguide-multiple $\Lambda$-type system.[33-35] In this paper, we further investigate theoretically manipulation single photon propagation properties in atom-waveguide chiral coupling system by phase difference between two coherent fields. We show that, the asymmetrical degree of the transmission can vary between 0 and 1 by controlling the phase difference. Our results may find applications in designing all-optical quantum devices at single-photon level.
2 Model and Method
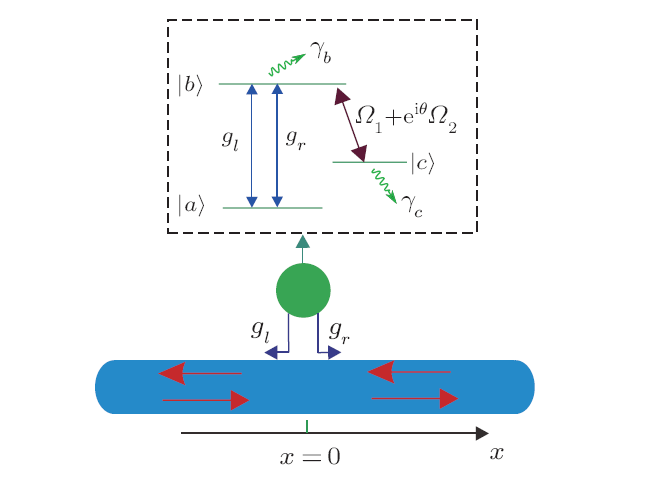
The system we consider in this study is shown in Fig. 1. An atom with three energy levels chirally couples to the waveguide. The transition between states $|a\rangle$ and $|b\rangle$ couples to the waveguide. The coupling strength between the transition $|a\rangle \Leftrightarrow|b\rangle$ and the right (left) propagating photon in the waveguide is $g_{r} (g_{l})$. The transition between the states $|b\rangle$ and $|c\rangle$ is decoupled from the waveguide. Instead, it is resonantly driven by two coherent fields. The equivalent Rabi frequency of the two coherent fields can be expressed asFig. 1
 New window|Download| PPT slide
New window|Download| PPT slideFig. 1(Color online) The system considered in the manuscript. $\Lambda$ system interacting with a one-dimensional waveguide. The transition between $|a\rangle$ and $|b\rangle$ chiral couples to the waveguide. The transition between $|b\rangle$ and $|c\rangle$ is resonantly driven by two coherent fields. The phase difference between the two coherent fields is $\theta$.
where $\Omega_{1}$ and $\Omega_{2}$ are the Rabi frequencies of each of the coherent fields. $\theta$ is the phase difference between the two fields, which can be controlled by the time delay between the two fields.[31] In this study, we will discuss how to control the single photon asymmetrical transmission properties by modulating the phase difference $\theta$.
The Hamiltonian describing the system is given by ($\hbar=1$)[36-37]
where $c^{\dagger}_{R/L}(x)$ denotes creating a right/left propagation photon at $x$ in the waveguide. $v_{g}$ is the velocity of the propagation photon. $\omega_{b}$ is the frequency of energy level $|b\rangle$. Here, we have set the energy level $|a\rangle$ as the reference. $\gamma_{b}(\gamma_{c})$ denotes the energy loss rate of $|b\rangle (|c\rangle)$. Since the coupling is chiral, $g_{r}\neq g_{l}$. When $g_{r}=g_{l}$, the coupling is non-chiral. $\sigma_{mn} (m, n=a,b,c)$ is the dipole transition operator.
Since we only consider the single photon diode, the wavefunction can be expressed as
where $|0,m\rangle (m=a,b,c)$ denotes no photon in the system and the atom in state $|m\rangle$. $e_{m}$ represents the corresponding probability amplitude. $\phi_{r/l}(x)$ denotes the wavefunction of right/left propagating photon at $x$. Supposing that a single photon with frequency $\omega$ incidents from the left of the waveguide, we can write $\phi_{r/l}(x)$ as[36-37]
where $k=\omega/v_{g}$. $h(x)$ is the step function with $h(0)=1/2$. $t_{lr}$ and $r_{lr}$ respectively denote the transmission and reflection amplitudes for the single photon incident from the left of the waveguide. From Schrödinger equation $H|\Psi\rangle=\omega|\Psi\rangle$, after some calculations, one can obtain
where $G_{r/l}=g^{2}_{r/l}/v_{g}, \delta=\omega-\omega_{b}, \Omega^{2}=|\Omega_{1}+e^{-i\theta}\Omega_{2}|^{2}$. When the single photon incidents from the right of the waveguide, one can obtain the transmission (reflection) amplitude $t_{rl}$ ($r_{rl}$) by exchanging the positions of $G_{l}$ and $G_{r}$ in Eqs. (5a) and (5b).
3 Results and Discussions
In this section, we show how to control single photon routing by manipulating the phase difference $\theta$.3.1 Ideal Case with $G_{l}=0$, $\gamma_{c}=0$
Firstly, we discuss the phase controlled single photon routing for the ideal case. When $G_{l}=0,\gamma_{c}=0$ are satisfied, Eqs. (5a), (5b) degenerate intoIf there is no driving fields $\Omega_{1}$ or $\Omega_{2}$, the system degenerates into a two-level system. One can obtain that when $G_{r}=\gamma_{b}$ and $\omega=\omega_{b}$, $t_{lr}=r_{lr}=0$. It means that the photon with energy $\omega=\omega_{b}$ will be scattered into the free space when it incidents from the left of the waveguide. Thus, the transmission probability is zero. However, when the photon incidents from the right of the waveguide, it will not interact with the atom due to $G_{l}=0$. It can be transmitted with probability of 1. Thus a diode is realized.
When the driving fields are applied, one can obtain that when $\omega=\omega_{T_{lr=0}}=\omega_{b}\pm|\Omega_{1}+e^{-i\theta}\Omega_{2}|$, both of $t_{lr}$ and $r_{lr}$ can reach the minimum value of 0. But when the photon incidents from the right of the waveguide, it can propagate freely. Thus, the frequency of the photon for realization of the perfect diode is shifted from $\omega_{b}$ to $\omega_{T_{lr=0}}=\omega_{b}\pm|\Omega_{1}+e^{-i\theta}\Omega_{2}|$. One can use dressed state picture to understand this effect. When the transition between $|b\rangle$ and $|c\rangle$ is driven by the two fields, the state $|b\rangle$ splits into two states with frequency $\omega_{b}+|\Omega_{1}+e^{-i\theta}\Omega_{2}|$ and $\omega_{b}-|\Omega_{1}+e^{-i\theta}\Omega_{2}|$, respectively. Thus, when the photon with frequency $\omega_{b}+|\Omega_{1}+e^{-i\theta}\Omega_{2}|$ or $\omega_{b}-|\Omega_{1}+e^{-i\theta}\Omega_{2}|$ incidents from the left, it will be scatted into the free space. It is interesting to note that if the system is driven by a single coherent field, for the resonant photon with $\omega=\omega_{b}$, one needs to turn off the coherent field to realize the diode. But in this proposal, instead of turning off the two coherent fields, one can manipulate the phase different $\theta$ to the realize the diode effect for the resonant photon while the coherent fields keep on.
Since $\omega_{T_{lr=0}}$ depends strongly on the phase difference $\theta$, one can manipulate single photon asymmetric transmission by controlling $\theta$. It is easy to obtain that when
the photon will be scatted into the free space. Here, we have supposed $\Omega_{1}=\Omega_{2}=\Omega_{0}$. Figure 2(a) shows $T_{lr}\equiv|t_{lr}|^{2}$ as functions of $\theta$ and $\omega$. It exhibits that when $\delta=\omega-\omega_{b}=\pm 2\Omega_{0}$, $\theta=2n\pi$, $T_{lr}$ reaches the minimum value of 0. $n$ is an integer. The results are consistent with the theoretical analysis. Figure 2(b) is cut from Fig. 2(a). It exhibits clearly that one can control $\theta$ to realize $T_{lr}=0$. It is also notable that when $\theta=(2n+1)\pi$, $T_{lr}$ reaches the minimum value of 0 for the resonant photon even the two coherent fields keep on. This effect results from the destructive interference between the two driving fields.
Fig. 2
 New window|Download| PPT slide
New window|Download| PPT slideFig. 2(Color online) Phase difference controlled $T_{lr}$. (a) $T_{lr}$ as functions of $\delta$, and $\theta$. (b) is cut from (a) at $\delta=0, 0.01G_{r}$ and $0.02G_{r}$, respectively. In the calculations, $\gamma_{b}=G_{r}, G_{l}=0, \gamma_{c}=0, \Omega_{0}=0.1G_{r}$.
3.2 Nonideal Case
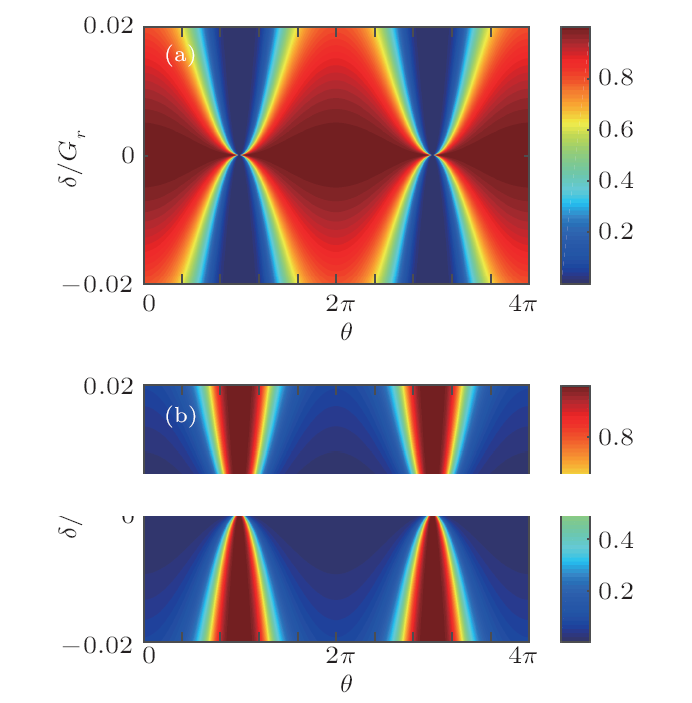
Now, we study the asymmetric transmission of single photon in the case of $G_{l}\neq0$. We first discuss the case of $\gamma_{c}=0$. One can find from Eqs. (5a), (5b) that if $G_{r}=G_{l}+\gamma_{b}$, and $\theta$ satisfies Eq. (7), $t_{lr}$ reaches the minimum value of 0. It means that the single photon can not transmit from the left to the right. However, if the photon incidents from the right, the transmission is not zero. Thus, one can realize the asymmetric transmission. Different from the case of $G_{l}=0$, $T_{lr}$ can not reach the maximum value of 1. To describe the degree of the asymmetric transmission, we introducewhere $T_{rl}=|t_{rl}|^{2}$. If there is no asymmetric transmission effect, $T_{lr}=T_{rl}=0$, thus $\Delta T$ reaches the minimum of 0. However, if $T_{lr}$ or $T_{rl}$ is zero, $|\Delta T|$ is equal to 1. The degree of the asymmetric transmission reaches the maximum value. It is easy to check that when $G_{r}-G_{l}=\pm\gamma_{b}$ and $\cos\theta=[(\omega-\omega_{b})^{2}-2\Omega_{0}^{2}]/(2\Omega_{0}^{2})$, $\Delta T$ can reach $\mp1$. So, one can control $\Delta T$ by manipulating $\theta$ for the fixed $\Omega_{0}$. Figures 3(a) and 3(b) respectively show $T_{lr}$ and $\Delta T$ as functions of $\theta$ and $\delta$. It exhibits clearly that for a given $\delta$, one can manipulate $\theta$ to reach high value of $\Delta T$. It also shows that when $\delta=0$, one can tune $\theta$ to be $(2n+1)\pi$ to obtain $\Delta T=1$.$\gamma_{c}$ is often neglected in many reports. However, it can strongly affect the results if $\gamma_{c}$ is comparable with $\gamma_{b}$. Equation (5a) shows that if
Fig. 3
 New window|Download| PPT slide
New window|Download| PPT slideFig. 3(Color online) Phase difference controlled $T_{lr}$ (a) and $\Delta T$ (b). In the calculations, $\gamma_{b}=0.75G_{r}, G_{l}=0.25G_{r}, \Omega_{0}=0.1G_{r}$.
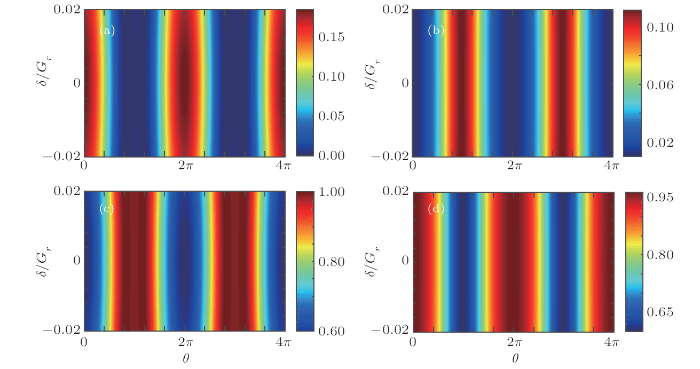
are satisfied, $t_{lr}=0$. Figures 4(a) and 4(b) show $T_{lr}$ as functions of $\theta$ and $\delta$ with $\gamma_{c}=0.1G_{r}$ and $\gamma_{c}=0.5G_{r}$, respectively. It exhibits clearly that the maximum values of $T_{lr}$ are different due to population leaking. Figures 4(c) and 4(d) exhibit $\Delta T$ varying with $\theta$ and $\delta$ for the cases of $\gamma_{c}=0.1G_{r}$ and $\gamma_{c}=0.5G_{r}$, respectively. It shows that the values of $\theta$ for getting the maximum values of $\Delta T$ are quite different, which is consistent with previous analysis. Thus, $\gamma_{c}$ may play important roles in coherently controlling the single photon diode.
Fig. 4
 New window|Download| PPT slide
New window|Download| PPT slideFig. 4(Color online) Phase difference controlled single photon transmission when $\gamma_{c}$ is not zero. (a) and (c) respectively exhibit $T_{lr}$ and $\Delta T$ with $\gamma_{c}=0.1G_{r}$ as functions of $\delta$ and $\theta$. (b) and (d) respectively show $T_{lr}$ and $\Delta T$ with $\gamma_{c}=0.5G_{r}$. In the calculations, $ G_{l}=0.25G_{r}$, $\gamma_{b}+\gamma_{c}+G_{l}=G_{r}$, $\Omega_{0}=0.1G_{r}$.
4 Summary
In summary, we investigated coherent controlling single photon asymmetric transmission in the atom-waveguide system with chiral coupling. We deduced the conditions to reach the maximum value of $\Delta T$ for the cases with and without considering of $\gamma_{c}$. The degree of asymmetric transmission $\Delta T$ can reach the ideal value of $\pm1$ by manipulating the phase difference between the two coherent fields even for the resonant single photon. The results may find applications in designing all-optical quantum devices at single-photon level.Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 2]
[Cited within: 1]
[Cited within: 2]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 2]
