删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Doubly Excited F States of Two-Electron Atoms under Weakly Coupled Plasma Environment

本站小编 Free考研考试/2022-01-02
S. Dutta1,2, J. K. Saha,3,?, S. Bhattacharyya4, T. K. Mukherjee2 Belgharia Texmaco Estate School, Belgharia, Kolkata 700056, India;
Department of Physics, Narula Institute of Technology, Agarpara, Kolkata 700109, India;
Department of Physics, Aliah University, IIA/27, Newtown, Kolkata 700160, India;
Department of Physics, Acharya Prafulla Chandra College, New Barrackpore, Kolkata 700131, India

Corresponding authors: ?E-mail:jksaha.phys@aliah.ac.in

Received:2018-12-31Online:2019-07-1
Fund supported:*Supported under Grant.No. EMR/2017/000737
from DST-SERB, Govt. of India, Grant.No. 23(Sanc.)/ST/P/S&T/16G-35/2017
from DHESTB, Govt. of West Bengal, India, and by the DHESTB, Govt. of West Bengal, India under Grant.No. 249(Sanc.)/ST/P/S&T/16G-26/2017


Abstract
Precise energy eigenvalues of metastable bound doubly excited $^{1,3}{\rm F}^{e}$ states originating from $2pnf$,($n=4$--6) configuration of helium-like ions $(Z=\text{2--4})$ under weakly coupled plasma (WCP) environment have been estimated within the framework of Ritz variational method. The wavefunction is expanded in explicitly correlated Hylleraas type basis set. The screened Coulomb potential is considered mimic the WCP environment. The atomic systems tend towards gradual instability and the number of excited metastable bound states reduces with increasing plasma strength. The wavelengths corresponding to $2pnf (^{1,3}{\rm F}^{e}) \rightarrow 2pn^\prime d (^{1,3}{\rm D}^{o})$ ($n=4$--6; $n^\prime=3$--6) transitions occurring between doubly excited states of plasma embedded two-electron ions are also reported.
Keywords： two-electron atom;doubly excited states;variational method;weakly coupled plasma;Hylleraas co-ordinate


PDF (383KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
S. Dutta, J. K. Saha, S. Bhattacharyya, T. K. Mukherjee. Doubly Excited 1,3Fe States of Two-Electron Atoms under Weakly Coupled Plasma Environment *. [J], 2019, 71(7): 853-860 doi:10.1088/0253-6102/71/7/853

1 Introduction

Doubly excited states (DESs) of two-electron atom is a topic of active interest in recent times, both from theoretical and experimental aspects.[1-9] The abundance of such DESs is noted in various astrophysical observations as well as in high temperature laboratory plasma.[10-19] The DESs of two-electron atom having unnatural parity ($\pi = (-1)^{L+1}$, $L$ is the total angular momentum quantum number) and lying below the second ionization threshold, are metastable bound. These states favorably can decay to a lower state via radiative process rather than decaying through non-radiative autoionization channel. Examples of such DESs of unnatural parity are $^{1,3}$P$^e$, $^{1,3}$D$^o$, $^{1,3}$F$^e$ states arising out of dominant $pp$, $pd$, $pf$ configurations respectively.

Atomic systems under external environments have been studied by various researchers during the past several decades, as they provide useful information about the environment. A large number of investigations[20-30] are there in the literature on the modified properties of plasma embedded atomic systems. Extensive review articles[31-32] are available on this topic. Plasma coupling strength ($\Gamma$) is defined as the ratio between average inter-particle electrostatic energy to the average thermal kinetic energy. The high temperature and low density classical plasma are categorized as weakly coupled ($\Gamma <1$). According to the Debye-Hückel theory[33] a short range Yukawa-type or screened Coulomb model potential is considered to mimic the modified inter-particle interaction under WCP environment. Due to its simplicity and effectiveness, such screened Coulomb potential has been used widely by researchers for the investigation of spectral and structural properties of atomic systems under WCP environment. In this model, plasma electron density ($n_{e}$) and temperature ($T$) are combinedly expressed through the plasma screening length ($D$).[33] As the screened Coulomb potential is more positive in nature than the "pure" Coulomb potential, in general, with the decrease of plasma screening length $(D)$, the energy levels are pushed up and the gap between two successive energy level decreases.[20] This causes the transition energy to decrease and a red shift[21] may be observed. However, it is remarkable that for some specific transitions between two doubly excited energy levels, the wavelengths get blue shifted or show a pattern with both red and blue shift w.r.t. the plasma screening length $(D)$.[21]

In the present work, we have estimated the non-rel-ativistic energy eigenvalues of doubly excited metastable bound $2pnf\,(n=4$--6) ($^{1,3}$F$^e$) states of two-electron ions ($Z=2$--4) as well as the $2s$ and $2p$ states of the respective one-electron ions under WCP environment. According to the Debye-Hückel theory,[33] in a two-electron Hamiltonian, the effect of plasma screening should be reflected in both the one-particle electron-nucleus attraction terms and the electron-electron repulsion term of the total potential. Although the effect of screening on the electron-nucleus attraction term predominates overthe electron-electron repulsion term in determining the properties of plasma embedded two electron atom, we have considered the effect of screening on both attractive electron-nucleus part and repulsive electron-electron part in the potential. Computationally, it is difficult to include the effect of screening in repulsive electron-electron part even for a partially correlated CI type basis constructed with Slater-type orbitals as the analytic solution of the corresponding basis integrals becomes extremely cumbersome.[34-35] However, we have been able to develop the methodology to estimate the basis integral for the trial wavefunction is expanded in multi-exponent Hylleraas type basis set in a way that the effect of screening in repulsive electron-electron part has been considered fully without any perturbative approximation. Ritz variational method is used to determine the energy eigenroots. The wavelengths for the dipole allowed transitions between doubly excited metastable bound states $2pnf$ [$n=4$--6] $(^{1,3}$F$^e)$ and $2pn'd$ ($n'=3$--6) $(^{1,3}$D$^o)$ are determined for different values of plasma screening length ($D$). The non-relativistic energy-eigenvalues of $2pnd$ ($n=3$--6) ($^{1,3}$D$^o$) states are taken from an earlier work of Saha et al.[21] The details of the methodology are given in Sec. 2 followed by the discussion on the results in Sec. 3 and finally concluded in Sec. 4.

2 Method

The non-relativistic Hamiltonian (in a.u.) of a two-electron atom immersed in WCP environment may be written as

$$ H=\sum_{i=1}^{2}\Big(-\frac{1}{2}\nabla_{i}^{2}-Z\frac{e^{-{r_{i}}/{D}}}{r_{i}}\Big) +\frac{e^{-{r_{12}}/{D} }}{r_{12}}\,, $$
where, in case of screening by both ions and electrons, the Debye screening length ($D$) reads as[33]

$$ D = \Big(\frac{kT}{4\pi (1+Z_{e})n_e}\Big)^{{1}/{2}}\,. $$
For a fully ionized plasma comprising of a single nuclear species, the effective nuclear charge is $Z_{e}=Z$ whereas in case of screening by electrons only, $Z_{e}=0$. After seperation of the centre of mass coordinates, the wave function of $^{1,3}$F$^{e}$ states due to dominant $pf$ configuration of a two-electron atom can be written in terms of six co-ordinates $(r_1, r_2, \theta_{12}; \theta ,\varphi ,\psi )$ as,[36-37]

$$ \Psi =f_{3}^{0}D_{3}^{0}+f_{3}^{2+}D_{3}^{2+}+f_{3}^{2-}D_{3}^{2-}\,, $$
where, $D_{L}^{\kappa \pm}$ are the rotational harmonics and functions of three Eulerian angles ($\theta$, $\varphi$, $\psi$) that define the orientation of the triangle formed by the two electrons and the nucleus in space; $\kappa$ is the angular momentum quantum number about the body fixed axis of rotation.[36] The radial parts of the wavefunction are given by $f_{3}^{0}=-F_{1}\sin\theta_{12}$, $f_{3}^{2+}=({\sqrt{15}}/{6})F_{1}\sin 2\theta_{12}$ and $f_{3}^{2-}=({\sqrt{15}}/{6})F_{2}(1-\cos 2\theta_{12})$; where, $F_{1}=(f\mp\tilde{f})$, $F_{2}=(f\pm\tilde{f})$ with the condition $\tilde{f}=f(r_{2},r_{1})$ and $\theta_{12}$ is the angle between $\vec{r}_1$ and $\vec{r}_2$. The upper sign corresponds to the singlet state and the lower sign to the triplet state. The trial radial wave function corresponding to $pf$ configurations is expanded in Hylleraas basis set as

$$ f(r_1, r_2, r_{12})=\sum_{i=1}^{A}r_{1}^{l_{i}+3} r_{2}^{m_{i}+1} r_{12}^{n_{i}} \\ \quad \times\Big[\sum_{k_{1}=1}^{p}C_{ik_{1}k_{1}}\eta_{k_{1}}(1)\eta_{k_{1}}(2) \\ \quad + \sum_{k_{1}=1}^{p}\sum_{k_{2}=1}^{p}C_{ik_{1}k_{2}}\eta_{k_{1}}(1)\eta_{k_{2}}(2)\Big]\,, $$
with the features: (a) The powers of $r_{1}$, $r_{2}$ and $r_{12}$ satisfies $(l_{i},m_{i},n_{i})\geq(0,0,0)$; (b) $A$ is the total number of ($l_{i},m_{i},n_{i}$) set considered in the calculation; (c) $\eta_i (j) = e^{-\rho_i r_j}$ are the Slater-type orbitals where $\rho$'s are the non-linear parameters; (d) $p$ denotes the total number of non-linear parameters; (e) In the double sum of Eq. (4), $k_{1} < k_{2}$; (f) $C_{ik_{1}k_{2}}$ are the linear variational parameters. The effect of the radial correlation is incorporated through different $\rho$'s in the wave function whereas, the angular correlation effect is taken care of through different powers of $r_{12}$. The number of terms in the basis set expansions for the trial radial wave function $f$ is therefore $N=[{p(p+1)}/{2}]\times A$. In the present case, we have considered a nine-exponent ($p=9$) basis set where the non-linear parameters are taken in a geometrical sequence following $\rho_{i}=\rho_{i-1}\gamma$, $\gamma$ is the geometrical ratio. After choosing the proper trial radial wave function, the energy eigenvalues are obtained by solving the generalized eigenvalue equation.[38] The details regarding the analytic evaluation of the correlated basis integrals are discussed in Dutta et al.[38]

The variational equation for the $nl$-state of the respective one-electron atoms under WCP environment can be written as

$$ \delta\int\Big[\Big(\frac{\partial f}{\partial r}\Big)^{2} +\frac{l(l+1)}{r^{2}}-E+Z\frac{e^{-{ r}/{D}}}{r}\Big] d r =0\,. $$
The radial function $f(r)$ is expanded in terms of a pure exponential basis set as

$$ f(r)=\sum_{i}C_{i}e^{-\sigma_{i}r}\,. $$
We have used 101 number of terms in the basis set and the exponents are taken in a geometrical sequence $\sigma_{i}=\sigma_{i-1}\beta$, $\beta$ is the geometrical ratio. The energy eigenvalues $E$'s and linear variational coefficients $C_{i}$'s are determined by matrix diagonalization procedure. All calculations are carried out in quadruple precision. Such procedure is repeated for different plasma screening length ($D$) considered in the present case.

3 Results and Discussion

Table 1 shows the convergence behavior of the energy eigenvalues of $2pnf$ ($n=4$--6) $(^{1,3}$F$^e)$ states of He with respect to the total number of terms $N=540$ and $N=675$ in the 9-exponent basis set for three different Debye screening lengths $D=100$, 50, and 20 (in a.u.). It can be seen from Table 1 that, all the energy eigenvalues converge at least up to sixth decimal place for $D=100$ a.u. and $D=50$ a.u. whereas, energies of $2p5f$ and $2p6f$ converge up to fourth and third decimal places respectively for $D=20$ a.u. The energy values of $2pnf$ ($n=4$--6) $(^{1,3}$F$^e)$ states of two-electron ions $(Z=2$--4) in the presence of WCP environment are given in Tables 2--4 respectively. Only the values obtained from the wave function of maximum basis size ($N=675; A=15$) are reported in Tables 2--4. It is observed that as the plasma screening length ($D$) decreases, the two-electron energy levels are pushed towards the continuum. Such behaviour is quite consistent with the fact that the screened Coulomb potential becomes more and more positive with respect to the decrease in plasma screening length ($D$). Moreover, Tables 2--4 show that for all the ions the singlet states are more bound than the triplet states from low to moderate plasma screening. At high screening (i.e. at low values of screening length $D$), we see that the singlet and triplet states become exactly or nearly degenerate. As the plasma screening increases, the two-electron energy levels become largely affected by the continuum embedded states through configuration interactions. At very high screening region, the energy values of two-electron states come very close to the one-electron continuum and tend to merge into the $2p$ threshold of the respective one-electron system.


Table 1
Table 1Energy eigenvalues (-E) for the 2pnf (n = 4-6)1,3Fe states of He for different number of terms N in the basis set with respect to different Debye screening length (D). All quantities are given in a.u.
DN-E
lFe3Fe
2p4f2p5f2p6f2p4f2p5f2p6f
1005400.503 0550.492 0220.486 4010.503 0470.492 0170.486 397
6750.503 0550.492 0220.486 4010.503 0470.492 0170.486 397
505400.476 0900.466 5430.462 4940.476 0830.466 5390.462 493
6750.476 0900.466 5430.462 4940.476 0830.466 5390.462 493
205400.406 0870.405 7920.405 5500.406 0860.405 7920.405 550
6750.406 0870.405 8560.405 7090.406 0860.405 8560.405 709

New window|CSV


Table 2
Table 2Variation of energy eigenvalues (-E) for the 2pnf (n = 4-6)1,3 Fe states of He and 2s, 2p states of He+ w.r.t. the Debye screening length (D). All quantities are given in a.u.
D1Fe3FeHe+(2s)He+(2p)
2p4f2p5f2p6f2p4f2p5f2p6f
1000.503 0550.492 0220.486 4010.503 0470.492 0170.486 3970.480 2960.480 247
0.502 956a0.491 928a0.486 314 5a0.502 952a0.491 925 5a0.486 313a
0.503 060 68b0.503 052 113b
900.499 9650.489 0580.483 5720.499 9570.489 0520.483 5690.478 1430.478 083
800.496 1360.485 4000.480 1000.496 1280.485 3940.480 0970.475 4620.475 386
700.491 2670.480 7750.475 7360.491 2590.480 7700.475 7330.472 0310.471 932
0.491 074a0.480 599 5a0.475 583 5a0.491 070 5a0.480 597a0.475 580 5a
600.484 8690.474 7420.470 0870.484 8620.474 7370.470 0850.467 4840.467 350
500.476 0900.466 5430.462 4940.476 0830.466 5390.462 4930.461 1730.460 981
0.475 737 5a0.466 241 5a0.462 223 5a0.475 733 5a0.466 237a0.462 197a
0.476 090 624b0.476 087 092b
400.463 3000.454 7730.451 7820.463 2930.454 7700.451 7810.451 8230.451 525
0.462 784a0.454 351a0.462 78a0.454 334a
300.442 9730.436 5450.435 9130.442 9680.436 5430.435 9130.436 5450.436 025
0.442 158 5a0.442 148 5a
200.406 0870.405 8560.405 7090.406 0860.405 8560.405 7090.407 1040.405 970
0.406 087 6b0.406 087 1b
100.322 8480.322 6990.321 4850.322 8480.322 6990.321 4850.327 0850.322 761
aRef. [34], bRef. [35].

New window|CSV


Table 3
Table 3Variation of energy eigenvalues (-E) for the 2pnf (n = 4-16) 1,3 Fe states of Li+ and 2s, 2p states of Li2+ w.r.t. the Debye length (D). All quantities are given in a.u.
D1Fe3FeLi2十(2s)Li2十(2p)
2p4f2p5f2p6f2p4f2p5f2p6f
1001.203 6001.158 0001.133 7341.203 5101.157 9371.133 6931.095 2981.095 248
901.198 2971.152 8351.128 7271.198 2071.152 7721.128 6871.092 0331.091 973
801.191 7031.146 4331.122 5421.191 6141.146 3711.122 5031.087 9641.087 887
701.183 2841.138 2881.114 7061.183 1951.138 2271.114 6681.082 7481.082 648
601.172 1591.127 5781.104 4571.172 0711.127 5171.104 4201.075 8231.075 687
501.156 7751.112 8621.090 4781.156 6881.112 8031.090 4421.066 1821.065 987
401.134 1071.091 3811.070 2831.134 0221.091 3261.070 2511.051 8401051 537
301.097 3931.057 0981.038 5791.097 3121.057 0481.038 5531.028 2511.027 719
201.027 8130.993 9140.982 0191.027 7450.993 8790.982 0080.982 2270.981 057
100.848 9310.846 9060.844 9000.848 9120.845 4280.841 7740.852 9470.848 554

New window|CSV


Table 4
Table 4Variation of energy eigenvalues (_E) for the 2pnf (n = 4-6) 1,3 Fe states of Be2+ and 2s, 2p states of Be3+w.r.t. the Debye screening length (D). All quantities are given in a.u.
D1Fe3FeBe3十（2幻Be3十（2p)
2p4f2p5f2p6f2p4f2p5f2p6f
1002.216 9392.114 0952.058 8542.216 6862.113 9232.058 7451.960 2981.960 249
902.216 9382.114 0952.051 6462.209 1652.106 5462.051 5361.955 9231.955 862
802.200 0522.097 5542.042 7122.199 8002.097 3822.042 6031.950 4651.950 388
702.188 0722.085 8612.031 3512.187 8212.085 6912.031 2431.943 4641.943 364
602.172 2022.070 4282.016 4172.171 9522.070 2592.016 3111.934 1591.934 022
502.150 1792.049 1141.995 9052.150 0862.048 9511.995 8061.921 1861.920 990
402.117 5772.017 7841.965 9942.117 3322.017 6211.965 8951.901 8481.901 543
302.064 3501.967 1881.918 2782.064 1101.967 0331.918 1921.869 9371.869 400
201.961 9361.871 7801.830 3411.961 7131.871 6461.830 2731.807 2921.806 102
101.685 1961.628 2461.623 0641.685 0481.628 1991.619 2161.628 4141.623 879

New window|CSV

The $2s$ and $2p$ threshold energies of respective one-electron atoms are also included in Tables 2--4 for a comprehensive analysis of the position of two-electron energy levels. The departure from Coulomb potential facilitates the removal of $l$-degeneracy in the one-electron atoms and it is evident that the $2s$ level remains more bound compared to the $2p$ level as $D$ decreases. Figure 1 illustrates the comparative behavior of different doubly excited triplet $2p4p$ (P$^e)$, $2p4d$ (D$^o)$ and $2p4f$ (F$^e)$ states below He$^+(2p)$ threshold. The energy values of $2p4p$ ($^3$P$^e)$ and $2p4d$ $(^3$D$^o)$ states of helium, immersed in WCP environment have been taken from Refs. [20] and [21] respectively. In Fig. 1, we have shown the position of triplet $2p4p$, $2p4d$, $2p4f$ energy levels of helium along with the $2s$ and $2p$ thresholds of He$^+$ at different plasma screening strength. We note that at low screening regions when the system is almost equivalent to a free system, the one-electron $2s$ and $2p$ levels are merged on each other due to their $l$-degeneracy. These levels are split when $l$-degeneracy is sufficiently lifted at a higher screening in presence of plasma environment which is evident from the diagram. It is seen from Fig. 1 that the $2p4p$ $(^3$P$^e)$ and $2p4d$ $(^3$D$^o)$ states always lie below both the $2s$ and $2p$ thresholds of He$^+$, but the $2p4f$ $(^3$F$^e)$ level crosses the $2s$ threshold of He$^+$ when the plasma screening length ($D$) is sufficiently small. Hence, at a low value of $D$, the $2p4f$ $(^3$F$^e)$ level of helium merges to the one-electron continuum.

Fig. 1

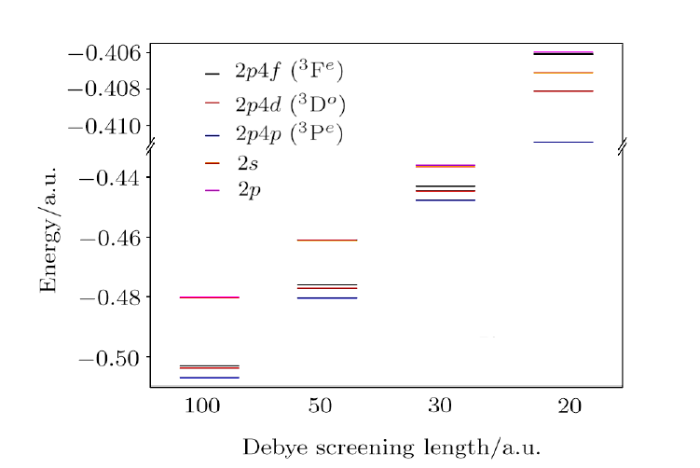New window|Download| PPT slide
Fig. 1Relative positions of $2p4f$ ($^3$F$^e$), $2p4d$ ($^3 $D$^o$) and $2p4p$ ($^3$P$^e$) energy levels of He and $2s$, $2p$ levels of He$^+$ in different plasma conditions.



We have also estimated the energy (in meV) corresponding to the

$$ 2pnf \;(^{1,3}{\rm F}^e) \rightarrow 2pn'd (^{1,3}{\rm D}^o) $$

transitions $(n=4$--6; $n'=3$--6) for different two-electron atoms ($Z=2$--4) embedded in WCP environment. The $2pn'd (^{1,3}$D$^o)$ energy values are taken from Saha et al.[21] and the results are exhibited in Tables 5--7 for $Z=2$--4 respectively. We mention that the absolute values of the difference between the position of the energy levels are given. The sequence for transition we maintain in the table is $2pnf \rightarrow 2pnd$ whereas in all the cases the $2pnf$ states are not high lying. For instance, in the case of triplet states of Li$^+$, $2p4f$ state lies energetically higher than $2p3d$ and $2p4d$ states but lower than the $2p5d$ and $2p6d$ states. We have used the conversion relation 1 a.u. of energy $= 27.21138$ eV.[39] It is worthwhile to mention that for $2pn'd (^3$D$^o) \rightarrow 2p3p (^3$P$^e)$ transitions in WCP environment, an initial blue shift followed by a red shift with respect to decreasing plasma screening length was reported in Ref. [21] whereas in the present case no such behavior is seen for $$ 2pnf (^3{\rm F}^e) \rightarrow 2pn'd (^3{\rm D}^o)$$ transitions. The transition energies, in a systematic manner, follow either a blue shift or a red shift for a particular transition scheme. For example, the $2p4f (^3$F$^e) \rightarrow 2p3d (^3$D$^o)$ line for $Z=4$ gets a gradual red shift with respect to decreasing plasma screening length ($D$) and a blue shift is observed for the $2p4f (^3$F$^e) \rightarrow 2p4d (^3$D$^o)$ of the same ion under similar conditions. Such features are evident from Fig. 2 where the $2p4f(^{1,3}$F$^e)\rightarrow 2pnd(^{1,3}$D$^o)$ transition energies $(n=3$--6) of $Z=4$ are plotted as a function of Debye screening length ($D$).


Table 5
Table 5Absolute values of the 2pnf (1,3Fe) →2pn’d(1,3D°) (n = 4-6; n’ = 3-6) transition energies (in meV) of plasma embedded He below the He+ (2p) threshold under Debye screening.
Debye screening length (D) in a.u.
Transition1009080706050403020
1Fe ^ 1D°
2p4f ^ 2p3d854.25851.72848.21843.20835.57823.21801.09754.79623.78
^ 2p4d71.7072.0172.4473.0173.8175.0676.9779.8177.62
^ 2p5d*264.68360.44381.82413.23
^ 2p6d*433.29
2p5f — 2p3d1154.461148.521140.351128.691111.151082.971033.10929.71630.08
^ 2p4d371.91368.81364.58358.50349.40334.82308.98254.7383.92
—2p5d*35.5363.6389.69127.74
—2p6d*133.06
2p6f — 2p3d1307.431297.781284.571265.821237.821193.171114.51946.91634.08
— 2p4d524.89518.07508.80495.63476.06445.02390.38271.9487.92
— 2 p5 d188.5085.6254.539.39
— 2p6d19.89
3Fe 3D°
2p4f — 2p3d734.25732.05729.02724.65718.03707.29688.04647.69532.15
— 2p4d21.9322.5923.4824.7526.6029.4934.2842.8455.08
—2p5d*288.62284.67279.28271.66
—2p6d*445.89
2p5f — 2p3d1034.401028.791021.081010.07993.54966.98919.97822.52538.40
— 2p4d322.07319.32315.55310.17302.12289.18266.21217.6761.33
— 2 p5 d11.5312.0712.7913.77
—2p6d*145.74
2p6f — 2p3d1187.311177.991165.241147.141120.141077.101001.31839.68542.41
— 2p4d474.99468.52459.71447.24428.72399.29347.55234.8365.34
— 2 p5 d164.44161.26156.95150.84
— 2p6d7.17
*pf level lines energetically lower than the pd level.

New window|CSV


Table 6
Table 6Absolute values of the 2pnf (1,3Fe) → 2pn’d(1,3D°) (n = 4-6; n’ = 3-6) transition energies (in meV) of plasma embedded Li+ below the Li2+ (2p) threshold under Debye screening.
Debye screening length (D) in a.u.
Transition1009080706050403020
1pe → 1D°
2p4f → 2p3d3229.533226.993223.503218.433210.713198.093175.373127.692997.69
→ 2p4d190.39190.91191.65192.69194.25196.75201.14209.82230.55
→ 2p5d*1148.051143.861138.061129.781117.301097.24
→ 2p6d*1848.711840.331828.781812.331787.67
2p5f — 2p3d4470.374464.074455.364442.834423.824393.024338.014224.173920.13
→ 2p4d1431.231427.991423.511417.091407.361391.681363.781306.301152.99
—2p5d92.7993.2293.8094.6295.8197.69
—2p6d*607.87603.24596.92587.93574.56
2p6f — 2p3d5130.685120.085105.475084.535052.985002.124912.114728.104243.81
— 2p4d2091.542084.002073.622058.792036.522000.781937.881810.231476.67
— 2 p 5 d753.10749.23743.90736.32724.96706.79
— 2p6d52.4452.7753.1853.7754.59
3→ 3D°
2p4f — 2p3d2839.042836.782833.642829.132822.232810.972790.702748.172632.07
— 2p4d44.1944.9746.0747.6449.9953.7860.4773.87107.00
—2p5d*1216.581212.101205.911197.051183.721162.29
—2p6d*1885.171876.471864.501847.421821.85
2p5f — 2p3d4079.144073.134064.774052.774034.614005.143952.523843.813553.62
— 2p4d1284.291281.321277.191271.281262.371247.951222.291169.511028.54
— 2 p 5 d23.5224.2525.2126.5928.6531.88
—2p6d*645.07640.12633.38623.78609.48
2p6f — 2p3d4738.854728.514714.254693.844663.114613.624526.004347.083876.64
— 2p4d1944.001936.711926.671912.351890.871856.421795.771672.791351.57
— 2 p 5 d683.23679.64674.69667.67657.15640.35
—2p6d*14.6415.2716.1017.2919.02
*pf level lines energetically lower than the pd level.

New window|CSV


Table 7
Table 7Absolute values of the 2praf (1,3Fe) → 2pn’d(1,3 D°) (n = 4-6; n’= 3-6) transition energies (in meV) of plasma embedded Be2+ below the Be3+(2p) threshold under Debye screening.
Debye screening length (D) in a.u.
Transition1009080706050403020
1Fe → 1D°
2p4f → 2p3d6948.146945.646942.186937.136929.456916.186894.026845.826713.53
→ 2p4d309.27309.91310.81312.08314.03317.18322.84334.38364.21
→ 2p5d*2649.022644.542638.322629.382615.822593.85
→ 2p6d*4217.374208.404196.014178.254151.41
2p5f — 2p3d9746.649740.199731.299718.449698.869666.279609.529489.749166.80
→ 2p4d3107.773104.463099.923093.383083.443067.283038.342978.292817.48
—2p5d149.48150.02150.80151.92153.59156.24
—2p6d*1418.871413.851406.901396.941382.00
2p6f — 2p3d11249.8011238.8111223.5911201.7311168.5811114.1411018.8010820.5410294.42
— 2p4d4610.934603.074592.224576.684553.164515.144447.624309.093945.09
— 2 p 5 d1652.631648.631643.101635.211623.301604.11
— 2p6d84.2984.7685.4086.3587.71
3F→ → 3do
2p4f — 2p3d6267.786265.496262.346257.716250.676509.086218.236174.166053.13
— 2p4d68.3369.6370.3572.0074.5477.1386.03101.20140.68
—2p5d*2758.912754.212747.672738.342724.122705.26
—2p6d*4274.574265.364252.624234.404206.86
2p5f — 2p3d9064.109057.909049.279036.819017.888987.008931.508815.768503.97
— 2p4d2864.652862.042857.282851.102841.752829.152799.302742.802591.53
— 2 p 5 d37.4138.2039.2640.7643.0846.77
—2p6d*1478.251472.951465.691455.301439.65
2p6f — 2p3d10565.5710554.8010539.8810518.4110485.8810433.1510339.0410144.799629.79
— 2p4d4366.124358.944347.904332.714309.754275.304206.844071.833717.34
— 2 p 5 d1538.881535.101529.871522.371511.081492.91
— 2p6d23.2223.9524.9326.3128.35
*pf level lines energetically lower than the pd level.

New window|CSV

Fig. 2

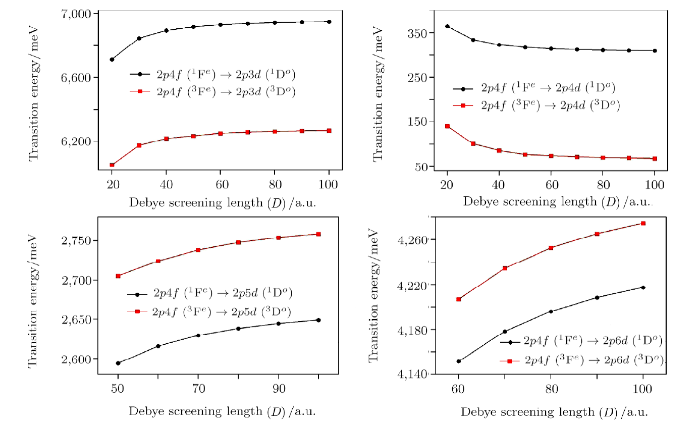New window|Download| PPT slide
Fig. 2Variation of transition energies (meV) for $2p4f (^{1,3}$F$^e)\rightarrow 2pnd(^{1,3}$D$^o)$ transitions $(n=3$--6) of Be$^{2+}$ in presence of weakly coupled plasma.



4 Conclusion

We report the behaviour of doubly excited energy levels of helium-like ions in WCP environment considering screened Coulomb potential. The two-electron energy levels as well as the respective one-electron thresholds become more positive as the plasma screening length decreases. The position of different doubly excited states has been compared extensively. The transition wavelengths between doubly excited states are found to undergo a gradual blue shift or a red shift with respect to the variation in plasma screening length. Such features have implications in interpreting complex atomic spectra like those of laboratory plasma experiments or astrophysical observations.

The authors have declared that no competing interests exist.


Reference By original order
By published year
By cited within times
By Impact factor

M. A. Albert, S. Laulan, S. Barmaki , Can. J. Phys.97 ( 2019)317, https://doi.org/https://ctp.itp.ac.cn/article/2019/0253-6102/10.1139/cjp-2018-0222.
[Cited within: 1]

D. Busto, L. Barreau, M. Isinger , et al., J. Phys. B 51 044002, ( 2018).


F. F. Goryaev, L. A. Vainshtein, A. M. Urnov , At. Data Nucl. Data Tables 113 ( 2017)117.


S. Kajita, K. Suzuki, H. Tanaka, N. Ohno ,Phys. Plasmas. 25 ( 2018)063303.


S. Kar, Y. Wang, W. Li, X. Sun ,Few-Body Sys. 56 ( 2015)10.


A. Müller, A. Borovik Jr., K. Huber , et al., Phys. Rev. A 97 ( 2018)022709.


A. Müller, E. Lindroth, S. Bari , et al., Phys. Rev. A 98 ( 2018)033416.


R. Si, S. Li, K. Wang, et al., Astron. Astrophys. 600 ( 2017)A85.


J. M. N. Djiokap and A. F. Starace ,J. Optics 19 ( 2017)09.
[Cited within: 1]

S. Nakazaki, K. Sakimoto, Y. Itikawa ,Phys. Scr. 47 ( 1993)359.
[Cited within: 1]

W. Schwanda and K. Eidman ,Phys. Rev. Lett. 69 ( 1992)3507.


St. Boddeker, S. Gunter, A. Konies , et al., Phys. Rev. E 47( 1990)2785.


A. B. C. Walker Jr. and H. R. Rugge , Astrophys. J. 164 ( 1971)181.


G. A. Doschek, P. Meekins, R. W. Kerplin, et al., Astrophys. J. 164 ( 1971)165.


J. L. Culhane, et al., Sol. Phys. 136 ( 1991)89.


U. Feldman , Phys. Scr. 46 ( 1992)202.


RESIK & Diogeness NEWS, Week, (2002), website: .
URL

J. Sylwester, B. Sylwester, K. J. H. Phillips , Astrophys. J. 681 ( 2008)L117.


C. Chang and W. Cui , Astrophys. J. 663 ( 2007)1207.
[Cited within: 1]

J. K. Saha, S. Bhattacharyya, T. K. Mukherjee, P. K. Mukherjee ,J. Phys. B 42 ( 2009)245701.
[Cited within: 3]

J. K. Saha, S. Bhattacharyya, T. K. Mukherjee, P. K. Mukherjee , J. Quant. Spectrosc. Radiat. Transfer 111 ( 2010)675.
[Cited within: 6]

J. K. Saha, T. K. Mukherjee, P. K. Mukherjee, B. Fricke , Eur. Phys. J. D 62 ( 2011)205.


J. K. Saha, T. K. Mukherjee, P. K. Mukherjee, B. Fricke , Eur. Phys. J. D 66 ( 2012)43.


J. K. Saha, S. Bhattacharyya, T. K. Mukherjee , Int. Rev. At. Mol. Phys. 3 ( 2012)1.


J. K. Saha, T. K. Mukherjee, P. K. Mukherjee, B. Fricke ,Phys. Plas. 20 ( 2013)042703.


S. Bhattacharyya, J. K. Saha, T. K. Mukherjee ,Phys. Rev. A 91 ( 2015)042515.


S. Dutta, J. K. Saha, S. Bhattacharyya, T. K. Mukherjee , Int. Rev. At. Mol. Phys. 6 ( 2015)73.


S. Dutta, J. K. Saha, T. K. Mukherjee ,Phys. Plas. 22 ( 2015)062103.


S. Dutta, J. K. Saha, R. Chandra, T. K. Mukherjee ,Phys. Plas. 23 ( 2016)042107.


J. K. Saha, S. Bhattacharyya, T. K. Mukherjee ,Phys. Plas. 23 ( 2016)092704.
[Cited within: 1]

A. N. Sil, S. Canuto, P. K. Mukherjee ,Adv. Quantum Chem. 58 ( 2009) 115 and references therein for comprehensive list of works till (2009).
[Cited within: 1]

S. Dutta, J. K. Saha, S. Bhattacharyya, T. K. Mu-kherjee ,Asian J. Phys. 25 ( 2016)1331.
[Cited within: 1]

A. I. Akhiezer, I. A. Akhiezer, R. A. Polovin , et al., Plas-ma Electrodynamics Linear Response Theory
Pergamon, Oxford(1975) 1.
[Cited within: 4]

S. Kar and Y. K. Ho , Int. J. Quantum Chem. 108 ( 2008)1491.
[Cited within: 2]

S. Kar and Y. K. Ho ,Phys. Rev. A 79 ( 2009)062508.
[Cited within: 2]

A. K. Bhatia and A. Temkin ,Rev. Mod. Phys. 36 ( 1964)1050.
[Cited within: 2]

T. K. Mukherjee and P. K. Mukherjee ,Phys. Rev. A 50 ( 1994)850.
[Cited within: 1]

S. Dutta, A. N. Sil, J. K. Saha, T. K. Mukherjee , Int. J. Quantum Chem. 118 ( 2017)e25577.
[Cited within: 2]

NIST, Scientific and Technical Databases, Atomic and Molecular Physics.
[Cited within: 1]

相关话题/Doubly Excited States

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.