 ,2,?
,2,? Corresponding authors: ?E-mail:
Received:2019-03-13Online:2019-07-1
| Fund supported: |

Abstract
Keywords:
PDF (1683KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Chao Feng, Yu Chen. Tunable Range Interactions and Multi-Roton Excitations for Bosons in a Bose-Fermi Mixture with Optical Lattices *. [J], 2019, 71(7): 869-875 doi:10.1088/0253-6102/71/7/869
1 Introduction
In ultracold atom experiments, short-range interactions between atoms can be controlled by all kinds of techniques, such as Feshbach resonances[1] and optical lattices.[2] In contrast, tunable long-range interactions are more difficult to access. Nevertheless, searching methods to control long-range interactions between atoms is growing vigorously these years.[3-16] The main reason is that many new phenomena emerge through competitions between the short-range interactions and the long-range interactions. For example, long-range interactions in Bose-Einstein condensates can lead to roton-like excitations in the single-particle excitation spectrum,[11] which serves as a percusor of crystallization phase.There are several possible ways to introduce long-range interactions in quantum gases. One method is through dipole-dipole interactions.[3-7] This method is intrinsically dependent on the atoms, thus it is hard to be tuned. Another method is through interactions between a cavity field and atoms.[9-11] Recently, there are a lot of progresses in both single mode[11] and multimode cavities.[17-18] However, the mode is always chosen by the cavity field rather than spontaneously. Beyond these two approaches, there is a third way to realize long-range interactions between atoms, which lends the help from quantum gas mixtures.[19-28] Following these realizations of long-range interactions, roton-like excitations are found and supersolid phase are presented.[11,19,29-36]
In recent years, there are a lot of new experimental progresses[23-27] in the field of Bose-Fermi mixtures. Importantly, a Bose-Fermi superfluid mixture is realized[25] and fermion-induced Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction[37] is observed.[27] These new advances drive us to study how to control the induced interactions in a Bose-Fermi mixture. When fermions are put into a lattice, the induced interaction by fermions is strongly influenced by the change of Fermi surface shape. Previous theoretical studies are mostly focused on a case where the lattice fermion density is fixed at the half-filling.[19-21] In that case, the induced interactions between bosons are infinite-range RKKY-type, where a supersolid phase[19-24] at commensurate momentum is expected. However, more general results for arbitrary filling and less deep lattice for three-dimensional Bose-Fermi mixtures is still missing. In this article, we study the boson-boson interactions and the excitation spectrum of the bosons in a Bose-Fermi mixture where the fermions experience an optical lattice. We find that the range of the fermion-mediated interactions can be tuned by the lattice depth and the fermion density. Moreover, we find there may emerge multi-roton minimum in Bogoliubov spectrum, when the fermion density is not exactly at half-filling. Most importantly, the range and the mode of the fermion-mediated interactions can be tuned by the lattice depth and the fermion density.
The following of the article is arranged into three parts. First, we introduce the system and the formulation for the induced interactions and the Bogoliubov spectrum. Then, we revisit the fermion-induced interactions and the Bogoliubov spectrum for bosons, which is mixed with fermions in free space. Finally, we discuss the tunable range interactions and multi-roton excitations for bosons in a Bose-Fermi mixture with optical lattices.
2 Fermion-Induced Interactions in Bose-Fermi Mixtures
Here we consider a Bose-Fermi mixture system which could be described by the following hamiltonian,where $\hat{H}_B$, $\hat{H}_F$, $\hat{H}_{\rm BF}$ are hamiltonians of the boson fields, the fermion fields, and the contact interactions between them. $\phi({{r}})$ is a complex boson field operator. $\psi({{r}})$ is a spinless fermion field operator. $g_{B}$ and $g_{{BF}}$ are boson-boson and boson-fermion interaction strengths respectively. $m_B$ and $\mu_B$ are the mass and the chemical potential of bosons. $H_0=-({\nabla^2}/{2m_{F}})+V({{r}})-\mu_{F}$ is the single body hamiltonian for fermions. $m_{F}$ is the mass of fermions and $\mu_{F}$ is the chemical potential of fermions. $V({{r}})$ is an optical lattice potential, which is applied to the fermions only. This is possible because the shift frequency between the laser field and atomic gases can be different for fermions and bosons.
Integrating out fermion fields up to the second order of $g_{{BF}}$ (the detail of this integration is given in Appendix A), the effective induced interaction can be given as
where
$$V_{\rm ind}({r},{r}')=g_{BF}^2\chi({r},{r}')\,, \\ \chi({r},{r}',T)=\sum_nG_F({r},{r}';i\omega_n)G_F({r}',{r};i\omega_n)$$
is the static structure factor. Here
$$ G_F({r},{r}';\tau-\tau')\equiv \langle T_\tau\psi({r},\tau)\psi^\dagger({r}',\tau')\rangle$$ is the free fermion's propagator in imaginary time,
$$G_F({r},{r}';i\omega_n)=\int_0^\beta d\tau \text{e}^{i\omega_n(\tau-\tau')}G_F({r},{r}';\tau-\tau')$$
($\omega_n=2\pi\beta(n+1/2)$, $n\in {\mathbb{Z}}$, $\beta=1/k_{B}T$, and $T$ is the temperature).
In a translational invariant system, $V_{\rm ind}({r},{r}')=V_{\rm ind}({r}-{r}')$ gives the information of the effective fermion-mediated interactions between bosons. Based on the effective hamiltonian for bosons including the fermion-mediated interactions, we can obtain the excitation spectrum of bosons by Bogoliubov theory as
where $\alpha=\langle \phi\rangle$ is the superfluid order parameter. Before diving into the detail calculations of the spectrum, we first analyze the influence of $V_{\rm ind}({{k}})$ on the spectrum. $V_{\rm ind}({{k}})$ is negative. To access a roton-like structure, threre must be a nonzero ${{k}}$, such that $|V_{\rm ind}({{k}})|\gg |V_{\rm ind}(0)|$. If they are close, then by increasing boson-fermion interaction will drop roton minimum and superfluid velocity at the same time. Thus superfluidity may be destroyed before a roton is formed. $V_{\rm ind}(0)$ is proportional to $-N(0)$, where $N(\epsilon)$ is the fermion density of states. In three-dimensional systems, $N(0)$ is usually finite.
In the following paragraphs, we first show the result of $V_{\rm ind}({{r}})$ and Bogoliubov spectrum $\epsilon_{{k}}$ for fermions without optical lattices. Then we show how optical lattice depth and fermion density affect the induced interaction $V_{\rm ind}({{r}})$ and the Bogoliubov spectrum $\epsilon_{{k}}$.
3 Fermions Without Lattices
In this section, we suppose $V({{r}})=0$ for free fermions. Then the static structure factor in momentum space $\chi({q},T)$ is the Fourier transformation of $\chi({{r}}-{{r}}',T)$,It can be calculated by the following formula
where $G_F({{k}},\text{i}\omega_n)=\text{i}\omega_n-|{{k}}|^2+k_{F}^2$ and we have taken $m_{F}=1/2$, $\mu_{F}=k_{F}^2$. Inserting the Green's function's expression into Eq. (8), we can calculate the susceptibility. At zero temperature, we can obtain an analytical expression of the static structure factor (see Appendix B for calculation detail) as
Similar calculation can be carried out for finite temperature, but the expression is no longer analytical.
Then we carry out a Fourier transformation of $V_{\rm ind}({q})=g_{BF}^2\chi({q},T)$ to real space. In the real space, the induced interaction $V_{\rm ind}({{r}})=g_{BF}^2\chi({{r}})$ is oscillating from negative values to positive values. In other words, these interactions are RKKY-type, which has been discovered long ago.[41-42] The finite temperature static structure factor can be also calculated numerically, whose result is presented in Fig. 1. We find the low temperature induced interaction is not quite different from the zero temperature result. Recently, this is observed in Cheng Chin's group's experiments.[26-27]
Fig. 1
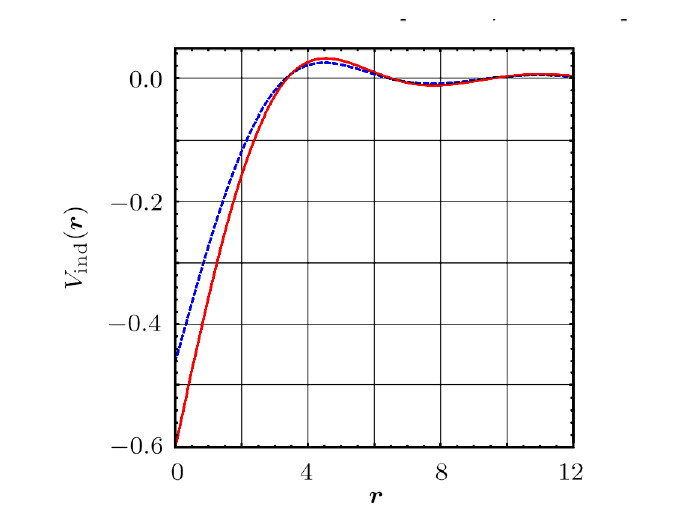 New window|Download| PPT slide
New window|Download| PPT slideFig. 1(Color online) Fermion-induced interactions $V_{\rm ind}({{r}})$ in real space. The red line is the zero temperature result, and the blue line is the low temperature result. In general, the free fermions induce an RKKY-type interaction in the real space.
We find the induced interaction in the short-range $r\ll 1/k_{F}$ is attractive. Therefore, if the boson-boson repulsive interaction is not strong enough, the RKKY interaction may lead to an instability alike attractive interactions in a Bose-Einstein condensate. In that case, there will be a phase separation for the Bose-Fermi mixture. To ensure the short-range interaction being repulsive, we require $g_{B}^{}+g_{BF}^2\chi(0)>0$. In this parameter region, the superfluid sound velocity is not zero. Since $V_{\rm ind}({{k}})$ is monotonously decreasing function of $k$, this potential can not give rise to a roton-like structure in Bogoliubov spectrum. We also work out the low temperature induced interaction, which is shown in Fig. 1 as blue line.
4 Fermions with Lattices
According to Eq. (6), the requirement of obtaining a roton-like minimum in Bogoliubov spectrum is $V_{\rm ind}({{k}}\neq 0)$ being much larger than $V_{\rm ind}(0)$. For free fermions, we have $|V_{\rm ind}({{k}}\neq 0)|<|V_{\rm ind}(0)|$. Therefore it is impossible to get a roton-like structure. However, the fermion model can be described by a tight-binding model, when the optical lattice is deep enough. We can find, the Fermi Surface (FS) is nested at momentum ${Q}_\pi=(\pm\pi,\pm\pi,\pm\pi)/\lambda$ at half-filling case, where $\lambda$ is the lattice constant. In this situation, the static structure factor $\chi({Q}_\pi)$ is divergent. The system has a density order instability. This is similar to the previous two-dimensional Bose-Fermi mixtures[19] and cavity fermions.[38-40] Indeed, there is another possibility of instability at momentum zero. The static structure factor $\chi(0)$ is $-N(0)$ where $N(\epsilon)$ is the fermion density of states (DOS) at energy $\epsilon$. In two-dimensional system, the DOS at zero energy for half-filling is logarithmic divergent because of Van-Hove singularity. The existence of two instabilities will lead to a competition between the instability at ${q}=0$ and ${q}={Q}_\pi$. However, in three-dimensional space, $N(0)$ is finite, therefore we only have instability at ${Q}_\pi$. For this reason, the three-dimensional Bose superfluid is always stable for weak Bose-Fermi interactions.In the following, we present the calculation for the induced interaction for fermion in optical lattices $V({{r}})=V_P(\cos^2 (k_0x)+\cos^2 (k_0y)+\cos^2 (k_0z))$, where $V_P$ is the laser pumping strength. The Bloch wave function can be expressed in terms of Mathieu function as $\phi_{n{{k}}}({{r}})=\text{e}^{\text{i}{{k}}\cdot{{r}}}M_{n_xk_x}(x)M_{n_yk_y}(y)M_{n_zk_z}(z)$, where ${{k}}=(k_x,k_y,k_z)$ is in the first Brillouin zone, $n=(n_x,n_y,n_z)$ is the band index. Here we denote the modified band energy for the $n_{\rm th}$ band is $\epsilon_{n{{k}}}$. In terms of these definitions, the single particle's Green's function can be expressed as
Therefore, the zero temperature static structure factor can be obtained as
Here we employ a tight-binding model with nearest neighbor (NN) hopping and the next nearest neighbor (NNN) hopping to simplify the fermions in an optical lattice. The tight-binding model reads
$$ \hat{H}_{\rm TB}\!=\!\Big(2t\sum_{i=x,y,z}\cos(k_i \lambda) +2t'\sum_{i=x,y,z}\cos(2k_i\lambda)-\mu\Big)c_{{k}}^\dagger c_{{k}}, $$
where $c_{{k}}$ is the lowest band fermion annihilation operator. $t$ and $t'$ can be fitted from exact energy band dispersion. In general, $|t'/t|$ approaches zero quickly when $|V_P/E_r|>3$.
Before we go to detail, we analyze the FS nesting property at half-filling. If $t'=0$, we can find $\epsilon_{{{k}}+{Q}_\pi}=-\epsilon_{{k}}$. The FS has a perfect nesting at ${q}={Q}_\pi$. The perfect nesting will be weakened by the presence of NNN hoping or the density being not exact at half-filling. In the following subsections, we present how NNN hopping and filling have their effect on the induced interactions and Bogoliubov spectrum.
4.1 Lattice Depth Effect on the Induced Interactions
First we fix the chemical potential to be $0.1t$. By tuning $V_P$ from small to large, $t'/t$ shrinks to zero. Here we denote the nesting momentum as ${q}_{\rm max}$, which is the momentum for largest $\chi({q})$. Then we can discuss how ${q}_{\rm max}$ and $V_{\rm ind}({q}_{\rm max})$ change against the lattice strength.With chemical potential being fixed, we vary the optical lattice depth $V_P$ from $-E_r$ to $-5E_r$. Then we obtain $V_{\rm ind}({q})=g_{BF}^2\chi({q})$ from Eq. (11), where $g_{BF}/E_r$ is fixed as $0.1$. The corresponding figures of $V_{\rm ind}({q})$ are given in Fig. 2. We find the induced interaction peak in momentum space shifts from a ring around ${Q}_\pi$ to exact at ${Q}_\pi$ as the pumping field increases. At the same time, we find the contrast between $V_{\rm ind}({q}_{\rm max})$ and $V_{\rm ind}(0)$ increases from 2 to 5 as the lattice strength increases from $-E_r$ to $-5E_r$. From these results, we predict the interaction range is increasing when the lattice depth is increasing.
Fig. 2
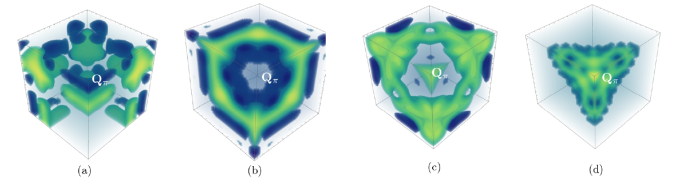 New window|Download| PPT slide
New window|Download| PPT slideFig. 2(Color online) Induced interaction in momentum space $V_{\rm ind}({q})$. The momentum space is restricted to the cubic region $q_{i=x,y,z}\in[0,\pi/\lambda]$. In (a), (b), (c), (d), we show $V_{\rm ind}({q})$ for different fermion optical lattice strength. $V_P=-E_r$ in (a), $V_P=-2E_r$ in (b), $V_P=-3E_r$ in (c) and $V_P=-5E_r$ in (d). The chemical potential $\mu$ is mixed as $0.1t$. The corner in the center of each figure is ${Q}_\pi=(\pi,\pi,\pi)/\lambda$ point.
Here we show what peaks in momentum space imply in real space potential. Assuming $V_{\rm ind}({q})$ is peaked at ${q}_{\rm max}^j$ and can be approximated as $\sum_j 1/(({q}-{q}^j_{\rm max})^2+1/r_*^2)$, where summation over $j$ is summation over different peaks and $r_*$ is an effective range. By Fourier transformation we have
Then we can see the oscillation factor comes from $e^{i{q}_{\rm max}^j\cdot{{r}}}$ and the width $1/r_*$ in momentum space implies the range of the potential in real space. The range of the interaction strength depends on how sharp is the peak of $V_{\rm ind}({q})$ in momentum space.
Further, we give the Bogoliubov spectrum of bosons in different lattice depth. One can find roton like excitations emerge, as is shown in Fig. 3. One can find when the lattice depth is not so deep, the roton position is not around ${Q}_\pi\;(K)$ point.
Fig. 3
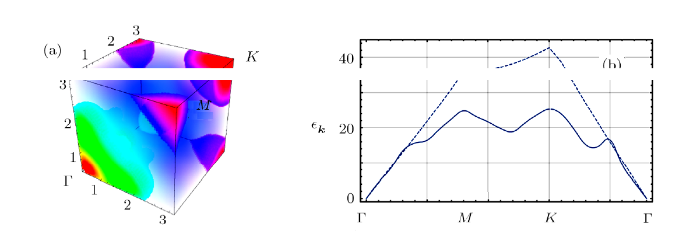 New window|Download| PPT slide
New window|Download| PPT slideFig. 3(Color online) In (a), we show the Bogoliubov spectrum for $V_P=-2E_r$ case. $g_{B}n_{B}/E_r=4.05$ and $g_{BF}^2/E_r^2=0.0045$. Red color is small energy value and violet color is for large energy value. In (b), we show the dispersion of bosons in a path from $\Gamma$ point to $M$ point, to $K$ point then return to $\Gamma$ point. A reference dispersion is presented in dashed line when we turn off the boson-fermion interactions.
4.2 Fermion Density Effect on the Induced Interactions
Here we fix the lattice depth to be $V_P=-5E_r$. In this situation, the FS nesting is almost perfect. And the induced interaction is divergent at the momentum ${Q}_\pi$. After driving the filling away from the half-filling, we find the momentum ${q}_{\rm max}$ where $V_{\rm ind}({q})$ is peaked shifts from ${Q}_\pi$ to incommensurate momentums. We show the induced $V_{\rm ind}({q})$ in momentum space in Fig. 4. And the chemical potential is equal to $t$, $0.5t$, and $0.1t$ in Figs. 4(a), 4(b), and 4(c) inrespectively. We see the induced interaction peaks in $(\pm\pi,\pm\pi,0)$, $(0,\pm\pi,\pm\pi)$, and $(\pm\pi,0,\pm\pi)$ for $\mu=t$. As the chemical potential approaches zero, the induced interaction peaks around ${Q}_\pi=(\pm\pi,\pm\pi,\pm\pi)$ point, forming a circle around ${Q}_\pi$ point. Meanwhile, the contrast between the peak $V_{\rm ind}({q}_{\rm max})$ and $V_{\rm ind}(0)$ diverges in the process of $\mu$ approaching $0$. The peak of induced interaction becomes larger and larger as the chemical potential approaches zero. If we translate these information in real space, that is, the induced interaction's oscillation pattern is changed and the range is enlarged when the fermion density approaches half-filling.Fig. 4
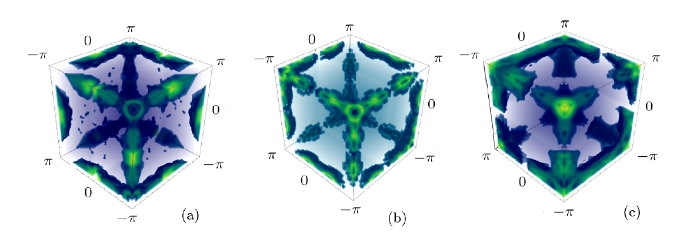 New window|Download| PPT slide
New window|Download| PPT slideFig. 4(Color online) The static structure factor in momentum space $\chi_0({q})$. In these figures we only show the largest region of the static structure factor. In (a), the chemical potential is $\mu=t$; In (b), the chemical potential is $\mu=0.5t$; and in (c), the chemical potential is $\mu=0.1t$. The brighter color is for larger $\chi({q})$, and the darker color is for smaller $\chi({q})$. Three axes are $q_x$, $q_y$, and $q_z$ direction, from $-\pi$ to $\pi$. Beyond this range, the static structure factor is almost zero, suppressed by the band gap.
Then we study how single-particle excitation spectrum of the bosons is changed by $V_{\rm ind}({q})$. First, we conclude that we can not have both superfluid and roton structure in the same time for relative low filling (but not close to zero). The reason is that the contrast between $V_{\rm ind}({q}_{\rm max})$ and $V_{\rm ind}(0)$ is not large when $\mu$ is not close to $0$. Meanwhile, the superfluid sound velocity will be reduced severely when $g_{BF}$ is large enough to give rise to a roton structure. Therefore, the system will experience a collapse where bosons and fermions are separated before a roton-like excitation can be generated in Bogoliubov spectrum.
Second, around $\mu=0$, a roton-like excitation is possible. This is because the contrast between $V_{\rm ind}({q}_{\rm max})$ and $V_{\rm ind}(0)$ is large when the fermion density is close to half-filling. When the nesting momentum becomes incommensurate, there could be multi-roton structure in Bogoliubov spectrum. Here we show the single-particle excitation spectrum of bosons in deep fermion lattice limit ($V_P=-5E_r$) in Fig. 4. In Fig. 5(a), we show the Bogoliubov spectrum $\epsilon_{{k}}$ with $\mu_{F}=0.1t$. $g_{BF}^2/E_r^2$ is taken as $0.0039$. In Fig. 5(b), we show the Bogoliubov spectrum $\epsilon_{{k}}$ with $\mu_{F}=0.5t$, $g_{BF}^2/E_r^2=0.004\,31$. The boson interaction energy is taken as $g_{B}n_B/E_r=4.05$. In Fig. 5(c), we give the Bogoliubov spectrum along ${\Gamma MK\Gamma}$ circle in momentum space. The dotdashed line is the Bogoliubov spectrum without Fermi gases. We observe more than one roton minimum in Fig. 5(c) for different fermion density (dashed line and solid line).
Fig. 5
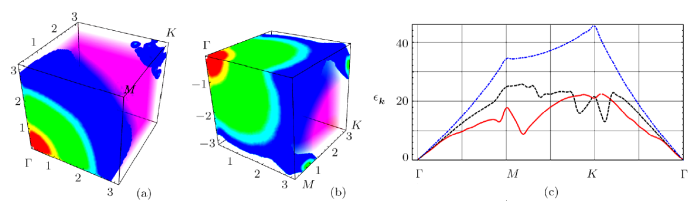 New window|Download| PPT slide
New window|Download| PPT slideFig. 5(Color online) In (a) and (b) we give the Bogoliubov spectrum for Bose gases mixed with Fermi gases in deep lattice. The chemical potential of the Fermi gases is $\mu=0.1t$ and $\mu=0.5t$ ($t<0$) in (a) and (b) respectively. In (c), the blue dot-dashed line is for the Bogoliubov spectrum of the interacting Bose gases alone, while the black dashed line and the red solid line are Bogoliubov spectrum of Bose gases mixed with lattice fermions along $\Gamma MK\Gamma$ route in the first Brilluin zone.
5 Conclusion
To summarize, we find boson-fermion interactions in a Bose-Fermi mixtures can induce an RKKY-type interaction between bosons. We can control the momentum pattern and the interaction range by tuning the lattice depth and the fermion density. In three-dimensional systems, the fermion-mediated interactions are strongly affected by the Fermi surface properties like FS nesting. On the other hand, unlike the two-dimensional case, the lattice fermion density of states in three-dimensional system is always finite, rather than a logarithmic divergence in two-dimensional system. This property ensures a roton-like excitation in Bogoliubov spectrum without instability at zero momentum. In some special fillings close to half-filling, multi-roton structure in Bogoliubov spectrum is observed. Therefore the Bose-Fermi mixture is an ideal system to study the interaction range effect, incommensurate density orders and the competing density orders.Appendix A: Deduction of Eq. (5)
Following the hamiltonian $\hat{H}$ given in Eq. (1), the partition function of the system can be written in a path integral form as,
where $\phi({{{r}}},\tau)$, $\psi({{{r}}},\tau)$ are a complex bosonic field and a complex fermionic field, whose boundary conditions are $\phi({{{r}}},0)=\phi({{{r}}},\beta)$ and $\psi({{{r}}},0)=-\psi({{{r}}},\beta)$. $\beta=1/k_{B} T$ is the inverse temperature.
From the action, one can observe the second line of the action is completely bilinear term of fermionic field $\psi$.
If one denotes a Green function operator in virtual time as $\hat{G}_0^{-1}(\tau)=\partial_\tau+\hat{H}_0$,
then by integrating the fermionic field we obtain
where $x=({{{r}}}.\tau)$ is a four vector. $\tau\in[0,\beta]$ is imaginary time. Applying integration over fermionic field $\psi$, $\bar{\psi}$ and make use of the Grassman number integral $\int \prod_{ij}d \bar{\psi}_i d \psi_j e^{\bar{\psi}_i A_{ij}\psi_j}=\det \hat{A}$, where $\hat{A}=\{A_{ij}\}$ is the matrix, then we can obtain an action with only the bosonic fields. As now there are only fermion bilinear terms, an exact integration over fermionic field is possible, and the result is
where $\hat{G}$ should be comprehend as an operator $\hat{G}=\{ G_{x,x'}\}$ and $\hat{\phi}\phi(x)$ is diagonal in real space.Making use of $\ln \det (\hat{A})={\rm Tr}\ln (\hat{A})$, we have
Considering $g_{BF}$ is a small parameter, we expand the $\ln$ function to a second order form, that is
Here trace is over different $x$, $x'$. The first term always vanishes. If we only consider the case where $\tau=\tau'$, then the second term is
As we know $\chi({{{r}}},{{{r}}}')=\langle \hat{G}_0(x,x')\hat{G}_0(x',x)\rangle$ is the equal time density correlation function, therefore this term can be interpreted as
Now we obtain Eq. (5).
Appendix B: Deduction for Eq. (8)
We start from Eq. (8). By inserting $G_F({{{k}}},\text{i}\omega_n)=\text{i}\omega_n-k^2+k_{F}^2$, we have
Here we introduce $b(x)=k_{F}^2-({q^2}/{4})(1-x^2)$. If $q<2k_{F}$, $b(x)\geq0$ for all $x$. If $q>2k_{F}$, it is possible that $b(x)<0$.
First, we consider the case for $q<2k_{F}$ where $b(x)>0$ for all $x$.Here we set $\beta(k^2-b)=t$ which leads to $k=\sqrt{t/\beta+b}$. One key integral in Eq. (A10) can be calculated as
Therefore, at zero temperature, in $\beta\rightarrow\infty$ limit, we have
Second, we consider $q>2k_{F}$ case. In this case, a different approach is taken directly at zero temperature, which is much simpler then above method. (Above method is more suitable for $q<2k_{F}$ case)
Here we set $\cos\theta=x$. The condition for $x$ is $x>(k_{F}^2-k^2-q^2)/2kq$. Because $k_{F}^2-k^2-q^2/2kq<-1$, therefore $x$ can take any value.
Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 4]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 5]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 3]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
