M. Farasat Shamir^,?, Adnan Malik^,?Department of Sciences and Humanities, National University of Computer and Emerging Sciences, Lahore Campus, Pakistan

Corresponding authors: ^?E-mail:farasat.shamir@nu.edu.pk^?E-mail:adnanmaths2017@gmail.com

Received:2018-10-16Online:2019-05-1

Fund supported:

National University of Computer and Emerging Sciences (NUCES), Pakistan

Abstract
The aim of this paper is to investigate modified $f(R,\phi)$ theory of gravity, where $R$ and $\phi$ represent the Ricci scalar and scalar potential respectively. Specifically, we take the spherically symmetric spacetime to discuss the possible emergence of compact stars. We study the physical behavior of compact stars by considering 4U 1820-30, SAX J 1808-3658 and Her X1, which are three popular models of compact stars. The graphical analysis of energy density, radial pressure, tangential pressure, energy conditions as well as stability of compact stars has been shown. It is concluded that behavior of these three stars is usual for $f(R,\phi)$ gravity models with some specific choices of model parameters.
Keywords： $f(R,\phi)$ gravity;spherically symmetric spacetime;compact stars;Klein-Gordon equation


PDF (2136KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
M. Farasat Shamir, Adnan Malik. Behavior of Anisotropic Compact Stars in $f(R,\phi)$ Gravity. [J], 2019, 71(5): 599-609 doi:10.1088/0253-6102/71/5/599

1 Introduction

Different ideas have been presented to explain the cause of current cosmic expansion. There are two ways to justify this apparently mysterious issue. One way is to introduce a new form of energy component commonly known as dark energy to solve the problem. However this approach has some difficulties because dark energy has never been detected or observed directly. Instead of the use of first option, one can modify the Einstein theory of general relativity (GR). Modification of gravity seems to explain the issue of cosmic expansion and may provide better understanding of the nature of gravity.

It is expected that alternative or modified models can give better explanation of the issues of dark energy. These alternative models are called as modified theories of GR, some of which are $f(R)$, $f(R,G)$, $f(R,T)$, $f(G)$, $f(G,T)$, $f(R, R_{\alpha\beta}R^{\alpha\beta}, \phi)$, and $f(R, \phi)$ theories of gravity, where $R$, $T$, $G$, $R_{\alpha\beta}$ and $\phi$ represent Ricci scalar, the trace of the energy momentum tensor, the Gauss-Bonnet invariant, Ricci tensor and scalar potential respectively. These modern theories of gravity are expected to explain the concept of dark energy, which seems to be responsible for current cosmic expansion. Buchdahl was the first who proposed $f(R)$ gravity in 1970.^[1] Stellar structure as well as hydrostatic equilibrium have been investigated by considering the Lane-Emden equation in $f(R)$ gravity.^[2] Harko presented modified $f(R,T)$ theory.^[3] Recently, Sharif and Ikram^[4] proposed $f(G,T)$ gravity and studied the energy conditions. Zubair and Kousar^[5] discussed cosmological reconstruction and energy bounds in a new general $f(R, R_{\alpha\beta}R^{\alpha\beta}, \phi)$ gravity. The same authors also studied the first and second laws of black hole thermodynamics.^[6] Capozziello and Laurentis^[7] introduced the scalar field in the action and discussed the $f(R,\phi)$ gravity. They discussed a new technique to address and solve the inconsistencies of GR. In a recent paper,^[8] density perturbations in the cosmic microwave background within general $f(R,\phi)$ models of gravity are investigated and it is concluded that density perturbation obtained from observations may be recovered naturally, with high precision. Therefore, modified theories of gravity look attention grabbing in explaining the nature of universe.

In astrophysics, study of compact star is a fascinating topic of research.^[9-16] Compact stars are generally being referred to as the black holes, quark stars, neutron stars, and hybrid stars. These stars have high densities because of their massive size. Many investigations have been done for finding the solutions of the field equations for spherically symmetric anisotropic configurations in different contexts.^[17-18] The nuclear density turns anisotropic at the core of the compact stars.^[19] The numerical simulations may be used to study the nature of the compact stars by using equation of state (EoS) parameter from Tolman-Oppenheimer-Volkoff (TOV) equation. Mak and Harko^[20] explored some exact solutions to find the physical parameters such as the radial pressure, energy density and tangential pressures for spherically symmetric compact objects. Some interested results can be seen for a through study in Refs. ^[21-27].

In this article, we are interested to examining the physical behavior of compact star using spherically symmetric space time. We study the stability of anisotropic compact stars using $f(R,\phi)$ gravity. The plan of our present study is as follows: In Sec. 2, we give the field equations of $f(R,\phi)$ theory of gravity and find the expressions for radial pressure, energy density, and tangential pressure. In Sec. 3, we develop the scalar field by using Klein-Gordon equation for three famous compact stars namely SAX J 1808-3658, 4U 1820-30, and Her X1. We further discuss the physical behavior of energy density and pressure evolution, energy conditions, TOV equation, matching conditions, EOS parameters, and stability analysis. Concluding discussion is given in Sec. 4.

2 Anisotropic Matter Distribution in $f(R,\phi)$ Gravity

An interesting family of extended theories of gravity may be categorized as the scalar tensor theories.^[28] A general class of higher order scalar tensor theories is obtained by the following effective action^[29]

(1)$ S= \frac{1}{2K} \int d^4x \sqrt{-g} (f(R,\phi) + w(\phi)\phi_{; \alpha}\phi^{; \alpha}+ L_{m}) , $
where $f(R,\phi)$ is an analytic function of Ricci Scalar $R$ and the scalar field $\phi$. For our convince we use $f(R,\phi)\equiv f$. Here $g$ is the determinant of metric tensor $g_{\mu \nu}$. The field equations of $f(R,\phi)$ gravity are obtained by varying the action $S$ in Eq. (1) with respect to the metric tensor

(2)$ f_{R}R_{\mu\nu}-\frac{1}{2}[f+w(\phi)\phi_{; \alpha}\phi^{; \alpha}]g_{\mu\nu} + w (\phi)\phi_{; \mu}\phi_{; \nu}-f_{R; \mu\nu} +g_{\mu\nu}\Box{f_{R}}=kT_{\mu\nu} ,$
where $w$ is an arbitrary function of $\phi$, $\nabla_{\mu}$ represents the covariant derivative, $\Box\equiv\nabla_{\mu}\nabla^{\nu}$ and $f_{R}\equiv{\partial f}/{\partial{R}}$ etc. Similarly, Klein-Gordon equation is obtained by varying the action $S$ in Eq. (1) with respect to the scalar field $\phi$^[29]

(3)$ 2 w (\phi)\Box \phi+w_{\phi}(\phi)\phi_{; \alpha}\phi^{;\alpha}-f_{\phi}=0 , $
where $w_{\phi}={dw}/{d\phi}$ and $f_{\phi}={\partial f}/{\partial \phi}$.

(4)$ T_{\xi\eta}^{m}=(\rho+p_{t})u_{\xi}u_{\eta} -p_{t}g_{\xi\eta}+(p_{r}-p_{t})v_{\xi}v_{\eta} ,$
where $\rho$, $p_{r}$, and $p_{t}$ represent the energy density, radial pressure, and tangential pressure respectively. Here $u_{\xi}=e^{a/2}\delta_{\xi}^{0}$ and $v_{\eta}=e^{b/2}\delta_{\eta}^{1}$. In this work, we consider the $f(R,\phi)$ model^[31]

(5)$ f(R,\phi)=\phi(R+\alpha R^{2}) ,$
where $\alpha$ is any non zero constant and $\phi\equiv \phi(r)$. We further consider the following spherically symmetric line element

(6)$ d{s}^{2}=e^{a(r)}dt^{2}-e^{b(r)}dr^{2}-r^{2} (d\theta^{2}+\sin^{2}\theta d\phi^{2}) . $
Using line element (6) along with energy-momentum tensor (4) in Eq. (2), we get

(7)$ \rho= e^{-b}\Bigl[\frac{1}{2}w(\phi)\phi^{\prime 2}+\frac{1}{4} \Bigl(a^{\prime 2}+2a^{\prime\prime}-a'b' +\frac{4a'}{r}\Bigr)f_{R} \\ -\Bigl(\frac{b'}{2}+\frac{2}{r}\Bigr) f'_{R}-f^{\prime\prime}_{R}\Bigr]-\frac{f}{2} , $
(8)$ p_{r}= e^{-b}\Bigl[\frac{1}{2}w(\phi)\phi^{\prime 2}-\frac{1}{4} \Bigl(a^{\prime 2}+2a^{\prime\prime}-a'b'-\frac{4b'}{r}\Bigr)f_{R} \\ +\Bigl(\frac{a'}{2}+\frac{2}{r}+b'\Bigr)f'_{R}\Bigr]+\frac{f}{2} , $
(9)$ p_{t}= e^{-b}\Bigl[-\frac{1}{2}w(\phi)\phi^{\prime 2}+\frac{1}{2} \Bigl(\frac{b'}{r}-\frac{a'}{r}+\frac{2e^{b}}{r^{2}} -\frac{2}{r^{2}}\Bigr)f_{R} \\ +\Bigl(\frac{a'}{2}+\frac{1}{r}+\frac{b'}{2}\Bigr)f'_{R}+f^{\prime\prime}_{R}\Bigr] +\frac{f}{2} . $
It is mentioned that prime denotes the radial derivative. These equations (7)-(9) are involving many unknown functions with high non linearity. So following Krori and Barua^[32] approach, we choose $a(r) = Yr^{2} + Z$ and $b(r) = Xr^{2}$, where $X$, $Y$, and $Z$ are constants. The values of these constants will be found by using some physical assumptions. It is worthwhile to mention here that we use the software $MATHEMATICA$ for the further analysis.

3 Physical Aspects of Compact Stars in $f(R, \phi)$ Gravity

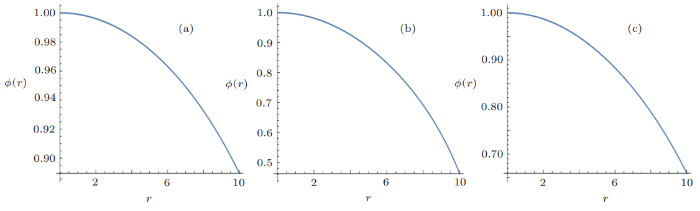
This section presents the physical behavior of energy density, pressure evolution, energy conditions, TOV equation, solutions regarding EOS, matching conditions and stability analysis for different stars namely Her X-1, SAX J 1808.4-3658 and 4U 1820-30. We choose $w(\phi)=w_0 \phi^m$, where $m$ is any arbitrary non-zero constant. It would be worthwhile to mention here that the use of Klein-Gordon equation (3) is necessary for respective solutions. Thus, for Her X-I star, we use $f(R,\phi)$ model (5) and line element (6) to obtain

(10)$ 2r^2e^{-0.0069062764281r^2}(4-4e^{0.0069062764281r^2}+0.004041836005200007r^2 +0.00004504479555181816r^4 )-e^{-0.0138125528562r^2} \\ \times(4e^{0.0069062764281r^2}-4 -0.004041836005200007r^2-0.00004504479555181816r^4 )^2-8r^4\Bigl[\Bigl(\frac{2}{r}+ 0.0111736410464r\Bigr)\phi'(r) \\ +\phi^{\prime\prime}(r)\Bigr]\phi(r)^3e^{-0.0069062764281r^2} -12r^4(\phi(r)^2\phi'(r)^2e^{-0.0069062764281r^2}) =0 , (10) $
which is a second order highly nonlinear differential equation. It is mentioned that for the sake of simplicity, we have chosen $w_0=1=m$ i.e. $w(\phi)=\phi$. By taking some suitable boundary conditions, we find the numerical solution of Eq. (10) as shown in Fig. 1(a). We obtain the following cubic function to approximate $ \phi(r)$ for Her X-I star by using suitable interpolation technique

(11)$ \phi(r) = 0.00000382193425644503r^3 - 0.001161081370864423r^2 + 0.0002321016161451929r + 0.9999651866685453 . $
Similarly, the corresponding numerical solutions for $\phi(r)$ for other two stars namely SAX J 1808.4-3658 and 4U 1820-30 stars are shown in Figs. 1(b) and 1(c) respectively. Moreover, the approximate cubic functions are given by

(12)$ \phi(r) = -0.000034122847109647934r^3 - 0.004956515547590018r^2 + 0.0009923267949312952r + 0.9998511339193368 . $
(13)$ \phi(r) = -0.000052265490526779855r^3 - 0.0029353251840551417r^2 + 0.0005886330015268344r + 0.9999116789170257 . $

Fig. 1

New window|Download| PPT slide
Fig. 1(Color online) Numerical solution of $\phi(r)$ for Her X-1, SAX J 1808.4-3658, and 4U 1820-30.

3.1 Her X-1 Candidate

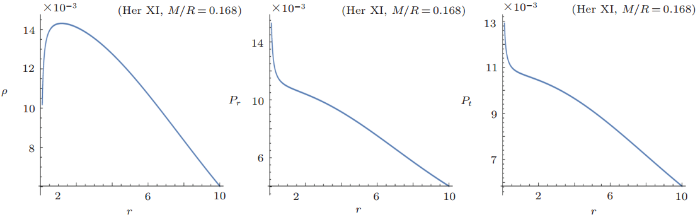
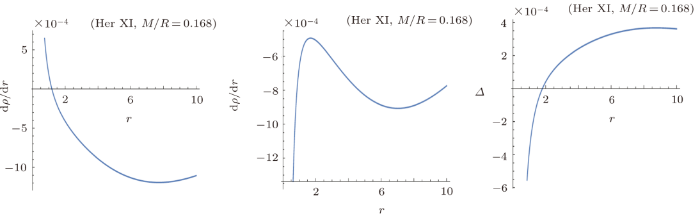
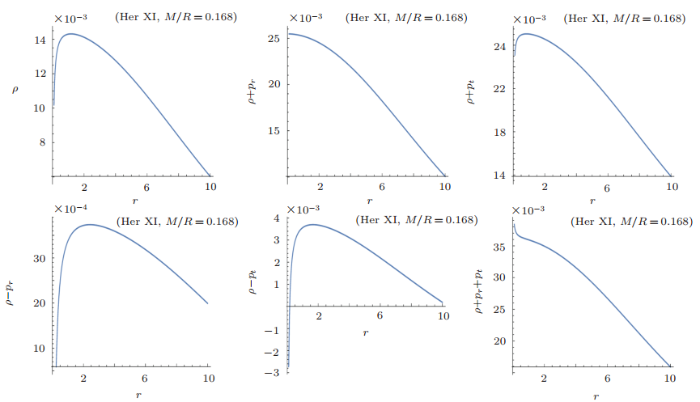
The graphical behavior of energy density, radial and tangential pressure for Her X-I candidate is presented in Fig. 2, which shows that all these graph are positive and decreasing. However, all these quantities approach to zero as we move away from the center of star. The variation of the radial derivative of density has the decreasing and monotonic behavior. The anisotropic measurement $\bigtriangleup=({2}/{r})(p_t-p_r)$ has the opposite behavior as compared to the behavior of the radial derivative of density as shown in Fig. 3. The anisotropic measurement is directed inward when tangential pressure is less than radial pressure. It is directed outward when radial pressure is less than tangential pressure. The variation of the radial derivative of radial pressure has the negative behavior as shown in Fig. 3.

Fig. 2

New window|Download| PPT slide
Fig. 2(Color online) Behavior of energy density $\rho~[{\rm MeV/fm^3}]$, radial pressure $P_{r}~[{\rm MeV/fm^3}]$ and tangential pressure $P_{t}~[{\rm MeV/fm^3}]$ versus radial coordinate $r(\rm km)$ for Her X-1 candidate.

Fig. 3

New window|Download| PPT slide
Fig. 3(Color online) Behavior of ${d\rho}/{dr}$, ${dp_r}/{dr}$ and $\bigtriangleup$ for Her X-1 candidate.



The importance of energy conditions can not be denied. These conditions must hold for the viability model under consideration. Some interesting results have been reported in cosmology using the energy bounds.^[33-35] Null energy conditions (NEC), weak energy conditions (WEC), strong energy conditions (SEC), and dominant energy conditions (DEC) are defined as

$ \textbf{NEC}: \rho + p_r\geq 0, \quad \rho+p_t\geq 0, \\ \textbf{WEC}: \rho\geq 0,\quad \rho + p_r\geq 0,\quad \rho+p_t\geq 0, \\ \textbf{SEC}: \rho + p_r\geq 0, \quad \rho+p_t\geq 0,\quad \rho + p_r+2p_t\geq 0, \\ \textbf{DEC}: \rho > |p_r|, \quad \rho >|p_t| . $

For the present analysis, the energy conditions plot is shown in Fig. 4 for only Her X-1. It is noticed from the graph that NEC, WEC, and SEC are satisfied. However, DEC is slightly violated near the center of star but holds as we move towards the boundary of star. It can be concluded that all the energy conditions satisfied for $0.2 \leq r \leq 10$. The TOV equation is expressed as

(14)$ \frac{dp_r}{dr}+\frac{v'(\rho+p_r)}{2}+\frac{2(p_r-p_t)}{r}=0 . $
We can write from Eq. (14) as

(15)$ F_h+F_g+F_a=0 , $
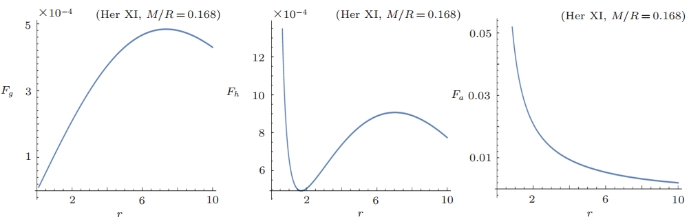
which suggests that TOV equation is the combination of hydrostatic force $F_h$, gravitating force $F_g$ and anisotropic pressure force $F_a$ where

(16)$ F_h=-\frac{dp_r}{dr},\quad F_g=Yr(\rho+p_r),\quad F_a=\frac{2(p_r-p_t)}{r} . $
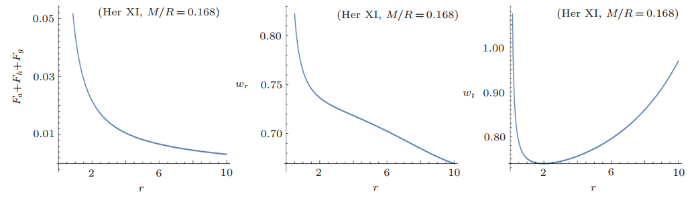
Individual behavior of these forces is shown in Fig. 5 and the combined effect of TOV equation is described in Fig. 6. It is clear that TOV equation is satisfied for Her X-I star candidate ultimately. In literature, parameters of EoS have been used differently according to the nature of fluid in cosmological contexts.^[41-43] Radial EoS parameter and tangential EoS parameter are given as^[44]

(17)$ w_r=\frac{p_r}{\rho},\quad w_t=\frac{p_t}{\rho} . $
The graphical representation of EOS parameters $w_r$ and $w_t$ is shown in Fig. 6. It is observed that these EOS parameters are satisfied for the usual range $0<w_r<1$, $0<w_t<1$. There are many choices for the matching conditions but we consider Schwarzchild exterior solution for the present work.^[36-38] Therefore, the metric is

(18)$ ds^2 = (1-\frac{2M}{r})dt^2-\frac{1}{(1-({2M}/{r}))} dr^2 \\ -r^{2}d\theta^2-r^2\sin^2\theta d\varphi^2 . $
Now for solving the field equations at $r=R$, the interior metric (6) requires these matching conditions

(19)$ g_{tt}^{-}=g_{tt}^{+} ,\quad g_{rr}^{-}=g_{rr}^{+} ,\quad \frac{\partial g_{tt}^{-}}{\partial r}=\frac{\partial g_{tt}^{+}}{\partial r} ,$
where $(-)$ represents the interior solutions and (+) represents the exterior solutions. Now after the comparison of both spacetimes i.e. exterior as well as interior metrics, we obtain the constants $X$, $Y$ and $Z$ as

(20)$ X=\ln\Bigl(1-\frac{2M}{R}\Bigr)^{{-1}/{R^2}} , $
(21)$ Y=\frac{M}{R^3}-\frac{2M^2}{R^4} ,$
(22)$ Z=\ln\Bigl(1-\frac{2M}{R}\Bigr)-\Bigl(\frac{M}{R}-\frac{2M^2}{R^2}\Bigr) ,$
where $M$ is the Schwarzchild mass and $R$ is the Schwarzchild radius of the compact star. The constants $X$ and $Y$ are given in the following table.^[39-40]

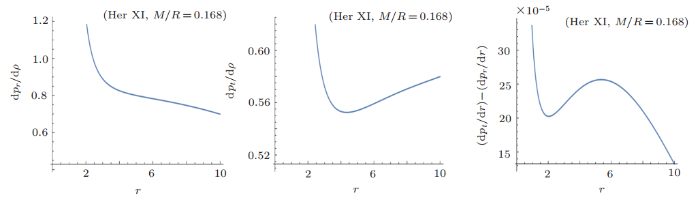
The radial sound speed $v_{sr}^{2}$ and transverse sound speed $v_{\rm st}^{2}$ is used for determining the stability, which are defined as

(23)$ v_{\rm sr}^{2}=\frac{dp_r}{d\rho}, \quad\quad v_{\rm st}^{2}=\frac{dp_t}{d\rho} . $
and the following bounds must be satisfied^[45]

(24)$ 0\leq v_{\rm sr}^{2}\leq 1 ,\quad\quad 0\leq v_{\rm st}^{2}\leq 1 . $
Moreover, the expressions for radial and transverse sound speed are obtained using the corresponding constants in Table 1. It can seen in Fig. 7 that bound for transverse case is satisfied and radial sound speed satisfies only for $3 \leq r \leq 10$. However, differences of the propagations of the sound speeds for Her X-I star are also satisfied $\mid \upsilon_{\rm sr}^2-\upsilon_{\rm st}^2\mid <1$ as shown in Fig. 7. So, proposed model of Her X-I star is stable.


Table 1
Table 1The constants X and Y of the compact star.

New window|CSV

Fig. 4

New window|Download| PPT slide
Fig. 4(Color online) Plots of energy conditions for Her X-1 candidate.

Fig. 5

New window|Download| PPT slide
Fig. 5(Color online) Behavior of gravitating force, hydrostatic force and pressure anisotropic force for Her X-1 candidate.

Fig. 6

New window|Download| PPT slide
Fig. 6(Color online) Behavior of TOV equation, radial EoS parameter, and tangential EoS parameter with respect to the radial coordinate for Her X-1 candidate.

Fig. 7

New window|Download| PPT slide
Fig. 7(Color online) Behavior of $v_{\rm sr}^2$, $v_{\rm st}^2$, and $v_{\rm st}^2-v_{\rm sr}^2$ with respect to the radial coordinate for for Her X-1 candidate.

Fig. 8

New window|Download| PPT slide
Fig. 8(Color online) Behavior of energy density $\rho[\rm MeV/fm^3]$, radial pressure $P_{r}[\rm MeV/fm^3]$, and tangential pressure $P_{t}[\rm MeV/fm^3]$ versus radial coordinate $r(\rm km)$ for SAX J 1808.4-3658 candidate.

Fig. 9

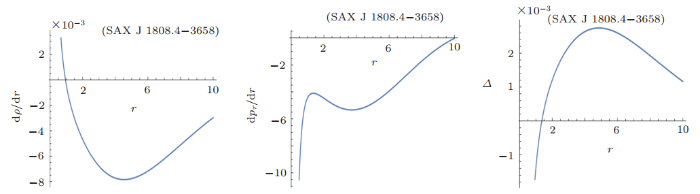
New window|Download| PPT slide
Fig. 9(Color online) Behavior of ${d\rho}/{dr}$, ${dp_r}/{dr}$, and $\Delta$ for SAX J 1808.4-3658 candidate.



The graphical behavior of energy density, radial pressure and tangential pressure for SAX J 1808.4-3658 Star candidate is shown in Fig. 8. The energy density and tangential pressure has positive and decreasing behavior. The radial pressure has negative behavior as we move away from the center of star, which is the validation of expansion of universe. Figure 9 shows that the anisotropic measurement is directed outward because radial pressure is less than tangential pressure. The variation of the radial derivative of density and radial pressure has the negative behavior as shown in Fig. 9.

The energy conditions for SAX J 1808.4-3658 are shown in Fig. 10. It is noticed that NEC, WEC, DEC, and SEC are satisfied. The graphical behavior of hydrostatic force $F_h$, gravitating force $F_g$, and anisotropic pressure force $F_a$ is shown in Fig. 11, which shows that all these forces have positive behavior. The combination of all these forces namely TOV equation is satisfied as shown in Fig. 12.

Fig. 10

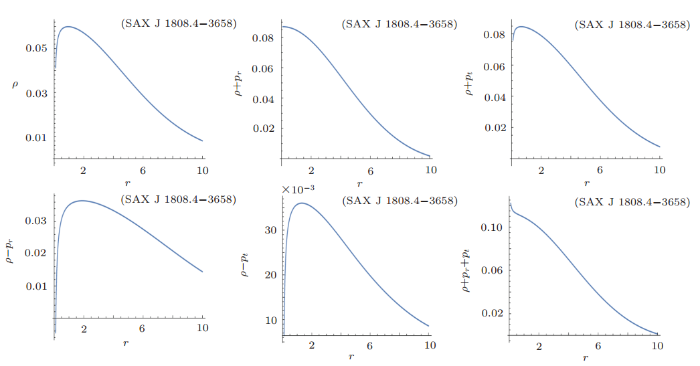New window|Download| PPT slide
Fig. 10(Color online) Plots of energy conditions with respect to radius $r$ for SAX J 1808.4-3658 candidate.

Fig. 11

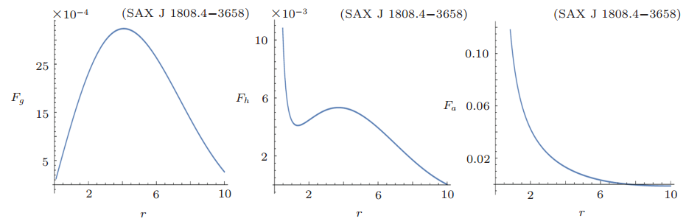New window|Download| PPT slide
Fig. 11(Color online) Behavior of gravitating force, hydrostatic force, and pressure anisotropic force for 1808.4-3658 candidate.

Fig. 12

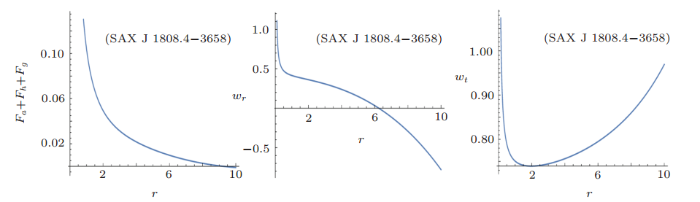New window|Download| PPT slide
Fig. 12(Color online) Behavior of TOV equation, radial EoS parameter, and tangential EoS parameter with respect to the radial coordinate for SAX J 1808.4-3658 candidate.



The radial EoS parameter and tangential EoS parameter's behavior can also be seen in Fig. 12. It can be observed that tangential parameter is satisfied but radial pressure parameter is only satisfied for $0 \leq r \leq 6$. The transverse sound speed is satisfied and radial sound speed is satisfied only for $2 \leq r \leq 10$. The differences of the propagations of the sound speeds for SAX J 1808.4-3658 star are also satisfied for $0 \leq r \leq 7$ as shown in Fig. 13. Hence, proposed model for SAX J 1808.4-3658 star is stable for $2 \leq r \leq 7$.

Fig. 13

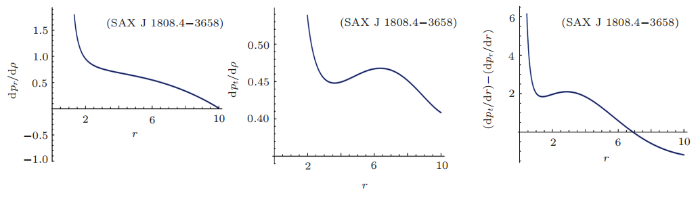New window|Download| PPT slide
Fig. 13(Color online) Behavior of $v_{\rm sr}^2$, $v_{\rm st}^2$ and $v_{\rm st}^2-v_{\rm sr}^2$ with respect to the radial coordinate for SAX J 1808.4-3658 candidate.

Fig. 14

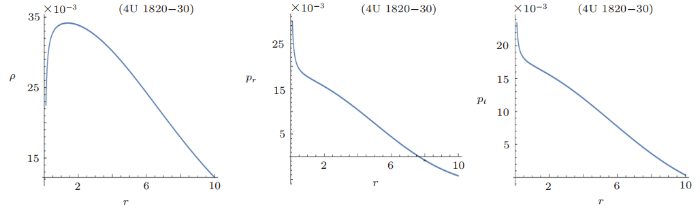New window|Download| PPT slide
Fig. 14(Color online) Behavior of energy density $\rho~[\rm MeV/fm^3]$, radial pressure $P_{r}~[\rm MeV/fm^3]$ and tangential pressure $P_{t}~[\rm MeV/fm^3]$ versus radial coordinate $r~(\rm km)$ for 4U 1820-30 candidate.

Fig. 15

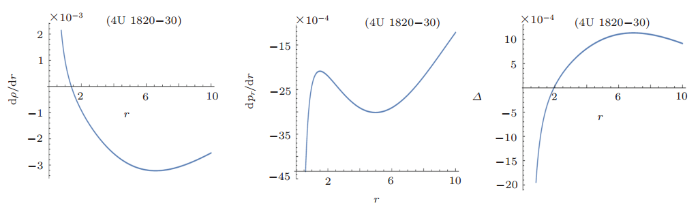New window|Download| PPT slide
Fig. 15(Color online) Behavior of ${d\rho}/{dr}$, ${dp_r}/{dr}$ and $\delta$ for 4U 1820-30 candidate.



The graphical analysis of energy density for 4U 1820-30 candidate is positive and monotonic behavior as shown in Fig. 14. The radial pressure has the decreasing behavior and positive behavior for $0\leq r \leq 8$. But radial pressure has the negative behavior when we move away from radial coordinate at 8. The tangential pressure's behavior can be shown in Fig. 14, which shows that pressure is positive as well as decreasing. It can be noticed that radial derivative of density and the anisotropic measurement has opposite behavior as shown in Fig. 15. The positive behavior of anisotropic measurement shows that tangential pressure is greater than radial pressure.

Fig. 16

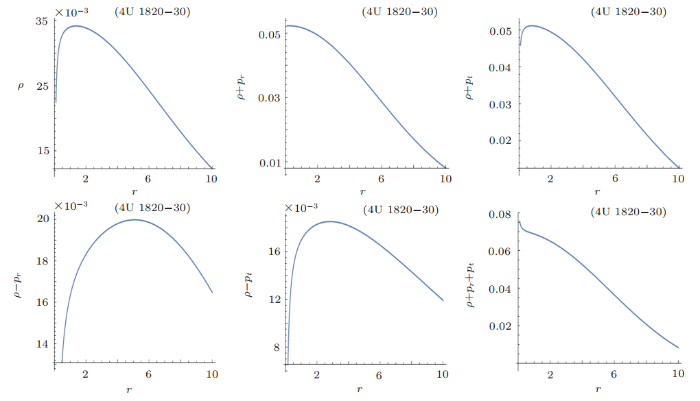New window|Download| PPT slide
Fig. 16(Color online) Plots of energy conditions with respect to radius $r$ for 4U 1820-30 candidate.

Fig. 17

New window|Download| PPT slide
Fig. 17(Color online) Behavior of gravitating force, hydrostatic force, and pressure anisotropic force for 4U 1820-30 candidate.

Fig. 18

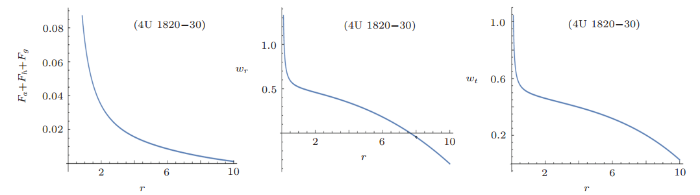New window|Download| PPT slide
Fig. 18(Color online) Behavior of TOV equation, radial EoS parameter and tangential EoS parameter with respect to the radial coordinate for 4U 1820-30 candidate.



The radial derivative of radial pressure is negative as shown in Fig. 15. The plots of energy conditions with respect to radial coordinates can be shown in Fig. 16, which shows that NEC, WEC, DEC and SEC hold for 4U 1820-30 candidate.

The behavior of gravitating force, hydrostatic force and pressure anisotropic force for 4U 1820-30 candidate is positive as shown in Fig. 17 and TOV equation is shown in Fig. 18, which shows that this model satisfies for this star. The tangential EoS parameter is satisfied but radial EoS parameter is satified only for $0\leq r \leq 8$ as shown in Fig. 18. The radial sound speed is satisfied for $4 \leq r \leq 10$ and transverse sound speed is satisfied for $3 \leq r \leq 10$ as shown in Fig. 19. The difference of these two forces can be shown in Fig. 19, which shows that it is satisfied for $0 \leq r \leq 9$. Hence, the proposed model is stable for 4U 1820-30 star for $3 \leq r \leq 9$.

Fig. 19

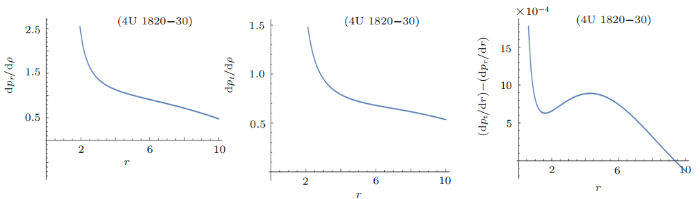New window|Download| PPT slide
Fig. 19(Color online) Behavior of $v_{\rm sr}^2$, $v_{\rm st}^2$, and $v_{\rm st}^2-v_{\rm sr}^2$ with respect to the radial coordinate for 4U 1820-30 candidate.

4 Conclusion

In this paper, we consider $f(R,\phi)=\phi(R+\alpha R^2)$ model and examine the physical behavior of the compact stars in $f(R,\phi)$ theory of gravity. In this regard, we prefer three compact stars namely, SAX J 1808-3658, Her X1, and 4U 182030 for the analysis of modified gravity model. We use Krori and Barua approach of metric function, that is, $a = Yr^2 + Z$ and $b = Xr^2$, where $X$, $Y$, and $Z$ are constants calculated by the matching conditions. We also develop three different scalar field functions for three stars by using the Klein-Gordon equation.

The energy density has been plotted with respect to radial coordinate $r$ for these stars. It can be observed that density has monotonic behavior and it goes to zero when we move away from the center of all three graphs. The radial pressure for Her X-I star has decreasing as well as positive behavior but it has some different behavior for SAX J 1808-3658 and 4U 182030 candidates. The values of radial pressure become negative with the movement away from the center. It is interesting to notice that the negative behavior of radial pressure near the core of star suggests the presence of dark energy which may be responsible for the expansion of universe. The tangential pressure's behavior for all these stars is similar.

The variation of radial derivative of density has the positive behavior near the center of star, but it becomes negative when we move on the radial coordinate. The physical behavior of variation of radial derivative of radial pressure has negative behavior as shown in figures. It is also noticed that $\Delta > 0$ when tangential pressure is greater than radial pressure and $\Delta < 0$ when tangential pressure is less than radial pressure. The graphical description shows that anisotropic force for all stars is directed outward. For the present analysis of energy conditions of Her X-1 star, it is noticed from the graph that NEC, WEC and DEC are satisfied but DEC is violated near the center of star but these conditions hold as we move towards the boundary of star. It can be concluded that all the energy conditions are satisfied for Her X-1 when $0.2 \leq r \leq 10$. It is also observed that all the energy conditions for SAX J 1808-3658 and 4U 182030 are satisfied for $0\leq r \leq10 $.

The gravitating force, hydrostatic force, and anisotropic pressure force have the similar behavior for Her X1 and 4U 182030 star but it has quite different for SAX J 1808-3658. The combination of all these forces namely TOV equation for three compact stars is satisfied. It is observed that the radial EoS parameter satisfies the usual range $0<w_r<1$ for Her X-I star. But for SAX J 1808-3658 and 4U 182030 stars satisfied the inequality for $0\leq r \leq6$ and $0\leq r \leq8$ respectively. The tangential EoS parameter for 4U 182030 star satisfies the usual range $0<w_t<1$ and it satisfies only $0.5\leq r \leq8$ for Her X-I and SAX J 1808-3658 stars.

The evolution of radial sound speed for strange star candidates Her X-1 and SAX J 1808-3658 hold for $2 \leq r \leq 10$ and it holds for 4U 182030 star in the range of $4 \leq r \leq 10$. While the transverse radial sound speed is satisfied for Her X-1 and SAX J 1808-3658 stars but for 4U 182030 star, it holds only for $4 \leq r \leq 10$. Furthermore, differences of the propagations of the sound speeds for Her X-I star are also satisfied $\mid \upsilon_{\rm sr}^2-\upsilon_{\rm st}^2\mid <1$ as shown in Fig. 7. Similarly, it hold for SAX J 1808-3658 and 4U 182030 star in the region of $2 \leq r \leq 7$ and $3 \leq r \leq 9$ respectively. Hence, it can be concluded that Her X-I star is more stable than SAX J 1808-3658 and 4U 182030 stars in $f(R,\phi)$ theory of gravity for the considered parameters.

Acknowledgement

Many thanks to the anonymous reviewers for valuable comments and suggestions to improve the paper.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] H. A. Buchdahl , Mon. Not. R. Astron. Soc. 150 (1970)1.
[Cited within: 1]

[2] S. Capozziello, M. De Laurentis, S. D. Odintsov, A. Stabile and , Phys. Rev. D 83 (2011)6.
[Cited within: 1]

[3] T. Harko , Mon. Not. R. Astron. Soc. 413 (2011)3095.
[Cited within: 1]

[4] M. Sharif and A. Ikram , Eur. Phys. J. C 76 (2016)640.
[Cited within: 1]

[5] M. Zubair and F. Kousar , Eur. Phys. J. C 76 (2016)254.
[Cited within: 1]

[6] M. Zubair and F. Kousar , Phys. Dark Universe 14 (2016) 116.
[Cited within: 1]

[7] S. Capozziello and M. D. Laurentis , Phys. Rep. 509 (2011)167.
[Cited within: 1]

[8] F. Hammad , Phys. Rev. D 96 (2017)064006.
[Cited within: 1]

[9] T. Chiba , JCAP 03 (2005)008.
[Cited within: 1]

[10] S. Arapoglu, C. Deliduman, and K. Y. Eksi , JCAP 07 (2011)020.


[11] A. V. Astashenok, S. Capozziello, and S. D. Odintsov , Phys. Rev. D 89 (2014)103509.


[12] H. R. Kausar and I. Noureen , Eur. Phys. J. C 74 (2014)2760.


[13] G. Abbas, A. Kanwal, and M. Zubair , Astrophys. Space Sci. 357 (2015)109.


[14] A. V. Astashenok, S. Capozziello, and S. D. Odintsov , JCAP 01 (2015)001.


[15] K. V. Staykov, D. D. Doneva, and S. S. Yazadjiev , Eur. Phys. J. C 75 (2015)607.


[16] S. Capozziello, M. De Laurentis, R. Farinelli, and S. D. Odintsov , Phys. Rev. D 93 (2016)023501.
[Cited within: 1]

[17] S. K. Maurya and Y. K. Gupta , Astrophys. Space Sci. 344 (2013)243.
[Cited within: 1]

[18] S. D. Maharaj, J. M. Sunzu, and S. Ray , Eur. Phys. J. Plus 129 (2014)3.
[Cited within: 1]

[19] R. Ruderman , Annu. Rev. Astron. Astrophys. 10 (1972)427.
[Cited within: 1]

[20] M. K. Mak and Harko , T. Int. J. Mod. Phys. D 13 (2004)149.
[Cited within: 1]

[21] S. Nojiri and S. D. Odintsov , Phys. Rep. 505 (2011)59.
[Cited within: 1]

[22] A. Paliathanasis , et al., Phys. Rev. D 89 (2014)104042.


[23] S. Nojiri and S. D. Odintsov , Int. J. Geom. Meth. Mod. Phys. 4 (2007)115.


[24] S. Capozziello, M. D. Laurentis, and S. D. Odintsov , Eur. Phys. J. C 72 (2012)2068.


[25] S. Capozziello, M. D. Laurentis, S. D. Odintsov, and A. Stabile , Phys. Rev. D 83 (2011)064004.


[26] A. V. Astashenok, S. Capozziello, M. D. Laurentis, and S. D. Odintsov , JCAP 1501 (2015)001.


[27] S. Capozziello, M. D. Laurentis, R. Farinelli, and S. D. Odintsov , Phys. Rev. D 93 (2016)023501.
[Cited within: 1]

[28] A. Stabile and S. Capozziello , Phys. Rev. D 87 (2013)064002.
[Cited within: 1]

[29] G. Lambiase, M. Sakellariadou, A. Stabile, and A. Stabile , JCAP 1507 (2015)003.
[Cited within: 2]

[30] K. D. Krori and J. J. Barua , Phys. A. Math. Gen. 8 (1975)508.


[31] S. Bahamonde , et al., Universe 1 (2015)186.
[Cited within: 1]

[32] K. D. Krori and J. J. Barua , Phys. A. Math. Gen. 8 (1975)508.
[Cited within: 1]

[33] K. Atazadeh and F. Darabi , Gen. Relativ. Gravity 46 (2014)1664.
[Cited within: 1]

[34] O. Bertolami and M. C. Sequeira , Phys. Rev. D 79 (2009)104010.


[35] L. Balart and E. C. Vagenas , Phys. Lett. B 730 (2014)14.
[Cited within: 1]

[36] A. Cooney, S. DeDeo, and D. Psaltis , Phys. Rev. D 82 (2010)064033.
[Cited within: 1]

[37] R. Goswami, A. M. Nzioki, S. D. Maharaj, and S. G. Ghosh , Phys. Rev. D 90 (2014)084011.


[38] A. Ganguly, R. Gannouji, R. Goswami, and S. Ray , Phys. Rev. D 89 (2014)064019.
[Cited within: 1]

[39] J. M. Lattimer and A. W. Steiner , Astrophy. J. 784 (2014)123.
[Cited within: 1]

[40] X. D. Li , et al., Phys. Rev. Lett. 83 (1999)3776.
[Cited within: 1]

[41] K. V. Staykov, D. D. Doneva, S. S. Yazadjiev, and K. D. Kokkotas , JCAP 10 (2014)006.
[Cited within: 1]

[42] M. Malaver , Frontiers Math. App. 1 (2014)9.


[43] S. A. Ngubelanga, S. D. Maharaj, and S. Ray , Astrophys. Space Sci. 357 (2016)74.
[Cited within: 1]

[44] M. Zubair, G. Abbas, and I. Noureen , Astrophys. Space Sci. 361 (2016)8.
[Cited within: 1]

[45] L. Herrera , Phys. Lett. A 165 (1992)206.
[Cited within: 1]