Bilal Shoaib¹, Muhammad Haneef^,1,?, Humayun Khan¹, Bakhtawar ^1,21 Lab of Theoretical Physics, Department of Physics, Hazara University, Mansehra 21300, Pakistan
2 Department of Physics, Women University, Mardan 23200, Pakistan

Corresponding authors: * E-mail:haneef.theoretician@gmail.com

Received:2018-09-29Online:2019-04-1


Abstract
A new scheme focusing on the surface plasmon polariton interferometry between the metal and dielectric interface is introduced. The phase shift is measured by using surface plasmon polariton wave, generated at the interface of metallic and dielectric media. The phase shift of SPPs is modified under phase and amplitude control of complex conductivity for interferometry. The control fields strongly influence the phase shift of SPPs for detection of molecular motion. The phase shift of SPPs is further modified by Plasmon polariton Fizeaus dragging effect. We measure $20\%$-$25\%$ fractional change in delay and their phases shift between two left and right SPPs modes. Our results may have significant applications in sensor interferometer technology.
Keywords： surface plasmon polariton;Fizeaus dragging


PDF (1646KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Bilal Shoaib, Muhammad Haneef, Humayun Khan, Bakhtawar . Surface Plasmon Polariton Fizeaus Dragging: via Relative Rotational Sensing. [J], 2019, 71(4): 435-440 doi:10.1088/0253-6102/71/4/435

1 Introduction

Over the years the field of light matter interaction, which can best be described by quantum optics at the quantum mechanical level, has been a hot topic of research.^[1-10] A Plasmon is a quantum of plasma oscillations of the electron density in a conducting media. Surface plasmon is the oscillation of plasma at the interface of two media.^[11] If the plasma oscillations become in resonance with the incident photons, this phenomenon is known as surface plasmon resonance. When electromagnetic waves interact with free electrons of the metal then the free electrons respond collectively by oscillating in resonance with incident waves and constitute surface plasmon polaritons (SPPs). Likely, SPPs are the surface waves, which are propagating along the interface of the two media must have opposite permittivities. Its intensity is maximum at the interface and decays gradually in the direction perpendicular to it.^[12]

The main applications of SPPs can be seen in the plasmonster technology. Plasmonster is a sensitive instrument like a transistor, which is based on Plasmon polariton waves. Many optical properties are described by using polariton waves. These waves can be used in many plasmonic devices i.e. the waveguides,^[13] plasmonic chips,^[14] quantum processors,^[15] optical microscopes, and magnetic recorders.^[16] Data storage, solar cells, biosensors, and chemical sensors are the main applications of it.^[17]

The SPPs and localized Plasmon at the interface of metal-dielectric surfaces open up an earlier inaccessible length scale for optical research, with promising applications in the photonics for the minimization of the circuit size.^[11] Besides this, the SPPs also play a vital role in near field optics^[18] and single-molecule optical sensing.^[19-20]

A research group of Refs. ^[21-22] have developed a theoretical model, which describes scattering of SPPs due to symmetric circular defect present on an otherwise planer metallic surface. They also obtained an expression for the dispersion of SPPs in a metal vacuum interface. Existence of long range SPP modes of vibrations are noted in a symmetric film structure^[23] and polarization dependent features of the long range SPPs^[24] are examined.

Numerous research articles have been published on SPPs.^[25-27] The Fizeaus dragging effect on SPPs due to relative motion of the medium is not studied. In this article we study the Fizeaus dragging effect on the SPPs due to relative motion of the proposed molecular medium and spin coherent effect. This Fizeaus dragging effect is then modified by coherent control fields, phase and amplitude of complex conductivity. Large sensitivity for motional sensing is calculated due to phase shift in the plasmonic waves created by spin coherence. We theoretically predicted the largest SPP Fizeaus dragging effect due to a moving medium. This study can be used for sensor technology and interferometry. Our theoretical idea will lead to the study of inertial effect with the collective state of atoms motion and can be helpful in designing new type of sensors interferometry.

2 Model of the Atomic System

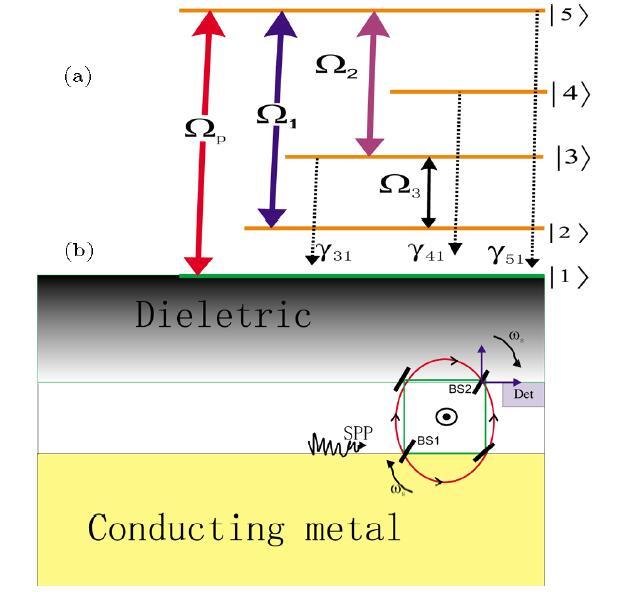
Here we propose a five level cascade type atomic system. This atomic system consists of states $\left\vert 1\right\rangle $, $\left\vert 2\right\rangle $, $\left\vert 3\right\rangle $, $\left\vert 4\right\rangle $, and $\left\vert 5\right\rangle $. The probe field is coupled between the states $\left\vert 1\right\rangle $ and $\left\vert 5\right\rangle $. This probe field has Rabi frequency $\Omega_{p}$. The control fields are coupled between the states $\left\vert 2\right\rangle $ and $\left\vert 5\right\rangle $, $\left\vert 3\right\rangle $ and $\left\vert 5\right\rangle $, $\left\vert 2\right\rangle $ and $\left\vert 3\right\rangle $ which are having frequencies $\Omega_{1},\Omega_{2}$ and $\Omega_{3}$ respectively. The decay parts of the system are represented by $\gamma_{31}, \gamma_{41}$ and $\gamma_{51}$ as shown in Fig. 1(a). In Fig. 1(b), the Mach-Zehnder type sagnac interferometer is shown in combination with Fig. 1(a). The interaction part of the hamiltonian for the proposed system is given below.

Fig. 1

New window|Download| PPT slide
Fig. 1(Color online) (a) Schematic of five levels energy diagram driven by three coherent control fields and probe field. (b) Mach-Zehnder type sagnac interferometer is shown.



(1)$ H_I =-\frac{\hbar}{2}[\Omega_{p}e^{-i\Delta_pt} \left\vert 1\right\rangle \left\langle 5\right\vert+\Omega _{1}e^{-i\Delta_1t}\left\vert 2\right\rangle \left\langle 5\right\vert+\Omega _{2}e^{-i\Delta_2 t} \\ \left\vert 3\right\rangle \left\langle 5\right\vert +\Omega _{3}e^{-i\Delta_3 t}\left\vert 2\right\rangle \left\langle 3\right\vert]+ {\rm H.c}\,. $

The general equation for the density of matrix is given below.^[28-30]

(2)$ \dot\rho=-\frac{i}{\hbar}[ H_I,\rho]-\frac{1}{2}\gamma_{ij}\sum( \sigma^\dagger \sigma \rho+\rho \sigma^\dagger \sigma-2\sigma \rho \sigma^\dagger)\,. $

First part of the above master equation exhibits interaction picture and the second part shows the decay term. The

$\sigma^{\dagger}$ is the raising operator and $\sigma$ is the lowering operator. To simplify the master equation for density matrix we obtain the following coupling equations

(3)$\dot{\tilde{\rho}}_{15} =\frac{i}{2}\Omega_p\tilde\rho_{55} -\frac{i}{2}\Omega_p\tilde\rho_{11}-\frac{i}{2} \Omega_1\tilde\rho_{12}-i\triangle_p\tilde\rho_{15} \\ -\frac{1}{2}\tilde\rho_{15}(\gamma_{51}+\gamma_{41}+\gamma_{31})\,,$

(4) $\dot{\tilde{\rho}}_{12}= \frac{i}{2}\Omega_p\tilde\rho_{52}-\frac{i}{2} \Omega_1^{*}\tilde\rho_{15}-\frac{i}{2} \Omega_3^{*}\tilde\rho_{13}-i(\triangle_1-\triangle_p)\tilde\rho_{12} \\ -\frac{1}{2}\tilde\rho_{12}(\gamma_{51}+\gamma_{41}+\gamma_{31})\,, \\$

(5) $\dot{\tilde{\rho}}_{13}= \frac{i}{2}\Omega_p\tilde\rho_{53}-\frac{i}{2}\Omega_2^{*}\tilde\rho_{15}-\frac{i}{2} \Omega_3^{*}\tilde\rho_{12}-i(\triangle_2-\triangle_p)\tilde\rho_{13} \\ -\frac{1}{2}\tilde\rho_{13}(\gamma_{51}+\gamma_{41}+\gamma_{31})\,, $

where $\Omega_{P}$ is taken in the first order perturbation, while $\Omega_{1,2,3}$ are taken in all order of perturbations. The atoms are initially prepared in the ground state $\left\vert 1\right\rangle$ while at other states their probability is zero. Under these conditions, we have $\tilde{\rho}_{11}^{(0)}=1$, $\tilde{\rho}_{55}^{(0)}=0$, $\tilde{\rho}_{52}^{(0)}=\tilde{\rho}_{53}^{(0)}=0$. Using the expression

(6)$ Z(t)=int^{t}_{-infty}e^{-M(t-t^\prime)}Bd t^\prime=M^{-1}B\,, $

the above set of equations are solved for $\tilde{\rho}_{15}^{(1)}$, $\tilde{\rho}_{12}^{(1)}$, and $\tilde{\rho}_{13}^{(1)}$ where $Z(t)$ and $B$ are column matrices and $M$ is a $3\times3$ matrix. The susceptibility for the given atomic system is given here.

(7)$ \chi=\frac{2N\varrho^2_{15}}{\hbar\varepsilon_0\Omega_p} \tilde{\rho}_{15}^{(1)}\,. $

The dispersion relation for surface plasmon polariton is written as:^[29,31]

(8)$ k_{\rm sp}=\frac{2\pi}{\lambda} \sqrt{\frac{(1+4\pi\chi)n^2_m}{1+4\pi\chi+n^2_m}}\,, $

where $k_{\rm sp}=k_0n_{\rm sp}$ and $n_m$ is the refractive index of a conducting medium.^[29,31]

(9)$ \qquad\quad n_{m}=\pm\sqrt{\frac{\mu_0c^2(T_1\pm\sqrt{T^2_1+T^2_2})}{2(\omega_{0}+\Delta_p)}} \\ \pm i\sqrt{\frac{\mu_0c^2(-T_1\pm\sqrt{T^2_1+T^2_2})}{2(\omega_{0}+\Delta_p)}}\,, $

(10)$ T_1=\epsilon_0(\omega_{0}+\Delta_p) |\mu_{m}||\epsilon_{m}|\cos(\varphi_1+\varphi_2) \\ -|\mu_{m}||\sigma|\sin(\varphi_2+\varphi_3)\,, $

(11)$ T_2=\epsilon_0(\omega_{0}+\Delta_p) |\mu_{m}||\epsilon_{m}|\sin(\varphi_1+\varphi_2) \\ +|\mu_{m}||\sigma|\cos(\varphi_2+\varphi_3)\,, $

where $\varphi_{1,2,3}$ are the phases of complex permittivity, permeability $\mu_m$ and complex conductivity of metallic medium.^[31] The complex index of refraction of surface plasmon is written as:

(12)$ n^{\rm sp}_r=\sqrt{\frac{(1+4\pi\chi)n^2_m}{1+4\pi\chi+n^2_m}}\,. $

The phase velocity is written as $c/n^{\rm sp}_r$. Consider that the plasmon polariton waves propagate in the Mach-Zehnder Interferometer as shown in Fig. 1(b). The plasmon-polariton waves propagate in a circular path of radius $R$. For the clockwise direction the relativistic phase front velocity is $v^{(+)}_r$ and for counter clockwise is $v^{(-)}_r$.^[32]

(13)$ v^{\pm}_r=\frac{v_p\pm v}{1\pm v_pv/c^2}\,. $

Here $v_p$ represents phase velocity in the absence of rotation, $S^{\pm}=\pi R\pm V t^{\pm}$ and $v=\omega_sR$ is the tangential velocity. Further $t^{\pm}=S^{\pm}/v^{\pm}_r$. The time delay between the plasmon polariton waves and the phase shift without Fizeaus dragging effect are given in the following.^[32]

(14)$ \qquad\quad \Delta t_0=t^{-}-t^{+}=\pi R\frac{v^{+}-v^{-}+2v}{(v^{+}+v)(v^{-}-v)}\,, $

(15)$ \Delta \phi_0=\frac{2\pi c}{\lambda}\Delta t\,. $

The time delay between the plasmon polariton waves and the phase shift in the presence of Fizeaus dragging effect is:^[32]

(16)$ \Delta t=[(n^{\rm sp}_r)^2(1-\alpha)]\Delta t_0\,, $

(17)$ \Delta \phi=[(n^{\rm sp}_r)^2(1-\alpha)]\Delta \phi_0\,, $

where, the Fizeaus dragging parameter^[33] is

(18)$ \alpha=1-\frac{1}{(n^{\rm sp}_r)^2}+\frac{\omega}{n^{\rm sp}_r}\Bigl[\frac{\partial n^{\rm sp}_r}{\partial \omega}\Bigr]\,. $

Slow plasmon can be modelled as a dark state polariton.^[33]

(19)$ \psi=\xi(z,t)\cos\theta(t)-\sqrt{N}\sin \theta(t)\rho_{\sigma}(Z,t)\exp(i k_{\rm eff}z)\,, $

where $z$ is the spatial coordinate, "$t$" is time coordinate, $\xi(z,t)$ is plasmon polariton amplitude and $\sqrt{N}\rho_{\sigma}(Z,t)$ is collective spin coherence. When the plasmon polariton field propagates along the interface of the two medium, part of the field is converted into the collective spin coherence. Due to motion of the plasma ensemble the exponent $\exp(i k_{{{\rm eff}}}z)$ can be extended to $\exp(i k_{\rm eff}z_0+\nu (\Delta t_0,\Delta t))$,^[33] where $z_0$ is the initial position of the media interface. When the plasmon polariton field leave the ensemble, the collective atomic coherence is converted back to the plasmonic waves field with an additional phase shift $k_{\rm eff}\nu (\Delta t_0,\Delta t)$. The sensitivity is written as $\Delta\nu_0,\Delta\nu=(\Delta\phi_0,\Delta\phi)/k_{\rm eff}(\Delta t_0,\Delta t)$.^[33] The fractional change in the phase shifts and sensitivity, from without plasmon polariton dragging to plasmon polariton dragging is written as: $\Delta F_{\phi}=(\Delta\phi-\Delta\phi_0)/\Delta\phi_0$ and $\Delta F_{\nu}=(\Delta\nu-\Delta\nu_0)/\Delta\nu_0$.

3 Results and Discussion

The results are presented for motional sensing using the collective state of plasma at room temperature. For the phase sensitivity, surface plasmon polariton waves generated at the interface of two media is under consideration in this theoretical work. The atomic decay rate $\gamma$ is assumed to be $36.1$ MHz and all other parameters are scaled to this decay rate $\gamma$. The parameters $\hbar,\mu_0,\epsilon_0=1$ and $c=1$ are taken in atomic units.^[30,34-38]

In Fig. 2 the plots are traced for refractive index of surface plasmon polariton waves generated at the interface of two media. The refractive index of surface plasmon polariton waves enhances with conductivity and decreases with control field's rabi frequency $\Omega_1$. This can be confirmed from Fig. 2(a). Furthermore, the refractive index enhances with the conductivity and also with the control field's rabi frequency $\Omega_3$ as shown in Fig. 2(b). These behaviors of surface plasmon polariton modify the slow plasmon group velocity, phase variation, and sensitivity.

Fig. 2

New window|Download| PPT slide
Fig. 2(Color online) Refractive index of surface plasmon polariton vs. conductivity $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$. (a) $\Omega_{2,3}=2\gamma$, $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$; (b) $\Omega_{1,2}=2\gamma$. $\Omega_3=5\gamma,10\gamma,15\gamma,20\gamma,25\gamma,30\gamma$.



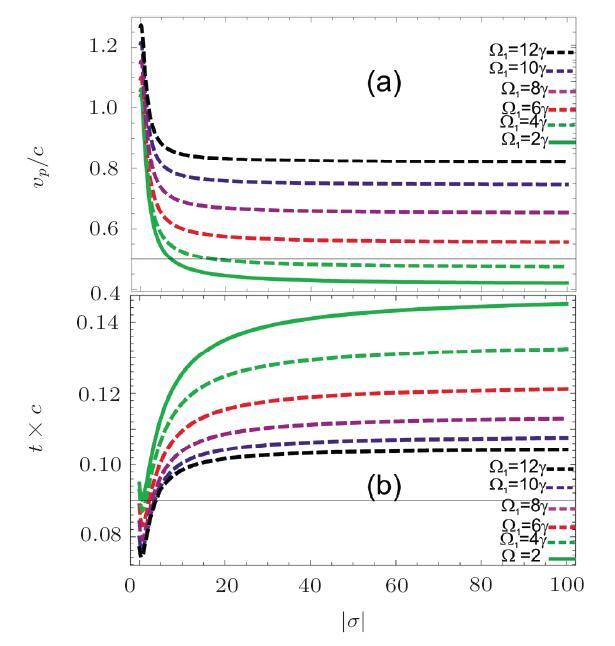
In Fig. 3 the phase velocity $v_p$ and phase delay time vs. conductivity of surface plasmon polariton at the interface of two media. At zero conductivity amplitude $|\sigma|$ the phase velocity of surface plasmon polariton is nearly $1.3~c$, where $c$ is the vacuum speed of light. As the conductivity increases from $0$ MS/m to $100$ MS/m, the phase velocity of surface plasmon waves decreases and becomes saturated at high conductivity values. The phase velocity increases with the Rabi frequency of control field and becomes saturated at low conductivity value as shown in Fig. 3(a). The phase delay time of surface waves enhances with conductivity and decreases with the control field's frequency as shown in Fig. 3(b). The phase delay time at zero conductivity and at control field of $2\gamma$ is $0.3$ ns, while at $100$ S/m is $0.5$ ns as shown by solid line. The dashed lines are at $4\gamma, 6\gamma, 8\gamma, 10\gamma$, and $12\gamma$ respectively.

Fig. 3

New window|Download| PPT slide
Fig. 3(Color online) Phase velocity and transit times can be calculated from $v_p/c$ and $t\times c$ of surface plasmon polariton vs. conductivity $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$ , $\Omega_{2,3}=2\gamma$. $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$.



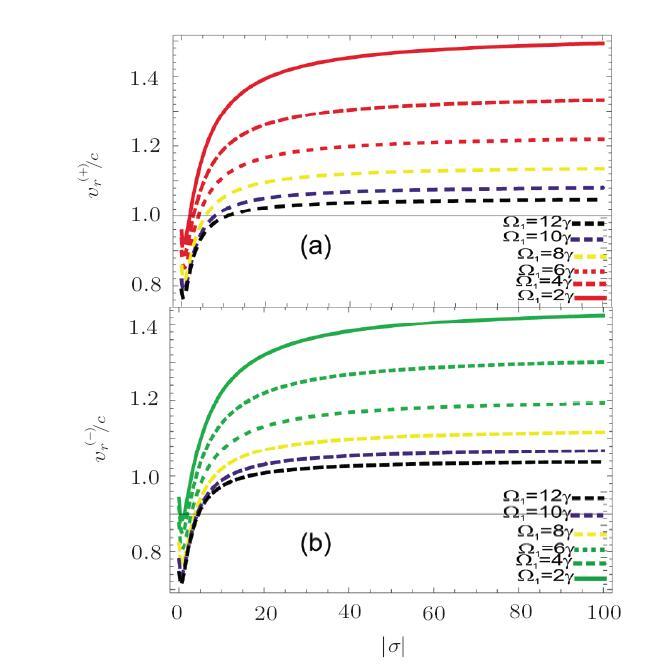
Figure 4 shows relativistic velocities $v^{(\pm)}_p$ of surface plasmon polariton waves in clock wise and anticlock wise direction after passing through a beam splitter. There is a small change in the relativistic speed of surface plasmon polariton in clock wise/anticlock wise directions as can be seen in Figs. 4(a)-4(b). The other behaviors of relativistic velocity are in matching with that of phase velocity for the increase in conductivity and control field intensity.

Fig. 4

New window|Download| PPT slide
Fig. 4(Color online) Relativistic velocity of surface plasmon polariton vs. conductivity $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$. $\Omega_{2,3}=2\gamma$, $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$, $v=20$ m/s.



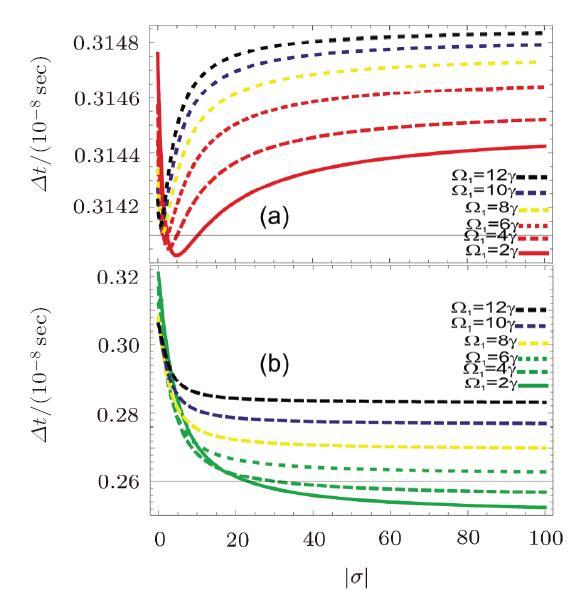
Figure 5 shows the plots of delay times between clock wise and anticlock wise pulses of plasmon polaritons after traversing the splitter mirror of the interferometer. The delay time between the two beam is effected by conductivity as will as Fizeaus dragging effect. Figure 5(a) is plotted for without Fizeaus dragging effect and Fig. 5(b) is plotted in the presence of Fizeaus dragging effect. When there is no Fizeaus dragging effect, the delay time first decreases and then increases with conductivity but in the presence Fizeaus dragging effect, the delay time decreases with conductivity. The delay time between the two pulses without Fizeaus dragging effect, at zero conductivity and $2\gamma$ of the control field is $3.1$ ns but this delay time enhances to $3.2$ ns due to Fizeaus dragging effect. The delay time, without Fizeaus dragging effect increases with conductivity and decreases with conductivity in the presence of Fizeaus dragging effect. The Fizeaus dragging effect is inversely proportion to the square of the refractive index of SPPs. The refractive of SPPs is directly depended on conductivity. The delay and phase shift is directly related to refractive index. Therefore the delay and phase continually reduce with increase of conductivity amplitude up to saturation limit. However the delay time increases with control field's rabi frequency.

Fig. 5

New window|Download| PPT slide
Fig. 5(Color online) Delays between two surface plasmon polariton vs. conductivity without and in the presence of Fizeaus dragging effect $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$. $\Omega_{2,3}=2\gamma$. $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$, $v=20$ m/s.



Figure 6 exhibits the phase shift without and in the presence of Fizeaus dragging effect between the two plasmon polariton beams. The phase shift without Fizeaus dragging effect initially decreases with conductivity and then enhances with high amplitude of complex conductivity. The control field also strongly effects the phase shift and enhances it as shown by solid and dashes lines in Fig. 6(a). The Fizeaus dragging effect decreases the phase shift with the increase of amplitude of complex conductivity. The phase shift have also saturation point at higher value amplitude of complex conductivity.

Fig. 6

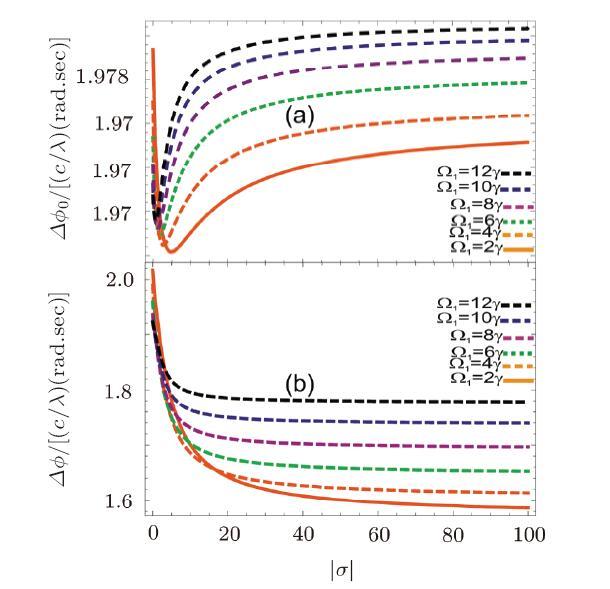New window|Download| PPT slide
Fig. 6(Color online) Phases shifts between two surface plasmon polariton waves vs. conductivity without and in the presence Fizeaus dragging effect $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$. $\Omega_{2,3}=2\gamma$, $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$, $v=20$ m/s.



In Fig. 7, the velocity sensitivity vs. amplitude of complex conductivity of the conducting medium without and in the presence of Fizeaus dragging effect is shown. The sensitivity is nearly $12$ m/s with amplitude of complex conductivity. The sensitivity decreases with conductivity and increases with control field Rabi frequency. Using the value of the effective wave vector $k_{\rm eff} =1.61 \times10^{7}~{\rm m}^{-1}$ and $\Delta t_0, \Delta t$. We calculated the sensitivity 12 m/s for molecular speed through by surface plasmon polaritons. This is higher than the sensitivity calculated at velocity width $\Delta \nu_a=8K_bT{\rm ln}2/\rm m$^[33] that is $1.76$ m/s at large Fizeaus dragging effect in a moving electromagnetically induced transparent medium, where $K_b=1.380~648~52\times 10^{-23}~ {\rm m^2 \cdot kg \cdot s^{-2}\cdot K^{-1}}$ is Boltzmann constant, $T$ is absolute temperature and m is molecular mass.

Fig. 7

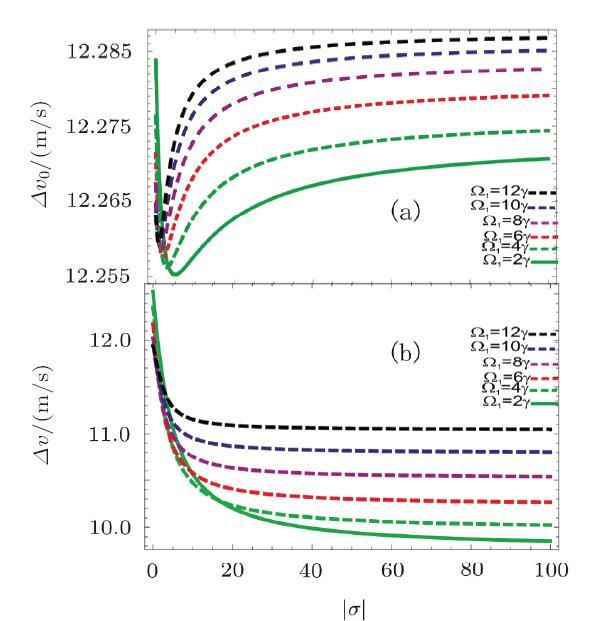New window|Download| PPT slide
Fig. 7(Color online) Sensitivity vs. conductivity without and in the presence of Fizeaus dragging effect $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$. $\Omega_{2,3}=2\gamma$, $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$, $v=20$ m/s.



The fractional change in phase shifts and sensitivity from without Fizeaus dragging effect to Fizeaus dragging effect vs. amplitude of complex conductivity is shown in Fig. 8. The fractional change in phase shifts from without Fizeaus dragging effect to Fizeaus dragging effect is about 25$\%$ at amplitude of complex conductivity of $100$ S/m. The fractional change in sensitivity is the same at these values. The fractional change in sensitivity as well as phase shift decreases with control field. This can be confirmed from Figs. 8(a)-8(b).

Fig. 8

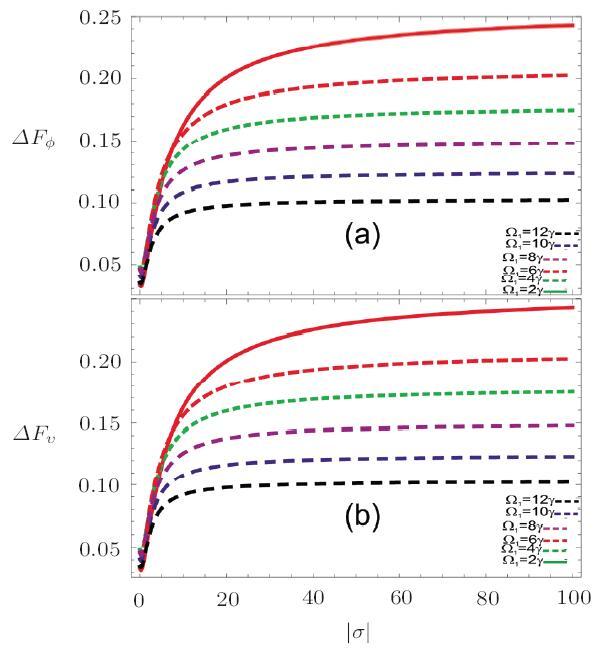New window|Download| PPT slide
Fig. 8(Color online) Fractional change in phase shifts and sensitivity vs. conductivity without and in the presence of Fizeaus dragging effect $\gamma=10$ MHz, $\Delta_p=0\gamma$, $\Delta_{1,2}=0\gamma$, $\gamma_{31,41,51}=2\gamma$, $o_{15}=1$, $\varphi(\varphi_{i=1,2,3})=0$, $\omega_p=1000\gamma$. $\Omega_{2,3}=2\gamma$, $\Omega_1=2\gamma,4\gamma,6\gamma,8\gamma,10\gamma, 12\gamma$, $v=20$ m/s.

4 Conclusion

The surface plasmon polariton interferometry between metal and dielectric interface is introduced in this article. In this theoretical work plasmon polariton dispersion relation, refractive index and phase velocity is calculated. The relativistic velocity between clock wise and counter cloak wise polariton beams are modified with the phase and amplitude of complex conductivity and also by the control fields strength. A significant phase shift is calculated between two left and right circular modes for surface plasmon polariton waves generated at the interface of conducting and dielectric medium. The phase shift and and fractional changes are measured with the amplitude complex conductivity of conducting medium. Furthermore the phase shifts and sensitivity are manipulated with the strength of control field. The phase shifts and sensitivity are also modified with Fizeaus dragging effect of SPPs. It is noted that the sensitivity decreases with conductivity and increases with the control fields rabi frequency. The effective wave vector $k_{\rm eff} =1.61\times 10^{7}/{\rm m}$^[33] and the delay times $\Delta t_0$, $\Delta t$ is used and velocity sensitivity of 12m/s is noted for surface Plasmon polariton, which is higher than velocity sensitivity calculated under Doppler broadening. A large Fizeaus dragging effect in SPPs is noted. A $25\%$ fractional change is calculated for phase shift Fizeaus dragging effect SPPs. The results show potential applications in applied SPPs interferometry technologies.

The authors have declared that no competing interests exist.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1] R. Loudon , "The Quantum Theory of Light", 3rd Edition, Oxford University Press, Oxford( 2000).
[Cited within: 1]

[2] H. Khan and M. Haneef, Can. J. Phys. 96(2017) 98.


[3] X. M. Hong, S. B. Wan, W.L. Hong, C. Chun , Chin. Phys. B 25 (2016) 080309.
DOI:10.1088/1674-1056/25/8/080309URL
We present a Trojan-horse attack on the practical two-way continuous-variable quantum key distribution system. Our attack mainly focuses on the imperfection of the practical system that the modulator has a redundancy of modulation pulsewidth, which leaves a loophole for the eavesdropper inserting a Trojan-horse pulse. Utilizing the unique characteristics of two-way continuous-variable quantum key distribution that Alice only takes modulation operation on the received mode without any measurement, this attack allows the eavesdropper to render all of the final keys shared between the legitimate parties insecure without being detected. After analyzing the feasibility of the attack, the corresponding countermeasures are put forward.

[4] H. L. Jin, D. R. Hai, X. P. Shi , et al., Chin. Phys. B 25 (2016) 124208.
DOI:10.1088/1674-1056/25/12/124208URL
Modulation instabilities in the randomly birefringent two-mode optical fibers(RB-TMFs) are analyzed in detail by accounting the effects of the differential mode group delay(DMGD) and group velocity dispersion(GVD) ratio between the two modes, both of which are absent in the randomly birefringent single-mode optical fibers(RB-SMFs). New MI characteristics are found in both normal and anomalous dispersion regimes. For the normal dispersion, without DMGD,no MI exists. With DMGD, a completely new MI band is generated as long as the total power is smaller than a critical total power value, named by Pcr, which increases significantly with the increment of DMGD, and reduces dramatically as GVD ratio and power ratio between the two modes increases. For the anomalous dispersion, there is one MI band without DMGD. In the presence of DMGD, the MI gain is reduced generally. On the other hand, there also exists a critical total power(Pcr), which increases(decreases) distinctly with the increment of DMGD(GVD ratio of the two modes) but varies complicatedly with the power ratio between the two modes. Two MI bands are present for total power smaller than Pcr, and the dominant band can be switched between the low and high frequency bands by adjusting the power ratio between the two modes. The MI analysis in this paper is verified by numerical simulation.

[5] H. Khan and M. Haneef, Laser Phys. 27(2017) 055201.
DOI:10.1088/1555-6611/aa658fURL

[6] A. Farmani, A. Mir, Z. Sharifpour , Appl. Surf. Sci. 453(2018) 358.
DOI:10.1016/j.apsusc.2018.05.092URL

[7] H. Khan, M. Haneef , Bakhtawar, Chin. Phys. B 27 (2018) 014201.
DOI:10.1088/1674-1056/27/1/014201URL
We propose a new scheme for the coherent control of birefringent light pulses propagation in a four-level atomic medium. We modify the splitting of a light pulse by controlling the electric and magnetic responses. The Doppler broadening effect is also noted on the propagation of the birefringent pulses. The dispersions of the birefringence beams are oppositely manipulated for delay and advancement of time at a Doppler width of 10 . A time gap is created between the birefringence beams, which protects from hacking of information. The time gap is then closed to restore the pulse into the original form by a reverse manipulation of the dispersion of the birefringence beams, i.e., introducing another medium whose transfer function is the complex conjugate of that of the original medium. The results are useful for secure communication technology.

[8] H. Khan and Haneef, Laser Phys. 27(2017) 055201.


[9] M. Haneef, S. Mohammad, J. Akbar , et al., Chin. Phys.Lett. 29(2012) 073201.
DOI:10.1088/0256-307X/29/7/073201URL
The photodetachment of a hydrogen negative ion (H) near a partially reflecting surface with a spherical shape is investigated by a theoretical imaging method. Analytical expressions for the detached electron flux and total photodetachment cross section are derived. It is found that two parameters, i.e. curvature radius and reflection parameter , control the photodetachment spectra. Furthermore, these parameters can be used for the classification, identification and revelation of minor details like curvature of different types of surfaces.

[10] Bakhtawar, M. Haneef , B. A. Bacha, et al., Chin.Phys. B. 27(2016) 114215.
[Cited within: 1]

[11] W. L. Barens, A. Dereux, T. W. Ebbesen , Nature (London) 424(2003) 824.
DOI:10.1038/nature01937 [Cited within: 2]

[12] A. B . Evlyukhin and S. I.Bozhevolnyi, Phys. Lett. 3(2006) 396.
[Cited within: 1]

[13] M. I. Stockman , Nano Lett. 6(2006) 2604.
DOI:10.1021/nl062082gURLPMID:17090099 [Cited within: 1]
Abstract I predict that a nanoscopic, high-permittivity layer on the surface of a plasmonic metal can cause total external reflection of surface plasmon polaritons (SPPs). Such a layer can be used as a mirror in nanoplasmonics, in particular for resonators of nanolasers and spasers and can also be used in adiabatic nanooptics. I also show that the earlier predicted slow propagating SPP modes, especially those with negative refraction, are highly damped.

[14] E. Ozbay , Science 311 (2006) 189.
[Cited within: 1]

[15] R. Kolesov, B. Grotz, G. Balasubramanian , et al., Nature Physics 5 (2009) 470.
[Cited within: 1]

[16] S. Zhang, H. Wei, K. Bao , et al., Phys. Rev.Lett. 107(2011) 096801.
DOI:10.1103/PhysRevLett.107.096801URLPMID:21929259 [Cited within: 1]
Chiral surface plasmon polaritons (SPPs) can be generated by linearly polarized light incident at the end of a nanowire, exciting a coherent superposition of three specific nanowire waveguide modes. Images of chiral SPPs on individual nanowires obtained from quantum dot fluorescence excited by the SPP evanescent field reveal the chirality predicted in our theoretical model. The handedness and spatial extent of the helical periods of the chiral SPPs depend on the input polarization angle and nanowire diameter as well as the dielectric environment. Chirality is preserved in the free-space output wave, making a metallic nanowire a broad bandwidth subwavelength source of circular polarized photons.

[17] S. Zeng, D. Billargeat, H. P. Ho, K. T. Yong , Chem. Soc. Rev. 43(2014) 3426.
DOI:10.1039/c3cs60479aURLPMID:24549396 [Cited within: 1]
The main challenge for all electrical, mechanical and optical sensors is to detect low molecular weight (less than 400 Da) chemical and biological analytes under extremely dilute conditions. Surface plasmon resonance sensors are the most commonly used optical sensors due to their unique ability for real-time monitoring the molecular binding events. However, their sensitivities are insufficient to detect trace amounts of small molecular weight molecules such as cancer biomarkers, hormones, antibiotics, insecticides, and explosive materials which are respectively important for early-stage disease diagnosis, food quality control, environmental monitoring, and homeland security protection. With the rapid development of nanotechnology in the past few years, nanomaterials-enhanced surface plasmon resonance sensors have been developed and used as effective tools to sense hard-to-detect molecules within the concentration range between pmol and amol. In this review article, we reviewed and discussed the latest trend and challenges in engineering and applications of nanomaterials-enhanced surface plasmon resonance sensors (e.g., metallic nanoparticles, magnetic nanoparticles, carbon-based nanomaterials, latex nanoparticles and liposome nanoparticles) for detecting ard-to-identify biological and chemical analytes. Such information will be viable in terms of providing a useful platform for designing future ultrasensitive plasmonic nanosensors.

[18] C. Girard , Rep. Prog. Phys. 68(2005) 1883.
DOI:10.1088/0034-4885/68/8/R05URL [Cited within: 1]

[19] S. M. Nie and S. R. Emery , Science 275 (1997) 1102.
[Cited within: 1]

[20] K. Kneipp, Y. Wang, H. Kneipp , et al., Phys. Rev.Lett. 78(1997) 1667.
DOI:10.1103/PhysRevLett.78.1667URL [Cited within: 1]

[21] A. V. Shchegrov, I. V. Novikov, A. A. Maradudin , Phys. Rev. Lett. 78(1997) 4269.
DOI:10.1103/PhysRevLett.78.4269URL [Cited within: 1]

[22] M. Kretschmann and A. A. Maradudin , Phys. Rev. B 66 (2002) 245408.
DOI:10.1103/PhysRevB.66.245408URL [Cited within: 1]

[23] P. Berini , Opt. Lett. 24(1999) 241011.
[Cited within: 1]

[24] R. Charbonneau, P. Berini, E. Berolo, E. L. Shrzek , Opt. Lett. 25(2000) 844.
DOI:10.1364/OL.25.000844URL [Cited within: 1]

[25] B. Hecht, H. Bielefeldt, L. Novotny , et al., Phys. Rev.Lett. 77(1996) 1889.
DOI:10.1103/PhysRevLett.77.1889URL [Cited within: 1]

[26] H. Ditlbacher, J. R. Krenn, G. Schider , et al., Appl. Phys.Lett. 81(2002) 1762.
DOI:10.1063/1.1506018URL
We report the experimental realization of highly efficient optical elements built up from metal nanostructures to manipulate surface plasmon polaritons propagating along a silver/polymer interface. Mirrors, beamsplitters, and interferometers produced by electron-beam lithography are investigated. The plasmon fields are imaged by detecting the fluorescence of molecules dispersed in the polymer.

[27] J. Lin, J. B. P. Mueller, Q. Wang , et al., Science 340 (2013) 331.
[Cited within: 1]

[28] S. Ahmad, A. Ahmad, B. A. Bacha , et al., Eur. Phys. J. Plus 132 (2017) 506.
[Cited within: 1]

[29] N. Khan, B. A. Bacha, A. Iqbal , et al., Phys. Rev. A 96 (2017) 013848.
DOI:10.1103/PhysRevA.96.013848URL [Cited within: 2]

[30] B. A. Bacha and M. S. A. Jabar , J. Optics 20 (2018) 095703.
DOI:10.1088/2040-8986/aad6a9URL [Cited within: 2]

[31] A. Ali, B. A. Bacha, M. S. A . Jabar, et al., Laser Phys. 26(2016) 095204.
DOI:10.1088/1054-660X/26/9/095204URL [Cited within: 3]
Conductivity-dependent surface plasmon polariton (SPP) propagation is investigated at the interface between a metal and a tripod-type atomic medium. Our theoretical investigations show that the SPP propagation depends on the conductivity of the metallic medium and the coherent driving fields applied in the atomic medium up to a saturation limit. Further, the SPPs drag and rotate with collective spinning of the proposed structure. The rotation is modified with the spin angular velocity of the whole structure. A maximum rotation of6565±4 microradians is observed. Our results may find applications in plasmonster technology.

[32] M. S. Shahriar, G. S. Pati, R. Tripathi , et al., Phys. Rev. A 75 (2007) 053807.
DOI:10.1103/PhysRevA.75.053807URL [Cited within: 3]

[33] P. C. Kuan, C. Huang, W. S. Chan , et al., Nature Commun. 7(2016) 13030.
DOI:10.1038/ncomms13030URL [Cited within: 6]

[34] R. L. Chern , J. Optics 15 (2013) 075702.
DOI:10.1088/2040-8978/15/7/075702URL [Cited within: 1]
In this paper, the author studies the features of wave propagation in chiral media. A general form of wave equations in biisotropic media is employed to derive concise formulas for the reflection and transmission coefficients. These coefficients are represented as a composite form of Fresnel equations for ordinary dielectrics, which reveal the circularly polarized nature of chiral media. The important features of negative refraction and a backward wave associated with left-handed waves are analyzed.

[35] A. Ghosh and P. Fischer, Phys. Rev. Lett. 97(2006) 173002.
DOI:10.1103/PhysRevLett.97.173002URLPMID:17155470
Abstract A light beam changes direction as it enters a liquid at an angle from another medium, such as air. Should the liquid contain molecules that lack mirror symmetry, then it has been predicted by Fresnel that the light beam will not only change direction, but will actually split into two separate beams with a small difference in the respective angles of refraction. Here we report the observation of this phenomenon. We also demonstrate that the angle of reflection does not equal the angle of incidence in a chiral medium. Unlike conventional optical rotation, which depends on the path-length through the sample, the reported reflection and refraction phenomena arise within a few wavelengths at the interface and thereby suggest a new approach to polarimetry that can be used in microfluidic volumes.

[36] D. L . Jaggard and A. R.Mickelson, Appl. Phys. 18(1979) 211.


[37] F. Ghafoor, B. A. Bacha, S. Khan , Phys. Rev. A 91 (2015) 053807.
DOI:10.1103/PhysRevA.91.053807URL
A gain-based four-level atomic medium for the stability in superluminal light propagation using control field and inverse Doppler shift as coherence generators is studied. In regimes of weak and strong control field, a broadband and multiple controllable transparency windows are, respectively, identified with significantly enhanced group indices. The observed Doppler effect for the class of high atomic velocity of the medium is counterintuitive in comparison to the effect of the class of low atomic velocity. The intensity of each of the two pump fields is kept less than the optimum limit reported in [M. D. Stenner and D. J. Gauthier, Phys. Rev. A 67, 063801 (2003), 10.1103/PhysRevA.67.063801] for stability in the superluminal light pulse. Consequently, superluminal stable domains with the generated coherence are explored.

[38] J. B. Pendry , Science 306 (2004) 1353.
[Cited within: 1]