摘要: 根据高强度聚焦超声(HIFU)治疗中超声散射回波信号的特点, 本文利用变分模态分解(VMD)与多尺度排列熵(MPE)对生物组织变性识别进行了研究. 首先对生物组织中的超声散射回波信号进行变分模态分解, 根据各阶模态的功率谱信息熵值分离出噪声分量和有用分量; 对分离出的有用信号进行重构并提取其多尺度排列熵; 然后通过Gustafson-Kessel (GK)模糊聚类确定聚类中心, 采用欧氏贴近度与择近原则对生物组织进行变性识别. 将所提方法应用于HIFU治疗中超声散射回波信号实验数据, 用遗传算法对多尺度排列熵的参数优化后, 对293例未变性组织和变性组织的超声散射回波信号数据进行了多尺度排列熵分析, 发现变性组织的超声散射回波信号的多尺度排列熵值要高于未变性组织; 多尺度排列熵可以较好地识别生物组织是否变性. 相对于EMD-MPE-GK模糊聚类以及VMD-小波熵(WE)-GK模糊聚类变性识别方法, 本文所提方法中变性与未变性组织特征交叠区域数据点更少, 聚类效果和分类性能更好; 本实验环境下生物组织变性识别结果表明, 该方法的识别率更高, 高达93.81%.
关键词: 高强度聚焦超声 /
变分模态分解 /
功率谱信息熵 /
多尺度排列熵 English Abstract Recognition of denatured biological tissue based on variational mode decomposition and multi-scale permutation entropy Liu Bei Hu Wei-Peng Zou Xiao Ding Ya-Jun Qian Sheng-You School of Physics and Electronics, Hunan Normal University, Changsha 410081, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11474090, 11774088, 61502164) and the Natural Science Foundation of Hunan Province, China (Grant No. 2016JJ3090).Received Date: 26 September 2018Accepted Date: 26 October 2018Available Online: 01 January 2019Published Online: 20 January 2019Abstract: It is an important practical problem to accurately recognize whether biological tissue is denatured during high intensity focused ultrasound (HIFU) treatment. Ultrasonic scattering echo signals are related to some physical properties of biological tissues. According to the characteristics of ultrasonic scattering echo signals, the recognition of denatured biological tissues is studied based on the variational mode decomposition (VMD) and multi-scale permutation entropy (MPE) in this paper. The ultrasonic echo signals are decomposed into various modal components by the VMD. The noise components and the useful components are separated according to the power spectrum information entropy of various modal components. The separated useful signals are reconstructed and the MPE are extracted. Furthermore, Gustafson-Kessel (GK) fuzzy clustering analysis is employed to obtain the standard clustering center, and the recognition of denatured biological tissues is carried out by Euclid approach degree and principle of proximity. The proposed method is applied to ultrasonic scattering echo signal during HIFU treatment. In order to determine the parameters of MPE algorithm for ultrasonic scattering echo signals, the embedding dimension of the MPE is discussed, and the scale factor of the MPE algorithm is optimized by genetic algorithm. When the delay time and the embedding dimension are 2 and 7 respectively, the MPE values decrease with scale factor increasing. Assuming that the scale factor is 12 from optimization results, the 293 ultrasonic scattering echo signals from normal tissues and denatured tissues are analyzed by the MPE. It is found that the MPE values of the denatured tissues are higher than those of the normal tissues. The MPE can be used to distinguish normal tissues and denatured tissues. Comparing with the recognition methods of the EMD-MPE-GK fuzzy clustering method and the VMD-WE-GK fuzzy clustering, the proposed method has good clustering performance and separability. Its partition coefficient (PC) is close to 1 and the Xie-Beni (XB) index is smaller. There are fewer feature points in the overlap region between MPE features of denatured tissues and normal tissues. The recognition results of denatured biological tissues in this experimental environment show that the recognition rate based on this method is higher, reaching up to 93.81%.Keywords: high intensity focused ultrasound /variational mode decomposition /power spectrum information entropy /multi-scale permutation entropy 全文HTML --> --> --> 1.引 言 高强度聚焦超声(high intensity focused ultrasound, HIFU)治疗是一种新的无创肿瘤治疗技术. 它通过聚焦方式将声能聚集于治疗靶区, 使靶区产生高温, 从而使病变组织细胞内的蛋白质发生固化、变性和坏死, 同时又不损伤靶区之外的正常组织. 通过监测生物组织的变性情况, 能掌握HIFU的治疗效果, 对确保HIFU治疗的安全高效有重要意义[1 -3 ] . 迄今为止, 超声领域的研究人员从多个方面对所取得的超声信号进行研究, 期望提取出能准确反映组织损伤变性的特征参数, 如回波能量、声衰减系数、频率偏移、声速和熵等[4 -8 ] . 当组织温度升高到65 ℃以上时, 背散射信号能量会发生显著变化[4 -9 ] . Seip和Ebbini[10 ] 采用回波信号的能量特征来检测组织损伤变性, 实验结果表明, 信号能量识别准确率达到82%. 在文献[11 ]中, 生物组织的超声衰减系数特征被用于估计组织损伤区域的温度. 盛磊等[6 ] 利用频率偏移等特征参数检测HIFU导致的组织凝固性坏死. 声速可以非侵入式地估计组织温度, 但是声速受非线性以及热膨胀的影响, 导致通过声速变化测量体内温度的准确性大大降低[7 -12 ] . 明文等[8 ] 采用超声散射回波信号的小波熵(wavelet entropy, WE)特征对HUFU治疗过程中的组织损伤变性进行评价研究, 同时对组织样本进行损伤级归类. 但到目前为止, 将超声回波信号的多尺度排列熵(multi-scale permutation entropy, MPE)特征用于生物组织变性识别是否有效的研究还未见报道.[13 ] , 并且文献[14 ]已经将其应用至从人体获得的超声回波信号, 然而, EMD存在端点效应、模态混叠问题[15 ] . 为了解决上述问题, Dragomiretskiy和Zosso[15 ] 提出一种新的变分模态分解(variational mode decomposition, VMD)方法, 能较好地抑制信号EMD过程中的端点效应和模态混叠现象, 对噪声具有更强的鲁棒性.[16 -18 ] . 排列熵作为一种非线性分析算法, 具有计算简单、抗噪能力强、鲁棒性强的优点, 因此被广泛应用于时间序列的复杂性分析中[19 ] . 多尺度排列熵将多尺度和排列熵结合起来, 可以更加有效地分析序列信息[20 ,21 ] . 本文从非线性角度分析生物组织中的超声散射回波信号, 利用多尺度排列熵算法研究未变性生物组织和变性生物组织超声散射回波信号的差异, 为HIFU治疗诊断提供有效的依据和帮助. 然而, 若MPE算法中嵌入维数和尺度因子参数设置不合理, 将导致算法无法达到最佳的处理效果. 同时, 由于生物组织从未变性状态到变性状态的演变是一个渐变的过程[22 ] , 因此提取的组织变性特征具有一定的模糊性, GK模糊聚类算法为解决这类问题提供了一条有效途径[23 ] .2.原理与方法 22.1.VMD理论 2.1.VMD理论 VMD是一种基于维纳滤波, 希尔伯特变换和外差解调的新型多分量信号分解算法. VMD可以将一个实际信号$f\left( t \right)$ 分解成$K$ 个离散的模态${\mu _k}\left( {k = 1,2,3,\cdots,K} \right)$ , 与EMD算法不同, ${\mu _k}$ 在频域中的带宽都具有特定的稀疏属性, 是调幅调频(AM-FM)信号, 可以有效地抑制EMD中出现的模态混叠现象. 每个${\mu _k}$ 紧凑围绕相应的中心频率, 并且其带宽通过高斯平滑解调获得. VMD处理过程中的约束变分问题为$\left\{ {{{\mu }_k}} \right\} \!=\! \left\{ {{\mu _1},{\mu _2},\cdots,{\mu _K}} \right\}$ 和$\left\{ {{{\omega }_k}} \right\} = \left\{ {{\omega _1},{\omega _2},\cdots,}\right.$ $\left.{{\omega _K}} \right\}$ 分别为分解的$K$ 个模态及其对应中心频率的集合. 同时引入二次惩罚参数$\alpha $ 和拉格朗日乘法算子$\lambda \left( t \right)$ 来求解(1 )式的约束变分问题. 增广拉格朗日函数为2 )式的鞍点, 并在频域内迭代更新${\mu _k}$ , ${\omega _k}$ 及$\lambda $ .$K$ 个模态分量的具体步骤如下:$\left\{ {{\mu }_k^1} \right\}$ , $\left\{ {{\omega }_k^1} \right\}$ , ${\lambda ^1}$ 和$n$ 为0;${\mu _k}$ 和${\omega _k}$ 分别由(3 )式和(4 )式迭代更新:5 )式更新$\lambda $ :$\varepsilon $ 为判别精度, $\varepsilon > 0$ ;$K$ 个模态分量.2.2.功率谱信息熵 -->2.2.功率谱信息熵 基于功率谱信息熵判断各模态分量为有效超声散射回波信号还是噪声以及无效超声散射回波信号的方法流程如下.7 )式求解信息熵, 并根据熵值判断该模态是否为噪声分量或无效超声散射信号:$H\left( x \right)$ 为功率谱信息熵, 其中${p_i}$ 表示功率谱分段后第$i$ 段所对应的概率, $M$ 表示总共的分段数.2.3.多尺度排列熵 -->2.3.多尺度排列熵 多尺度排列熵是在排列熵基础上的改进, 基本思想是将时间序列进行多尺度粗粒化,然后计算其排列熵. 计算具体步骤如下.$N$ 的时间序列${X} = \left\{ {{x_i},i =}\right. $ $\left.{ 1,2,\cdots,N} \right\}$ 进行粗粒化处理, 得到粗粒化序列$y_j^{\left( s \right)}$ s 为尺度因子; [N/s ]表示对N/s 取整.$y_j^{\left( s \right)}$ 进行时间重构得到$m$ 为嵌入维数, $\tau $ 为延迟时间; $l$ 为第$l$ 个重构分量, $l = 1,2,\cdots,N - (m - 1)\tau $ .${S}\left( r \right) = \left( {{l_1},{l_2},\cdots,{l_m}} \right)$ . 其中, $r = 1,2,\cdots,R,$ 且$R \leqslant m!$ . 计算每一种符号序列出现的概率${P_r}$ .10 )式计算每个粗粒化序列的排列熵, 由此得到时间序列在多尺度下的排列熵.${P_r} = {1/{m!}}$ 时, ${H_{\rm{p}}}\left( m \right)$ 达到最大值$\ln \left( {m!} \right)$ ; 通常将多尺度排列熵值${H_{\rm{p}}}(m)$ 进行归一化处理, 即$\overline {{H_{\rm{p}}}\left( m \right)} $ 为归一化处理后的排列熵值. 在上述多尺度排列熵算法中, 尺度因子s 的取值对熵值影响较大. 若s 取值过大, 将有可能造成信号之间的复杂度差异被抹除, 故尺度因子的取值选取很重要. 本文选用多尺度排列熵偏度的平方函数作为遗传算法的目标函数来优化尺度因子参数, 求其最小值. 将时间序列${X_s}$ 所有尺度下的排列熵组成序列$\overline {{{H}_{{\rm{p}}X}}(m)} = \left\{ {\overline {{H_{{\rm{p}}1}}(m)} ,\overline {{H_{{\rm{p}}2}}(m)} ,\overline {{H_{{\rm{p}}3}}(m)}, \cdots,\overline {{H_{{\rm{p}}s}}(m)} } \right\}$ , 通过(12 )式计算偏度${\rm{SKe}}$ ,$H_{\rm{p}}^{\rm{m}}({{X}_s})$ 为序列$\overline {{H_{{\rm{p}}X}}(m)} $ 的均值, $H_{\rm{p}}^{\rm{d}}({{X}_s})$ 为序列$\overline {{H_{{\rm{p}}X}}(m)} $ 的标准差, $E\left( · \right)$ 为数学期望, 适应度函数为2.4.GK聚类与变性识别 -->2.4.GK聚类与变性识别 GK模糊聚类算法是利用协方差矩阵能自适应动态度量的模糊聚类算法, 假设输入数据为${X} = \left\{ {{x_1},{x_2},\cdots,{x_n}} \right\}$ , GK模糊聚类的目标函数为$\theta \geqslant 1$ 为模糊指数, 模糊指数会影响聚类效果, 其值太大会导致各类之间相互重叠; ${D_{ij}}$ 为第$j$ 个样本与第$i$ 类聚类中心的马氏距离, $D_{ij}^2$ 是一个平方内积范数.${{Z}_i} = \det {\left( {{{F}_i}} \right)^{\frac{1}{n}}}{F}_i^{ - 1}$ 为正定对称矩阵, 由聚类协方差矩阵${{F}_i}$ 决定. 同时GK模糊聚类的聚类中心${V} = {\left( {{\nu _1},{\nu _2},\cdots{\nu _c}} \right)^{\rm{T}}}$ 和隶属度矩阵${U} = {\left[ {{u_{ij}}} \right]_{c \times n}}$ 可通过最小化目标函数求得, 其中c 为聚类中心的数目, n 为样本个数, ${\nu _i}\left( {i = 1,2,\cdots,c} \right)$ 为第$i$ 个聚类中心, ${u_{ij}}$ 表示$j$ 个元素属于第$i$ 类隶属度, 且满足14 )式取得极小值, 其必要条件为$c$ 以及模糊指数$\theta $ , 根据(16 )式对隶属度矩阵${U}$ 进行初始化, 通过(18 )式计算聚类中心${\nu _i}$ ;${{F}_i}$ ${{F}_i}$ 求出正定对称矩阵${{Z}_i}$ , 之后根据(15 )式计算出平方内积范数$D_{ij}^2$ ; 利用得到的平方内积范数$D_{ij}^2$ , 根据(17 )式更新隶属度矩阵${U}$ , 若不满足$\left\| {{{U}^{\left( {L + 1} \right)}} - {{U}^{\left( L \right)}}} \right\| < \eta $ , 则增加迭代次数, 若满足判断式, 则终止迭代运算.- Beni (XB)指数进行检验.$\delta $ 为类的平均方差, ${d_{\min }}$ 是类间最短模糊距离; 对于聚类效果评价, 其中PC越接近1, 代表划分越清晰, 反之划分越模糊; XB越小, 代表类间分离的聚类就越好.A 、标准聚类中心模糊子集B , 其计算如下:${u_A}\left( {{u_i}} \right)$ 和${u_B}\left( {{u_i}} \right)$ 分别为样本${u_i}$ 对模糊子集A 和B 的隶属度函数; $n$ 为待识别样本个数. 根据择近原则, 通过计算待识别样本与标准聚类中心的欧氏贴近度大小判别生物组织是否变性, 若待识别样本与变性组织标准聚类中心欧氏贴近度最大, 即识别为变性组织; 若待识别样本与未变性组织标准聚类中心欧氏贴近度最大, 即识别为未变性组织. 最后与实际生物组织切片损伤变性结果对比, 得出变性识别率.3.模拟仿真及应用实例 23.1.信号分解与去噪 3.1.信号分解与去噪 为研究EMD与VMD算法对噪声的鲁棒性, 对含噪仿真信号进行分析, 所采用的仿真信号表达式为$f\left( t \right) = 0.5\cdot\cos (2{\text{π}} \cdot 2t) + 0.4 \cdot\cos (2{\text{π}}\cdot 24t) \;+ $ $0.4\times $ $\cos (2{\text{π}} \cdot 288t) + \eta$ , 其中$\eta $ 为高斯白噪声, 标准偏差取0.1. 仿真信号及各对应成分如图1 所示.图 1 仿真信号及其对应非噪声成分的时域图 (a)加入噪声的仿真信号时域图; (b)对应非噪声成分的时域图Figure1. Time-domain diagram of the simulated signal and its non-noise components: (a) Time-domain diagram of the simulated signal with added noise; (b) time-domain diagram corresponding to non-noise components.图2 为加入噪声的仿真信号经EMD和VMD处理后的结果. 由图2(b) 可以明显看出, 随着EMD分解层数增多, 分解结果出现严重失真, 产生虚假分量, 即模态混叠现象. 而根据图2(a) 的VMD结果, 发现分解得到的前三个单频模态分量与原信号对应各成分比较一致, 说明VMD可以较好地解决信号分解过程中的模态混叠现象, VMD对噪声具有较强的鲁棒性.图 2 VMD与EMD的结果 (a)VMD方法; (b)EMD方法Figure2. Results of VMD and EMD: (a) VMD method; (b) EMD method.图3(a) 为实验获得的超声回波信号. 实验中用HIFU辐照新鲜离体猪肉组织来改变其特性, 通过B超监控来获取超声回波信号, 并经数字示波器(Model MDO3032; Tektronix)转化为数字信号后进行保存. B超探头的中心频率为3.5 MHz. 预先设定VMD算法中的分解模态的个数K = 5, 超声回波信号经VMD算法分解后, 不同K 值下各模态分量如图3(b) 所示.图 3 实际超声回波信号与VMD结果 (a)实际超声回波信号; (b)超声回波信号VMD结果Figure3. Actual ultrasonic echo signals and their VMD results: (a) Actual ultrasonic echo signals; (b) VMD results of ultrasonic echo signals.3.2.多尺度排列熵的计算 -->3.2.多尺度排列熵的计算 通过筛选功率谱信息熵值在0.13—0.35的模态分量对信号进行重构, 对重构后的信号进行参数优化后的MPE分析, 利用遗传算法来优化尺度因子s . 参数设置为: 最大进化代数为100; 种群最大数量为20; 交叉概率为0.4; 变异概率为0.09; 超声回波信号的截取点数为675, 一般来说, 嵌入维数m 通常取3—8, 延迟时间$\tau = 2$ . 对重构后的超声散射回波信号进行尺度因子参数优化, 取整后得到多尺度排列熵算法的尺度因子优化参数. 三组样本的MPE参数优化结果: 第一组和第二组样本的MPE分析中, 尺度因子参数为12; 第三组样本的MPE分析中, 尺度因子参数为13.图4 为嵌入维数m 分别取3, 5和7时样本1的MPE随尺度因子的变化情况.图 4 不同嵌入维数时变性与未变性情况的MPE分布 (a) m = 3; (b) m = 5; (c) m = 7Figure4. MPE distribution of denatured and undenatured cases with different embedding dimension: (a) m = 3; (b) m = 5; (c) m = 7.图4 可以明显看出, 嵌入维数m = 3和5时, 变性组织与未变性组织各尺度因子下的MPE值有较多交叠, 此时MPE不能较好地区分变性组织和未变性组织; 而嵌入维数m = 7时, 变性组织和未变性组织的MPE值有明显区别, 变性组织的多尺度排列熵值要明显高于未变性组织的熵值. 表1 为嵌入维数为7时, 三组样本中变性与未变性组织的各尺度排列熵平均值.尺度因子s 样本1 样本2 样本3 未变性 变性 未变性 变性 未变性 变性 1 0.7068 0.7396 0.7085 0.7408 0.7028 0.7366 2 0.6504 0.7163 0.6491 0.7013 0.6449 0.6958 3 0.6200 0.6855 0.6194 0.6718 0.6145 0.6715 4 0.5836 0.6498 0.5839 0.6361 0.5781 0.6378 5 0.5569 0.6241 0.5575 0.6176 0.5530 0.6151 6 0.5328 0.5994 0.5329 0.5962 0.5273 0.5934 7 0.5142 0.5780 0.5130 0.5771 0.5087 0.5776 8 0.4954 0.5609 0.4958 0.5618 0.4908 0.5602 9 0.4792 0.5458 0.4796 0.5453 0.4737 0.5418 10 0.4657 0.5313 0.4646 0.5325 0.4622 0.5320 11 0.4536 0.5152 0.4506 0.5246 0.4471 0.5173 12 0.4384 0.5139 0.4379 0.5188 0.4350 0.5059 13 0.4364 0.4626 0.4367 0.4686 0.4289 0.5042
表1 三组样本在嵌入维数m = 7时各尺度下排列熵平均值Table1. The average entropy of the three samples at each scale when the embedding dimension m = 7.表1 可见, 嵌入维数为7时, 尺度因子改变, 同一样本的MPE值发生变化; 尺度因子越大, MPE值越小, 且在不同尺度因子下, 变性组织的MPE值均高于未变性组织的MPE值. 另外, 尺度因子为12时, 第一组样本与第二组样本变性状态与未变性状态的MPE平均熵值差别较大, 与本文尺度因子参数优化结果相符合; 三组样本的MPE值随尺度因子的变化趋势类似. 后续研究中, 延迟时间$\tau $ 为2, 嵌入维数m 取为7, 综合考虑优化结果选取尺度因子s 为12. 通过以上分析可以发现, MPE特征可以作为识别生物组织是否变性的一个重要特征参数.3.3.GK聚类与生物组织变性识别 -->3.3.GK聚类与生物组织变性识别 取超声散射回波信号的重构后信号293例数据, 构成20组样本. 随机选取其中150例数据(共10组样本)作为已知样本, 后143例数据(10组样本)作为待识别样本, 选取各自的参数优化后的MPE值作为特征参量. 提取的特征向量经过GK模糊聚类算法处理后, 结合择近原则计算欧氏贴近度, 从而实现生物组织变性的模式识别. 为进一步验证所提方法的有效性, 分别采用EMD-MPE方法以及文献[8 ]报道的WE分析(VMD-WE)方法提取特征参量, 最后采用GK模糊聚类对生物组织变性分类识别, 图5 分别为利用EMD-MPE, VMD-WE和VMD-MPE提取组织超声散射回波信号多尺度排列熵的特征向量、经GK模糊聚类后的二维空间分布以及二维等高线. 计算可得出各种方法的聚类PC, XB以及变性识别率, 识别结果见表2 . 由图5 可以看出, 带有组织变性与未变性特征的超声散射回波信号经本文方法处理后, 多尺度排列熵特征参量按照变性与未变性基本分布在2个聚类中心的周围, 并且不同类型之间区分较为明显, 相较于EMD-MPE-GK聚类和VMD-WE-GK聚类方法, 本文方法变性与未变性特征二维空间交叠区域数据点更少, 而且隶属度等高线区分变性组织与未变性组织的误识别数据点更少, 类内变性MPE特征更紧密, 分类效果更理想, 这说明基于VMD, MPE和GK模糊聚类的算法对生物组织是否变性具有较好的分类识别效果.图 5 不同聚类方法对未变性与变性生物组织超声散射回波信号的聚类效果 (a) EMD-MPE-GK; (b) VMD-WE-GK; (c) VMD-MPE-GKFigure5. Clustering effect on ultrasonic scattering echo signals of undenatured and denatured biological tissues through different clustering methods: (a) EMD-MPE-GK; (b) VMD-WE-GK; (c) VMD-MPE-GK.聚类方法 PC XB 识别率/% VMD-MPE-GK 0.8119 4.498 93.81 EMD-MPE-GK 0.8088 11.589 87.44 VMD-WE-GK 0.790 14.878 85.29
表2 变性与未变性组织识别结果Table2. Recognition results of denatured and undenatured tissues.表2 可知, 对比VMD-MPE-GK聚类方法与EMD-MPE-GK聚类方法的识别结果, VMD分解重构信号的XB更小, PC与变性识别率高于EMD分解重构信号; 对比VMD-MPE-GK聚类方法与VMD-WE-GK聚类方法的识别结果, MPE的聚类效果优于WE, 且变性识别率更高. 基于VMD, MPE和GK模糊聚类的生物组织变性识别方法能够较准确地识别生物组织是否变性, 变性识别率高达93.81%, 且本文所提方法相较于EMD-MPE-GK聚类和VMD-WE-GK聚类方法, PC系数更接近1, XB指数更小, 从而证明了所提方法对生物组织变性识别分类的优越性.4.结 论 本文针对HIFU治疗中超声散射回波信号的特点, 利用VMD与MPE对生物组织变性识别进行了研究, 得出以下结论. 





































































































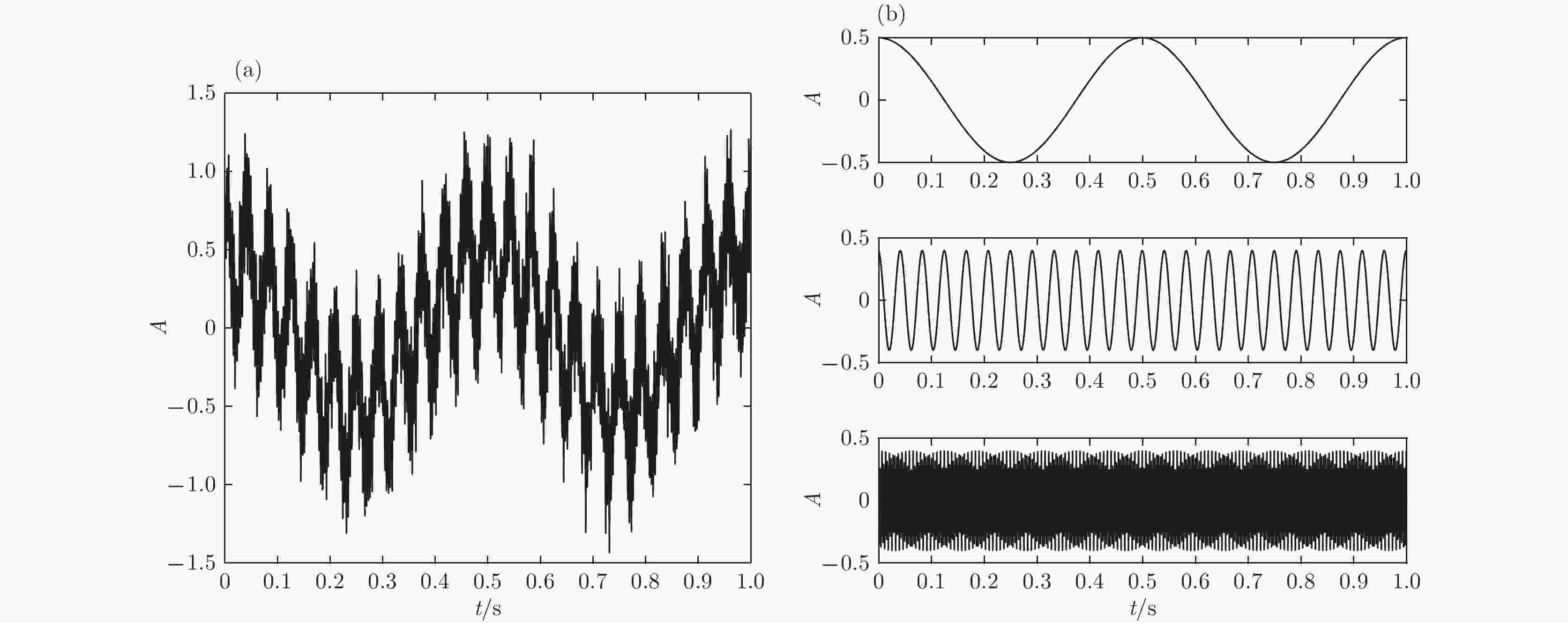 图 1 仿真信号及其对应非噪声成分的时域图 (a)加入噪声的仿真信号时域图; (b)对应非噪声成分的时域图
图 1 仿真信号及其对应非噪声成分的时域图 (a)加入噪声的仿真信号时域图; (b)对应非噪声成分的时域图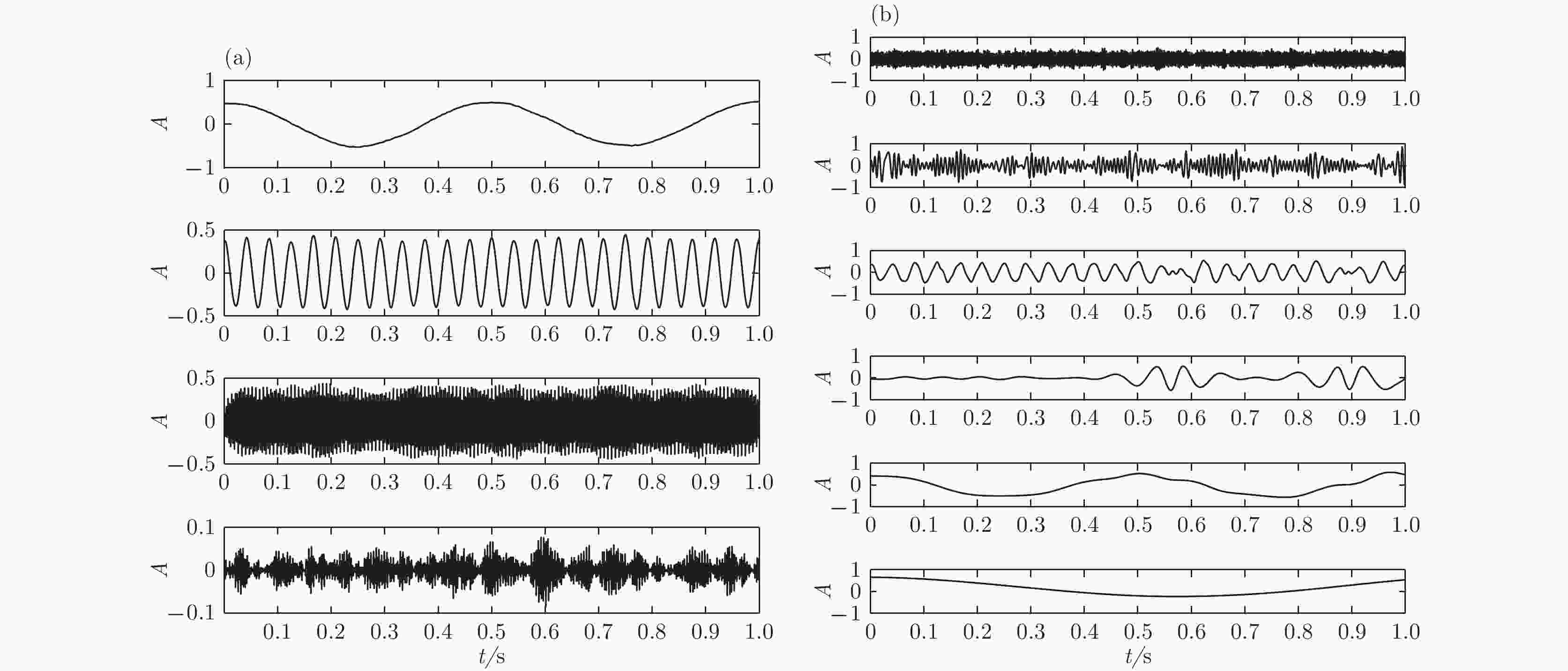 图 2 VMD与EMD的结果 (a)VMD方法; (b)EMD方法
图 2 VMD与EMD的结果 (a)VMD方法; (b)EMD方法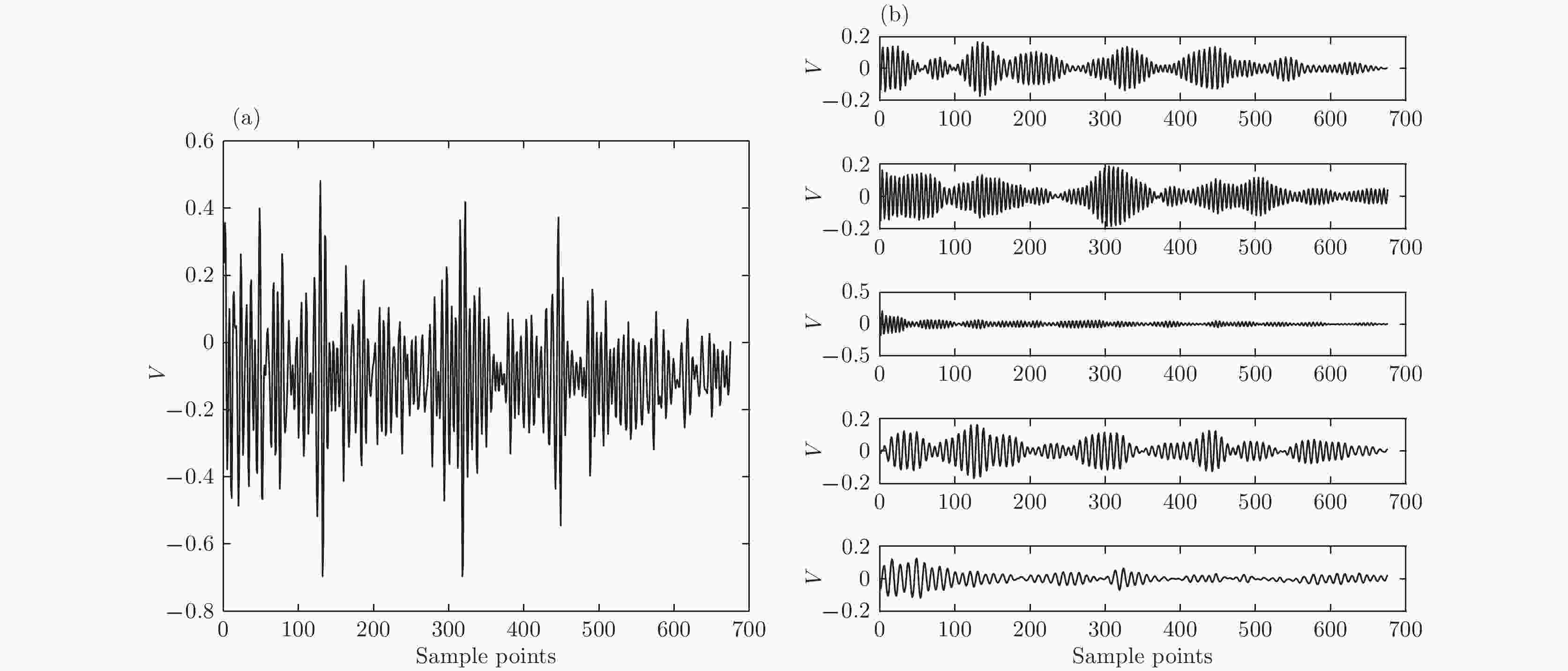 图 3 实际超声回波信号与VMD结果 (a)实际超声回波信号; (b)超声回波信号VMD结果
图 3 实际超声回波信号与VMD结果 (a)实际超声回波信号; (b)超声回波信号VMD结果
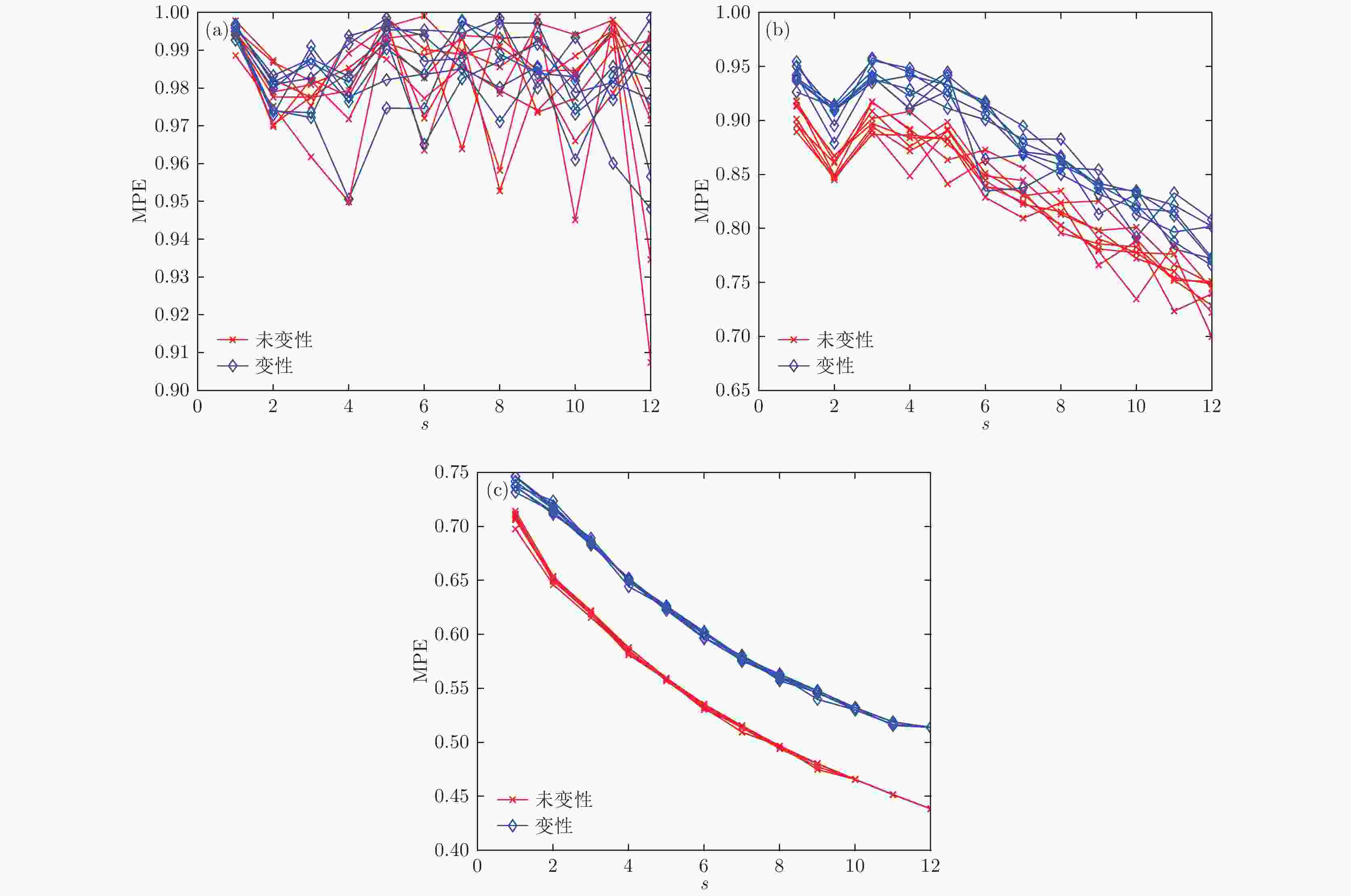 图 4 不同嵌入维数时变性与未变性情况的MPE分布 (a) m = 3; (b) m = 5; (c) m = 7
图 4 不同嵌入维数时变性与未变性情况的MPE分布 (a) m = 3; (b) m = 5; (c) m = 7
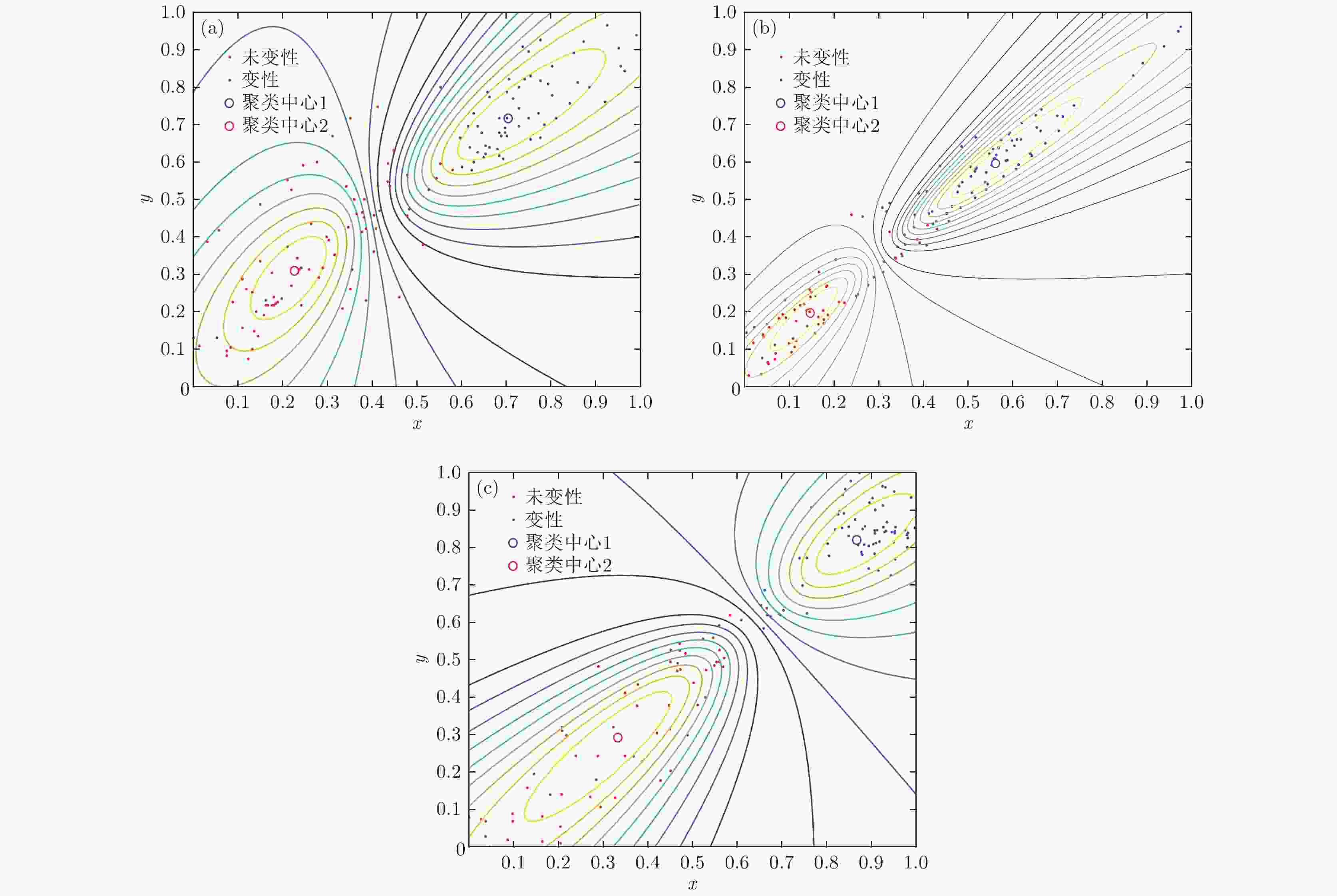 图 5 不同聚类方法对未变性与变性生物组织超声散射回波信号的聚类效果 (a) EMD-MPE-GK; (b) VMD-WE-GK; (c) VMD-MPE-GK
图 5 不同聚类方法对未变性与变性生物组织超声散射回波信号的聚类效果 (a) EMD-MPE-GK; (b) VMD-WE-GK; (c) VMD-MPE-GK