近日,中国科学院物理研究所/北京凝聚态物理国家研究中心的研究组发展出了一套自动计算材料拓扑性质的新方法,在近4万种材料中发现了8千余种拓扑材料,十几倍于过去十几年间人们找到的拓扑材料的总和,并据此建立了拓扑电子材料的在线数据库。国际学术刊物《自然》于今天在线发表了该成果【1】。什么是拓扑材料?它们有什么用处?所谓“新方法”何以一下找到了如此多的新拓扑材料?本文将回答这些问题,让您一窥这一新工作背后的门道。
拓扑材料是什么
拓扑学是数学的重要分支,它的研究对象是在连续的形变下空间的不变性。比如,一个物体上面有多少洞(是指贯穿前后的洞,不是坑),这个洞的数目就是在连续形变下的一个不变量。因为具有相同的“洞数”(学名是“欧拉数”),一个有把儿的茶杯可以连续地变成一个游泳圈,而不可以连续地变成一个球。在上世纪80年代对量子霍尔效应态的研究中,人们认识到,就像几何形体一样,固体中电子的波函数也具有这样的“拓扑不变量”,称为“陈数”(因数学家陈省身得名);对于量子霍尔效应态而言,陈数直接对应了量子化的霍尔电导。由于电子的波函数生活在无穷维的希尔伯特空间,我们无法像欧拉数那样直观地去理解陈数,但是它们之间确实有一些共性。首先,它们都是分立取值的:我们无法想象有1.5个洞的形状,也不存在陈数为分数的电子波函数;再者,它们在连续形变下都是不变的:量子化的霍尔电导对外界的扰动是如此稳定,以至于可以用它来校准欧姆这个国际单位。
对于电子波函数中的拓扑,下一次认识的飞跃出现在2005年前后。在一系列理论工作中,人们意识到,除了陈数之外,对称性可以带来新的拓扑不变量。具有这些新的拓扑不变量的绝缘体,后来被称为“拓扑绝缘体”。我们拿几何形状做类比,如果说人们之前所理解的简单绝缘体是一个球的话,拓扑绝缘体就是游泳圈(有一个洞)。而带给我们这个新的拓扑不变量的对称性,是时间反演不变性(时间反演不变性等同于要求体系没有磁性,也没有外加磁场)。拓扑绝缘体被发现没多久,人们就意识到,“时间反演不变性能够带来新的拓扑不变量”这一事实,不过是一大类普遍现象的冰山一角:对于几乎任何常见的对称性,比如晶体中的平移、镜面反射、旋转……都有可能存在其对应的新的拓扑不变量。寻找自然界中新的拓扑不变量,以及具备了这些拓扑不变量的材料,是过去十几年中凝聚态物理研究中的热点问题。
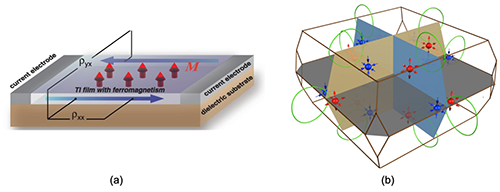 |
| 图1:知名的一些拓扑材料。(a)量子反常霍尔效应态也叫陈绝缘体。其特点是霍尔电导的值为e2/h的整数倍,同时边界上有一个或数个单向行走的边界态,它们被称为手性边界态。量子反常霍尔效应在磁性原子掺杂的三硒化二铋薄膜中的发现,引起了国际学术界的轰动,该系列成果还荣获了2018年度国家自然科学一等奖。(b)外尔半金属。其特点是材料体内的费米面由一系列“外尔点”(红色和蓝色的点)组成,每个外尔点都是贝里曲率的奇异点,可以带来“量子反常”、“表面费米弧”等物理效应。外尔半金属在砷化钽体系中的理论、实验发现,被美国物理学会评选为125年来该学会旗下杂志发表的49项重要成果之一。 |
认识到电子的波函数可能具有某种特殊的拓扑结构,固然是物理理论的一大进展,但是跟我们的实际生活有多大联系呢?一般认为,拓扑材料的边界态具有“背散射通道禁闭”等特点,可以用来制作超低能耗的电子元件;有人在利用拓扑材料边界态电子的“动量-自旋锁合”的特点设计自旋电子器件;还有人设想利用拓扑超导体边界的“马约拉那零模式”来设计量子比特等等……因此,研究拓扑材料,或者说具有非零的拓扑不变量的材料,具有基础科学和应用技术的双重意义。
前期的理论工作
要研究拓扑材料,第一步就是要将它们从浩如烟海的化合物中寻找出来。究竟具有什么样的化学式,拥有哪样的晶体结构的材料,才会有非零的拓扑不变量呢?这个问题长期困扰着领域内的科学家。从原理上讲,拓扑不变量的信息已经包含在了所有价带的电子波函数中,而后者可以用第一性原理计算的方法得到。但在实际操作中,由于某些拓扑不变量的表达式非常繁难,此类计算需要具有深厚材料物理和拓扑物理学背景的专家,同时也会耗费大量的时间。事实上,每一类新的拓扑材料的成功预言,都在领域内引起了广泛关注。在“艰难搜索”拓扑材料的过程中,多数科学家在直觉上认为拓扑性质是在自然界中是罕见的,需要构成原子的外层电子轨道、晶体结构、自旋轨道耦合等种种因素的巧妙平衡。
2017年,“拓扑量子化学”【2】和“对称性指标理论”【3】的提出,让人们看到了在上述“土法炼钢”方法之外寻找拓扑材料可能性。这两项工作表明,关于一个能带系统的拓扑不变量的信息,有一大部分其实已经蕴含于在高对称动量点的价带电子波函数的对称性之中;而后者——我们称为能带的对称性数据,人们知道是可以通过全自动的方法计算得到的。根据这个理论,人们可以通过计算任何材料的对称性数据来判断它是否具有拓扑性质。这是计算预言拓扑材料方法的重大突破。
2017年底,中科院物理所的方辰研究员、方忠研究员、博士研究生宋志达(现普林斯顿大学博士后)、张田田在上述工作的基础上更进一步,得到了从对称性数据到所有拓扑不变量的完整对应【4,5】。简单来说,拓扑材料又分为拓扑绝缘体、拓扑半金属、拓扑晶体绝缘体等等,它们每一类中又按不同的拓扑不变量的取值有着进一步的分类;而只有这些更细致的分类,才能表达材料全部的拓扑性质。根据物理所研究组的新理论,不仅可以判断一个材料是否具有拓扑性质,还能指出具备(不具备)哪些拓扑性质。该研究组将此成果称为“拓扑词典”,其中对称性数据是“词”,拓扑不变量的取值是“义”。根据这本“词典”,人们只需计算出任何材料的对称性数据,就可以查出它的拓扑不变量来。
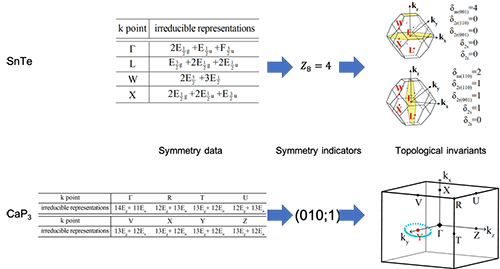 |
| 图2:“拓扑词典”的使用方法。对于给定的材料(上为碲化锡,下为三磷化钙),先通过第一性原理计算软件获得所有的对称性数据(symmetry data),这个对称性数据就是我们要查的“词”。接下来由对称性数据,先转换成“对称性指标”,再进而得到所有可能的拓扑不变量(即词典中的“义”)。注意,对于弱自旋轨道耦合的体系(如下面一排),该词典给出的“义”则是拓扑能带交点在动量空间的可能构型。 |
在“词典”出版后的拓扑材料研究领域可以说是“山雨欲来风满楼”,接下来需要做的事情已经再显然不过了:根据新的理论设计一套全自动判别拓扑材料并计算拓扑不变量的算法,然后用它来以全自动的方式寻找新的拓扑材料。这是难得一见的、可以取得突破性进展的机会,物理所的研究人员不可能放过。2018年初,方辰研究员与翁红明研究员、方忠研究员,以及博士研究生张田田、蒋毅、宋志达组成了研究团队,设计出了自动计算材料拓扑性质的全流程。在这套流程中,通过一系列的逻辑判断,我们给了每一种材料一个”拓扑标签“。这个标签是以下8个之中的一个:“高对称点半金属”、“高对称线半金属”、“一般动量点半金属”、“拓扑绝缘体”、“拓扑晶体学绝缘体”、“磁性材料”、“普通金属”和“普通绝缘体”。其中,前五个标签表示该材料是拓扑材料,后三类为非拓扑材料(或者叫无法判别其拓扑性质的材料)。对于每类拓扑材料他们又进行了细分,就不在这里详细写出了。研究小组扫描了共计约40000种无机晶体材料,并发现其中约8000种是拓扑材料。由于计算的所有材料都是曾经在实验上合成过的,这也就意味着世界上存在着起码8000余种具有拓扑性质的实际材料——这与之前人们认为拓扑材料是特殊的和稀有的直觉大相径庭。用全自动算法得到的这8000余种材料,不仅包括了几乎所有前人用老方法在十几年间找到的拓扑材料,还包括了大量的新拓扑材料,这些材料的拓扑性质之前从未被研究过。
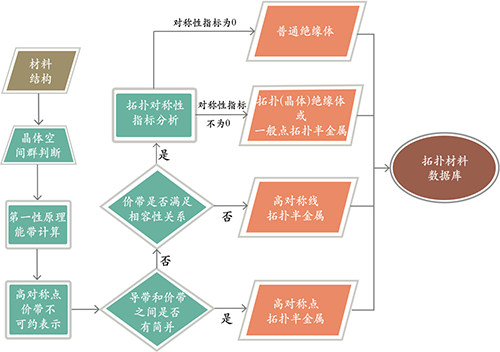 |
| 图3:文献【1】中所使用的自动计算任意晶体材料的自动化流程。其中棱形的绿色模块表示逻辑判断,而平行四边形的橙色模块则代表输出结果。根据这一流程,对于任何一个材料,我们都会得到一个确定的“标签”,这个标签告诉我们这一材料是否属于拓扑材料,以及属于哪一种拓扑材料。这里对于任何材料,文献【1】都分别考虑了有自旋轨道耦合和无自旋轨道耦合两种设置,这是与文献【6,7】有所区别之处。 |
所谓“英雄所见略同”,另有两个研究小组,也于同一天同一刊物上发表了他们的独立研究成果【6,7】。其中一个小组是来自美国的普林斯顿大学、西班牙巴斯克大学和德国马克斯-普朗克研究所的科学家,另一小组是来自南京大学和美国哈佛大学的科学家。他们两个小组的工作内容,同样是通过计算能带高对称点的对称性数据从而得到材料的拓扑性质,方法和物理所研究小组采用的方法一致,三个研究组得到的结果也彼此相洽、相互印证。
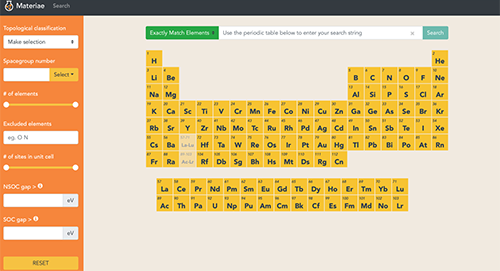 |
| 图4:中科院物理所-中科院计算机网络信息中心合作建立的在线数据库(Materiae),在元素周期表中点选材料,在左边输入(可选)筛选条件,然后按下搜索键即可得到含有这些元素的所有拓扑材料的列表。该网站的网址为http://materiae.iphy.ac.cn/。 |
从“拓扑电子材料目录”建立的过程我们可以看出,最后那“临门一脚”的三篇《自然》可能是关注度最高的,但对于深耕于领域的业内人士而言,从两年前“拓扑量子化学”和“对称性指标”这两篇论文出现的时候开始,此方向的研究范式已悄然改变,而在2017年底的“拓扑词典”出现之后,一种全自动计算拓扑性质的方法更是呼之欲出。也难怪最后会出现三路人马争相发表自己的“目录”了。“拓扑电子材料目录”的面世,代表了拓扑材料这一领域开始从“寻找新材料”转向“研究新材料”。这8000余种拓扑材料像是给物理学家、材料学家打开了无数的门,从每一扇门看过去,很多本以为熟悉的材料有了新的研究角度,而许多之前被忽视的材料也出现了新的闪光点。
致谢
文献【1,4,5】中的研究工作得到了科技部重点研发计划、国家自然科学基金、中国科学院科研信息化项目和先导项目等项目的支持。
参考文献
【1】Zhang, T., et al. Catalogue of Topological Electronic Materials. Nature 566, 475 (2019)
【2】Bradlyn, B., et al. Topological quantum chemistry. Nature, 547(7663), 298 (2017)
【3】Po, H. C., Vishwanath, A., & Watanabe, H. Symmetry-based indicators of band 343 topology in the 230 space groups. Nature Communications, 8(1), 50 (2017)
【4】Song, Z., Zhang, T., Fang, Z., & Fang, C. Quantitative mappings between 345 symmetry and topology in solids. Nature communications, 9(1), 3530 (2018)
【5】Song, Z., Zhang, T., & Fang, C. Diagnosis for Nonmagnetic Topological 353 Semimetals in the Absence of Spin-Orbital Coupling. Physical Review X, 8(3), 354 031069 (2018)
【6】Vergniory, M. G., Elcoro, L., Felser, C., Bernevig, B. A. & Wang. Z. A complete catalogue of high-quality topological materials. Nature 566, 480 (2019)
【7】Tang, F., Po, H. C., Vishwanath, A. & Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 566, 486 (2019)
Nature566,475(2019).pdf
