Hao Wang ^1,
, Ke-Yan Ma ^1,,
, Si-Ying Liu ^1,
, Jing-Bin Lu ^1,,
,

Corresponding author: Ke-Yan Ma, mky@jlu.edu.cn

Corresponding author: Jing-Bin Lu, ljb@jlu.edu.cn

1.College of Physics, Jilin University, Changchun 130012, China
Received Date:2021-04-11
Available Online:2021-09-15
Abstract:The semimagic nucleus ⁹⁰Zr, with Z = 40 and N = 50, is investigated in terms of large scale shell model calculations. A logical agreement is obtained between the available experimental data and predicted values. The calculated results indicate that the low-lying states are primarily dominated by the proton excitations from the fp orbitals across the Z = 38 or 40 subshell into the high-j $1g_{9/2}$ orbital. For the higher-spin states of ⁹⁰Zr, the breaking of the N = 50 core plays a crucial role, and the contribution of different orbitals to each state are discussed in this article. The evolution from neutron core excitations to proton excitations is systematically studied along the neighboring N = 50 isotones. Furthermore, the strong $\Delta I$ = 1 sequence demonstrates an abrupt backbend attributed to the alignment of the valence nucleons in fp proton orbitals and is proposed to have a $\pi(fp)^{-2}(1g_{9/2})^{2} \otimes $$ \nu(1g_{9/2})^{-1}(2d_{5/2}/1g_{7/2})^{1}$ configuration before the backbend, based on the shell model calculations. The properties of this sequence before the backbend indicate a general agreement with the fingerprints of magnetic rotation; hence, the sequence with the $\pi(fp)^{-2}(1g_{9/2})^{2} \otimes \nu(1g_{9/2})^{-1}(2d_{5/2}/1g_{7/2})^{1}$ configuration is suggested as a magnetic rotational band arising from shears mechanism.

HTML

--> --> -->

The study on level structures is significantly interesting in weakly deformed and nearly spherical nuclei [1-9]. In particular, the nuclei with $ N \sim 50$ in the $ A \sim 90$ mass region provide a suitable laboratory to study the mechanism of particle-hole excitations. The low-lying states of these nuclei are well described within the shell model framework, mainly exhibiting the characteristics of single-particle excitations [5-10]. With an increase in the excitation energy, the medium spin states are predominated by the multi-quasiparticle excitations outside the inert core. As the energy and spin further increase, the higher-spin states could be dominated by the excitation of the neutron across the N = 50 core into the next major shell, such as the breaking of the N = 50 core. This phenomenon a critical topic in the $ A \sim 90$ mass region, and has been reported systematically in the N = 50 isotones [6-22]. However, the relevant research for ⁹⁰Zr nucleus with N = 50 is relatively insufficient [23-26], and earlier studies on this nucleus mainly focus on lower-spin states. Hence, it is necessary to further investigate level structures and explore possible neutron core excitations in a semimagic nucleus ⁹⁰Zr, using the large scale shell model calculations. Accordingly, the evolution from the neutron core excitations to proton excitations across the Z = 38 or 40 subshell along the N = 50 isotones (⁸⁵Br, ⁸⁶Kr, ⁸⁷Rb, ⁸⁸Sr, ⁸⁹Y, ⁹⁰Zr, ⁹¹Nb, ⁹²Mo, ⁹³Tc, ⁹⁴Ru) is systematically discussed in the present work.
In addition, the magnetic rotation is another significantly interesting topic in our current study. It can be sufficiently interpreted by the tilted axis cranking covariant density functional theory (TAC-CDFT) [27-30]. In addition, semiclassical calculations can also provide a logical description for the shears mechanism [31-34]. In the A $ \sim 90$ mass region, many magnetic rotational bands have been reported in Br, Kr, Rb, and Sr nuclei [35-42], which are strong ?I = 1 bands based on the high-j particle-hole configurations. Interestingly, a similar structure also emerges in the ⁹⁰Zr nucleus, and a detailed discussion on this structure is presented in Sec. IIIC.

The level structures of ⁹⁰Zr are investigated via large scale shell model calculations with the NUSHELLX code [43]. The GWB model space and GWBXG interaction are adopted in the code. The model space comprises four proton orbitals ($1 f_{5/2} $, $2 p_{3/2} $, $2 p_{1/2} $, $1 g_{9/2} $) and six neutron orbitals ($2 p_{1/2} $, $1 g_{9/2} $, $1 g_{7/2} $, $2 d_{5/2} $, $2 d_{3/2} $, $3 s_{1/2} $) relative to an inert ⁶⁶Ni (Z = 28, N = 38) core. The single-particle energies relative to the ⁶⁶Ni core are set as $ \varepsilon^{\pi}_{1f_{5/2}} $ = ?5.322 MeV, $ \varepsilon^{\pi}_{2p_{3/2}} $ = ?6.144 MeV, $ \varepsilon^{\pi}_{2p_{1/2}} $ = ?3.941 MeV, $ \varepsilon^{\pi}_{1g_{9/2}} $ = ?1.250 MeV, $ \varepsilon^{\nu}_{2p_{1/2}} $ = ?0.696 MeV, $ \varepsilon^{\nu}_{1g_{9/2}} $ = ?2.597 MeV, $ \varepsilon^{\nu}_{1g_{7/2}} $ = 5.159 MeV, $ \varepsilon^{\nu}_{2d_{5/2}} $ = 1.830 MeV, $ \varepsilon^{\nu}_{2d_{3/2}} $ = 4.261 MeV, and $ \varepsilon^{\nu}_{3s_{1/2}} $ = 1.741 MeV. These single-particle energies and the corresponding values of the strengths of the residual interactions are adopted to calculate level energies and provide an optimal description of the spectra for nuclei with $ N \sim 50$ in the $ A \sim 90$ mass region [7-9, 44].

The semimagic nucleus ⁹⁰Zr has 12 valence protons and 12 valence neutrons in the configuration space. Considering the large dimensionality of the matrices involved, truncations are employed to make the calculations feasible. In this study, two sets of shell model calculations (SM1 and SM2) are performed. For the SM1 configuration space, no neutron excitation is allowed across the N = 50 magic core, and the valence protons are redistributed in the $1 f_{5/2} $, $2 p_{3/2} $, $2 p_{1/2} $, and $1 g_{9/2} $ single-particle orbitals. SM2 adopts the same proton configuration space as SM1, and the influence of neutron core excitation $ {\nu} (1 g_{9/2} ) ^{-1} (2 d_{5/2} /1 g_{7/2} ) ^{1} $ is considered, i.e., one neutron is allowed from the completed filled $1 g_{9/2} $ orbital across the N = 50 core into the $2 d_{5/2} $ or $1 g_{7/2} $ orbitals.
2

-->

A.Proton excitations and neutron core breaking

The level scheme of ⁹⁰Zr deduced from Ref. [23] and the results of the shell model calculations (SM1 and SM2) are compared in Fig. 1. The main partitions of the wave function for each state within SM1 and SM2 are summarized in Table 1.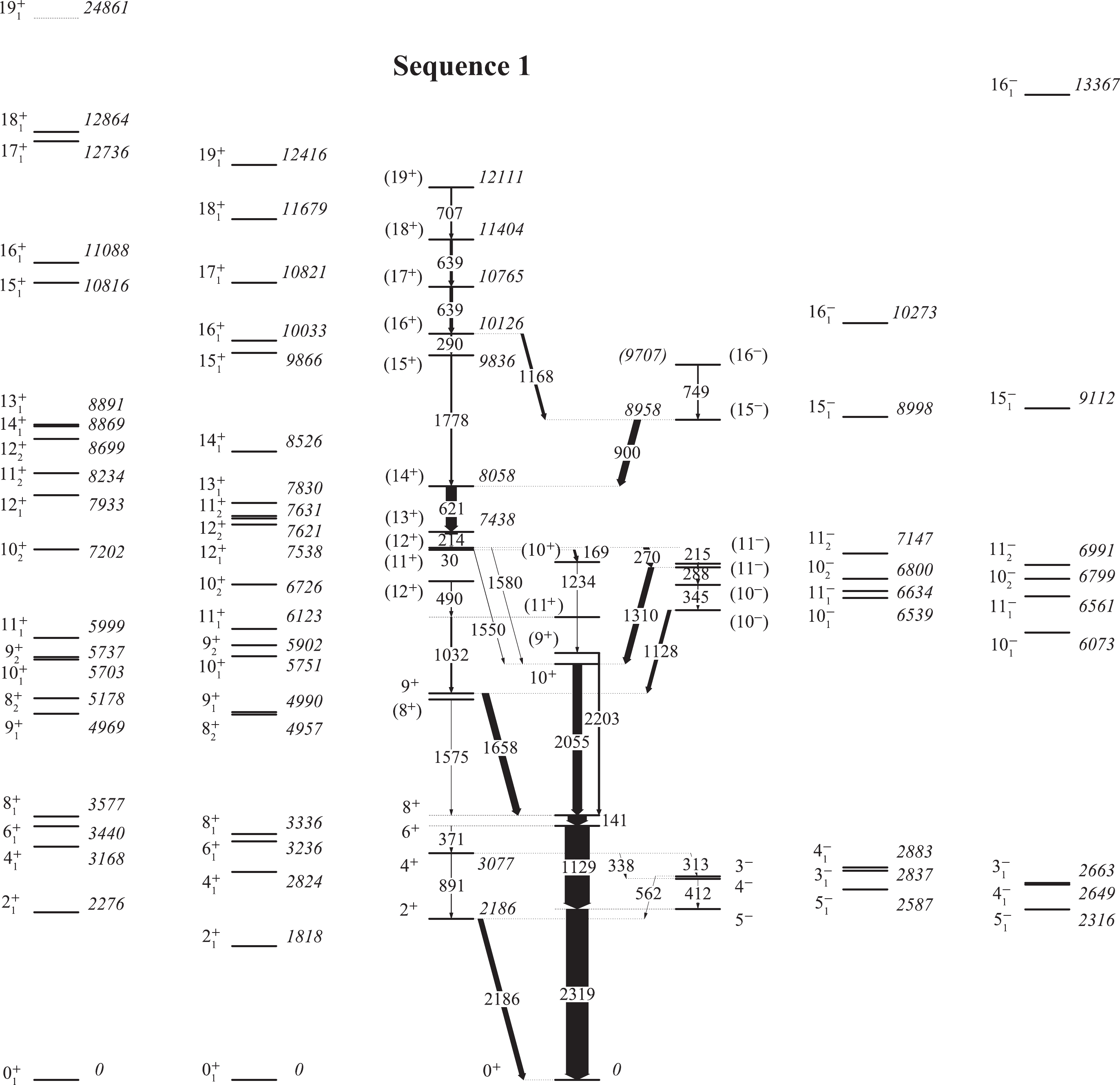
Figure1. Level scheme of ⁹⁰Zr deduced from Ref. [23], compared with the results obtained from the shell model calculations (SM1 and SM2).

$ I^{\pi} (\hbar) $	$E_{ ({\rm {exp.}})}$/keV	SM1					SM2
		$ E_{\rm (cal.)} $/keV	Wave function $ \pi\otimes\nu $	Seniority ν	Partitions (%)		$ E_{\rm (cal.)} $/keV	Wave function $ \pi \otimes\nu $	Seniority ν	Partitions (%)
$ 0_{1}^{+} $	0	0	6 4 2 0 $ \otimes $ 2 10 0 0	0	45.25		0	6 4 2 0 $ \otimes $ 2 10 0 0	0	30.26
			6 4 0 2 $ \otimes $ 2 10 0 0	0	22.45			6 4 0 2 $ \otimes $ 2 10 0 0	0	20.89
$ 2_{1}^{+} $	2186	2276	6 4 0 2 $ \otimes $ 2 10 0 0	2	50.68		1818	6 4 0 2 $ \otimes $ 2 10 0 0	2	36.62
			4 4 2 2 $ \otimes $ 2 10 0 0	2	16.21			4 4 2 2 $ \otimes $ 2 10 0 0	2	16.69
$ 4_{1}^{+} $	3077	3168	6 4 0 2 $ \otimes $ 2 10 0 0	2	54.83		2824	6 4 0 2 $ \otimes $ 2 10 0 0	2	40.93
			4 4 2 2 $ \otimes $ 2 10 0 0	2	14.36			4 4 2 2 $ \otimes $ 2 10 0 0	2	15.55
$ 6_{1}^{+} $	3448	3440	6 4 0 2 $ \otimes $ 2 10 0 0	2	59.52		3236	6 4 0 2 $ \otimes $ 2 10 0 0	2	48.94
			4 4 2 2 $ \otimes $ 2 10 0 0	2	12.43			4 4 2 2 $ \otimes $ 2 10 0 0	2	14.05
$ 8_{1}^{+} $	3589	3577	6 4 0 2 $ \otimes $ 2 10 0 0	2	63.07		3336	6 4 0 2 $ \otimes $ 2 10 0 0	2	50.65
			4 4 2 2 $ \otimes $ 2 10 0 0	2	12.07			4 4 2 2 $ \otimes $ 2 10 0 0	2	13.48
$ 8_{2}^{+} $	5164	5178	5 4 1 2 $ \otimes $ 2 10 0 0	2	47.53		4957	5 4 1 2 $ \otimes $ 2 10 0 0	4	40.82
			5 3 2 2 $ \otimes $ 2 10 0 0	2	25.20			6 3 1 2 $ \otimes $ 2 10 0 0	4	19.89
$ 9_{1}^{+} $	5247	4969	5 4 1 2 $ \otimes $ 2 10 0 0	4	73.08		4990	5 4 1 2 $ \otimes $ 2 10 0 0	4	66.91
			5 3 2 2 $ \otimes $ 2 10 0 0	4	11.91			5 3 2 2 $ \otimes $ 2 10 0 0	4	10.64
$ 9_{2}^{+} $	5792	5737	6 3 1 2 $ \otimes $ 2 10 0 0	4	67.49		5902	5 4 1 2 $ \otimes $ 2 10 0 0	4	44.86
			5 4 1 2 $ \otimes $ 2 10 0 0	4	13.93			6 3 1 2 $ \otimes $ 2 10 0 0	4	21.38
$ 10_{1}^{+} $	5644	5703	5 4 1 2 $ \otimes $ 2 10 0 0	4	76.91		5751	6 3 1 2 $ \otimes $ 2 10 0 0	4	38.86
			5 3 2 2 $ \otimes $ 2 10 0 0	4	13.72			5 4 1 2 $ \otimes $ 2 10 0 0	4	20.99
$ 10_{2}^{+} $	7026	7202	4 4 0 4 $ \otimes $ 2 10 0 0	4	55.80		6726	4 4 0 4 $ \otimes $ 2 10 0 0	4	48.21
			4 4 2 2 $ \otimes $ 2 10 0 0	4	8.65			4 3 1 4 $ \otimes $ 2 10 0 0	4	7.85
$ 11_{1}^{+} $	6280	5999	5 4 1 2 $ \otimes $ 2 10 0 0	4	73.52		6123	5 4 1 2 $ \otimes $ 2 10 0 0	4	65.31
			5 3 2 2 $ \otimes $ 2 10 0 0	4	14.18			5 3 2 2 $ \otimes $ 2 10 0 0	4	12.46
$ 11_{2}^{+} $	7194	8234	4 4 0 4 $ \otimes $ 2 10 0 0	4	34.60		7631	6 4 0 2 $ \otimes $ 2 9 0 1	4	34.74
			5 3 0 4 $ \otimes $ 2 10 0 0	4	24.19			4 4 2 2 $ \otimes $ 2 9 0 1	4	16.23
$ 12_{1}^{+} $	6770	7933	4 4 0 4 $ \otimes $ 2 10 0 0	4	62.69		7538	4 4 0 4 $ \otimes $ 2 10 0 0	4	51.58
			4 3 1 4 $ \otimes $ 2 10 0 0	6	12.98			4 3 1 4 $ \otimes $ 2 10 0 0	6	10.90
$ 12_{2}^{+} $	7224	8699	5 3 0 4 $ \otimes $ 2 10 0 0	4	29.17		7621	6 4 0 2 $ \otimes $ 2 9 0 1	4	38.10
			4 4 0 4 $ \otimes $ 2 10 0 0	4	26.84			4 4 2 2 $ \otimes $ 2 9 0 1	4	17.05
$ 13_{1}^{+} $	7438	8891	5 3 0 4 $ \otimes $ 2 10 0 0	6	38.03		7830	6 4 0 2 $ \otimes $ 2 9 0 1	4	42.29
			4 4 0 4 $ \otimes $ 2 10 0 0	6	33.83			4 4 2 2 $ \otimes $ 2 9 0 1	4	17.69
$ 14_{1}^{+} $	8058	8869	4 4 0 4 $ \otimes $ 2 10 0 0	6	70.98		8526	6 4 0 2 $ \otimes $ 2 9 0 1	4	40.74
			4 3 1 4 $ \otimes $ 2 10 0 0	6	22.62			4 4 2 2 $ \otimes $ 2 9 0 1	4	14.72
$ 15_{1}^{+} $	9836	10816	5 3 0 4 $ \otimes $ 2 10 0 0	6	29.71		9866	5 4 1 2 $ \otimes $ 2 9 0 1	6	54.25
			5 2 1 4 $ \otimes $ 2 10 0 0	6	22.90			4 4 2 2 $ \otimes $ 2 9 0 1	6	7.32
$ 16_{1}^{+} $	10126	11088	5 3 0 4 $ \otimes $ 2 10 0 0	6	38.12		10033	5 4 1 2 $ \otimes $ 2 9 0 1	6	73.92
			5 2 1 4 $ \otimes $ 2 10 0 0	8	27.82			5 3 2 2 $ \otimes $ 2 9 0 1	6	13.27
$ 17_{1}^{+} $	10765	12736	3 4 1 4 $ \otimes $ 2 10 0 0	8	53.79		10821	5 4 1 2 $ \otimes $ 2 9 0 1	6	66.57
			4 3 1 4 $ \otimes $ 2 10 0 0	8	32.73			5 3 2 2 $ \otimes $ 2 9 0 1	6	14.64
Continued on next page

Table1.Main partitions of the wave functions for ⁹⁰Zr with SM1 and SM2 configuration spaces. The wave function for a particular angular momentum state would contain several partitions. Each partition is of the form $P = \pi[p(1),\ p(2),\ p(3),\ p(4)] \otimes \nu[n(1) $, $n(2),\ n(3),\ n(4)]$, where $ p(i) $ represents the number of valence protons occupying the $ 1f_{5/2} $, $ 2p_{3/2} $, $ 2p_{1/2} $, and $ 1g_{9/2} $ orbitals, and $ n(j) $ represents the number of valence neutrons in the $ 2p_{1/2} $, $ 1g_{9/2} $, $ 1g_{7/2} $, and $ 2d_{5/2} $ orbitals.

It can be seen from Fig. 1 that the $2 _{1}^{+} $, $4 _{1}^{+} $, $6 _{1}^{+} $, and $8 _{1}^{+} $ states are well reproduced in both SM1 and SM2. As presented in Table 1, two sets of calculations predict that the above states are predominated by the $ \pi(fp)^{-2}(1g_{9/2})^{2} $ configurations, including the proton excitations from the completely filled $2 p_{1/2} $ orbital into the $1 g_{9/2} $ orbital, and the angular momentum of the $8 _{1}^{+} $ state arises from the full alignment of two $1 g_{9/2} $ protons. With an increase in the excitation energy, the higher $8 ^{+}_{2} $ and $9 ^{+}_{1} $ states are primarily dominated by the coupling of two proton holes in fp orbitals and two unpaired proton particles in the $1 g_{9/2} $ orbital, namely $ \pi(1f_{5/2})^{-1}(2p_{1/2})^{-1}(1g_{9/2})^{2} $ configurations. As presented in Table 1, both SM1 and SM2 calculations give the same results for the $9 ^{+}_{2} $ and $10 ^{+}_{1} $ states, with $ \pi (fp) ^{-2} (1 g_{9/2} ) ^{2} $ configurations. It should be noted that the 1575, 1658, 2203, and 2055 keV rays are de-excited from the observed ($8 ^{+} $), $9 ^{+} $, ($9 ^{+} $), and $10 ^{+} $ states, respectively. In the neighboring isotone ⁹²Mo [9], the presence of high-energy transitions of approximately 2 MeV at the levels I = 8 $ \sim 10 \hbar $ is suggested as an experimental indication of nucleons across the Z = 38 subshell, which supports the interpretation of excitations across the Z = 38 subshell for the aforementioned states in the ⁹⁰Zr nucleus. SM2 predicts that the $10 _{2}^{+} $ state is mainly dominated by the excitations of two $ 2p_{1/2} $ and $ 1f_{5/2} $ protons across the Z = 40 and 38 closed subshells into the high-j $ 1g_{9/2} $ orbital. As presented in Fig. 1, the energy difference between the predicted $11 ^{+}_{1} $ and $9 ^{+}_{1} $ states of SM2 is 1133 keV, which is close to the energy of the observed 1032 γ ray. The shell model calculations indicate that the $11 ^{+}_{1} $ state mainly decays to the $9 ^{+}_{1} $ state by the transition with E2 multipolarity. Thus, the observed first ($11 ^{+} $) state may correspond to the predicted $11 ^{+}_{1} $ state with an energy of 6123 keV obtained from the SM2 calculations, which is also consistent with the temporary spin-parity assignment suggested in Ref. [23]. It is predicted that the $11 _{1}^{+} $ state has the same configuration as the $9 _{1}^{+} $ state, i.e., the $ \pi(1f_{5/2})^{-1} $$ (2p_{1/2})^{-1}(1g_{9/2})^{2} $ configuration, mixed with $ \pi(1f_{5/2})^{-1} $$ (2p_{3/2})^{-1}(1g_{9/2})^{2} $ configuration. For the $12 _{1}^{+} $ state, it has the same $ \pi(fp)^{-4}(1g_{9/2})^{4} $ configuration as the $10 _{2}^{+} $ state.
In Table 1, it can be observed that the primary contribution to the positive-parity states from the $2 ^{+}_{1} $ state to the $8 ^{+}_{1} $ state comes from the $2 p_{1/2} $ proton excitations. For the states from $8 ^{+}_{2} $ to the $12 ^{+}_{1} $ state, the proton excitations of $1 f_{5/2} $ begin to participate in the contribution of the angular momentum. In general, the states from the $0 _{1}^{+} $ ground state to the $12 _{1}^{+} $ state (0 $ \sim 7000 $ keV), are reproduced satisfactorily in both SM1 and SM2. However, for the states above the $12 _{1}^{+} $ state, the values for the excitation energies, calculated within the two different configuration spaces (SM1 and SM2), exhibit significant differences.
It can be seen from Fig. 1 that the predicted energies of the $11 _{2}^{+} $ and $12 _{2}^{+} $ states in SM2, which involve neutron core excitations, are more reasonable than those in SM1. Within SM2 calculations, the observed $11 _{2}^{+} $ and $12 _{2}^{+} $ states could be interpreted as $ \pi(fp)^{-2}(1g_{9/2})^{2} \otimes \nu(1g_{9/2})^{-1} $$ (2d_{5/2})^{1} $ configurations with seniority ν = 4, including the coupling of two unpaired $ 1g_{9/2} $ protons and one $1 g_{9/2} $ neutron hole as well as a single $ 2d_{5/2} $ neutron located above N = 50 core, while both states are assigned to the $ \pi(fp)^{-4}(1g_{9/2})^{4} $ configurations in SM1 calculations. It should be noted that the order of levels $11 ^{+}_{2} $ and $12 ^{+}_{2} $ is opposite in SM2 and is normal in SM1 compared to the data. Considering the differences in configurations obtained by SM1 and SM2, the inverse order of levels $11 ^{+}_{2} $ and $12 ^{+}_{2} $ given by SM2 may be attributed to the influence of the neutron-proton interaction [45], as an additional neutron is excited to the $2 d_{5/2} $ orbital. Furthermore, the excitation energies for the observed $11 ^{+}_{2} $ and $12 ^{+}_{2} $ states are very close to each other (about 30 keV), and the predicted energy difference between the both states in SM2 is only 10 keV. Such a small energy difference is significantly sensitive to change of configuration space, which is also likely to affect the order of levels in the shell model calculations. In addition, the presence of high-energy 1550 and 1580 keV transitions decaying from the second ($11 ^{+} $) and ($12 ^{+} $) states may be an experimental indication of the N = 50 core breaking. Similar features are also observed in ⁹¹Nb [8], ⁹²Mo [9], ⁹⁴Ru [11, 17], and $ ^{96,97,98} {\rm{Ru}}$ [46]. For example, in the neighboring N = 50 isotone ⁹⁴Ru, the initial states of the high-energy 2200, 2402, 2584, and 2565 keV transitions, namely $13 ^{-}_{3} $, $13 ^{-}_{4} $, $14 ^{-}_{1} $, and $15 ^{-}_{1} $ states, respectively, also involve the breaking of the N = 50 core.
The improved description for the $11 _{2}^{+} $ and $12 _{2}^{+} $ states in SM2 indicates that the neutron core excitations may play a significant role in the higher-spin states of ⁹⁰Zr. It is clear from Fig. 1 and Table 1 that within SM2 calculations, the observed ($13 ^{+} $) and ($14 ^{+} $) states may correspond to the calculated $13 _{1}^{+} $ and $14 _{1}^{+} $ states, with the $ \pi(fp)^{-2}(1g_{9/2})^{2} \otimes \nu(1g_{9/2})^{-1}(2d_{5/2})^{1} $ configurations contributing maximally. In addition, the energy difference between the calculated $13 _{1}^{+} $ and $14 _{1}^{+} $ states is 696 keV, which is close to the energy of the observed 621 keV γ ray [23]. Nevertheless, in SM1 calculations, the predicted excitation energies of $13 _{1}^{+} $ and $14 _{1}^{+} $ states are 1453 and 811 keV higher than the experimental values, respectively, and the order of these two states is inverted. As can be deduced from Fig. 1, the calculated $15 _{1}^{+} $, $16 _{1}^{+} $, $17 _{1}^{+} $, and $18 _{1}^{+} $ states of SM2 may correspond to the experimental levels at 9836, 10126, 10765, and 11404 keV, respectively. The deviations between predicted excitation energies and experimental ones are less than 280 keV, whereas using the SM1 configuration space leads to relatively large differences of $1.0 \sim 2.0$ MeV. Within SM2 calculations, the aforementioned states are predominated by $ \pi(1f_{5/2})^{-1}(2p_{1/2})^{-1} $$ (1g_{9/2})^{2} \otimes \nu(1g_{9/2})^{-1}(2d_{5/2})^{1} $ configurations with seniority ν = 6, including the excitation of a single $ 1g_{9/2} $ neutron across the N = 50 core into the $ 2d_{5/2} $ orbital. This further indicates that the contribution from the particle-hole excitations across the N = 50 inert core cannot be ignored. The observed ($19 ^{+} $) state with an energy of 12111 keV may correspond to the calculated $19 _{1}^{+} $ state of SM2 at an energy of 12416 keV. Although it has the same proton configuration as that of the $18 _{1}^{+} $ state, it involves neutron excitations across the N = 50 core into the $ 1g_{7/2} $ orbital, i.e., the $ \pi(1f_{5/2})^{-1}(2p_{1/2})^{-1}(1g_{9/2})^{2} \otimes $$ \nu(1g_{9/2})^{-1}(1g_{7/2})^{1} $ configuration. However, in the SM1 configuration space, the predicted $19 ^{+} $ is significantly higher than the experimental one, with a difference of more than 10 MeV. In general, it can be inferred from Fig. 1 that the predicted energies of higher-spin states within the SM2 configuration space are more logical than those in SM1.
A similar situation also emerges in the negative-parity states of ⁹⁰Zr. As can be seen from Fig. 1, the calculations within SM2 containing neutron core excitations provide an improved description for higher-spin states in comparison with the SM1. Hence, the breaking of the N = 50 core plays an important role in the higher-spin states of ⁹⁰Zr, for positive-parity states as well as negative-parity states. The calculated $16 _{1}^{-} $ state primarily originates from the configuration of $ \pi(fp)^{-3}(1g_{9/2})^{3} \otimes \nu(1g_{9/2})^{-1} $$ (2d_{5/2})^{1} $ with ν = 6. For the other negative-parity states of ⁹⁰Zr, the predicted excitation energies within SM1 and SM2 configuration spaces are in logical agreement with the experimental ones. The observed state with an energy of 8958 keV, corresponding to the predicted $15 _{1}^{-} $ state at an energy of 8998 keV, could be interpreted as the configuration of $ \pi(1f_{5/2})^{-2}(2p_{1/2})^{-1}(1g_{9/2})^{3} $, involving the excitations of two $1 f_{5/2} $ proton holes across the Z = 38 subshell. The $10 _{2}^{-} $ and $11 _{2}^{-} $ states have the same configurations, i.e., $ \pi(1f_{5/2})^{-1}(2p_{3/2})^{-1}(2p_{1/2})^{-1}(1g_{9/2})^{3} $. For the $10 _{1}^{-} $ state, it mainly arises from the coupling of one $1 f_{5/2} $ proton hole and three $1 g_{9/2} $ proton particles. The $3 _{1}^{-} $ state could be described as the $ \pi(2p_{3/2})^{-1}(1g_{9/2})^{1} $ configuration, with seniority ν = 2. The calculated wave functions of $4 _{1}^{-} $ and $ 5_{1}^{-} $ states indicate a multiplet character, with the predominated $ \pi(2p_{1/2})^{-1}(1g_{9/2})^{1} $ configuration.
2 -->

B.Evolution from the neutron core excitations to proton excitations

The core excitations are systematically observed in N = 50 isotones, generally for the higher-spin states. However, we note that some specific lower-spin states also include the breaking of the N = 50 core. To further understand the core breaking of the lower-spin states, the systematic study of the states for the N = 50 even-even isotones ⁸⁶Kr [47], ⁸⁸Sr [6], ⁹⁰Zr [23, 48], ⁹²Mo [9], ⁹⁴Ru [11], and odd-A isotones ⁸⁵Br [49], ⁸⁷Rb [50], ⁸⁹Y [7], ⁹¹Nb [8], ⁹³Tc [10], is presented in Figs. 2(a) and 2(b), respectively, where the states, including the neutron core excitations, are marked in red.
Figure2. (color online) Excitation energies for the low-lying states in the N = 50 (a) even-even isotones ⁸⁶Kr [47], ⁸⁸Sr [6], ⁹⁰Zr [23, 48], ⁹²Mo [9], and ⁹⁴Ru [11], and (b) odd-A isotones ⁸⁵Br [49], ⁸⁷Rb [50], ⁸⁹Y [7], ⁹¹Nb [8], and ⁹³Tc [10]. The states including the neutron excitations across the N = 50 core are marked in red.

In Fig. 2(a), the $6 _{1}^{+} $ and $7 _{1}^{+} $ states of ⁸⁶Kr [47] and ⁸⁸Sr [6] are predominated by the $ \nu(1g_{9/2})^{-1}(2d_{5/2})^{1} $ configurations, associated with the breaking of the N = 50 core. Conversely, in ⁹⁰Zr, the $6 _{1}^{+} $ and $7 _{1}^{+} $ states mainly arise from the proton configurations $ \pi (fp) ^{-2} (1 g_{9/2})^{2} $. In the heavier ⁹²Mo and ⁹⁴Ru nuclei, the $6 _{1}^{+} $ and $7 _{1}^{+} $ states are also mainly dominated by the coupling of the two unpaired $1 g_{9/2} $ protons, without neutron core excitations.
This indicates an evolution from the neutron core excitations to proton excitations for low-lying states, along the N = 50 even-even isotones. This phenomenon appears to be related to the change in the proton Fermi surface. With the decrease in the proton number from ⁹⁰Zr to ⁸⁶Kr, the proton Fermi surface moves away from the $ 1g_{9/2} $ orbital, i.e., the proton excitations from the fp orbitals into the $1 g_{9/2} $ orbital become more difficult. In fact, it can be deduced from Fig. 2(a) that for the yrast $6 ^{+} $ and $7 ^{+} $ states, the neutron core excitations seem to be more favored than proton excitations. In contrast, as the protons increase from ⁹⁰Zr to ⁹⁴Ru, the proton excitations become relatively easy.
A similar situation also emerges at the 23/$2 ^{+} $ states in the N = 50 odd-A isotones. From Fig. 2(b), the yrast 23/$2 ^{+} $ states of ⁸⁷Rb [50] and ⁸⁹Y [7] nuclei, with Z < 40, are dominated by the neutron core excitations. The yrast 23/$2 ^{+} $ states of the ⁹¹Nb [8] and ⁹³Tc [10] nuclei, with Z > 40, are generated by the proton excitations instead of the neutron core excitations, whereas the yrare 23/$2 ^{+} $ state of ⁹¹Nb includes the neutron core excitation. In particular, the ⁹⁰Zr nucleus with Z = 40, of which the proton Fermi surface lies at the $2 p_{1/2} $ orbital, may be a critical nucleus for the structural evolution along the N = 50 isotones.
In addition, for the $8 _{1}^{+} $ states with $ \pi(1g_{9/2})^{2} $ configurations in even-even nuclei, the excitation energies decrease with increasing proton numbers, as illustrated inFig. 2(a). Similarly, in Fig. 2(b), the excitation energies of the 9/$2 _{1}^{+} $ and 13/$2 _{1}^{+} $ states in the odd-A nuclei also exhibit a decreasing character. The behavior of the aforementioned excitation energies also indicates the influence of the change in the proton Fermi surface.
2 -->

C.Possible magnetic rotation

In Fig. 1, the positive-parity sequence 1 primarily comprises relatively strong M1 transitions with absent E2 crossover transitions. To further interpret this sequence, the observed spins I are presented in Fig. 3(a) as a function of the rotational frequency $ \hbar\omega $, where $ \hbar\omega(I) = $$ [E(I) - E(I - 2)]/2 $. In Fig. 3(a), a sudden backbend occurs at $ \hbar\omega \approx $ 1.2 MeV, owing to the alignment of the two fp proton holes, which agrees well with the shell model prediction. Based on SM2 calculations, we suggest that the sequence 1 of ⁹⁰Zr has the $ \pi(fp)^{-2}(1g_{9/2})^{2} \otimes $$ \nu(1g_{9/2})^{-1}(2d_{5/2}/1g_{7/2})^{1} $ configuration before the sharp backbend.
Figure3. (color online) (a) Angular momentum as a function of rotational frequency $ \hbar\omega$ for sequence 1 in nucleus ⁹⁰Zr. (b) Comparative dynamic moment of inertia $ J^{2}$ versus $ \hbar\omega$ plot for the magnetic rotational bands in ⁸³Kr [51], ⁸⁴Rb [36], and ⁸⁵Sr [41], with the M1 sequence in ⁹⁰Zr. The dash line indicates the value for the rigid spherical rotor.

In this mass region, the high-j particles and holes are known to play active roles in the magnetic rotation [35]. In fact, these basic conditions for the occurrence of magnetic rotation can be satisfied in the positive-parity sequence 1. Hence, it is interesting to investigate whether sequence 1 emerges from magnetic rotation. Accordingly, the dynamic moment of inertia $ J^{(2)} $ of sequence 1 in ⁹⁰Zr and those of the magnetic rotational bands in the neighboring ⁸³Kr [38], ⁸⁴Rb [35, 36], and ⁸⁵Sr [41] nuclei are presented in Fig. 3(b), where $ J^{(2)} $ of sequence 1 is similar to those of magnetic rotational bands in the neighboring nuclei. Another typical characteristic of magnetic rotation is the decrease in $ B(M1) $ values with increasing spin. The $ B ( M 1)$ values for sequence 1 in nucleus ⁹⁰Zr [23] and magnetic rotational bands in ⁸³Kr [51], ⁸⁴Rb [36], and ⁸⁵Sr [42], are plotted in Fig. 4. As illustrated in Fig. 4, the $ B(M1) $ values of ⁹⁰Zr exhibit a decreasing tendency with increasing spin up to $ I^{\pi} = 14^{+} $, similar to magnetic rotational bands of ⁸³Kr, ⁸⁴Rb, and ⁸⁵Sr. Meanwhile, the $ B ( M 1)$ values of these nuclei are close to each other, approximately 1.0 $ \mu^{2}_{N} $. Hence, we suggest that the positive-parity sequence 1 of ⁹⁰Zr before the backbend ($ \sim 14^{+} $) may also be a candidate magnetic rotational band.
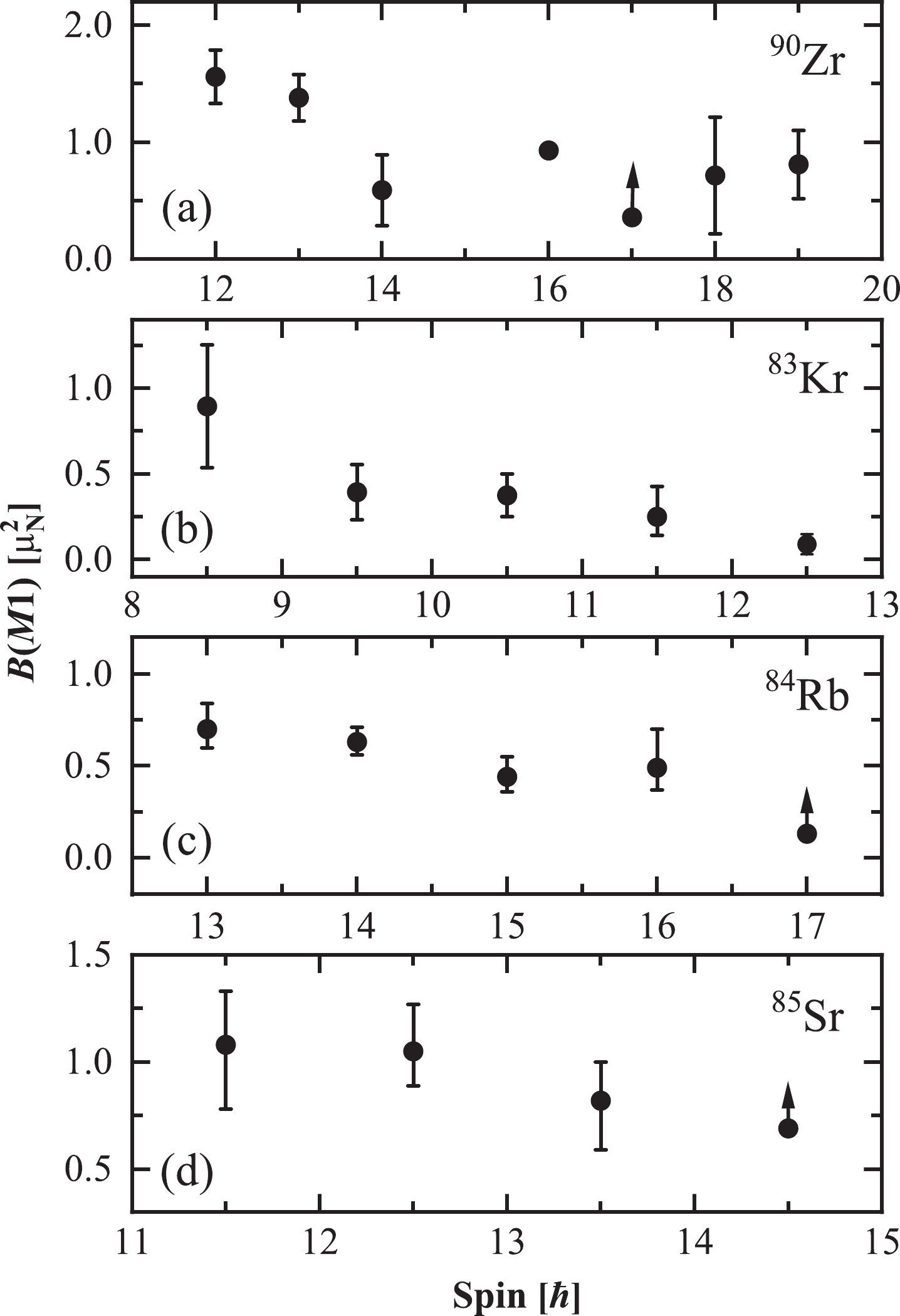Figure4. Comparison of transition rates $ B(M1)$ for sequence 1 of nucleus (a) ⁹⁰Zr [23] and $ B(M1)$ values for magnetic rotational bands in (b) ⁸³Kr [51], (c) ⁸⁴Rb [36], and (d) ⁸⁵Sr [42] nuclei.

In order to examine the conjecture of magnetic rotation, the theoretical reduced transition probabilities $ B(M1) $ for sequence 1 before the backbend are presented as a function of the rotational frequency based on the large scale shell model calculations in the insert of Fig. 5, where the calculated $ B(M1) $ values are large (about several $ \mu_{N}^{2} $) and exhibit a smooth decreasing trend with the increasing spin, which is consistent with the characteristic of magnetic rotation.
Figure5. (color online) Effective interaction as a function of shears angle. The solid curve represents the fit to the experimental data for $ V_{2}$ = 2.51 MeV. The insert presents the experimental and calculated B(M1) values of the candidate magnetic rotational band in ⁹⁰Zr.

To further elucidate the shears mechanism, we perform the semiclassical calculations proposed by A. O. Macchiavelli and R. M. Clark et al. [31-34], based on a schematic model with the objective of extracting information on the effective interaction. The calculated energies of sequence 1 are presented as a function of shears angle θ, in comparison with the available data, as illustrated in Fig. 5, where the shears angle decreases gradually with spin increasing. In addition, the data are logically reproduced for $ V_{2} $ = 2.51 MeV before the band crossing. Meanwhile, we estimate that the interaction strength per proton/neutron-hole pair is $ \sim 840 $ keV for ⁹⁰Zr, which is close to the value $ \sim 900$keV adopted for the magnetic rotational band in the neighboring ⁸⁴Rb [34]. Primarily, the positive-parity sequence 1 of ⁹⁰Zr before the backbend may originate from the shears mechanism.

Large scale shell model calculations were performed for ⁹⁰Zr based on two different configuration spaces. Although SM1 calculations reproduce the lower-spin states well, they fail to logically describe higher-spin states. In contrast to SM1, the SM2 configuration space, including the neutron core excitations, provides an improved description of the higher-spin states. The SM2 calculations predict that the higher-spin states of ⁹⁰Zr can be predominated by (i) proton excitations from the fp orbitals across the Z = 38 or 40 subshell into the higher orbitals, and (ii) neutron excitations from the interior of the N = 50 core to the next major shell. This indicates that the neutron core excitations play a significant role in the higher-spin states of ⁹⁰Zr. Meanwhile, the evolution from the neutron core excitations to proton excitations was systematically studied along the neighboring N = 50 isotones for lower-spin states, and ⁹⁰Zr may be the critical nucleus for the evolution. Furthermore, based on lifetime measurements and characteristics of sequence 1, the positive-parity ?I = 1 of sequence 1 before the backbend is proposed as a candidate magnetic rotational band with the $ \pi(fp)^{-2}(1g_{9/2})^{2} \otimes $$ \nu(1g_{9/2})^{-1}(2d_{5/2}/1g_{7/2})^{1} $ configuration.