Bing Li ^1,2,
, Na Tang ^1,2,
, Feng-Shou Zhang ^1,2,3,,
,

Corresponding author: Feng-Shou Zhang, fszhang@bnu.edu.cn

1.The Key Laboratory of Beam Technology and Material Modification of Ministry of Education, College of Nuclear Science and Technology, Beijing Normal University, Beijing 100875, China
2.Beijing Radiation Center, Beijing 100875, China
3.Center of Theoretical Nuclear Physics, National Laboratory of Heavy Ion Accelerator of Lanzhou, Lanzhou 730000, China
Received Date:2021-02-04
Available Online:2021-08-15
Abstract:The isospin effects of projectile fragmentation at intermediate energies are investigated using an isospin-dependent Boltzmann-Langevin model. The collisions of mass-symmetric reactions including ⁵⁸Fe, ⁵⁸Ni + ⁵⁸Fe, and ⁵⁸Ni at intermediate energies, in the 30 to 100 MeV/A range, are studied for different symmetry energies. Yield ratios of the isotopic, isobaric, and isotonic pairs of fragments from the intermediate-mass region using three symmetry energies are extracted as functions of the N/Z ratio of the composite systems in the entrance channel and the incident energies. It is found that the yield ratios are sensitive to symmetry energies, especially for neutron-rich systems, and the calculations using soft symmetry energy are closer to the experimental data. The isospin effect is stronger for the soft symmetry energy, owing to the competition of the repulsive Coulomb force and the symmetry energy attractive force on the proton. For the first time, the splits are presented, revealing a transition from the isospin equilibrium at lower energies to translucency at intermediate energies. The results show a degree of transparency in that intermediate mass fragments undergo a transition from dependence on the composite systems in the entrance channel to reliance on the projectile and target nuclei.

HTML

--> --> -->

In the past decades, isospin dynamics in nuclear reactions at Fermi energies have been widely studied, both experimentally and theoretically [1-18]. Moreover, nuclear fragmentation is very important for studying the reaction mechanisms of nuclear collisions [19, 20] and for constraining the density dependence of the symmetry energy, which is essential for nuclear-astrophysics, nuclear structure, and nuclear reactions [21-23]. Isospin observables, including the neutron/proton or triton/³He yield ratio, the neutron-proton differential flow, the isoscaling of fragments, and the isospin diffusion, have been widely studied, for analyzing the density dependence of the symmetry energy [24-32]. In contrast, many puzzles remain related to the isospin effects, especially in the projectile fragmentation, a well-established technique for producing rare isotope beams.
In heavy-ion collisions at intermediate energies, ranging from the Fermi energy to 100-200 MeV/nucleon, the isospin equilibration is always related to the production of fragments. The first attempt to study the isospin degree of freedom at the Fermi energy was reported in Ref. [33], where the reaction of $ E/A $ = 53 MeV and A = 40 projectiles with A = 58 targets was measured. It was concluded that isotopic ratios must maintain some memory of the entrance channel. Similar studies were also performed on other reaction systems at other energies, all showing that the isospin transport continues until equilibrating [34-37]. The isospin transport effects include the isospin drift driven by the density gradient [38-41], and the isospin diffusion related to the isospin transport between the projectile and target nuclei [42-45]. These two mechanisms are related to the symmetry energy in the equation of state (EOS) of asymmetrical nuclear matter. The study of the symmetry energy has garnered significant attention in recent years [46-53], because it can influence dissipative reactions, such as fragment emissions.
At intermediate energies, the fragmentation reaction is the main reaction mechanism, where a composite system splits into several fragments. Different theoretical transport models have been developed for describing the dynamics of fragmentation under certain approximations. One of these is the quantum molecular dynamics model (QMD) [54], in which the nucleon is considered a Gaussian wave packet with a finite width. Another is the semi-classical Boltzmann-Uehling-Uhlenbeck (BUU) model [55, 56], which has been extensively applied for describing one-body observables in nuclear collisions. However, the BUU model cannot be used for describing a fermion system's properties far from equilibrium, such as multi-fragmentation and subthreshold particle production [57-60]. The BUU model has been extended to consider the correlation effects between nucleons, using the Boltzmann-Langevin equation (BLE) [58-70]. It is well known that the BLE has been successfully used for describing fragmentation reactions [61, 62]. It incorporates a fluctuation into the collision term of the dynamical evolution of the system. By introducing the isospin effect into the BLE, we obtain the isospin-dependent Boltzmann-Langevin equation (IBLE). Another method that incorporates fluctuations into mean-field dynamics is the stochastic mean-field approach (SMF) [71, 72], and fragmentation characteristics have been analyzed using that approach [10, 73, 74]. A comprehensive comparison of these transport theories can facilitate future research, and many studies have been published on this subject. Xu and Zhang et al. compared different heavy-ion transport simulations under controlled conditions, including nine Boltzmann-Uehling-Uhlenbeck-type codes and nine quantum-molecular-dynamics-type codes [75, 76].
In this study, we determine our model's feasibility and then apply the IBLE model to investigate the isospin effects of projectile fragmentation in the mass-symmetric reactions including ⁵⁸Fe, ⁵⁸Ni + ⁵⁸Fe, and ⁵⁸Ni, at energies in the 30 to 100 MeV/nucleon range. The remainder of this paper is organized as follows. A brief introduction of the IBLE and the model test is given in Sec. II. The results and discussion are presented in Sec. III. Finally, conclusions are presented in Sec. IV.

The BUU equation and other one-body transport equations do not incorporate two-body correlation effects; thus, they fail to describe dynamical fluctuations [61, 62]. By incorporating the fluctuating collision term into the BUU equation, we obtain the isospin-dependent Boltzmann-Langevin equation. The fluctuating single particle density $ \hat{f}({{r}},{{p}},t) $ is determined by the so-called isospin-dependent Boltzmann-Langevin equation [58, 59, 61, 62, 68-70]:

$ \left(\frac{\partial}{\partial{t}}+\frac{{{p}}}{m} \cdot \bigtriangledown_{r}-\bigtriangledown_{r}U(\hat{f})\cdot\bigtriangledown_{p}\right) \hat{f}({{r}},{{p}},t) = K(\hat{f})+\delta K({{r}},{{p}},t). $

(1)

The left side of the above equation describes the Vlasov propagation, determined by the nuclear mean field $ U(\hat{f}) $. On the right side, $ K(\hat{f}) $ and $ \delta K({{r}},{{p}},t) $ denote the collision term and the fluctuating collision term, respectively [62]. The collision term $ K(\hat{f}) $ has the usual BUU form but is described by the fluctuating density $ \hat{f}({{r}},{{p}},t) $, that is:

$ \begin{aligned}[b] K(\hat{f_{1}}) = &\int {\rm d}{{p}}_{2}{\rm d}{{p}}_{3}{\rm d}{{p}}_{4}W(12;34)\\ &[\hat{f_{3}}\hat{f_{4}}(1-\hat{f_{1}})(1-\hat{f_{2}})-\hat{f_{1}}\hat{f_{2}}(1-\hat{f_{3}})(1-\hat{f_{4}})], \end{aligned} $

(2)

where $ \hat{f_{i}} $ = $ \hat{f}({{r}},{{p}}_{i},t) $ denotes the diagonal elements of single particle density; $ W(12;34) $ is the transition rate, which can be expressed by the collision cross section $ ({{p}}_{1},{{p}}_{2}) \rightarrow ({{p}}_{3},{{p}}_{4}) $ as

$ W(12;34) = \frac{{\rm d}\sigma}{{\rm d}\Omega}\delta({{p}}_{1}+{{p}}_{2}-{{p}}_{3}-{{p}}_{4}) \delta(\epsilon_{1}+\epsilon_{2}-\epsilon_{3}-\epsilon_{4}), $

(3)

where $ \epsilon_{i} $ are the single particle energies. The fluctuating collision term can be characterized by the following correlation function:

$ \langle{\delta K({{r}}_{1},{{p}}_{1},t_{1}) \delta K({{r}}_{2},{{p}}_{2},t_{2})}\rangle = C({{p}}_{1},{{p}}_{2})\delta({{r}}_{1}-{{r}}_{2}) \delta(t_{1}-t_{2}). $

(4)

The brackets in Eq. (4) denote local ensemble averaging, generated during a short time interval $ \Delta t $. When averaging inside one of the subensembles, one is performing the so-called local averaging [58, 59, 61, 62, 68-70]. We simulate Eq. (1) using the projection method [57, 61, 66], which projects fluctuations onto a series of multipole moments of the momentum distribution. We truncate the multipole moments to the first two non-vanishing terms, i.e., the quadrupole moment and the octupole moment ($ Q_{20}+Q_{30} $), because we posit that a few low-order multipole moments are sufficient for describing dynamical fluctuations. The quadrupole and octupole moments of the momentum distribution can be described as

$ \begin{aligned}[b] Q_{20} =& \int{{\rm d}{{r}}{\rm d}{{p}}\hat{Q}_{20}\hat{f}({{r}},{{p}},t)}\\ =& \int{{\rm d}{{r}}{\rm d}{{p}}(2{{p}}_{z}^{2}-{{p}}_{x}^{2}-{{p}}_{y}^{2})\hat{f}({{r}},{{p}},t)}, \end{aligned} $

(5)

$ \begin{aligned}[b] Q_{30} =& \int{{\rm d}{{r}}{\rm d}{{p}}\hat{Q}_{30}\hat{f}({{r}},{{p}},t)}\\ =& \int{{\rm d}{{r}}{\rm d}{{p}}({{p}}_{z}(2{{p}}_{z}^{2}-3{{p}}_{x}^{2}-3{{p}}_{y}^{2}))\hat{f}({{r}},{{p}},t)}.\end{aligned} $

(6)

where the beam axis is along the z-axis.
In this model, the interaction nuclear potential, which includes the isospin degree of freedom for nucleons, is given as

$ \begin{aligned}[b] U_{\tau}(\rho,\delta,{{p}}) =& \alpha\frac{\rho}{\rho_{0}}+\beta\left(\frac{\rho}{\rho_{0}}\right)^{\gamma}+E_{\rm sym}^{\rm loc}(\rho)\delta^{2}\\ &+\frac{\partial E_{\rm sym}^{\rm loc}(\rho)}{\partial \rho}\rho\delta^{2}+E_{\rm sym}^{\rm loc}(\rho)\rho\frac{\partial\delta^{2}}{\partial\rho_{\tau}}+U_{\rm MDI}, \end{aligned} $

(7)

where $ \delta = (\rho_{n}-\rho_{p})/\rho $ is the isospin asymmetry; $ \rho_{0} $ is the normal nuclear matter density; $ \rho $, $ \rho_{p} $ and $ \rho_{n} $ are the total, proton, and neutron densities, respectively. Here, we adopt the parameters of soft EOS plus MDI as SM from Table 1 [54].

EOS	α/MeV	β/MeV	γ	K/MeV
SM	?390	320	1.14	200
HM	?130	59	2.09	380

Table1.Two sets of parameters adopted in IBLE.

$E_{\rm sym}^{\rm loc}$ is the local part of the symmetry energy, according to Ref. [52]. It can be written as

$ E_{\rm sym}^{\rm loc}(\rho) = \frac{1}{2}C_{\rm sym}\left(\frac{\rho}{\rho_{0}}\right)^{\gamma_{s}}. $

(8)

The parameters $ \gamma_{s} $ = 0.5, 1.0, and 2.0 are applied, corresponding to the soft, linear, and hard symmetry energies, respectively. The coefficient value of $C_{\rm sym}$ is 29.4 MeV. The density dependence of the symmetry energy for different $ \gamma_{s} $ is shown in Fig. 1. The symmetry energy increases with increasing density for the three cases, and the symmetry energy is approximately 30 MeV at normal density. At subsaturation densities, higher symmetry energies are obtained for smaller $ \gamma_{s} $, while this trend is reversed at suprasaturation densities.
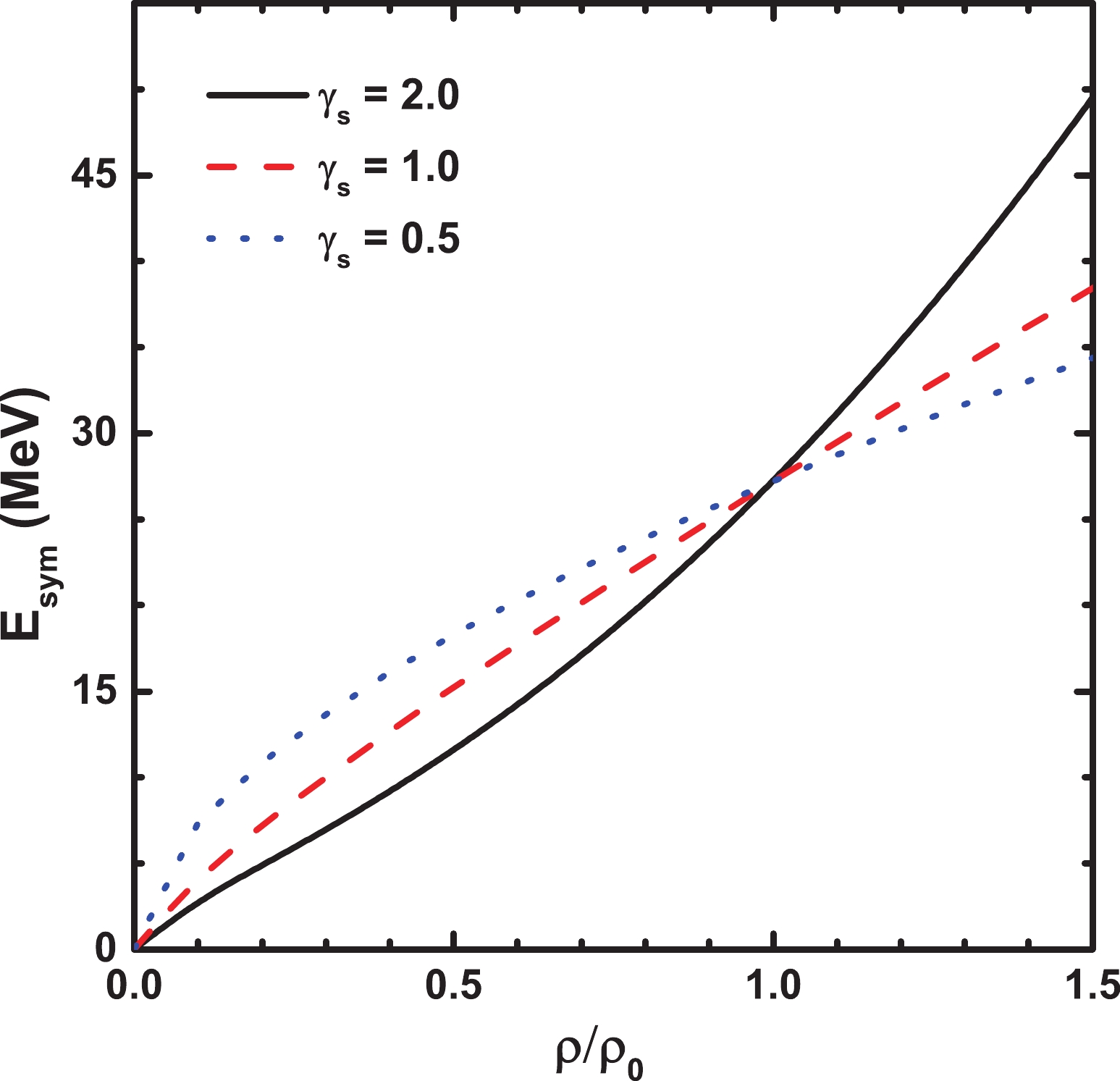Figure1. (color online) Density dependence of the symmetry energy. The cases $ \gamma_{s}$ = 2.0, 1.0, and 0.5 are presented as the black solid line, red dashed line, and blue dotted line, respectively.

The $U_{\rm MDI}$ is momentum-dependent potential, which is given by [77, 78]

$ U_{\rm MDI} = \frac{t_{4}}{\rho_{0}}\int\hat{f}({{r}},{{p}})[\ln(t_{5}({{p}}-{{p{'}}})^{2}+1)]^{2}{\rm d}{{p{'}}}, $

(9)

where $ t_{4} $ = 1.57 MeV, $ t_{5} $ = 0.0005 MeV^-2.
We construct clusters using the so-called coalescence model [62, 79-83], in which particles with relative momenta smaller than $ P_{0} $ and relative distances smaller than $ R_{0} $ are considered to belong to one cluster [62, 84, 85]. Here, we set $ R_{0} $ and $ P_{0} $ as 3.5 fm and 300 MeV/c, respectively. Simulations are conducted for 5000 events with impact parameter values ranging from 0 to 7 fm [86], and the number of test particles is set as 20 for the four reactions in the results.
We first test the IBLE model for describing the mass distributions of B element in the reaction of ⁴⁰Ca+⁹Be at $ E_{in} = 140 $ MeV/nucleon, and compare the results with calculations from EPAX and data from experiment [87].
As shown in Fig. 2, the black solid and blue dashed lines represent the IBLE and EPAX parametrization results, respectively. The red circles present the experimental data, which were taken from Ref. [87]. Clearly, the measured mass distribution is reasonably reproduced by the IBLE model. The most stable nuclides ¹⁰B and ¹¹B yield the largest cross sections. For the ¹¹B nuclide, we underestimate the cross section using the IBLE model, and the difference is within one order of magnitude. However, these results are consistent with the EPAX calculations, which also underestimate the cross section of the ¹¹B nuclide. It is worth mentioning that our results indicate more neutron-deficient and neutron-rich nuclides, compared with the experimental data and EPAX parametrization results, because we simulate more events, which results in lower nuclide cross sections. Therefore, the IBLE model can be applied for calculating the cross sections and yields of fragments in projectile fragmentation reactions.
Figure2. (color online) Mass distributions of B elements in the ⁴⁰Ca+⁹Be reaction at 140 MeV/nucleon. IBLE calculations are shown as the black solid line. EPAX simulations are shown as the blue dashed line. Experimental fragmentation data are shown as red circles. The experimental data and EPAX calculations are taken from Ref. [87].

We focus on the isospin observable yield ratios of isotopic, isobaric, and isotonic pairs of fragments from different aspects. The mass-symmetric reactions including ⁵⁸Fe, ⁵⁸Ni + ⁵⁸Fe, and ⁵⁸Ni at incident energies in the 30 to 100 MeV/nucleon range are applied. We adopt the ratios of the isotopic pairs of fragments differing by one neutron, isobaric pairs of fragments differing by one proton, and isotonic pairs of fragments differing by one proton, as in Ref. [86]. The same total mass of the composite system allows us to investigate the effects of the N/Z ratio on the fragments' emission [73].
2

-->

A.Symmetry energy dependence

To determine the effect of the symmetry energy on intermediate fragments, we begin our discussion by comparing the calculated yield ratios of the isobaric pairs of fragments for different symmetry energies with available experimental data. Figure 3 shows the mass distributions of Li and Be elements in the reactions of ⁵⁸Ni+⁵⁸Ni (N/Z = 1.07) and ⁵⁸Fe+⁵⁸Fe (N/Z = 1.23), which have a larger difference in N/Z, at 30 MeV/nucleon. In the reaction of ⁵⁸Ni+⁵⁸Ni, the isotope cross sections of Li and Be for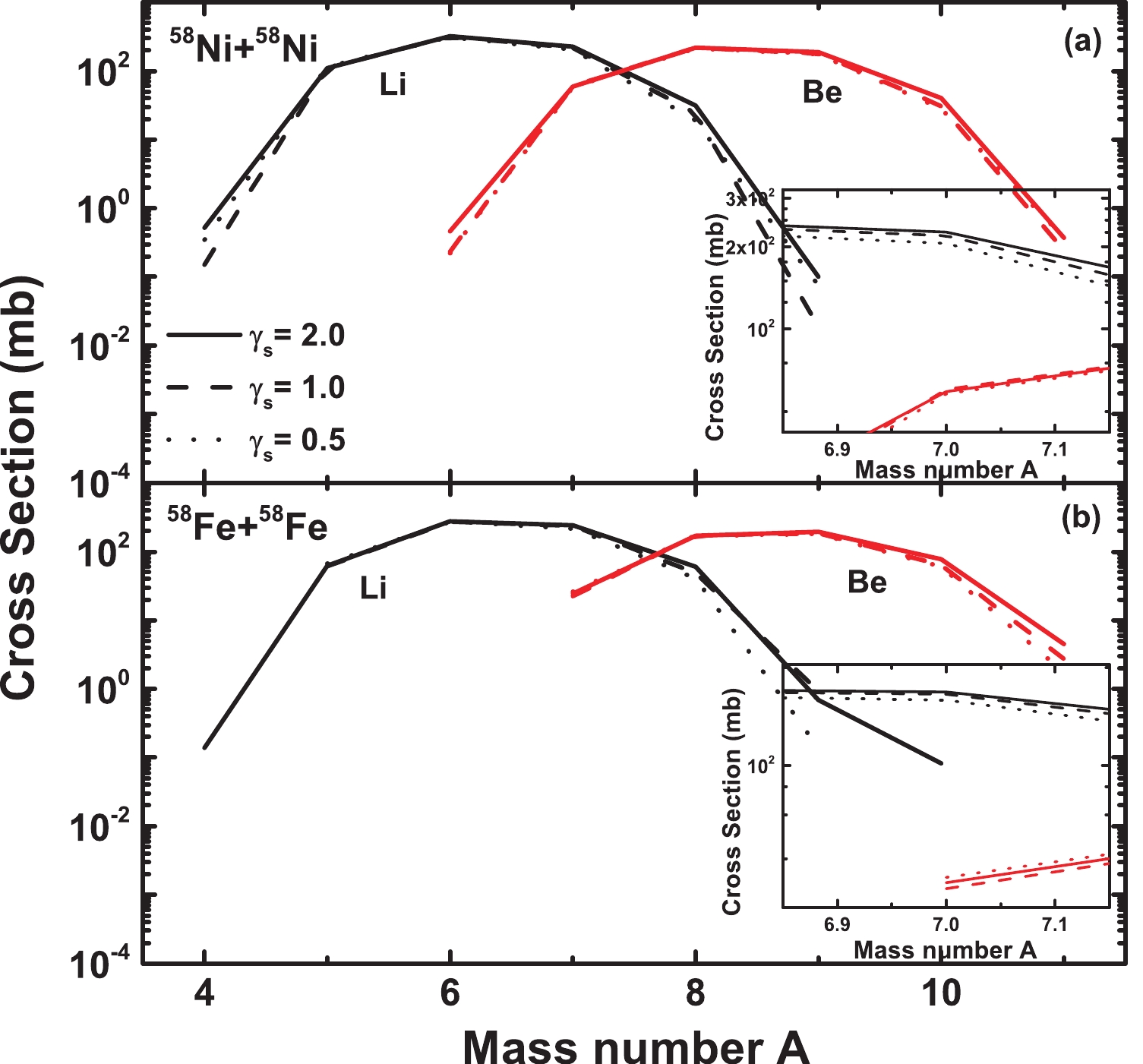 $ \gamma_{s} $ = 2.0 are wider than $ \gamma_{s} $ = 1.0 and 0.5. In the reaction of ⁵⁸Fe+⁵⁸Fe, this phenomenon is the same in the neutron-rich region, and is not obvious in the proton-rich region. The ⁵⁸Fe+⁵⁸Fe system has a higher N/Z ratio, so it is more likely to produce neutron-rich fragments. Therefore, the effect in the proton-rich region is diminished in the ⁵⁸Fe+⁵⁸Fe system. The two insets show the magnifications around A = 7, for the mirror nuclei ⁷Li and ⁷Be. The isospin effects in the neutron-rich system ⁵⁸Fe+⁵⁸Fe are more obvious, for which the cross sections of ⁷Be with different $ \gamma_{s} $ differ greatly.
Figure3. (color online) Mass distributions for Li (black lines) and Be (red lines) elements in the reactions of ⁵⁸Ni+⁵⁸Ni (N/Z = 1.07) and ⁵⁸Fe+⁵⁸Fe (N/Z = 1.23) at 30 MeV/nucleon. The two insets show the magnifications around A = 7.

Using the data in Table 2, we analyze the ratios as a function of the N/Z ratio of the composite systems, from more neutron-deficient 1.07 to more neutron-rich 1.23. Three symmetry energies are adopted, i.e., $ \gamma_{s} = 2.0 $ (hard), $ \gamma_{s} = 1.0 $ (linear), and $ \gamma_{s} = 0.5 $ (soft). Our calculations for the three sets of symmetry energy parameters using the IBLE model overestimate the measured data to the first order. However, the calculated isobaric yield ratios $Y_{\rm ^{7}Li/^{7}Be}$ with the soft symmetry energy are much closer to the experimental values. So far, no theoretical model has been able to replicate the experimental data, including QMD, GEMINI, and BUU models [86, 88]. Therefore, a relatively well-developed theoretical model for introducing isospin dependent nuclear collisions is necessary. Secondly, the ratios of the three symmetry energies in this table are functions of the N/Z ratios of the composite systems ($ (N/Z)_{cs} $). This shows the isospin dependence exactly, i.e., the higher N/Z ratio of the composite system, the higher N/Z ratio of the reaction products, and the higher the yield of the neutron-rich fragments.

system	$(N/Z)_{cs}$	Ycal			Yexp [86]
		$\gamma_{s} = 2.0$	$\gamma_{s} = 1.0$	$\gamma_{s} = 0.5$
58Ni+58Ni	1.07	3.814	3.632	3.535	2.992
58Ni+58Fe	1.15	6.310	5.271	5.342	4.016
58Fe+58Ni	1.15	6.330	5.583	5.169	4.272
58Fe+58Fe	1.23	9.997	9.461	8.488	5.744

Table2.Yield ratios of the isobaric pair of fragments $Y_{\rm ^{7}Li/^{7}Be}$ for the four reactions with different N/Z ratios of the composite systems($(N/Z)_{cs}$), using the three sets of symmetry energy parameters at 30 MeV/nucleon, compared with the experimental data.

The dependence of the yield ratio on the symmetry energy is obvious for the isobaric pair of fragments. In general, the distributions of the three symmetry energies are approximately the same. Stiffer symmetry energy leads to higher yield ratios for the isobaric pair of fragments. This phenomenon becomes more apparent in more neutron-rich systems, such as the ⁵⁸Fe+⁵⁸Fe reaction. At subnormal densities, as shown in Fig. 1, smaller $ \gamma_{s} $ yields higher symmetry energies. Thus, there is a small symmetry energy of $ \gamma_{s} = 2.0 $, and the proportion of the Coulomb energy dominates the interaction potential. The repulsive Coulomb force can enhance the protons' emission, increasing the neutron abundance of the fragments. In contrast, the symmetry energy can attract protons in neutron-rich systems, decreasing the neutron abundance of the fragments [53]. Different yield ratios of the ⁵⁸Fe+⁵⁸Ni and ⁵⁸Ni+⁵⁸Fe reactions indicate that the isospin degree of freedom is not completely equilibrated. There must be some memory of the entrance channel, and the emission fragments are affected by both the projectile and target nuclei [33, 86]. Overall, the strong dependence of the calculated yield ratio on the symmetry energy illustrates the importance of the isospin degree of freedom in projectile fragmentation, and the isospin effect is stronger for soft symmetry energies [10, 53].
2 -->

B.Incident energy dependence

We analyze the energy effect on the yield ratios of the isotopic, isobaric, and isotonic pairs of fragments, for different symmetry energies. Previous studies have shown that there is a transition from the isospin equilibrium at low energies to translucency at intermediate energies. This means that the isotopic, isobaric, and isotonic compositions of fragments will strongly depend on the N/Z ratios of the projectile and target but not much on the (N/Z)_cs ratio of the composite system in the entrance channel [22, 33, 34, 50, 88-90]. We perform simulations for the four reactions at 30, 50, 70, and 100 MeV/nucleon from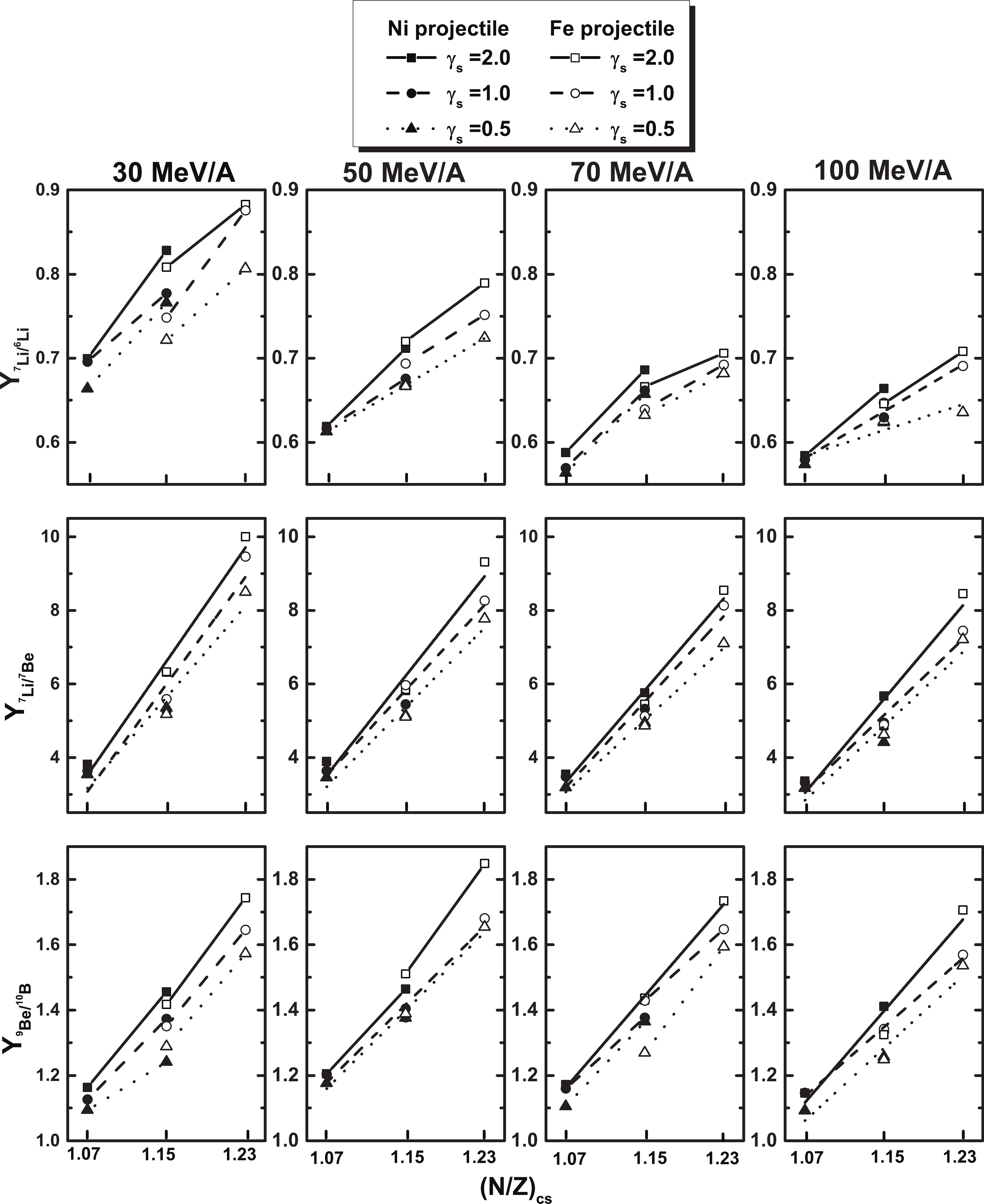 $ b = 0 $ to 7 fm. In addition, we compare two reaction systems with the largest isospin differences: ⁵⁸Fe+⁵⁸Fe and ⁵⁸Ni+⁵⁸Ni, with (N/Z)_cs = 1.23 and 1.07. The results are shown in Fig. 4 to Fig. 6.
Figure4. Yield ratios of isotopic (upper row), isobaric (middle row), and isotonic (lower row) pairs of fragments from the four reactions at 30, 50, 70, and 100 MeV/nucleon, plotted as a function of the N/Z ratio of the composite system in the entrance channel. The four reactions are the same as in Table 2.

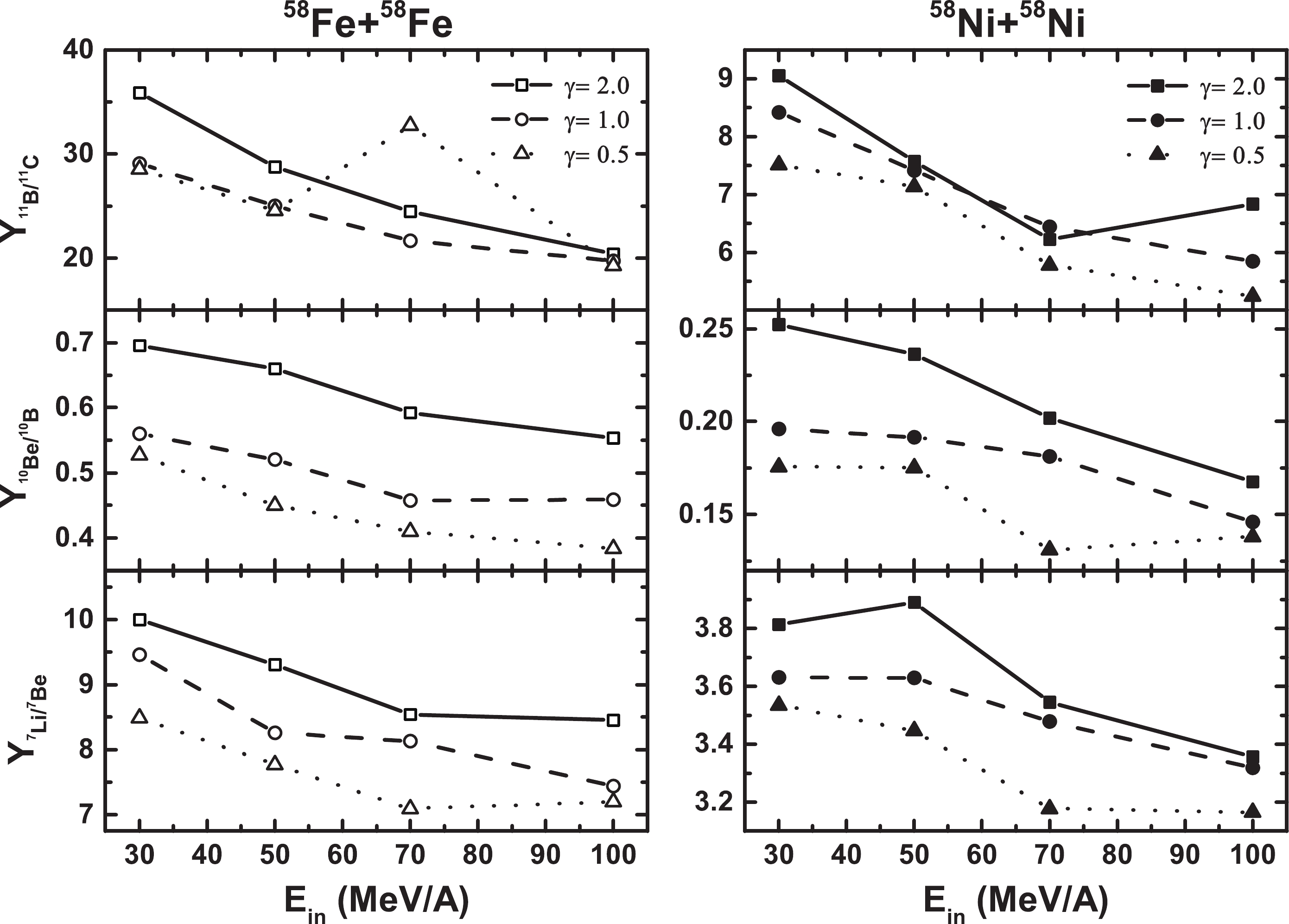Figure6. The same as Fig. 5 but for the isobaric pair of fragments.

From Fig. 4, it is obvious that as the energy increases, the isotopic (upper row), isobaric (middle row), and isotonic (lower row) yield ratios decrease, especially the isotopic and isobaric yield ratios. The descending trend is more moderate for higher incident energies, resulting in the closer yield ratios for the three symmetry energies at higher incident energies. This phenomenon indicates the weakening of the isospin effect with increasing energy, as nucleon-nucleon collisions become dominant at high energies. The yield ratios are functions of the N/Z ratio of the composite system in the entrance channel, but they do not all fall on a single line, as in Ref. [86]. As for the yield ratios of the isobaric pair of fragments, we report linear fits to these ratios because the symbols are too close to obtain the split. These results do not agree with previous data [88], where a split at an incident energy of 45 MeV/nucleon was reported experimentally, but none of the theoretical calculations reproduced the split. For the yield ratios of the isotopic and isotonic pairs of fragments, we observed some splits with three parameters of symmetry energies. The ratios for the reactions of Ni as a projectile do not overlap with that of Fe as a projectile, especially the ratios for the ⁵⁸Fe+⁵⁸Ni and ⁵⁸Ni+⁵⁸Fe reactions, which have the same N/Z ratios of the composite systems. These illustrate that intermediate mass fragment emissions depend not only on composite systems but also on the projectile and target nuclei. Moreover, the isospin degree of freedom does not reach equilibrium even at lower energies, which may be owing to the onset of nuclear transparency [89]. It is worth mentioning that this phenomenon of isospin nonequilibrium has also been discussed in Ref. [50].
Figures 5 and 6 present the yield ratios of the isotopic (Fig. 5) and isobaric (Fig. 6) pairs of fragments for the ⁵⁸Fe+⁵⁸Fe and ⁵⁸Ni+⁵⁸Ni reactions, plotted as a function of the incident energies in the 30 to 100 MeV/nucleon range. The yield ratios for the Ni+Ni reaction are lower than that for the Fe+Fe reaction, as the N/Z ratio of the composite system for the Fe+Fe reaction is relatively larger. This indicates that fragments are more neutron-rich in neutron-rich reaction systems. As the incident energy increases, the general trend of the yield ratio is to decrease but not sequentially. This phenomenon may be owing to the fact that the energy effect weakens for incident energies above 100 MeV/nucleon. It is worth noting that the yields of intermediate mass fragments in the projectile fragmentation change little for incident energies above 100 MeV/nucleon [87].
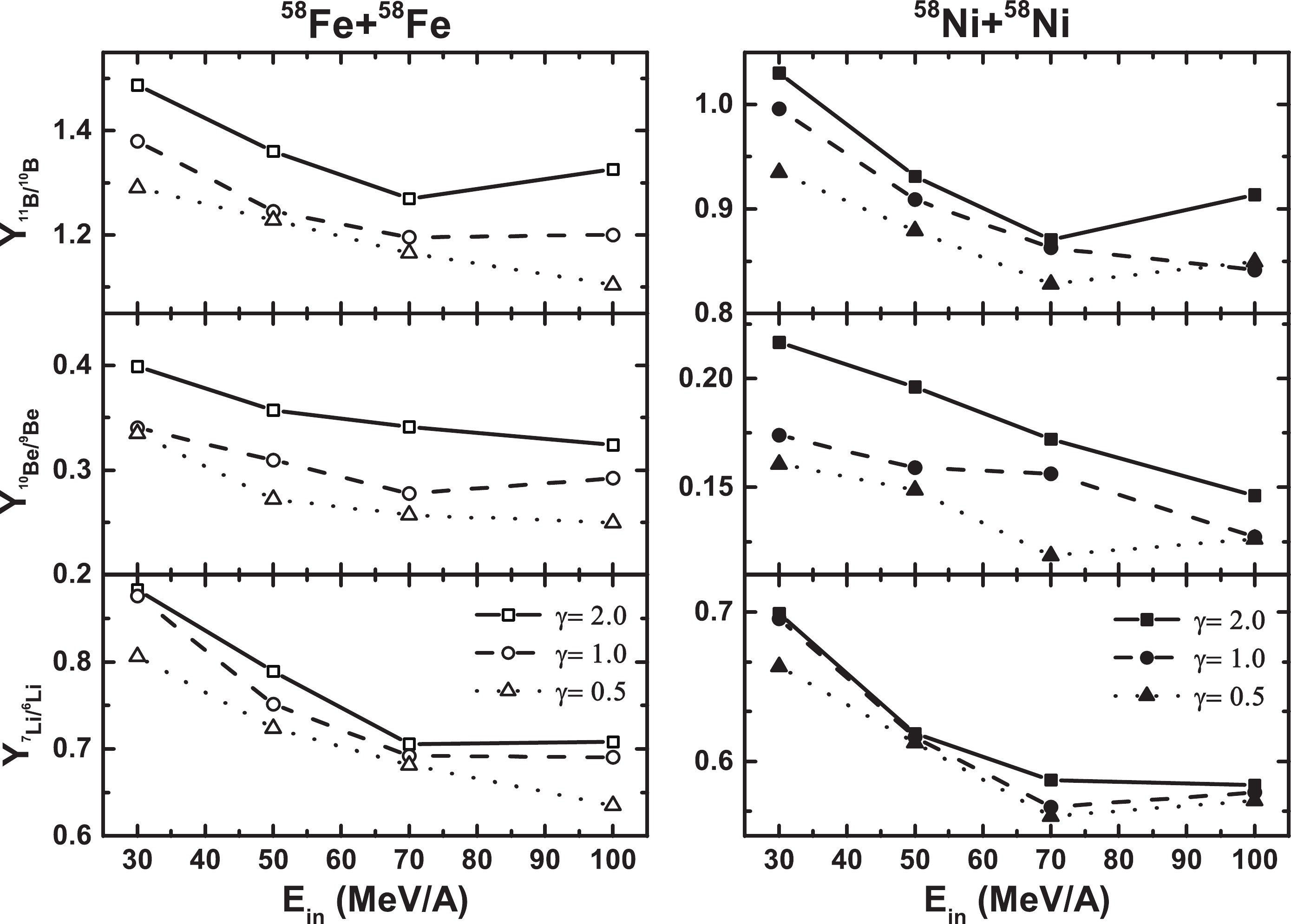Figure5. Yield ratios for the isotopic pair of fragments, for the ⁵⁸Fe+⁵⁸Fe and ⁵⁸Ni+⁵⁸Ni reactions, plotted as a function of the incident energy in the 30 to 100 MeV/nucleon range.

In addition, in Fig. 5, the ratios of the isotopic pair of fragments for the symmetry energy parameter $ \gamma_{s} = 2.0 $ are higher than that for $ \gamma_{s} = 1.0 $, and they are both higher than that for $ \gamma_{s} = 0.5 $. This phenomenon is the same as in Table 2 and Fig. 4 and mainly arises owing to the competition between the repulsive Coulomb force and the symmetry energy attractive force on the proton. In Fig. 6, the isobaric yield ratios of ¹¹B/¹¹C for the Fe+Fe reaction at 70 MeV/A with $ \gamma_{s} = 0.5 $ are higher than that for $ \gamma_{s} = 2.0 $, while the isobaric yield ratios of ¹¹B/¹¹C for the Ni+Ni reaction at 70 MeV/nucleon with $ \gamma_{s} = 2.0 $ are higher than that for $ \gamma_{s} = 1.0 $. Comparing the isobaric yield ratio of ¹¹B/¹¹C with the isotopic yield ratio of ¹¹B/¹⁰B, we conclude that the yield of the unstable nuclide ¹¹C increases for $ \gamma_{s} = 2.0 $ and decreases for $ \gamma_{s} = 0.5 $. It is clear that the indicated value must not be considered as an absolute estimate, but it shows only a trend toward different behaviors of the symmetry energy.

In this paper, the mass distribution of the intermediate mass fragment B in the ⁴⁰Ca+⁹Be projectile fragmentation reaction at E_in = 140 MeV/nucleon was simulated using the IBLE model. The results agreed fairly well with the experimental data, demonstrating that the IBLE model is adequate for describing projectile fragmentation at intermediate energies. The intermediate mass fragment productions from the mass-symmetric reactions including ⁵⁸Fe, ⁵⁸Ni + ⁵⁸Fe, and ⁵⁸Ni at energies in the 30 to 100 MeV/nucleon range were studied, and the dependence of the isospin observable yield ratios on the symmetry energies and incident energies was analyzed. It was found that the yield ratios of the isobaric pair of fragments $Y_{\rm ^{7}Li/^{7}Be}$ with the soft symmetry energy of $ \gamma_{s} $ = 0.5 were closer to the experimental data. The yield ratios were extremely sensitive to the symmetry energy, caused by the competition of the Coulomb force and the symmetry energy force. The repulsive Coulomb force and the symmetry energy attractive force on the proton reduced the ratios for the symmetry energy parameter $ \gamma_{s} = 0.5 $. The isospin effect was more evident for the soft symmetry energy. The yield ratios for the three symmetry energies decreased with increasing incident energies. The splits were firstly presented for isotopic and isotonic pairs of fragments using the IBLE model framework, which denote the transition from isospin equilibrium at low energy to translucency at intermediate energies. As the incident energy increased, the isospin degree of freedom reached equilibrium posterior to the timescale of intermediate mass fragment productions. Therefore, intermediate mass fragments depend on not only the composite system in the entrance channel but also the projectile and target nuclei. The isospin effect was more pronounced in the neutron-rich system ⁵⁸Fe+⁵⁸Fe, in which the results obtained for the three symmetry energies were relatively different. These results may be helpful for studying nuclear interactions in the dynamics of projectile fragmentation. The isospin effects in projectile fragmentation and effective isospin observables need to be studied more extensively.