HTML
--> --> -->In the present work we focus on tetraquarks composed of a single flavor, charm quarks only, using a diquark-antidiquark picture
The first work on the all-charm tetraquark was published in 1975 by Iwasaki [14]. In a subsequent paper Chao studied the T4c in the diquark-antidiquark picture with orbital excitations, and its production in e+e- annihilation [15], including an interesting analysis of the possible decay channels. Later, in the eighties and nineties, several works with different approaches addressed the question of the existence of this
On the experimental side, recent measurements of J/ψ pair production are very promising and might be the ideal starting point to search for the all-charm tetraquark. They have been studied at the LHC, by the LHCb [32, 33], CMS [34] and ATLAS [35] collaborations. Double
Most of the predictions for the T4c mass lead to values around 6 GeV, and therefore lie well above the experimentally known range for charmonium (which is concentrated within 3 - 4.5 GeV). This energy gap makes the all-charm tetraquark a special object in the sector of exotic multiquarks. The most discussed tetraquark candidates (the X, Y, Z states) are in the same mass range as conventional charmonium states and this can lead to confusion.
The absence of light quarks in the T4c makes it unlikely to be a meson-meson molecule, since it is not easy to describe this binding in terms of pion exchange or light vector meson exchange. If it exists, the T4c is bound by QCD forces and studying its spectrum will lead to a more complete understanding of QCD interactions. If it does not exist we have to understand why.
We will describe the T4c as a two-body non-relativistic system, made of a cc diquark and a
Why do we choose the Cornell model? We choose it because it is able to capture the essential aspects of the heavy quark-antiquark interactions. It has almost never been too wrong and when it was, there was something really new happening. Moreover, the quark-antiquark potential can be continuously improved [37] and its parameters can be adjusted so as to incorporate the most recent experimental information on the charmonium spectrum. Finally, we will study systems with angular momentum and all kinds of spin interactions. With more constituents, we may form systems with higher spin and total angular momentum. With the Cornell model (unlike in some other approaches) we can identify the individual contribution of each one of these interactions.
We choose to work with diquarks, not only because they simplify the calculations, but also because there is some evidence of diquark clustering in baryons. In the case of heavy diquarks the interaction has a stronger short distance component, in which the perturbative one-gluon exchange may be attractive. In particular, the cc diquark became more interesting after the prediction of the Tcc [38] and even more so after the very recent discovery of the baryon
In the literature we find some calculations which are very simple and strongly based on the existing empirical information, as in Ref. [30], and some which are very sophisticated, such as the lattice calculations of Ref. [25] or the QCD sum rules calculations of [28]. Our model is at an intermediate level, being more precise than the estimates made in Ref. [30] and more transparent than the results found in Refs. [25, 28], where it is very difficult to access the role of spin interactions. Ideally, all these approaches should converge and the origin of the remaining discrepancies should be well understood. At the end of this work we will present a comparison with the results obtained in other approaches.
| $\begin{eqnarray}{V}_{C+L}^{(0)}={V}_{V}+{V}_{S}\Rightarrow {V}^{(0)}(r)={\kappa }_{s}\displaystyle \frac{{\alpha }_{s}}{r}+br,\end{eqnarray}$ | (1) |
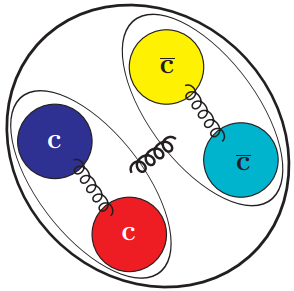Figure1. (color online) Pictorial representation of the all-charm tetraquark in the diquark-antiquark scheme.where κs, sometimes called the "color factor", is related to the color configuration of the system (it can be negative or positive), αs is the QCD fine structure constant and b, sometimes called "string tension", is related to the strength of the confinement. One could also add a constant term, which would act as a zero-point energy.
Usually, in heavy quark bound states the kinetic energy of the constituents is small compared to their rest energy, hence a non-relativistic approach with static potentials can be a reasonable approximation. In two-body problems involving a central potential, it is convenient to work in the center-of-mass frame (CM), where one can use spherical coordinates to separate the radial and angular parts of the wavefunction, and the kinetic energy is written in terms of the reduced mass μ = (m1 m2)/(m1 + m2). We start with the time-independent Schr?dinger equation:
| $\begin{eqnarray}\left[\displaystyle \frac{1}{2\mu }\left(-\displaystyle \frac{{{\rm{d}}}^{{\rm{2}}}}{{\rm{d}}{r}^{2}}+\displaystyle \frac{\ell (\ell +1)}{{r}^{2}}\right)+{V}^{(0)}(r)\right]\;y(r)=Ey(r).\end{eqnarray}$ | (2) |
| $\begin{eqnarray}{V}_{{\rm{SS}}}={C}_{{\rm{SS}}}(r)\;{{\boldsymbol{S}}}_{1}\cdot {{\boldsymbol{S}}}_{2},\end{eqnarray}$ | (3) |
| $\begin{eqnarray}{V}_{{\rm{LS}}}={C}_{{\rm{LS}}}(r){\boldsymbol{L}}\cdot {\boldsymbol{S}},\end{eqnarray}$ | (4) |
| $\begin{eqnarray}{V}_{{\rm{T}}}={C}_{{\rm{T}}}(r)\left(\displaystyle \frac{({{\boldsymbol{S}}}_{1}\cdot {\boldsymbol{r}})({{\boldsymbol{S}}}_{2}\cdot {\boldsymbol{r}})}{{{\boldsymbol{r}}}^{2}}-\displaystyle \frac{1}{3}({{\boldsymbol{S}}}_{1}\cdot {{\boldsymbol{S}}}_{2})\right),\end{eqnarray}$ | (5) |
| $\begin{eqnarray}{C}_{{\rm{SS}}}(r)=\displaystyle \frac{2}{3{m}^{2}}{\nabla }^{2}{V}_{V}(r)=-\displaystyle \frac{8{\kappa }_{s}{\alpha }_{s}\pi }{3{m}^{2}}{\delta }^{3}(r),\end{eqnarray}$ | (6) |
| $\begin{eqnarray}{C}_{{\rm{LS}}}(r)=\displaystyle \frac{1}{2{m}^{2}}\displaystyle \frac{1}{r}\left[3\displaystyle \frac{d{V}_{V}(r)}{dr}-\displaystyle \frac{{\rm{d}}{V}_{S}(r)}{{\rm{d}}r}\right]\\=-\displaystyle \frac{3{\kappa }_{s}{\alpha }_{s}}{2{m}^{2}}\displaystyle \frac{1}{{r}^{3}}-\displaystyle \frac{b}{2{m}^{2}}\displaystyle \frac{1}{r},\end{eqnarray}$ | (7) |
| $\begin{eqnarray}{C}_{{\rm{T}}}(r)=\displaystyle \frac{1}{{m}^{2}}\left[\displaystyle \frac{1}{r}\displaystyle \frac{{\rm{d}}{V}_{V}(r)}{{\rm{d}}r}-\displaystyle \frac{{{\rm{d}}}^{2}{V}_{V}(r)}{{\rm{d}}{r}^{2}}\right]=-\displaystyle \frac{12{\kappa }_{s}{\alpha }_{s}}{4{m}^{2}}\displaystyle \frac{1}{{r}^{3}},\end{eqnarray}$ | (8) |
These spin-dependent terms are proportional to 1/m2, which justifies their treatment as first-order perturbation corrections in heavy quark bound states. The expectation value of their radial-dependent coefficients can be calculated using the wavefunction obtained with the solution of the Schr?dinger equation.
This framework appears frequently in quarkonium spectroscopy, but a better agreement between predicted states and the experimental data for
| $\begin{eqnarray}{V}_{{\rm{SS}}}^{(0)}=-\displaystyle \frac{8\pi {\kappa }_{s}{\alpha }_{s}}{3{m}^{2}}{\left(\displaystyle \frac{\sigma }{\sqrt{\pi }}\right)}^{3}{{\rm{e}}}^{-{\sigma }^{2}{r}^{2}}{{\boldsymbol{S}}}_{1}\cdot {{\boldsymbol{S}}}_{2}.\end{eqnarray}$ | (9) |
The expectation value of the operator of the spin-orbit interaction can be calculated in terms of the quantum numbers of total angular momentum J (defined by the vector sum: J = L + S), total spin S, and orbital angular momentum
The tensor interaction demands a bit of algebra. For convenience, we redefine the tensor operator with an extra factor 12, which we remove from its radial coefficient in Eq. (8):
| $\begin{eqnarray}\begin{array}{ll}{{\boldsymbol{S}}}_{12}&\equiv 12\left(\displaystyle \frac{({{\boldsymbol{S}}}_{1}\cdot {\boldsymbol{r}})({{\boldsymbol{S}}}_{2}\cdot {\boldsymbol{r}})}{{{\boldsymbol{r}}}^{2}}-\displaystyle \frac{1}{3}({{\boldsymbol{S}}}_{1}\cdot {{\boldsymbol{S}}}_{2})\right)\\ &=4[3({{\boldsymbol{S}}}_{1}\cdot \hat{r})({{\boldsymbol{S}}}_{2}\cdot \hat{r})-{{\boldsymbol{S}}}_{1}\cdot {{\boldsymbol{S}}}_{2}].\end{array}\end{eqnarray}$ | (10) |
| $\begin{eqnarray}\begin{array}{ll}&1)\;\;\;\;\ell \ne 0\;\;\;\;{\rm{and}}\;\;\;\;S=1\;\;({\rm{triplet}}),\\ &2)\;\;\;\;J=\ell,\;\;{\rm{or}}\;\;J=\ell -1,\;\;\;\;{\rm{or}}\;\;\;\;J=\ell +1.\end{array}\end{eqnarray}$ | (11) |
| $\begin{eqnarray}{\langle {{\boldsymbol{S}}}{_{12}\rangle }_{\displaystyle \frac{1}{2}\otimes \displaystyle \frac{1}{2}\to S=1,\ell \ne 0}}=\left\{\begin{array}{cl}-\displaystyle \frac{2\ell }{(2\ell +3)},&{\rm{if}}&\;J=\ell +1,\\ +2,&{\rm{if}}&\;J=\ell,\\ -\displaystyle \frac{2(\ell +1)}{(2\ell -1)},&{\rm{if}}&\;J=\ell -1,\end{array}\right.\end{eqnarray}$ | (12) |
Notice that in order to obtain these three general cases of non-vanishing diagonal matrix elements of the tensor operator for two spin 1/2 particles in Eq. (12), it is necessary to make use of a few relations that are valid only for Pauli matrices [48, 49], like its eigenvalues and the anticommutation relation. Therefore, we cannot use this result in the diquark-antidiquark tensor interaction (if we wish to treat it as a two-body problem), since the diquarks can have spin 0 or 1. This issue will be discussed later when we address the tetraquark interaction.
Regarding the wavefunction, we will consider only pure states where
Solving the eigenvalue equation (2), one can obtain the interaction energy E and the wavefunction y(r) of the two-body system under consideration, where both depend on the number of nodes of the wavefunction n (or principal quantum number N = n + 1), on the orbital angular momentum number
An interesting quantity that can be used to check the validity of the non-relativistic approximation is the velocity of the constituents in each of the systems in consideration: the quark velocity inside the meson or the diquark velocity inside the tetraquark. As discussed in Ref. [53], the mean square velocity can be obtained from the kinetic energy, which can be calculated directly from the Hamiltonian, or using the virial theorem:
| $\begin{eqnarray}\begin{array}{lll}&\langle {{\boldsymbol{v}}}^{2}\rangle =\displaystyle \frac{1}{2\mu }(E-\langle {V}^{(0)}(r)\rangle );&\langle {{\boldsymbol{v}}}^{2}\rangle =\displaystyle \frac{1}{4\mu }\langle r\displaystyle \frac{{\rm{d}}}{{\rm{d}}r}{V}^{(0)}(r)\rangle,\end{array}\end{eqnarray}$ | (13) |
| $\begin{eqnarray}\mu =\displaystyle \frac{{m}_{1}{m}_{2}}{{m}_{1}+{m}_{2}}=\displaystyle \frac{m}{2},\;\;{\rm{for}}\;\;{m}_{1}={m}_{2}.\end{eqnarray}$ | (14) |
One interesting aspect of the non-relativistic approach is that, even though the charmonium system is not completely non-relativistic, a surprisingly good reproduction of its mass spectrum can be obtained. As discussed in Ref. [54], where a charmonium model is developed with completely relativistic energy and also with non-relativistic kinetic energy, good agreement with the experimental data can be obtained with both methods, just by using a different set of parameters in the effective potential employed.
The value of the square modulus of the wavefunction at the origin, |Ψ(0)|2, is an important quantity. If the spin-spin interaction was treated as a first-order perturbation without the Gaussian smearing, it would be proportional to |Ψ(0)|2 because of the Dirac delta. Decay widths can also be calculated using the wavefunction or its derivative at the origin. Only S-wave states (
| $\begin{eqnarray}|\Psi (0){|}^{2}=|{Y}_{0}^{0}(\theta,\phi ){R}_{n,\ell }(0){|}^{2}=\displaystyle \frac{|{R}_{n,\ell }(0){|}^{2}}{4\pi },\;\;{\rm{for}}\;\;\ell =0.\end{eqnarray}$ | (15) |
| $\begin{eqnarray}|Ψ (0){|}^{2}=\displaystyle \frac{\mu }{2\pi }\;\left\langle \displaystyle \frac{{\rm{d}}}{{\rm{d}}r}{V}^{(0)}(r)\right\rangle \Rightarrow |R(0){|}^{2}=2\mu \;\left\langle \displaystyle \frac{{\rm{d}}}{{\rm{d}}r}{V}^{(0)}(r)\right\rangle .\end{eqnarray}$ | (16) |
In more sophisticated quarkonium models, such as the relativized potential model of Ref. [44], the coupling constant αs is considered as a "running" parameter, that changes according to the energy scale of each bound state. However, we have chosen to adopt the non-relativistic model of Ref. [47], where αs is as a constant in the potential, which is also a common approach in many charmonium models.
The values of αs, the charm quark mass mc, the string tension b, and the Gaussian parameter σ, will be obtained from a fit of the charmonium experimental data, and once the best set is found, they are kept fixed to generate the whole mass spectrum.
2
2.1.Charmonium
In order to get good estimates for diquarks and tetraquarks, we first study the spectrum of charmonium. In this case, the color factor κs in Eq. (1) should be that of a color singlet state, since forAfter having solved the Schr?dinger equation, the mass of a particular state will be given by:
| $\begin{eqnarray}M(c\bar{c})=2{m}_{c}+{E}_{c\bar{c}}+{\langle {V}_{{\rm{Spin}}}^{(1)}\rangle }_{c\bar{c}}.\end{eqnarray}$ | (17) |
| $\begin{eqnarray}{\chi }^{2}=\displaystyle \sum _{i}^{n}{({M}_{i}^{{\rm{calc}}}-{M}_{i}^{\exp })}^{2}\cdot {w}_{i}.\end{eqnarray}$ | (18) |
2
2.2.Diquarks
In the study of tetraquarks, we shall treat the full four-body problem as three two-body problems. Repeating the steps described in the previous subsection, we first compute the mass spectrum of the diquark, then we do the same for the antidiquark and finally we solve the Schr?dinger equation once again for a two-body system composed of the diquark and antidiquark. The inspiration for this factorization is the color structure behind it.A diquark is a cluster of two quarks which can form a bound state. This binding is caused by one-gluon exchange between the quarks. In this interaction the factor κs can be negative, then the short distance part (∝ 1/r) of the potential will be attractive. The SU(3) color symmetry of QCD implies that, when we combine two quarks in the fundamental (3) representation, we obtain:
Notice that going from the color factor -4/3 (for quark-antiquark in the singlet color state) to the color factor -2/3 (for quark-quark in the antitriplet color state) is equivalent to introducing a factor 1/2, which one would expect to be a global factor since it comes from the color structure of the wavefunction. Because of that, it is very common to extend this factor 1/2 to the whole potential describing the quark-quark interaction. This rule is motivated by the interactions inside baryons, where two quarks can also be considered to form a color-antitriplet diquark, which can then interact with the third quark and form a color-singlet baryon. Since this seems to give satisfactory results in baryon spectroscopy, it has also been extended to diquarks inside tetraquarks. The general rule would be simply
The calculation of the total mass of the diquark is completely analogous to the
2
2.3.Tetraquarks
The all-charm tetraquark will be treated as a two-body (cc -| $\begin{eqnarray}M({T}_{4c})={m}_{cc}+{m}_{\bar{c}\bar{c}}+{E}_{[cc][\bar{c}\bar{c}]}+{\langle {V}_{{\rm{Spin}}}^{(1)}\rangle }_{[cc][\bar{c}\bar{c}]}.\end{eqnarray}$ | (19) |
For the spin-spin and spin-orbit corrections, we can obtain the angular factors from the spin, orbital and total angular momentum quantum numbers. However, for the tensor correction we only have a general result (in terms of eigenvalues) for the interaction between two spin 1/2 particles, shown in Eq. (12). Then, for a proper treatment of the tensor interaction in the diquark-antidiquark system we will explicitly apply the tensor operator on the angular part of the tetraquark wavefunction, as we will describe below.
Let us focus on the spatial and spin components of the wavefunction. We factorize the radial wavefunction from the angular one that combines orbital angular momentum and spin, which are coupled using Clebsh-Gordan coefficients. We will use the indices 1 and 2 for the two quarks inside the diquark, and 3 and 4 for the two antiquarks inside the antidiquark (see Fig. 2).
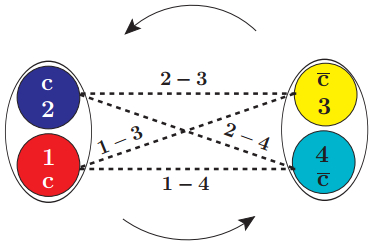Figure2. (color online) Pictorial representation of the tensor interaction between diquark and antidiquark. The arrows represent the orbital angular momentum.To illustrate our procedure to treat tensor interactions, we present one specific example with total spin ST = 2, LT = 1 and JT = 2. Sd and
| $\begin{eqnarray}\begin{array}{l} [({S}_{d}=1)\otimes ({S}_{\bar{d}}=1)\to ({S}_{{\rm{T}}}=2)]\otimes ({L}_{{\rm{T}}}=1)\to |{J}_{{\rm{T}}},{M}_{{J}_{{\rm{T}}}}\rangle \\=|2,2{\rangle }_{{J}_{{\rm{T}}}} =\sqrt{\displaystyle \frac{2}{3}}|2,2{\rangle }_{{S}_{{\rm{T}}}}\otimes |1,0{\rangle }_{{L}_{{\rm{T}}}}-\displaystyle \frac{1}{\sqrt{3}}|2,1{\rangle }_{{S}_{{\rm{T}}}}\otimes |1,1{\rangle }_{{L}_{{\rm{T}}}}\\ =\sqrt{\displaystyle \frac{2}{3}}|1,1{\rangle }_{12}\otimes |1,1{\rangle }_{34}{Y}_{1}^{0}(\theta,\varphi )-\displaystyle \frac{1}{\sqrt{3}}(\displaystyle \frac{1}{\sqrt{2}}|1,1{\rangle }_{12}\otimes |1,0{\rangle }_{34}+\displaystyle \frac{1}{\sqrt{2}}|1,0{\rangle }_{12}\otimes |1,1{\rangle }_{34}){Y}_{1}^{1}(\theta,\varphi )\\ =\sqrt{\displaystyle \frac{2}{3}}(|\uparrow \uparrow {\rangle }_{12}\otimes |\uparrow \uparrow {\rangle }_{34}){Y}_{1}^{0}(\theta,\varphi )-\displaystyle \frac{1}{\sqrt{3}}(\displaystyle \frac{1}{\sqrt{2}}|\uparrow \uparrow {\rangle }_{12}\otimes |\displaystyle \frac{\uparrow \downarrow +\downarrow \uparrow }{\sqrt{2}}{\rangle }_{34}+\displaystyle \frac{1}{\sqrt{2}}|\displaystyle \frac{\uparrow \downarrow +\downarrow \uparrow }{\sqrt{2}}{\rangle }_{12}\otimes |\uparrow \uparrow {\rangle }_{34}){Y}_{1}^{1}(\theta,\varphi )\\ =\sqrt{\displaystyle \frac{2}{3}}(\uparrow \uparrow \uparrow \uparrow ){Y}_{1}^{0}(\theta,\varphi )-\displaystyle \frac{1}{\sqrt{3}}(\displaystyle \frac{1}{2}(\uparrow \uparrow \uparrow \downarrow +\uparrow \uparrow \downarrow \uparrow +\uparrow \downarrow \uparrow \uparrow +\downarrow \uparrow \uparrow \uparrow )){Y}_{1}^{1}(\theta,\varphi ).\end{array}\end{eqnarray}$ | (20) |
We now explicitly apply the tensor operator on the above angular wavefunction and we note that within our approximations, it is equivalent to apply this operator directly on the diquark-antidiquark pair (in spin 1 basis) or consider a sum of four tensor interactions between each quark-antiquark pair (spin 1/2 basis) as illustrated in Fig. 2, as would be expected from the angular momentum algebra1). We have:
| $\begin{eqnarray}\begin{array}{ll}{{\boldsymbol{S}}}_{d-\bar{d}}&=12\left(\displaystyle \frac{({{\boldsymbol{S}}}_{d}\cdot {\boldsymbol{r}})({{\boldsymbol{S}}}_{\bar{d}}\cdot {\boldsymbol{r}})}{{{\boldsymbol{r}}}^{2}}-\displaystyle \frac{1}{3}({{\boldsymbol{S}}}_{d}\cdot {{\boldsymbol{S}}}_{\bar{d}})\right)\\ &={{\boldsymbol{S}}}_{14}+{{\boldsymbol{S}}}_{13}+{{\boldsymbol{S}}}_{24}+{{\boldsymbol{S}}}_{23}.\end{array}\end{eqnarray}$ | (21) |
Since the tetraquark is treated as a two-body system, the expectation value of the radial wavefunction between every
In order to deal with the generalization of the tensor interaction to the tetraquark case, we will rewrite the tensor in a form that allows us to recover the same results that we already know for the particular case of two spin 1/2 particles and that can also be used as a generalization to other cases, such as the interaction between two spin 1 diquarks. The operator S12 in Eq. (10) is a "rank-2" tensor which can be written in terms of spin operators and spherical harmonics, as shown in textbooks [63]. An extensive discussion of this approach can be found in Ref. [49].
The following functional form does not use any particular relation or eigenvalues for spin 1/2 particles, only general properties of angular momentum elementary theory. One can write the unity vector
| $\begin{eqnarray}{{\boldsymbol{S}}}_{12}=4[{T}_{0}+{T}_{{0}^{\prime}}+{T}_{1}+{T}_{-1}+{T}_{2}+{T}_{-2}]\end{eqnarray}$ | (22) |
| $\begin{eqnarray}\begin{array}{ll}{T}_{0}=&2\sqrt{\displaystyle \frac{4\pi }{5}}{Y}_{2}^{0}(\theta,\phi ){S}_{1z}{S}_{2z},\\ {T}_{{0}^{\prime}}=&-\displaystyle \frac{1}{4}2\sqrt{\displaystyle \frac{4\pi }{5}}{Y}_{2}^{0}(\theta,\phi )({S}_{1+}{S}_{2-}+{S}_{1-}{S}_{2+}),\\ {T}_{1}=&\displaystyle \frac{3}{2}\sqrt{\displaystyle \frac{8\pi }{15}}{Y}_{2}^{-1}(\theta,\phi )({S}_{1z}{S}_{2+}+{S}_{1+}{S}_{2z}),\\ {T}_{-1}=&-\displaystyle \frac{3}{2}\sqrt{\displaystyle \frac{8\pi }{15}}{Y}_{2}^{1}(\theta,\phi )({S}_{1z}{S}_{2-}+{S}_{1-}{S}_{2z}),\\ {T}_{2}=&3\sqrt{\displaystyle \frac{2\pi }{15}}{Y}_{2}^{-2}(\theta,\phi ){S}_{1+}{S}_{2+},\\ {T}_{-2}=&3\sqrt{\displaystyle \frac{2\pi }{15}}{Y}_{2}^{2}(\theta,\phi ){S}_{1-}{S}_{2-}.\end{array}\end{eqnarray}$ | (23) |
To close this subsection, we discuss the tetraquark quantum numbers, as in Refs. [64, 65]. We can use the diquark-antidiquark basis to label the possible quantum numbers JPC of the tetraquark. We shall use the following notation:
| $\begin{eqnarray}|{T}_{4Q}\rangle =|{S}_{d},{S}_{\bar{d}},{S}_{{\rm{T}}},{L}_{{\rm{T}}}{\rangle }_{{J}_{{\rm{T}}}},\end{eqnarray}$ | (24) |
| $\begin{eqnarray}\begin{array}{ll}{C}_{{\rm{T}}}&={(-1)}^{{L}_{{\rm{T}}}+{S}_{{\rm{T}}}},\\ {P}_{{\rm{T}}}&={(-1)}^{{L}_{{\rm{T}}}}.\end{array}\end{eqnarray}$ | (25) |
| $\begin{eqnarray}|{0}^{++}{\rangle }_{T4c}=|{S}_{cc}=1,{S}_{\bar{c}\bar{c}}=1,{S}_{{\rm{T}}}=0,{L}_{{\rm{T}}}=0{\rangle }_{{J}_{{\rm{T}}}=0},\\ |{1}^{+-}{\rangle }_{T4c}=|{S}_{cc}=1,{S}_{\bar{c}\bar{c}}=1,{S}_{{\rm{T}}}=1,{L}_{{\rm{T}}}=0{\rangle }_{{J}_{{\rm{T}}}=1},\\ |{2}^{++}{\rangle }_{T4c}=|{S}_{cc}=1,{S}_{\bar{c}\bar{c}}=1,{S}_{{\rm{T}}}=2,{L}_{{\rm{T}}}=0{\rangle }_{{J}_{{\rm{T}}}=2}.\end{eqnarray}$ | (26) |
| ST | LT | JT | JPC |
| 0 | 0 | 0 | 0++ |
| 1 | 0 | 1 | 1+- |
| 2 | 0 | 2 | 2++ |
| 0 | 1 | 1 | 1-- |
| 1 | 1 | 2 | 2-+ |
| 1 | 1 | 1 | 1-+ |
| 1 | 1 | 0 | 0-+ |
| 2 | 1 | 3 | 3-- |
| 2 | 1 | 2 | 2-- |
| 2 | 1 | 1 | 1-- |
Table1.Results for the JPC quantum numbers of the T4c with
2
3.1.Charmonium
In order to get good estimates of diquark and tetraquark properties, we first study the spectrum of the conventional charmonium states to observe how well we can fit the experimental data. In our model we considered the zeroth-order potential of the form Coulomb plus linear plus smeared spin-spin interactions. We separate the spin triplet (S=1) and spin singlet (S=0) before solving the Schr?dinger equation. Using κs = -4/3, S1 = S2 = 1/2 and S = 0 or S = 1, we replace the operator S1 · S2 by the constant [S(S+1)-S1(S1+1) - S2(S2+1)]/2 and we find the wavefunction y(r) and the eigenvalue E. In Fig. 3 we show the zeroth-order potential for total spin 0 or 1. Later the spin-orbit and tensor corrections are included, splitting orbitally-excited states.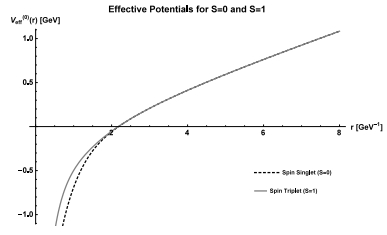
Figure3. Effective Potentials: Coulomb plus linear plus smeared spin-spin, for S = 0 and S = 1. Parameters are αs = 0.5202, b = 0.1463 GeV2, σ = 1.0831 GeV.We performed a fit with experimental values from the PDG [67]. The four parameters were allowed to vary in the following range: 1.1 < mc < 1.9 GeV, 0.1 < αs < 0.7, 0.050 < b < 0.450 GeV2, 0.7 < σ< 1.3 GeV. The results are also very similar to those from Refs. [46, 47], which were obtained with the fit of 11
| $\begin{eqnarray}\begin{array}{rlll}{m}_{c}&=& 1.4622\ {\rm{GeV}},&{\alpha }_{s}&=&0.5202,\\ b&=&0.1463\ {{\rm{GeV}}}^{2},&\sigma&=&1.0831\ {\rm{GeV}}.\end{array}\end{eqnarray}$ | (27) |
In Table 2 we present the wavefunction properties. Notice that the inclusion of the spin-spin interaction in the zeroth-order potential creates a small difference between the wavefunction of the spin singlet and spin triplet. The spin 0 states receive a negative contribution from this interaction in the potential, which causes the short-distance region of the potential (small r coordinate) to be "more negative", generating states with smaller root mean square radius, higher value of the wavefunction at the origin, and higher quark velocity.
| N2S+1 | M(0)/GeV | |R(0)|2/GeV3 | ||
| 11S | 2.9924 | 1.5405 | 0.375 | 0.336 |
| 13S | 3.0917 | 1.1861 | 0.421 | 0.253 |
| 11P | 3.5105 | 0 | 0.678 | 0.257 |
| 13P | 3.5191 | 0 | 0.689 | 0.246 |
| 21S | 3.6317 | 0.7541 | 0.839 | 0.308 |
| 23S | 3.6714 | 0.7092 | 0.867 | 0.293 |
| 11D | 3.7951 | 0 | 0.899 | 0.280 |
| 13D | 3.7958 | 0 | 0.901 | 0.278 |
| 21P | 3.9334 | 0 | 1.071 | 0.324 |
| 23P | 3.9427 | 0 | 1.082 | 0.315 |
| 31S | 4.0481 | 0.6088 | 1.210 | 0.364 |
| 33S | 4.0755 | 0.5914 | 1.230 | 0.357 |
| 21D | 4.1591 | 0 | 1.258 | 0.350 |
| 23D | 4.1604 | 0 | 1.261 | 0.348 |
| 41S | 4.3933 | 0.5430 | 1.531 | 0.424 |
| 43S | 4.4150 | 0.5340 | 1.547 | 0.419 |
Table2.Results for charmonium
The spin-dependent interactions are very important in charmonium spectroscopy because they can test the QCD dynamics in the heavy quark context, lying between the perturbative and the non-perturbative regime. Particularly interesting is the role of the spin-spin interaction in orbitally-excited states. It is convenient to define the spin-average mass of a multiplet (spin here means J), also known as "center-of-weight" or "center-of-gravity" (c.o.g.):
| $\begin{eqnarray}\langle M({N}^{2S+1}{\ell }_{J})\rangle =\displaystyle \frac{\displaystyle \sum _{J}(2J+1)M({N}^{2S+1}{\ell }_{J})}{\displaystyle \sum _{J}(2J+1)},\ ({\rm{c}}.{\rm{o}}.{\rm{g}}.)\end{eqnarray}$ | (28) |
| $\begin{eqnarray}\langle M({1}^{3}{P}_{J})\rangle =\displaystyle \frac{5M({1}^{3}{P}_{2})+3M({1}^{3}{P}_{1})+M({1}^{3}{P}_{0})}{9}.\end{eqnarray}$ | (29) |
In Table 3 we present the results for the masses including the spin interactions. Note that the contribution of the spin-spin interaction to orbitally-excited states is not zero, especially in the P-wave, even though the wave function at the origin is still compatible with zero. Because of that the spin singlet in orbitally-excited states is slightly different from the spin-average (c.o.g.). The experimental measurements of 1P states suggest that they should be very close (see Table 4 for experimental values). As pointed out in Ref. [68], a precise measurement of the difference between the c.o.g. of the 13PJ states and the singlet 11P1 can provide useful information about the spin-dependent interactions in heavy quarks. Actually, the prediction for hc(11P1) is already close to the experimental value and even more so if one considers its mass as the spin-average of the 3PJ states (as done in Ref. [47] for the calculations where its mass was required). Also, the inclusion of the recently measured χc2(2P) [69, 70] did not affect the resulting set much, even though the prediction for its mass is a little higher than the experimental value.
| N2S+1 | E(0) | M(0)/MeV | Mf/MeV | ||||||
| 11S0 | 491.9 | -584.4 | 246.2 | -85.6 | 68.1 | 2992.4 | 0 | 0 | 2992.4 |
| 13S1 | 370.6 | -504.0 | 279.4 | 21.4 | 167.4 | 3091.7 | 0 | 0 | 3091.7 |
| 13P0 | 359.5 | -246.6 | 480.0 | 2.0 | 594.8 | 3519.1 | -63.9 | -29.4 | 3425.8 |
| 13P1 | 359.5 | -246.6 | 480.0 | 2.0 | 594.8 | 3519.1 | -32.0 | 14.7 | 3501.8 |
| 11P1 | 375.2 | -253.1 | 471.1 | -7.0 | 586.2 | 3510.5 | 0 | 0 | 3510.5 |
| 13P2 | 359.5 | -246.6 | 480.0 | 2.0 | 594.8 | 3519.1 | 32.0 | -2.9 | 3548.1 |
| 21S0 | 450.6 | -287.3 | 573.8 | -29.7 | 707.4 | 3631.7 | 0 | 0 | 3631.7 |
| 23S1 | 428.5 | -281.7 | 590.4 | 9.8 | 747.1 | 3671.4 | 0 | 0 | 3671.4 |
| 13D1 | 407.0 | -175.4 | 639.7 | 0.2 | 871.5 | 3795.8 | -8.8 | -3.9 | 3783.1 |
| 13D2 | 407.0 | -175.4 | 639.7 | 0.2 | 871.5 | 3795.8 | -2.9 | 3.9 | 3796.7 |
| 11D2 | 408.8 | -175.9 | 638.5 | -0.6 | 870.8 | 3795.1 | 0 | 0 | 3795.1 |
| 13D3 | 407.0 | -175.4 | 639.7 | 0.2 | 871.5 | 3795.8 | 5.9 | -1.1 | 3800.6 |
| 23P0 | 460.4 | -186.2 | 742.1 | 2.2 | 1018.4 | 3942.7 | -59.9 | -26.1 | 3856.7 |
| 23P1 | 460.4 | -186.2 | 742.1 | 2.2 | 1018.4 | 3942.7 | -29.9 | 13.0 | 3925.8 |
| 21P1 | 474.4 | -190.8 | 733.1 | -7.5 | 1009.1 | 3933.4 | 0 | 0 | 3933.4 |
| 23P2 | 460.4 | -186.2 | 742.1 | 2.2 | 1018.4 | 3942.7 | 29.9 | -2.6 | 3970.0 |
| 31S0 | 532.8 | -215.4 | 826.5 | -20.1 | 1123.8 | 4048.1 | 0 | 0 | 4048.1 |
| 33S1 | 521.9 | -215.3 | 837.7 | 6.9 | 1151.2 | 4075.5 | 0 | 0 | 4075.5 |
| 23D1 | 508.6 | -145.8 | 873.0 | 0.3 | 1236.1 | 4160.4 | -11.6 | -3.7 | 4145.1 |
| 23D2 | 508.6 | -145.8 | 873.0 | 0.3 | 1236.1 | 4160.4 | -3.9 | 3.7 | 4160.2 |
| 21D2 | 511.3 | -146.5 | 871.0 | -1.0 | 1234.8 | 4159.1 | 0 | 0 | 4159.1 |
| 23D3 | 508.6 | -145.8 | 873.0 | 0.3 | 1236.1 | 4160.4 | 7.7 | -1.1 | 4167.1 |
| 41S0 | 620.4 | -179.5 | 1044.0 | -15.8 | 1469.0 | 4393.3 | 0 | 0 | 4393.3 |
| 43S1 | 613.2 | -180.6 | 1053.0 | 5.6 | 1490.7 | 4415.0 | 0 | 0 | 4415.0 |
Table3.Results for charmonium
| N2S+1 | Mf | Exp. [67] | Meson | JPC |
| 11S0 | 2992.4 | 2983.4 | ηc(1S) | 0-+ |
| 13S1 | 3091.7 | 3096.900 | J/ψ(1S) | 1-- |
| 13P0 | 3425.8 | 3414.75 | χc0(1P) | 0++ |
| 13P1 | 3501.8 | 3510.66 | χc1(1P) | 1++ |
| 11P1 | 3510.5 | 3525.38 | hc(1P)? | 1+- |
| 13P2 | 3548.1 | 3556.20 | χc2(1P) | 2++ |
| 13P (c.o.g.) | (3519.1) | (3525.303) | - | - |
| 21S0 | 3631.7 | 3639.2 | ηc(2S) | 0-+ |
| 23S1 | 3671.4 | 3686.097 | ψ(2S) | 1-- |
| 13D1 | 3783.1 | 3773.13 | ψ(3770) | 1-- |
| 13D2 | 3796.7 | - | - | 2-- |
| 11D2 | 3795.1 | - | - | 2-+ |
| 13D3 | 3800.6 | - | - | 3-- |
| 13D (c.o.g.) | (3795.8) | - | - | - |
| 23P0 | 3856.7 | - | * | 0++ |
| 23P1 | 3925.8 | - | - | 1++ |
| 21P1 | 3933.4 | - | - | 1+- |
| 23P2 | 3970.0 | 3927.2 | χc2(2P) | 2++ |
| 23P (c.o.g.) | (3942.7) | - | - | - |
| 31S0 | 4048.1 | - | - | 0-+ |
| 33S1 | 4075.5 | 4039 | ψ(4040) | 1-- |
| 23D1 | 4145.1 | 4191 | ψ(4160) | 1-- |
| 23D2 | 4160.2 | - | - | 2-- |
| 21D2 | 4159.1 | - | - | 2-+ |
| 23D3 | 4167.1 | - | - | 3-- |
| 23D (c.o.g.) | (4158.9) | - | - | - |
| 41S0 | 4393.3 | - | - | 0-+ |
| 43S1 | 4415.0 | 4421 | ψ(4415) | 1-- |
| ? In Ref. [47] the hc(1P) is taken as the spin-average (c.o.g.) of the P-wave states, which is in better agreement with experimental data. * See text for discussion about the ηc0(2P) and the X(3915). | ||||
Table4.Comparison of charmonium
In the 2014 edition of the PDG [71] the X(3915) was assigned as the 23 P0
Finally, in Table 4 we compare the results of the model with the experimental data, which are illustrated in the mass spectrum presented in Fig. 4. We can see that the agreement with the experimental data is satisfactory.
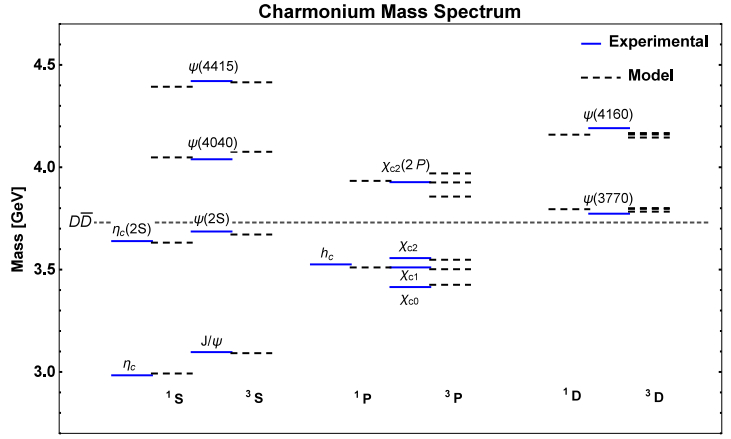Figure4. (color online) Spectrum of charmonium. Solid lines: experimental data [67]. Dashed lines: results from the model. Parameters are mc = 1.4622 GeV, αs = 0.5202, b = 0.1463 GeV2, and σ = 1.0831 GeV. Each state is shown with experimental data on the left and model results on the right. Notice that for some of the calculated states there is no experimental data to compare with.2
3.2.Diquarks
We now present our calculations for heavy diquarks composed of two charm quarks cc (which are equivalent for antidiquarksIn Tables 5 and 6 we present the results for the diquark wavefunctions and masses, respectively. For completeness we also show diquarks in the 1P, 2S and 2P states. Because of the restrictions due to the Pauli exclusion principle the possibilities are much less numerous. Also, since the P-wave introduces a (-1) factor in the parity, the antisymmetric restriction in the wavefunction implies that their total spin S should be 0 if they are in the antitriplet color state.
| N2S+1 | M(0)/GeV | |R(0)|2/GeV3 | ||
| 13S | 3.1334 | 0.3296 | 0.593 | 0.123 |
| 11P | 3.3530 | 0 | 0.906 | 0.141 |
| 23S | 3.4560 | 0.2370 | 1.147 | 0.167 |
| 21P | 3.6062 | 0 | 1.395 | 0.190 |
Table5.Results for diquark cc wavefunctions. Parameters from the charmonium fit are: mc = 1.4622 GeV, αs = 0.5202,
| N2S+1 | E(0) | M(0)/MeV | Mf/MeV | ||||||
| 13S1 | 180.4 | -173.9 | 197.9 | 4.7 | 209.0 | 3133.4 | 0 | 0 | 3133.4 |
| 11P1 | 206.7 | -93.3 | 316.2 | -0.9 | 428.7 | 3353.0 | 0 | 0 | 3353.0 |
| 23S1 | 244.8 | -105.7 | 389.8 | 2.9 | 531.7 | 3456.0 | 0 | 0 | 3456.0 |
| 21P1 | 277.5 | -72.3 | 477.9 | -1.2 | 681.9 | 3606.2 | 0 | 0 | 3606.2 |
Table6.Results for the cc diquark. Parameters from the charmonium fit are: mc = 1.4622 GeV, αs = 0.5202,
In Table 7 we show a few results from other works about cc diquarks. Due to differences in the models and presentation in each reference, we show only the information that can be compared to our results. In particular, we select only the results that correspond to the (attractive) antitriplet-color configuration. As can be seen, the 1S diquark is very similar in all the models, with a mass around 3.1 GeV.
| N | Mcc/GeV | |R(0)|2/GeV3 | Ref. | |
| 1S | 3.13 | (0.523)2=0.2735 | 0.58 | [77] |
| 2S | 3.47 | (0.424)2=0.1798 | 1.12 | [77] |
| 2P | 3.35 | - | 0.88 | [77] |
| 1S | 3.226 | - | - | [59] |
| 1S | 3.067 | - | - | [2] mod. Ⅰ |
| 1S | 3.082 | - | - | [2] mod. Ⅱ |
| 1P | 3.523 | - | - | [2] mod. Ⅰ |
| 1P | 3.513 | - | - | [2] mod. Ⅱ |
| 1S | 3.204 | - | - | [30] |
Table7.Results for cc diquarks from other works.
2
3.3.Tetraquarks
As discussed above, the diquark-antidiquark tetraquark is treated as a two-body system. The diquark masses were presented in the previous subsection and the parameter set was obtained from a fit to the charmonium data. The tetraquark spectrum is calculated by replacing the charm quark mass by the diquark mass mcc.We now present the spectrum of the all-charm tetraquark considering the ground states 1S and the first orbital excitations 1P (relative to the diquark-antidiquark system), including all the possible combinations of total spin and total angular momentum. We also include the radial excitations 2S and 2P, in a total of 20 T4c states built with two cc diquarks, each of them being in an antitriplet color state and spin 1 (13S1). These 20 states were built considering the coupling of the total spin of the tetraquark ST (composed of the coupling of the total spins of the diquark Sd and antidiquark
In our model the spin-spin interaction is treated non-perturbatively. In mesons and diquarks we had only two possibilities for total spin when combining two spin 1/2 particles S = 0, 1. Now, since we consider spin 1 diquark and antidiquark, we have three possibilities for total spin ST = 0, 1, 2, and therefore three different zeroth-order potentials, and consequently three wavefunctions for each NLT state, as presented in Table 8. The splitting structure from the perturbative corrections (spin-orbit and tensor) also has more possibilities, as presented in Table 9 with the masses of the 20 T4c states. In Fig. 5 we show the mass spectrum.
| N2ST+1LT | M(0)/GeV | |R(0)|2/GeV3 | ||
| 11S | 5.9694 | 8.4219 | 0.232 | 0.199 |
| 13S | 6.0209 | 7.8384 | 0.241 | 0.183 |
| 15S | 6.1154 | 6.6727 | 0.264 | 0.153 |
| 11P | 6.5771 | 0 | 0.471 | 0.119 |
| 13P | 6.5847 | 0 | 0.478 | 0.115 |
| 15P | 6.5984 | 0 | 0.491 | 0.107 |
| 21S | 6.6633 | 2.8414 | 0.588 | 0.131 |
| 23S | 6.6745 | 2.8528 | 0.595 | 0.130 |
| 25S | 6.6981 | 2.8616 | 0.610 | 0.129 |
| 21P | 6.9441 | 0 | 0.785 | 0.132 |
| 23P | 6.9500 | 0 | 0.790 | 0.130 |
| 25P | 6.9610 | 0 | 0.800 | 0.126 |
Table8.Results for T4c wavefunctions and ground state (13S1) diquark and antidiquark. Parameters are mcc = 3133.4 MeV, αs = 0.5202, b = 0.1463 GeV2, and σ = 1.0831 GeV.
| N2ST+1LT JT | E(0) | M(0)/MeV | Mf/MeV | JPC | ||||||
| 11S0 | 624.0 | -966.6 | 151.1 | -106.0 | -297.3 | 5969.4 | 0 | 0 | 5969.4 | 0++ |
| 13S1 | 574.8 | -928.0 | 157.6 | -50.2 | -245.8 | 6020.9 | 0 | 0 | 6020.9 | 1+- |
| 15S2 | 479.4 | -847.5 | 172.5 | 44.3 | -151.3 | 6115.4 | 0 | 0 | 6115.4 | 2++ |
| 11P1 | 372.6 | -371.8 | 325.3 | -15.8 | 310.3 | 6577.1 | 0 | 0 | 6577.1 | 1-- |
| 13P0 | 358.9 | -364.3 | 330.7 | -7.4 | 318.0 | 6584.7 | -59.4 | -44.8 | 6480.4 | 0-+ |
| 13P1 | 358.9 | -364.3 | 330.7 | -7.4 | 318.0 | 6584.7 | -29.7 | 22.4 | 6577.4 | 1-+ |
| 13P2 | 358.9 | -364.3 | 330.7 | -7.4 | 318.0 | 6584.7 | 29.7 | -4.5 | 6609.9 | 2-+ |
| 15P1 | 335.4 | -350.8 | 340.7 | 6.4 | 331.7 | 6598.4 | -75.9 | -27.2 | 6495.4 | 1-- |
| 15P2 | 335.4 | -350.8 | 340.7 | 6.4 | 331.7 | 6598.4 | -25.3 | 27.1 | 6600.2 | 2-- |
| 15P3 | 335.4 | -350.8 | 340.7 | 6.4 | 331.7 | 6598.4 | 50.6 | -7.7 | 6641.2 | 3-- |
| 21S0 | 410.8 | -397.0 | 404.6 | -21.8 | 396.6 | 6663.3 | 0 | 0 | 6663.3 | 0++ |
| 23S1 | 408.7 | -398.2 | 408.7 | -11.4 | 407.8 | 6674.5 | 0 | 0 | 6674.5 | 1+- |
| 25S2 | 403.0 | -400.7 | 416.8 | 12.3 | 431.4 | 6698.1 | 0 | 0 | 6698.1 | 2++ |
| 21P1 | 414.9 | -262.9 | 537.5 | -12.0 | 677.4 | 6944.1 | 0 | 0 | 6944.1 | 1-- |
| 23P0 | 407.8 | -260.0 | 541.2 | -5.7 | 683.3 | 6950.0 | -47.9 | -35.6 | 6866.5 | 0-+ |
| 23P1 | 407.8 | -260.0 | 541.2 | -5.7 | 683.3 | 6950.0 | -23.9 | 17.8 | 6943.9 | 1-+ |
| 23P2 | 407.8 | -260.0 | 541.2 | -5.7 | 683.3 | 6950.0 | 23.9 | -3.6 | 6970.4 | 2-+ |
| 25P1 | 394.5 | -254.2 | 548.7 | 5.2 | 694.3 | 6961.0 | -63.1 | -22.2 | 6875.6 | 1-- |
| 25P2 | 394.5 | -254.2 | 548.7 | 5.2 | 694.3 | 6961.0 | -21.0 | 22.2 | 6962.1 | 2-- |
| 25P3 | 394.5 | -254.2 | 548.7 | 5.2 | 694.3 | 6961.0 | 42.1 | -6.3 | 6996.7 | 3-- |
Table9.Results for T4c masses using ground state (13S1) diquarks. Parameters are mcc = 3133.4 MeV, αs = 0.5202, b = 0.1463 GeV2, and σ = 1.0831 GeV.
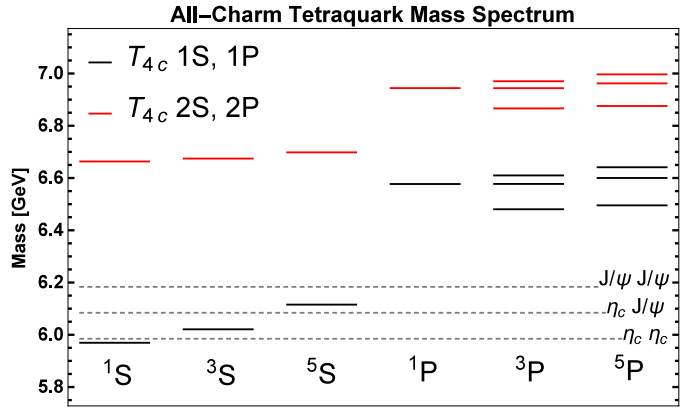Figure5. (color online) Spectrum of T4c obtained with the model, using ground state (13S1) diquark and antidiquark. Parameters are mcc = 3133.4 MeV, αs = 0.5202, b = 0.1463 GeV2, and σ = 1.0831 GeV.From Table 8 we can observe that the tetraquark is very compact. In fact, its
As suggested in Ref. [15], the two-body approximation is better for orbitally-excited states, such as the P-wave considered here, since the centrifugal barrier would suppress overlap at the origin. As we can see in Table 8, the compactness of the T4c is also reflected in the value of the wavefunction at the origin for the 1S states, which is very large.
In Table 9 we see that the compactness of the 1S states is mainly caused by the Coulomb interaction. This suggests that the one-gluon exchange is indeed the dominant mechanism responsible for the very strong binding between diquark and antidiquark, which causes the energy eigenvalue E to be negative. This also implies that the spin-spin interaction is strong. In this case we must have in mind that the factors coming from S1 · S2 are larger for the coupling of two spin 1 than for two spin 1/2 particles. It is interesting to see that even though the spin-dependent terms are now suppressed by a factor
In Fig. 5 we can see that the masses of the 20 states are concentrated in the range between 6 and 7 GeV. Among the 1S states, the lowest one, with JPC = 0++, lies very close to the ηc pair threshold. Within our uncertainties (both from the choice of parameters as well as the assumption of the diquark-antidiquark structure), we cannot say whether this state is below or above such a threshold. If it is above, it could be seen as a narrow state in the ηcηc invariant mass. If it is below, then it would be stable against the rearrangement in
The second lowest state, with quantum numbers JPC = 1+-, could rearrange itself into ηcJ/ψ. However, this state seems to be more than 50 MeV below this two-meson threshold, and therefore it should be stable. The highest 1S state, with quantum numbers JPC = 2++, is also more than 50 MeV below the corresponding J/ψ pair threshold. It could still decay into
In order to be consistent with our
| (M1 + M2) | |||||
| JPC | N2ST+1LT JT | MT4c | M1 M2 | Model | Exp. |
| 0++ | 11S0 | 5969.4 | ηc(1S) ηc(1S) | 5984.8 | 5966.8 |
| 1+- | 13S1 | 6020.9 | J/ψ(1S) ηc(1S) | 6084.1 | 6080.3 |
| 2++ | 15S2 | 6115.4 | J/ψ(1S) J/ψ(1S) | 6183.4 | 6193.8 |
| 0-+ | 13P0 | 6480.4 | ηc(1S) χc0(1P) | 6418.2 | 6398.1 |
| 1-+ | 13P1 | 6577.4 | ηc(1S) χc1(1P) | 6494.2 | 6494.1 |
| 1-- | 15P1 | 6495.4 | ηc(1S) hc(1P) | 6502.9 | 6508.8 |
| 1-- | 11P1 | 6577.1 | |||
| 2-+ | 13P2 | 6609.9 | ηc(1S) χc2(1P) | 6540.5 | 6539.6 |
| 2-- | 15P2 | 6600.2 | J/ψ(1S) χc1(1P) | 6593.5 | 6607.6 |
| 3-- | 15P3 | 6641.2 | J/ψ(1S) χc2(1P) | 6639.8 | 6653.1 |
Table10.Comparison of 1S and 1P T4c masses with the lowest S-wave two
One of these orbitally-excited states is of particular interest, since it presents exotic quantum numbers that cannot be obtained as a simple
Next, we comment on the results of other works which also investigate the existence and properties of this state composed of four charm quarks. Some of them also consider a sextet structure for the diquarks (which can also lead to a color singlet tetraquark). In the following tables we present a compilation of the main results.
First, we show the results of Ref. [2] in Tables 11 and 12. In this work a variational method with Gaussian trial wavefunctions was employed to study all-heavy tetraquarks, using a four-body coordinate system. The interactions were described with a potential due to the exchange of color octets in two-body forces. Two potentials were used: model I is a Cornell-type (Coulomb plus linear) and the model II is of the form A+Brβ. Also, a version of the MIT bag model was used with the Born-Oppenheimer approximation. Both color structures were considered,
| NLT | model | color | |
| 1S | 6.437 | I | |
| 1S | 6.450 | II | |
| 1S | 6.383 | I | |
| 1S | 6.276 | Bag | |
| 1S | 6.252 | Bag | |
| 1P | 6.718 | I | |
| 1P | 6.714 | II | |
| 1P | 6.832 | I | |
| 1P | 6.822 | Ⅱ |
Table11.Results for the T4c mass (without spin-corrections) from Ref. [2].
| N | JP(C) | SS/GeV | LS + T/GeV | model | color | |
| 1S | 6.383 | 0+ | 0.017 | - | I | |
| 1S | 6.437 | 0+ | -0.011 | - | I | |
| 1S | 6.437 | 1+ | 0.003 | - | I | |
| 1S | 6.437 | 2+ | 0.032 | - | I | |
| 1P | 6.832 | 1-- | 0.011 | 0 | I | |
| 1P | 6.718 | 0-+ | 0.010 | -0.023 | I | |
| 1P | 6.718 | 1-- | 0.020 | -0.024 | I |
Table12.Results for the spin shifts of the T4c from Ref. [2].
In Table 13 we compile the results of Refs. [66, 78], where the T4c production was studied. The estimates for the T4c are very similar to those presented in this work. The authors used the diquark results of Ref. [77], where the cc diquark was calculated as a baryon constituent (we also compared these diquark results with ours). The same strategy of dividing the problem into two-body problems was used, but only S-wave states were calculated, and the spin-spin splitting was considered between each spin 1/2 constituent pair, using the wavefunction at the origin of the diquark or of the charmonium, depending on the interacting pair. It is interesting to see that the 0++ state is very close to our result, and the 1+- is also below the ηcJ/ψ threshold. However, the 2++ is about 20 MeV above the J/ψ J/ψ threshold, indicating that this state could be seen in the J/ψ J/ψ invariant mass.
| NLT | |ψ(0)|/GeV3/2 | JPC | color | |||
| 1S | 6.12 | 0.47 | 0.29 | 0++ | 5.97 | |
| 1S | 6.12 | 0.47 | 0.29 | 1+- | 6.05 | |
| 1S | 6.12 | 0.47 | 0.29 | 2++ | 6.22 |
Table13.Results for the T4c from Refs. [66, 78].
In Table 14 we compare our results for the S-wave T4c with those of the recent diquark-antidiquark studies: those with antitriplet diquarks [66, 78], and those with the color-magnetic model [27] and with QCD sum rules [28].
| JPC | Mfinal/GeV | Ref. [66, 78] | Ref. [27] | Ref. [28] |
| 0++ | 5.9694 | 5.966 | 5.617-6.254 | 6.44-7.15 |
| 1+- | 6.0209 | 6.051 | 5.720-6.137 | 6.37-6.51 |
| 2++ | 6.1154 | 6.223 | 5.777-6.194 | 6.51-6.37 |
Table14.Comparison of our results for the S-wave T4c.
In Table 15 we compare our results with the contribution of each term used to calculate the 0++ T4c in Ref. [30], which was based in meson and baryon masses. The constant V0 is obtained as twice the constant term S obtained from the fit of baryon and meson masses (which is added only into baryon masses, related to the QCD string junction, as discussed in that reference). Remember that in our model the spin-spin interaction is contained in the energy eigenvalue.
| JPC | mc/MeV | mcc/MeV | E/MeV | V0 | SS/MeV | ||
| 0++ | 1462.2 | 3133.4 | -297.3 | - | (-106.0) | 5969.4 | This work |
| 0++ | 1655.6 | 3204.1 | -388.3 | 330.2 | -158.5 | 6191.5 | Ref. [30] |
Table15.Comparison of our results for the 0++ T4c with Ref. [30].
Finally, in Table 16 we compare our results for the P-wave T4c with the old diquark-antidiquark predictions of Chao [15], the recent diquark-antidiquark predictions of QCD sum rules [28] and with lattice results [24].
| JPC | N2ST+1LTJT | Mfinal/GeV | Ref. [15] | Ref. [28] | Ref. [24] |
| 1-- | 11P1 | 6.5771 | 6.55-6.82 | 6.83-6.84 | 6.420 |
| 1-- | 15P1 | 6.4954 | 6.39 |
Table16.Comparison of our results for the P-wave T4c.
The use of the Cornell potential allows us to study the charmonium spectrum without the confining interactions, which can easily be "switched off" by choosing the string tension to be zero. We can thus repeat all our calculations and check whether we find bound diquark states and also a bound T4c. We have done these calculations and we find both diquark and tetraquark bound states. The obtained diquark and T4c ground states have masses equal to mcc = 2881.4 MeV and T4c = 5.3-5.4 GeV (for the lowest 1S states), respectively, as shown in the Appendix. These results can have applications in the context of relativistic heavy ion collisions, where a deconfined medium is formed (the quark-gluon plasma, QGP). Our results suggest that the T4c can be formed and perhaps survive in the QGP phase.
2
3.4.The role of $6-\bar{6}$ configurations
The tetraquark composed of four quarks of the same flavor is constrained by the Pauli exclusion principle, which restricts the possibilities of the diquark wave function. The most favorable case is the one presented in the previous sections, where quarks in the diquark are in the attractive antitriplet color state (antisymmetric), in the ground state 1S with no orbital nor radial excitations (symmetric) and with total spin S = 1 (symmetric), resulting in an antisymmetric wave function appropriate for identical fermions. A diquark in the repulsive color sextet configuration (symmetric) should either have total spin S = 0 (antisymmetric) or have an internal orbital excitation. This excitation strongly disfavors the compactness of the diquarks, which underlies the assumption that the dynamics is dominated by one-gluon exchange. Therefore, any internal orbital excitation in the diquarks can be safely neglected, and we end up with two orthogonal building blocks: the antitriplet diquark with spin 1 and the sextet diquark with spin 0. There could be some mixing between these two states. We know that spin 0 diquarks can only form tetraquarks with total spin ST = 0, therefore the tetraquarks composed of sextet diquarks would only mix with four of the 20 states presented in this work, i. e. the states 1S and 1P with quantum numbers JPC = 0++ 1-- and both respective radial excitations. All the other states are necessarily composed of pure antitriplet diquarks, since to have spin 1 sextet diquarks one would need both diquark and antidiquark with one unit of internal orbital excitation, which is highly unlikely.The exchange of one gluon between a quark inside the diquark and an antiquark inside the antidiquark could mix the color states
Let us now present results for the pure
| N2ST+1LT | M(0)/GeV | |R(0)|2/GeV3 | ||
| 11S | 3.8611 | 70.7780 | 0.127 | 0.820 |
| 11P | 5.8902 | 0 | 0.302 | 0.341 |
| 21S | 6.0176 | 16.3850 | 0.368 | 0.376 |
| 21P | 6.7567 | 0 | 0.539 | 0.322 |
Table17.Results for T4c wavefunctions using ground state (11S0) diquark and antidiquark (sextet). Parameters are mcc = 2mc = 2.9243 MeV, αs = 0.5202, and b = 10 bcc/4 = 10 × 0.1463/4 GeV2.
| N2ST+1LTJT | E(0) | M(0)/MeV | Mf/MeV | JPC | ||||||
| 11S0 | 2397.0 | -4589.0 | 204.6 | 0 | -1987.6 | 3861.1 | 0 | 0 | 3861.1 | |
| 11P1 | 996.1 | -1473.0 | 518.9 | 0 | 41.6 | 5890.2 | 0 | 0 | 5890.2 | |
| 21S0 | 1101.0 | -1566.0 | 634.8 | 0 | 169.0 | 6017.6 | 0 | 0 | 6017.6 | |
| 21P1 | 941.9 | -958.9 | 925.0 | 0 | 908.1 | 6756.7 | 0 | 0 | 6756.7 |
Table18.Results for T4c masses using ground state (11S0) diquarks (sextet - antisextet). Parameters are mcc = 2mc = 2.9243 MeV, αs = 0.5202, and b = 10bcc/4=10×0.1463/4 GeV2.
Before concluding we would like to add a remark on the scale dependence of our results. The one-loop QCD running coupling is given by:
| $\begin{eqnarray*}{\alpha }_{s}({Q}^{2})=\displaystyle \frac{12\pi }{(33-2{N}_{f}){\rm{ln}}({Q}^{2}/{\Lambda }^{2})}.\end{eqnarray*}$ |
An alternative way to compute running coupling effects was described in Ref. [81], where the authors compare (using their formula 2.23) αs in bottomonium with αs in charmonium with a simple formula. Adapting their formula to our context, it reads:
| $\begin{eqnarray*}{\alpha }_{s}({T}_{4c})=\displaystyle \frac{{\alpha }_{s}(\psi )}{1+\left[\displaystyle \frac{{\alpha }_{s}(\psi )}{12\pi }\right](33-2{N}_{f}){\rm{ln}}({m}_{{T}_{4c}}^{2}/{m}_{\psi }^{2})}\end{eqnarray*}$ |
This was the first calculation of the T4c spectrum with a non-relativistic diquark-antidiquark model. It was meant to check whether this approach reproduces what we know from the lattice calculations, from QCD sum rules and from the results of the Bethe-Salpeter approach. In this sense it is a preliminary calculation which we believe has passed the test. Further improvement could be made in the future by including a systematic analysis of the uncertainties, moving towards "precision physics". The real novelty of this work would be the power to identify the components of the masses and determine the role of the spin interactions, which are very difficult to isolate in the lattice and in QCD sum rules calculations.
We explored a diquark-antidiquark configuration, including P-wave tetraquarks, and we extended the spin-dependent interactions between diquarks, including a consistent strategy to deal with the tensor interaction between two objects of spin 1. The fact that our model is relatively simple compared to the four-body approach and to the relativistic models allows us to study many of the T4c properties with clarity, especially the role of the spin interactions.
We were able to study the behavior of the all-charm tetraquark when radial and orbital excitations are included, investigating the contribution of the one-gluon exchange, the confinement and the spin-dependent interactions, providing for the first time detailed results which elucidate the dynamics of the diquark-antidiquark structure.
The inclusion of one orbital excitation in the tetraquark also leads to a significant increase in the possibilities of quantum numbers and to the prediction of the exotic state with JPC = 1-+. The orbitally-excited
Our model is simple and instructive, especially in what concerns spin interactions. For the lowest T4c states our predictions are compatible with those made with other approaches. For the higher states, in particular those with orbital excitations, we make novel predictions which can be tested. In this region our predictions are more reliable, since the diquark-antidiquark spatial separation is bigger.
Our results and the others found in the recent literature on the T4c tetraquark, taken together, should encourage a careful experimental search for these states at LHCb and Belle Ⅱ.
| N2ST+1LTJT | E(0) | Mf/MeV | JPC | |||||
| Diquark | ||||||||
| 13S1 | 41.4 | -85.3 | 1.0 | -42.9 | 2881.4 | 1+ | 1.378 | 0.028 |
| Tetraquark | ||||||||
| 11S0 | 472.7 | -809.0 | -98.0 | -434.3 | 5328.4 | 0++ | 0.291 | 0.164 |
| 13S1 | 408.0 | -751.9 | -44.0 | -387.8 | 5374.9 | 1+- | 0.315 | 0.142 |
| 15S2 | 289.4 | -633.3 | 33.4 | -310.4 | 5452.3 | 2++ | 0.374 | 0.100 |
TableA1.Results for lowest T4c states (1S) using ground state (13S1) diquarks. Both diquark and tetraquark are calculated without the linear confinement term. Parameters are mcc = 2881.4 MeV, αs = 0.5202, b = 0, and σ = 1.0831 GeV.
These 1S states are deeply bound. As we can see in Table A1, the binding energy for the lowest state, with JPC = 0++, is larger than -400 MeV, where about 100 MeV come from the spin-spin interaction. The resulting mass of 5.3 GeV is compatible with the results of Ref. [23], where a state with a dominant ηcηc component and mass 5.3
For the excited tetraquark states 2S, 1P and 2P, the binding energy is around -90 MeV and the spin-dependent interactions are of the order of 10 MeV, with masses around 5.6-5.7 GeV.
