删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

1978-2016年中国农业生态效率时空演变及趋势预测

本站小编 Free考研考试/2021-12-29

侯孟阳¹^,²^,, 姚顺波¹^,²^,

1. 西北农林科技大学经济管理学院,杨凌 712100

2. 西北农林科技大学资源经济与环境管理研究中心,杨凌 712100

Spatial-temporal evolution and trend prediction of agricultural eco-efficiency in China: 1978-2016

HOUMengyang¹^,²^,, YAOShunbo¹^,²^,

1. College of Economics & Management, Northwest A& F University, Yangling 712100, China;

2. Research Center for Resource Economics and Environment Management, Northwest A& F University, Yangling 712100, China;

通讯作者:通讯作者：姚顺波(1964-), 男, 博士, 教授, 博导, 研究方向为资源经济与环境管理、林业政策效果评估。E-mail: yaoshunbo@163.com
收稿日期:2017-12-8
修回日期:2018-06-24
网络出版日期:2018-11-25
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

林业公益性行业科研专项经费(201504424);教育部人文社会科学重点基金(14JJD790031);国家自然科学基金项目(71473195)

作者简介:
-->作者简介：侯孟阳(1988-), 男, 博士生, 研究方向为资源经济与环境管理、农业经济与生态。E-mail: houmengyang@outlook.com

展开

摘要
基于1978-2016年中国各省市面板数据,采用超效率SBM模型测算省际农业生态效率,在时间序列分析和空间相关性分析的基础上,构建传统和空间马尔可夫概率转移矩阵,探讨中国农业生态效率的时空动态演变特征,并预测其长期演变的趋势。研究发现：① 中国农业生态效率呈现出在波动中稳定上升的“双峰”分布特征,且波峰高度的差距在缩小,但整体仍处于较低水平,农业生态效率仍存在较大提升空间,东部地区农业生态效率提升较中西部地区更加显著;② 中国农业生态效率整体上向高水平方向转移的趋势显著,但农业生态效率的演变具有维持原有状态的稳定性,且较难实现跨越式转移。地理空间格局在农业生态效率时空演变过程中发挥着重要作用,空间集聚特性显著,农业生态效率较高的省市具有正向的溢出效应,而农业生态效率较低的省市具有负的溢出效应,从而在空间格局上逐渐形成“高高集聚、低低集聚、高辐射低、低抑制高”的“俱乐部收敛”现象;③ 从长期演变的趋势预测来看,多数省市农业生态效率逐渐向上转移为较高水平,并逐渐演变为由低到高渐次递增的格局,在农业生态效率较低的地理背景下,其长期演变的稳定状态表现为偏“单峰”分布,而在农业生态效率较高的地理背景下,其长期演变为较高水平集聚的偏“双峰”分布。最后,分析当前研究需要改进的方向,并提出控制农业污染排放量、地区间农业生态政策联动、加强地区间农业生态合作交流与借鉴等能够有效提升中国农业生态效率及缩小省市间差距。

关键词：农业生态效率;时空演变;趋势预测;超效率SBM模型;空间马尔可夫链;中国
Abstract
Based on the panel data of 30 provinces in China from 1978 to 2016, the super efficiency SBM model was used to measure the inter-provincial agricultural eco-efficiency in our study. On the basis of time series analysis and spatial correlation analysis, traditional and spatial Markov probability transfer matrices were constructed to explore the spatial and temporal evolution of agricultural eco-efficiency of China, and the long-term trends were also predicted. The result shows that: (1) The agricultural eco-efficiency in China presents a "double-peak" distribution with stable rise in fluctuation, and the gap between peak heights is narrowing, but the overall level is still relatively low. Therefore, there is still room for improvement in agricultural eco-efficiency. Besides, the agricultural eco-efficiency improvement in the eastern region is more significant than that in the central and western regions. (2) The trend of China's agricultural eco-efficiency shifting to a higher level is significant, but the evolution of agricultural eco-efficiency has maintained the stability of the original state, and it is difficult to achieve a leap-forward shift. The geospatial structure plays an important role in the spatial-temporal evolution of agricultural eco-efficiency and the spatial agglomeration is significant. The provinces with higher agricultural eco-efficiency have positive spillover effects, while those with lower agricultural eco-efficiency have negative spillover effects. As a result, the "club convergence" phenomenon of "high agglomeration, low concentration, high radiates low, and low inhibits high" has been gradually formed in the spatial pattern. (3) From the long-term trend prediction, the agricultural eco-efficiency in most provinces gradually shifts upward to a relatively high level, and gradually evolves from a low-to-high incremental pattern. In the context of the low agricultural eco-efficiency, its long-term stable evolution is manifested as a "partial unimodal" distribution; while under the geographical background of higher agricultural eco-efficiency, it has evolved into a "double-peak" distribution of higher-level agglomeration for a long time. Finally, we analyze the shortcomings and what needs to be improved for current research. What's more, we propose that controlling agricultural pollution emissions, inter-regional agro-ecological policy linkages, and strengthening inter-regional agro-ecological cooperation, exchange, and learning can effectively improve China's agricultural eco-efficiency and narrow the gap between provinces.

Keywords：agricultural eco-efficiency;spatial-temporal evolution;trend prediction;super efficiency SBM model;spatial Markov chain;China

-->0
PDF (2922KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
侯孟阳, 姚顺波. 1978-2016年中国农业生态效率时空演变及趋势预测[J]. 地理学报, 2018, 73(11): 2168-2183 https://doi.org/10.11821/dlxb201811009
HOU Mengyang, YAO Shunbo. Spatial-temporal evolution and trend prediction of agricultural eco-efficiency in China: 1978-2016[J]. Acta Geographica Sinica, 2018, 73(11): 2168-2183 https://doi.org/10.11821/dlxb201811009

1 引言

“三农”是国家稳定和安全的重要基础。1978年改革开放以来,中国农业经济取得了巨大成就,以占世界不到10%的耕地养活了世界20%左右的人口^[1],且粮食连年增产,2016年中国粮食产量达到6.1624亿t,改革开放以来年均增长率1.82%,而农业产值由1978年的1397亿元增长到2016年的63671亿元,年均增长率10%左右。伴随着农业经济的快速发展,也带来了一系列的生态恶化、环境污染、资源浪费等问题,《第一次全国污染源普查公报（2010）》^[2]数据显示,2007年农业污染源中的化学需氧量、总氮、总磷的排放量分别为1324.09万t、270.46万t和28.47万t,占各自污染总排放量的比重分别为43.71%、57.19%和67.27%;《全国农业可持续发展规划（2015-2030）》^[3]报告也显示,农业内源性污染严重,化肥、农药利用率不足1/3,农膜回收率不足2/3,秸秆焚烧现象严重,从而导致了严重的农业内源性污染,并影响了中国农业生产的可持续发展。中央农村工作会议明确提出了建立资源节约型和环境友好型的“两型农业”,期望最大限度地减弱农业生产的负外部性,党的“十九大”报告也指出,建设生态文明是中华民族永续发展的千年大计,必须树立和践行绿水青山就是金山银山的理念,既要创造更多的物质财富和精神财富以满足人民日益增长的美好生活需要,也要提供更多优质生态产品以满足人民日益增长的优美生态环境需要。在当前农业生态环境面临严峻形势的背景下,农业经济发展过程中如何保持资源消耗、生态保护的统筹协调,即农业发展不仅要重视其经济效应,还要重视其生态效益。
“两型”农业的发展需要协调农业投入产出与资源消耗、环境保护三者间的关系,因而考察农业生产效率必须将农业的生态负外部性纳入投入产出过程的衡量中,以生态影响的视角考察农业生产效率,也可称为农业生态效率。生态效率首先由德国****Schaltegger等^[4]提出,并由世界可持续发展工商理事会（WBCSD）^[5]和经合组织（OECD）^[6]推广,生态效率可看作与达到地球承载能力的资源环境投入与满足人类生产生活需求的产出之间相互协调的关系,即在经济和环境之间达到一种平衡。具体到农业生产方面,农业生态效率则是指以尽可能小的资源消耗和环境污染,得到尽可能多的农业产出,并保证农产品质量^[7]。依照该农业生态效率的要求,在农业生态效率评价中不但要重视期望产出（农业经济效益）最大化,还要重视非期望产出（资源消耗、环境破坏）最小化,以符合“两型”农业的可持续发展理念。
当前****们对农业生产效率、农业生态效率的研究,已经从微观^[8,9,10]、中观^[11,12]、宏观^[13,14]等不同层次进行了广泛深入的探讨,涉及到指标体系构建^{[7, 15-16]}、影响因素分析^[17,18,19]等多方面内容,测算方法主要包括随机前沿法（Stochastic Frontier Approach, SFA）和数据包络分析法（Data Envelopment Analysis, DEA）、超效率DEA、三阶段DEA及非期望SBM模型^{[7-8, 13-15]}等,以DEA为基础的评价方法,其中由于非期望SBM模型将负外部性产出纳入模型,有效解决了投入产出的松弛现象,已逐渐成为测定生态效率的主流模型。在农业非期望产出方面,已有研究通常将农业面源污染^{[1, 7]}或者农业碳排放量^{[15, 20]},或者这两种非期望产出都纳入模型^[21],鉴于当前效率测定方法已渐成熟,本文采用非期望SBM模型测算中国农业生态效率。另外,围绕生态效率时空演变特征的研究,多数文献采用的DEA与探索性空间数据分析（ESDA）相结合^[20,21,22]的方法是研究效率在时间和空间动态演化的成熟方法,但ESDA较多注重不同年份截面数据的比较分析,而在面板数据的动态性和异质性分析方面存在一定局限性^[22],难以揭示某些经济现象演变的动态变化过程。
整体而言,当前文献仍可以从以下几个方面进行扩展,一方面,考虑农业环境污染等非期望产出的SBM模型的应用也已渐成熟,而现有采用非期望SBM模型的文献则较少考虑效率为1的Decision Making Unit（DMU）的进一步对比,而超效率SBM模型能够有效解决该问题;另一方面,考虑到现有ESDA方法对面板数据分析的局限性,且鲜有文献对农业生态效率的演变趋势进行预测,而空间马尔可夫链（Spatial Markov chain）能够深入分析面板数据在时间演变和空间背景下的内在演变规律,并对其长期演变趋势进行预测^{[23,24,25,26]}。基于此,本文以1978-2016年中国各省市面板数据为研究单元,以狭义农业（种植业）为研究对象,将农业碳排放作为非期望产出,采用超效率SBM模型对中国农业生态效率进行测定,在时间序列和空间相关性分析的基础上,构建传统和空间马尔可夫概率转移矩阵,通过转移矩阵的对比,分析农业生态效率的时空动态演化特征,并预测其长期演变的趋势,旨在探索农业生态效率在发展演变过程中周围邻域对自身发展的影响,为进一步加强农业生态合作、缩小地区生态不均衡提供科学的理论支撑。

2 研究方法

2.1 基于非期望产出的超效率SBM模型

在农业生产过程中,通常期望化肥、农药、农膜等化学制品的过度使用产生的环境污染越小越好,这种越小越好的产出即为非期望产出。基于非期望产出的SBM模型是首先由Tone^[27]2001年提出的测算生态效率的模型,SBM模型能够有效解决径向和角度的传统数据包络模型（DEA）模型造成的投入要素的“拥挤”或“松弛”现象,但SBM模型与传统DEA模型存在的相同问题,即对于效率都为1的DMU,难以进一步区分有效率DMU之间的差异,Tone在SBM模型的基础上,进一步定义了超效率SBM模型^[28],它是超效率DEA模型和SBM模型相结合的一种模型,其综合了两种模型的优势,相比一般的SBM模型,超效率SBM模型能够对处于前沿面的有效率DMU进一步对比区分,模型构建为：

Min ρ = \frac{\frac{1}{m} \overset{m}{\sum_{i = 1}} (\frac{\overset{?}{x}}{x_{ik}})}{\frac{1}{r_{1} + r_{2}} (\frac{\overset{r_{1}}{\sum_{s = 1}} \overset{ˉ}{y^{d}}}{y_{sk}^{d}} + \frac{\overset{r_{2}}{\sum_{q = 1}} \overset{ˉ}{y^{u}}}{y_{qk}^{u}})}

（1）

\{\begin{array}{l} \overset{?}{x} \geq \overset{n}{\sum_{j = 1, \neq k}} x_{ij} λ_{j}; \overset{ˉ}{y^{d}} \leq \overset{n}{\sum_{j = 1, \neq k}} y_{sj}^{d} λ_{j}; \overset{ˉ}{y^{d}} \geq \overset{n}{\sum_{j = 1, \neq k}} y_{qj}^{d} λ_{j}; \overset{?}{x} \geq x_{k}; \overset{ˉ}{y^{d}} \leq y_{k}^{d}; \overset{ˉ}{y^{u}} \geq y_{k}^{u}; \\ λ_{j} \geq 0, i = 1,2, ?, m; j = 1,2, ?, n, j \neq 0; s = 1,2, ?, r_{1}; q = 1,2, ?, r_{2}; \end{array}

（2）
式中：假设有n个DMU,每个DMU由投入m,期望产出r₁和非期望产出r₂构成;x、y^d、y^u为相应的投入矩阵、期望产出矩阵和非期望产出矩阵中的元素,ρ为生态效率值。

2.2 非参数Kernel密度估计

Kernel密度估计（Kernel Density Estimation）属于密度制图^[29],从本质上说,它是一个通过离散采样点进行表面内插的过程,即通过平滑的方法,用连续的密度曲线代替直方图,以更好地描述变量的分布形态,凭借其优良的统计特性,较直方图估计更加准确且平滑性好。其基本原理为：Kernel密度估计作为非参数估计方法,可用连续密度曲线描述随机变量的分布形态,设随机变量的密度函数为f（x）,对于随机变量Y有n个独立同分布的观测值,分别为y₁, y₂, …, y_n,则Kernel密度函数的估计量为^[30]：

f (x) = \frac{1}{nh} \overset{n}{\sum_{i = 1}} K (\frac{y_{i} - y}{h})

（3）
式中：n为研究区域个数;h为窗宽（bandwidth）;

K (\cdot)

为随机核函数,是一种加权函数或平滑函数,包括Gaussian(Normal) Kernel、Epanechnikov Kernel、Triangular Kernel、Quartic Kernel等类型。窗宽的选择决定了所估计密度函数的平滑程度,窗宽越大,核估计的方差越小,密度函数曲线越平滑,但估计的偏差越大,因此,最佳窗宽的选择必须在核估计的方差和偏差之间进行权衡,使均方误差最小,根据叶阿忠^[30]的相关研究,对应的最佳窗宽h = cN^-0.2（c为常数）。本文采用Gaussian Kernel分布的核密度函数,窗宽设定为h = 0.9SeN^-0.2（即c = 0.9Se,Se是随机变量观测值的标准差）。Kernel密度估计在Eviews软件内完成。

2.3 空间相关性分析

农业生态效率由于不同地区之间的资源禀赋、农业经济、空间背景等的不同而存在差异,根据地理学第一定律（Tobler's First Law of Geography）,空间单元中的每一个事物或现象并非孤立存在的,都是有联系的,邻近事物或现象之间的联系程度较远距离的事物更加紧密,意味着相邻地区的农业生产活动可能相互影响。空间自相关能够表示邻近地区的影响的大小,而地区空间分布的差异性可能存在空间自相关性,也即某地区的地理位置不仅影响其自身的农业生态效率,同时也会影响其邻域的农业生态效率。在这种情况下,需要对地区农业生态效率的空间自相关性进行度量,空间自相关分析包括全局空间自相关和局部空间自相关,本文以全局空间自相关来了解地区农业生态效率的空间关联和空间差异,在空间统计学中,常用的度量空间自相关程度的统计指标为Moran's I指数,其计算公式为：

I = \frac{n \overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} w_{ij} (x_{i} - \overset{?}{x}) (x_{j} - \overset{?}{x})}{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} w_{ij} \overset{n}{\sum_{i = 1}} (x_{i} {- \overset{?}{x})}^{2}}

（4）
式中：n为样本量;x_i、x_j为空间位置i和j的观察量;w_ij表示空间位置i和j的邻近关系,当i和j邻近时,w_ij = 1;反之为0。全局Moran's I指数的取值范围为[-1, 1],大于0为空间正相关,小于0为负相关,等于0为不相关。

2.4 空间马尔可夫链理论基础

传统马尔可夫链是根据俄国数学家马尔科夫（A.A Markov）的随机过程理论提取出来的,通过构造状态转移概率矩阵来测量事件发生的状态及其发展变化趋势,该过程中,在给定当前知识或信息的情况下,过去（即当期以前的历史状态）对于预测将来（即当期以后的未来状态）是无关的,即“无后效性”,也称为“马尔可夫性”。许多经济现象的演变过程存在“无后效性”特征,具体到农业生态效率,其演变过程同样存在“无后效性”。假设P_ij为某地区农业生态效率从t年的状态i转移到t+1年的状态j的转移概率,可采用转移的频数近似估算状态转移概率P_ij = n_ij/n_i,其中,n_ij表示在样本考察期内由t年状态i转移到t+1年状态j的城市数量,n_ij示在样本考察期内属于状态i的城市数量,且满足

\sum_{j} P_{ij} = \sum_{j} P {X_{n + 1} = j |X_{n} = i} = 1

。如果将农业生态效率划分为N种类型,即N个状态,则可以构造出N×N的状态转移概率矩阵（表1）,另外,根据农业生态效率类型的向上（提高）、不变和向下（降低）变化来定义转移的方向。
Tab. 1
表1
表1马尔可夫链状态转移概率矩阵(N = 4)
Tab. 1The probability transfer matrix of Markov chain (N=4)

t_i/t_i₊₁	1	2	3	4
1	P₁₁	P₁₂	P₁₃	P₁₄
2	P₂₁	P₂₂	P₂₃	P₂₄
3	P₃₁	P₃₂	P₃₃	P₃₄
4	P₄₁	P₄₂	P₄₃	P₄₄

新窗口打开
空间马尔可夫链分析则是把空间滞后的概念引入转移概率矩阵,这是因为区域经济增长及其他经济现象的演变在地理位置上并非孤立的、随机的,而是与相邻地区紧密联系、相互影响的。空间马尔可夫链弥补了传统马尔可夫链分析对研究区域的空间关联影响的忽视,用于揭示某经济现象时空演变与地区空间背景之间的内在联系。以某地区在初始年份的空间滞后类型为条件,将传统的N×N阶状态转移概率矩阵分解为N个N×N转移条件概率矩阵（表2）,使得能够分析在不同地理背景条件下,某地区农业生态效率提高或降低的可能性,以第N个条件矩阵为例,P_ij（N）表示以某地区在t年的空间滞后类型N为条件,该年由状态i转移到t+1年状态j的一步空间转移概率。某地区的空间滞后类型由其生态效率值在初始年份的空间滞后值来分类确定,空间滞后值是该区域邻近地区农业生态效率值的空间加权平均,通过地区农业生态效率值和空间权重矩阵的乘积来计算,即

\sum_{j} W_{ij} Y_{j}

,其中Y_j表示某地区生态效率值,W_ij表示空间权重矩阵W的元素。本文采用公共边界原则来确定空间权重矩阵,即地区相邻,则W_ij=1,否则W_ij = 0^[24,25,26]。由于海南省特殊的地理位置,权重矩阵的计算假定海南省与广东省相邻。
Tab. 2
表2
表2空间马尔可夫链状态转移条件概率矩阵(N=4)
Tab. 2The conditional probability transfer matrix of spatial Markov chain (N=4)

空间滞后	t_i/t_i₊₁	1	2	3	4
1	1	P_11/1	P_12/1	P_13/1	P_14/1
	2	P_21/1	P_22/1	P_23/1	P_24/1
	3	P_31/1	P_32/1	P_33/1	P_34/1
	4	P_41/1	P_42/1	P_43/1	P_44/1
2	1	P_11/2	P_12/2	P_13/2	P_14/2
	2	P_21/2	P_22/2	P_23/2	P_24/2
	3	P_31/2	P_21/2	P_21/2	P_21/2
	4	P_41/2	P_42/2	P_43/2	P_44/2
3	1	P_11/3	P_12/3	P_13/3	P_14/3
	2	P_21/3	P_22/3	P_23/3	P_24/3
	3	P_31/3	P_21/3	P_21/3	P_21/3
	4	P_41/3	P_42/3	P_43/3	P_44/3
4	1	P_11/4	P_12/4	P_13/4	P_14/4
	2	P_21/4	P_22/4	P_23/4	P_24/4
	3	P_31/4	P_21/4	P_21/4	P_21/4
	4	P_41/4	P_42/4	P_43/4	P_44/4

新窗口打开
通过比较传统马尔科夫转移矩阵（表1）和空间马尔科夫转移矩阵（表2）的相对应元素,能够了解某地区农业生态效率向上或向下的转移概率大小与周围邻域之间的关系,从而探讨不同空间背景对农业生态效率转移之间的空间溢出效应。如若P₁₂> P_12/1,则表示某城市生态效率在不考虑邻域的情况下,由状态1转移为状态2的概率要大于考虑邻域情况下,且城市与处于状态1的城市为邻时,由状态1转移为状态2的概率;如果空间背景对状态转移无影响,则有P₁₂= P_12/1。
马尔可夫过程在长时间的转移之后,如果系统存在一种平衡状态,即平衡状态时系统处于同一状态的概率是相同的,不依赖于初始状态,也不再随时间的推移而改变,此时的概率分布即是平稳分布^[29]。利用马尔可夫概率转移矩阵可以求得该随机过程的平稳分布,能够预测某经济现象（本文为农业生态效率）的动态演变趋势。假定传统马尔可夫链

{X_{n}, n = 0,1, 2, ?}

,状态空间,p_ij为一步转移概率,

{π_{i}, i \in S}

为各状态的概率分布,若

{π_{i}, i \in S}

满足方程组

π_{i} = \sum_{j}^{=} π_{j} p_{ij}

（

i = 0,1, 2, ?

）,则概率分布

{π_{i}, i \in S}

为传统马尔可夫链的平稳分布。将其推广到空间马尔可夫链,根据相似的原理求得每个空间滞后类型下的空间平稳分布,取转移概率最大值作为所对应状态可能的演变趋势。

3 研究对象与指标体系构建

3.1 研究对象与数据来源

广义的农业为农牧渔业,狭义的农业则指种植业,本文以狭义农业为研究内容测算农业生态效率,研究对象为全国30个省市（直辖市、自治区,不包括港澳台）,考虑到西藏自治区特殊的资源禀赋和农业生产条件,及数据的可获取性,未将其加入实证。以改革开放实施的初始年份1978年为起点,截止到2016年共39年为研究的时间区间。本文所用农业相关数据均来源于《中国农村统计年鉴》、各省市统计年鉴、各省市60年统计资料、及《全国农业机械化统计资料汇编1949-2004》,缺失数据根据插值法进行推算。另外,重庆在1997年之前、海南在1988年之前的数据通过各自统计年鉴和60年统计资料获取,并调整四川、广东相应年份的数据,最终得到了30个省市1978-2016年共39年的面板数据。国界线及省界线的矢量数据来源于2017年国家基础地理信息中心公布的全国1∶100万基础地理数据库（www.webmap.cn）,本文使用的空间坐标系统为Krasovsky_1940_Albers。

3.2 研究指标体系构建

农业生态效率本质上是以尽可能少的农业资源投入和最少的环境代价获得尽可能大的农业经济产出和生态保护,其综合反映了农业经济与资源利用、环境保护协调共赢的关系,本文农业生态效率的评价指标的选取参考已有研究^{[7, 20-21]}中的农业投入产出指标体系,结合数据的可得性及统计口径的一致性,最终以土地、劳动力、机械动力、灌溉、化肥、农药等作为地区农业资源投入指标,以农业总产值作为期望产出指标,以农业碳排放作为非期望产出,构建中国农业生态效率指标体系（表3）。
Tab. 3
表3
表3农业生态效率指标体系
Tab. 3The index system of agricultural eco-efficiency evaluation index

指标	变量	变量说明	备注
资源投入	土地投入	农作物播种总面积/千hm²	反映农业生产中的实际耕作面积
	劳动投入	农业从业人员/万人	以第一产业从业人员×(农业总产值/农林牧渔业总产值)进行折算
	机械投入	农业机械总动力/万kW	农业机械是农业现代化的代表性工具
	用水投入	有效灌溉面积/千hm²	农业用水主要是用来灌溉,以此来代理
	化肥投入	农用化肥施用量/万t (折纯量)	化肥、农药、农膜、柴油等的使用是农业生产过程中主要的污染源
	农药投入	农药使用量/万t
	农膜投入	农膜使用量/万t
	能源投入	农用柴油使用量/万t
期望产出	农业产出	农业总产值/亿元	折算到1978年不变价,以剔除价格变化的影响
非期望产出	碳排放	农业碳排放量/万t	参考李波等^[31]、王宝义等^[21]

新窗口打开
农业非期望产出主要包括农业碳排放和农业面源污染两类,有的****以农业碳排放作为非期望产出^[20],有的****将农业面源污染作为非期望产出^[7],有的****将两类同时作为非期望产出^[21],两类指标的测算均为各污染源排放量乘以各自的碳排放系数或无效利用系数（流失系数）,本文选择农业碳排放作为非期望产出,一方面考虑到农业碳排放包含的范围较农业面源污染更广泛,另一方面也考虑到农业碳排放更容易量化,以及研究的时间区间（1978-2016年）造成的数据可获得性。农业碳排放的测试参考李波等^[31]的碳排放模型及测算系数,选取了化肥、农药、农膜、农用柴油、灌溉耗电耗水、翻耕流失等六类直接或间接的碳排放,参照该研究,六大类碳源排放系数分别为化肥0.8956（kg/kg）、农药4.9341（kg/kg）、农膜5.18（kg/kg）、柴油0.5927（kg/kg）、农业灌溉20.476（kg/hm²）和农业翻耕312.6（kg/km²）。

4 结果分析

4.1 中国农业生态效率测定及时间序列分析

首先,通过对比各省市农业生产投入产出数据,可以发现多数省市第一产业从业人员经历了“上升→下降”式的倒“U”型过程,整体而言,现阶段呈现下降走势,而其他的投入指标除农作物播种面积变化较稳定外,呈现出不同程度的上升走势,这意味着伴随城镇化进程,大量农村劳动力的外出迁移,中国的农业经济发展已经由劳动力与机械化等物质生产要素“互补”的阶段向机械化等物质生产要素对劳动力“替代”转化的阶段,但物质生产要素对劳动力投入的不断替代过程,不仅带来了农业期望产出的增加,也不可避免地牺牲生态而造成了农业污染源排放量的增长。然后,基于DEA-SOLVER Pro 5.0软件,采用非径向（Non-Oriented）、规模报酬可变（VRS）的超效率SBM模型,测算中国1978-2016年30个省市的农业生态效率,求解各年份平均值,并采用通常的11∶8∶12东中西的区域划分方法,对不同区域农业生态效率均值进行对比分析（图1）。① 通过观察图1走势,各年份平均农业生态效率基本上处在0.7以下的水平,整体上中国农业生态效率处于较低水平,意味着中国农业的两型发展存在较大的资源节约和环境保护空间,1978-2016年间,中国农业生态效率呈现出在波动中稳定上升的走势,波动性主要体现在1978-2000年间,但变化幅度较小,2000年之后开始呈现稳定上升走势,21世纪以来,中央一号文件连续多年聚焦农业,关注“三农”问题,并明确提出“要鼓励发展循环农业、生态农业”,显示出政府对农业可持续发展能力的重视,避免了农业生态效率的下滑。② 通过对比东中西三个区域的农业生态效率,同样以2000年为界分为两个阶段,1978-2000年间的农业生态效率排名为西部>东部>中部,而在2000-2016年间的农业生态效率排名为东部>西部>中部,但中西部之间的差距较小,显示出随着农业经济的不断发展,东部地区农业技术水平的进步显著,且更加重视农业现代化,有意识保持农业生产、资源节约与环境保护之间的协调,而中西部地区农业技术水平发展缓慢,农业机械化程度较低,农业经济发展方式相对较粗放。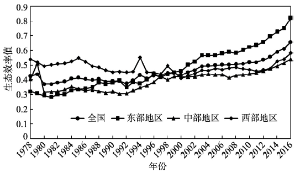

显示原图|下载原图ZIP|生成PPT
图11978-2016中国农业生态效率演变走势
-->Fig. 1The evolutionary trend of agricultural eco-efficiency in China from 1978 to 2016
-->

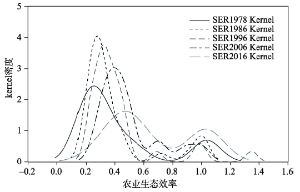
为继续探索各省市农业生态效率随时间演变的集聚差异,采用高斯正态分布的非参数Kernel核密度函数^{[29, 32]},选择1978年、1986年、1996年、2006年和2016年5个年份为观测时点进行核密度估计^[31],得到不同时点的分布状况（图2）。波峰的高度反映各省农业生态效率的集聚程度,由图2可以看出,中国农业生态效率整体上呈现出从左至右、波峰从高到低的“双峰”演变分布特征,显示出中国农业生态效率随时间变化而稳定提升的走势,多数省市由低水平集聚逐渐向“高—低”数量差异缩小的趋势转变。改革开放初期,多数省市的农业生态效率在低水平上集聚,进入90年代后,随着农业环保意识增强、农村劳动力转移、农业机械化水平进步加快,各省市农业生态效率呈现不同程度的提升,但各省之间资源禀赋、经济实力等仍存在差异,各省市农业生态效率的差距开始增大,形成了多个不同幅度的波峰,但低水平集聚的波峰呈逐渐下降,而到了2016年,双峰分布的波峰高度差距缩小,表明低水平农业生态效率与高水平农业生态效率的差距进一步缩小,逐渐形成“低低集聚、高高集聚”的近似“俱乐部收敛”的“双峰”式演变格局。

显示原图|下载原图ZIP|生成PPT
图2中国农业生态效率的Kernel密度估计
-->Fig. 2The Kernel density estimation of agricultural eco-efficiency in China
-->

4.2 中国农业生态效率的时间演变特征

由农业生态效率的时间分析和Kernel密度分析只能简单地刻画生态效率的时间变化走势及演变差异,并不能深刻反映其内在的时空演变规律。首先求解传统马尔可夫链概率转移矩阵,将1978-2016年间30省市按照农业生态效率的高低差异划分为不同类型的状态空间,考虑到各类型的省市观测量大致相同,按照分位数的划分方法^[28],以1/4、1/2、3/4分位数为界限,将农业生态效率值划分为4个相邻但不相互交叉的完备区间：（0.1603, 0.2939]、（0.2939, 0.3676]、（0.3676, 0.5046]及（0.5046, 1.8182],这4种状态类型的完备区间分别用k =1, 2, 3, 4来表示,k越大表示地区农业生态效率越高,另外,根据图1的演变走势,将整个研究期大致分为两个阶段：1978-2000年和2001-2016年,根据状态类型的划分分别求得传统的马尔可夫概率转移矩阵（表4）。
Tab. 4
表4
表41978-2016年中国农业生态效率的传统马尔可夫概率转移矩阵
Tab. 4Traditional Markov probability transfer matrix of agricultural eco-efficiency in China from 1978 to 2016

t\t+1	1978-2000年					2001-2016年
t\t+1	n	1	2	3	4	n	1	2	3	4
1	259	0.8842	0.1158	0	0	35	0.8857	0.1143	0	0
2	201	0.1095	0.7811	0.1095	0	91	0	0.8352	0.1648	0
3	106	0	0.1315	0.7642	0.1043	185	0	0.0270	0.9135	0.0595
4	124	0	0.0161	0.0726	0.9113	169	0	0	0.0118	0.9882

新窗口打开
表4对角线上的元素表示地区农业生态效率的状态类型未发生转移的概率,反映该地区农业生态效率演变的稳定性,而非对角线上的元素则表示地区农业生态效率在不同状态类型之间发生转移的概率,据此得出农业生态效率在未考虑地理空间格局下的演变特征：① 各省市农业生态效率具有维持原有状态的稳定性。所有对角线上的元素均显著大于非对角线上的元素,对角线上的元素最小值为0.7642,最大值为0.9882,即无论在哪个时期,某省市农业生态效率在当年属于某类型,在随后的年份仍属于该类型的概率至少为76%;另外,对角线两端的类型维持稳定性的概率最大（类型1和4）,农业生态效率存在向低水平和高水平收敛的可能性,也即“俱乐部收敛”;② 农业生态效率整体上具有向高水平方向转移的显著性趋势,从两个阶段转移频次来看,2001-2016年期间的类型1、2的数量明显少于1978-2000年期间,而类型3、4的数量则多于1978-2000年期间,但不同阶段内的转移也存在差异,1978-2000年期间,类型2和类型3向上或向下转移的概率差距较小,且P₂₂和P₃₃的差距也较小,表明该阶段各省市农业生态效率变化较稳定,而在2001-2016年期间,则P₂₁= 0 < P₂₃= 0.1648,P₃₂= 0.0270 < P₃₄= 0.0595,该阶段内各省市农业生态效率不断提高的可能性更大;③ 农业生态效率很难实现跨越式转移。农业生态效率的转移几乎发生在对角线两侧,从非对角线元素看,非对角线上的概率显著小于对角线上的概率,其最大值为0.1648,仅为对角线上概率最小值的21.57%,意味着在两个连续年份之间,农业生态效率实现跨越式转移的概率极小（如1→3）,表明各省市农业生态的改善是一个相对稳定持续的过程,短期内难以实现跨越式的发展演变。

4.3 中国农业生态效率的空间演变特征

随着中国农业市场经济的日趋完善和区域间开放程度的扩大,农业生产要素的空间流动性越来越频繁,农业生产之间的空间联系越来越紧密^[7],邻近省市之间的农业生态效率区位效应将越发显著。为深入了解不同省市农业生态效率的时空演变差异,构建空间马尔可夫链概率转移矩阵,对比两个矩阵中的相对应元素,探究在有无空间背景影响的前提下,某省市农业生态效率类型的转移概率与邻近省市之间的关系。首先测算1978-2016年农业生态效率全局Moran's I指数进行空间相关性检验,不同年份农业生态效率Moran's I指数均为正（0.1245~0.2780）,除个别年份外,均在5%（或10%）的显著性水平上通过检验,表明中国农业生态效率在空间分布上呈较显著的正相关性,地理空间格局是影响中国农业生态效率的重要因素,邻近省市之间农业生态效率的影响存在空间依赖性,某省市的农业生态效率不但会影响其周围省市,也会受周围邻近省市的影响。基于ArcGIS 10.4平台绘制1978-2000年和2001-2016年两个时期的农业生态效率类型转移的空间分布图（图3）。图3显示,① 在1978-2000年期间,农业生态效率向上转移的省市共有13个,主要集中在东部沿海和湖北、湖南、四川、陕西等若干中西部省份,而向下转移的省市共有7个,且主要集中在中西部省份,类型不变的省份则有10个,整体上反映出该时期内农业生态效率变化的空间格局与省市自身的经济实力、技术水平具有较大的关联性;② 在2001-2016年期间,农业生态效率向上转移的省市共有19个,中西部地区的数量增长明显,东部地区增长较稳定,农业生态效率向下转移的省市只有1个,而状态类型保持不变的省份仍有10个,但省份发生变化,表明该时期内农业生态效率整体上提升较显著,且逐渐向中西部地区扩散,空间溢出效应显著。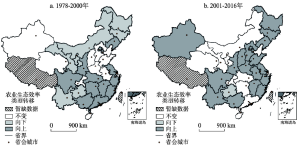

显示原图|下载原图ZIP|生成PPT
图3分阶段中国农业生态效率类型转移的空间分布格局
-->Fig. 3Spatial distribution of agricultural eco-efficiency type transfer in China in different stages
-->

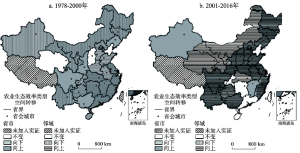
传统马尔可夫概率转移矩阵没有考虑周围邻域类型转移的影响,农业生态效率的向上或向下转移在空间上并不是孤立的,而是与周围邻域相铺相成、切实关联的。在传统马尔可夫概率转移矩阵的基础上,引入地理空间背景因素,以各省市在初始年份的空间滞后类型为条件构建空间马尔可夫概率转移矩阵。空间马尔可夫概率转移矩阵是以不同地区在初始年份的空间滞后类型为条件得到的,上述研究的两个时期的划分显示,农业生态效率的类型转移在时间上存在不稳定性,同样的,分别建立1978-2000年和2001-2016年两个时期的空间马尔可夫概率转移矩阵（表5）,并绘制空间格局分布图（图4）,考察不同省市所处的周围邻域对农业生态效率产生的影响。

显示原图|下载原图ZIP|生成PPT
图4分阶段中国农业生态效率类型转移及邻域转移的空间分布格局
-->Fig. 4Spatial distribution of agricultural eco-efficiency type transfer and adjacent in China in different stages
-->

Tab. 5
表5
表51978-2016年中国农业生态效率的空间马尔可夫概率转移矩阵
Tab. 5Spatial Markov probability transfer matrix of agricultural eco-efficiency in China from 1978 to 2016

空间滞后	t\t+1	1978-2000年					2001-2016年
空间滞后	t\t+1	n	1	2	3	4	n	1	2	3	4
1	1	86	0.8721	0.1279	0	0	0	0	0	0	0
	2	75	0.1200	0.7600	0.1200	0	0	0	0	0	0
	3	38	0	0.0789	0.8421	0.0789	0	0	0	0	0
	4	31	0	0.0645	0.0323	0.9032	0	0	0	0	0
2	1	70	0.8714	0.1286	0	0	25	0.9600	0.0400	0	0
	2	31	0.1613	0.7419	0.0968	0	40	0	0.9250	0.0750	0
	3	13	0	0.0769	0.7692	0.1538	30	0	0.0333	0.9000	0.0667
	4	47	0	0	0.0426	0.9574	49	0	0	0	1.0000
3	1	51	0.8824	0.1176	0	0	10	0.7000	0.3000	0	0
	2	52	0.0577	0.8269	0.1154	0	37	0	0.7568	0.2432	0
	3	36	0	0.1111	0.7222	0.1667	123	0	0.0163	0.9431	0.0407
	4	45	0	0	0.1111	0.8889	70	0	0	0.0143	0.9857
4	1	52	0.9231	0.0769	0	0	0	0	0	0	0
	2	43	0.0930	0.7907	0.1163	0	14	0	0.7143	0.2857	0
	3	19	0	0.0526	0.6842	0.2632	32	0	0.0625	0.7813	0.1563
	4	1	0	0	1	0	50	0	0	0.0200	0.9800

新窗口打开
空间马尔可夫概率转移矩阵除了具有与传统马尔可夫概率转移矩阵的共性特征外,通过两个时期的空间分布格局（图4）前后对比发现,当某省市农业生态效率向上转移时,其周围省市也向上转移的数量在增加,周围省市农业生态效率向下转移的数量在减小。另外,对比表4和表5的矩阵,还可以得出以下空间演变特征：① 地理空间格局在中国农业生态效率动态演变过程中发挥着重要作用。在不同的邻域背景下,各省市农业生态效率的类型转移概率并不相同,也不等于相对应的传统马尔可夫概率转移矩阵,否则,空间滞后的影响将不存在,比如,在不考虑地理空间格局的情况下,P₁₂= 0.1158,而当某省市与类型2的省市相邻时,其在1978-2000年期间的P_12/2= 0.1286,考虑空间背景分析农业生态效率的演变转移具有其必要性。② 在考虑地理空间格局的影响下,与不同类型的省市相邻,某省市农业生态效率类型转移的概率不尽相同,比如,在1978-2000年期间,P_23/2= 0.0968< P₂₃= 0.1095< P_23/3= 0.1154、P_21/2= 0.1613> P₂₁= 0.1095 > P_21/3= 0.0577,在2001-2016年期间,则P_23/2= 0.0750 < P₂₃= 0.1648 < P_23/3= 0.2432,一般来说,与农业生态效率较高的省市为邻,其向上转移的概率将增大,而与农业生态效率较低的省市为邻,其向下转移的概率将增大,可见,农业生态效率较低的省市对周围省市具有负向影响作用,而农业生态效率较高的省市对邻近省市具有正向溢出效应。③ 空间马尔可夫概率转移矩阵为“俱乐部收敛”现象的存在提供了空间意义上的解释。也即若某省市以农业生态效率较低的省市（1或2）为邻,其向上转移会受到抑制,向下转移的可能性将提高,如上述P_21/2= 0.1613 > P₂₁= 0.1095,而若是以农业生态效率较高的省市（3或4）为邻,则会收到邻近省市正的辐射作用,向上转移的可能性将提高,如P_34/4= 0.1563 > P₃₄= 0.0595,容易形成高低各自集聚的“俱乐部收敛”现象,也即“双峰”式分布。
以上通过矩阵之间的对比分析,结果显示空间背景格局对中国农业生态效率的时空演变产生重要的影响,农业生态效率较高的省市带动周围省市向上转移的可能性增大,具有正向的溢出效应,而农业生态效率较低的省市则抑制周围省市向上转移的可能性增大,并将继续维持农业生态效率低水平的状态,产生负向的溢出效应,从而在空间格局上逐渐形成“高高集聚、低低集聚、高辐射低、低抑制高”的“俱乐部收敛”现象,因而,空间马尔可夫链为“俱乐部收敛”现象的存在提供了空间意义上的解释^[24]。
为验证地理空间格局对中国农业生态效率的影响是否具有统计学上的显著意义,通过假设检验进行验证。原假设是农业生态效率的转移在空间上相互独立,其转移的概率大小与空间滞后类型无关,以至于能够直接采用传统马尔可夫概率转移矩阵来计算。构造似然比统计量对原假设进行检验^[33]：

Q = - 2 \log \{\overset{k}{\prod_{l = 1}} \overset{k}{\prod_{i = 1}} \overset{k}{\prod_{j = 1}} {[\frac{P_{ij}}{p_{ij} (l)}]}^{n_{ij} (l)}\}

（5）
式中：p_ij、p_ij(l)、n_ij(l)

(l = 1,2, ?, k)

分别表示不考虑地理空间格局的转移概率、空间滞后类型为l的条件下的空间转移概率以及相应的城市观察数量。统计量Q服从自由度为k(k-1)²的

χ^{2}

分布。根据该公式,分别求得1978-2000年和2001-2016年期间的统计量Q,计算求得

Q_{1978 - 2000}

= 46.52、

Q_{2000 - 2016}

= 48.61,对自由度进行相应调整后,由4×(4-1)²= 36分别变为30,在α=0.05的显著性水平下,

Q_{1978 - 2000} > χ^{2} (30)

= 43.77,而在α = 0.03的显著性水平下,

Q_{2001 - 2016} > χ^{2} (30)

= 46.98,因此,这两个时期均可以拒绝中国农业生态效率的类型转移在空间上相互独立的原假设,但2001-2016年期间的显著性高于1978-2000年期间,可见,随着农业现代化的发展、技术水平的进步、农业生产要素的空间流动性越来越频繁,农业生态效率的空间溢出效应将越发显著。

4.4 中国农业生态效率时空演变的趋势预测

空间马尔可夫概率转移矩阵显示中国农业生态效率的演变将会逐渐形成“俱乐部”收敛,但在长期的演变过程中是否仍将保持该收敛特性呢?由于中国各省市农业生态效率的类型转移具有维持原有状态的稳定性,但目前转移过程仍未达到一种平稳状态,状态类型的相互转移过程仍将继续。马尔可夫概率转移的极限分布是各类型转移达到均衡状态时的概率分布,也就是说,对于农业生态效率状态类型的n步概率转移矩阵,当

n \to \infty

时,便可得该状态概率转移的极限分布,而加入空间滞后的空间马尔可夫概率转移矩阵,可根据每一个空间滞后类型求得各自的极限分布,从而可以预测中国农业生态效率长期演变的发展趋势。由于此前的研究将1978-2016年分成了两个阶段,为了便于求解整体的极限分布,此处重新测算了整个研究时点的传统和空间马尔可夫概率转移矩阵,利用这两个矩阵测算两种背景条件下的极限分布（表6）,并与初始状态的概率分布进行对比。
Tab. 6
表6
表6中国农业生态效率类型转移的演变趋势预测
Tab. 6The evolutionary trend prediction of agricultural eco-efficiency type transfer in China

	空间滞后	1	2	3	4
初始状态		0.4667	0.2000	0.1000	0.2333
不考虑空间滞后的极限分布		0.1005	0.1582	0.2672	0.4741
考虑空间滞后的极限分布	1	0.0769	0.1247	0.2303	0.5681
	2	0.0476	0.0507	0.1948	0.7069
	3	0.0707	0.1558	0.4024	0.3711
	4	0.0866	0.1114	0.3357	0.4663

新窗口打开
在不考虑空间滞后的情况下,求解的极限分布与初始状态对比发现,处于类型1和2的省市数量在减小,而处于类型3和4的省市明显增加,表明中国各省市农业生态效率随时间推移的提升效果显著,多数省市向上转移为较高及以上水平（26.72%、47.41%）,只有少数省份向下转移或保持较低及以下水平。从极限分布的形状看,中国农业生态效率的转移并未出现“高高集聚、低低集聚”的局面,而是呈现出由低到高渐次递增的演变格局^[24],因而,在长期演变过程中,中国农业生态效率逐步向高水平发展,可见,由传统马尔可夫概率转移矩阵总结出的“俱乐部收敛”的“双峰”式特性在长期演变过程中将会演变为偏“单峰”式分布,短期内农业生态效率相对较低的省市随着农业现代化发展、生态环保意识增强等因素影响下,生态效率将逐步向上转移到较高水平,转移过程是稳定的、持续的,但仍有少数省份提升缓慢。
在考虑空间滞后的情况下,在不同的地理空间格局背景下,中国农业生态效率在长期演变中的转移概率存在显著差异。在与较低水平（类型1、2）农业生态效率的省市为邻时,其农业生态效率的长期演变的稳定状态同样呈现出由低到高渐次递增的格局,处于高水平（类型4）的省市数量分别为56.81%、70.69%,均高于传统极限分布的47.41%,“单峰”式的分布更加明显,显示出在该地理背景下,中国农业生态效率长期提升的潜力巨大;与较高水平（类型3、4）农业生态效率的省市为邻时,其长期演变逐渐形成高水平集聚（类型3、4）的偏“双峰”式分布,高低各自集聚的“俱乐部收敛”将逐渐消失,且与该类型的省市为邻时,处在该类型的省市的数量最大,比如,与类型3的省市为邻时,处在类型3的省市的数量为40.24%,均高于其他类型。整体而言,中国农业生态效率的长期演变趋势受地理空间格局的影响较显著。

5 结论

本文以1978-2016年中国各省市面板数据为研究单元,以狭义农业为研究对象,采用超效率SBM模型对省际农业生态效率进行测定,在基于Kernel密度估计的时间分析和全局Moran's I指数的空间相关性分析的基础上,构建传统和空间马尔可夫概率转移矩阵,通过矩阵的对比分析农业生态效率的时空动态演变特征,并预测其长期演变的趋势,探讨地理空间格局在农业生态效率时空演变过程中产生的影响。得到以下主要结论：
（1）从时间演变的差异来看,基于折线图和Kernel密度估计的中国农业生态效率呈现出在波动中稳定上升的走势,波动性主要集中在1978-2000年间,2001-2016年期间东部地区农业生态效率提升较中西部地区较显著,但整体仍处于较低水平,农业生态效率仍存在较大提升空间。Kernel密度估计图显示,中国农业生态效率演变的波峰呈现出由高向低转演变的“双峰”分布特征,且波峰高度的差距在缩小,逐渐形成“低低集聚、高高集聚”的“俱乐部收敛”格局。
（2）从空间演变的格局来看,全局Moran's I指数的结果显示,中国农业生态效率在空间分布上具有较显著的正相关性,省际农业生态效率之间存在空间依赖性。传统马尔可夫概率转移矩阵显示,农业生态效率整体上向高水平方向转移的趋势显著,农业生态效率的演变具有维持原有状态的稳定性,且较难实现跨越式转移,矩阵两端类型保持不变的概率最大,存在“低低集聚、高高集聚”的可能性。空间马尔可夫概率转移矩阵与传统转移矩阵的对比显示,除具有共有特性外,地理空间格局对农业生态效率时空演变过程中发挥着重要作用,空间溢出效应明显,在不同空间背景下,不同省市的农业生态效率类型转移的概率具有差异,某省市与农业生态效率较高的省市为邻,其向上转移的概率增加,而与农业生态效率较低的省市为邻,其向下转移的概率将增大,也即是农业生态效率较高的省市具有正向的溢出效应,而农业生态效率较低的省市具有负的溢出效应,从而在空间格局上逐渐形成“高高集聚、低低集聚、高辐射低、低抑制高”的“俱乐部收敛”,能够与时间演变特征相呼应。
（3）从长期演变的趋势来看,多数省市农业生态效率逐渐向上转移为较高水平,其演变特征由“俱乐部收敛”逐渐演变为由低到高渐次递增的格局,转移过程是稳定的、持续的。在不同地理空间格局下,与农业生态效率较低的省市为邻时,其长期演变的稳定状态同样呈现出由低到高渐次递增的过程,“单峰”分布更加明显,此背景下农业生态效率具有巨大的提升潜力,而与农业生态效率较高的省市为邻时,其长期演变将会由高低各自集聚的“俱乐部收敛”逐渐演化为较高水平（类型3、4）集聚的偏“双峰”分布。
基于超效率SBM模型和空间马尔可夫概率转移矩阵的中国农业生态效率时空演变特征及趋势预测,总结得出以下启示：
（1）基于非期望产出的超效率SBM模型能够充分考虑资源环境对农业生态效率的影响,并能够对效率为1的DMU进一步对比,但本文未考虑导致农业生态效率损失的各种社会经济因素,由于农业生态效率的损失是各种因素共同影响的结果,未来的研究可考虑结构变化、政策变化、技术变化、城镇化、外商直接投资（FDI）等因素,深入探讨农业生态效率损失的影响因素。
（2）空间马尔可夫概率转移矩阵是研究不同经济现象（农业生态效率）时空演变特征,并对长期演变趋势进行预测的有效方法之一,不仅强调了研究对象前后年份之间的紧密关联,也强调了地理空间格局对农业生态效率演变过程中产生的影响,将空间滞后条件纳入农业生态效率损失影响因素的计量模型构建空间面板计量模型,是未来深入研究的重要方向。
（3）中国农业生态效率的长期演变趋势显示,农业生态效率较低的省市存在巨大的提升潜力,中国农业现代化仍面临资源节约、环境保护的艰巨任务,需要按照“两型农业”发展的要求,继续深入转变农业经济发展方式,注重资源的节约保护和农业污染排放量的控制,加强农业科技创新与推广,实行更加严格的农业生态政策,明确生态事故主体责任;基于不同的地理空间格局、资源禀赋及农业经济发展水平,邻近省市之间应建立完备的生态农业合作机制、农业生态政策联动机制,加强农业生态合作与交流,农业生态效率较高的省市应发挥其辐射带动作用,而农业生态效率较低的省市应发挥其主观能动性,借鉴邻近农业生态效率较高省市的生态农业管理经验,并结合自身发展条件,寻求农业经济增长与资源节约、环境保护之间协调发展的均衡点,并改善省市间农业生态效率差距。
The authors have declared that no competing interests exist.

1978-2016年中国农业生态效率时空演变及趋势预测

本站小编 Free考研考试/2021-12-29

Spatial-temporal evolution and trend prediction of agricultural eco-efficiency in China: 1978-2016

1 引言