删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于矢量网格的城市土地利用邻里模式研究

本站小编 Free考研考试/2021-12-29

李也¹^,, 龚咏喜²^,³, 张兆东²^,³, 冯长春¹^,

1. 北京大学城市与环境学院,北京 100871

2. 哈尔滨工业大学（深圳）深圳市城市规划与决策仿真重点实验室,深圳 518055

3. 哈尔滨工业大学（深圳）建筑学院,深圳 518055

On the neighborhood patterns of urban land use using vector grids

LIYe¹^,, GONGYongxi²^,³, ZHANGZhaodong²^,³, FENGChangchun¹^,

1. College of Urban and Environmental Sciences, Peking University, Beijing 100871, China

2. Shenzhen Key Laboratory of Urban Planning and Decision Making, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, Guangdong, China

3. School of Architecture, Harbin Institute of Technology (Shenzhen), Shenzhen 518055, Guangdong, China;

通讯作者:通讯作者：冯长春(1957-), 男, 山西安泽人, 教授, 博士生导师, 主要从事区域发展与城镇化、城市与区域规划、土地与房地产经济研究。E-mail: fcc@urban.pku.edu.cn
收稿日期:2017-09-29
修回日期:2018-07-19
网络出版日期:2018-11-25
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

国家自然科学基金项目(41771169, 41371169);国土资源部公益性行业科研专项(201511010-3A);广东省科技计划项目(2013B040401003)

作者简介:
-->作者简介：李也(1988-), 男, 天津人, 博士生, 主要从事土地利用方面研究。E-mail: lyzero88712@163.com

展开

摘要
城市土地利用的空间分布特征一直是城市地理和城市规划领域关注的重点问题,对城市土地利用空间模式的研究有助于理解城市系统的运行状态。在分析现有城市空间结构和城市土地利用模式的基础上,从两个方面对现有基于富集因子的分析方法提出改进,一是采用矢量网格以减少分析的误差,二是采用斜网格和曼哈顿距离来对空间临近关系进行界定。采用这一方法对深圳市2015年6类城市土地利用数据进行分析,得到邻里尺度上各类用地之间富集度随距离变化的3种模式。模式I中,同类用地间的富集度在短距离内较大,且其值随着距离的增加而减小并趋于0,表明同类用地间在较短距离内相互吸引,而吸引力随着距离增加而减弱。在不同类型用地间的模式II和模式III中,富集度在较短距离内为负值,但是在模式II中,富集度随着距离的增加而逐渐增加并趋于0,表明不同用地间短距离内相互排斥,且排斥作用随着距离增加而减弱;而在模式III中,富集度则随着距离增加而快速上升到正值,然后逐渐下降并趋于0,表明不同类型用地在较短距离内相互排斥,但随着距离增加很快变为相互吸引,最后吸引力随着距离增加慢慢减弱。结果表明,相对于基于栅格网的分析方法,基于矢量斜网格的分析方法能够显著降低分析误差。

关键词：城市土地利用;邻里模式;富集因子;矢量网格
Abstract
The spatial distribution of urban land use is an important issue in urban geography and urban planning, and the research on the spatial patterns of urban land use could help us to understand the status of urban systems. We reviewed the research progress on urban spatial structure and urban land use patterns, and we improved the existing methods of enrichment factors from two aspects to analyze the neighborhood patterns of urban land use. The first was to adopt vector grids instead of raster grids to decrease errors, and the second was to use fastigiated grids and Manhattan distance to measure the neighborhood. We used the proposed method to analyze six types of urban land uses in Shenzhen in 2015 and identified three neighborhood patterns that revealed the variation of enrichment degrees between different types of urban land uses with respect to distance. Pattern I showed that the enrichment degree between the same urban land use type was high over short distances and became low over increasing distances, indicating the attraction of the same type of urban land use within short distances and the decrease of attraction over long distances. The value of the enrichment degree between different types of land uses was negative over short distances in both Pattern II and Pattern III. In Pattern II the enrichment degree gradually increased to 0 when the distance increased, demonstrating the repulsion between different types of land uses over short distances and the decrease of repulsion over long distances. In Pattern III the enrichment degree increased quickly to a positive value, then decreased gradually to 0, which revealed repulsion between different types of land uses over short distances, and the interaction became attraction over long distance. Compared with the method based on raster grids, the proposed method based on fastigiated vector grids can reduce the error of neighborhood patterns of urban land uses.

Keywords：urban land use;neighborhood pattern;enrichment factor;vector grid

-->0
PDF (4178KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
李也, 龚咏喜, 张兆东, 冯长春. 基于矢量网格的城市土地利用邻里模式研究[J]. 地理学报, 2018, 73(11): 2236-2249 https://doi.org/10.11821/dlxb201811014
LI Ye, GONG Yongxi, ZHANG Zhaodong, FENG Changchun. On the neighborhood patterns of urban land use using vector grids[J]. Acta Geographica Sinica, 2018, 73(11): 2236-2249 https://doi.org/10.11821/dlxb201811014

1 引言

城市是由多种要素组成的复杂系统,土地利用是城市复杂系统中的基本要素,城市土地利用的空间分布是各要素相互作用、相互影响的结果^[1,2]。对城市土地利用空间分布的研究一直是城市地理学、城市规划等相关领域研究的重要内容。早期对城市用地空间分布的研究主要是从宏观层面出发,相继提出了同心圆结构、扇形结构和多核心等城市空间结构,以解释和理解城市用地的空间分布规律^[3]。近年来,微观角度的城市土地利用空间分布特征成为人文地理学领域关注的热点,相关研究从微观视角探讨单一尺度城市用地的空间分布特征,如分析街区尺度土地利用混合特征及其对居民职住分离的影响^[4],或者分析城市道路、土地利用分区等因素对土地利用变化的作用^[5]。
在微观尺度对城市用地空间模式的提取,更多的是服务于用地变化的预测和多情景模拟^[6,7],特别是为元胞自动机（Cellular Automata, CA）模型提供用地变化转换的规则。CA是模拟土地利用变化空间分布的模型^[8],广泛用于区域和城市等多个尺度的土地利用变化模拟^[8,9]。用地邻里尺度上的相互作用和转换是CA模型的基础^[9,10,11],如提出富集因子的概念用于测量和分析用地的邻域特征和土地利用变化的规律,并将这些特征和规律作为CA模型的转换规则,从而实现对土地利用变化的模拟^[12]。富集因子以及基于富集因子的CA模型在后续研究中得到进一步扩展和应用,除了借助富集因子提取用地邻域关系的变化趋势,探求土地利用格局的邻域关系外^[13],更多研究重点关注如何利用富集因子校准土地利用模型中的转换规则,从而改善CA模型的土地利用变化模拟结果^{[8, 10, 12, 14]}。
可以看到,微观层面用地模式的研究主要服务于地理CA模型演化规则的提取,而对城市用地模式分析和提取的方法关注不够,对土地利用邻里尺度规律和模式的研究较少。现有研究多以栅格数据作为用地模式分析和提取的数据基础和模型基础^{[8,9,10,11,12]}。用地数据由矢量转换为栅格数据时,将损失部分用地信息,而损失的信息量与各类用地的空间形状、用地分类的详细程度有关,且具有空间尺度敏感性,将随着选择的网格单元的变大而变大。针对这一问题,部分****采用矢量数据提取和分析土地利用空间分布特征,提高对城市用地变化分析的精度,这也是当前研究的重要方向之一^[15,16,17]。考虑到在城市中街区大多采取棋盘式空间布局,不同用地之间主要是通过实际的道路网络产生相互作用,现有研究多采用欧式距离以及Moore邻接来定义邻域,也难以反映这一特点。
本文以深圳市为例,对现有基于栅格数据的富集因子分析方法进行改进,提出基于矢量斜网格的富集因子分析方法,并对深圳市2015年6类城市土地利用空间分布特征进行分析,得到各类用地在邻里尺度上的3种空间分布模式,最后对比基于矢量斜网格和基于栅格网的分析结果,显示基于栅格网方法的用地邻里特征结果具有较大误差,而采用矢量网格的方法则可以避免这一误差。

2 研究区域与数据

深圳市位于珠江口东岸,是中国第一个经济特区,也是中国第一个没有农村的高度城市化地区。全市土地总面积1948.69 km²,根据土地利用现状图统计,深圳市2015年建设用地面积为916 km²。随着经济的快速发展,深圳市城市空间逐渐向关外扩张,原分布于关内的加工工业逐步搬迁到关外及东莞、惠州等珠三角其他城市,代之而起的主要是高科技企业、高端制造业以及服务业。为了优化城市发展空间,协调关内关外发展,从2010年7月1日起启动特区内外一体化进程,将经济特区扩大到全市。
本文使用的主要数据为2015年深圳市城市土地利用现状图,来自深圳市规划和国土资源委员会。根据分析的需要对深圳市城市土地利用现状图中的用地类型进行归并,得到居住用地、商业用地、政府社团用地、工业用地、交通用地和其他用地等6大类用地（图1）。

显示原图|下载原图ZIP|生成PPT
图1归并后的深圳市2015年城市土地利用图
-->Fig. 1Urban land use of Shenzhen in 2015 after combination
-->

3 研究方法

3.1 富集因子

地理学第一定律Tobler定律认为,任何事物之间都是相关的,但在空间上相近的事物之间更加相关^[18]。分析邻里尺度上土地利用的特征,能够更好的发现土地利用的模式和特征,并有助于研究城市空间中不同用地之间的相互作用情况。
富集因子（Enrichment Factor, EF）是一种用来研究邻里尺度上不同用地之间空间模式的方法,该方法能够为CA模型提供土地利用变化的转换规则^[12]。给定空间位置,富集因子是该位置一定邻域内某种土地利用类型出现的次数相对于这类用地在整个研究区域出现次数的相对值,即：

F_{i, k, d} = \frac{\frac{n_{k, d, i}}{n_{d, i}}}{\frac{N_{k}}{N}}

（1）
式中：i为一个栅格单元,代表了一个空间位置;d为给定的邻域距离;k为土地利用类型;n_k_,_d_,_i为位置i距离为d的邻域内用地k的栅格单元的个数;n_d_,_i为位置i距离为d的邻域内栅格单元的个数;N_k为研究区域内用地k的栅格单元个数;N为研究区域内所有栅格单元的个数;F_i_,_k_,_d为位置i距离为d邻域内用地k的富集因子。
富集因子反映了当前位置的用地周围一定邻域范围内指定类型用地的相对集中程度。但要反映研究区域内不同用地之间的邻里模式,则需要根据大量空间单元的富集因子进行统计,计算研究区域中用地类型l在给定距离d的邻域范围内,某种用地类型k的富集因子的平均值,即：

{\overset{?}{F}}_{l, k, d} = \frac{\sum^{} F_{i, k, d}}{N_{l}}

（2）
式中：L为研究区域内土地利用类型l的栅格单元集合;N_l为研究区域内土地利用类型为l的栅格单元的数目。
同时还应计算富集因子的标准差,以判断均值是否能够反映用地的邻里模式,即：

S_{l, k, d} = \sqrt[]{\frac{1}{N_{l} - 1} {\sum^{} (F_{i, k, d} - {\overset{?}{F}}_{l, k, d})}^{2}}

（3）
通过计算富集因子的平均值来发现不同类型用地之间出现的空间模式,并通过标准差来检验这种模式的有效性,以分析土地利用邻里的相互作用以及土地利用变化的规律^{[19,20,21,22,23]}。

3.2 邻域、Moore邻接、Manhattan距离与斜网格

邻域是计算富集因子并分析土地用模式的基础,现有研究多基于Moore邻接来定义邻域^[10]。Moore邻域是以研究单元为中心并与其8个方向邻接的9个单元（包括中心单元）空间范围（图2a）。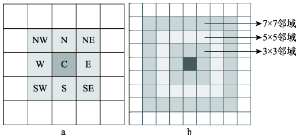

显示原图|下载原图ZIP|生成PPT
图2Moore邻域与距离
-->Fig. 2Moore neighborhood and distance
-->

基于Moore邻接,对于给定距离d,中心单元

c (i, j)

,该单元的邻域可以定义为：

Neighbor (m, n, d) = \{c (i, j) ||i - m| \leq d 且 |j - n| \leq d\}

（4）
式中：

c (i, j)

为i行j列的网格单元;

Neighbor (m, n, d)

为与中心单元（m, n）行距与列距都不大于d的网格单元的集合。距离为d的邻域为以给定网格单元为中心的（2d+1）×（2d+1）个单元。当所使用的网格单元为矢量时,基于Moore邻接并测度距离的单元称之为矢量正网格（图2b）。
在CA模型中采用Moore邻接来定义邻域,可以较好地反应相邻土地利用之间的交互作用及其土地利用模式,但在对城市土地利用模式的研究中,不同场所间相互作用的基础是连接场所的道路,相互作用的强度取决于实际街道的距离,因此要求在所定义的邻域和邻接关系中边界线距离中心单元的距离相同,而Moore邻接显然与这一要求不相符合。
现代城市布局多呈规则网格状态,虽然两点之间的距离可采用直线距离来测度,但连接两个地点的线路实际是街道,对实际连接路线的测度方式多为街区距离。街区距离也称为Manhattan距离,是两个点之间坐标轴方向的距离差之和,即：

Manh (p_{1}, p_{2}) = |p_{1} (x) - p_{2} (x)| + |p_{1} (y) - p_{2} (y)|

（5）
Manhattan距离是对城市中不同地点间相互影响的实际路径测度,因此从理论上看,将它作为富集因子计算的基础更为合理。同时也要考虑到,基于Manhattan距离计算富集因子,仍然要使中心单元与邻域范围的边界的距离相等。由于现有的栅格数据无法实现斜网格,斜网格都是基于矢量数据实现,本文称为矢量斜网格,即将图2中的正网格旋转45°得到的斜网格作为富集因子计算的基本空间单元（图3）。斜网格以给定单元为中心的9个单元格邻接为基础建立指定距离d的邻域,且给定单元的中心与一定距离邻域边界的Manhattan距离均相同。采用Manhattan距离时,其值在一般情况下也比两点之间的直线距离要大。

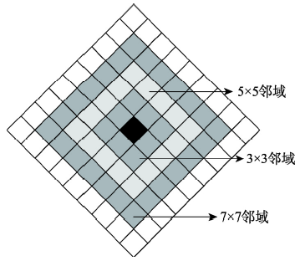显示原图|下载原图ZIP|生成PPT
图3基于斜网格和Manhattan距离的邻域范围
-->Fig. 3Neighborhood based on fastigiated grids and Manhattan distance
-->

3.3 栅格网格与矢量网格

现有方法中,计算富集因子一般采用栅格数据,当原始数据为矢量数据时,需要先转换为栅格数据。栅格数据中每个栅格单元只能属于一类用地,因此用地数据从矢量转换为栅格时,会将一个网格单元内的多种用地类型转变为单一的用地类型,从而造成用地信息损失,而网格单元越大,这种误差就越大,具有明显的尺度效应。在研究区域较小,土地利用的形状较为破碎或者呈点或者线性的地块时,采用栅格网格来分析土地利用的邻里模式将损失很多信息。城市受人类活动影响较大,用地景观较为破碎,建设用地分类较细,这些都可能导致较大的误差。
因此,本文基于矢量斜网格对富集因子进行重新定义并分析城市用地的邻里模式。下文不经特别说明,所指的网格均为斜网格,所指的距离均为Manhattan距离。对于一个给定矢量网格i,其距离为d的斜网格邻域内某种土地利用类型k的富集因子为：

F_{i, k, d} = \frac{\frac{a_{k, d, i}}{a_{d, i}}}{\frac{A_{k}}{A}}

（6）
式中：a_k_,_d_,_i为斜网格i在距离为d的邻域内用地类型k的面积;a_d_,_i为斜网格在距离为d的邻域的总面积;A_k为整个研究区域内土地利用类型k的面积;A为整个研究区域的面积;F_i_,_k_,_d为矢量网格i在距离d内土地利用类型k的富集因子。
在研究区域内,采用矢量网格计算得到的富集因子与采用栅格网格所得到的值有所不同。在栅格单元情况下,当前栅格单元为单一的土地利用类型;而在矢量网格单元情况下,一个网格单元可能包含多种土地利用类型。因此在研究区域内距离为d的邻域内,用地类型k在用地类型l周围的富集因子要以l在当前网格单元中的面积为权重来计算富集因子的平均值,即：

{\overset{?}{F}}_{l, k, d} = \frac{\sum^{} a_{i, l} \times F_{i, k, d}}{\sum a_{i, l}} = \frac{\sum^{} a_{i, l} \frac{\times a_{k, d, i}}{a_{d, i}}}{A_{l} \frac{\times A_{k}}{A}} = \frac{\sum^{} (a_{i, l} \sum^{} \frac{a_{j, k}}{a_{d, i}})}{A_{l} \frac{\times A_{k}}{A}}

（7）
式中：a_i_,_l为栅格单元i内土地利用类型l的面积;D_i_,_d为网格i距离为d邻域网格的集合。对于一个理想的平面以及给定的邻域距离d,任意网格邻域d内的面积a_d_,_i相同,记为a_d。因此,根据式（7）,对于给定的邻域距离d,用地类型k在l附近的富集因子均值和用地类型l在k附近的富集因子均值分别为：

{\overset{?}{F}}_{l, k, d} = \frac{\sum^{} (a_{i, l} \sum^{} a_{j, k})}{a_{d} \times A_{l} \frac{\times A_{k}}{A}} = \frac{\sum^{} \sum^{} a_{i, l} \times a_{j, k}}{a_{d} \times A_{l} \frac{\times A_{k}}{A}}

（8）

{\overset{?}{F}}_{k, l, d} = \frac{\sum^{} (a_{i, k} \sum^{} a_{j, l})}{a_{d} \times A_{l} \frac{\times A_{k}}{A}} = \frac{\sum^{} \sum^{} a_{i, k} \times a_{j, l}}{a_{d} \times A_{l} \frac{\times A_{k}}{A}}

（9）
由于式（8）和式（9）的分母部分实际上是在邻域距离d内所有网格内用地k和用地l面积的乘积之和,其值是相等的。因此从理论上来说,一对用地类型之间在给定距离d邻域内,它们之间富集因子均值是对称的,也就是说对于用地类型l和k,l距离d邻域内k的富集因子均值与k距离d的邻域内l的富集因子均值相等,即：

{\overset{?}{F}}_{l, k, d} = {\overset{?}{F}}_{k, l, d}

（10）
但在实际计算中,研究区域有边界,边界附近网格的邻域有可能会超出边界范围,从而导致

{\overset{?}{F}}_{l, k, d}

和

{\overset{?}{F}}_{k, l, d}

有一定的误差。考虑到用地间富集因子均值的对称性,下面对于两类用地间富集因子的描述将不再区分中心网格用地类型和邻域范围内的用地类型,而简称为这两类用地间的富集因子。
对于富集因子误差的计算,也要考虑其权重,即：

S_{l, k, d} = \sqrt[]{{\frac{\sum^{} a_{i, l} (F_{i, k, d} - {\overset{?}{F}}_{l, k, d})}{(N_{l} - 1) \sum^{} a_{i, l}}}^{2}}

（11）
在现有方法的基础上,通过将正网格改变为斜网格,采用Manhattan距离作为邻域计算的距离范式,并以矢量网格代替栅格网格,就形成一种适应性更强的富集因子及其误差的计算方法。

4 分析结果

根据上述方法对归并后的深圳市2015年6类城市土地利用数据计算不同用地间的富集因子,每一个斜网格的边长为200 m,则对角线长度为

200 \times \sqrt[]{2}

=282.84 m,一个网格的中心到相邻网格的中心,其Manhattan距离为282.84 m,到网格距离为1的邻域边界线的Manhattan距离为424.26 m,从中心网格到网格距离为d的邻域边界,其Manhattan距离为282.84×d+141.42 m。

4.1 深圳市城市土地利用富集因子

在基于栅格网格富集因子的土地利用邻里特征分析中,其最小邻域为距离值为1的3×3网格,因为如果为0则是网格单元本身,每个栅格单元均为单一土地利用类型,距离为0的富集因子没有意义。基于矢量网格计算富集因子时,距离为0时网格的邻域为矢量网格本身,由于每个网格单元中可以包含多种土地利用类型,因此在距离为0时的富集因子是有意义的。
基于矢量网格和Manhattan距离,计算深圳市2015年6类城市土地利用网格距离为1的富集因子均值及其标准差（表1）。如果土地利用类型l和k在网格距离为d邻域范围内的富集因子均值大于1,则说明l和k在d个网格邻域范围内呈现出相对集聚的空间特征;反之则呈现相对分散的空间特征。
Tab. 1
表1
表1深圳市2015年6类城市土地利用的富集因子均值及标准差(d = 1)
Tab. 1The means and standard deviations of EF (F_l_,_k_,_d₌₁) of the 6 types of urban land use neighborhood pattern (d=1) of Shenzhen in 2015

邻域土地利用类型(k)			居住用地	商业用地	工业用地	政府社团用地	交通用地	其他用地
中心单元土地利用类型 (l)	居住用地	均值	3.85	1.91	1.03	1.42	1.42	0.30
		标准差	1.71	1.70	1.24	1.69	1.69	0.74
		变异系数	0.44	0.89	1.21	1.19	1.19	2.50
	商业用地	均值	1.91	9.71	1.10	1.52	1.74	0.30
		标准差	2.69	8.85	2.05	2.92	3.29	1.33
		变异系数	1.41	0.91	1.86	1.93	1.90	4.39
	工业用地	均值	1.03	1.10	3.11	0.66	1.28	0.37
		标准差	1.01	1.18	1.24	0.92	1.35	0.78
		变异系数	0.98	1.07	0.40	1.39	1.06	2.10
	政府社团用地	均值	1.41	1.52	0.66	6.22	1.22	0.46
		标准差	1.49	1.69	1.08	4.85	1.83	1.21
		变异系数	1.05	1.11	1.62	0.78	1.50	2.62
	交通用地	均值	1.42	1.74	1.28	1.22	2.48	0.46
		标准差	0.75	0.92	0.77	0.94	1.77	0.71
		变异系数	0.53	0.53	0.60	0.77	0.71	1.54
	其他用地	均值	0.30	0.30	0.37	0.46	0.46	1.51
		标准差	0.34	0.37	0.33	0.44	0.46	0.43
		变异系数	1.17	1.21	0.91	0.95	1.00	0.28

注：加黑值为每类用地周围富集因子均值最高的值,加下划线值为所有大于1的富集因子均值。

新窗口打开
从表1可以看出,在给定距离d邻域内,一对用地类型之间富集因子均值是对称的,例如网格距离为1时,居住用地邻域内工业用地的富集因子均值为1.03,而工业用地邻域内居住用地的富集因子均值也为1.03,对于其他土地利用类型之间也是如此。表1中部分土地利用类型之间的值并不完全对称,而是存在细小的差别,这是因为边界附近网格邻域超出范围导致的结果。
表1中以加黑的方式标出每类用地周围富集因子均值最高的值,对所有大于1的富集因子均值加下划线,在对角线上同类用地间富集因子均值为该行和该列的最大值。这说明在网格距离为1的邻域范围内,同类用地高度集聚。这其中以商业用地最为集中,其富集因子均值为9.71;而政府社团用地的富集因子均值为6.22,表现出较高的空间集聚特征;其他如居住用地、工业用地和交通用地也表现出类似的特征,富集因子均值最小的为其他用地,说明其分布不够集中,这是因为这一类型的土地面积较大,与整个研究区域相比其相对集中程度较低。
除了同类用地之间的空间集聚特征外,不同用地间富集因子均值大于1的情况在表1中以下划线标出。不同用地间的富集因子均值大于1,说明在1个网格距离的邻域范围内,相对于整个研究区这两种类型用地分布相对集中。在网格距离为1时,共有13对不同用地类型间的组合,其中富集因子均值大于1的有9对,这些用地间在1个网格距离的邻域内表现出相对集聚的特征;而其他用地与所有非其他用地的富集因子均值都小于1,除此之外富集因子均值小于1的仅有工业用地与政府社团用地,说明工业用地与政府社团用地在1个网格距离内相互排斥。
计算富集因子均值的标准差和变异系数（表1）。总体来说,其标准差都比较小。在变异系数方面,表中的对角线为各土地利用类型与自身富集因子的变异系数,在富集因子均值较大的情况下,其误差比也都较小,说明各类用地间的空间特征较为稳定,变异系数最大的为商业用地对其他用地,高达4.39,其对应的均值为0.30。表1中其他用地富集因子的变异系数都比较大,这表明其他用地在各类用地1个网格距离邻域内的土地利用空间特征不明显。

4.2 深圳市城市土地利用邻里模式

为了分析城市土地利用空间特征随距离变化的情况,以网格距离为自变量绘制某种用地类型邻域内各种土地利用类型富集因子均值的变化。由于富集因子大于1时表明在邻域内某种土地利用类型相对集中,则对富集因子均值取自然对数后,其值大于0;当富集因子均值小于1时,取对数后则小于0,表明两种类型土地利用之间相对分散。
假设网格中心用地类型为l,其周围一定范围内用地类型为k,则将某个研究区域内给定用地类型k在用地类型l网格距离为d的邻域内富集因子均值的自然对数值称为用地类型k在用地类型l网格距离为d的邻域内的富集度（Enrichment Degree, ED）。由富集因子对用地类型的对称性可知,富集度的计算中用地l和用地k也具有对称性。当两类用地的富集度大于0,则说明这两类用地在给定的邻域内相对集聚,如果小于0,则说明这两类用地在给定的邻域内相对分散。
根据深圳市2015年6类城市土地利用数据计算各类用地富集度随距离的变化情况,如图4所示。其中,横坐标的距离是指200 m×200 m斜网格的个数,而网格距离d的实际距离为Manhattan距离下的282.84×d+141.42 m。图4中横坐标的网格距离从0~50,因此实际从网格中心到邻域范围的Manhattan距离为从141.42 m到14283.42 m。

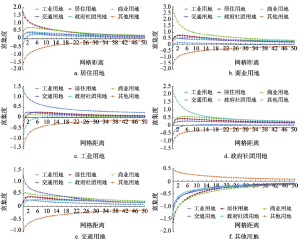显示原图|下载原图ZIP|生成PPT
图4深圳市2015年城市土地利用富集度随距离的变化
-->Fig. 4The urban land use ED as a function of the distance of Shenzhen in 2015
-->

从图4可以看到,在网格距离从0~50的邻域范围内,当网格中心用地类型和邻域用地类型相同时,其富集程度最高,并且富集度随着距离的增加而减弱,当距离达到一定值,使得邻域可以覆盖整个城市范围时,其值接近于0。这一特征可以用图5的模式I来描述,模式I主要是用来描述同类用地之间富集度随距离变化的情况。

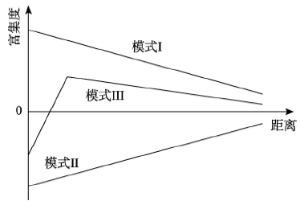显示原图|下载原图ZIP|生成PPT
图5城市土地利用富集度随距离变化的模式
-->Fig. 5Patterns of ED over distance of urban land use
-->

在网格距离为0的情况下,不同用地间的富集度一般都处于一个较小的值,且一般小于0,说明在距离很近的情况下,非同类用地之间具有相互排斥的作用。在开展具体研究时,对于边长为s的斜网格,网格距离为0实际表示在Manhattan距离为

s / \sqrt[]{2}

的邻域范围内的用地模式,从理论上来说,当s取值足够小,直到每个网格内仅包含一种类型用地时,则同类用地富集度的起始值为一个大于0的值,而不同类型用地间的富集因子为0,富集度为负无穷大。
当距离逐渐变大时,非同类用地间的富集度变化可以分为两类。一类是随着距离的增加,邻域用地的富集度也逐渐变大,并逐渐接近0,图5的模式II描述了这一特征。在这种情况下,邻域用地与中心网格用地之间在空间上存在明显的相互排斥,这种排斥作用随着距离的增加而减弱,例如其他用地和非其他用地之间都存在空间互斥的特征,政府社团用地和工业用地之间在较小的邻域范围内也基本表现出这一特征。另外一类是随着距离增加邻域用地的富集度快速增加,到达一个大于0的最大值,之后随着距离的增加富集度下降并趋于0,图5的模式III描述了这一特征。这种情况表明,两类用地之间在较小邻域范围内相互排斥,而随着距离的增加排斥作用减弱,并转变为相互吸引,达到较高的集聚程度,但这种空间集聚特征随着距离的进一步增加而减弱。
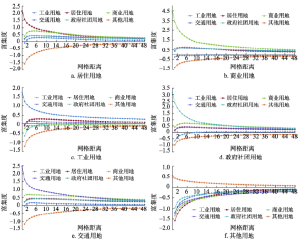
总体上来说,其他用地邻里范围各类用地富集度较小（图4e）,本文主要研究城市建设用地的邻里模式,因此下面将主要分析居住用地、商业用地、工业用地、政府社团用地和交通用地周围各类用地的富集度变化情况。
除去自身外,居住用地周围富集度最高的是商业用地（图4a）。这表明商业用地和居住用地在邻里尺度的分布相对集中。这种分布特征的形成,一方面由于商业设施需要为居民提供较为便利的服务,另一方面商业用地接近居住用地也可以吸引更多的客流,提高商业用地的效率。交通用地和政府社团用地在2~4个网格距离附近的富集度也较高,这与交通用地和政府社团用地的功能相吻合（图4a）：交通用地多呈狭长的线状,需要连接居民住所和其他类型的用地,这样才能满足居民完成各种社会活动的交通需求;而政府社团用地,特别是医疗、教育等公共服务设施用地需要在全市分散分布,服务于居民,因此这类用地在居住用地周围富集度也较高。总体上来看,居住用地附近1个网格距离之内的工业用地分布较少,这样可以减少工业生产对居民日常生活的影响,同时由于开展工业生产需要大量的人力资源,因此工业用地和居住用地的富集度在4个网格距离达到较高的值。
商业用地附近0个网格距离内富集度最高的非同类用地是交通用地（图4b）,表明商业用地周围需要较为完善的交通配套;随着距离的增加,富集度较高的用地类型变为居住用地和政府社团用地,政府社团用地在商业用地周围的高富集度与这两类用地较多位于关内且相伴出现有关。在商业用地周围,建设用地中富集程度最低的是工业用地,说明商业用地和工业用地之间集聚特征不明显。
总体上,在4个网格距离内,工业用地周围的交通用地富集度较高,商业用地和居住用地则处于较低的富集水平,但后两者的富集度随着距离增加而增长到较大的值（图4c）,这归结于工业生产需要运送原材料与产品,同时需要居住在附近的工作人员以及配套的商业设施。此外,政府社团用地在工业用地附近的富集度较低,这两类用地之间存在明显的空间排斥现象（图4c）。
在政府社团用地周围,商业用地、居住用地和交通用地的富集度随距离变化相似,在2~6个网格距离开始达到较高的集聚程度,而工业用地的空间集聚程度在7个网格距离内均低于全市水平,大于7个网格距离的相对集中程度也基本与全市持平（图4d）,说明在政府社团用地与商业用地、居住用地和交通用地之间相互吸引的关系较为明显,而与工业用地的吸引力则没有那么强烈。
交通用地周围几类建设用地的富集情况如图4e所示。交通用地周围的商业用地、居住用地和政府社团用地富集度较高,工业用地次之,其中商业用地富集度最高,表明总体上交通用地能很好的连接各类建设用地。

5 讨论与结论

5.1 讨论

相对于现有基于栅格网分析方法,基于矢量网格的土地利用邻里模式方法更具优势。从矢量数据转为栅格数据时会将网格用地类型转化为该网格内面积占优的用地类型,而损失该网格内其他的用地信息。为了说明矢量网格和栅格网格对用地邻里模式分析的影响,下面将分别比较基于Manhattan距离的矢量斜网格和基于Moore邻接的矢量正网格,以及矢量斜网格和栅格网格对用地富集度计算结果的影响。
在基于Manhattan距离的矢量斜网格和基于Moore邻接的矢量正网格的比较中,以边长200 m的矢量正网格为基本空间单元,计算各类用地间富集度随距离的变化情况。限于篇幅,本文仅列出居住用地和商业用地周围各类用地富集度随距离变化情况（图6）。将图6a、图6b分别与图4a和4b比较,可以发现,二者的差别比较细微,这说明采用矢量斜网格或者采用矢量正网格对土地利用富集度计算结果影响不大,但是采用矢量斜网格更能够达到理论上的自洽,其他各类用地情况与这两类用地相似。

显示原图|下载原图ZIP|生成PPT
图6基于Moore邻接的城市土地利用富集度随距离的变化
-->Fig. 6The urban land use ED as a function of the distance based on Moore neighborhood
-->

实际上,可以将矢量斜网格看作是矢量正网格旋转45°得到的网格（图7）。两种网格下分析空间的重叠率达到91%,同时考虑到用地分布的空间自相关,则基于矢量斜网格和基于Moore邻接的正网格得到的富集度及其随距离的变化情况相差较小就容易理解。

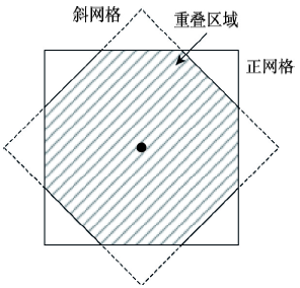显示原图|下载原图ZIP|生成PPT
图7基于Manhattan距离的矢量斜网格和基于Moore邻接的矢量网格
-->Fig. 7The fastigiated grid based on Manhattan distance and the vector grid based on Moore neighborhood
-->

比较矢量斜网格和栅格网对用地富集度计算结果的影响时,由于现有的栅格数据都是基于正网格,因此首先模拟将边长200 m的矢量正网格转换为栅格网格,即在每个网格中取面积最大的用地类型作为该网格的栅格用地类型,且其面积为整个网格的面积,其他各类用地面积设置为0,然后基于Moore邻接分析各类用地的富集度,如图8所示。需要注意的是,由于栅格方法中,网格距离为0时,不同用地类型间的富集因子平均值都为0,取对数后为非法值。因此,不同类型用地之间网格距离为0时的富集度值空缺（图8）。

显示原图|下载原图ZIP|生成PPT
图8基于栅格网的2015年深圳市城市土地利用富集度随距离的变化
-->Fig. 8The urban land use ED as a function of the distance based on raster grids in 2015
-->

基于栅格网格的同类用地间富集度都高于斜网格计算结果（图8）,这是因为同类用地在较小的网格距离内存在较高的相对集聚,而从矢量数据到栅格数据的转换过程中,信息损失导致对同类用地间富集度被高估,而且同类用地富集度的高估现象在分析的邻域范围内一直存在;相应的,基于栅格网格提取不同用地之间的富集因子为0,富集度则为负无穷大,这也是由于矢量数据转换为栅格数据时的信息损失导致的结果。
图8和图4的对比表明,基于矢量斜网格和基于栅格网格提取的土地利用富集度计算结果有较大差别。除了同类用地的富集度被高估外,基于栅格网方法计算不同类型用地的富集度也存在较大误差,且这种误差也会随着距离的变化而变化。为了详细分析栅格网计算结果的误差,下面采用基于栅格网的富集度与基于矢量斜网格的富集度的差值作为分析指标,当差值大于0时,表明基于栅格网得到的富集度被高估,反之则表明被低估。限于篇幅,仅对商业用地和工业用地周围各类用地富集度的误差进行分析。采用栅格网的同类用地间富集度高估最严重,而这种被高估的程度会随着距离的增加而减弱（图9）。图9a表明,采用栅格网计算富集度时,除本身外,商业用地周围交通用地的富集度高估最为严重,其次是政府社团用地;而工业用地富集度则被严重低估。在工业用地邻域范围内,商业用地富集度低估最为严重（图9b）,另一类被低估的用地类型为交通用地;居住用地的富集程度在较小邻域范围内被低估,但随着距离的增加又被高估。总体来看,基于栅格网的各类用地邻域内其他用地的富集度误差最小,这与其他用地面积较大且形状比较方正,从矢量数据到栅格数据的转换损失的信息量比较小有关系。基于栅格网计算的结果中,无论是同类用地还是不同用地间的富集度,其误差都呈现出随距离增加而减小的趋势。

显示原图|下载原图ZIP|生成PPT
图9基于栅格网富集度计算结果的误差分析
-->Fig. 9Errors of enrichment degree based on raster grids
-->

同时,基于栅格数据的用地邻里模式分析方法得到的结果具有空间尺度效应,一般而言,栅格单元越大,提取用地邻里模式时损失的信息量就越大。以工业用地为例,采用边长500 m的矢量斜网格和栅格网分别分析其周围各类用地富集度（图10）,发现采用栅格网得到的结果与采用矢量斜网格得到的结果相差很大,采用矢量斜网格时工业用地周围居住用地、交通用地以及商业用地的富集度都大于0,而采用栅格网后仅居住用地富集度大于0,商业用地和交通用地的富集度都小于0,特别是商业用地,由于采用栅格网导致的误差,使得该类用地由工业用地周围富集度较高的用地类型成为富集度最低的用地类型。比较200 m网格和500 m网格的误差分析结果也可以得到相同的结论。因此,在进行用地邻里模式的分析时,采用栅格网作为分析的基础具有明显的空间尺度效应,栅格的网格越大,计算得到的富集度结果与实际的误差就越大。

显示原图|下载原图ZIP|生成PPT
图10比较不同网格对工业用地周围边长500 m网格用地富集度随距离变化的影响
-->Fig. 10Comparison of the land use ED as a function of the distance based on 500 m grids in the neighborhood of industry land use using vector tilted grids and raster grids
-->

通过对城市土地利用邻里模式的比较分析,可以认为相比于现有基于栅格数据及栅格网的方法,基于矢量网格的方法能够减少因为数据转换带来的信息损失,并避免给分析结果带来误差。

5.2 结论

邻里尺度城市土地利用模式,特别是不同类型用地之间的伴随关系随着距离而变化的情况能够反映不同类型用地之间的吸引与排斥关系,这对于从微观角度理解城市土地利用以及城市动态空间和交互具有重要意义。本文基于矢量网格和Manhattan距离的富集因子分析不同类型用地在邻里尺度一定距离上的吸引和排斥情况,以及这种吸引和排斥随着距离变化的特征,总结归纳土地利用在邻里尺度上的模式,有助于从微观的视角理解城市空间及其空间交互的关系,也有助于理解城市中的空间交互以及城市土地利用的演变。
本文以深圳为例,采用深圳市2015年6类城市土地利用数据,对居住用地、商业用地、工业用地、政府社团用地、交通用地以及其他用地的土地利用邻里模式进行分析,得到3种城市土地利用邻里模式：同类用地之间的模式I,即在较小距离内同类用地高度富集,并且富集度随着距离的增加而降低,并趋向于0;不同用地类型之间的模式II,即在较小距离内两类用地之间相互排斥,富集度小于0,并且这种排斥的程度随着距离的增加而减弱,并最后趋于0;以及不同用地类型之间的模式III,即不同类型用地在较短距离内富集度小于0,表现出相互排斥的特征,但随着距离增加很快变为相互吸引,富集度上升至一个大于0的高值,然后随着距离的增加而逐渐减少并慢慢趋于0。整体上来说,模式I和模式III表现出用地之间相互吸引关系,而模式II则表现出不同用地之间的相互排斥。
深圳市2015年6类城市土地利用数据的富集度分析表明,6类用地之间,同类型用地都遵循模式I,即同类用地在空间上相对集聚,其他用地与居住用地、商业用地、工业用地、政府社团用地、交通用地等用地之间都遵循模式II,即其他用地和5类建设用地之间在邻里尺度上有明显的空间排斥,而在5类建设用地之间,除去政府社团用地和工业用地之间基本遵循模式II外,其他用地之间都遵循模式III,表现出一定程度上的空间吸引特征。
基于富集因子和富集度分析邻里尺度上的土地利用模式,并与智能刷卡记录和出租车轨迹等大数据以及社会感知等方法结合起来^{[24,25,26,27]},能够更好的理解城市系统中用地模式和空间行为之间的关系,这也是未来的工作方向。
The authors have declared that no competing interests exist.

基于矢量网格的城市土地利用邻里模式研究

本站小编 Free考研考试/2021-12-29

On the neighborhood patterns of urban land use using vector grids

1 引言

2 研究区域与数据