删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

黄河小北干流汛期和非汛期冲淤过程模拟

本站小编 Free考研考试/2021-12-29

邵文伟, 吴保生, 王彦君, 章若茵
清华大学水沙科学与水利水电工程国家重点实验室,北京 100084

Simulation of sedimentation processes in dry and wet seasons in the Xiaobeiganliu reach of the Yellow River

SHAOWenwei, WUBaosheng, WANGYanjun, ZHANGRuoyin
State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China
通讯作者:通讯作者:吴保生(1959-), 男, 河南安阳人, 教授, 博士生导师, 主要从事水力学及河流动力学方面的研究。E-mail: baosheng@tsinghua.edu.cn
收稿日期:2017-04-26
修回日期:2018-02-19
网络出版日期:2018-05-20
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

国家重点研发计划(2017YFC0405202)

国家自然科学基金重点项目(51639005)

作者简介:
-->作者简介：邵文伟(1985-), 男, 浙江金华人, 博士生, 主要从事河流地貌与河道演变研究。E-mail: shao_ww@mail.tsinghua.edu.cn

展开

摘要
滞后性是河流系统自动调整的重要特征之一。根据河道演变的滞后响应机制,在考虑上游来水来沙和下游侵蚀基准面（潼关高程）共同影响的基础上,建立了能够模拟河道汛期和非汛期冲淤过程的滞后响应模型,并采用黄河小北干流1960-2015年的冲淤资料进行参数率定（1960-2001年）和模型验证（2002-2015年）。结果表明该模型能较好地模拟小北干流汛期和非汛期的冲淤过程。汛期和非汛期累计冲淤量的模拟效果优于单个冲淤量;累计冲淤量和单个冲淤量的模拟效果汛期要优于非汛期。三门峡水库修建后,1960-2015年间小北干流汛期和非汛期的冲淤过程表现出时段差异。根据建立的滞后响应模型,本文分析了来水来沙和潼关高程对小北干流汛期和非汛期各个特征时段冲淤的贡献率,汛期和非汛期的第一时段（1960-1970年,1960-1968年）主要受到潼关高程的影响,但是后续时段主要受到来水来沙的影响。

关键词：小北干流;冲淤;潼关高程;滞后响应模型;汛期和非汛期
Abstract
Delayed response is one of important characteristics of self-adjustment in fluvial processes. Based on the mechanism of delayed response in fluvial processes, a delayed response model, considering the effects of water-sediment regime and the base level (Tongguan elevation), was developed to simulate the sedimentation processes in wet and dry seasons. The measured data in the period of 1960-2001 was used to estimate the parameters, and the measured data in the period of 2002-2015 was used to validate this model. Results showed that the proposed model could reasonably simulate the sedimentation processes in wet and dry seasons in the Xiaobeiganliu reach. This model performed better for cumulative sediment storage than single sediment storage in wet and dry seasons. Besides, this model also performed better for cumulative and single sediment storage in wet season than in dry season. Since the closure of Sanmenxia Dam, the sedimentation processes in wet and dry seasons in the Xiaobeiganliu has changed obviously in different periods during 1960-2015. Using this model, the contributions of water-sediment regime and the Tongguan elevation on sedimentation in different periods were analyzed. The sedimentation process was mainly affected by the Tongguan elevation in the period of 1960-1970(wet season) and 1960-1968(dry season). However, it was dominated by water- sediment regime after 1970(wet season) and 1968(dry season).

Keywords：Xiaobeiganliu reach;silt and scour;Tongguan elevation;delayed response model;wet and dry seasons

-->0
PDF (1884KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
邵文伟, 吴保生, 王彦君, 章若茵. 黄河小北干流汛期和非汛期冲淤过程模拟[J]. 地理学报, 2018, 73(5): 880-892 https://doi.org/10.11821/dlxb201805008
SHAO Wenwei, WU Baosheng, WANG Yanjun, ZHANG Ruoyin. Simulation of sedimentation processes in dry and wet seasons in the Xiaobeiganliu reach of the Yellow River[J]. Acta Geographica Sinica, 2018, 73(5): 880-892 https://doi.org/10.11821/dlxb201805008

1 引言

河流是地表输送水流和泥沙的主要通道,对维持生态环境有重要的意义^[1,2]。近些年来,受人类活动和气候变化的双重影响,河流系统的调整幅度发生了前所未有的变化^[3]。调整过程中河流通常表现出自动调整的趋向性,遵循平衡倾向性和系统能量分配规律原则^[4,5,6],即当来水来沙条件或边界条件发生改变时,河段将通过堆积和冲刷过程的调整,按照能耗最小或者方差最小理论,最终建立一个与外部条件相适应的新平衡状态。
滞后性是河流系统自动调整的重要特征之一^[7]。钱宁^[5]指出滞后性是因为河流系统通过自我调整以消除外界干扰后产生的变化,但从发生变化到消除变化以实现平衡需要经历一定的时间。进一步研究表明这一时间过程可大致分成反应、调整和平衡3个阶段^[8,9]。由于河道的调整速率与当前状态和平衡状态之间的差值成正比^[7],河道的调整速率一般表现为先增加后减小的特征^[10]。受流域来水来沙和地质地貌等因素影响,不同河流调整速率存在一定差异。大江大河调整时间会更长,时间尺度从一年到几十年不等^[9]。极端气候事件以及人类活动（水库,采沙）则会显著缩短响应时间,加速河道自身的调整过程^[11]。
人们最初基于变率方程模拟河道自动调整中的滞后响应过程^[12]。王兆印等^[13]据此建立了渭河下游河道冲淤量的计算方法,模拟了1960-2001年渭河下游的累计冲淤过程。吴保生^[14,15]根据变率方程提出了滞后响应模型的单步和多步模式,较好地模拟了水库冲淤、平滩面积和平滩流量的演变过程。郑珊等^[16]建立了考虑侵蚀基准面和来水来沙共同作用下的滞后响应模型,并应用于渭河下游和小北干流河道冲淤过程的模拟。以上模型多考虑年际尺度上的河床演变过程,然而季节性河流汛期和非汛期在来水来沙以及冲淤变化上存在巨大差异,调整速率也显著不同,以年为尺度的滞后响应模型势必掩盖了季节性河流汛期和非汛期冲淤变化特点,因此有必要建立能够模拟汛期和非汛期河床演变的滞后响应模型。黄河小北干流位于三门峡水库上游,是黄河中游产沙区的末端,汛期和非汛期冲淤存在显著差异。本文在分析黄河小北干流汛期和非汛期冲淤过程基础上,建立了能够模拟汛期和非汛期冲淤过程的滞后响应模型,并以此分析了不同时段来水来沙和潼关高程对河道冲淤变化的影响。

2 研究区概况

黄河中游禹门口（龙门）至潼关河段称为小北干流,全长135.2 km（图1）。在距今~150 ka BP的更新世早中期,古三门湖盆被切穿^[17],黄河侵蚀基准面下降了40 m左右,小北干流经历了下切和堆积过程,形成了多级阶地^[18]。小北干流为典型的游荡型河段,河道宽浅散乱,比降0.3‰~0.6‰,弯曲系数1.0~1.4。河床平均宽度8.5 km,河床组成粗,河漫滩两侧为高出河床50~200 m的黄土台塬。河道平面形态为两头宽中间窄的哑铃状,据此把小北干流分为3大段：① 上段为禹门口至庙前（61断面）,全长42.5 km,河道宽浅,汾河于左岸汇入,禹门口以下河宽瞬间增加到3 km左右;② 中段为庙前至夹马口（54断面）,全长30 km,河道较窄;③ 下段为夹马口至潼关,河长60 km,是小北干流最宽的河段。小北干流主要支流有左岸的汾河和涑水河以及右岸的涺水,来水来沙量相对较小。渭河在潼关汇入黄河（图1）。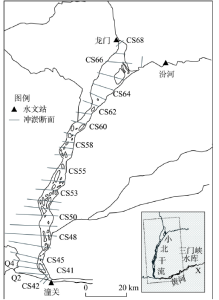

显示原图|下载原图ZIP|生成PPT
图1黄河小北干流概况图
-->Fig. 1Map showing the location of the Xiaobeiganliu reach in the Yellow River
-->

小北干流来水来沙受到上游水库、水土保持措施以及河道整治工程的影响。特别是龙羊峡水库和刘家峡水库在1986年联合运用后,对小北干流的来水来沙产生了显著的影响。来水来沙明显减小,汛期水量和沙量占全年水量百分比减少,大流量和大沙量出现的机率降低及中小流量历时变长。
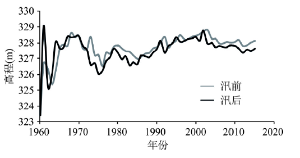
三门峡水库对小北干流的河床演变有着巨大的影响。三门峡水库于1960年9月下闸蓄水运用,坝址距离潼关113.5 km。自投入使用以来,水库依次历经蓄水拦沙、滞洪排沙和蓄清排浑3个阶段^[19],相应潼关高程（潼关断面1000 m³/s流量相应的水位）的变化过程如图2所示。自1973年采取蓄清排浑运用方式后的1974-1985年,水沙条件与水库运用方式比较适应,潼关高程相对稳定。1986年以后潼关高程再次呈上升趋势,1995-2001年期间在328.1~328.3 m之间变化。为了适应来水来沙条件的变化,降低并控制潼关高程,消除水库运用对渭河的不利影响,2003年之后（2002年11月）开始,在三门峡水库开展了“非汛期控制318 m”的原型试验：非汛期最高运用水位严格控制在318 m以下,汛期平水期按305 m控制,潼关高程有所降低。

显示原图|下载原图ZIP|生成PPT
图21960-2015年间潼关高程的变化过程
-->Fig. 2Variation of the Tongguan elevation during 1960-2015
-->

3 研究方法

3.1 数据与资料

本文收集了1960-2015年间黄河小北干流汛期和非汛期的来水来沙和冲淤量资料。数据来源于文献^[20]、黄河泥沙公报、黄河水文年鉴和黄河年度咨询报告。冲淤量根据断面法计算。小北干流由潼关至龙门常设淤积断面34个,断面平均间距4830 m（图1）。由下游往上游依次命名为黄淤41断面（CS41）,黄淤42断面（CS42）直至黄淤68断面（CS68）。除部分缺测外,断面每年至少在汛前（5、6月份）和汛后（9、10月份）各测量1次。

3.2 汛期和非汛期滞后响应模型

河流受到外部扰动后,河床特征变量的调整速率一般与其当前状态和平衡状态之间的差值成正比,用速率方程表示为：

\begin{matrix} \frac{dy}{dt} = β (y_{e} - y) \end{matrix}

（1）
式中：y为特征变量,本文中为河道累计冲淤量;t为计算时段;y_e为河道适应外界扰动而建立的新平衡状态;

\begin{matrix} β \end{matrix}

为比例系数,又称为河道的调整速率参数,反映了河道受到外部扰动后调整速率的快慢。
吴保生^[14,15]根据速率方程,建立了能够反映河床演变过程的模拟方法,取得良好的效果。以河道的累计冲淤量为特征变量,分别得到了河道冲淤量的单步和多步计算方法：

\begin{matrix} y = (1 - e^{- βt}) + y_{0} e^{- βt} \end{matrix}

（2）

\begin{matrix} y_{n} = (1 - e^{- βΔt}) \overset{n}{\sum_{i = 1}} (e^{- (n - i) βΔt} y_{e, i}) + e^{- nβΔt} y_{0} \end{matrix}

（3）
式中：y₀为冲淤量初始值;y_n为第n个时段的累计冲淤量;y_e_,_i为第i时刻的平衡冲淤量。
无论是单步模式还是多步模式,模型的关键问题是如何确定平衡冲淤量y_e。郑珊等^[16]在前人研究的基础上,假设平衡淤积体是纵剖面为三角形的锥体,并协同考虑了水沙条件和河道侵蚀基准面对河道平衡冲淤量的双重影响,进一步细化了河道沖淤量平衡态的计算方法。其平衡冲淤量描述公式如下：

\begin{matrix} y_{e} = \frac{KBΔ Z^{2}}{2 J_{0}} (1 + \frac{k W_{f}^{a} W_{sf}^{b}}{ΔZ}) \end{matrix}

（4）
式中：K为小北干流冲淤平衡时潼关河床高程与潼关高程抬升值（ΔZ,单位m）间的关系系数;B为平衡淤积体的横向平均宽度（m）;J₀为初始河床比降;k为平衡淤积体翘尾巴高度与汛期来水（W_f）和汛期来沙（W_sf）的关系系数;a、b分别为关于来水和来沙的参数。
将式（4）分别代入到式（2）和（3）中,得到考虑上游来水来沙和下游侵蚀基准面的单步和多步计算模型^[16]：

\begin{matrix} y = (1 - e^{- βt}) \frac{KBΔ Z^{2}}{2 J_{0}} (1 + \frac{k W_{f}^{a} W_{sf}^{b}}{ΔZ}) + y_{0} e^{- βt} \end{matrix}

（5）

\begin{matrix} y_{n} = (1 - e^{- βt}) \frac{KBΔ Z^{2}}{2 J_{0}} \overset{n}{\sum_{i = 1}} [e^{- (n - i) βt} (1 + \frac{k W_{f, i}^{a} W_{sf, i}^{b}}{Δ Z_{i}})] + e^{- nβt} y_{0} \end{matrix}

（6）
假设汛期和非汛期的河道调整速率,计算时段和平衡冲淤量分别为β_f和β_d、t_f和t_d以及y_ef和y_ed。以某一非汛期作为初始时刻,记初始时刻的冲淤量为y₀。记经过第一个非汛期（t_d）末的冲淤量为y_d₁,根据式（2）可以计算得到：

\begin{matrix} y_{d 1} = (1 - e^{- β_{d} t_{d}}) y_{ed 1} + y_{0} e^{- β_{d} t_{d}} \end{matrix}

（7）
经过第1个汛期t_f后,汛末的累计冲淤量为y_f₁,将上一时段非汛期末的计算值即式（7）代入到式（2）,可得到：

\begin{matrix} y_{f 1} = (1 - e^{- β_{f} t_{f}}) y_{ef 1} + (1 - e^{- β_{d} t_{d}}) e^{- β_{f} t_{f}} y_{ed 1} + y_{0} e^{- β_{d} t_{d} - β_{f} t_{f}} \end{matrix}

（8）
记第2个非汛期末的累计冲淤量为

\begin{matrix} y_{d 2} \end{matrix}

\begin{matrix} y_{0} \end{matrix}

则为上一时段的计算值y_f1,可以得到：

\begin{matrix} y_{d 2} = (1 - e^{- β_{d} t_{d}}) y_{ed 2} + (1 - e^{- β_{f} t_{f}}) e^{- β_{d} t_{d}} y_{ef 1} + (1 - e^{- β_{d} t_{d}}) e^{- β_{f} t_{f} - β_{d} t_{d}} y_{ed 1} + y_{0} e^{- 2 β_{d} t_{d} - β_{f} t_{f}} \end{matrix}

（9）
记第2个汛期末的累计冲淤量为y_f₂,y₀则为上一时段的计算值y_d₂,可以得到：
（10）
记第3个非汛期末的累计冲淤量为y_d₃,y₀则为上一时段的计算值y_f₂,可以得到：

\begin{matrix} y_{d 3} = (1 - e^{- β_{d} t_{d}}) y_{ed 3} + (1 - e^{- β_{d} t_{d}}) y_{ed 2} e^{- β_{f} t_{f} - β_{d} t_{d}} + (1 - e^{- β_{d} t_{d}}) e^{- 2 β_{f} t_{f} - 2 β_{d} t_{d}} y_{ed 1} + \\ (1 - e^{- β_{f} t_{f}}) y_{ef 2} e^{- β_{d} t_{d}} + (1 - e^{- β_{f} t_{f}}) y_{ef 1} e^{- β_{f} t_{f} - 2 β_{d} t_{d}} + y_{0} e^{- 3 β_{d} t_{d} - 2 β_{f} t_{f}} \end{matrix}

（11）
多次迭代计算后,非汛期和汛期的冲淤量的多步递推模式可用下式表示：

\begin{matrix} y_{di} = \overset{n}{\sum_{i = 1}} (1 - e^{- β_{d} t_{d}}) y_{edi} e^{- (n - i) (β_{f} t_{f} + β_{d} t_{d})} + \overset{n - 1}{\sum_{i = 1}} (1 - e^{- β_{f} t_{f}}) y_{efi} e^{- [(n - i) β_{d} t_{d} + (n - i - 1) β_{f} t_{f}]} + y_{0} e^{- [n β_{d} t_{d} + (n - 1) β_{f} t_{f}]} \end{matrix}

（12）

\begin{matrix} y_{fi} = \overset{n}{\sum_{i = 1}} (1 - e^{- β_{f} t_{f}}) y_{efi} e^{- (n - i) (β_{f} t_{f} + β_{d} t_{d})} + \overset{n - 1}{\sum_{i = 1}} (1 - e^{- β_{d} t_{d}}) y_{edi} e^{- [(n - i) β_{d} t_{d} + (n - i + 1) β_{f} t_{f}]} + y_{0} e^{- n (β_{d} t_{d} + β_{f} t_{f})} \end{matrix}

（13）
式中：y_di、y_fi分别表示汛期末和非汛期末的累计冲淤量。考虑平衡淤积体的表达方式,将（4）式分别带入式（12）和式（13）,可得到计算汛期和非汛期冲淤过程的滞后响应模型：

\begin{matrix} y_{di} = \frac{KB}{2 J_{0}} [\overset{n}{\sum_{i = 1}} (1 - e^{- β_{d} t_{d}}) Δ Z_{i}^{2} (1 + \frac{k_{d} W_{d}^{a} W_{sd}^{b}}{Δ Z_{i}}) e^{- (n - i) (β_{f} t_{f} + β_{d} t_{d})} + \\ \overset{n - 1}{\sum_{i = 1}} (1 - e^{- β_{f} t_{f}}) Δ {Z_{i}}^{2} (1 + \frac{k_{d} W_{d}^{a} W_{sd}^{b}}{Δ Z_{i}}) e^{- [(n - i) β_{d} t_{d} + (n - i - 1) β_{f} t_{f}]}] + y_{0} e^{- [n β_{d} t_{d} + (n - 1) β_{f} t_{f}]} \end{matrix}

（14）

\begin{matrix} y_{fi} = \frac{KB}{2 J_{0}} \overset{n}{\sum_{i = 1}} (1 - e^{- β_{f} t_{f}}) Δ Z_{i}^{2} (1 + \frac{k W_{fi}^{a} W_{sfi}^{b}}{Δ Z_{i}}) e^{- (n - i) (β_{f} t_{f} + β_{d} t_{d})} + \\ \overset{n - 1}{\sum_{i = 1}} (1 - e^{- β_{d} t_{d}}) Δ Z_{i}^{2} (1 + \frac{k W_{fi}^{a} W_{sfi}^{b}}{Δ Z_{i}}) e^{- [(n - i) β_{d} t_{d} + (n - i + 1) β_{f} t_{f}]} + y_{0} e^{- n (β_{d} t_{d} + β_{f} t_{f})} \end{matrix}

（15）
式中：y_di、f_fi分别表示为第i个汛期末和非汛期末的累计冲淤量,式（14）和式（15）相减可以得到单个汛期和非汛期的冲淤量。考虑到单步模式依赖于上一个时段的实测值,故本文仅考虑多步模式计算。

4 研究结果

4.1 汛期冲淤过程

小北干流年内冲淤过程表现为汛期淤积和非汛期冲刷（图3a）。1960-2015年间汛期累计淤积泥沙41.46亿m³,汛期平均冲淤量为0.74±0.95亿m³。根据累计曲线（图3b）,可将小北干流汛期冲淤过程分为4个阶段,即1960-1970年、1971-1985年、1986-1998年、1999-2015年。其中,1960-1970年为快速淤积阶段,共淤积泥沙18.95亿m³,单个汛期淤积速率为1.72亿m³（表1）。1971-1985年间单个汛期淤积速率迅速降为0.54亿m³。1986-1998年间,淤积速率比前一时期增加了0.25亿m³,仅次于第一时期。1999-2015年间,汛期累计淤积仅为3.01亿m³,平均单个汛期淤积0.18亿m³。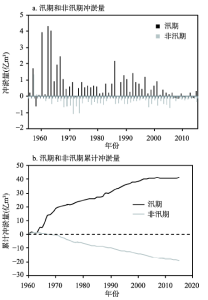

显示原图|下载原图ZIP|生成PPT
图31960-2015年小北干流汛期和非汛期冲淤量及其累计冲淤量
-->Fig. 3Sediment storage and cumulative sediment storage in the Xiaobeiganliu reach in the period of 1960-2015
-->

Tab. 1
表1
表1小北干流汛期各特征时段的冲淤量及来水来沙特征
Tab. 1Sediment storage and the character of the water-sediment regime in wet season in the Xiaobeiganliu reach at different periods

时期	汛期来水(亿m³)	来沙量(亿t)	含沙量(kg/m³)	来沙系数(kg/m⁶)	淤积量(亿m³)	淤积速率(亿m³/a)
1960-1970年	194.34	10.26	52.81	0.029	18.95	1.72
1971-1985年	161.82	5.80	35.85	0.024	8.05	0.54
1986-1998年	89.25	4.37	48.93	0.058	11.16	0.86
1999-2015年	77.89	1.20	15.45	0.021	3.01	0.18
1960-2015年	125.88	4.95	39.32	0.033	41.16	0.74

新窗口打开

4.2 非汛期冲淤过程

小北干流非汛期河道以冲刷为主,共冲刷泥沙18.79亿m³,平均冲刷量为0.34±0.33亿m³（表2）。依据非汛期冲淤量累计曲线（图3b）,非汛期的冲淤过程可分为1960-1968年（微淤）,1969-1977年（快速冲刷）,1978-1998年（冲刷）,1998-2006年（快速冲刷）和2007-2015年（缓慢冲刷）5个时段。1960-1968年非汛期,共淤积泥沙0.28亿m³,年淤积泥沙0.03亿m³,冲淤交替,河道整体略有淤积。1969-1977年非汛期冲刷速率在5个时期中最高。1978-1998年非汛期,冲刷速率下降到0.34亿m³。1999-2006年非汛期的冲刷速率仅次于1969-1977年。2007-2015年平均冲刷量仅次于1960-1966年。
Tab. 2
表2
表2小北干流非汛期各个时期的冲淤量及其来水来沙特征
Tab. 2Sediment storage and the character of the water-sediment regime in dry season in the Xiaobeiganliu reach at different periods

时期	非汛期来水(亿m³)	来沙量(亿t)	含沙量(kg/m³)	来沙系数(kg/m⁶)	淤积量(亿m³)	淤积速率(亿m³/a)
1960-1968年	134.47	0.91	6.78	0.011	0.28	0.03
1969-1977年	134.27	0.83	6.19	0.010	-5.90	-0.66
1978-1998年	124.70	0.91	7.29	0.012	-7.05	-0.34
1999-2006年	102.78	0.60	5.85	0.012	-4.16	-0.52
2007-2015年	113.58	0.13	1.13	0.002	-1.74	-0.22
1960-2015年	120.38	0.69	5.70	0.010	-18.79	-0.34

新窗口打开

4.3 滞后响应模型

式（14）和式（15）为计算汛期末和非汛期末累计冲淤量的滞后响应模型,它基于汛期和非汛期水沙条件,同时考虑潼关高程的影响。为确定模型参数,本文将1960-2001年时段作为模型的率定期,2002-2015年作为模型的验证期,模型的率定和验证均在汛期和非汛期尺度上进行。根据1960-2001年黄河小北干流汛期和非汛期的来水来沙,实测累计冲淤量和潼关高程,通过标准差分进化算法（DE）率定参数,主要参数如表3所示。标准差分进化算法是由N（种群规模）个D（待率定参数）维参数矢量在搜索空间进行并行直接的搜索。具体是通过差分变异和交叉操作产生后代群体,应用最优函数将子个体和对应父个体进行选择操作,从而把最优者保存到下代直至选取最优参数^[21]。在该模型中,包括了河道调整参数β等6个参数,其确定方法为：基于已有研究,河道调整参数β取值主要在0~0.2之间;B为淤积体的横向平均宽度,考虑到小北干流最宽约为20 km,B的取值设为0~20 km;K为侵蚀基准面高程的抬升值（潼关高程变化值）与河道淤积平衡时潼关河床的淤积高度的关系系数的平方,一般认为与1比较接近^[16];k为平衡淤积体上延高度与来水来沙的关系系数,考虑到上延高度与汛期水沙正相关,故k为正值,而小北干流非汛期上延高度减小,故k为负值;a和b分别为来水和来沙参数,考虑到河道冲淤一般与来水负相关,与来沙正相关,故a的范围设为-1~0,而b设为0~1。
Tab. 3
表3
表3汛期及非汛期冲淤量滞后响应模型的计算参数
Tab. 3Parameters of delayed response model in wet and dry seasons

J₀	β	K	B(km)	k	a	b
非汛期0.00046	0.03	0.9	9.98	-15.00	-0.23	0.52
汛期0.00046	0.17	0.9	9.98	110.15	-0.16	0.27

新窗口打开
在参数估计时首先设置好参数的取值范围,运行DE,设置种群规模为1000,经过1000次随机搜索后得到较为可靠的一组参数。模型率定和验证期的模拟效果以相对均方根误差（RRMSE）和决定系数（R²）来评价,其中RRMSE的计算公式如下：

\begin{matrix} RMSE = \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} (S_{i} - O_{i})^{2}} \end{matrix}

（16）

\begin{matrix} RRMSE = \frac{RMSE}{\overset{?}{O}} \times 100 % \end{matrix}

（17）
式中：

\begin{matrix} RMSE \end{matrix}

为均方根误差;

\begin{matrix} RRMSE \end{matrix}

为相对均方根误差;S_i和O_i分别为第i个模拟值和观测值;

\begin{matrix} \overset{?}{O} \end{matrix}

为观测值平均值。
根据以上参数,计算得到1960-2001年间小北干流汛期末和非汛期末的累计冲淤量,点绘在图4中,该累计值为某个汛期或非汛期前期所有时段的冲淤量之和。从图4a可知,模型率定期（1960-2001年）累计冲淤过程的模拟值与实测值十分吻合。误差分析表明率定期的相对均方根误差（RRMSE）为9.3%,表明模型能很好的模拟河道的冲淤过程。从图4b可知,累计冲淤量模拟值和实测值的决定系数R²达到0.97,点子基本上落在直线（y = x）上,两者回归函数的斜率为0.98,与1十分接近,表明本文建立的模型能很好的模拟河道的冲淤过程。

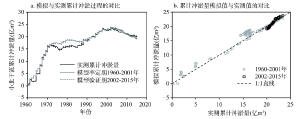显示原图|下载原图ZIP|生成PPT
图4率定期(1960-2001年)和验证期(2002-2015年)小北干流汛期和非汛期模拟与实测累计冲淤积过程的对比、累计冲淤量模拟值与实测值的对比
-->Fig. 4Comparison between simulated and measured cumulative sedimentation processes, and simulated and measured cumulative sediment storage in the calibration period (1960-2001) and validation period (2002-2015) in the Xiaobeignaliu reach
-->

为验证模型的准确性,根据表3的参数计算了小北干流汛期和非汛期在2002-2015年的累计冲淤量（图4a）。由图4可知,验证期模拟与实测累计冲淤量的变化趋势相一致。误差分析表明,验证期的RRMSE和R²分别为2.7%和0.98,这表明本文所建立的模型能够较好的模拟汛期和非汛期累计淤积过程。
以上分析的是汛期末和非汛期末的累计值,本文进一步计算了单个汛期和非汛期的冲淤量。根据式（14）和式（15）得到的汛期末和非汛期末累计冲淤量,得到了单个汛期和非汛期的冲淤量以及相应的累计冲淤量,点绘在图5和图6中。率定期汛期累计冲淤过程模拟值与实测值较为吻合（图5a）,发现点子基本落在直线（y = x）上,R²达到0.98（图5b）,RRMSE为4.2%。回归分析表明两者线性回归函数的斜率为0.99,几乎等于斜率1,表明本文建立的模型能很好的模拟汛期的累计冲淤量。率定期单个汛期冲淤量模拟值和实测值的RRMSE降为66%,R²降低为0.59（图5c）,相关性要低于累计值,点子相对发散。

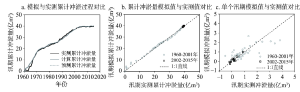显示原图|下载原图ZIP|生成PPT
图5率定期(1960-2001年)和验证期(2002-2015年)小北干流汛期模拟与实测累计冲淤过程的对比、汛期累计冲淤量模拟值与实测值的对比以及单个汛期模拟值与实测值的对比
-->Fig. 5Comparison between simulated and measured cumulative sedimentation processes, cumulative sediment storage, and sediment storage in wet season in the Xiaobeiganliu reach in calibration period (1960-2001) and validation period (2002-2015)
-->

显示原图|下载原图ZIP|生成PPT
图6率定期(1960-2001年)和验证期(2002-2015年)小北干流非汛期模拟与实测累计冲淤过程的对比、非汛期累计冲淤量模拟值与实测值的对比以及单个非汛期模拟值与实测值的对比
-->Fig. 6Comparison between simulated and measured cumulative sedimentation processes, cumulative sediment storage, and sediment storage in dry season in the Xiaobeiganliu reach in calibration period (1960-2001) and validation period (2002-2015)
-->

图5a虚线为汛期验证期模拟值。从图5a可知,验证期汛期累计冲淤变化趋势与实测趋势基本吻合,R²为0.99,RRMSE为0.9%。相对而言,验证期单个汛期冲淤量模拟值和实测值间存在一定的误差,单个汛期冲淤量的RRMSE为15%,R²为0.72。以上表明本文所建立的模型能够较好的模拟汛期累计冲淤量过程,但对单个汛期冲淤量的模拟存在一定的误差。
非汛期率定期模拟和实测累计冲淤过程整体上较为吻合（图6a）,但模拟效果要低于汛期。从图6b可知,模拟值和实测值的点子也基本落在直线y = x上,而且两者的线性回归函数的斜率为0.96,也较接近1,但R²为0.96,要低于汛期（图5b）。和非汛期累计冲淤（图6b）以及汛期沖淤模拟效果相比（图5b、5c）,率定期单个非汛期冲淤量模拟值和实测值的点子相对更为发散,相关性要更低,R²为0.32,RRMSE为78.7%。
图6a虚线为非汛期验证期模拟值。从图6a可知,验证期模拟值的冲淤变化趋势基本反映实际变化趋势,R²为0.93,RRMSE为3.85%。相比之下,验证期单个非汛期冲淤量模拟值和实测值的R²为0.40,RRMSE为44.9%（图6c）。与汛期类似,以上分析表明本文所建立的模型能够较好的模拟非汛期累计冲淤过程,但对单个非汛期冲淤量的模拟还存在较大的误差。

5 讨论

5.1 滞后响应模型分析

鉴于多数河流在汛期和非汛期的来水来沙条件存在显著的差异,本文构建了基于汛期和非汛期的滞后响应模型,并模拟了小北干流河道在汛期和非汛期的冲淤过程,取得了较好的模拟效果。以上结果显示,汛期和非汛期累计冲淤量的模拟效果优于单个汛期和非汛期冲淤量;无论是冲淤量还是累计冲淤量,汛期的模拟效果要优于非汛期。
汛期模拟效果相对较优,这与小北干流冲淤变化与潼关高程和汛期来沙量存在较好关系有关。图7表明汛期的冲淤变化与潼关高程和上游来水来沙的关系都十分显著。从图5c可知,虽然R²为0.68,但单个汛期的点子仍然相对分散,特别是在上游来沙较大的年份。主要原因是滞后响应模型是通过当前值与平衡值间的差值来计算河道的累计冲淤变化。所以在累计冲淤量的基础上,进一步计算单个汛期和非汛期的冲淤量,会导致模拟效果降低。此外,小北干流的来水来沙过程复杂,在某些大沙年,如1964年、1966年、1969年和1970年等,小北干流多发生高含沙水流,甚至有发生不同程度的揭河底冲刷,影响河道的冲淤规律,从而影响模拟效果。

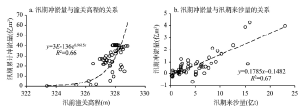显示原图|下载原图ZIP|生成PPT
图7小北干流汛期冲淤量与潼关高程、汛期来沙量的关系
-->Fig. 7Relationships between cumulative sediment storage in wet season and the Tongguan elevation, and sediment storage and sediment load in wet season in the Xiaobeiganliu reach
-->

非汛期的模拟效果低于汛期,特别是单个非汛期的模拟存在较大误差。可能的原因是非汛期冲淤过程受到更多因素的影响,与来水来沙和潼关高程相关性相对低,这与邓安军等^[22]的研究是一致的。而且,非汛期模拟效果较差的原因还可能与三门峡水库的运用有关。从年内来看,三门峡水库非汛期水位变动很大,水库运用方式包括防凌前蓄水、防凌蓄水和春灌蓄水等,水位变动非常大,导致非汛期冲淤复杂;而汛期的水位变化则相对处于平稳的状态,基本保持在305 m左右。此外,同单个汛期模拟值和实测值的点子分散情况类似,本模型模拟河道冲淤量的累计变化,进一步计算单个非汛期的冲淤量,误差会进一步增大,从而降低模拟效果。
河道的调整参数β反映的是河道在某时刻的调整能力。比较小北干流汛期和非汛期的调整参数,可以看到汛期的调整参数（0.17）要明显高于非汛期（0.04）,表明汛期河道的调整速率要明显的高于非汛期,这与黄河流域河道的冲淤主要受汛期来水来沙影响是一致的。
本文以累计冲淤量来模拟小北干流河床的冲淤演变,达到了较好的效果（图4,图5,图6）。这表明本模型能反应河床演变中的滞后响应现象,同时对预测水库长期的冲淤变化有一定的意义。然而,在历年汛期和非汛期冲淤量计算上,本文虽然能在一定程度上模拟单个汛期的冲淤量,但对单个非汛期冲淤量的预报还存在较大误差。精确模拟单个汛期和非汛期的冲淤量,从而为水库运用调度来调控库区冲淤提供有效指导,具有重要的使用价值,有待深入研究。

5.2 小北干流冲淤的影响因素分析

针对不同的水沙和边界条件,冲积性河流会做出相应的冲淤调整（包括比降、河宽和边界组成等）,建立新平衡以适应外部环境的改变^[5],同时这一新平衡的建立过程具有时间和空间上的差异性^[23]。在水沙和侵蚀基准面作用下,小北干流汛期和非汛期冲淤过程表现出时间差异,具有不同的特征时段（图3）,充分证明了这一点。探讨各个时段哪种因素对冲淤起到主要作用,具有重要意义。因此,本文采用基于汛期和非汛期的滞后响应模型,定量分析潼关高程和来水来沙对不同特征时段汛期和非汛期河道冲淤的影响程度。
定义设计潼关高程为不同时段潼关高程的初始值,并在每一个特征时段内保持不变。以实测的水沙过程和设计潼关高程计算河道的冲淤量,那么就可以得到各时段仅受来水来沙作用下的冲淤量。
汛期各时段1960-1970年、1971-1985年、1986-1998年和1999-2015年的初始值分别为324 m、327.6 m、327.1 m和328.4 m,计算结果如表4所示。由表4可知,1960-1970年,如果潼关高程保持324 m不变,则小北干流汛期冲淤过程仅受到来水来沙的影响。模拟结果表明1960-1970年小北干流汛期因来水来沙累计淤积泥沙2.2亿m³,因潼关高程抬升多淤积泥沙15.11亿m³,表明潼关高程是影响此时段内河床淤积的主要原因。与1960-1970年相反的是,1971-1985年、1986-1998年和1999-2015年计算结果表明这3个时期的冲淤主要是受到来水来沙的影响。
Tab. 4
表4
表41960-2015年间潼关高程和来水来沙对不同时期小北干流汛期冲淤量的贡献率
Tab. 4Contribution rate of water-sediment regime and Tongguan elevation on the sediment storage in wet season in the Xiaobeiganliu reach at different periods during 1960-2015

时段	设定高程	模拟冲淤量^a	模拟冲淤量^b	水沙引起的冲淤量		潼关高程引起的冲淤量
时段	(m)	(亿m³)	(亿m³)	绝对值(亿m³)	贡献率	绝对值(亿m³)	贡献率
1960-1970年	324.00	2.20	16.01	2.20	0.14	13.81	0.86
1971-1985年	327.64	7.06	8.61	7.06	0.82	1.55	0.18
1986-1998年	327.08	7.97	11.09	7.97	0.72	3.12	0.28
1999-2015年	328.40	9.49	6.97	9.49	1.36	-2.51	-0.36
1960-2015年	324.00	5.85	42.68	5.85	0.14	36.83	0.86

注：a为根据设定的潼关高程计算的累计冲淤量;b为根据实测的潼关高程计算的累计冲淤量。

新窗口打开
非汛期各特征时段1960-1968年、1969-1977年、1978-1998年、1999-2006年和2007-2015年对应的初始高程分别为324 m、328.3 m、326.8 m、328.2 m和327.8 m,计算结果如表5所示。由表可知,1960-1968年非汛期主要是受到潼关高程的影响,贡献率到达了79%。而另一个潼关高程抬升期1978-1998年,潼关高程的贡献率下降到了4%,对非汛期的冲淤不起到任何作用。1969-1977年、1999-2006年和2007-2015年,3个时段的潼关高程为下降的趋势,除了1969-1977年贡献率分别为15%,其余两个时期接近0。表明虽然潼关高程降低是造成了一定溯源冲刷,但是主要还是由水沙变化引起的沿程冲刷为主。
Tab. 5
表5
表51960-2015年间不同时段潼关高程和来水来沙对小北干流非汛期冲淤量的贡献率
Tab. 5Contribution rate of water-sediment regime and Tongguan elevation on the sediment storage in dry season in the Xiaobeiganliu reach at different periods during 1960-2015

时段	设定高程	模拟冲淤量^a	模拟冲淤量^b	水沙引起的冲淤量		潼关高程引起的冲淤量
时段	(m)	(亿m³)	(亿m³)	绝对值(亿m³)	贡献率	绝对值(亿m³)	贡献率
1960-1968年	324	-0.12	-0.56	-0.12	0.21	-0.44	0.79
1969-1977年	328.3	-2.65	-3.10	-2.65	0.85	-0.45	0.15
1978-1998年	326.8	-8.81	-9.23	-8.81	0.96	-0.41	0.04
1999-2006年	328.2	-4.50	-4.48	-4.50	1.00	0.02	0.00
2007-2015年	327.8	-4.92	-4.86	-4.92	1.00	0.06	0.00
1960-2015年	324	-3.20	-22.22	-3.20	0.14	19.02	0.86

注：a为根据设定的潼关高程计算的累计冲淤量;b为根据实测的潼关高程计算的累计冲淤量。

新窗口打开

6 结论

根据河道演变的滞后响应机制,在考虑上游来水来沙和下游侵蚀基准面（潼关高程）共同影响的基础上,建立了能够计算河道汛期和非汛期冲淤量的滞后响应模型。将滞后响应模型应用于小北干流汛期和非汛期的冲淤量计算,定量分析潼关高程和来水来沙对不同特征时段汛期和非汛期河道冲淤的影响程度。结论如下：
（1）小北干流汛期和非汛期的冲淤过程具有明显的时间差异,可分为多个特征时段。小北干流汛期的冲淤过程可分为1960-1970、1971-1985年、1986-1998年和1999-2015年4个时段;小北干流非汛期的冲淤过程可分为5个阶段,分别为1960-1968、1969-1977年、1978-1998年、1999-2006年和2007-2015年。
（2）建立了能够模拟汛期和非汛期冲淤变化的滞后响应模型,并较好的模拟了小北干流1960-2015年间汛期和非汛期的冲淤过程,计算精度较高。率定期的汛期和非汛期累计冲淤量模拟效果较好,R²分别为0.98和0.96。模拟单个汛期和非汛期的冲淤量时,率定期的汛期和非汛期的R²分别为0.59和0.32,但验证期汛期和非汛期的R²为0.72和0.40,模拟效果低于累计冲淤量。
（3）根据建立的滞后响应模型,本文定量分析了来水来沙和潼关高程在汛期和非汛期各个特征时段的贡献率。发现潼关高程主要是影响汛期和非汛期在第一特征时段（1960-1970年,1960-1968年）冲淤变化的主要因素。随着水库的改建,运用方式以及来水来沙的变化,上游来水来沙成为影响河道汛期和非汛期冲淤变化的主要因素。
（4）本文建立的滞后响应模型对非汛期的模拟精度要低于汛期,可能和非汛期来水来沙过程和三门峡水库的运用水位变动有关,还需要进一步的研究以提高模拟效果。
The authors have declared that no competing interests exist.

黄河小北干流汛期和非汛期冲淤过程模拟

本站小编 Free考研考试/2021-12-29

Simulation of sedimentation processes in dry and wet seasons in the Xiaobeiganliu reach of the Yellow River

1 引言

2 研究区概况