张厦^1,2, 姜泉江¹, 梁广¹, 余金培¹
1. 中国科学院微小卫星创新研究院, 上海 201203;
2. 中国科学院大学, 北京 100049
2019年12月30日 收稿; 2020年3月26日 收修改稿
基金项目: 国家自然科学基金(61601295)、上海市启明星计划(18QA1404000)和国家重点研发计划(2017YFB0502902)资助
通信作者: 余金培，E-mail: yujp@microsate.com

摘要: DVB-S2X标准在DVB-S2标准的基础上增加多种高阶APSK(amplitude phase shift keying)调制方式，其中16APSK调制增加8+8APSK星座图。主要分析16APSK星座图的特点，并提出一种新的软解调优化算法。该算法与LLR算法和Max-log-MAP算法相比，计算复杂度显著降低。仿真结果表明，优化算法性能损失小，在工程应用中具有较好的实用性。
关键词: DVB-S2X8+8APSKLDPC软解调
A soft demodulation optimization algorithm of 16APSK signal for DVB-S2X standard
ZHANG Sha^1,2, JIANG Quanjiang¹, LIANG Guang¹, YU Jinpei¹
1. Innovation Academy for Microsatellites, Chinese Academy of Sciences, Shanghai 201203, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China


Abstract: Multiple high-order APSK modulation schemes are added in the DVB-S2X standard on the basis of the DVB-S2 standard, and an 8+8APSK constellation is added based on the original 16APSK. In this paper, characteristics of a 16-APSK constellation are mainly analyzed, and a new soft demodulation optimization algorithm is proposed. Compared with the LLR algorithm and the Max-log-MAP algorithm, the proposed algorithm has the significantly reduced computational complexity. Simulation results of the three algorithms show that the optimization algorithm is small in performance loss and has good practicability in engineering application.
Keywords: DVB-S2X8+8APSKLDPCsoft demodulation
2005年，第二代数字卫星电视广播标准DVB-S2发布，该标准在DVB-S的基础上采用新的纠错编码方式BCH+LDPC，增加新的调制体制16APSK(amplitude phase shift keying)和32APSK以及新的工作模式，即可变编码及调制方式VCM(variable coding and modulation)和自适应编码方式ACM(adaptive modulation and coding)等^[1]。通过以上新技术的应用，DVB-S2能显著改善卫星传输的带宽利用率，并提高传输功率效率。经过十几年的发展，该标准已经成为全球应用最为广泛的下一代卫星电视广播标准^[2]。
随着数字卫星电视广播行业和其他媒体传输需求的增加，高容量卫星技术的进步和硬件平台的飞速发展，DVB组织从2011年底开始研究DVB-S2的扩展标准，并于2014年3月发布了DVB-S2X。DVB-S2标准采用4种调制方式：QPSK，8PSK，16APSK和32APSK。其中16APSK星座图模式为4+12APSK，32APSK星座图模式为4+12+16APSK, 16APSK和32APSK在广播服务中属于可选项^[3]。而DVB-S2X采用更多高阶的调制方式：BPSK，QPSK，8PSK，8APSK，16APSK，32APSK，64APSK，128APSK和256APSK。其中16APSK和32APSK星座图在DVB-S2标准的基础上，增加了8+8APSK和4+8+4+16APSK星座图，64APSK为可选项^[4]。DVB-S2X标准通过引入更高阶的调制方式，进一步提高了现行标准的频谱利用率。
高阶调制技术的采用使得卫星通信系统的传输能力得到极大提高，但是计算复杂度也有很大增加。目前，在实际的卫星接收中，64APSK及更高的调制方式实现难度极高，降低高阶调制解调方式的计算复杂度成为当前研究热点。DVB-S2X标准中，高阶调制技术与LDPC编译码结合使用，解调不再采用传统的硬解调方式，而是采用软解调方式，即解调端输出编码比特的软信息至译码器，再由译码器进行硬判决译码。软输出解调器通常采用基于最大对数后验概率准则的对数似然比(log-likelihood ratio, LLR)算法计算高阶调制信号的软输出解调信息，但计算复杂度较高，在卫星硬件平台实现比较困难，因此其简化算法的研究很有实用意义。目前针对DVB-S2标准的16APSK、32APSK调制信号的软解调算法已经有很多人做过研究^[5-9]，但针对DVB-S2X标准新采用的调制方式的研究还较少。本文主要研究DVB-S2X标准新采用的8+8APSK调制方式，并根据星座图的特点提出一种降低计算复杂度的软解调算法。
1 16APSK星座图描述DVB-S2X标准中的16APSK调制方式采用2种星座图，一种是4+12APSK星座图，即由2个同心圆组成，内圆含有4个星座点，外圆含有12个星座点，如图 1(a)所示；另一种是8+8APSK星座图，即由2个同心圆组成，内圆含有8个星座点，外圆含有8个星座点，如图 1(b)所示。其中R₁代表内圆半径，R₂代表外圆半径，γ=R₂/R₁，不同的编码速率对应不同的γ值。DVB-S2X标准采用的4+12APSK星座图相比于DVB-S2标准增加了多种编码速率以及多种γ值，具体的对应关系见表 1。
Fig. 1

	Download: JPG larger image
图 1 4+12APSK星座图和8+8APSK星座图 Fig. 1 4+12APSK Constellation and 8+8APSK Constellation 图 1 4+12APSK星座图和8+8APSK星座图 Fig. 1 4+12APSK Constellation and 8+8APSK Constellation -->

Table 1

表 1 不同码率对应的γ值Table 1 γ corresponding to different code rates 码长nldpc LDPC码标识符 调制/编码频谱效率 γ 64 800 26/45 2.30 3.70 3/5 2.39 3.70 28/45 2.48 3.50 23/36 2.54 3.10 25/36 2.77 3.10 13/18 2.88 2.85 140/180 3.11 3.60 154/180 3.42 3.20 16 200 7/15 1.83 3.32 8/15 2.09 3.50 26/45 2.27 3.70 3/5 2.36 3.70 32/45 2.80 2.85

表 1 不同码率对应的γ值Table 1 γ corresponding to different code rates

DVB-S2X标准中，8+8APSK调制方式与5种不同的编码速率相结合, 分别对应具体的5种星座图。其中3种编码速率(90/180、96/180、100/180)相对应的γ值如表 2所示，相位$ \emptyset $值如表 3所示。编码速率为18/30、20/30，DVB-S2X标准给出了具体的坐标值，具体星座图坐标参见文献[4]。
Table 2

表 2 nldpc=64 800不同码率对应的γTable 2 γ corresponding to different code rates when nldpc=64 800 LDPC码标识符 调制/编码频谱效率 γ 90/180 2.00 2.19 96/180 2.13 2.19 100/180 2.22 2.19

表 2 nldpc=64 800不同码率对应的γTable 2 γ corresponding to different code rates when nldpc=64 800

Table 3

表 3 码率90/180、96/180、100/180对应的相位角$ \emptyset $Table 3 Phase angles $ \emptyset $ corresponding to code rates 90/180, 96/180, 100/180 星座点 R $ \emptyset $/π p=q=0 p=0, q=1 p=1, q=0 p=q=1 0qp0 R1 1/8 15/8 7/8 9/8 0qp1 R1 3/8 13/8 5/8 11/8 1qp0 R2 1/8 15/8 7/8 9/8 1qp1 R2 3/8 13/8 5/8 11/8

表 3 码率90/180、96/180、100/180对应的相位角$ \emptyset $Table 3 Phase angles $ \emptyset $ corresponding to code rates 90/180, 96/180, 100/180

调制器根据如上星座图特性，将编码得到的二进制向量映射到星座点，其中每个信号点对应一个4 bit向量{b₃b₂b₁b₀}，其中b₃，b₂，b₁，b₀∈{0, 1}，b₃表示最高位，b₀表示最低位。
2 16APSK解调算法调制器输出的信号表示为s_k=s_I+j×s_Q，调制信号经过高斯白噪声信道，解调器接收到的信号可以表示为

$r_{k}=I_{k}+j \times Q_{k}.$

(1)

现在分别对应用比较成熟的硬解调算法、软解调LLR算法和Max-log-MAP算法进行介绍，并提出简化Max-log算法，以期降低计算复杂度。文中解调算法都针对8+8APSK星座图。
2.1 硬解调算法硬解调算法是根据欧式距离来判断信号所处位置，再根据查找表逐符号判决。该算法首先根据接收信号的振幅R判断信号处于内圆还是外圆，再根据接收信号的相位$ \emptyset $′判断接收信号具体的星座点。一旦确定接收信号的星座点，使用查找表即可一次性判决4 bit符号。具体算法如下：
1) 计算接收信号振幅

$R=\sqrt{\left(I_{k}\right)^{2}+\left(Q_{k}\right)^{2}}.$

(2)

2) 计算接收信号相位

$\emptyset^{\prime}=\tan ^{-1}\left(\frac{Q_{k}}{I_{k}}\right).$

(3)

3) 根据8+8APSK查找表进行硬判决。
2.2 软解调算法软解调算法主要是与LDPC编译码和Turbo编译码联合使用，将解调器输出的软信息送入译码器，在译码器逐比特硬判决出数字符号0或1^[10]。软解调算法计算每比特符号的概率似然比LLR，根据似然比进行判决。基于最大后验概率准则，映射比特b_i的对数似然比函数定义为

$\begin{aligned}\operatorname{LLR}\left(b_{i}\right)&=\log \frac{P\left(b=0 \mid r_{k}\right)}{P\left(b=1 \mid r_{k}\right)} \\&=\log \left(\frac{\sum\nolimits_{x}^{X \in S_{0}^{i}} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2}}} \mathrm{e}^{-\frac{\left|r_{k}-s_{i}\right|^{2}}{2 \sigma^{2}}}}{\sum\nolimits_{X}^{X \in S_{1}^{i}} \frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^{2}}} \mathrm{e}^{-\frac{\left|r_{k}-s_{i}\right|^{2}}{2 \sigma^{2}}}}\right),\end{aligned}$

(4)

式中：s_i表示调制后的信号，S₀ⁱ表示比特b_i=0的星座点，S₁ⁱ表示比特b_i=1的星座点，σ²表示噪声方差。
为降低软解调算法的计算复杂度，目前应用比较广泛的是对数似然比算法，以及简化算法Max-log-MAP。8+8APSK星座图的LLR算法首先计算出每比特的软信息LLR(b_i)，具体计算公式如下

$\begin{gathered}\operatorname{LLR}\left(b_{3}\right)=\\\log \frac{P_{0}+P_{1}+P_{2}+P_{3}+P_{4}+P_{5}+P_{6}+P_{7}}{P_{8}+P_{9}+P_{10}+P_{11}+P_{12}+P_{13}+P_{14}+P_{15}}, \\\operatorname{LLR}\left(b_{2}\right)=\\\log \frac{P_{0}+P_{1}+P_{2}+P_{3}+P_{8}+P_{9}+P_{10}+P_{11}}{P_{4}+P_{5}+P_{6}+P_{7}+P_{12}+P_{13}+P_{14}+P_{15}},\\\operatorname{LLR}\left(b_{1}\right)=\\\log \frac{P_{0}+P_{1}+P_{4}+P_{5}+P_{8}+P_{9}+P_{12}+P_{13}}{P_{2}+P_{3}+P_{6}+P_{7}+P_{10}+P_{11}+P_{14}+P_{15}},\\\operatorname{LLR}\left(b_{0}\right)=\\\log \frac{P_{0}+P_{2}+P_{4}+P_{6}+P_{8}+P_{10}+P_{12}+P_{14}}{P_{1}+P_{3}+P_{5}+P_{7}+P_{9}+P_{11}+P_{13}+P_{15}}.\end{gathered}$

(5)

分子中的P_i代表b_i=0的星座点，分母中的P_i代表b_i=1的星座点，其中$ {P_i}{\rm{ = }}\frac{1}{{\sqrt {2\pi {\sigma ^2}} }}{{\rm{e}}^{ - \frac{{{{\left| {{r_k} - {s_i}} \right|}^2}}}{{2{\sigma ^2}}}}}, i = 0, 1, \cdots , 15$，表达式中s_i是调制后对应的星座点，r_k是接收到的信号。式(5)中包含较多的对数和指数运算，计算复杂度偏高。为降低计算复杂度，目前应用比较广泛的是Max-log-MAP算法^[11]。
Max-log-MAP算法主要采用式(6)的近似算法，可大大降低LLR算法的计算复杂度。由于该算法对系统性能的影响很小，得到了很好的工程应用。

$\begin{aligned}\ln \left(\mathrm{e}^{x}+\mathrm{e}^{y}\right) &=\max (x, y)+\ln \left(1+\mathrm{e}^{-|x-y|}\right) \\& \approx \max (x, y).\end{aligned}$

(6)

8+8APSK星座图的Max-log-MAP算法计算每比特的软信息LLR(b_i)表示如下

$\begin{gathered}\operatorname{LLR}\left(b_{3}\right)=\max \left(P_{0}, P_{1}, P_{2}, P_{3}, P_{4}, P_{5}, P_{6}, P_{7}\right)- \\\max \left(P_{8}, P_{9}, P_{10}, P_{11}, P_{12}, P_{13}, P_{14}, P_{15}\right), \\\operatorname{LLR}\left(b_{2}\right)=\max \left(P_{0}, P_{1}, P_{2}, P_{3}, P_{8}, P_{9}, P_{10}, P_{11}\right)- \\\max \left(P_{4}, P_{5}, P_{6}, P_{7}, P_{12}, P_{13}, P_{14}, P_{15}\right), \\\operatorname{LLR}\left(b_{1}\right)=\max \left(P_{0}, P_{1}, P_{4}, P_{5}, P_{8}, P_{9}, P_{12}, P_{13}\right)- \\\max \left(P_{2}, P_{3}, P_{6}, P_{7}, P_{10}, P_{11}, P_{14}, P_{15}\right), \\\operatorname{LLR}\left(b_{0}\right)=\max \left(P_{0}, P_{2}, P_{4}, P_{6}, P_{8}, P_{10}, P_{12}, P_{14}\right)- \\\max \left(P_{1}, P_{3}, P_{5}, P_{7}, P_{9}, P_{11}, P_{13}, P_{15}\right),\end{gathered}$

(7)

其中$ {P_i}{\rm{ = }} - \frac{{{{\left| {{r_k} - {s_i}} \right|}^2}}}{{2{\sigma ^2}}}, i = 0, 1, \cdots , 15$.
Max-log-MAP算法计算复杂度比LLR算法降低很多，但对于高阶的调制解调算法，还存在很大的计算量。
2.3 简化Max-log算法文献[12]根据星座图的图形特点并结合Max-log-MAP算法对4+12APSK做了相关优化，进一步降低了算法的复杂度。本文结合文献[12]的算法思想，对8+8APSK解调算法进行优化，并根据8+8APSK星座图特有的图形特点，进一步优化算法，提出简化Max-log算法，降低计算复杂度。
文献[12]提出的算法主要根据星座图中每比特所具有的特性，先比较该比特对应16个星座点的概率值大小，排除概率值较小的星座点，从而无需计算便可排除一些概率值的计算，降低了计算复杂度。例如对于文献[12]提到的QPSK，b₁比特在Q≥0时，P₂≥P₃，P₀≥P₁，在Q < 0时，P₂ < P₃，P₀ < P₁，所以LLR(b₁)可以表示为

$\begin{aligned}\operatorname{LLR}\left(b_{1}\right) &=\max \left(P_{0}, P_{1}\right)-\max \left(P_{2}, P_{3}\right) ,\\& \approx \begin{cases}P_{0}-P_{2},& Q \geqslant 0. \\P_{1}-P_{3}, & Q<0\end{cases}\end{aligned}$

(8)

根据8+8APSK星座图特点，本文提出的简化Max-log算法如下：
1) b₀位判决
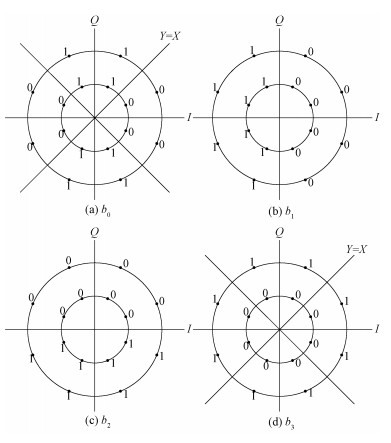
如图 2(a)所示，b₀位信息关于I轴、Q轴都对称，所以将b₀位信息的判决放在第1象限进行。第1象限中，在直线Y=X上方，b₀均为1，在直线Y=X下方，b₀均为0。根据b₀位的图形特征，可以判断当|r_I|≥|r_Q|时，b₀=0，当|r_I| < |r_Q|时，b₀=1。采用软解调LLR算法和Max-log-MAP算法进行解调时，解调器输出的软信息在译码器是根据软信息的正负性进行硬判决，所以软信息LLR(b₀)可以表示为

$\operatorname{LLR}\left(b_{0}\right) \approx \operatorname{abs}\left(r_{I}\right)-\operatorname{abs}\left(r_{Q}\right).$

(9)

Fig. 2

	Download: JPG larger image
图 2 bi位 Fig. 2 bi bit 图 2 bi位 Fig. 2 bi bit -->

2) b₁位判决
如图 2(b)所示，当r_I≥0时，b₁=0，当r_I < 0时，b₁=1，软信息LLR(b₁)与r_Q无关。结合Max-log-MAP算法的判决思想，可将软信息LLR(b₁)近似表示为r_I，即

$\operatorname{LLR}\left(b_{1}\right) \approx r_{I}$

(10)

3) b₂位判决
如图 2(c)所示，当r_Q≥0时，b₂=0，当r_Q < 0时，b₂=1，软信息LLR(b₂)与r_I无关。结合Max-log-MAP算法的判决思想，可将软信息LLR(b₂)近似表示为r_Q，即

$\operatorname{LLR}\left(b_{2}\right) \approx r_{Q}$

(11)

4) b₃位判决
如图 2(d)所示，b₃位信息关于I轴、Q轴都对称。为了降低计算复杂度，b₃信息的判决可以在第1象限进行。此时$ P_{i}=-\frac{|| r_{k}\left|-s_{i}\right|^{2}}{2 \sigma^{2}}, i=0, 1, 8, 9$。根据文献[12]的改进算法，LLR(b₃)=max(P₀, P₁)-max(P₈, P₉)。第1象限星座图关于Y=X直线对称。由此特点可得，当|r_I|≥|r_Q|时，P₀≥P₁，P₈≥P₉，当|r_I| < |r_Q|时，P₀ < P₁，P₈ < P₉。故

$\operatorname{LLR}\left(b_{3}\right) \approx \begin{cases}P_{0}-P_{8}, & \left|r_{I}\right| \geqslant\left|r_{Q}\right| ,\\ P_{1}-P_{9}, & \left|r_{I}\right|<\left|r_{Q}\right|.\end{cases}$

(12)

综上所述，8+8APSK星座图软解调简化Max-log算法具体表示如下：
1) 计算软信息LLR(b₀)

$\operatorname{LLR}\left(b_{0}\right)=\operatorname{abs}\left(r_{I}\right)-\operatorname{abs}\left(r_{Q}\right).$

2) 计算软信息LLR(b₁)

$\operatorname{LLR}\left(b_{1}\right)=r_{I}.$

3) 计算软信息LLR(b₂)

$\operatorname{LLR}\left(b_{2}\right)=r_{Q}.$

4) 计算软信息LLR(b₃)

$\operatorname{LLR}\left(b_{3}\right)= \begin{cases}P_{0}-P_{8}, & \left|r_{I}\right| \geqslant\left|r_{Q}\right|, \\ P_{1}-P_{9}, & \left|r_{I}\right|<\left|r_{Q}\right| .\end{cases}$

5) 将计算得到的软信息LLR(b_i), i=0, 1, 2, 3送入译码端进行译码。
简化Max-log算法在计算b₀位、b₁位、b₂位的软信息时是根据星座图的图形特点求解的，并没有复杂的代数运算，相比于文献[12]中的优化算法，计算复杂度进一步降低。
3 仿真分析设输入信号为随机信号，信道采用加性高斯白噪声信道，LDPC的码长为64 800，迭代次数为50，分别对码率90/180、18/30、20/30进行仿真，系统模型如图 3所示。
Fig. 3

	Download: JPG larger image
图 3 系统模型 Fig. 3 System model 图 3 系统模型 Fig. 3 System model -->

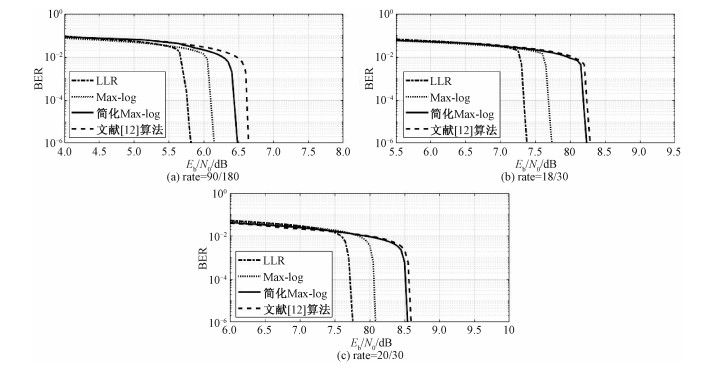
通过仿真将简化Max-log算法与LLR算法、Max-log-MAP算法、文献[12]算法进行误码性能比较，如图 4所示。本文简化Max-log算法与LLR算法、Max-log-MAP算法、文献[12]算法计算复杂度比较如表 4所示。由图 4(a)可得，码率为90/180，当误码率达到10^-6时，简化Max-log算法与Max-log-MAP算法相比，有0.5 dB编码增益的差距，与LLR算法相比，存在0.7 dB编码增益的差距，与文献[12]算法相比，存在0.05 dB编码增益的差距。由图 4(b)可得，码率为18/30，当误码率达到10^-6时，简化Max-log算法与Max-log-MAP算法相比，有0.5 dB编码增益的差距，与LLR算法相比，存在0.8 dB编码增益的差距，与文献[12]算法相比，存在0.05 dB编码增益的差距。由图 4(c)可得，码率为20/30，当误码率达到10^-6时，简化Max-log算法与Max-log-MAP算法相比，有0.5 dB编码增益的差距，与LLR算法相比，存在0.7 dB编码增益的差距，与文献[12]算法相比，存在0.05 dB编码增益的差距。
Fig. 4

	Download: JPG larger image
图 4 码率90/180、18/30和20/30 BER曲线图 Fig. 4 BER performance when code rate=90/180, 18/30, and 20/30 图 4 码率90/180、18/30和20/30 BER曲线图 Fig. 4 BER performance when code rate=90/180, 18/30, and 20/30 -->

Table 4

表 4 计算复杂度比较Table 4 Comparison of computational complexityfor 8+8APSK 解调算法 比较 指数/对数 加法 乘法 LLR 0 16/4 72 128 Max-log 8 0/0 68 64 文献[12]算法 4 0/0 11 35 简化Max-log算法 3 0/0 6 16

表 4 计算复杂度比较Table 4 Comparison of computational complexityfor 8+8APSK

表 4中的数据表示每个接收符号r_k经过解调器输出4 bit软信息LLR(b_i), i=0, 1, 2, 3时需要进行的计算量。4种算法计算量的数据是根据4 bit软信息LLR(b_i)计算公式中包含的运算符号得到的。由表 4可得，简化Max-log算法与Max-log-MAP算法、LLR算法、文献[12]算法相比计算复杂度有了明显的下降。
4 总结本文分析DVB-S2X标准中的16APSK星座图特点，针对8+8APSK调制方式提出简化Max-log算法，该算法有效降低了计算复杂度，大大节省了硬件资源。
与文献[12]算法、Max-log-MAP算法相比，简化Max-log算法的性能下降较小，与LLR算法相比，该算法的性能虽然有所下降，但由于简化Max-log算法在硬件上容易实现，复杂度显著降低，因此在工程应用中具有很好的实用价值。

参考文献

[1]	卢六翮. DVB-S2X技术解析[J]. 广播与电视技术, 2014, 41(7): 97-99.
[2]	李远东, 凌明伟. 第三代DVB卫星电视广播标准DVB-S2X综述[J]. 电视技术, 2014, 38(12): 28-31, 44.
[3]	European Telecommunications Standard Institute. Digital video broadcasting (DVB); Second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications; Part 1: DVB-S2: EN 302307-1 V1.4.1[S/OL]. (2014-11-01)[2019-12-29]. https://dvb.org/specifications.
[4]	European Telecommunications Standard Institute. Digital video broadcasting (DVB); Second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications; Part Ⅱ: S2-Extensions (DVB-S2X): EN 302307-2 V1.2.1[S/OL]. (2014-11-01)[2019-12-29]. https://dvb.org/specifications.
[5]	Cho K, Hyun K, Yoon D, et al. An approximated soft decoding algorithm of 16-APSK signal for DVB-S2[C]//2007 Digest of Technical Papers International Conference on Consumer Electronics. Las Vegas, NV, USA: IEEE, 2007: 1-2.
[6]	Ali P, Hussain F, Jeong J. A new demapping technique for 16-APSK modulation for digital video broadcasting in AWGN channel[C]//2008 Third International Conference on Convergence and Hybrid Information Technology. Busan, Korea (South): IEEE, 2008: 9-12.
[7]	段红光, 张源. GMR-1卫星通信16-APSK信号软解码算法[J]. 信息通信, 2016(2): 22-24. Doi:10.3969/j.issn.1673-1131.2016.02.011
[8]	Yao E X, Yang S, Jiang W. A simplified soft decision demapping algorithm of 16-APSK signals in AWGN channels[C]//2010 Second International Conference on Networks Security, Wireless Communications and Trusted Computing. Wuhan, China: IEEE, 2010: 103-106.
[9]	Zhang J J, Zhu L D, Guo Y T, et al. A new method of demodulation for 16APSK/32APSK[C]//Proceedings of 2012 5th Global Symposium on Millimeter-Waves. Harbin, China: IEEE, 2012: 477-481.
[10]	许大正, 刘爱军. DVB-S2标准中联合LDPC译码的16-APSK星座迭代软判决算法研究[J]. 宇航学报, 2011, 32(3): 634-639. Doi:10.3873/j.issn.1000-1328.2011.03.027
[11]	Allpress S, Luschi C, Felix S. Exact and approximated expressions of the log-likelihood ratio for 16-QAM signals[C]//Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, 2004. Pacific Grove, CA, USA: IEEE, 2004: 794-798.
[12]	Park J W, Ryu C D, Sunwoo M H, et al. Simplified soft-decision demapping algorithm for DVB-S2[C]//2009 International SoC Design Conference (ISOCC). Busan, Korea(South): IEEE, 2009: 444-447.