陈菲菲^1,2, 孙志华^1,2, 叶雪^1,2
1. 中国科学院大学数学科学学院, 北京 100049;
2. 中国科学院大数据挖掘与知识管理重点实验室, 北京 100190
2015年06月01日 收稿; 2015年11月20日 收修改稿
基金项目: 国家自然科学基金（10901162，U1430103，11571340）、中国科学院大学校长基金、中国科学院大数据挖掘与知识管理重点实验室开放课题和安徽省振兴计划团队项目（统计学前沿问题及应用）资助
通信作者: 孙志华

摘要: 对失效信息随机缺失时的可加危险率模型的估计进行研究。充分利用失效信息和缺失信息的概率模型的信息，通过构建估计方程，得到回归参数和基准累积风险函数的3个估计。证明了所提估计的渐近正态性，并进行数值模拟研究其有限样本性质。利用数值模拟研究比较所提估计与文献中的估计的有限样本性质，并通过分析一个实际数据验证了本文方法的有效性。
关键词: 删失信息随机缺失可加危险率模型加权估计方程插补估计
Statistic inference of additive hazards model when censoring indicators are missing at random
CHEN Feifei^1,2, SUN Zhihua^1,2, YE Xue^1,2
1. School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China;
2. Key Laboratory of Big Data Mining and Knowledge Management, Chinese Academy of Sciences, Beijing 100190, China


Abstract: In this work, we consider a semi-parametric additive hazards regression model for right-censored data with censoring indicators missing at random.By employing the information of the response and censoring probability models, we propose three estimators of the regression coefficient and the baseline cumulative hazard function.We prove that the proposed estimators are consistent and asymptotically normal.Simulation studies are conducted to evaluate the numerical performance of the proposed estimators in comparison with the existing estimators.A real data set is analyzed to validate the effectiveness of the proposed methods.
Key words: censoring informationmissing at randomadditive hazards regression modelweighting estimating equationimputation estimating
在很多研究领域，数据经常出现右删失的情况，比如研究个体的中途退出或失去跟踪都会导致生存时间的右删失. 令T和C分别表示分布函数为F和G的生存时间和删失时间变量，当生存数据出现右删失时，仅观察到X=:min(T,C).通常假定在给定p 维协变量Z时，T和C条件独立.
记删失指示变量δ=I(T≤C)，I(A)表示A的示性函数.删失指示变量δ不是总能观测到，有时会出现缺失的现象.例如，某些研究个体的医学记录丢失了； 另外，当获取死亡信息需要进行解剖时，昂贵的解剖代价往往使得许多个体的解剖没有进行，从而使死亡原因无法收集到，这时失效信息也缺失了. 令ξ表示失效信息缺失的指示变量，当观测到δ时ξ=1，否则ξ=0.
若δ缺失的概率既与δ本身的值无关，又与观测到的变量X和Z的值无关，即P{ξ=1|δ,X,Z}=P{ξ=1}，则称δ的缺失为完全随机缺失(MCAR)；若δ缺失的概率仅仅与X和Z的值相关，但是与δ本身的值无关，即P{ξ=1|δ,X,Z}=P{ξ=1|X,Z}，则称δ的缺失为随机缺失(MAR)；若δ的缺失与δ本身有关，则称δ的缺失为非随机缺失(MNAR). 通常假设数据的缺失是MAR的，且在很多情形下这是合乎情理的^[1].大量的统计文献在做统计推断时将数据的随机缺失假设作为基本准则，例如文献^[2]对失效原因随机缺失的竞争风险数据进行研究；文献^[3]对响应变量随机缺失的半参数回归模型进行研究；文献^[4]研究死亡原因随机缺失时生存函数的半参数估计.本文考虑失效信息δ是随机缺失的，关于失效信息缺失的研究也有很多，如文献^[5-8]等.
本文中，我们利用可加危险率模型研究协变量Z对生存时间T的影响.可加危险率模型是一种较为常见的半参数回归模型，在可加危险率回归模型下，条件风险率函数λ(t|Z)=λ₀(t)+β′₀Z，其中λ₀(t)是未知的基准风险函数，β₀是p维未知回归参数. 关于可加危险率模型的研究有很多，可参考文献^[9-11]等.
我们的目的是估计未知的回归参数β₀和基准风险函数λ₀(t). 对可加危险率模型，当失效信息随机缺失时，文献^[12]采用逆概率加权的思想，构建关于未知参数β₀和λ₀(t)的简单加权估计方程组和完全增广加权估计方程组，并证明了估计的渐近性质；文献^[13]亦对同种类型的数据进行研究，通过一种基于核的插补方法(Kernel-assisted imputation estimating method)得到一组关于β₀和λ₀(t)的估计方程组，从而得到β₀和λ₀(t)的估计.上述估计方法在构建估计方程组时，均使用了条件概率P{δ=1|X,Z}的非参数核估计.我们知道，非参数核方法受到“维数祸根”的困扰，从而在一定程度上 限制了方法在协变量维数比较高时的使用.
我们发现，有时是可以获得关于删失模型P{δ=1|X,Z}的信息的，比如当生存时间和删失时间都服从威布尔分布时，根据P{δ=1|X=x}=$\frac{{{\lambda }_{t}}\left( x \right)}{{{\lambda }_{t}}\left( x \right)+{{\lambda }_{c}}\left( x \right)}=\frac{1}{1+{{\lambda }_{c}}\left( x \right)/{{\lambda }_{t}}\left( x \right)}$，其中λ_t(x)和λ_c(x)分别表示T和C的风险函数，文献^[14]表明θ₁/(θ₁+x^θ₂),θ₁>0,θ₂∈R是一个可供选择的模型. 更多关于对P{δ=1|X,Z}进行参数模型假定的细节可参考文献^[14]. 显然，假定P{δ=1|X,Z}具有参数形式，就可避免非参数光滑方法的使用，从而避免“维数祸根”的问题. 即使协变量的维数比较高，本文所提的方法也是有效的.
1 模型介绍假设我们观测到一个独立同分布的样本{X_i,ξ_i,ξ_iδ_i,Z_i}_i=1ⁿ. 进一步假定参数概率模型：

$\begin{align} & \pi ({{V}_{i}},\alpha )=P\{{{\xi }_{i}}=1|{{V}_{i}}\}, \\ & \omega ({{V}_{i}},\gamma )=P\{{{\delta }_{i}}=1|{{V}_{i}}\}, \\ \end{align}$

其中，π(·,α)和ω(·,γ)表示形式已知的函数，α和γ表示未知参数，V_i=(X_i,Z′_i)′. 对可加危险率回归模型,条件危险率函数有如下形式

$\lambda \left( t|Z \right)={{\lambda }_{0}}\left( t \right)+\beta {{\prime }_{0}}Z,$

(1)

其中λ₀(t)是未知的基准危险率函数，β₀是p维未知回归参数.
显然$\pi ({{V}_{i}},\alpha )=E\{{{\xi }_{i}}|{{V}_{i}}\},\omega ({{V}_{i}},\gamma )=E\{{{\delta }_{i}}|{{V}_{i}}\}$分别表示给定V_i时ξ_i和δ_i的条件期望，因而可使用已有的二元数据分析的方法对缺失模型和删失模型进行分析，可假定π(V_i,α)和ω(V_i,γ)满足常见的逻辑回归模型.另外，文献^[14]给出删失参数模型需满足$P\left\{ \delta =1|X=x \right\}=\frac{{{\lambda }_{t}}\left( x \right)}{{{\lambda }_{t}}\left( x \right)+{{\lambda }_{c}}\left( x \right)}.$该文同时还给出了一些具体可行的参数模型假设，比如当λ_c(x)通过链接函数Ψ(x,γ)对λ_t(x)产生乘积效应，即λ_t(x)=Ψ(x,γ)λ_c(x)，其中γ是未知参数，那么可给出$P\left\{ \delta =1|X=x \right\}=\frac{\Psi \left( x,\gamma \right)}{1+\Psi \left( x,\gamma \right)}.$.更多关于对P{δ=1|X}进行参数模型假定的细节可参考文献^[14].
对可加危险率模型，若失效信息没有缺失，令${{N}_{i}}\left( t \right)=I({{X}_{i}}\le t,{{\delta }_{i}}=1),{{N}^{u}}_{i}\left( t \right)=I({{X}_{i}}\le t),{{Y}_{i}}\left( t \right)=I({{X}_{i}}\ge t)$，那么

$\begin{align} & {{M}_{i}}\left( t \right)={{N}_{i}}\left( t \right)-\int\limits_{0}^{t}{{{Y}_{i}}\left( s \right)\{{{\lambda }_{0}}\left( s \right)+\beta {{\prime }_{0}}{{Z}_{i}}\}\text{d}s} \\ & ={{\delta }_{i}}N_{i}^{u}\left( t \right)-\int\limits_{0}^{t}{{{Y}_{i}}\left( s \right)\{{{\lambda }_{0}}\left( s \right)+\beta {{\prime }_{0}}{{Z}_{i}}\}\text{d}s}, \\ & \left( i=1,2,\ldots ,n \right). \\ \end{align}$

是零均值的鞅过程.根据鞅的性质，可得到关于未知回归参数β₀的估计方程^[9]

$\sum\limits_{i=1}^{n}{\int_{0}^{\tau }{\{{{Z}_{i}}-Z-\left( t \right)\}[\text{d}{{N}_{i}}\left( t \right)-{{Y}_{i}}\left( t \right)\beta {{\prime }_{0}}{{Z}_{i}}\text{d}t]}}=0,$

(2)

其中$\bar{Z}\left( t \right)=\frac{\sumolimits_{i=1}^{n}{{{Z}_{i}}{{Y}_{i}}\left( t \right)}}{\sumolimits_{i=1}^{n}{{{Y}_{i}}\left( t \right)}}$，τ是给定的满足P(X_i≥τ)>0且Λ₀(τ)<∞的正常数，一般取τ=max{X_i}，其中Λ₀(t)=$\int\limits_{0}^{t}{{{\lambda }_{0}}\left( s \right)\text{d}s}$表示基准累积风险函数.
2 参数概率模型的估计这一节考虑参数概率模型中未知参数α和γ的估计. 因为ξ和δ均服从条件伯努利分布，可以构建如下的似然函数：

${{L}_{n}}\left( \alpha \right)=\Pi _{i=1}^{n}{{\{\pi ({{V}_{i}},\alpha )\}}^{{{\xi }_{i}}}}{{\{1-\pi ({{V}_{i}},\alpha )\}}^{1-{{\xi }_{i}}}},$

(3)

${{L}_{n}}\left( \gamma \right)=\Pi _{^{i=1}}^{n}{{\{\omega ({{V}_{i}},\gamma )\}}^{{{\xi }_{i}}{{\delta }_{i}}}}{{\{1-\omega ({{V}_{i}},\gamma )\}}^{{{\xi }_{i}}(1-{{\delta }_{i}})}}.$

(4)

求解使上面似然函数达到最大的α和γ，分别记为${{\hat{\alpha }}_{n}}$和${{\hat{\gamma }}_{n}}$.在估计${{\hat{\gamma }}_{n}}$时，我们只用到对应ξ_i=1的观测数据，也即只使用了失效信息完全观察到的数据.在随机缺失条件下，由上面似然函数得到的估计方程是相合的. 下面引理给出估计的渐近正态性.
引理 2.1?若附录中的条件(C1)—(C3)成立，则有

$\begin{align} & \sqrt{n}\left( {{{\hat{\alpha }}}_{n}}-\alpha \right)=\frac{V_{\alpha }^{-1}}{\sqrt{n}}\sum\limits_{i=1}^{n}{\frac{{\pi }'\left( {{V}_{i}},\alpha \right)}{\pi \left( {{V}_{i}},\alpha \right)}}\frac{{{\xi }_{i}}-\pi \left( {{V}_{i}},\alpha \right)}{1-\pi \left( {{V}_{i}},\alpha \right)}+{{o}_{p}}\left( 1 \right), \\ & \sqrt{n}\left( {{{\hat{\gamma }}}_{n}}-\gamma \right)=\frac{V_{\gamma }^{-1}}{\sqrt{n}}\sum\limits_{i=1}^{n}{\frac{{\omega }'\left( {{V}_{i}},\gamma \right)}{\omega \left( {{V}_{i}},\gamma \right)}}\frac{{{\delta }_{i}}-\omega \left( {{V}_{i}},\gamma \right)}{1-\omega \left( {{V}_{i}},\gamma \right)}+{{o}_{p}}\left( 1 \right), \\ \end{align}$

这里

$\begin{align} & {{V}_{\alpha }}=E\left[ \frac{\pi \prime ({{V}_{i}},\alpha )}{\pi ({{V}_{i}},\alpha )}\frac{\pi \prime {{({{V}_{i}},\alpha )}^{\text{T}}}}{1-\pi ({{V}_{i}},\alpha )} \right], \\ & {{V}_{\gamma }}=E\left[ \frac{\omega \prime ({{V}_{i}},\gamma )}{\omega ({{V}_{i}},\gamma )}\frac{\omega \prime {{({{V}_{i}},\gamma )}^{\text{T}}}}{1-\omega ({{V}_{i}},\gamma )}\pi ({{V}_{i}},\alpha ) \right], \\ \end{align}$

π′(V_i,α)和ω′(V_i,γ)分别为π(V_i,α)和ω(V_i,γ)关于α和γ的一阶导数.
3 逆概率加权估计当失效信息随机缺失时，因为有些δ_i是缺失的，因此估计方程(2)不能直接使用.利用逆概率加权方法，可以构建零均值的随机过程

$M_{i}^{[1]}\left( t \right)=\frac{{{\xi }_{i}}}{\pi ({{V}_{i}},\alpha )}\left[ {{N}_{i}}\left( t \right)-\int_{0}^{t}{{{Y}_{i}}\left( s \right)}\{{{\lambda }_{0}}\left( s \right)+\beta {{\prime }_{0}}{{Z}_{i}}\}\text{d}s \right],$

进一步可构建下面的估计方程组：

$\begin{align} & \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}}}{{Z}_{i}}\left[ \text{d}{{N}_{i}}\left( t \right)-{{Y}_{i}}\left( t \right){{{{\beta }'}}_{0}}{{Z}_{i}}\text{d}t-{{Y}_{i}}\left( t \right) \right. \\ & \left. \text{d}{{\Lambda }_{0}}\left( t \right) \right]=0, \\ \end{align}$

(5)

$\sum\limits_{i=1}^{n}{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}}[\text{d}{{N}_{i}}\left( t \right)-{{Y}_{i}}\left( t \right){{{\beta }'}_{0}}{{Z}_{i}}\text{d}t-{{Y}_{i}}\left( t \right)\text{d}{{\Lambda }_{0}}\left( t \right)]=0,$

(6)

对任意的向量a，记${{a}^{\otimes 2}}=a{a}'$.解上述方程组，可得β₀和Λ₀的逆概率加权估计有如下形式：

$\begin{align} & {{{\hat{\beta }}}_{1n}}={{\left[ \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}}}{{Y}_{i}}\left( t \right){{\left\{ {{Z}_{i}}-{{{\bar{Z}}}^{*}}\left( t \right) \right\}}^{\otimes 2}}\text{d}t \right]}^{-1}} \\ & \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}}}\left\{ {{Z}_{i}}-{{{\bar{Z}}}^{*}}\left( t \right) \right\}\text{d}{{N}_{i}}\left( t \right), \\ \end{align}$

(7)

${{{\hat{\Lambda }}}_{1n}}\left( t \right)=\int\limits_{0}^{t}{\frac{\sumolimits_{i=1}^{n}{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\left[ \text{d}{{N}_{i}}\left( s \right)-{{Y}_{i}}\left( s \right){{{{\hat{\beta }}'}}_{1n}}{{Z}_{i}}\text{d}s \right]}}{\sumolimits_{i=1}^{n}{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}{{Y}_{i}}\left( s \right)}}},$

(8)

其中

${{{\bar{Z}}}^{*}}\left( t \right)=\frac{\sumolimits_{i=1}^{n}{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}{{Z}_{i}}{{Y}_{i}}\left( t \right)}}{\sumolimits_{i=1}^{n}{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}{{Y}_{i}}\left( s \right)}}$

首先给出${{\hat{\beta }}_{1n}}$的渐近正态性.
定理3.1?若附录中条件(C1)—(C5)成立，那么

$\sqrt{n}\left( {{{\hat{\beta }}}_{1n}}-{{\beta }_{0}} \right)={{A}^{-1}}\left( {{n}^{-1/2}}\sum\limits_{i=1}^{n}{{{\phi }_{1i}}} \right)+{{o}_{p}}\left( 1 \right).$

其中

$\begin{align} & A=E[\int\limits_{0}^{\tau }{{{Y}_{i}}\left( t \right){{\{{{Z}_{i}}-\bar{z}\left( t \right)\}}^{\otimes 2}}\text{d}t]}, \\ & \bar{z}\left( t \right)=E[{{Z}_{i}}{{Y}_{i}}\left( t \right)\left] /E \right[{{Y}_{i}}\left( t \right)], \\ & {{\phi }_{1i}}=\int\limits_{0}^{\tau }{\frac{{{\xi }_{i}}}{\pi ({{V}_{i}},\alpha )}}\{{{Z}_{i}}-\bar{z}\left( t \right)\}\text{d}{{M}_{i}}\left( t \right)+{{B}_{1\alpha }}V_{_{\alpha }}^{-1}{{S}_{\alpha i}}, \\ & {{B}_{1\alpha }}=E[-\int\limits_{0}^{\tau }{\{{{Z}_{i}}-\bar{z}\left( t \right)\}}\frac{{{\xi }_{i}}\pi \prime {{({{V}_{i}},\alpha )}^{\text{T}}}}{{{\pi }^{2}}({{V}_{i}},\alpha )}\text{d}{{M}_{i}}\left( t \right)], \\ & {{S}_{\alpha i}}=\frac{\pi \prime ({{V}_{i}},\alpha )}{\pi ({{V}_{i}},\alpha )}\frac{{{\xi }_{i}}-\pi ({{V}_{i}},\alpha )}{1-\pi ({{V}_{i}},\alpha )}. \\ \end{align}$

根据定理3.1，由中心极限定理可知$\sqrt{n}\left( {{{\hat{\beta }}}_{1n}}-{{\beta }_{0}} \right)$依分布收敛于均值为0、 协方差矩阵为${{A}^{-1}}E({{\phi }_{1i}}\phi _{1i}^{T}){{({{A}^{-1}})}^{\text{T}}}$的正态分布.
采用传统的plug-in方法，可得到渐近方差${{A}^{-1}}E({{\phi }_{1i}}\phi _{1i}^{T}){{({{A}^{-1}})}^{\text{T}}}$的相合估计为${{A}^{-1}}(\frac{1}{n}\sum\limits_{i-1}^{n}{{{{\hat{\phi }}}_{1i}}\hat{\phi }_{1i}^{T}}){{({{\hat{A}}^{-1}})}^{\text{T}}}$，其中

$\begin{align} & \hat{A}=\frac{1}{n}\int\limits_{0}^{\tau }{{{Y}_{i}}\left( t \right){{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}}^{\otimes 2}}\text{d}t,} \\ & {{{\hat{\phi }}}_{1i}}=\int\limits_{0}^{\tau }{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}}\left[ \text{d}{{N}_{i}}\left( t \right)-{{Y}_{i}}\left( t \right) \right. \\ & \left. \left( \text{d}{{{\hat{\Lambda }}}_{1n}}\left( t \right)+{{{{\hat{\beta }}'}}_{1n}}{{Z}_{i}}\text{d}t \right) \right]+{{{{\hat{B}}'}}_{1n}}\hat{V}_{\alpha }^{-1}{{{\hat{S}}}_{\alpha i}}, \\ & {{{\hat{B}}}_{1\alpha }}=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ -\int\limits_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}}\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right.} \\ & \left. \left\{ \text{d}{{N}_{i}}\left( t \right)-{{Y}_{i}}\left( t \right)\left( \text{d}{{{\hat{\Lambda }}}_{1n}}\left( t \right)+{{{{\hat{\beta }}'}}_{1n}}{{Z}_{i}}\text{d}t \right) \right\} \right], \\ & {{{\hat{V}}}_{\alpha }}=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ \frac{{\pi }'\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\frac{{\pi }'{{\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}^{\text{T}}}}{1-\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right]}, \\ & {{{\hat{S}}}_{\alpha i}}=\frac{{\pi }'\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\frac{{{\xi }_{i}}-\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}{1-\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}. \\ \end{align}$

下面考察${{\hat{\Lambda }}_{1n}}\left( t \right)$的渐近正态性.
定理3.2?在定理3.1成立的条件下，有

$\sqrt{n}\left( {{{\hat{\Lambda }}}_{1n}}\left( t \right)-{{\Lambda }_{0}}\left( t \right) \right)={{n}^{-1/2}}\sum\limits_{i=1}^{n}{{{\psi }_{1i}}\left( t \right)+{{o}_{p}}\left( 1 \right),}$

其中

$\begin{align} & {{\psi }_{1i}}\left( t \right)=\int\limits_{0}^{t}{\frac{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},\alpha \right)}\text{d}{{M}_{i}}\left( s \right)}{\mu \left( s \right)}}-C{{\left( t \right)}^{\text{T}}}{{A}^{-1}}{{\phi }_{1i}}-{{D}_{1\alpha }}\left( t \right)V_{\alpha }^{-1}{{S}_{\alpha i}}, \\ & \mu \left( t \right)=E\left[ {{Y}_{i}}\left( t \right) \right],C\left( t \right)=\int\limits_{0}^{t}{\bar{z}\left( s \right)\text{d}s}, \\ & {{D}_{1\alpha }}\left( t \right)=E\left[ \int_{0}^{t}{\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},\alpha \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},\alpha \right)\mu \left( s \right)}\text{d}M\left( s \right)} \right]. \\ \end{align}$

根据定理3.2，$\sqrt{n}\left( {{{\hat{\Lambda }}}_{1n}}\left( t \right)-{{\Lambda }_{0}}\left( t \right) \right)$依分布收敛于一个均值为0的高斯过程，且在(s,t)的渐近协方差函数为E(ψ_1i(s)ψ_1i(t)).易得E(ψ_1i(s)ψ_1i(t))的相合估计为$\frac{1}{n}\sum\limits_{i=1}^{n}{\left( {{{\hat{\psi }}}_{1i}}\left( s \right){{{\hat{\psi }}}_{1i}}\left( t \right) \right)}$其中

$\begin{align} & {{{\hat{\psi }}}_{1i}}\left( t \right)= \\ & \int\limits_{0}^{t}{\frac{\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\left[ \text{d}{{N}_{i}}\left( s \right)-{{Y}_{i}}\left( s \right)\left\{ \text{d}{{{\hat{\Lambda }}}_{1n}}\left( s \right)+{{{{\hat{\beta }}'}}_{1n}}{{Z}_{i}}\text{d}s \right\} \right]}{\frac{1}{n}\sumolimits_{i=1}^{n}{{{Y}_{i}}\left( s \right)}}}- \\ & \hat{C}\left( t \right)=\int\limits_{0}^{t}{\bar{Z}\left( s \right)\text{d}s,\hat{\mu }\left( t \right)=\frac{1}{n}\sum\limits_{i=1}^{n}{{{Y}_{i}}\left( t \right)}}, \\ & {{{\hat{D}}}_{1\alpha }}\left( t \right)=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ \int\limits_{0}^{t}{\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)\hat{\mu }\left( s \right)}}\left\{ \text{d}{{N}_{i}}\left( s \right)- \right. \right.} \\ & \left. {{Y}_{i}}\left( s \right)\left( \text{d}{{{\hat{\Lambda }}}_{1n}}\left( s \right)+{{{{\hat{\beta }}'}}_{1n}}{{Z}_{i}}\text{d}s \right) \right\}. \\ \end{align}$

4 增广加权估计上面构建的逆概率加权估计只用到了完全观测样本(对应ξ_i=1的个体)的信息.忽略不完全观测样本(ξ_i=0 的个体)可能会使结果的有效性降低.尤其当缺失比率较高时，这种现象更为严重. 注意到

$\begin{align} & M_{i}^{\left[ 2 \right]}\left( t \right)=\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},\alpha \right)}{{N}_{i}}\left( t \right)+ \\ & \left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},\alpha \right)} \right)\omega \left( {{V}_{i}},\gamma \right)N_{i}^{u}\left( t \right)- \\ & \int\limits_{0}^{t}{{{Y}_{i}}\left( s \right)\left\{ {{\lambda }_{0}}\left( s \right)+{{{{\beta }'}}_{0}}{{Z}_{i}} \right\}}\text{d}s, \\ \end{align}$

是零均值的随机过程.
考虑下面的关于β₀和Λ₀的增广加权估计方程：

$\begin{align} & \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{{{Z}_{i}}\left[ \frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\text{d}{{N}_{i}}\left( t \right)+\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right)\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right) \right.}} \\ & \left. \text{d}N_{i}^{u}\left( t \right)-{{Y}_{i}}\left( t \right){{{{\beta }'}}_{0}}{{Z}_{i}}\text{d}t-{{Y}_{i}}\left( t \right)\text{d}{{\Lambda }_{0}}\left( t \right) \right]=0, \\ \end{align}$

(9)

$\begin{align} & \sum\limits_{i=1}^{n}{\left[ \frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\text{d}{{N}_{i}}\left( t \right)+\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right)\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right) \right.} \\ & \left. \text{d}N_{i}^{u}\left( t \right)-{{Y}_{i}}\left( t \right){{{{\beta }'}}_{0}}{{Z}_{i}}\text{d}t-{{Y}_{i}}\left( t \right)\text{d}{{\Lambda }_{0}}\left( t \right) \right]=0, \\ \end{align}$

(10)

解上述方程组，可得β₀和Λ₀的增广加权估计有如下形式：

$\begin{align} & {{{\hat{\beta }}}_{2n}}={{\left[ \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{{{Y}_{i}}\left( t \right){{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}}^{\otimes 2}}\text{d}t}} \right]}^{-1}} \\ & \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}}}\left[ \frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\text{d}{{N}_{i}}\left( t \right)+ \right. \\ & \left. \left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right)\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)\text{d}N_{i}^{u}\left( t \right) \right], \\ \end{align}$

(11)

$\begin{align} & {{{\hat{\Lambda }}}_{2n}}\left( t \right)=\int\limits_{0}^{t}{\sum\limits_{i=1}^{n}{\left\{ \frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\text{d}{{N}_{i}}\left( s \right)+ \right.}}\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right) \\ & \left. \omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)\text{d}N_{i}^{u}\left( s \right)-{{Y}_{i}}\left( s \right){{{{\hat{\beta }}'}}_{2n}}{{Z}_{i}}\text{d}s \right\}/\sum\limits_{i=1}^{n}{{{Y}_{i}}\left( s \right)}. \\ \end{align}$

(12)

我们给出记号：

$\begin{align} & {{S}_{\gamma i}}=\frac{{\omega }'\left( {{V}_{i}},\gamma \right)}{\omega \left( {{V}_{i}},\gamma \right)}\frac{{{\delta }_{i}}-\omega \left( {{V}_{i}},\gamma \right)}{1-\omega \left( {{V}_{i}},\gamma \right)}{{\xi }_{i}}, \\ & {{\phi }_{2i}}=\int\limits_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{z}\left( t \right) \right\}\text{d}M_{i}^{\left[ 2 \right]}\left( t \right)+{{B}_{2\alpha }}V_{\alpha }^{-1}{{S}_{\alpha i}}+{{B}_{2\gamma }}V_{\gamma }^{-1}{{S}_{\gamma i}}} \\ & {{B}_{2\alpha }}=E\left[ \int_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{z}\left( t \right) \right\}\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},\alpha \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},\alpha \right)}\left( \omega \left( {{V}_{i}},\gamma \right)-{{\delta }_{i}} \right)\text{d}N_{i}^{u}\left( t \right)} \right], \\ & {{B}_{2\gamma }}=E\left[ \int_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{z}\left( t \right) \right\}\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},\alpha \right)} \right){\omega }'{{\left( {{V}_{i}},\gamma \right)}^{\text{T}}}\text{d}N_{i}^{u}\left( t \right)} \right]. \\ \end{align}$

下面定理给出${{\hat{\beta }}_{2n}}$的渐近正态性.
定理4.1?在定理3.1成立的条件下，

$\sqrt{n}\left( {{{\hat{\beta }}}_{2n}}-{{\beta }_{0}} \right)={{A}^{-1}}\left( {{n}^{-1/2}}\sum\limits_{i=1}^{n}{{{\phi }_{2i}}} \right)+{{o}_{p}}\left( 1 \right).$

由定理4.1可得$\sqrt{n}\left( {{{\hat{\beta }}}_{2n}}-{{\beta }_{0}} \right)$依分布收敛于均值为0、协方差矩阵为${{A}^{-1}}E\left( {{\phi }_{2i}}\phi _{2i}^{\text{T}} \right){{\left( {{A}^{-1}} \right)}^{\text{T}}}$的正态分布. 我们可以给出渐近方差${{A}^{-1}}E\left( {{\phi }_{2i}}\phi _{2i}^{\text{T}} \right){{\left( {{A}^{-1}} \right)}^{\text{T}}}$的相合估计：${{A}^{-1}}\left( \frac{1}{n}\sum\limits_{i=1}^{n}{{{{\hat{\phi }}}_{2i}}\hat{\phi }_{2i}^{\text{T}}} \right){{\left( {{{\hat{A}}}^{-1}} \right)}^{\text{T}}}$，其中

$\begin{align} & {{{\hat{\phi }}}_{2i}}=\int\limits_{0}^{\tau }{\left\{ {{z}_{i}}-\bar{z}\left( t \right) \right\}\left[ \frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\text{d}{{N}_{i}}\left( t \right)+\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right) \right.} \\ & \left. \omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)\text{d}N_{i}^{u}\left( t \right)-{{Y}_{i}}\left( t \right)\left( \text{d}{{{\hat{\Lambda }}}_{2n}}\left( t \right)+{{{{\hat{\beta }}'}}_{2n}}{{Z}_{i}}\text{d}t \right) \right]+ \\ & {{{\hat{B}}}_{2\alpha }}\hat{V}_{\alpha }^{-1}{{{\hat{S}}}_{\alpha i}}+{{{\hat{B}}}_{2\gamma }}\hat{V}_{\gamma }^{-1}{{{\hat{S}}}_{\gamma i}}, \\ & {{{\hat{B}}}_{2\alpha }}=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ \int\limits_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}} \right.} \\ & \left. \left( \omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)-{{\delta }_{i}} \right)\text{d}N_{i}^{u}\left( t \right) \right], \\ \end{align}$

$\begin{align} & {{{\hat{B}}}_{2\gamma }}=\frac{1}{n}\sum\limits_{i=1}^{n}{\int\limits_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right)}} \\ & \left. {\omega }'{{\left( {{V}_{i}}{{{\hat{\gamma }}}_{n}} \right)}^{\text{T}}}\text{d}N_{i}^{u}\left( t \right) \right], \\ & {{{\hat{V}}}_{\gamma }}=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ \frac{{\omega }'\left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}{\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}\frac{{\omega }'{{\left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}^{\text{T}}}}{1-\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right) \right]}, \\ & {{{\hat{S}}}_{\gamma i}}=\frac{{\omega }'\left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}{\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}\frac{{{\delta }_{i}}-\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}{1-\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}{{\xi }_{i}}. \\ \end{align}$

下面的定理4.2给出${{{\hat{\Lambda }}}_{2n}}\left( t \right)$的渐近性质.
定理4.2?在定理3.1成立的条件下，有

$\sqrt{n}\left( {{{\hat{\Lambda }}}_{2n}}\left( t \right)-{{\Lambda }_{0}}\left( t \right) \right)={{n}^{-1/2}}\sum\limits_{i=1}^{n}{{{\psi }_{2i}}\left( t \right)}+{{o}_{p}}\left( 1 \right),$

其中

$\begin{align} & {{\psi }_{2i}}\left( t \right)=\int\limits_{0}^{t}{\frac{\text{d}M_{i}^{\left[ 2 \right]}\left( s \right)}{\mu \left( s \right)}}-C{{\left( t \right)}^{\text{T}}}{{A}^{-1}}{{\phi }_{2i}}+ \\ & {{D}_{2\alpha }}\left( t \right)V_{\alpha }^{-1}{{S}_{\alpha i}}+{{D}_{2\gamma }}\left( t \right)V_{\gamma }^{-1}{{S}_{\gamma i}}, \\ & {{D}_{2\alpha }}\left( t \right)=E\left[ \int\limits_{0}^{t}{\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},\alpha \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},\alpha \right)\mu \left( s \right)}\left( \omega \left( {{V}_{i}},\gamma \right)-{{\delta }_{i}} \right)\text{d}N_{i}^{u}\left( s \right)} \right], \\ & {{D}_{2\gamma }}\left( t \right)=E\left[ \int\limits_{0}^{t}{\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},\alpha \right)} \right)\frac{{\omega }'{{\left( {{V}_{i}},\gamma \right)}^{\text{T}}}}{\mu \left( s \right)}\text{d}N_{i}^{u}\left( s \right)} \right]. \\ \end{align}$

由定理4.2，进一步可得到$\sqrt{n}\left( {{{\hat{\Lambda }}}_{2n}}\left( t \right)-{{\Lambda }_{0}}\left( t \right) \right)$依分布收敛于一个均值为0的高斯过程，且在(s,t)的渐近协方差函数为E(ψ_2i(s)ψ_2i(t)).我们给出E(ψ_2i(s)ψ_i(t))的相合估计$\frac{1}{n}\sum\limits_{i=1}^{n}{\left( {{{\hat{\psi }}}_{2i}}\left( s \right){{{\hat{\psi }}}_{2i}}\left( t \right) \right)}$，其中

$\begin{align} & {{{\hat{\psi }}}_{2i}}\left( t \right)=\int\limits_{0}^{t}{\left\{ \frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}\text{d}{{N}_{i}}\left( s \right)+\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right) \right.} \\ & \omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)\text{d}N_{i}^{u}\left( s \right)-{{Y}_{i}}\left( s \right)\left\{ \text{d}{{{\hat{\Lambda }}}_{2n}}\left( s \right)+ \right. \\ & \left. \left. {{{{\hat{\beta }}'}}_{2n}}{{Z}_{i}}\text{d}s \right\} \right\}/\left\{ \frac{1}{n}\sum\limits_{i=1}^{n}{{{Y}_{i}}\left( s \right)} \right\}- \\ & \hat{C}{{\left( t \right)}^{\text{T}}}{{{\hat{A}}}^{-1}}{{{\hat{\phi }}}_{2i}}+{{{\hat{D}}}_{2\alpha }}\left( t \right)\hat{V}_{\alpha }^{-1}{{{\hat{S}}}_{\alpha i}}+ \\ & {{{\hat{D}}}_{2\gamma }}\left( t \right)\hat{V}_{\gamma }^{-1}{{{\hat{S}}}_{\gamma i}}, \\ \end{align}$

$\begin{align} & {{{\hat{D}}}_{2\alpha }}\left( t \right)=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ \int\limits_{0}^{t}{\frac{{{\xi }_{i}}{\pi }'{{\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)}^{\text{T}}}}{{{\pi }^{2}}\left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)\hat{\mu }\left( s \right)}\left( \omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)-{{\delta }_{i}} \right)\text{d}N_{i}^{u}\left( s \right)} \right]}, \\ & {{{\hat{D}}}_{2\gamma }}\left( t \right)=\frac{1}{n}\sum\limits_{i=1}^{n}{\left[ \int\limits_{0}^{t}{\left( 1-\frac{{{\xi }_{i}}}{\pi \left( {{V}_{i}},{{{\hat{\alpha }}}_{n}} \right)} \right)\frac{{\omega }'{{\left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)}^{\text{T}}}}{\hat{\mu }\left( s \right)}}\text{d}N_{i}^{u}\left( s \right) \right]}. \\ \end{align}$

5 基于模型的插补估计在处理缺失数据时，插补是一种常用的方法.下面考虑一种基于模型的插补方法. 当ξ_i=1，I(X_i≤t,δ_i=1)=δ_iI(X_i≤t)是可以观察到的.但是ξ_i=0时，因为δ_i的值缺失了，因此I(X_i≤t,δ_i=1)无法由观察数据得到.此时，对δ_i用其条件均值ω(V_i,γ)替代,以此得到下面零均值的随机过程

$\begin{align} & M_{i}^{\left[ 3 \right]}\left( t \right)={{\xi }_{i}}{{N}_{i}}\left( t \right)+\left( 1-{{\xi }_{i}} \right)\omega \left( {{V}_{i}},\gamma \right)N_{i}^{u}\left( t \right)- \\ & \int\limits_{0}^{t}{{{Y}_{i}}\left( s \right)\left\{ {{\lambda }_{0}}\left( s \right)+{{{{\beta }'}}_{0}}{{Z}_{i}} \right\}\text{d}s,} \\ \end{align}$

那么可得如下关于β₀和Λ₀的估计方程：

$\begin{align} & \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{{{Z}_{i}}\left[ {{\xi }_{i}}\text{d}{{N}_{i}}(t)+(1-{{\xi }_{i}})\omega ({{V}_{i}},{{{\hat{\gamma }}}_{n}})\text{d}N_{i}^{u}(t)- \right.}} \\ & \left. {{Y}_{i}}\left( t \right){{{{\beta }'}}_{0}}{{Z}_{i}}\text{d}t-{{Y}_{i}}\left( t \right)\text{d}{{\Lambda }_{0}}\left( t \right) \right]=0, \\ \end{align}$

(13)

$\begin{align} & \sum\limits_{i=1}^{n}{\left[ {{\xi }_{i}}\text{d}{{N}_{i}}\left( t \right)+\left( 1-{{\xi }_{i}} \right)\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right) \right.\text{d}N_{i}^{u}\left( t \right)-} \\ & \left. {{Y}_{i}}\left( t \right){{{{\beta }'}}_{0}}{{Z}_{i}}\text{d}t-{{Y}_{i}}\left( t \right)\text{d}{{\Lambda }_{0}}\left( t \right) \right]=0, \\ \end{align}$

(14)

解上述方程组，可得β₀和Λ₀的基于模型的插补估计有如下形式：

$\begin{align} & {{{\hat{\beta }}}_{3n}}={{\left[ \sum\limits_{i=1}^{n}{\int_{0}^{\tau }{{{Y}_{i}}\left( t \right){{\left\{ {{Z}_{i}}-\bar{Z}\left( t \right) \right\}}^{\otimes 2}}\text{d}t}} \right]}^{-1}}\sum\limits_{i=1}^{n}{\int_{0}^{\tau }{\left\{ {{Z}_{i}}- \right.}} \\ & \left. \bar{Z}\left( t \right) \right\}\left[ {{\xi }_{i}}\text{d}{{N}_{i}}\left( t \right)+\left( 1-{{\xi }_{i}} \right)\omega \right. \\ & \left. \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)\text{d}N_{i}^{u}\left( t \right) \right], \\ \end{align}$

(15)

$\begin{align} & {{{\hat{\Lambda }}}_{3n}}\left( t \right)=\int\limits_{0}^{t}{\left\{ \sum\limits_{i=1}^{n}{{{\xi }_{i}}\text{d}{{N}_{i}}\left( s \right)+\left( 1-{{\xi }_{i}} \right)\omega \left( {{V}_{i}},{{{\hat{\gamma }}}_{n}} \right)\text{d}N_{i}^{u}\left( s \right)} \right.}- \\ & \left. {{Y}_{i}}\left( s \right){{{{\hat{\beta }}'}}_{3n}}{{Z}_{i}}\text{d}s \right\}/\sum\limits_{i=1}^{n}{{{Y}_{i}}\left( s \right)}. \\ \end{align}$

(16)

与定理4.1和定理4.2相似，${{\hat{\beta }}_{3n}}$和${{\hat{\Lambda }}_{3n}}\left( t \right)$的渐近性质由下面的定理给出.
定理5.1?在定理3.1成立的条件下，我们有

$\begin{align} & \sqrt{n}\left( {{{\hat{\beta }}}_{3n}}-{{\beta }_{0}} \right)={{A}^{-1}}\left( {{n}^{-1/2}}\sum\limits_{i=1}^{n}{{{\phi }_{3i}}} \right)+{{o}_{p}}\left( 1 \right), \\ & \sqrt{n}\left( {{{\hat{\Lambda }}}_{3n}}\left( t \right)-{{\Lambda }_{0}}\left( t \right) \right)={{n}^{-1/2}}\sum\limits_{i=1}^{n}{{{\psi }_{3i}}\left( t \right)+{{o}_{p}}\left( 1 \right),} \\ \end{align}$

其中

$\begin{align} & {{\phi }_{3i}}=\int\limits_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{z}\left( t \right) \right\}}\text{d}M_{i}^{\left[ 3 \right]}\left( t \right)+{{B}_{3\gamma }}V_{\gamma }^{-1}{{S}_{\gamma i}}, \\ & {{B}_{3\gamma }}=E\left[ \int_{0}^{\tau }{\left\{ {{Z}_{i}}-\bar{z}\left( t \right) \right\}\left( 1-{{\xi }_{i}} \right)}{\omega }'{{\left( {{V}_{i}},\gamma \right)}^{\text{T}}}\text{d}N_{i}^{u}\left( t \right) \right], \\ & {{\psi }_{3i}}\left( t \right)=\int\limits_{0}^{t}{\frac{\text{d}M_{i}^{\left[ 3 \right]}\left( s \right)}{\mu \left( s \right)}-C{{\left( t \right)}^{\text{T}}}{{A}^{-1}}{{\phi }_{3i}}+{{D}_{3\gamma }}\left( t \right)V_{\gamma }^{-1}}{{S}_{\gamma i}}, \\ & {{D}_{3\gamma }}\left( t \right)=E\left[ \int\limits_{0}^{t}{\left( 1-{{\xi }_{i}} \right)\frac{{\omega }'{{\left( {{V}_{i}},\gamma \right)}^{\text{T}}}}{\mu \left( s \right)}\text{d}N_{i}^{u}\left( s \right)} \right]. \\ \end{align}$

由定理5.1可得$\sqrt{n}\left( {{{\hat{\beta }}}_{3n}}-{{\beta }_{0}} \right)$依分布收敛于均值为0、协方差矩阵为${{A}^{-1}}E\left( {{\phi }_{^{3i}}}\phi _{3i}^{\text{T}} \right){{\left( {{A}^{-1}} \right)}^{\text{T}}}$的正态分布，$\sqrt{n}\left( {{{\hat{\Lambda }}}_{3n}}\left( t \right)-{{\Lambda }_{0}}\left( t \right) \right)$依分布收敛于均值为0、在(s,t) 的渐近协方差函数为E(ψ_3i(s)ψ_3i(t))的高斯过程，与前面类似的讨论即可得到其渐近方差和渐近协方差函数的相合估计.
6 数值模拟和实例分析6.1 数值模拟本节通过数值模拟对回归参数β₀的3个估计结果${{\hat{\beta }}_{1n}},{{\hat{\beta }}_{2n}}$和$的有限样本性质进行研究. 对考虑的可加危险率模型λ(t|Z)=λ₀(t)+β′₀Z，基准风险函数取为λ₀(t)≡0.5，回归系数β₀=1. 协变量考虑2种情形：Z～Uniform(0,2)和Z～Bernoulli(0.5). 由可加危险率模型λ(t|Z)=λ₀(t)+β₀Z，根据风险函数和密度函数的关系，可以生成生存时间变量T_i,i=1,2,…,n. 假定删失时间变量C的风险函数为(λ₀(t)+β₀Z)/exp(γ₁Z+γ₂)，并据此生成删失时间变量C_i,i=1,2,…,n. 样本量n取为100和200.
设定响应概率模型P{ξ_i=1|V_i}=π(V_i,α)的参数形式为

$\pi \left( {{V}_{i}}\alpha \right)=\frac{\exp \left( {{{{\alpha }'}}_{1}}{{V}_{i}}+{{\alpha }_{2}} \right)}{1-\exp \left( {{{{\alpha }'}}_{1}}{{V}_{i}}+{{\alpha }_{2}} \right)}.$

考虑到$\omega \left( v,\gamma \right)=\frac{{{\lambda }_{t}}}{{{\lambda }_{t}}+{{\lambda }_{c}}}$,其中λ_t和λ_c分别表示T和C的风险函数，因此可求得

$P\left\{ {{\delta }_{i}}=1|{{X}_{i}},{{Z}_{i}} \right\}=\omega \left( {{V}_{i}},\gamma \right)=\frac{\exp \left( {{\gamma }_{1}}{{Z}_{i}}+{{\gamma }_{2}} \right)}{1+\exp \left( {{\gamma }_{1}}{{Z}_{i}}+{{\gamma }_{2}} \right)},$

考虑不同的删失率和缺失率，这通过取不同的参数的值达到.参数不同的取值以及相应的删失率和缺失率详见表 1.
Table 1

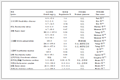表 1 模型参数设置Table 1 Parametric model settings 删失率 缺失率 20% 40% α γ α γ Z～Uniform(0,2) 20% [1.50,-0.71]’ [1.00,0.48]’ [0.50,-0.38]’ [1.00,0.48]’ 40% [0.50,0.70]’ [1.00,-0.56]’ [0.50,-0.30]’ [1.00,-0.56]’ Z～Bernoulli(0.5) 20% [1.00,0.15]’ [2.00,0.68]’ [0.50,-0.25]’ [2.00,0.68]’ 40% [0.50,0.90]’ [2.00,-0.49]’ [0.50,-0.16]’ [2.00,-0.49]’

表 1 模型参数设置Table 1 Parametric model settings

基于1 000次重复模拟的结果，计算所提的回归参数β的3种估计的偏差(BIAS)，样本标准差(SSE)，估计的标准差(ESE)和基于正态近似的95%的覆盖率(CP). 我们也给出文献^[12-13]所提估计的偏差，样本标准差，估计的标准差和基于正态近似的95%的覆盖率，具体结果列于表 2和表 3.
Table 2

表 2 Z～Uniform(0,2)时的模拟结果Table 2 Simulation results when Z～Uniform(0,2) 删失率 估计 缺失率 20% 40% BIAS SSE ESE CP BIAS SSE ESE CP n=100 20% ${{\hat{\beta }}_{1}}$ 0.015 2 0.325 2 0.348 9 0.962 0 0.025 0 0.374 0 0.488 0 0.977 0 ${{\hat{\beta }}_{2}}$ 0.008 6 0.304 8 0.299 2 0.946 0 0.021 9 0.317 7 0.302 3 0.935 0 ${{\hat{\beta }}_{3}}$ 0.012 5 0.286 3 0.292 4 0.952 0 0.021 9 0.289 9 0.298 9 0.948 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.053 3 0.313 4 0.381 7 0.983 0 0.053 3 0.365 0 0.438 8 0.979 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.060 9 0.305 7 0.381 7 0.987 0 0.007 1 0.312 6 0.438 8 0.983 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ 0.148 1 0.289 8 0.375 1 0.988 0 -0.065 0 0.276 6 0.374 7 0.977 0 40% ${{\hat{\beta }}_{1}}$ 0.044 0 0.383 3 0.445 6 0.975 0 0.035 1 0.441 6 0.618 4 0.987 0 ${{\hat{\beta }}_{2}}$ 0.040 6 0.367 3 0.341 9 0.938 0 0.026 3 0.383 5 0.360 9 0.979 0 ${{\hat{\beta }}_{3}}$ 0.039 9 0.340 5 0.340 3 0.950 0 0.024 8 0.319 1 0.358 7 0.967 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.053 6 0.383 0 0.465 9 0.982 0 0.060 6 0.438 6 0.519 6 0.973 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.031 9 0.363 8 0.465 9 0.987 0 0.000 3 0.370 6 0.519 6 0.984 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ 0.022 9 0.351 2 0.438 3 0.984 0 0.062 1 0.329 4 0.435 1 0.975 0 n=200 20% ${{{\hat{\beta }}}_{1}}$ 0.007 7 0.228 3 0.241 8 0.950 0 0.004 5 0.253 6 0.335 5 0.988 0 ${{{\hat{\beta }}}_{2}}$ 0.004 2 0.216 0 0.211 8 0.940 0 0.003 7 0.219 1 0.214 1 0.942 0 ${{{\hat{\beta }}}_{3}}$ 0.005 0 0.200 0 0.206 8 0.953 0 0.003 9 0.198 3 0.211 5 0.964 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.030 2 0.217 2 0.261 2 0.983 0 0.029 2 0.241 5 0.294 1 0.980 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.034 7 0.213 7 0.261 2 0.983 0 -0.011 7 0.213 2 0.294 1 0.987 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ 0.131 4 0.205 2 0.259 2 0.978 0 -0.069 3 0.188 8 0.259 6 0.979 0 40% ${{{\hat{\beta }}}_{1}}$ 0.009 0 0.254 7 0.312 4 0.977 0 0.014 2 0.293 7 0.424 2 0.988 0 ${{{\hat{\beta }}}_{2}}$ 0.008 3 0.242 2 0.241 7 0.943 0 0.015 2 0.254 9 0.253 7 0.953 0 ${{{\hat{\beta }}}_{3}}$ 0.006 8 0.223 6 0.240 5 0.964 0 0.011 8 0.214 1 0.251 1 0.972 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.016 7 0.254 8 0.315 1 0.980 0 0.035 6 0.286 4 0.347 8 0.981 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.000 6 0.240 9 0.315 1 0.986 0 -0.004 8 0.249 4 0.347 8 0.988 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ -0.005 8 0.230 5 0.300 6 0.984 0 -0.058 7 0.222 0 0.302 4 0.983 0 注：${{{\hat{\beta }}}_{1}}$本文的逆概率加权估计；$\hat{\beta }_{1}^{\left[ S \right]}$；文献[12]的简单加权估计；${{{\hat{\beta }}}_{2}}$本文的增广加权估计；$\hat{\beta }_{2}^{\left[ S \right]}$：文献[12]的增广加权估计；${{{\hat{\beta }}}_{3}}$：本文的基于模型的插补估计；$\hat{\beta }_{3}^{\left[ Q \right]}$：文献[13]的插补估计；BIAS：偏差；SSE：样本标准差；ESE：估计标准差；CP：基于正态近似的95%的覆盖率.

表 2 Z～Uniform(0,2)时的模拟结果Table 2 Simulation results when Z～Uniform(0,2)

Table 3

表 3 Z～Bernoulli(0.5)时的模拟结果Table 3 Simulation results when Z～Bernoulli(0.5) 删失率 估计 缺失率 20% 40% BIAS SSE ESE CP BIAS SSE ESE CP n=100 20% ${{{\hat{\beta }}}_{1}}$ 0.020 3 0.270 7 0.280 6 0.958 0 0.016 0 0.311 1 0.360 6 0.966 0 ${{{\hat{\beta }}}_{2}}$ 0.019 3 0.258 9 0.243 2 0.926 0 0.018 2 0.261 2 0.249 8 0.943 0 ${{{\hat{\beta }}}_{3}}$ 0.018 9 0.250 5 0.240 8 0.934 0 0.020 5 0.246 7 0.247 2 0.951 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.022 8 0.260 8 0.291 4 0.971 0 0.026 8 0.275 8 0.314 5 0.983 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.021 8 0.260 2 0.291 4 0.969 0 0.014 7 0.260 2 0.314 5 0.987 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ 0.030 6 0.247 6 0.287 0 0.981 0 -0.084 8 0.230 6 0.288 8 0.958 0 40% ${{{\hat{\beta }}}_{1}}$ 0.036 1 0.302 4 0.341 4 0.970 0 0.035 0 0.353 5 0.458 8 0.977 0 ${{{\hat{\beta }}}_{2}}$ 0.034 0 0.286 8 0.275 0 0.946 0 0.026 1 0.304 4 0.289 3 0.933 0 ${{{\hat{\beta }}}_{3}}$ 0.031 9 0.269 1 0.273 6 0.962 0 0.025 2 0.259 8 0.287 0 0.973 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.038 9 0.293 5 0.336 7 0.983 0 0.040 4 0.327 9 0.362 5 0.978 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.031 1 0.286 1 0.336 7 0.984 0 0.016 9 0.301 6 0.362 5 0.983 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ 0.013 6 0.274 8 0.327 1 0.983 0 -0.072 8 0.264 8 0.327 9 0.969 0 n=200 20% ${{{\hat{\beta }}}_{1}}$ 0.005 7 0.190 5 0.197 4 0.955 0 0.009 6 0.216 7 0.250 5 0.970 0 ${{{\hat{\beta }}}_{2}}$ 0.004 0 0.180 0 0.173 6 0.943 0 0.004 0 0.182 5 0.177 5 0.948 0 ${{{\hat{\beta }}}_{3}}$ 0.005 2 0.174 6 0.172 1 0.948 0 0.006 0 0.172 2 0.175 2 0.957 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.006 6 0.181 9 0.203 2 0.971 0 0.013 5 0.189 7 0.217 1 0.972 0 $\hat{\beta }_{2}^{\left[ S \right]}$ 0.005 9 0.180 7 0.203 2 0.974 0 0.001 5 0.182 8 0.217 1 0.982 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ 0.018 3 0.174 4 0.202 5 0.977 0 -0.091 4 0.161 2 0.201 1 0.952 0 40% ${{{\hat{\beta }}}_{1}}$ 0.002 3 0.210 9 0.237 1 0.972 0 0.004 9 0.246 0 0.314 2 0.981 0 ${{{\hat{\beta }}}_{2}}$ 0.003 8 0.199 0 0.192 6 0.954 0 0.000 9 0.213 7 0.203 6 0.937 0 ${{{\hat{\beta }}}_{3}}$ 0.004 7 0.186 9 0.191 8 0.947 0 0.002 8 0.182 8 0.202 0 0.966 0 $\hat{\beta }_{1}^{\left[ S \right]}$ 0.003 2 0.203 4 0.230 8 0.972 0 0.011 3 0.225 6 0.246 9 0.969 0 $\hat{\beta }_{2}^{\left[ S \right]}$ -0.002 4 0.200 6 0.230 8 0.976 0 -0.004 9 0.213 8 0.246 9 0.979 0 $\hat{\beta }_{3}^{\left[ Q \right]}$ -0.017 1 0.193 4 0.225 8 0.977 0 -0.089 9 0.185 1 0.227 3 0.962 0 注：${{{\hat{\beta }}}_{1}}$本文的逆概率加权估计；$\hat{\beta }_{1}^{\left[ S \right]}$；文献[12]的简单加权估计；${{{\hat{\beta }}}_{2}}$本文的增广加权估计；$\hat{\beta }_{2}^{\left[ S \right]}$：文献[12]的增广加权估计；${{{\hat{\beta }}}_{3}}$：本文的基于模型的插补估计；$\hat{\beta }_{3}^{\left[ Q \right]}$：文献[13]的插补估计；BIAS：偏差；SSE：样本标准差；ESE：估计标准差；CP：基于正态近似的95%的覆盖率.

表 3 Z～Bernoulli(0.5)时的模拟结果Table 3 Simulation results when Z～Bernoulli(0.5)

从模拟结果可以看出，本文所提的3个估计都有比较小的偏差，样本标准差和估计标准差；样本标准差和估计标准差比较接近. 当缺失概率和删失概率不是很大时，所提估计的覆盖率在95%附近.因此，所提的估计有比较好的有限样本性质.进一步比较所提的3个估计. 显然，增广加权估计和基于模型的插补估计，相比逆概率加权估计，具有更小的偏差，样本标准差和估计标准差及更加准确的覆盖率. 比较增广加权估计和基于模型的插补估计，后者具有更好的有限样本性质.前文提出回归系数和基准累积风险函数的增广加权估计时，就已指出，逆概率加权估计只用到了完全观测样本(对应ξ_i=1的个体)的信息，忽略了不完全观测样本(ξ_i=0的个体)的信息，可能会使结果的有效性降低. 增广加权估计中由于也采用了逆概率的方法，有时会导致结果稍逊于插补估计.
我们对所提的3个估计和文献中的估计：文献^[12]的简单逆概率加权估计和增广加权估计，以及文献^[13]的插补估计的有限样本性质进行比较. 发现我们所提的增广加权估计和基于模型的插补估计具有比文献中3个估计更好的有限样本性质： 具有更小的偏差，样本标准差和估计标准差和更加准确的覆盖率. 因为本文所提的增广加权估计和基于模型的插补估计充分地利用了参数模型的信息，因此相比采用非参数方法的文献中的3个估计更为准确，这是非常合理的. 这些说明我们所提的增广加权估计和基于模型的插补估计在参数模型假定正确时，的确更为有效.这种优势在样本量小(n=100)时尤其明显. 这也是合理的，当样本量比较大时，非参数方法的估计也比较准确，这时基于参数概率模型的方法和非参数概率模型的方法的差异就变小了.
6.2 实例分析本节我们通过对乳腺癌数据^[15]的分析验证所提出的估计方法.该数据来自ECOG(东部肿瘤协作组)的E1178临床试验，有169名患有第Ⅱ型乳腺癌的年长女性的相关信息.我们感兴趣的是注射它莫西芬病人的腋窝淋巴结数量对其生存时间的影响，该批病人中，共有86名病人接受了它莫西芬注射，其中21人死于乳腺癌(ξ=1,δ=1)，55人死于其他原因(ξ=1,δ=0)，而剩余10人死亡原因未知(ξ=0).我们建立可加危险率模型，利用本文所提的方法，采用与前面的模拟设置相同的参数模型结构对数据进行分析，具体结果见表 4.
Table 4

表 4 乳腺癌数据研究Table 4 Aanalysis of breast cancer data 方法 $\hat{\beta }\times {{10}^{3}}$ ESE×104 P-value IPW 0.129 4 0.599 5 0.030 9 FW 0.126 8 0.581 4 0.029 2 IM 0.123 4 0.572 4 0.031 2 Song1 0.140 2 0.699 2 0.044 9 Song2 0.138 5 0.699 2 0.047 6 Qiu 0.132 9 0.683 5 0.051 9 CC 0.120 6 0.633 3 0.056 9 注：IPW，FW和IM分别表示本文的逆概率加权，增广加权和基于模型的插补方法；Song1和Song2分别表示文献[12]的简单加权和增广加权方法；Qiu表示文献[13]的插补方法；CC表示Complete-Case方法.

表 4 乳腺癌数据研究Table 4 Aanalysis of breast cancer data

我们也利用文献^[12-13]中的方法，以及Complete-Case方法分析数据.文献中的方法用到删失概率函数和缺失概率函数的非参数估计，我们使用大拇指法则选择窗宽，所得结果见表 4. 从表 4的结果可以看出，乳腺癌病人的腋窝淋巴结数量是显著的，并且可以看出本文所提出方法的估计标准差明显小于文献中的方法，且检验的P值也要小一些.
7 结束语本文给出在失效信息随机缺失时可加危险率模型的回归参数和基准累积风险函数的逆概率加权估计、增广加权估计和基于模型的插补估计.本文结果表明 所得的估计计算简单并且具有良好的理论性质，其渐近协方差矩阵的也可由传统的plug-in方法得到. 通过数值模拟研究，我们发现当参数模型的假定正确时，本文所提的增广加权估计和基于模型的插补估计具有优于文献^[12-13]的估计的有限样本性质.乳腺癌数据的对比分析结果也证明了本文方法的良好效果.
参考文献

[1]	Little R J A, Rubin D B. Statistical analysis with missing data[M].2nd ed.New York: John Wiley & Sons, 2002.
[2]	Lu K, Tsiatis A A. Multiple imputation methods for estimating regression coefficients in the competing risks model with missing cause of failure[J].Biometrics, 2001, 57(4):1191–1197.DOI:10.1111/j.0006-341X.2001.01191.x
[3]	Wang Q, Linton O, H?rdle W. Semiparametric regression analysis with missing response at random[J].Journal of the American Statistical Association, 2004, 99(466):334–345.DOI:10.1198/016214504000000449
[4]	Sun Z, Wang Q. Semiparametric estimation of survival function with cause of death data missing at random[J].Journal of Applied Probability and Statistics, 2007, 2:189–209.
[5]	Zhou X, Sun L. Additive hazards regression with missing censoring information[J].Statistica Sinica, 2003, 13(4):1237–1257.
[6]	Wang Q, Ng K W. Asymptotically efficient product-limit estimators with censoring indicators missing at random[J].Statistica Sinica, 2008, 18(2):749–768.
[7]	Wang Q, Dinse G E. Linear regression analysis of survival data with missing censoring indicators[J].Lifetime Data Analysis, 2011, 17(2):256–279.DOI:10.1007/s10985-010-9175-8
[8]	Sun Z, Xie T, Liang H. Statistical inference for right-censored data with nonignorable missing censoring indicators[J].Science China Mathematics, 2013, 56(6):1263–1278.DOI:10.1007/s11425-012-4492-x
[9]	Lin D Y, Ying Z. Semiparametric analysis of the additive risk model[J].Biometrika, 1994, 81(1):61–71.DOI:10.1093/biomet/81.1.61
[10]	Yin G, Cai J. Additive hazards model with multivariate failure time data[J].Biometrika, 2004, 91(4):801–818.DOI:10.1093/biomet/91.4.801
[11]	Lu W, Liang Y. Analysis of competing risks data with missing cause of failure under additive hazards model[J].Statistica Sinica, 2008, 18(1):219.
[12]	Song X, Sun L, Mu X, et al. Additive hazards regression with censoring indicators missing at random[J].Canadian Journal of Statistics, 2010, 38(3):333–351.DOI:10.1002/cjs.v38:3
[13]	Qiu Z, Chen X, Zhou Y. A kernel-assisted imputation estimating method for the additive hazards model with missing censoring indicator[J].Statistics & Probability Letters, 2015, 98:89–97.
[14]	Dikta G. On semiparametric random censorship models[J].Journal of Statistical Planning and Inference, 1998, 66(2):253–279.DOI:10.1016/S0378-3758(97)00091-8
[15]	Goetghebeur E, Ryan L. Analysis of competing risks survival data when some failure types are missing[J].Biometrika, 1995, 82(4):821–833.DOI:10.1093/biomet/82.4.821
[16]	Pollard D.Empirical processes: theory and applications // NSF-CBMS regional conference series in probability and statistics.Institute of Mathematical Statistics and the American Statistical Association, 1990: 1-86.