LI Fei, YANG Fuzhong


School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
Received 2 April 2019; Revised 26 April 2019
Foundation items: Supported by the National Natural Science Foundation of China (11475178, Y4JT01VJ01)
Corresponding author: YANG Fuzhong, E-mail:
fzyang@ucas.ac.cn Abstract: The effective D-brane superpotential determines the vacuum structure and is the generating function of the Ooguri-Vafa invariants. It is of great significance in both physics and mathematics. In this work, the superpotential of the system with three D-branes is calculated by mirror symmetry, GKZ-system (hypergeometric system of Gel'fand, Kapranov, and Zelevinski) method, and the type Ⅱ/F-theory duality. On compact Calabi-Yau manifold, the superpotenial and geometric invariants of D-brane system in the three phases are studied. The calculations show that the superpotentials in the three phases are different. This implies that the enhanced gauge symmetry in low energy theory and geometric singularity may lead to the phase transition.
Keywords: superstringF-theorysuperpotentialOoguri-Vafa invariants
紧致Calabi-Yau流形中D膜系统的超势和几何不变量
李菲, 杨富中


中国科学院大学物理科学学院, 北京 100049
摘要: 有效的D膜超势决定真空结构,是Ooguri-Vafa不变量的生成函数。它对物理和数学都具有重要意义。利用镜像对称性、GKZ系统和Type Ⅱ/F-理论对偶的方法,计算带有3个D膜的系统的超势;研究在紧致Calabi-Yau流形中,处于3个相中的D膜系统的超势和几何不变量。计算结果显示,这3个相区中得到的超势是不同的,这意味着增加的规范对称性和几何奇异性导致了相变。
关键词: 超弦理论F-理论超势Ooguri-Vafa不变量
Mirror symmetry gives the equivalence between A-model determined by K?hler moduli of quantum geometry and B-model determined by complex structure moduli of the classical geometry in the topological string theory. Supersymmetry breaks from
N=2 to
N=1 when D-brane is included. Correspondingly, open-closed mirror symmetry
[1-2] between A and B models is developed. On the analogy of the prepotential in
N=2 supersymmetric topological string theory, the counterpart is called the non-perturbed holomorphic superpotential in
N=1 supersymmetric topological string theory
[3]. In this work, the D-brane superpotential is calculated by mirror symmetry, GKZ-system method, and the type Ⅱ/F-theory duality
[4-8].
Since there is no quantum correction and it is relatively easy to deal with, we calculate the effective superpotential on the side of B-model. Considering that the space-filling D5-branes wrap on a reducible curve
C=∑
iCi and
C is embedded in a divisor
D of Calabi-Yau 3-fold
M3, the effective superpotential is
| $\begin{array}{*{20}{c}}{{W_{N = 1}}(z,\hat z) = {\Pi _\gamma }(z,\hat z) = \int_\gamma {{\Omega ^{(3,0)}}} (z,\hat z),}\\{\gamma \in {H_3}\left( {{M_3},D} \right).}\end{array}$ | (1) |
The effective superpotential
[9] can be expressed as a linear combination of relative period
[10]:
| $\begin{array}{l}{W_{N = 1}}(z,\hat z) = \sum {{N_\alpha }} {\Pi _\alpha }(z,\hat z)\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {W_{{\rm{open }}}}(z,\hat z) + {W_{{\rm{closed }}}}(z,\hat z),\end{array}$ | (2) |
where
z and
$\hat{z}$ are closed and open parameters, respectively.
On the other hand, the type Ⅱ string theory is dual to F-theory
[11-12]. The D-brane superpotential in type Ⅱ string theory is dual to the background flux superpotential in F-theory
[11]. The D-brane superpotential of type Ⅱ on a compact Calabi-Yau threefold
M3 can be obtained in F-theory which is on a compact Calabi-Yau fourfold
M4. The superpotential of 4-form flux
G4 in F-theory compactified on the Calabi-Yau 4-fold
M4 is a section of the Hodge line bundle in the complex structure moduli space
Mcs(
M4). This superpotential is called Gukov-Vafa-Witten superpotential,
| $\begin{array}{l}{W_{{\rm{GVW}}}}\left( {{M_4}} \right) = \int_{{M_4}} {{G_4}} \wedge {\Omega ^{(4,0)}}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum {\left( {{N_\Sigma }\left( {{G_4}} \right){\Pi _\Sigma }(z,\hat z)} \right)} + O\left( {{g_s}} \right) + O\left( {{{\rm{e}}^{\left( { - \frac{1}{{{g_s}}}} \right)}}} \right).\end{array}$ | (3) |
The leading term on the right-hand side of the above equation is the D-brane superpotential
WN=1, and
gs is the string coupling strength.
In the weak coupling limit
gs→0, the D-brane superpotential
WN can be obtained from the GVW superpotential
WGVW of F-theory:
| $\begin{array}{l}{W_{N = 1}}\left( {{M_3},D} \right) = \sum {{N_\Sigma }} \left( {{G_4}} \right){\Pi _\Sigma }(z,\hat z)\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathop {\lim }\limits_{{g_s} \to 0} {W_{{\rm{GVW}}}}\left( {{M_4}} \right).\end{array}$ | (4) |
The system with three D-branes is more complex than the system with single or two D-branes. Complicated D-brane systems play the important role in the phenomenological applications such as superstring/ M/F-theory for MSSM. In this work, for the system with three D-branes on the hypersurface P(1, 1, 1, 1, 2), i.e., Sextic, the type Ⅱ string theory and F-theory duality
[12] are used to calculate the D-brane superpotential and Oogrui-Vafa invariants. The phase transitions, the parallel phase→the partial coincident phase→the complete coincident phase, correspond to the enhancement of gauge group
U(1)×
U(1)×
U(1)→
U(1)×
U(2)→
U(3), in the low energy effective theory.
1 Toric geometry of D-branes system and the generalized hyper-geometric system of Gel'fand, Kapranov, and Zelevinski (GKZ-hypergeomtric system)The Calabi-Yau manifolds in this paper are the hypersurfaces in ambient toric variety
[13-14]. For each pair of reflexive polyhedrons (
$\nabla $4, Δ
4) with a pair of complete fans (Σ(
$\nabla $4), Σ(Δ
4)), there is a pair of toric varieties (
PΣ($\nabla $4),
PΣ(Δ4)). The defining polynomial
P for the hypersurface
M3 in the homogeneous coordinates
xj of toric ambient space is
| $P = \sum\nolimits_{i = 0}^{p - 1} {{a_i}} \prod\nolimits_{v \in {\Delta _4}} {x_j^{ < v,v_i^* > + 1}} .$ | (5) |
The
n parallel D-branes are defined by reducible divisor:
| $\begin{array}{l}Q(D) = \prod\nolimits_{m = 0}^n {\left( {{\phi _m}{a_0} + {a_i}\sum\nolimits_{v \in {\Delta _4}} {x_j^{k < v,v_i^* > + 1}} } \right)} \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\nolimits_{k = 0}^n {{b_k}} \sum\nolimits_{v \in {\Delta _4}} {x_j^{k < v,v_i^* > + n}} .\end{array}$ | (6) |
The parallel D-brane geometry corresponds to the Coulomb phase of the gauge theory and the corresponding group is
U(1)×
U(1)…
U(1)
[11, 15].
The vertices of the parallel D-branes phase shaping the
$\tilde{\nabla }$5 are
| $\tilde v_j^* = \left\{ {\begin{array}{*{20}{l}}{\left( {v_j^*,0} \right)}&{j = 0, \cdots ,p - 1,}\\{\left( {mv_i^*,1} \right)}&{j = p + m,0 \le m \le n.}\end{array}} \right.$ | (7) |
The gauge group
U(1)×
U(1)…
U(1) is promoted to the
U(
N) group when parallel D-branes coincide, while the phase is translated to the Higgs branch.
We have got the enhanced polyhedron which defines the non-compact four-fold
$\tilde{X}$4*. Then the
P1 compactification can be obtained by adding the extra vertex. Combined with the compactifying point
$\tilde{v}$c*, all the points define the enhanced polyhedron
$\nabla $5. This means the real F-theory compact four-manifold is obtained.
The bases for choosing compactifying point are given as follows. 1) The origin is to be included in the enhanced polyhedron. 2) The polyhedron and dual polyhedron are convex polyhedron.
The relative period satisfies the differential equations of Picard-Fuchs
[16], and its differential operator derived by GKZ-system
[4] is
| $\begin{array}{*{20}{l}}{L\left( {{l^a}} \right) = \prod\nolimits_{k = 1}^{l_0^a} {\left( {{\vartheta _0} - k} \right)} \prod\nolimits_{l_j^a > 0} {\prod\nolimits_{k = 0}^{l_j^a - 1} {\left( {{\vartheta _j} - k} \right)} } - }\\{{{( - 1)}^{l_0^a}}{z_a}\prod\nolimits_{k = 1}^{ - l_0^a} {\left( {{\vartheta _0} - k} \right)} \prod\nolimits_{l_j^a} {\prod\nolimits_{k = 0}^{ - l_j^a - 1} {\left( {{\vartheta _j} - k} \right)} } ,}\end{array}$ | (8) |
where
${{\vartheta }_{j}}={{a}_{j}}\frac{\partial }{\partial {{a}_{j}}}$ are logarithmic derivative operators in the parameter
aj, and
aj defines the coefficients in the polynomial for the hypersurface.
la are Mori cone generators of toric variety
PΣ($\nabla $5). These generators are also known as the charge vectors of the gauged linear sigma model (GLSM),
a∈{1, …,
k}.
According to the generators of Mori cone, the local coordinates near the limit point of large complex structure in
M4 moduli space have the forms
| ${z_a} = {( - 1)^{l_0^a}}\prod\nolimits_j {a_j^{l_0^a}} .$ | (9) |
Mori cone and K?hler cone are dual to each other. The selection of Mori cone generator
la also gives a set of dual bases for K?hler cone, denoted as
Ja∈
H(1, 1)(
W4). The corresponding local coordinate is marked as
ka. Since the large complex structure limit point is dual to the large radius limit point, the
ka of K?hler moduli space are also known as flat coordinates.
Local solution of GKZ-system can be derived from basic cycle
w0,
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {w_0}(z;\rho ) = \sum {_{{m_1}, \cdots ,{m_a} \ge 0}} \\\frac{{\Gamma \left( { - \sum {\left( {{m_a} + {\rho _a}} \right)} l_0^a + 1} \right)}}{{\prod\nolimits_{1 \le i \le p} \Gamma \left( {\sum {\left( {{m_a} + {\rho _a}} \right)} l_i^a + 1} \right)}}{z^{m + \rho }}.\end{array}$ | (10) |
By using the Frobenius method, the complete cycle vector has the form,
| $\mathit{\boldsymbol{ \boldsymbol{\varPi} }}(z) = \left( {\begin{array}{*{20}{c}}{{\Pi _0} = {{\left. {{w_0}(z;\rho )} \right|}_{\rho = 0}}}\\{{\Pi _{1,i}} = {{\left. {{\partial _{\rho i}}\left( {{w_0};\rho } \right)} \right|}_{\rho = 0}}}\\{{\Pi _{2,n}} = \sum\nolimits_{{i_1},{i_2}} {{{\left. {{K_{{i_1}{i_2};n}}{\partial _{{\rho _{{i_1}}}}}{\partial _{{\rho _{{i_2}}}}}{w_0}(z;\rho )} \right|}_{\rho = 0}}} }\\ \ldots \end{array}} \right),$ | (11) |
n?1, …,
h, where
h equals the dimension of
H4(
$\tilde{M}$4). The
Ki1, i2; n are the combinatoric coefficients of the second derivative of
w0.
The mirror conjecture gives the dual periodic vectors on the side of A-model as follows:
| ${\mathit{\boldsymbol{ \boldsymbol{\varPi} }}^*}(k) = \left( {\begin{array}{*{20}{c}}{\Pi _0^* = 1}\\{\Pi _{1,i}^* = {k_i}}\\{\Pi _{2,n}^* = \sum\nolimits_{{i_1},{i_2}} {K_{{i_1}{i_2};n}^*} {k_{{i_1}}}{k_{{i_2}}} + {b_n} + F_n^{{\rm{inst}}}}\\ \ldots \end{array}} \right),$ | (12) |
where
ki=Π
1, i/Π
0 are the flat coordinates. The coefficients
Ki1i2;n* of the leading terms are related to the classical sector in superpotential (
Ki1i2; n*=
Ki1i2; n) and
bn are constants. The
Fninst stands for the instanton correction sector of the solutions.
Mirror map is given by
| ${k_i} = \frac{{\prod\nolimits_{1,i} {(z)} }}{{{\Pi _0}}}.$ | (13) |
The open and closed string parameters in K?hler moduli can be separated by linear combination of
ki. The instanton corrections are encoded as a power series expansion in
qi=exp(2πi
tI) and
$\hat{q}$i=exp(2πi
$\hat{t}$i)
| ${F^{{\rm{inst }}}}(t,\hat t) = \sum\nolimits_{\mathit{\boldsymbol{r,m}}} {{G_{\mathit{\boldsymbol{r,m}}}}} {q^\mathit{\boldsymbol{r}}}{q^\mathit{\boldsymbol{m}}} = \sum\nolimits_n {\sum\nolimits_{\mathit{\boldsymbol{r,m}}} {\frac{{{N_{\mathit{\boldsymbol{r,m}}}}}}{{{n^2}}}} } {q^{n\mathit{\boldsymbol{r}}}}{\hat q^{n\mathit{\boldsymbol{m}}}},$ | (14) |
where {
Gr, m} are open Gromov-Witten invariants and {
Nr, m} are Ooguri-Vafa invariants.
m represent the elements of
H1(
L) and
r represent the elements of
H2(
W3).
2 Model: D-brane system on the SexticThe hypersurface
P(1, 1, 1, 1, 2) is given by a polynomial
| $\begin{array}{l}P = {a_1}x_1^6 + {a_2}x_2^6 + {a_3}x_3^6 + {a_4}x_4^6 + {a_5}x_5^3 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_0}{x_1}{x_2}{x_3}{x_4}{x_5}.\end{array}$ | (15) |
The degree 6 hypersurface
P is in the ambient toric variety
PΣ(Δ4). The toric variety is determined by the vertices of the polyhedron Δ
4 as follows:
| ${{v_1} = (2, - 1, - 1, - 1),{v_2} = ( - 1,5, - 1, - 1),}$ |
| ${{v_3} = ( - 1, - 1,5, - 1),{v_4} = ( - 1, - 1, - 1,5),}$ |
| ${{v_5} = ( - 1, - 1, - 1, - 1).}$ |
The vertices of its dual polyhedron
$\nabla $4 are
| $v_0^* = (0,0,0,0),v_1^* = (1,0,0,0),$ |
| $v_2^* = (0,1,0,0),v_4^* = (0,0,0,1),$ |
| $v_5^* = ( - 2, - 1, - 1, - 1),v_3^* = (0,0,1,0).$ |
2.1 Parallel phase of three D-branes:
$\tilde{v}$c*=(-1, 1, 1, 1, -1) is selected as the compactifying point.
We consider the parallel D-branes defined by the reducible divisor
D=
D1+
D2+
D3, which can be written as the degree 15 homogeneous equations,
| $\begin{array}{l}Q = {b_0}{\left( {{x_1}{x_2}{x_3}{x_4}{x_5}} \right)^3} + {b_1}x_1^2x_2^2x_3^2x_4^2x_5^5 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_2}{x_1}{x_2}{x_3}{x_4}x_5^7 + {b_3}x_5^9\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \backsim \prod\nolimits_{i = 1}^3 {\left( {{\phi _i}{a_0}{x_1}{x_2}{x_3}{x_4}{x_5} + {a_1}x_5^3} \right)} .\end{array}$ | (16) |
The open-closed system is encoded in the enhanced polyhedron
$\tilde{\nabla }$5 whose vertices are
| ${\tilde v_0^* = (0,0,0,0,0),\tilde v_1^* = (1,0,0,0,0),}$ |
| ${\tilde v_2^* = (0,1,0,0,0),\tilde v_3^* = (0,0,1,0,0),}$ |
| ${\tilde v_4^* = (0,0,0,1,0),\tilde v_5^* = ( - 2, - 1, - 1, - 1,0),}$ |
| ${\tilde v_6^* = (0,0,0,0,1),\tilde v_7^* = (1,0,0,0,0),}$ |
| ${\tilde v_8^* = (2,0,0,0,1),\tilde v_9^* = (3,0,0,0,1).}$ |
The generators of Mori cone determined by
$\nabla $5 are given as follows:
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}\ \ \ 0&1&2&3&4&5&\ \ \ 6&\ \ \ 7&\ \ \ 8&\ \ \ 9&c\end{array}\\\ {{l^1} = \left( {\begin{array}{*{20}{l}}{ - 4}&0&1&1&1&1&{ - 2}&\ \ \ 2&\ \ \ 0&\ \ \ 0&0\end{array}} \right)}\\\begin{array}{*{20}{l}}{{l^2} = \left( {\begin{array}{*{20}{l}}\ \ \ 0&0&0&0&0&0&\ \ \ 1&{ - 2}&\ \ \ 1&\ \ \ 0&0\end{array}} \right)}\\{{l^3} = \left( {\begin{array}{*{20}{l}}\ \ \ 0&0&0&0&0&0&\ \ \ 0&\ \ \ 1&{ - 2}&\ \ \ 1&0\end{array}} \right).}\end{array}\\\begin{array}{*{20}{l}}{{l^4} = \left( {\begin{array}{*{20}{l}}{ - 1}&1&0&0&0&0&\ \ \ 0&\ \ \ 0&\ \ \ 1&{ - 1}&0\end{array}} \right)}\\{{l^5} = \left( {\begin{array}{*{20}{l}}{ - 3}&0&0&0&0&1&{ - 2}&\ \ \ 3&\ \ \ 0&\ \ \ 0&1\end{array}} \right)}\end{array}\end{array}$ | (17) |
A suitable set of bases is selected to visualize the closed and open moduli,
| $\begin{array}{*{20}{c}}{t = {k_1} + 2{k_2} + 2{k_3} + 2{k_4},}\\{{{\hat t}_1} = {k_2} + {k_3} + {k_4},{{\hat t}_2} = {k_3} + {k_4},{{\hat t}_3} = {k_4}.}\end{array}$ | (18) |
The leading terms of the relative periods are
| $\begin{array}{*{20}{c}}{\tilde \Pi _{2,1}^* = 3{t^2},\tilde \Pi _{2,2}^* = {{\left( {t - 2{{\hat t}_1}} \right)}^2},}\\{\tilde \Pi _{2,3}^* = \left( {t - 2{{\hat t}_2}} \right),\tilde \Pi _{2,4}^* = \left( {t - 2{{\hat t}_3}} \right).}\end{array}$ | (19) |
The
$\tilde{\Pi }$2, 1* only depends on the close moduli
t and is supposed to be the leading term of the bulk potential function
Ft(
t), while
$\tilde{\Pi }$2, 2*,
$\tilde{\Pi }$2, 3*, and
$\tilde{\Pi }$2, 4* are supposed to lead the D-brane superpotential
W(
t,
$\hat{t}$) which depends on both open
$\hat{t}$ and closed
t parameters.
Using algebraic coordinates as follows:
| ${z_1} = \frac{{{a_2}{a_3}{a_4}{a_5}b_1^2}}{{b_0^2}},{z_2} = \frac{{{b_0}{b_2}}}{{b_1^2}},{z_3} = \frac{{{b_1}{b_3}}}{{b_2^2}},{z_4} = \frac{{{a_1}{b_2}}}{{{a_0}{b_3}}}.$ | (20) |
the fundamental period and the logarithmic period are
| $\begin{array}{l}{\Pi _0}(z) = {w_0}(z;0),{\Pi _{1,i}} = {\left. {{\partial _{\rho i}}(z;\rho )} \right|_{{\rho _i} = 0}}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\Pi _{2,n}} = \sum\limits_{i,j} {{{\left. {{K_{i,j;n}}{\partial _{{\rho _i}}}{\partial _{{\rho _j}}}{w_0}(z;\rho )} \right|}_{\rho = 0}}} .\end{array}$ | (21) |
The flat coordinates are given by
| ${k_i} = \frac{{{\Pi _{1,i}}(z)}}{{{\Pi _0}}} = \frac{1}{{{\rm{2 \mathsf{ π} i}}}}\log {z_i} + \cdots .$ | (22) |
Then the mixed inverse mirror maps in terms of
qi=exp(2πi
ki) for {
i=1, 2, 3, 4} are
| $\begin{array}{l}{z_1} = {q_1} - 24q_1^2 + 2{q_1}{q_2} - 24q_1^2{q_2} + {q_1}q_2^2 + 2{q_1}{q_2}{q_3} - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 24q_1^2{q_2}{q_3} + 2{q_1}q_2^2{q_3} + 288q_1^2q_2^2q_3^2{q_4} + \cdots ,\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_2} = {q_2} + 12{q_1}{q_2} + 414q_1^2{q_2} - 2q_2^2 - 48{q_1}q_2^2 - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3q_2^2{q_3} + {q_2}{q_3} + 12{q_1}{q_2}{q_3} + 414q_1^2{q_2}{q_3} - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1944q_1^2q_2^2 + \cdots ,\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{{z_3} = {q_3} + {q_2}{q_3} + 12{q_1}{q_2}{q_3} + 414q_1^2{q_2}{q_3} + }\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 12{q_1}q_2^2{q_3} - 2q_3^2 - 3{q_2}q_3^2 - 36{q_1}{q_2}q_3^2}\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1242q_1^2{q_2}q_3^2 - 2{q_2}q_3^2 + \cdots ,}\end{array}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_4} = {q_4} + {q_3}{q_4} + {q_2}{q_3}{q_4} + 12{q_1}{q_2}{q_3}{q_4} + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 414q_1^2{q_2}{q_3}{q_4} + 12{q_1}q_2^2{q_3}{q_4} + q_4^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 12{q_1}q_1^2q_3^2{q_4} + q_3^2q_4^2 + \cdots .\end{array}$ | (23) |
According to the leading terms, we find the relative periods which correspond to the closed-string period and the D-brane superpotentials in the A-model as follows:
| $\begin{array}{l}{F_t}(t) = 3{t^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}\left( {15768q + 24117750{q^2} + \cdots } \right),\\{W_1}\left( {t,{{\hat t}_1}} \right) = {\left( {t - 2{{\hat t}_1}} \right)^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}\left( {4416q + 6465456{q^2} + } \right.\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 24{{\hat q}_1} + 6\hat q_1^2 + \frac{8}{3}\hat q_1^3 + \frac{3}{2}\hat q_1^4 + 160q\hat q_1^{ - 2} - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1632q\hat q_1^{ - 1} + 3952q{{\hat q}_1} - 2184q\hat q_1^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {6600{q^2}\hat q_1^{ - 4} + \cdots } \right),\\{W_2}\left( {t,{{\hat t}_2}} \right) = {\left( {t - 2{{\hat t}_2}} \right)^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}\left( {4416q + 6465456{q^2} + } \right.\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{24{{\hat q}_2} + 6\hat q_2^2 + \frac{8}{3}\hat q_2^3 + \frac{3}{2}\hat q_2^4 + }\\{160q\hat q_2^{ - 2} - 1632q\hat q_2^{ - 1} + 3952{{\hat q}_2} - }\\{\left. {2184q\hat q_2^2 + 6600{q^2}\hat q_2^{ - 4} + \cdots } \right)}\end{array}\\{W_3}\left( {t,{{\hat t}_3}} \right) = {\left( {t - 2{{\hat t}_3}} \right)^2} + \frac{1}{{4{\pi ^2}}}\left( {4416q + 6465456{q^2} + } \right.\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{24{{\hat q}_3} + 6\hat q_3^2 + \frac{8}{3}\hat q_3^3 + \frac{3}{2}\hat q_3^4 + }\\{160q\hat q_3^{ - 2} - 1632q\hat q_3^{ - 1} + 3952q{{\hat q}_3} - }\\{\left. {2184q\hat q_3^2 + 6600{q^2}\hat q_3^{ - 4} + \cdots } \right),}\end{array}\end{array}$ | (24) |
where
qi=exp(2πi
ti),
$\hat{q}$i=exp(2πi
$\hat{t}$i), {
i=0, 1, 2, 3}.
The disk invariants are shown in
Table 1.
Table 1
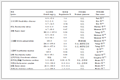 Table 1 Ooguri-Vafa invariants Nn1, n2, n3, n4 Table 1 Ooguri-Vafa invariants Nn1, n2, n3, n4  | 0 | 1 | 2 | 3 | 4 | | 0 | 0 | 24 | 0 | 0 | 0 | | 1 | 160 | -1 632 | 4 416 | 3 952 | -2 184 | | 2 | 6 560 | -96 816 | 576 576 | -2 314 128 | 6 464 352 | | 3 | 544 480 | -10 918 080 | 95 304 192 | -510 183 552 | 1 953 068 832 | | 4 | 59 891 520 | -1 532 438 472 | 17 665 503 360 | -125 289 517 560 | 627 335 745 792 | | Note: Ooguri-Vafa invariants Nn1, n2, n3, n4 from the off-shell superpotential W1(t, $\hat{t}$1) contributed by one of three parallel branes on the sextic. |
| Table 1 Ooguri-Vafa invariants Nn1, n2, n3, n4 |
2.2 Partial coincident phase of three D-branesThe part coincident represents the coincidence of two of the three D branes. "
$\tilde{v}$c*=(-1, 1, 1, 1, -1)" is selected as the compactifying point.
First, we ignore the interior point
$\tilde{v}$7* on the one-dimensional edge with
$\tilde{v}$6*,
$\tilde{v}$8* and
$\tilde{v}$9* to obtain the new charge vectors.
The generators of Mori cone determined by
$\nabla $5 are given:
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}\ \ \ 0&1&2&3&4&5&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 7}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 8}&c\end{array}\\\ {l^1} = \left( {\begin{array}{*{20}{l}}{ - 8}&0&2&2&2&2&{ - 2}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 2}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 0}&0\end{array}} \right)\\\ {l^2} = \left( {\begin{array}{*{20}{l}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&0&0&0&0&0&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 1}&{\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt}{-3}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ \ 2}&0\end{array}} \right).\\\begin{array}{*{20}{l}}{{l^3} = \left( {\begin{array}{*{20}{l}}{-1}&1&0&0&0&0&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 1}&{ - 1}&0\end{array}{\kern 1pt} } \right)}\\{{l^4} = \left( {\begin{array}{*{20}{l}}{ - 6}&0&0&0&0&2&{ - 1}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 3}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 0}&2\end{array}} \right)}\end{array}\end{array}$ | (25) |
A suitable set of bases is selected to visualize the closed and open moduli.
| $t = {k_1} + 2{k_2} + 4{k_3},{\hat t_1} = {k_2} + {k_3},{\hat t_2} = {k_3}.$ | (26) |
The leading terms of the relative periods are:
| $\tilde \Pi _{2,1}^* = 3{t^2},\tilde \Pi _{2,2}^* = {\left( {t - 2{{\hat t}_1}} \right)^2},\tilde \Pi _{2,3}^* = \left( {t - 2{{\hat t}_2}} \right).$ | (27) |
Using algebraic coordinate:
| ${z_1} = \frac{{a_2^2a_3^2a_4^2a_5^2b_1^2}}{{a_0^8b_0^2}},{z_2} = \frac{{{b_0}b_2^2}}{{b_1^3}},{z_3} = \frac{{{a_1}{b_1}}}{{{a_0}{b_2}}}.$ | (28) |
Then the mixed inverse mirror maps in terms of
qi=exp(2πi
ki) for {
i=1, 2, 3} are:
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_1} = {q_1} - 2520q_1^2 - 2{q_1}{q_2} + 7560q_1^2{q_2} + {q_1}q_2^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6300q_1^2q_2^2 + 6{q_1}{q_2}{q_3} + 22680q_1^2{q_2}{q_3} - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{q_1}{q_2}q_3^2 - 20160q_1^2q_2^2{q_3} + \cdots .\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_2} = {q_2} + 1260{q_1}{q_2} + 13384350q_1^2{q_2} + 3q_2^2 - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{q_2}{q_3} + 5040{q_1}q_2^2 - 34706700q_1^2q_2^2 - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2520{q_1}{q_2}{q_3} + \cdots .\\{z_3} = {q_3} - 2{q_2}{q_3} - 1260{q_1}{q_2}{q_3} + 3150{q_1}q_2^2{q_3} + q_3^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_2}q_3^2 - 13384350q_1^2{q_2}{q_3} + 1260{q_1}{q_2}q_3^2 + \cdots .\end{array}$ | (29) |
D-brane superpotentials in the A-model as follows:
| $\begin{array}{l}\begin{array}{*{20}{c}}{{F_t}(t) = 3{t^2} + \frac{1}{{4{\pi ^2}}}(498991500q + \cdots ),}\\{{W_1}\left( {t,{{\hat t}_1}} \right) = {{\left( {t - 2{{\hat t}_1}} \right)}^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}\left( {84453030q - 16{{\hat q}_1} - } \right.}\end{array}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{20\hat q_1^2 + \frac{{368}}{9}\hat q_1^3 - 77\hat q_1^4 + 12600q\hat q_1^{ - 2} + }\\{\left. {1212960q\hat q_1^{ - 1} + \cdots } \right),}\end{array}\\{W_2}\left( {t,{{\hat t}_2}} \right) = {\left( {t - 2{{\hat t}_2}} \right)^2} + \frac{1}{{4{\pi ^2}}}\left( {1578722769q + 88{{\hat q}_2} + } \right.\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 22\hat q_2^2 + \frac{{88}}{9}\hat q_2^3 + \frac{5}{2}\hat q_2^4 + 5671296q\hat q_2^{ - 2} - \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {89251824q\hat q_2^{ - 1} + \cdots } \right).\end{array}$ | (30) |
Second, we ignore the interior point
$\tilde{v}$8* on the one dimensional edge with
$\tilde{v}$6*,
$\tilde{v}$7* and
$\tilde{v}$9* to obtain the new charge vectors.
The generators of Mori cone determined by
$\nabla $5 are given:
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}\ \ \ 0&1&2&3&4&5&\ \ \ 6&\ \ \ 7&\ \ \ 8&c\end{array}\\\begin{array}{*{20}{l}}{{l^1} = \left( {\begin{array}{*{20}{l}}{ - 4}&0&1&1&1&1&{ - 2}&\ \ \ 2&\ \ \ 0&0\end{array}} \right)}\\{{l^2} = \left( {\begin{array}{*{20}{r}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 0}&0&0&0&0&0&\ \ \ 2&{ - 3}&\ \ \ 1&0\end{array}} \right).}\end{array}\\\begin{array}{*{20}{l}}{{l^3} = \left( {\begin{array}{*{20}{l}}{ - 2}&2&0&0&0&0&\ \ \ 0&\ \ \ 1&{ - 1}&0\end{array}} \right)}\\{{l^4} = \left( {\begin{array}{*{20}{l}}{ - 3}&0&0&0&0&1&{ - 2}&\ \ \ 3&\ \ \ 0&1\end{array}} \right)}\end{array}\end{array}$ | (31) |
A suitable set of bases is selected to visualize the closed and open moduli.
| $t = {k_1} + {k_2} + {k_3},{\hat t_1} = {k_2} + {k_3},{\hat t_2} = {k_3}.$ | (32) |
The leading terms of the relative periods are:
| $\tilde \Pi _{2,1}^* = 3{t^2},\tilde \Pi _{2,2}^* = {\left( {t - {{\hat t}_1}} \right)^2},\tilde \Pi _{2,3}^* = \left( {t - {{\hat t}_2}} \right).$ | (33) |
Using algebraic coordinate:
| ${z_1} = \frac{{{a_2}{a_3}{a_4}{a_5}b_1^2}}{{a_0^4b_0^2}},{z_2} = \frac{{b_0^2{b_2}}}{{b_1^3}},{z_3} = \frac{{a_1^2{b_1}}}{{a_0^2{b_2}}}.$ | (34) |
Then the mixed inverse mirror maps in terms of
qi=exp(2πi
ki) for {
i=1, 2, 3} are:
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_1} = {q_1} - 24q_1^2 - 2{q_1}{q_2} + {q_1}q_2^2 - 24q_1^2q_2^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3{q_1}{q_2}{q_3} - 2112q_1^2{q_2}{q_3} - 3{q_1}q_2^2{q_3} + \cdots .\\{z_2} = {q_2} + 24{q_1}{q_2} + 972q_1^2{q_2} + 3q_2^2 + 168{q_1}q_2^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 8136q_1^2q_2^2 - {q_2}{q_3} - 24{q_1}{q_2}{q_3} + \cdots .\\{\kern 1pt} {\kern 1pt} {z_3} = {q_3} - {q_2}{q_3} - 48{q_1}{q_2}{q_3} - 972q_1^2{q_2}{q_3} + q_3^2 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 12{q_1}q_2^2{q_3} + 1260q_1^2q_2^2{q_3} - 720{q_1}{q_2}q_3^2 + \cdots .\end{array}$ | (35) |
D-brane superpotentials in the A-model as follows:
| $\begin{array}{l}\begin{array}{*{20}{c}}{{F_t}(t) = 3{t^2} + \frac{1}{{4{\pi ^2}}}\left( {15768q + 24117750{q^2} + \cdots } \right),}\\{{W_1}\left( {t,{{\hat t}_1}} \right) = {{\left( {t - 2{{\hat t}_1}} \right)}^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}(4832q + }\end{array}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{6267312{q^2} - 14{{\hat q}_1} + \frac{{25}}{6}\hat q_1^2 - }\\{\left. {\frac{{94}}{{45}}\hat q_1^3 + \frac{{361}}{{280}}\hat q_1^4 + 160q\hat q_1^{ - 1} + \cdots } \right),}\end{array}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {W_2}\left( {t,{{\hat t}_2}} \right) = {\left( {t - 2{{\hat t}_2}} \right)^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}(4964q + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{6215169{q^2} + 10{{\hat q}_2} + \frac{{17}}{6}\hat q_2^2 + }\\{\left. {\frac{{62}}{{45}}\hat q_2^3 + \frac{{233}}{{280}}\hat q_2^4 - 8q\hat q_2^{ - 1} + \cdots } \right).}\end{array}\end{array}$ | (36) |
2.3 Complete coincident phase of three D-braneThe complete coincident means that the three D-branes coincide. We ignore the interior point
$\tilde{v}$7* and
$\tilde{v}$8*, and select
$\tilde{v}$c*=(-1, 1, 1, 1, -1) as the compactifying point.
The generators of Mori cone determined by
$\nabla $5 are given:
| $\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}\ \ \ 0&1&2&3&4&5&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 6}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 7}&c\end{array}\\{l^1} = \left( {\begin{array}{*{20}{l}}{ - 12}&0&3&3&3&3&{ - 2}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ 2}&0\end{array}} \right)\\{l^2} = \left( {\begin{array}{*{20}{c}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} - 3}&3&0&0&0&0&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{ - 1}&0\end{array}} \right)\\{l^3} = \left( {\begin{array}{*{20}{c}}{{\kern 1pt} {\kern 1pt} {\kern 1pt} - 3}&0&0&0&0&1&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&1\end{array}} \right)\end{array}$ | (37) |
A suitable set of bases is selected to visualize the closed and open moduli.
| $t = {k_1} + 2{k_2},\hat t = {k_2}.$ | (38) |
The leading terms of the relative periods are
| $\tilde \Pi _{2,1}^* = 3{t^2},\tilde \Pi _{2,2}^* = {(t - 2\hat t)^2}.$ | (39) |
Using algebraic coordinate:
| ${z_1} = \frac{{a_2^3a_3^3a_4^3a_5^3b_1^2}}{{a_0^{12}b_0^2}},{z_2} = \frac{{a_1^3{b_0}}}{{a_0^3{b_1}}}.$ | (40) |
Then the mixed inverse mirror maps in terms of
qi=exp(2πi
ki) for {
i=1, 2} are
| $\begin{array}{l}{z_1} = {q_1} - 369600q_1^2 - 2{q_1}{q_2} + 337444800q_1^2{q_2} + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {q_1}q_2^2 - 137496092160q_1^2q_2^2 + \cdots ,\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_2} = {q_2} + 184800{q_1}{q_2} + 525959313264q_1^2{q_2} + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} q_2^2 - 168168000{q_1}q_2^2 + \cdots .\end{array}$ | (41) |
D-brane superpotentials in the A-model as follows:
| $\begin{array}{l}\begin{array}{*{20}{c}}{{F_t}(t) = 3{t^2} + \frac{1}{{4{\pi ^2}}}(4465834118784q + \cdots ),}\\{{W_1}(t,\hat t) = {{(t - 2\hat t)}^2} + \frac{1}{{4{{\rm{ \mathsf{ π} }}^2}}}(1488611372928q + }\end{array}\\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{96\hat q + \frac{{156}}{5}{{\hat q}^2} + \frac{{1738}}{{105}}{{\hat q}^3} + \frac{{4101}}{{385}}{{\hat q}^4} - }\\{\left. {106456166409q{{\hat q}^{ - 1}} + \cdots } \right).}\end{array}\end{array}$ | (42) |
The disk invariants are shown in
Table 2.
Table 2
 Table 2 Ooguri-Vafa invariants Nn1, n2 Table 2 Ooguri-Vafa invariants Nn1, n2 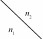 | 0 | 1 | 2 | 3 | 4 | | 0 | 0 | 96 | $\frac{36}{5}$ | $\frac{206}{35}$ | $\frac{\text{1098}}{385}$ | | 1 | 10525120 | -10645616640 | 1488611372928 | 7051829959360 | -31177934877120 | | 2 | $\frac{\text{157772524448128}}{5}$ | $-\frac{\text{720372241121229312}}{5}$ | $\frac{\text{224094978329177385216}}{5}$ | $-\frac{\text{22384150775562073309728}}{5}$ | $\frac{\text{2105098804709796887074752}}{5}$ | | 3 | 189118562604531816240 | -2459242077761323436440320 | 1833394255666692353022651648 | -392840595907256438117173347872 | 38513946045317628971822280844176 | | 4 | $\frac{\text{16619398618692876227958670080}}{11}$ | $-\frac{\text{2358605199330557588324499726491904}}{55}$ | $\frac{\text{3564211188496858798284818206686550464}}{55}$ | $-\frac{\text{297973584076238231487450398687549965584}}{11}$ | $\frac{\text{267806376573319047403184525034359361203328}}{55}$ | | *Ooguri-Vafa invariants Nn1, n2 from the off-shell superpotential W(t, $\hat{t}$) contributed by complete coincident branes on the Sextic. |
| Table 2 Ooguri-Vafa invariants Nn1, n2 |
3 SummaryThe superpotential and Ooguri-Vafa invariants of D-brane system with three D-branes on hypersurface
P(1, 1, 1, 1, 2), i.e., Sextic are calculated. Different from previous works on the systems with single and two D-branes, the system with three D-branes complicates the research.
The results show that there are three phases: parallel phase, partial coincident phase and complete coincident phase. The parallel phase of the D-brane system corresponds to the Coulomb branch of gauge theory, and the superpotential contributed by one of the three D-branes is identical to the one contributed by the D-brane system with single brane on the same Calabi-Yau manifold. The partial coincident phase of the D-brane system corresponds to the Coulomb-Higgs branch. The D-brane system changes from parallel D-brane phase to partial coincident D-brane phase, and that corresponds to the transition from the
U(1)×
U(1)×
U(1) to
U(1)×
U(2) in terms of gauge theory. The complete coincident phase of the D-brane system corresponds to the Higgs branch. The D-brane system changes from parallel D-brane phase to complete coincident D-brane phase, and that shows the feature of the phase transition from
U(1)×
U(1)×
U(1) to
U(3) in terms of gauge theory.
Therefore, in the low effective theory of the system with three D-branes on compact Calabi-Yau manifolds, the superpotentials have rich phase structures. On the other hand, these superpotentials have potential phenomenological applications. We also try to calculate the D-brane superpotential with the method of
A∞ structure and derived category approach and path algebras of quivers.
References | [1] | Lerche W, Vafa C, Warner N P. Chiral rings in N=2 superconformal theories[J]. Nuclear Physics B, 1989, 324(2): 427-474. DOI:10.1016/0550-3213(89)90474-4
|
| [2] | Hosomo S, Klemm A, Theisen S, et al. Mirror symmetry, mirror map and applications to Calabi-Yau hypersurfaces[J]. Communications in Mathematical Physics, 1995, 167(2): 301-350. DOI:10.1007/BF02100589
|
| [3] | Lerche W, Mayr P, Warner N. N=1 special geometry, mixed Hodge variations and toric geometry[EB/OL]. arXiv: hep-th/0208039. (2002-08-06)[2019-03-01]. http://html.rhhz.net/ZGKXYDXXB/https//arxiv.org/abs/hep-th/0208039.
|
| [4] | Xu F J, Yang F Z. Off-shell superpotenials and Oogrui-Vafa invariants of type Ⅱ/F-theory compactfication[J]. Chinese Physics C, 2014, 38(3): 033103. DOI:10.1088/1674-1137/38/3/033103
|
| [5] | Xu F J, Yang F Z. Type Ⅱ/F-theory superpotentials and Ooguri-Vafa invariants of compact Calabi-Yau threefolds with three deformations[J]. Modern Physics Letters A, 2014, 29(13): 1450062. DOI:10.1142/S021773231450062X
|
| [6] | Cheng S, Xu F J, Yang F Z. Off-shell D-brane/F-theory effective superpotentials and Ooguri-Vafa invariants of several compact Calabi-Yau manifolds[J]. Modern Physics Letters A, 2014, 29(12): 1450061. DOI:10.1142/S0217732314500618
|
| [7] | Zhang S S, Yang F Z. Mirror Symmetry, D-brane superpotential and Ooguri-Vafa invariants of compact Calabi-Yau Manifolds[J]. Chinese Physics C, 2015, 39(12): 121002. DOI:10.1088/1674-1137/39/12/121002
|
| [8] | Zou H, Yang F Z. Effective superpotentials of type Ⅱ D-brane/F-theory on compact complete intersection CalabiYau Threefolds[J]. Modern Physics Letters A, 2016, 31(15): 1650094. DOI:10.1142/S0217732316500942
|
| [9] | Jockers H, Soroush H. Effective superpotentials for compact D5-brane Calabi-Yau geometries[J]. Communications in Mathematical Physics, 2009, 290(1): 249-290. DOI:10.1007/s00220-008-0727-7
|
| [10] | Jockers H, Soroush M. Relative periods and open-string integer invariants for a compact Calabi-Yau hypersurface[J]. Nuclear Physics B, 2009, 821(3): 535-552. DOI:10.1016/j.nuclphysb.2009.05.019
|
| [11] | Alim M, Hecht M, Jockers H, et al. Hints for Off-Shell mirror symmetry in type Ⅱ/F-theory compactification[J]. Nuclear Physics B, 2010, 941(3): 303-338.
|
| [12] | Berglund P, Mayr P. Non-perturbative superpotentials in F-theory and string duality[J]. Journal of High Energy Physics, 2013. DOI:10.1007/JHEP01(2013)114
|
| [13] | Alim M, Hecht M, Mayr P, et al. Mirror symmetry for toric branes on compact hypersurfaces[J]. Journal of High Energy Physics, 2009. DOI:10.1088/1126-6708/2009/09/126
|
| [14] | Hosono S, Lian B H, Yau S T. GKZ-generalized hypergeometric systems in mirror symmetry of Calabi-Yau hypersurfaces[J]. Communications in Mathematical Physics, 1996, 182(3): 535-577. DOI:10.1007/BF02506417
|
| [15] | Jiang X T, Yang F Z. D-brane superpotentials, SU(2) Ooguri-Vafa invariants and type Ⅱ/F-theory duality[EB/OL]. arXiv: hep-th/1710.06184. (2018-04-06)[2019-03-01]. https://arxiv.org/abs/hep-th/1710.06184.
|
| [16] | Li S, Lian B H, Yau S T. Picard-Fuchs equations for relative periods and Abel-Jacobi map for Calabi-Yau hypersurfaces[J]. American Journal of Mathematics, 2012, 134(5): 1345-1384. DOI:10.1353/ajm.2012.0039
|