刘梦^1,2, 刘威^1,2, 周志刚¹
1. 中国科学院上海微系统与信息技术研究所, 上海 200050;
2. 中国科学院大学, 北京 100049
2018年12月25日 收稿; 2019年5月8日 收修改稿
基金项目: 中国科学院科技创新重点部署项目（KGFZD-135-18-013YT）资助
通信作者: 刘梦, E-mail:meng.liu@mail.sim.ac.cn

摘要: 稀疏码分多址（SCMA）是一种新型非正交多址技术，具有过载通信的特点。在高信噪比（E_b/N₀）场景下基于消息传递（MPA）的译码算法，误比特率性能不理想。因此，提出一种部分响应与稀疏码分多址联合调制译码模型，方案继承了SCMA在译码端的低复杂性和部分响应的高容错性。为进一步降低联合译码的误比特率，将部分响应的Viterbi译码级联至MPA迭代译码过程中，即每次迭代过程中变量节点都会进行一次Viterbi译码，从而组成新型联合译码模块。仿真结果表明，改进后联合编译码模型能够有效降低系统对E_b/N₀的需求，同时保持较低的误比特率。
关键词: 稀疏码分多址消息传递算法部分响应联合调制解调
Joint detection and decoding algorithm based on partial response and SCMA
LIU Meng^1,2, LIU Wei^1,2, ZHOU Zhigang¹
1. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China


Abstract: Sparse code multiple access (SCMA) is a new type of non-orthogonal multiple access technology with overload communication. In the high signal to noise ratio(E_b/N₀)scenario, based on the message passing (MPA) decoding algorithm, the bit error rate performance is not ideal. Therefore, a joint modulation and decoding model based on partial response and sparse code division multiple access is proposed. The scheme inherits the low complexity of SCMA at the decoding end and the high fault tolerance of partial response. In order to further reduce the bit error rate of the joint decoding, the Viterbi decoding of the partial response is cascaded into the MPA iterative decoding process, that is, the variable node performs a Viterbi decoding during each iteration, to form a new joint decoding module. The theoretical and simulation results show that the improved joint coding and decoding model effectively reduces the system's demand for E_b/N₀ and maintains a low bit error rate.
Keywords: sparse code multiple accessmessage passing algorithmpartial responsejoint detection and decoding
物联网和移动互联网的快速发展给第五代(5G)移动通信研究提出了诸多挑战，比如更低的系统时延、更高的吞吐量、超大规模的连接和更好的服务质量^[1]。稀疏码分多址(sparse code multiple access，SCMA)作为频率域的非正交多址技术^[2-3]，综合LDS技术的稀疏性和QAM调制的高效性，可以适应大规模连接、低时延和高吞吐量的通信场景，成为5G非正交多址技术中有竞争力的候选方案。
SCMA的核心思想是利用多维稀疏码本将信息流直接映射成复数域数据流，利用码本的非正交性，用户的信息将稀疏地分散在不同的子载波上。接收端使用基于因子图迭代的消息传递算法(message passing algorithm，MPA)^[4]解码作为次优解码方案，其本质是基于置信度传播(belief propagation，BP)算法^[5]的演进，相比最优性能的最大后验概率算法(maximum a posteriori probability，MAP)和极大似然算法(maximum likelihood algorithm，ML)，MPA算法计算复杂度更低。
原始MPA在因子图中沿着边缘传递所有节点的消息，直至达到最大迭代次数，但是当系统严重超载以及用户过多时复杂度会剧增。文献[6]提出将乘法与指数运算转化为加法与求极值运算的对数域max log-MPA算法方案，从运算角度简化复杂度，文献[7-8]研究FPGA上的MPA和log-MPA的定点和浮点实现，改进log-MPA算法方案，使其可以在性能和复杂性之间实现良好的权衡。基于部分边缘更新(partial marginalizition-based MPA，PM-based MPA)方案^[9]、用剪枝的思想暂停部分节点更新，从降低搜索路径长度角度降低计算复杂度。文献[10]根据信息论的定义，引入动态自适应边缘选择MPA(edge selected MPA，ES-MPA)方案，由每条边迭代更新产生的信息量决定是否进行下一轮FN节点到VN节点的更新，能够在BER和复杂度间取得良好平衡。SCMA接收端使用消息传递算法及优化译码方案，能有效降低译码复杂度，但在高SNR情境下，误比特率性能未成瀑布状分布。
为进一步提升高SNR场景下BER性能，降低高SNR的需求，本文在优化SCMA译码效率的前提下，在SCMA调制编码前级联部分响应信号模块，提出部分响应与稀疏多址联合调制模型。在不损失频带利用率的前提下，依然能够消除码间干扰(ISI)，提出MPA-Viterbi联合译码算法(MPA-VA)，能够有效降低SNR的需求，取得较低的误比特率。在部分响应系统译码算法方面，引入基于极大似然算法的Viterbi译码算法^[11]，利用相关编码特性在误比特率方面的优势，并且在Viterbi译码器之前加入白化匹配滤波器，有效提升Viterbi算法非线性递归运算的先验值。
1 联合编码模型虽然SCMA模块具有高过载率，但在高SNR环境中，误比特率不能显著下降。同时，部分响应是一种卷积编码^[12]，具有卷积编码的特性，可以提高符号之间的容错性部分。部分响应和稀疏码分多址联合调制解码模型继承了SCMA的高过载率和部分响应的高容错性，在大规模连接的情况下可以保持低误比特率，特别是在高信噪比情况中，联合调制模型BER性能有明显优势。
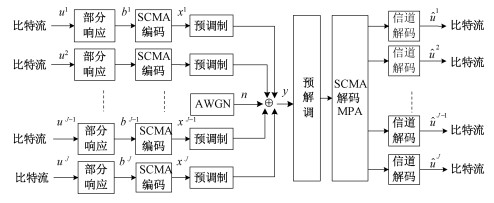
本方案在编码侧使用部分响应与稀疏码分多址联合调制，J个用户使用K资源块的SCMA下行传输流程如图 1所示，第j个用户发送的信息序列u^j首先经过部分响应模型，人为引入可控制的码间串扰，经过SCMA编码、调制过程，进入高斯信道发送到接收机端，接收机端通过MPA-VA联合译码算法获得估计序列${\hat u^J}$。
Fig. 1

	Download: JPG larger image
图 1 J个用户K个资源块的SCMA简化下行链路图 Fig. 1 Simplified downlink diagram of SCMA with J users and K resource blocks 图 1 J个用户K个资源块的SCMA简化下行链路图 Fig. 1 Simplified downlink diagram of SCMA with J users and K resource blocks -->

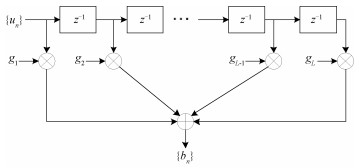
1.1 部分响应模型假设在理想信道的情况下，一个用户的输入比特流序列表示为u=[u₁, u₂, …, u_n]，经过部分响应模型，如图 2所示，在每个比特间引入的冗余码字^[12]为

${b_n} = \sum\limits_{l = 1}^L {{u_{n - (l - 1)}}} {g_l}, $

(1)

Fig. 2

	Download: JPG larger image
图 2 部分响应的离散模型 Fig. 2 Discrete model of partial response 图 2 部分响应的离散模型 Fig. 2 Discrete model of partial response -->

式中：u_n为二进制比特数据；这里的{g_l}，l∈[1, 2, …, L]，表示L个采样点的抽头系数。那么u经过部分响应实际上可看作一种编码效率为1/2的编码。
目前部分响应信号解码主要有两种概率译码方案：1)基于极大似然的检测方案(Viterbi)；2)基于最大欧氏距离的最大似然序列检测(MLSE)^[13]。
根据部分响应信道的码间串扰特性，可以看作单入单出的卷积码，因此可以使用成熟的BCJR或Viterbi译码算法来降低译码复杂度。本文使用Viterbi算法的考量在于，算法的最大似然译码特性，能够获得最小误比特率，且接近MLSE。
1.2 SCMA模型在SCMA模型中，J个用户共用K个资源块来传输数据。所有的用户经过部分响应模型的比特流为B=[b¹, b², …, b^j]，其中b^j=[b₁^j, b₂^j, …, b_n^j]，j∈[1, J]，表示第j个用户经过部分响应的比特流。比特流B进入SCMA编码器，根据码本进行映射f^j:b^j→x^j，得到X=[x¹, x², …, x^j]，其中x^j=[x₁^j, x₂^j, …，x_K^j]^T，x_K^j表示第j个用户发送到第k个资源块上的符号。
本文取J=6，K=4，则6个用户共用4个资源块方式用矩阵表示为

$\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}}0&1&1&0&1&0\\1&0&1&0&0&1\\0&1&0&1&0&1\\1&0&0&1&1&0\end{array}} \right].$

(2)

这里F_kj=1表示用户j占用资源块k；F_kj=0，表示用户j不占用资源块k，对应的因子图如图 3所示。
Fig. 3

	Download: JPG larger image
图 3 J=6, K=4的因子图 Fig. 3 Factor graph for J=6 and K=4 图 3 J=6, K=4的因子图 Fig. 3 Factor graph for J=6 and K=4 -->

各个用户发送的数据在每个资源块上进行叠加，经过高斯信道，在接收机端，接收信号可表示为

$\mathit{\boldsymbol{y}} = \sum\limits_{j = 1}^J {{\mathop{\rm diag}\nolimits} } \left( {{\mathit{\boldsymbol{h}}_j}} \right){\mathit{\boldsymbol{x}}^j} + \mathit{\boldsymbol{n,}}$

(3)

式中：y=(y₁, y₂, …, y_K)^T表示接收信号矢量，y_K表示第k个资源块上接收的符号；h_j=(h_{1, j}, h_{2, j}, …, h_{K, j})^T表示信道增益矢量，h_{K, j}表示第j个用户到第k个资源块上的信道增益因子；x^j=(x₁^j, x₂^j, …, x_K^j)^T表示用户j发送的码字，x_K^j表示第j个用户发送到第k个资源块上的符号，n=[n₁, n₂, …，n_K]^T，表示高斯白噪声矢量。
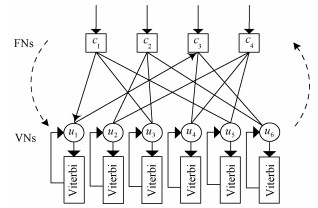
2 联合检测译码模型通过AWGN的接收信号，接收数据序列使用基于MPA和Viterbi的联合迭代解调模块，判决并输出估计序列。其中，MPA解码的核心单元是VNs与FNs之间的迭代更新，而这个迭代过程可以分两个步骤进行，本文联合译码算法在迭代更新过程中加入Viterbi译码算法。具体联合译码流程如图 4所示。
Fig. 4

	Download: JPG larger image
图 4 SCMA-PR联合因子图 Fig. 4 SCMA-PR joint factor graph 图 4 SCMA-PR联合因子图 Fig. 4 SCMA-PR joint factor graph -->

第1步：信号初始化。通过使用期望值和接收值的欧氏距离，从计算接收到的每个资源所有组合的附加码字的概率开始。由于缺少码字的先验信息，所以假设资源节点FNs在每个用户节点VNs取得每个符号的概率是相等的，即初始化时，第j个用户节点向第k资源节点的转移概率为

$\mathit{\boldsymbol{I}}_{j \to k}^{{\rm{init}}}(\mathit{\boldsymbol{x}}_m^j) = \frac{1}{M}, m = 1, \cdots , M, $

(4)

式中：M表示进制数，x_m^j表示x^j的第m个符号值。
接收机基于设定好的用户码本，计算每个资源节点FN上接收的不同比特信息的概率为

$\begin{array}{l}{P_{k, j}}\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} \sigma }}\exp \left( { - \frac{1}{{2{\sigma ^2}}}} \right.\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\parallel {y_k} - \sum\limits_{} {_{i \in {\xi _k}}{h_{k, i}}} {x_{k, i, m}}{\rm{ }}\left. {{\parallel ^2}} \right), \end{array}$

(5)

式中：P_{K, j}(x_m^j)是第j个用户节点VN到第k个资源节点FN的置信概率，y_K表示第k个资源节点FN上接收的符号信息，ξ_K表示第k个资源节点FN连接的用户节点VN的个数。
第2步：资源节点FN更新。将资源节点FN收到的先验概率信息式(5)与当前概率计算结果相结合，进行节点更新，

$I_{k \to j}^t\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \sum\limits_{} {_{\mathit{\boldsymbol{\tilde x}}_m^j}{P_{k, j}}} \left( {\mathit{\boldsymbol{x}}_m^j} \right)\prod\limits_{} {_{j \in {\xi _{k/j}}}I_{j \to k}^{l - 1}} \left( {\mathit{\boldsymbol{x}}_m^j} \right), $

(6)

式中：I_k→j^t(x_m^j)表示第t次迭代过程中，资源节点k到用户节点j的更新信息；j∈ξ_k/j，表示除去用户节点j的ξ_K。然后计算符号的外部信息为

${P_{k, j}}\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \prod\limits_{} {_{k \in {\xi _j}}I_{k \to j}^t} \left( {\mathit{\boldsymbol{x}}_m^j} \right), $

(7)

式中：ξ_j表示第j个用户节点VN连接的资源节点FN的个数。
第3步：Viterbi译码更新符号信息。Viterbi译码器接收的信号为式(7)，按Viterbi算法流程进行译码，符号的外部信息更新为

$P\left( {\mathit{\boldsymbol{x}}_m^j} \right) = {\rm{Viterbi(}}{P_k}\left( {\mathit{\boldsymbol{x}}_m^j} \right){\rm{)}}{\rm{.}}$

(8)

第4步：用户节点VN更新。用户节点VN接收的信息结合第3步更新的符号信息，进行和积操作，并对VN节点进行归一化操作，

$I_{j \to k}^t\left( {\mathit{\boldsymbol{x}}_m^j} \right) = {\rm{normalize(}}P\left( {\mathit{\boldsymbol{x}}_{jm}^{}} \right)\prod\limits_{} {_{\tilde k \in {\xi _j}/k}I_{k \to j}^{l - 1}} \left( {\mathit{\boldsymbol{x}}_m^j} \right){\rm{)}}, $

(9)

第5步：估计与软输出。在式(6)~式(9)之间进行t_max次迭代后，最终第j个VN节点经过估计后的LLR软输出为

${{\hat X}_j}\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \prod\limits_{} {_{k \in {\xi _j}}I_{k \to j}^{{t_{\max }}}} \left( {\mathit{\boldsymbol{x}}_m^j} \right).$

(10)

为表述清晰，具体VA-MPA运算伪代码流程，如下所示：
Table

算法1 VA-MPA联合译码算法 输入：y，H，tmax 初始化： 1. for all j=1:J and k∈[ξK] and m=1:M do 2.Ik→j0(xmj)=0，$I_{j \to k}^0\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \frac{1}{M}$ 3.end for 迭代计算： 4. for t=1 to t=tmax do 5. Calculate PK, j(xmj)via(5); 6. Calculate and propagate Ik→jt(xmj)via(6); 7. Calculate and propagate PK(xmj)via(7); 8. Calculate and propagate P(xmj)via(8); 9. Calculate and propagate Ij→kt(xmj)via(9); 10. t=t+1; 11. end for LLR软输出： 12. for all j=1 toj=J do 13. return ${{\hat X}_j}\left( {\mathit{\boldsymbol{x}}_m^j} \right)$ via (10) 14. end for

3 算法仿真与分析本文基于下行SCMA通信系统，采用文献[8]中给出的码本矩阵，仿真分析SCMA-PR联合调制译码设计方案在高斯信道中的BER性能。基于文献[4-10]中提出的标准MPA、PM-MPA和ES-MPA3种MPA算法，在前置部分响应模块后，使用联合译码模块进行解调。方案适当增加复杂度，提高在高信噪比下的BER性能。因此将在不同的信噪比下，分别对比MPA和VA-MPA、PM-MPA和VA-PM-MPA、ES-MPA和VA-ES-MPA的BER性能，从而验证本方案的性能。VA-PM-MPA表示级联Viterbi译码的PM-MPA译码算法，VA-ES-MPA同理。同时，将本文联合调制译码方案与文献[14-17]提出的Polar级联SCMA译码方案(BP-MPA)进行BER性能对比。仿真关键参数如表 1所示。
Table 1

表 1 部分响应与稀疏多址译码仿真参数Table 1 Partial response and sparse multiple access decoding simulation parameters 参数 取值(过载150%) 迭代次数tmax 5 变量节点数量J 6 功能节点数量K 4 资源重叠度ξj 2 用户重叠度ξK 3 回溯深度 5 多用户检测方式 MPA、PM-MPA和ES-MPA 调制 BPSK 传输信道模型 AWGN 进制数M 4 抽头系数个数L 6 抽头系数 g1=g2=g3=g6=1, g4=g5=0

表 1 部分响应与稀疏多址译码仿真参数Table 1 Partial response and sparse multiple access decoding simulation parameters

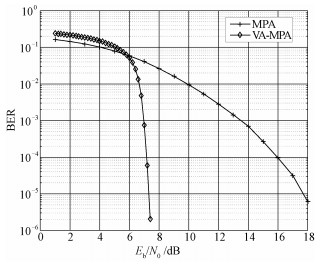
MPA与VA-MPA响应联合译码方案性能对比如图 5所示。从图中可看出：E_b/N₀在1~5 dB范围时，由于部分响应模块需要根据输入数据添加冗余比特，使得进入SCMA映射矩阵的比特数增加1倍，因此在低信噪比场景下VA-MPA的误比特率性能与MPA相比衰减约1 dB；在E_b/N₀>6 dB时，VA-MPA与MPA译码方案相比优势明显；当E_b/N₀在6~8 dB范围时，BER迅速从10^-2降到10^-6量级。当BER=10^-5时，本文方案较标准MPA方案的信噪比可改善10.4 dB。
Fig. 5

	Download: JPG larger image
图 5 MPA与VA-MPA译码误比特率对比图 Fig. 5 Comparison of BER performance between MPA and VA-MPA decoding algorithms 图 5 MPA与VA-MPA译码误比特率对比图 Fig. 5 Comparison of BER performance between MPA and VA-MPA decoding algorithms -->

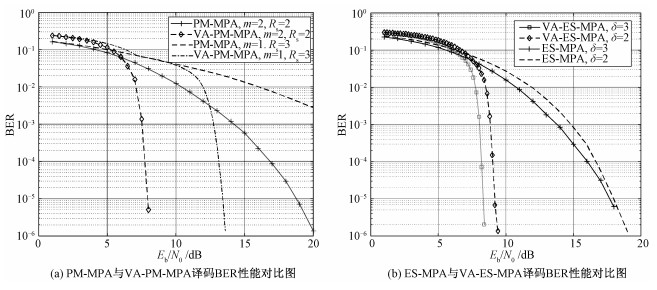
PM-MPA与VA-PM-MPA联合译码方案BER性能对比如图 6(a)所示。根据PM-MPA算法的特点，取两组m、R_s值进行对比，分别为m=1、R_s=3和m=2、R_s=2。由图中可知，在高信噪比场景下，VA-PM-MPA译码方案在误比特率方面始终优于PM-MPA。以m=1、R_s=3对比曲线为例，在信噪比2~11 dB, PM-MPA的BER性能逼近VA-PM-MPA方案，VA-PM-MPA方案优势不突出。对于m=2, R_s=2，在E_b/N₀>6 dB时，VA-PM-MPA译码方案与PM-MPA方案相比优势明显，随后E_b/N₀在6~8 dB范围内，BER迅速从10^-2降到10^-5量级。当BER=10^-5时，VA-PM-MPA方案较PM-MPA方案的信噪比可改善将近11 dB。
Fig. 6

	Download: JPG larger image
图 6 不同算法的误比特率性能对比图 Fig. 6 Comparison of BER performance among different algorithms 图 6 不同算法的误比特率性能对比图 Fig. 6 Comparison of BER performance among different algorithms -->

ES-MPA与VA-ES-MPA联合译码方案BER性能对比如图 6(b)所示。此处ES-MPA与VA-ES-MPA的仿真参数采用两组阈值进行对比，分别为δ=2、δ=3。对比两组曲线，在高信噪情况下，VA-ES-MPA方案的BER性能优势明显。以δ=3对比曲线为例, 当E_b/N₀>7 dB时，VA-ES-MPA相较于ES-MPA方案的BER值骤减且呈瀑布状，表明部分响应在高信噪比场景下优势明显。当BER=10^-5时，VA-ES-MPA方案较ES-MPA方案信噪比提高9 dB。对比两条VA-ES-MPA方案曲线，当BER=10^-5时，两组参数曲线的信噪比仅相差1.2 dB。
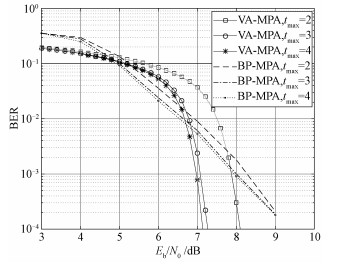
VA-MPA联合译码方案与BP-MPA联合译码方案性能对比如图 7所示，此处分别对两种方案迭代2、3、4次。对比两组曲线，在高信噪比的情况下，VA-MPA方案的BER性能优势明显。以迭代次数t_max=4为例，当E_b/N₀>6 dB时，VA-MPA相比较于Polar级联联合译码方案的BER值骤减且呈瀑布状，表明部分响应在高信噪比场景下优势明显; 当BER=10^-4时，VA-MPA方案较BP-MPA方案的信噪比可改善大约2 dB。
Fig. 7

	Download: JPG larger image
图 7 VA-MPA与BP-MPA译码误比特率对比图 Fig. 7 Comparison of BER performance between VA-MPA and BP-MPA decoding algorithms 图 7 VA-MPA与BP-MPA译码误比特率对比图 Fig. 7 Comparison of BER performance between VA-MPA and BP-MPA decoding algorithms -->

4 结束语本文综合部分响应的容错率和SCMA系统的稀疏性，提出部分响应与稀疏码分多址联合调制解码模型。在SCMA调制编码前级联部分响应模块，即使用部分响应的卷积特性将输入信号进行预编码。在接收侧，综合基于MLSE的Viterbi译码算法和MPA算法，给出新型MPA-VA联合译码方案。仿真结果表明，标准MPA、PM-MPA和ES-MPA3种SCMA译码方案，在联合VA译码后，BER性能曲线在高E_b/N₀情境下，呈瀑布状分布，并且优于Polar级联SCMA译码方案。表明，本文提出的联合编译码模型能够有效增加高E_b/N₀情况下的BER性能界。由于引入卷积编码，使系统整体计算复杂度有一定升高，因此在未来工作中，深入研究降低系统的计算复杂度是有必要的。

参考文献

[1]	Dai L, Wang B, Yuan Y, et al. Non-orthogonal multiple access for 5G:solutions, challenges, opportunities, and future research trends[J]. IEEE Communications Magazine, 2015, 53(9): 74-81.
[2]	Ma Z, Zhang Z Q, Ding Z G, et al. Key techniques for 5G wireless communications:network architecture, physical layer, and MAC layer perspectives[J]. Science China:Information Sciences, 2015, 58(4): 1-20.
[3]	Benjebbour A, Saito Y, Kishiyama Y, et al. Concept and practical considerations of non-orthogonal multiple access (NOMA) for future radio access[C]//2013 International Symposium on Intelligent Signal Processing and Communication Systems. IEEE, 2013: 770-774.
[4]	Nikopour H, Baligh H. Sparse code multiple access[C]//2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). IEEE, 2013: 332-336.
[5]	Kihara K, Nishimura T, Ohgane T, et al. Signal detection with belief propagation in faster-than-Nyquist signaling[C]//2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC). IEEE, 2017: 1790-1794.
[6]	Zhang S, Xu X, Lu L, et al. Sparse code multiple access: an energy efficient uplink approach for 5G wireless systems[C]//2014 IEEE Global Communications Conference. IEEE, 2014: 4782-4787.
[7]	Ghaffari A, Leonardon M, Cassagne A, et al. Toward high-performance implementation of 5G SCMA algorithms[J]. IEEE Access, 2019, 7: 10402-10414.
[8]	Liu J, Wu G, Li S, et al. On fixed-point implementation of Log-MPA for SCMA signals[J]. IEEE Wireless Communications Letters, 2016, 5(3): 324-327.
[9]	Mu H, Ma Z, Alhaji M, et al. A fixed low complexity message pass algorithm detector for up-link SCMA system[J]. IEEE Wireless Communications Letters, 2015, 4(6): 585-588.
[10]	Wang Y, Qiu L. Edge selection-based low complexity detection scheme for SCMA system[C]//2016 IEEE 84th Vehicular Technology Conference (VTC-Fall). IEEE, 2016: 1-5.
[11]	Forney G. Maximum-likelihood sequence estimation of digital sequences in the presence of intersymbol interference[J]. IEEE Transactions on Information theory, 1972, 18(3): 363-378.
[12]	Rusek F. Partial response and faster-than-Nyquist signaling[D]. Lund: Lund University, 2007.
[13]	Taherzadeh M, Nikopour H, Bayesteh A, et al. SCMA codebook design[C]//2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall). IEEE, 2014: 1-5.
[14]	Pan Z, Li E, Wen L, et al. Joint iterative detection and decoding receiver for polar coded SCMA system[C]//2018 IEEE International Conference on Communications Workshops (ICC Workshops). IEEE, 2018: 1-6.
[15]	张弩天.极化码的译码算法研究及其应用[D].成都: 电子科技大学, 2018.
[16]	符杰林, 张剑波, 王俊义. SCMA与极化码的联合检测译码技术[J]. 计算机应用研究, 2019(9): 1-6.
[17]	Pan Z, Li E, Zhang L, et al. Design and optimization of joint iterative detection and decoding receiver for uplink polar coded SCMA system[J]. IEEE Access, 2018, 6: 52014-52026.