一种基于层次稀疏的全极化SAR层析成像方法

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-25

杨牡丹^1,2, 魏中浩^1,2, 徐志林^1,2, 张冰尘¹, 洪文¹
1. 中国科学院电子学研究所空间信息处理与应用系统技术重点实验室, 北京 100190;
2. 中国科学院大学, 北京 100049
2019年1月7日收稿; 2019年3月7日收修改稿
基金项目: 国家自然科学基金（61331017）资助
通信作者: 杨牡丹, E-mail:yangmudan16@mails.ucas.ac.cn

摘要: SAR层析成像利用多航过复数据对观测目标进行高程向重构，全极化数据具有丰富的散射信息。将全极化数据与SAR层析成像相结合，利用城市建筑高程向散射体的稀疏性和全极化数据信号稀疏支撑集相同的特点，提出基于组稀疏约束和稀疏约束相结合的求解模型，并利用层次稀疏的方法对模型进行求解。通过Monte Carlo仿真实验将该模型法的性能与单极化层析成像模型和基于组稀疏的求解方法的性能进行对比，并将该方法应用到实测数据的半点目标仿真实验中。结果表明，本文提出的方法提高了高程向重建精度，且有更好的鲁棒性，在低信噪比下也能较好地恢复目标的高程向信息和后向散射系数。
关键词: SAR层析成像组稀疏稀疏全极化SAR
A full-polarimetric SAR tomography method based on hierarchical sparseness
YANG Mudan^1,2, WEI Zhonghao^1,2, XU Zhilin^1,2, ZHANG Bingchen¹, HONG Wen¹
1. Key Laboratory of Technology in Geospatial Information Processing and Application System, Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China

Abstract: SAR tomography employs the multiple-pass data to achieve the elevation location reconstruction of the observation target, while the fully polarimetric data owns rich scattering information. We combine the full-polarimetric data with SAR tomography. By considering the same characteristic of the sparsity of elevation scatters in urban building and the sparse support set in full-polarimetric data, a solution model based on group sparse constraint and sparse constraint, solved by hierarchical sparse method, is proposed. The performance of the method has been compared with those of the single-polarimetric tomography model and the group sparse-based solution method by Monte Carlo simulation experiments. Meanwhile, the method is also applied to semi-simulation of point target experiments based on real data. The results show that the proposed method improves the accuracy of elevation reconstruction and has better robustness, and it accurately recovers the elevation position and backscatter coefficient of the target at low SNR.
Keywords: SAR tomographygroup sparsesparsefull polarimetric SAR
合成孔径雷达(synthetic aperture radar, 简称SAR)^[1]是一种主动微波遥感手段，穿透能力强，具有全天时全天候对地观测能力，是对地观测重要手段之一。随着SAR技术的不断发展，获取目标信息更加丰富，促进了SAR相关技术的发展^[2-3]。SAR层析(SAR tomography，TomoSAR)将合成孔径原理扩展到高程向，通过多帧同一场景的观测复图像，对每个方位-距离分辨单元的高程向进行重建，获得SAR三维图像。该技术可有效分辨单个雷达分辨单元中混叠的多个散射体，解决叠掩问题。自SAR层析成像技术提出以来，得到国内外****广泛关注，相应的求解方法不断涌现。初期，谱估计方法^[4-5]被广泛运用，随着成像技术的发展，压缩感知技术被引入到SAR层析成像技术中^[6-7]，文献[8-9]中提出“?₁范数最小化降维，模型选择和估计重建”算法，并进行系统分析与论证。
极化合成孔径雷达(polarimetric synthetic aperture radar, Pol-SAR)^[10]是遥感领域研究热点之一。相较于传统的单极化数据，全极化数据提供更加丰富的目标散射信息。将全极化数据与SAR层析成像相结合，利用全极化数据能反映地面目标的几何结构、分布方向、介电特性等信息的能力，更准确地获取观测目标的高程向信息和更佳的成像性能。文献[11]提出利用多极化通道的结构相关性，在组稀疏框架下，用多极化数据的混合范数正则化代替单极化的?₁范数正则化，求解多极化SAR层析成像模型。文献[12]提出基于多次测量向量压缩感知模型和Tikhonov正则化理论的极化三维重构模型，并将其运用到人造目标的重构中。
本文提出全极化SAR层析成像技术运用到城市建筑的三维重构模型，城市建筑观测目标具有如下特点：同一分辨单元中散射体的个数较少，具有稀疏性，可用正则化惩罚项?₁刻画；全极化数据中，信号的稀疏性出现在不同极化数据的相同位置，即4个极化通道中，在相同位置，信号的幅度和相位不同，会同时为零或不为零，符合组稀疏的特性。组稀疏性是对传统信号稀疏性的扩展，针对对象是组，使得组内元素同时取零或同时取非零值，用于刻画的正则化惩罚项通过?_{2, 1}实现。整体场景的稀疏约束和不同极化通道的组稀疏约束相结合，得到多重约束SAR层析成像求解模型——层次稀疏模型，从而获得观测目标的高程向信息。该模型下，全极化数据的使用，能更充分利用观测目标的结构信息。城市建筑观测目标图像中，单个像素点中强散射元较少的特性，以及4个极化通道中支撑集相同的特点，仿真和实际数据实验表明，基于层次稀疏的全极化SAR层析成像求解模型，提高了高程向和后向散射系数精度，且有更好的鲁棒性。
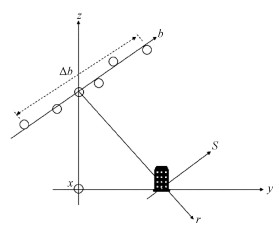
1 全极化SAR层析成像原理SAR层析成像是在SAR二维成像技术基础上发展得到的一种三维成像技术，其几何示意图如图 1所示。x, y, z分别表示方位向、水平向和垂直高度向；r, s, b分别表示斜距向、高程向和基线分布方向；Δb为高程向合成孔径长度。其原理是用对同一观测目标场景的不同航向(不同观测角度)的观测复数据，将合成孔径原理扩展到高程向，使其在高程向具有分辨能力，获得目标的高程向信息，重建三维观测场景。经过聚焦后的雷达图像，单个像素点的值是后向散射信号在高程向的积分，其第n帧雷达聚焦信号表达式为

${g_n} = \int\limits_{\Delta s} \gamma (s){\rm{exp}}\{ - {\rm{j}}2\pi {\xi _n}s\} {\rm{d}}s,\quad n = 1,2,3, \cdots ,N.$

(1)

Fig. 1

	Download: JPG larger image
图 1 SAR层析成像几何示意图 Fig. 1 Schematic of SAR tomography 图 1 SAR层析成像几何示意图 Fig. 1 Schematic of SAR tomography -->

式中：γ(s)表示与高程向位置有关的散射体辐射强度；Δs表示高程向的范围，在此范围内积分；ξ_ns表示高程向位置不同产生的相位，其中ξ_n=-2b_n/λr为高程向频率，b_n为该图形对应基线到主基线的垂直距离，λ为发射脉冲信号波长，r为观测目标到雷达的斜距。式(1)可看成是后向散射系数的傅里叶变换，可将该式沿高程向s进行离散化处理，则可得到如下形式的表达

${\mathit{\boldsymbol{g}}_{N \times 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{N \times L}} \cdot {\mathit{\pmb{\gamma}}_{L \times 1}} + {\mathit{\boldsymbol{n}}_{N \times 1}},$

(2)

式中：g_N×1=[g₁, g₂, …, g_N]^T；L为沿高程向离散化的个数；Φ_N×L为观测矩阵，Φ_{n, l}=exp{-j2πξ_ns_l}，s_l表示高程向L个离散中的第l个所在的高程向位置；γ_L×1为高程向离散化的后向散射系数；n_N×1为噪声项。
全极化SAR层析模型中，假设从不同位置和时间获得同一观测目标4种极化模式HH、HV、VH、VV下的SAR单视复图像，每种极化模式各N帧，经过配准、大气相位补偿等前期数据预处理后，某一方位向-距离向单元的观测数据可表示为

$\left[ {\begin{array}{*{20}{l}}{{\mathit{\boldsymbol{g}}_{{\rm{hh}}}}}\\{{\mathit{\boldsymbol{g}}_{{\rm{hv}}}}}\\{{\mathit{\boldsymbol{g}}_{{\rm{vh}}}}}\\{{\mathit{\boldsymbol{g}}_{{\rm{vh}}}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{hh}}}}}&0&0&0\\0&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{hv}}}}}&0&0\\0&0&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{vh}}}}}&0\\0&0&0&{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{vv}}}}}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{{\mathit{\pmb{\gamma}}_{{\rm{hh}}}}}\\{{\mathit{\pmb{\gamma}}_{{\rm{hv}}}}}\\{{\mathit{\pmb{\gamma}}_{{\rm{vh}}}}}\\{{\mathit{\pmb{\gamma}}_{{\rm{vv}}}}}\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{n}}_{{\rm{hh}}}}}\\{{\mathit{\boldsymbol{n}}_{{\rm{hv}}}}}\\{{\mathit{\boldsymbol{n}}_{{\rm{vh}}}}}\\{{\mathit{\boldsymbol{n}}_{{\rm{vv}}}}}\end{array}} \right].$

(3)

因为4种极化模式下的方位角相近，假定在小的方位角范围内后向散射结构相同，故可以将4种极化模式下对同一观测目标的观测矩阵表示为相同的形式，均为Φ，则有

${\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{hh}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{hv}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{vh}}}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{vv}}}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}.$

(4)

式(3)即可表示为

$\begin{array}{*{20}{l}}{[{\mathit{\boldsymbol{g}}_{{\rm{hh}}}},{\mathit{\boldsymbol{g}}_{{\rm{hv}}}},{\mathit{\boldsymbol{g}}_{{\rm{vh}}}},{\mathit{\boldsymbol{g}}_{{\rm{vv}}}}] = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}[{\mathit{\pmb{\gamma}}_{{\rm{hh}}}},{\mathit{\pmb{\gamma}}_{{\rm{hv}}}},{\mathit{\pmb{\gamma}}_{{\rm{vh}}}},{\mathit{\pmb{\gamma}}_{{\rm{vv}}}}] + }\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{\mathit{\boldsymbol{n}}_{{\rm{hh}}}},{\mathit{\boldsymbol{n}}_{{\rm{hv}}}},{\mathit{\boldsymbol{n}}_{{\rm{vh}}}},{\mathit{\boldsymbol{n}}_{{\rm{vv}}}}].}\end{array}$

(5)

式中：g_i∈${{\mathbb{C}}^{N\times 1}}$, i∈{hh, hv, vh, vv}分别表示在HH、HV、VH、VV极化模式下的目标信号观测向量，4种极化模式下的观测矩阵相同；γ_i∈${{\mathbb{R}}^{L\times 1}}$，i∈{hh, hv, vh, vv}表示观测目标的后向散射系数；n_i∈${{\mathbb{C}}^{N\times 1}}$, i∈{hh, hv, vh, vv}表示噪声扰动项。
2 全极化SAR层析重构方法2.1 重构方法建模前述得到式(5)的全极化SAR层析成像模型，同时考虑所有极化形式，得到如下综合表达式

$\mathit{\boldsymbol{G}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \hat \gamma }} + \mathit{\boldsymbol{N}},$

(6)

式中：综合的观测向量为G=[g_hhg_hvg_vhg_vv]，观测目标的后向散射系数为$\widehat{\mathrm{ }\!\!\gamma\!\!\text{ }}$=[γ_hhγ_hvγ_vhγ_vv]，噪声项为N=[n_hhn_hvn_vhn_vv]。观测目标的4个极化通道得到的后向散射系数示意图如图 2所示，由图中可知，4个极化通道的后向散射系数在相同位置，如椭圆框所示，即同一高程上，后向散射系数的稀疏性属性一致，即同时为零或同时不为零。当后向散射系数不为零时，4个极化通道值可以不同，式(6)的重构具有一定结构性，重构向量中的元素分组出现，支撑集一致，在重构模型中利用这种结构信息可以提高重构的精度和鲁棒性，这一特点可以用适于刻画组稀疏约束性的正则化惩罚项的?_{2, 1}混合范数实现，文献[12]中根据该结构关系，得到如下所示的重构模型

${\rm{arg}}{\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_x \frac{1}{2}\left\| {\mathit{\boldsymbol{G}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} \mathit{\pmb{\hat \gamma}} }}} \right\|{\kern 1pt} _2^2 + \lambda \left\| \mathit{\pmb{\gamma}} \right\|{\kern 1pt} _{2,1}^1,$

(7)

Fig. 2

	Download: JPG larger image
图 2 4个极化通道后向散射系数示意图 Fig. 2 Schematic of backscattering coefficients of four polarized channels 图 2 4个极化通道后向散射系数示意图 Fig. 2 Schematic of backscattering coefficients of four polarized channels -->

式中：λ为正则化参数。式(7)仅考虑全极化信号间的结构稀疏性，但整体观测场景同样具有稀疏性，故本文中根据?_{2, 1}的结果保证了组间稀疏的约束条件，对于同一组的元素，并非都为非零，因此可以对同一组内元素进一步进行稀疏约束，即对于整体观测场景的稀疏性用正则化惩罚?₁范数刻画，综上，得到如下所示的层次稀疏求解模型

$\begin{array}{*{20}{c}}{{\rm{arg}}{\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_x \frac{1}{2}\left\| {{\kern 1pt} \mathit{\boldsymbol{G}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} \mathit{\pmb{\hat \gamma}} }}{\kern 1pt} } \right\|{\kern 1pt} _2^2 + {\lambda _1}\left\| {{\kern 1pt} \mathit{\pmb{\gamma}}{\kern 1pt} } \right\|_{2,1}^1 + }\\{{\lambda _2}\left\| {{\kern 1pt} \mathit{\pmb{\gamma}}{\kern 1pt} } \right\|{{\kern 1pt} _1}.}\end{array}$

(8)

其中所述的范数数学表达式为

$\begin{array}{l}\left\| \mathit{\pmb{\gamma}} \right\|{{\kern 1pt} _{2,1}} = \sum\limits_{j = 1}^{j = L} {{\kern 1pt} {\kern 1pt} \times } \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {|{\mathit{\pmb{\gamma}}_{{\rm{hh}},j}}{|^2} + |{\mathit{\pmb{\gamma}}_{{\rm{hv}},j}}{|^2} + |{\mathit{\pmb{\gamma}}_{{\rm{vh}},j}}{|^2} + |{\mathit{\pmb{\gamma}}_{{\rm{vv}},j}}{|^2}} ,\\\left\| \mathit{\pmb{\gamma}} \right\|{{\kern 1pt} _1} = \sum\limits_{j = 1}^{j = L} {{\kern 1pt} {\kern 1pt} \times } \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {|{\mathit{\pmb{\gamma}}_{{\rm{hh}},j}}{|^2} + |{\mathit{\pmb{\gamma}}_{{\rm{hv}},j}}{|^2} + |{\mathit{\pmb{\gamma}}_{{\rm{vh}},j}}{|^2} + |{\mathit{\pmb{\gamma}}_{{\rm{vv}},j}}{|^2}} \right),\end{array}$

式中：${{\widehat{\mathrm{ }\!\!\gamma\!\!\text{ }}}_{i, j}}$, i∈{hh, hv, vh, vv}, j=1, 2, …L表示某极化方式下j指数对应的后向散射系数; λ₁，λ₂为正则化参数; 第1个惩罚项为?_{2, 1}混合范数惩罚项，用于表征组稀疏特性; 第2个惩罚项为?₁范数，用于约束成像区域的稀疏度。
2.2 重构模型求解方法实验对比中，针对式(7)所示的模型，参考文献[13]中的方法求解。形如式(8)的多重约束模型为层次稀疏模型^[14]，每个稀疏组间相互独立，可分解为对每组求解的子问题。本文中，每组采用阈值迭代算法求解，阈值迭代算法是经典的稀疏信号处理方法，利用优化函数的梯度实现每次迭代计算，计算复杂度更小，适用于大场景的稀疏成像问题。求解中，第k迭代公式为

$\begin{array}{l}{\mathit{\pmb{\gamma}}^{(k + 1)}} = {\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}(\left\| {{\kern 1pt} \mathit{\pmb{\gamma}}_i^{(k)} - \mathit{\pmb{\gamma}}_i^{(k)}{\kern 1pt} } \right\|{{\kern 1pt} _2} + {\lambda _1}\left\| {{\kern 1pt} \mathit{\pmb{\gamma}}{\kern 1pt} } \right\|{\kern 1pt} _{2,1}^1 + \\{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}}{{\lambda _2}\left\| {{\kern 1pt} \mathit{\pmb{\gamma}}{\kern 1pt} } \right\|{{\kern 1pt} _1}) = {H_{\left. 2 \right|{\kern 1pt} {\kern 1pt} 1,{\lambda _1}\mu }}([\mathit{\boldsymbol{\bar u}}_{{\rm{hh}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{hv}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{vh}}}^{(k)},}\\{\mathit{\boldsymbol{\bar u}}_{{\rm{vv}}}^{(k)}]).}\end{array}\end{array}$

(9)

式中：μ为步长，H(·)为混合范数阈值迭代函数，表达式为

$\begin{array}{l}{H_{\left. 2 \right|{\kern 1pt} {\kern 1pt} 1,{\lambda _1}\mu }}([\mathit{\boldsymbol{\bar u}}_{{\rm{hh}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{hv}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{vh}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{vv}}}^{(k)}]) = \\[\mathit{\boldsymbol{\bar u}}_{{\rm{hh}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{hv}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{vh}}}^{(k)},\mathit{\boldsymbol{\bar u}}_{{\rm{vv}}}^{(k)}]{\rm{max}}\left( {1 - \frac{{{\lambda _1}\mu }}{{{{\left\| {{\kern 1pt} \mathit{\boldsymbol{u}}_g^{(k)}{\kern 1pt} } \right\|}_{{\kern 1pt} 2}}}},0} \right).\end{array}$

式中:u_i, u_i, i∈{hh, hv, vh, vv}为迭代中间量，组阈值选择方法为

${\lambda _1}\mu = |\mathit{\boldsymbol{u}}_g^{(k)}{|_{K + 1}},$

式中:|u_g^(k)|_K+1表示取u_g^(k)中幅值第K+1大值，u_g^(k)为定义的组向量，其中第j个元素为

$\begin{array}{*{20}{l}}{{{(\mathit{\boldsymbol{u}}_g^{(k)})}_j} = (|{{(\mathit{\boldsymbol{\bar u}}_{{\rm{hh}}}^{(k)})}_j}{|^2} + |{{(\mathit{\boldsymbol{\bar u}}_{{\rm{hv}}}^{(k)})}_j}{|^2} + }\\{{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} |{{(\mathit{\boldsymbol{\bar u}}_{{\rm{vh}}}^{(k)})}_j}{|^2} + |{{(\mathit{\boldsymbol{\bar u}}_{{\rm{vv}}}^{(k)})}_j}{|^2}{)^{1/2}}.}\end{array}$

K表示稀疏度，具体步骤如下：
1) 估计残差

${\Delta ^{(k)}} = \sum\limits_{i \in \{ {\rm{hh,hv,vh,vv}}\} } {{\mathit{\boldsymbol{G}}_i}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} \mathit{\pmb{\gamma}} }}_i^{(k)};$

2) 梯度更新

$\begin{array}{*{20}{l}}{\mathit{\boldsymbol{u}}_i^{(k)} = \mathit{\pmb{\gamma}}_i^{(k)} + \mu \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i^{\rm{H}}{\Delta ^{(k)}},}\\{\mathit{\boldsymbol{\bar u}}_i^{(k)} = {\eta _{1/{\lambda _2}\mu }}(\mathit{\boldsymbol{u}}_i^{(k)}).}\end{array}$

式中阈值迭代的公式为

$\begin{array}{l}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\eta _{\left. 1 \right|{\lambda _2}\mu }}(\mathit{\boldsymbol{u}}_i^{(k)}) = \\\left\{ {\begin{array}{*{20}{l}}{{\rm{sgn}} (\mathit{\boldsymbol{u}}_i^{(k)})(|\mathit{\boldsymbol{u}}_i^{(k)}| - {\lambda _2}\mu ),}&{|\mathit{\boldsymbol{u}}_i^{(k)}| \ge {\lambda _2}\mu ,}\\{0,}&{|\mathit{\boldsymbol{u}}_i^{(k)}| < {\lambda _2}\mu .}\end{array}} \right.\end{array}$

式中sgn(·)为符号函数，式中函数的阈值选择方法为

${\lambda _2}\mu = |\mathit{\boldsymbol{\bar u}}_{{\rm{hh}}}^{(k)}{|_{K + 1}};$

3) 按照式(9)更新γ.
重复以上步骤直至满足收敛条件，由此得到全极化SAR层析的重构结果。
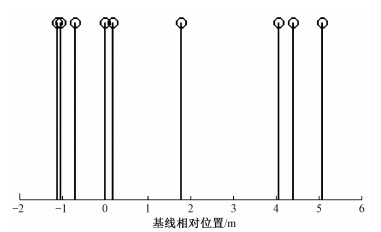
3 仿真和实测结果与分析在实验验证中，进行仿真实验和结合实测数据的半仿真实验对基于层次稀疏的全极化SAR层析模型的性能进行验证。实测数据为德国宇航局E-SAR传感器2007年在瑞典南部区域获取的帧L波段的二维SAR复图像数据^[15]，相应的系统参数见表 1，基线分布图如图 3，横坐标表示基线的相对垂直距离，选取一帧作为主图像，对应基线距离为0。为实验保持一致性，仿真实验的实验参数和基线分布与实测数据相同。仿真实验中，对比了不同信噪比下，3种求解模型重构结果的相对均方误差(relative mean square error, RMSE)和虚警率(false alarm rate, FAR)。定义如下：

$\begin{array}{*{20}{c}}{{\rm{RMSE}} = \frac{{\left\| {{\kern 1pt} \mathit{\pmb{\hat \gamma}} - \mathit{\pmb{\gamma}}{\kern 1pt} } \right\|{\kern 1pt} _2^2}}{{\left\| {{\kern 1pt} \mathit{\pmb{\gamma}}{\kern 1pt} } \right\|{\kern 1pt} _2^2}},}\\{{\rm{FAR}} = P(\mathit{\pmb{\hat \gamma}}(l) = \left. {0{\rm{ }}} \right|\mathit{\pmb{\gamma}}(l) \ne 0),l = 1,2, \cdots ,L.}\end{array}$

Table 1

表 1 实验系统参数Table 1 Experimental system parameters

参数	数值
基线数目	9
基线跨度/m	6.209
波长/m	0.230 6
观测近距/m	4 288

表 1 实验系统参数Table 1 Experimental system parameters

Fig. 3

	Download: JPG larger image
图 3 基线分布图 Fig. 3 Baseline distribution 图 3 基线分布图 Fig. 3 Baseline distribution -->

3.1 仿真实验处理仿真实验中，模拟点目标中存在两个散射体，高程向位置分别为10和-5 m，对应的后向散射系数分别为1和0.5。仿真实验中模拟不同噪声环境下，单极化模型、式(7)所示的组稀疏约束模型以及式(8)所示的层次稀疏模型，对目标后向散射系数和高程向位置的重构效果。图 4展示在信噪比为10和5 dB时，3种方式下的重建结果，图 4(a)中，当信噪比为10 dB时，层次稀疏模型方法能准确恢复散射体的高程向位置，对后向散射系数的重建也较准确，而单极化模型和组稀疏约束模型的高程向位置重建结果误差较小，但后向散射稀疏误差较明显；图 4(b)中，当信噪比为5 dB时，相较于其他两种模型，组稀疏约束和稀疏约束相结合模型在高程向位置和后向散射系数重建效果明显较优。
Fig. 4

	Download: JPG larger image
图 4 不同信噪比重建图 Fig. 4 Reconstruction figures at different SNR values 图 4 不同信噪比重建图 Fig. 4 Reconstruction figures at different SNR values -->

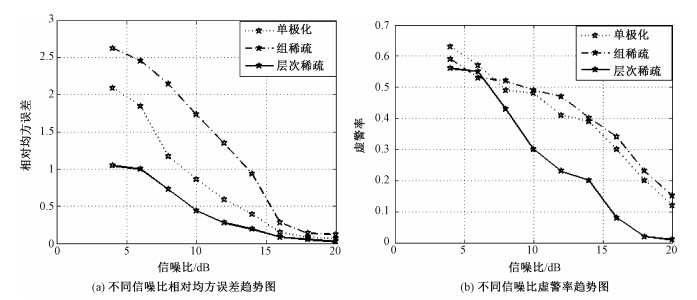
3种求解模型的相对均方误差和虚警率性能通过100次Monte Carlo实验得出，结果如图 5所示。图 5(a)为相对均方误差趋势图，当噪声较小时，层次稀疏模型重建结果与其他两种模型的相对均方误差均较小，相差不大，当信噪比较小时，层析稀疏模型重构结构也能保持在较低水平，结果明显优于单极化模型和组稀疏约束模型；图 5(b)为不同信噪比下的虚警率，不同信噪比下，层次稀疏模型的重建结果都呈现出较明显的优势。由图 5可知，除少数情况外，基于层次稀疏模型的重建结果在不同信噪比下均优于单极化和组稀疏模型方法。
Fig. 5

	Download: JPG larger image
图 5 不同信噪比对比图 Fig. 5 Comparison figures at different SNR values 图 5 不同信噪比对比图 Fig. 5 Comparison figures at different SNR values -->

由仿真实验结果可知，基于层次稀疏的SAR层析成像求解模型，以4个极化通道中相同位置信号同时为零或不为零特性为先验知识进行组稀疏约束，其重构结果相较于单通道的SAR层析成像模型和基于组稀疏约束的SAR层析成像模型，提高了高程向精度，且有更好的鲁棒性，在低信噪比下也能较准确恢复目标的高程向信息和后向散射系数。
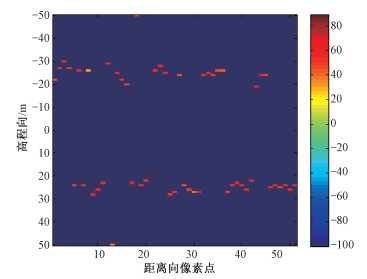
3.2 实测数据处理基于实测数据的半仿真实验中，选取观测区域的一个方位向切片场景，如图 6所示，图 6(a)为原始场景图，6(b)为局部放大，实验中在某一个像素点处加入二面角散射信息，高程向信息为20 m，从而获得半仿真的实验数据。基于该实验数据，用基于层次稀疏的全极化SAR层析成像模型及对应求解方法进行实验处理。选取的方位向切片区域的幅度较弱，将其作为二面角背景，选取其中一个像素点人工加入一个正二面角散射体目标，该二面角的边长设置为10倍的波长，根据边长和波长求得二面角S矩阵中的系数σ；在BioSAR 2007^[15]数据中设置了3个三面角，在图中找到对应三面角的3个像素点，由该像素点得到像素的幅值与S矩阵系数之间的对应关系；人工二面角像素点的相位由其高程向信息获得，由此可获得人工二面角像素点的幅值和相位信息，结合选定的目标区域，得到实验的观测数据。最后重建结果如图 7所示。图 7中圆圈表示选取的像素点真实，由图可知，该方法能正确重建得到该像素点的高程值。
Fig. 6

	Download: JPG larger image
图 6 实测数据场景图 Fig. 6 Scenes of measured data 图 6 实测数据场景图 Fig. 6 Scenes of measured data -->

Fig. 7

	Download: JPG larger image
图 7 线目标场景半仿真实验 Fig. 7 Semi-simulation experiment of the line target scene 图 7 线目标场景半仿真实验 Fig. 7 Semi-simulation experiment of the line target scene -->

4 结论本文提出的基于层次稀疏的全极化SAR层析成像求解模型，将全极化数据与SAR层析成像相结合，以4个极化通道中信号支撑集相同为先验知识进行组稀疏约束，整体观测场景的稀疏性用?₁正则化进行约束。仿真实验中，将该方法与单极化的SAR层析和基于组稀疏约束的SAR层析进行对比。实验结果表明，本文提出的求解方法综合性能更优，提高了高程向重构精度，对后向散射系数重构也有较好效果，且有更好的鲁棒性，在较低的信噪比下也能较好恢复高程向信息和后向散射系数信息。且在基于BioSAR 2007机载全极化数据的实验中，该模型也得到了较好的实验验证。

参考文献

[1]	Brown W M. Synthetic aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1967, AES-3(2): 217-229. Doi:10.1109/TAES.1967.5408745
[2]	肖垚, 刘畅. 基于稀疏求解的改进PCA方法在SAR目标识别中的应用[J]. 中国科学院大学学报, 2018, 35(1): 84-88.
[3]	向卫力, 李晓辉, 周胜勇, 等. 一种鲁棒的多尺度稀疏表示SAR目标识别方法[J]. 中国科学院大学学报, 2017, 34(1): 99-105.
[4]	Bordoni F, Lombardini F, Gini F, et al. Multibaseline cross-track SAR interferometry using interpolated arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1473-1482. Doi:10.1109/TAES.2005.1561898
[5]	Lombard F, Ender J, RoBing L, et al. Experiments of interferometric layover solution with the three-antenna airborne AER-Ⅱ SAR system[C]//IGARSS. 2004 IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2004, 5: 3341-3344.
[6]	Pang B, Dai D H, Liu J, et al. A super-resolving imaging algorithm of forward-looking SAR based on compressive sensing[C]//IEEE Geoscience and Remote Sensing Symposium. 2014: 572-575.
[7]	赵克祥, 毕辉, 张冰尘. 基于快速阈值迭代的SAR层析成像处理方法[J]. 系统工程与电子技术, 2017, 39(5): 1019-1023.
[8]	Zhu X, Bamler R. Super-resolution for 4-D SAR tomography via compressive sensing[C]//8th European Conference on Synthetic Aperture Radar. VDE, 2010: 1-4.
[9]	Zhu X X, Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247-258.
[10]	Cloude S. Polarisation:applications in remote sensing[M]. Oxford: Oxford University Press, 2010.
[11]	Aguilera E, Nannini M, Reigber A. A data-adaptive compressed sensing approach to polarimetric SAR tomography of forested areas[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 543-547. Doi:10.1109/LGRS.2012.2212693
[12]	Xing S Q, Li Y Z, Dai D H, et al. Three-dimensional reconstruction of man-made objects using polarimetric tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3694-3705. Doi:10.1109/TGRS.2012.2220145
[13]	Yuan M, Lin Y. Model selection and estimation in regression with grouped variables[J]. Journal of the Royal Statistical Society, 2006, 68(1): 49-67. Doi:10.1111/j.1467-9868.2005.00532.x
[14]	Liu X, Zhai D, Zhao D, et al. Image super-resolution via hierarchical and collaborative sparse representation[C]//Data Compression Conference (DCC), 2013. IEEE, 2013: 93-102.
[15]	Hajnsek I, Scheiber R, Ulander L et al. BioSAR 2007 technical assistance for the development of airborne SAR and geophysical measurements during the BioSAR 2007 experiment: final report without synthesis[R]. Paris: European Space Agency, 2008.