
 , 苏刚1
, 苏刚1

1. 中国科学院大学物理科学学院, 北京 100049;
2. 北京建筑大学理学院, 北京 102616;
3. 中国科学院大学材料科学与光电技术学院, 北京 100049
2018年4月20日 收稿; 2018年5月15日 收修改稿
基金项目: 国家自然科学基金(11474279)资助
通信作者: 闫清波, E-mail:yan@ucas.ac.cn
苏刚, gsu@ucas.ac.cn
摘要: 石墨二炔是近年实验上成功合成的一种新型二维碳材料,具有独特的结构、丰富的化学键和电子性质,拥有巨大的应用潜力。使用基于密度泛函理论的第一性原理方法,系统研究硅、锗、硼、氮、磷单元素替位掺杂的石墨二炔以及硼-氮、硼-磷双元素共掺杂的石墨二炔的电子结构。发现硅、锗掺杂的石墨二炔和硼-氮、硼-磷共掺杂的石墨二炔依然是半导体,带隙大小在0.004~0.49 eV;而硼、氮、磷掺杂的石墨二炔都变成了金属。本研究可为实验上通过掺杂手段调节石墨二炔的带隙和费米面位置提供理论依据。
关键词: 石墨二炔第一性原理计算掺杂电子结构
First-principles study on electronic structures of doped graphdiynes
ZHANG Zihan1, CUI Huijuan1,2, YAN Qingbo3

 , SU Gang1
, SU Gang1

1. School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China;
2. School of Science, Beijing University of Civil Engineering and Architecture, Beijing 102616, China;
3. College of Materials Science and Opto-Electronic Technology, University of Chinese
Abstract: Graphdiyne is a new type of two-dimensional carbon material successfully synthesized in recent years. It has a peculiar structure, rich hybrid bonds, and interesting electronic properties, and has a wide range of potential applications. We perform the first-principles calculations based on density functional theory to study the silicon, germanium, boron, nitrogen, and phosphorus doped graphdiynes and boron-nitrogen and boron-phosphorus co-doped graphdiynes systematically. Our results show that Si and Ge doped graphdiynes and B-N and B-P co-doped graphdiynes are semiconductors with band gaps from 0.004 to 0.49 eV, and B, N, and P doped graphdiynes all become conductors. The present study on the band structures of doped graphdiynes helps to engineer the band gap of graphdiyne and manipulate Fermi level of graphdiyne.
Keywords: graphdiynefirst-principles calculationsdopingelectronic structure
碳作为地球上分布最广泛的元素之一,一直以来就是科学家研究的热点。碳原子(C)通过不同的杂化方式可以形成多种具有优良性能的材料,如金刚石、石墨、石墨烯[1]、碳纳米管[2]、T-碳[3]等。这些材料在人们的生产生活中具有重要的应用或应用潜力[4-7]。Baughman等[8]通过计算预言一种碳原子通过sp和sp2杂化形成的新型碳同素异形体-石墨炔。这是一类只有单原子层厚度的二维材料,可以看作是由炔键连接起来的碳六元环构成。根据碳六元环间炔键的数目,可以将石墨炔划分为石墨一炔(graphyne)、石墨二炔(graphdiyne)……石墨n炔(graphyne-n)等。科学家一直在试图制备出石墨炔。2010年,李玉良课题组[9]使用六炔基苯在铜表面发生交联反应,成功实现石墨二炔薄膜的大面积(~3.6 cm2)合成,并且在实验上印证石墨二炔的确是拥有卓越性能的半导体材料。目前,在碳原子的sp和sp2方式杂化成键的材料中,实验上合成的有石墨二炔、石墨四炔[10]和Carbon Ene-Yne (CEY)[11]。
石墨二炔(graphdiyne, GD)具有P6/mmm空间群对称性,晶格常数为9.44?[12](1?=0.1 nm)。石墨二炔电子性质优异,是Γ点处的直接带隙半导体,可以方便地应用于光电子器件,带隙在0.46~1.22 eV之间[13]。实验上测得石墨二炔的吸收光谱,有3个吸收峰分别在0.56、0.89和1.79 eV处;通过Bethe-Salpeter方程(BSE)计算得到的3个激子峰分别在0.75、1.00和1.82 eV处[14],与实验一致。
石墨二炔的孔洞结构使其与其他二维材料相比具有的独特性质,预示其在锂离子电池电极材料和储氢材料方面有巨大应用前景,这些孔洞可以容纳大量的锂离子、氢气分子[15-17]等。石墨二炔上有规律地分布着三角孔,也使其可用作纳米选择性透过膜。由于石墨二炔三角孔的有效尺寸刚好与氦气的范德瓦尔斯直径相匹配,因此它也可以作为一种理想的将氦气与其他气体相分离的材料[18]。另外,石墨二炔还可作为一种非常高效的过滤膜用于水的提纯[19]。
施加应力可以对石墨二炔的能带结构进行调控,使其发生从半导体到半金属的转变[20]。通过理论研究发现,加氢或者卤化处理石墨二炔,可使其带隙从0.5 eV增加到5.2 eV[21]。掺杂是改进材料性质的常用手段,N掺杂的石墨二炔可用于氧还原反应催化剂[22],其催化效率可以达到商业化铂碳复合物的水平,而在材料的稳定性和对交叉效应的耐受性方面则比铂碳复合物更有优势。后续的研究发现,通过N-F共掺杂可以进一步改善石墨二炔材料在氧还原反应中的电催化表现[23]。N掺杂还可以提高石墨二炔用于锂电池负极材料时的容量和循环寿命[24]。通过理论计算发现,B掺杂可以提高石墨一炔的嵌锂电位和容量[25]。
通过掺杂可以调节石墨二炔的电子性质。我们利用第一性原理计算方法,系统研究硅(Si)、锗(Ge)、硼(B)、氮(N)、磷(P)单元素替位掺杂的石墨二炔(分别表示为SiGD、GeGD、BGD、NGD、PGD),以及硼-氮、硼-磷双元素共掺杂的石墨二炔(分别表示为BNGD、BPGD)的电子结构。发现硅、锗掺杂的石墨二炔和硼-氮、硼-磷共掺杂的石墨二炔依然是半导体,而硼、氮、磷掺杂的石墨二炔都变成了导体。对于本征石墨二炔,其费米面附近的电子能量状态主要由六元环上碳原子的2pz轨道起作用[26],在六元环上替位掺杂将直接改变六元环上的电荷分布,使杂质原子和其周围的碳原子之间发生电荷转移。硅、锗单原子掺杂降低了石墨二炔的对称性,使原本简并的能级退简并,从而降低带隙。硅、锗双原子掺杂的石墨二炔的带隙则分别小到0.004和0.013 eV。硼、氮、磷相对于碳缺电子或者多电子,从而显著降低或者升高了费米面的位置,使费米面穿过能带,带来了从半导体到导体转变。硼-氮、硼-磷双原子共掺杂是等电子掺杂,费米面基本保持不动。硼-磷共掺杂的石墨二炔还依然是直接带隙半导体,带隙大小比本征石墨二炔的带隙要小,带隙位置则略偏离Γ点。硼-氮共掺杂的石墨二炔是我们研究的12种掺杂石墨二炔结构中唯一的间接带隙半导体。
目前,N和B掺杂的石墨二炔以及B-N共掺杂的石墨二炔都已在实验上成功合成[22-24]。通过对掺杂石墨二炔形成能的计算,我们发现B, N为杂质元素时,形成能较小,而Si/Ge/P掺杂石墨二炔的形成能则较大。Si/Ge/P掺杂石墨二炔尚未有相关实验报道。通过在理论上研究不同杂质元素和不同掺杂方式对石墨二炔电子结构的影响,可为实验上通过掺杂手段调控石墨二炔的电子性质提供重要理论依据,改进石墨二炔在储能、电子器件等方面的性能。
1 计算方法我们利用基于密度泛函理论的第一性原理计算程序Vienna Ab-initio Simulation Package(VASP)[27]完成计算,使用广义梯度近似(GGA)下的Perdew-Burke-Ernzerhof(PBE)交换关联泛函[28]。赝势采用投影缀加波(PAW)方法[29-30]。动能截断取500 eV。自洽计算的收敛标准是总能量相差小于10-4 eV,结构驰豫计算的收敛标准是原子受力小于0.01 eV/?。自洽计算的K抽样选取以Γ点为中心的9×9×1格子,态密度计算的K抽样选取以Γ点为中心的35×35×1格子。能带计算的高对称点选K-Γ-M-K,掺杂之后对称性降低,增加R-Γ-S-R路径。垂直于石墨二炔平面方向取15?的真空层,以避免层间的相互作用。对本征石墨二炔和掺杂石墨二炔的计算都选取一个原胞(包含18个原子)来完成。
2 本征石墨二炔的能带结构和态密度首先计算优化后的本征石墨二炔的几何结构。优化后的石墨二炔晶格常数是9.46?,与之前的研究结果9.44?[12]吻合。之后计算石墨二炔的能带和态密度,如图 1(c)所示,选取费米能级的位置为能量零点。计算结果表明,石墨二炔是一种直接带隙半导体,在Γ点处有0.48 eV的带隙,与之前研究中使用局域密度近似(LDA)计算的带隙0.44 eV[14]基本一致,所获得的能带结构和态密度也与之前的研究结果一致,说明我们的计算方法可靠。
Fig. 1
 | Download: JPG larger image |
| (a)石墨二炔的几何结构(菱形虚线框表示原胞大小); (b)第一布里渊区及高对称点; (c)能带和态密度(虚线指出费米能级的位置)。 图 1 石墨二炔的结构和能带 Fig. 1 Structure and bandstructure of graphdiyne 图 1 石墨二炔的结构和能带 Fig. 1 Structure and bandstructure of graphdiyne --> | |
3 硅、锗掺杂石墨二炔的能带结构我们考虑两种方式的替位掺杂,分别在每个石墨二炔原胞的六边环上掺杂1个Si/Ge杂质原子(简称为SiGD-Ⅰ, GeGD-Ⅰ),如图 2(a)、2(c)所示,以及在六元环上的相对位置掺杂2个相同Si/Ge杂质原子(简称为SiGD-Ⅱ, GeGD-Ⅱ),如图 2(e)、2(g)所示。Si/Ge和C的价电子数相同,这4种掺杂方式均为等电子掺杂。一个石墨二炔原胞(18个原子)包含1个或2个杂质原子,掺杂浓度分别为5.6%和11.1%。计算能带时,由于掺杂之后对称性降低,我们选取路径K-Γ-M-K,R-Γ-S-R,如图 1(b)中所示,得到的能带结构展示在图 2(b), 2(d), 2(f)和2(h)中。Si, Ge和C的价电子数相同,是等电子掺杂,费米面未发生上下移动,且材料依然都是半导体。对于单原子替位掺杂的情况,如图 2(b)和2(d)所示,掺入Si和Ge时,都是Γ点处的直接带隙半导体,带隙分别为0.34和0.35 eV,小于本征石墨二炔的带隙0.48 eV。对于双原子对位掺杂的情况,如图 2(f)和2(h)所示,带隙位置从Γ点移动到K和Γ之间,还是直接带隙半导体,带隙变得非常小。对于Si和Ge掺杂,带隙分别是0.004 eV和0.013 eV。
Fig. 2
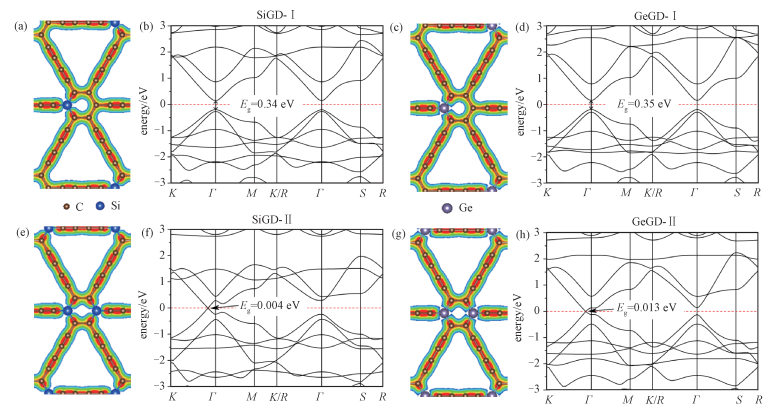 | Download: JPG larger image |
| 图 2 硅、锗掺杂石墨二炔的几何结构、电子密度和能带结构 Fig. 2 Geometric structures, charge densities, and bandstructures of Si/Ge-doped graphdiynes 图 2 硅、锗掺杂石墨二炔的几何结构、电子密度和能带结构 Fig. 2 Geometric structures, charge densities, and bandstructures of Si/Ge-doped graphdiynes --> | |
石墨二炔费米面附近的电子能量状态主要来自其六元环上C原子的2pz轨道的贡献[26]。在六元环上掺杂Si或Ge,由于Si和Ge的电负性都小于C,部分电荷从Si/Ge转移给了C,如图 2(a), 2(c), 2(e)和2(g)所示,六元环上sp2键是局域在面内的,决定费米面处电子性质的主要是pz电子,C的2pz轨道多出了来自Si/Ge的电子,提供施主能级,使导带下移(以带隙中心位置为参考),而Si/Ge的3pz/4pz轨道则部分空缺,提供受主能级,使价带上移,因此Si/Ge掺杂使带隙减小。随着掺杂浓度的提高,六元环上C原子的2pz轨道从Si/Ge处获得更多的电子,且部分空缺的Si/Ge的pz轨道数量更多,因此带隙进一步减小。我们认为在双原子掺杂情况中,带隙位置的改变与所选取的对位掺杂位置有关。
4 硼、氮、磷掺杂石墨二炔的能带结构现在考虑硼、氮、磷3种元素掺杂的情况,与第3节中的命名规则相同,按照掺杂元素的种类和浓度简称为BGD-Ⅰ, NGD-Ⅰ, PGD-Ⅰ, BGD-Ⅱ, NGD-Ⅱ, PGD-Ⅱ。从掺杂后的能带结构来看,掺B是p型掺杂,会使费米面下移,穿过价带,如图 3(g)和3(j)所示,掺杂之后的材料都变成了导体。BGD-Ⅰ的费米面下移0.74 eV(以带隙中心位置为参考点),BGD-Ⅱ的费米面下移1.17 eV。掺N是n型掺杂,会使费米面上移,穿过导带,如图 3(h)和3(k)所示,材料变成了导体。NGD-Ⅰ的费米面上移0.72 eV,NGD-Ⅱ的费米面上移1.12 eV。掺P也是n型掺杂,会使费米面上移,穿过导带,如图 3(i)和3(l)所示,材料变成了导体。PGD-Ⅰ的费米面上移0.83 eV,PGD-Ⅱ的费米面上移1.09 eV。双原子掺杂比单原子掺杂对费米面的改变更显著。
Fig. 3
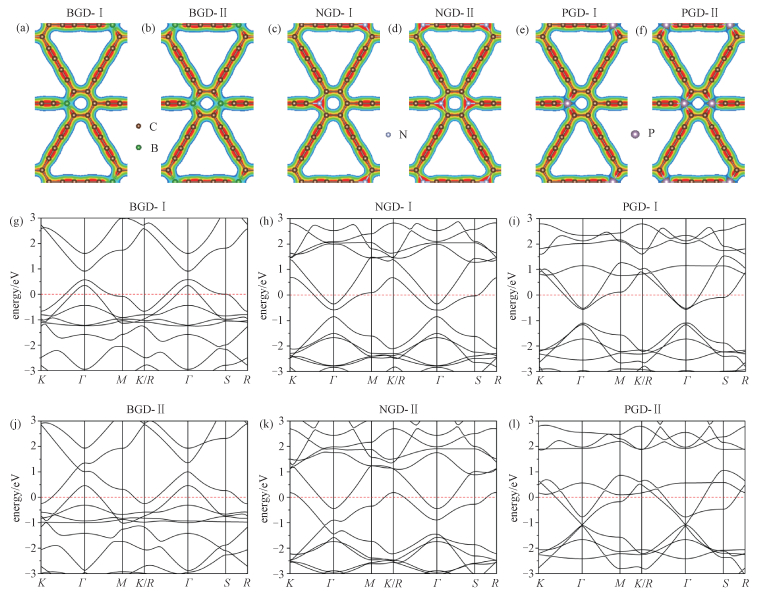 | Download: JPG larger image |
| 图 3 硼、氮、磷掺杂石墨二炔的能带结构 Fig. 3 Bandstructures of B/N/P-doped graphdiynes 图 3 硼、氮、磷掺杂石墨二炔的能带结构 Fig. 3 Bandstructures of B/N/P-doped graphdiynes --> | |
5 硼-氮、硼-磷共掺杂石墨二炔的能带结构我们考虑将石墨二炔六边环上相对的2个碳原子分别替换为硼和氮,以及硼和磷,研究硼-氮共掺杂石墨二炔(BNGD)、硼-磷共掺杂石墨二炔(BPGD)的能带结构。B比C少1个价电子,N, P比C多1个价电子,因此B-N和B-P共掺杂都是等电子掺杂方式,材料依然是半导体。BNGD的能带结构如图 4(b)所示,材料由直接带隙变成间接带隙,导带底和价带顶都转移到Γ和S之间,带隙大小为0.49 eV,和本征石墨二炔的带隙大小接近。BPGD的能带结构如图 4(d)所示,材料依然是直接带隙半导体,但带隙位置偏离了Γ点,转移到Γ和S之间,带隙则减小到0.26 eV。BNGD和BPGD的结构对称性与前面提到的Si/Ge/B/N/P单原子掺杂的对称性相同,带隙大小是可比拟的,都在0.26~0.49 eV之间,所不同的是共掺杂时,带隙不再是Γ点处的直接带隙,导带底和价带顶都偏离了Γ点,转移到Γ和S之间,这是因为共掺杂时,2种掺杂原子与C原子之间都存在着电荷转移,导致带隙位置发生变化。B-P共掺杂时,B和P的电子都部分转移给了周围的C,如图 4(c)所示,六元环上4个碳原子都从杂质原子获得电子,共同提供施主能级,因此带隙较小。而B-N共掺杂时,处于B邻位的C原子获得电子,处于N邻位的C原子失去电子,如图 4(a)所示,六元环两侧的电荷密度非常不平衡,对称性降低,可能导致间接带隙的出现。
Fig. 4
 | Download: JPG larger image |
| 图 4 共掺杂石墨二炔的几何结构、电子密度和能带结构 Fig. 4 Geometric structures, charge densities, and bandstructures of co-doped graphdiynes 图 4 共掺杂石墨二炔的几何结构、电子密度和能带结构 Fig. 4 Geometric structures, charge densities, and bandstructures of co-doped graphdiynes --> | |
6 掺杂石墨二炔的形成能形成能是衡量掺杂实现容易程度和掺杂材料稳定性的重要因素。我们计算了所有12种掺杂石墨二炔的形成能Ef
| ${E_{\rm{f}}} = {E_{{\rm{XCD}}}} - {E_{{\rm{GD}}}} + n{E_{\rm{C}}} - n{E_X}, $ |
Table 1
| 表 1 掺杂石墨二炔的形成能Table 1 Formation energies of doped graphdiynes eV |
单原子N掺杂的形成能为2.0 eV,双原子N掺杂的形成能为3.7 eV,分别为对应掺杂浓度下形成能最小的情况。实验上已经成功合成了N掺杂的石墨二炔[22-24],且掺杂浓度可以达到10%左右[24]。B为杂质元素时的形成能比较小,单原子掺杂时为3.3 eV,双原子掺杂时为6.5 eV。B掺杂石墨二炔也在实验上成功合成[23],然而掺杂浓度仅能实现到0.24%。Si, P, Ge由于原子半径较大,Si/P/Ge掺杂石墨二炔的形成能较大,目前都未有成功合成的报道。总体来看,双原子掺杂的形成能大致是单原子掺杂的2倍。对于Si/Ge掺杂,其双原子掺杂的形成能比单原子掺杂的2倍略大,对于B/P掺杂,双原子掺杂的形成能接近于单原子掺杂的2倍。对于N掺杂,双原子掺杂的形成能比单原子掺杂的2倍略小,亦反映了N掺杂容易实现。而B-N共掺杂的形成能3.7 eV,小于B单原子掺杂的形成能与N单原子掺杂的形成能之和5.3 eV,这点与B-P共掺杂不同,这表明N元素的存在有利于提高B的掺杂浓度,这已在实验上得到证实[23]。
7 总结我们计算了石墨二炔六元环上替位掺杂1个或在相对位置替位掺杂2个Si, Ge, B, N, P原子的掺杂石墨二炔的能带结构,与B-N和B-P共掺杂石墨二炔的能带结构。发现SiGD-Ⅰ, SiGD-Ⅱ, GeGD-Ⅰ, GeGD-Ⅱ和BNGD, BPGD是半导体,其中SiGD-Ⅰ, GeGD-Ⅰ是Γ点处的直接带隙半导体,带隙分别为0.34和0.35 eV,比本征石墨二炔略小,而SiGD-Ⅱ, GeGD-Ⅱ的带隙分别减小到0.004和0.013 eV,出现狄拉克锥状电子结构,锥点处于K和Γ之间。BPGD的带隙为0.26 eV,是直接带隙,带隙位置从Γ点转移到Γ和S之间;BNGD的带隙为0.49 eV,是我们研究的12种掺杂石墨二炔结构中唯一的一个间接带隙半导体,导带底和价带顶都在Γ和S之间。BGD, NGD和PGD都是导体,其中掺B是p型掺杂,费米面穿过价带,掺N和P是n型掺杂,费米面穿过导带。B/N/P单原子掺杂,即掺杂浓度为5.6%时,费米面相对带隙中心位置移动0.7 eV左右。B/N/P双原子掺杂,即掺杂浓度为11.1%时,费米面相对带隙中心位置移动1.1 eV左右。随着掺杂浓度的提高,费米面的位置改变更显著。我们还计算了研究的12种掺杂石墨二炔的形成能。发现B, N作为掺杂元素时,形成能较小,容易实现掺杂,也都有成功合成的报道;Si, Ge, P作为掺杂元素时,形成能较大,还没有相关实验报道。通过对掺杂石墨二炔能带结构的研究和比较,发现掺杂浓度和掺杂位置与带隙大小和费米面位置之间有密切关系,并分析原因,总结其中的规律。本研究为实验上通过掺杂手段调节石墨二炔带隙大小和费米面位置提供了理论依据,使其能在相关电子和光电子器件中得到有效应用。
参考文献
| [1] | Novoselov K S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films[J]. Science, 2004, 306(5696): 666-669. Doi:10.1126/science.1102896 |
| [2] | Iijima S. Helical microtubules of graphitic carbon[J]. Nature, 1991, 354(6348): 56. Doi:10.1038/354056a0 |
| [3] | Sheng X L, Yan Q B, Ye F, et al. T-carbon:a novel carbon allotrope[J]. Physical Review Letters, 2011, 106(15): 155703. Doi:10.1103/PhysRevLett.106.155703 |
| [4] | Schedin F, Geim A K, Morozov S V, et al. Detection of individual gas molecules adsorbed on graphene[J]. Nature Materials, 2007, 6(9): 652. Doi:10.1038/nmat1967 |
| [5] | Wang X, Zhi L, Müllen K. Transparent, conductive graphene electrodes for dye-sensitized solar cells[J]. Nano Letters, 2008, 8(1): 323-327. Doi:10.1021/nl072838r |
| [6] | Du H L, Li X Y. Molecular dynamics simulations for separation of H2/N2 by porous graphene[J]. Journal of Graduate University of Chinese Academy of Sciences, 2012, 29(3): 312-315. |
| [7] | Park H, Afzali A, Han S J, et al. High-density integration of carbon nanotubes via chemical self-assembly[J]. Nature Nanotechnology, 2012, 7(12): 787. Doi:10.1038/nnano.2012.189 |
| [8] | Baughman R H, Eckhardt H, Kertesz M. Structure-property predictions for new planar forms of carbon:Layered phases containing sp2 and sp atoms[J]. The Journal of Chemical Physics, 1987, 87(11): 6687-6699. Doi:10.1063/1.453405 |
| [9] | Li G, Li Y, Liu H, et al. Architecture of graphdiyne nanoscale films[J]. Chemical Communications, 2010, 46(19): 3256-3258. Doi:10.1039/b922733d |
| [10] | Gao J, Li J, Chen Y, et al. Architecture and properties of a novel two-dimensional carbon material-graphtetrayne[J]. Nano Energy, 2018, 43: 192-199. Doi:10.1016/j.nanoen.2017.11.005 |
| [11] | Jia Z, Zuo Z, Yi Y, et al. Low temperature, atmospheric pressure for synthesis of a new carbon Ene-yne and application in Li storage[J]. Nano Energy, 2017, 33: 343-349. Doi:10.1016/j.nanoen.2017.01.049 |
| [12] | Narita N, Nagai S, Suzuki S, et al. Optimized geometries and electronic structures of graphyne and its family[J]. Physical Review B, 1998, 58(16): 11009. Doi:10.1103/PhysRevB.58.11009 |
| [13] | Li Y, Xu L, Liu H, et al. Graphdiyne and graphyne:from theoretical predictions to practical construction[J]. Chemical Society Reviews, 2014, 43(8): 2572-2586. Doi:10.1039/c3cs60388a |
| [14] | Luo G, Qian X, Liu H, et al. Quasiparticle energies and excitonic effects of the two-dimensional carbon allotrope graphdiyne:theory and experiment[J]. Physical Review B, 2011, 84(7): 075439. Doi:10.1103/PhysRevB.84.075439 |
| [15] | Sun C, Searles D J. Lithium storage on graphdiyne predicted by DFT calculations[J]. The Journal of Physical Chemistry C, 2012, 116(50): 26222-26226. Doi:10.1021/jp309638z |
| [16] | Zhang S, Liu H, Huang C, et al. Bulk graphdiyne powder applied for highly efficient lithium storage[J]. Chemical Communications, 2015, 51(10): 1834-1837. Doi:10.1039/C4CC08706B |
| [17] | Li C, Li J, Wu F, et al. High capacity hydrogen storage in Ca decorated graphyne:a first-principles study[J]. The Journal of Physical Chemistry C, 2011, 115(46): 23221-23225. Doi:10.1021/jp208423y |
| [18] | Bartolomei M, Carmona-Novillo E, Hernández M I, et al. Graphdiyne pores:"ad hoc" openings for helium separation applications[J]. The Journal of Physical Chemistry C, 2014, 118(51): 29966-29972. Doi:10.1021/jp510124e |
| [19] | Bartolomei M, Carmona-Novillo E, Hernández M I, et al. Penetration barrier of water through graphynes' pores:first-principles predictions and force field optimization[J]. The Journal of Physical Chemistry Letters, 2014, 5(4): 751-755. Doi:10.1021/jz4026563 |
| [20] | Cui H J, Sheng X L, Yan Q B, et al. Strain-induced Dirac cone-like electronic structures and semiconductor-semimetal transition in graphdiyne[J]. Physical Chemistry Chemical Physics, 2013, 15(21): 8179-8185. Doi:10.1039/c3cp44457k |
| [21] | Koo J, Park M, Hwang S, et al. Widely tunable band gaps of graphdiyne:an ab initio study[J]. Physical Chemistry Chemical Physics, 2014, 16(19): 8935-8939. Doi:10.1039/C4CP00800F |
| [22] | Lv Q, Si W, Yang Z, et al. Nitrogen-doped porous graphdiyne:a highly efficient metal-free electrocatalyst for oxygen reduction reaction[J]. ACS applied materials & interfaces, 2017, 9(35): 29744-29752. |
| [23] | Zhang S, Cai Y, He H, et al. Heteroatom doped graphdiyne as efficient metal-free electrocatalyst for oxygen reduction reaction in alkaline medium[J]. Journal of Materials Chemistry A, 2016, 4(13): 4738-4744. Doi:10.1039/C5TA10579J |
| [24] | Zhang S, Du H, He J, et al. Nitrogen-doped graphdiyne applied for lithium-ion storage[J]. ACS Applied Materials & Interfaces, 2016, 8(13): 8467-8473. |
| [25] | Lu R, Rao D, Meng Z, et al. Boron-substituted graphyne as a versatile material with high storage capacities of Li and H2:a multiscale theoretical study[J]. Physical Chemistry Chemical Physics, 2013, 15(38): 16120-16126. Doi:10.1039/c3cp52364k |
| [26] | Chen C, Li J, Sheng X L. Graphdiyne nanoribbons with open hexagonal rings:existence of topological unprotected edge states[J]. Physics Letters A, 2017, 381(38): 3337-3341. Doi:10.1016/j.physleta.2017.08.034 |
| [27] | Kresse G, Furthmuler J. Efficient iterative schemes for ab initio total energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54(16): 11169. Doi:10.1103/PhysRevB.54.11169 |
| [28] | Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865. Doi:10.1103/PhysRevLett.77.3865 |
| [29] | Bl?chl P E. Projector augmented-wave method[J]. Physical Review B, 1994, 50(24): 17953. Doi:10.1103/PhysRevB.50.17953 |
| [30] | Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Physical Review B, 1999, 59(3): 1758-1775. Doi:10.1103/PhysRevB.59.1758 |
