季策^1,2, 王鑫¹, 耿蓉¹, 梁敏骏³
1. 东北大学 计算机科学与工程学院，辽宁 沈阳 110169;
2. 东北大学 医学影像智能计算教育部重点实验室，辽宁 沈阳 110169;
3. 东北大学 信息科学与工程学院，辽宁 沈阳 110819
收稿日期：2022-07-01
基金项目：中央高校基本科研业务费专项资金资助项目(N2116015, N2116020)。
作者简介：季策(1969－)，女，辽宁沈阳人，东北大学副教授。

摘要：针对时变信道环境下传统信道估计方法性能受限，其他基于深度学习的信道估计方法估计精度低或复杂度高的问题，提出一种基于长短期记忆结构的信道估计网络，由双向长短期记忆(bidirectional long short-term memory, BiLSTM)网络和多层感知器(multilayer perceptron, MLP)网络组成，即BiLSTM-MLP.首先，利用BiLSTM网络来学习信道的时变特性；然后，利用MLP网络进行去噪并重构信道估计.仿真结果表明，所提出的信道估计方法与传统方法相比，性能提升明显，与同类型的基于深度学习的估计方法相比，复杂度较低且性能更优.此外，所提方法还具有对不同导频密度的鲁棒性.
关键词：时变信道信道估计深度学习长短期记忆多层感知器
LSTM-Based Channel Estimation Method in Time-Varying Channels
JI Ce^1,2, WANG Xin¹, GENG Rong¹, LIANG Min-jun³
1. School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China;
2. Key Laboratory of Intelligent Computing in Medical Image, Ministry of Education, Northeastern University, Shenyang 110169, China;
3. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Xin, E-mail: 1660781760@qq.com.

Abstract: Aiming to address the limitations of traditional channel estimation methods in time-varying channel environments, as well as the low estimation accuracy or high complexity of deep learning-based channel estimation methods, a channel estimation network based on long short-term memory structure is proposed, which consists of a bidirectional long short-term memory(BiLSTM)network and a multilayer perceptron(MLP)network, namely BiLSTM-MLP. First, the BiLSTM network is used to learn the time-varying characteristics of the channel. Then, a MLP network is used to denoise and reconstruct the channel estimation. Simulation results show that the proposed channel estimation method has better performance than traditional methods, and has lower complexity and better performance compared with the same type of deep learning-based estimation methods. Furthermore, the proposed method is also robust to different pilot densities.
Key words: time-varying channelchannel estimationdeep learninglong short-term memory (LSTM)multilayer perceptron (MLP)
信道估计是无线通信系统接收机的关键模块，其估计质量的好坏对于整个系统的性能至关重要.但在实际应用中，由于接收机的移动，信道状态将在时域中改变，这种时变性会严重影响信道估计的质量.因此，如何在时变信道环境下获得精准的信道估计是无线通信系统当前面临的一大挑战.传统的信道估计方法，如最小二乘(least squares, LS)算法^[1]和最小均方误差(minimum mean square error, MMSE)算法^[2]，均是依赖于线性平稳的信道模型，然而时变信道是非线性和非平稳的，所以在时变信道环境下传统算法的性能会遭受严重的损失.虽然MMSE算法性能仍较为优越，但是其需要信道的先验统计信息，在实际应用中却很难知道真实的信道模型，而且MMSE算法需要矩阵的求逆运算，具有极高的计算复杂度.
近年来，随着人工智能的发展和计算机算力的提高，深度学习技术得到了广泛的应用，特别是在计算机视觉和自然语言处理领域，这也激励了通信领域的研究人员积极地尝试将该技术应用到无线通信领域^[3-4].文献[5]利用深度神经网络(deep neural network, DNN)来完成语音信号去噪和波束形成.文献[6]利用循环神经网络(recurrent neural network, RNN)对泊松信道下的信号进行解码.文献[7]将自编码器(autoencoder, AE)网络用于IEEE 802.11p系统下的信道估计，提出了一种基于数据导频辅助的误差补偿方案.文献[8]将DNN用于正交频分复用(orthogonal frequency division multiplexing, OFDM)系统中的联合信道估计与信号检测.文献[9]提出了一种基于双向长短期记忆(bidirectional long short-term memory, BiLSTM)网络的新型网络结构——CBR-Net，将其用于上行时变OFDM系统的信号检测，并取得了良好的信号恢复性能.对于时变信道下的信道估计问题，文献[10]提出了一种基于DNN的估计方法，DNN根据接收信号、导频信号和先前的信道估计计算出当前的信道估计，与传统算法相比有了明显的增益.文献[11]也提出了一种类似的基于DNN的信道估计方法，并将其应用于双选信道环境下的信道估计.然而，DNN是一种没有记忆的网络结构，虽然文献[10]将先前的信道估计输入到了网络中，但并没有充分利用信道在时域中的相关性.文献[12]提出了一种滑动双向门控循环单元(sliding bidirectional gated recurrent unit, SBGRU)网络，其原理是一种具有滑动结构的BiGRU网络，GRU是一种具有门结构的RNN，是LSTM的变体之一.SBGRU可以充分学习信道在时域中的相关性，滑动操作的引入可以利用特定时间窗口内的平均信道信息，与传统方法及基于DNN的估计方法相比，性能大幅提升，但同时滑动操作的引入也极大地提高了计算复杂度.
本文提出了一种基于LSTM的信道估计方法，由BiLSTM网络和多层感知器(multilayer perceptron, MLP)网络级联而成，即BiLSTM-MLP.BiLSTM-MLP方法首先利用BiLSTM网络来充分学习信道的时间相关性，再利用MLP网络对输出进行降维并去噪，给出最终的信道估计.仿真结果显示，对于时变环境下的信道估计问题，相比于LS算法和DNN估计方法，本文给出的BiLSTM-MLP方法的均方误差(mean square error，MSE)和误比特率(bit error rate，BER)性能得到大幅提升，与MMSE算法和SBGRU方法相比，在复杂度大大降低的同时MSE性能仍有一定的提升.此外，本文方法还具有对不同导频密度的鲁棒性.
1 系统模型1.1 发射信号结构发射信号结构遵循现有的IEEE标准，如图 1所示.1帧信号包含K个块，可以分为两部分.第一部分是前导训练块，第二部分是插入了导频符号的数据块.每个数据块包含N_S个数据符号和N_P个导频符号.因此，1个数据块共有N=N_S+N_P个符号，1帧信号共有L=NK个符号.导频符号以相等的间隔插入到每个块中，导频密度定义为N_S/N.
图 1(Fig. 1)

图 1 发射信号结构Fig.1 Transmit signal structure

1.2 时变信道模型无线通信环境通常被建模为瑞利衰落信道.多径效应和多普勒频移分别会导致频率选择性衰落和时间选择性衰落，本文重点考虑的是时间选择性衰落.
本文采用Clarke模型^[13]来描述时变信道，采用Jakes模型^[14]来描述时变特性，其功率谱为

(1)

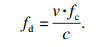其中，f_d是最大多普勒频移，由式(2)给出：

(2)

其中：v是接收机的移动速度；f_c是载波频率；c为光速.Jakes多普勒频谱的自相关为

(3)

其中，J₀(·)是第一类零阶贝塞尔函数.
1.3 信号流模型信号流模型如图 2所示.
图 2(Fig. 2)

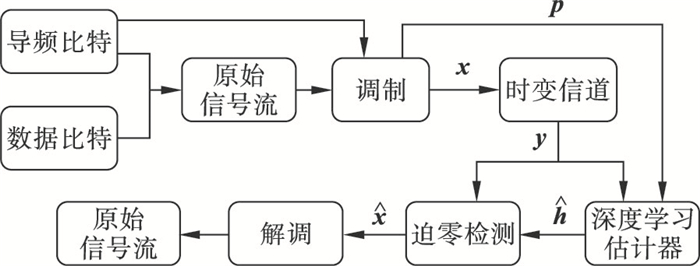图 2 信号流模型Fig.2 Signal flow model

在发射机端，首先将数据比特和导频比特组合生成原始信号流.原始信号流经调制后，生成发射信号x，再将x发送到时变信道，同时将调制后的导频p发送到深度学习估计器.在接收机端，深度学习估计器利用导频p和接收信号y给出信道估计.最后，本文采用迫零检测算法，通过计算 来恢复发射信号，再经解调后即可得到原始信号流.
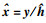
信道输入和输出的关系可以表示为

(4)

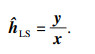其中：h表示时变信道频率响应；w表示均值为0，方差为σ_w²的加性高斯白噪声.本文设计了基于深度学习的信道估计器，而传统的信道估计算法一般为LS和MMSE.时变信道下LS算法可由式(5)给出^[1]：

(5)

利用式(5)可以计算得到导频位置处的信道估计，对于数据位置处的信道估计，需要由线性插值算法得到.数据位置i处相邻的导频位置由j, k(j < k)表示，则数据位置i处的信道估计可以表示为

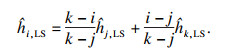(6)

时变信道下的MMSE算法可表示为^[2]

(7)

其中：I表示单位矩阵；R_hy表示信道响应与接收信号的互相关矩阵；R_yy表示接收信号的自相关矩阵；R_hh表示信道的自相关矩阵；σ_n²表示噪声的方差；σ_s²表示信号的方差.
2 基于LSTM的信道估计2.1 LSTM概述RNN是一种用于处理序列数据的神经网络，但序列数据的预测往往存在一种长期依赖问题，即当前状态的预测受很久之前信息的影响.一般的RNN容易出现梯度消失或爆炸的问题，从而不能捕获很久之前的信息，难以解决长期依赖问题.LSTM网络是一种特殊的RNN，是为了解决长期依赖问题而专门设计的^[15].
LSTM的结构如图 3所示，通过“门”结构来去除或增加信息到细胞状态中.“门”是一种让信息选择式通过的方法，负责控制和跟踪随时间变化的信息流.LSTM网络机制可以用以下4个主要步骤来描述.
图 3(Fig. 3)

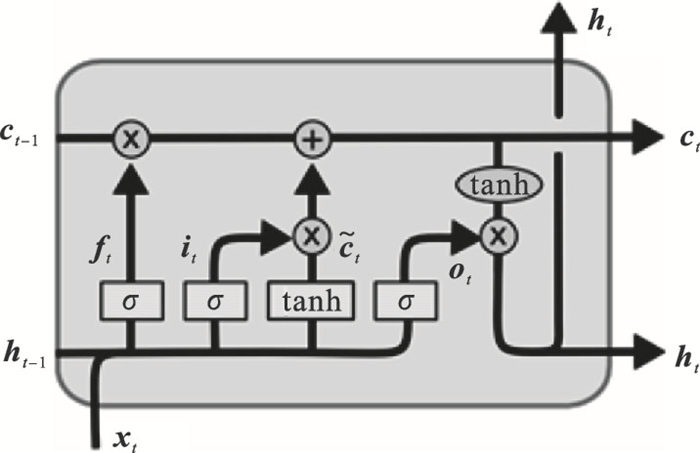图 3 LSTM细胞结构Fig.3 LSTM cell structure

1) 忘记无关的旧信息：LSTM单元将输入数据分类为相关信息和无关信息.从细胞状态中丢弃与未来数据预测无关的信息，通过遗忘门f_t来执行.遗忘门的计算如下：

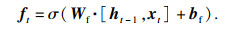(8)

其中：σ是Sigmoid函数，即 ；W_f和b_f是时间为t时的遗忘门权重矩阵和偏置向量；x_t和h_t-1分别表示维度为X_in的LSTM单元输入向量和维度为P的前一单元的隐藏状态.
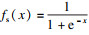
2) 存储相关的新信息：确定什么样的新信息会被添加到细胞状态中，包含2个部分：候选单元 存储的是计算得到的新信息，输入门i_t则决定应该从 中提取哪些信息，候选单元和输入门的定义如下：

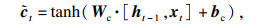(9)

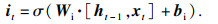(10)

其中：tanh是双曲正切函数，即tanh(x)= ；W_c, W_i和b_c, b_i分别是候选单元和输入门的权重矩阵和偏置向量.
3) 更新旧细胞状态：LSTM单元基于前面的2个步骤更新当前的细胞状态c_t，使得

(11)

其中，⊙表示哈达玛乘积，即2个矩阵的对应位置元素相乘.
4) 生成LSTM单元输出：通过输出门o_t来更新隐藏状态h_t，即确定输出值.输出被认为是细胞状态的过滤，输出门和遗忘门、输入门的计算方式相同.输出门和隐藏状态的计算如下：

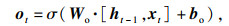(12)

(13)

其中，W_o和b_o是输出门的权重矩阵和偏置向量.
2.2 BiLSTM-MLP网络本文所设计的BiLSTM-MLP估计网络由1个BiLSTM网络和1个MLP网络组成，网络结构如图 4所示. 因为LSTM网络在时间序列数据预测方面表现优越，所以采用LSTM网络来预测信道状态信息(channel state information, CSI).并且考虑到时变信道状态h(t)与过去和将来的信道状态皆有关联，故采用双向结构，即为2个单向LSTM网络的组合，1个网络进行正向预测，另1个网络进行反向预测.
图 4(Fig. 4)

图 4 BiLSTM-MLP结构Fig.4 BiLSTM-MLP structure

将式(8)~(13)表示的LSTM单元操作简化并定义为双向模式：

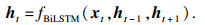(14)

其中，h_t-1和h_t+1分别是前一单元和后一单元的隐藏状态.MLP网络的作用是提高网络的去噪能力，并对输出进行维度变换，重构信道估计.采用的是两层MLP网络，第一层选用ReLU函数作为激活函数来处理LSTM的输出，第二层选用线性层将输出降维重构信道估计.MLP网络可以表示为

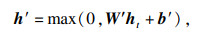(15)

(16)

其中：W′, W″和b′, b″分别是第一层和第二层的权重矩阵和偏置向量；h′和h″分别为每一层的输出.
BiLSTM-MLP网络的输入数据有接收信号y和原始导频信号p.由于深度学习平台只能处理实数，所以应对输入数据进行预处理，分离其实部和虚部将其合成为一个向量，因此最终的输入形式为：S_in=[Re(y^T), Re(p^T), lm(y^T), lm(p^T)]^T.将S_in输入到BiLSTM-MLP中，得到信道估计 ，可表示为

(17)

其中：f_BiLSTM-MLP(·)表示式(14)~(16)中给出的BiLSTM-MLP网络的计算过程；θ是网络的参数.
为了训练神经网络，需构造1个表示系统性能的损失函数，本文采用MSE(mean square error)函数，可表示为

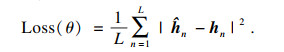(18)

要训练出1个性能优越的网络模型，需要不断地迭代更新参数θ来最小化损失函数，本文采用自适应矩估计(adaptive moment estimation, ADAM)算法来最小化Loss(θ)，直到网络达到收敛，ADAM算法公式如下：

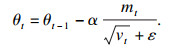(19)

其中：α是固定的学习率；m_t是梯度的指数平均数；v_t是二阶动量，将其作为α的分母可自适应地调整学习率的大小，ε>0，以防止分母为0.
测试时，网络的输入与训练阶段的输入具有相同的结构和统计特征.加载训练好的参数θ，完成测试数据的计算，获得信道估计 .
2.3 复杂度分析将本文所提方法与其他信道估计方法进行了计算复杂度的比较，复杂度的衡量标准是估计一帧信号的信道所需的浮点运算次数(FLOPs)，即实际运算过程中实数加减乘除计算的次数.传统方法的复杂度易于分析，由式(5)可知LS算法计算简单，相比其他方法复杂度较低.由式(7)可知MMSE算法在LS算法的基础上还涉及相关矩阵的计算，特别是矩阵求逆运算，而神经网络的计算仅涉及矩阵乘法和矩阵加法，故MMSE算法要比基于深度学习的估计方法复杂很多.因此，在下面的分析中，本文将重点比较3种基于深度学习的信道估计方法的复杂度：DNN, SBGRU与BiLSTM-MLP.
对于文献[10]中提出的DNN估计方法，其复杂度易于分析.记N_l, N分别表示DNN第l隐藏层的维度和隐藏层的总层数，第l隐藏层和第l+1隐藏层之间的转换需要进行乘法和加法运算的次数均为N_lN_l+1，则DNN估计方法的复杂度可以表示为

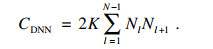(20)

文献[12]中提出的SBGRU估计方法，采用一个具有滑动结构的双向GRU网络窗来估计信道，其中网络的隐藏层数为2.对于SBGRU网络，P表示GRU隐藏层维度，W_L表示估计窗的长度，X_in和X_out表示其输入维度和输出维度.在第一隐藏层，需要3(PX_in+P²+P)次乘法运算和3(PX_in+P²)+P次加法运算；在第二隐藏层，其输入为第一层的隐藏状态h_t，需要3(2P²+P)次乘法运算和6P²+P次加法运算；输出层需要PX_out次加法运算和乘法运算.由于是双向结构，GRU网络的所有计算次数均需乘以2，而SBGRU网络估计1帧信号的信道共需要滑动L-W_L+1次，所以其计算复杂度可以表示为

(21)

因为BiLSTM-MLP网络与SBGRU的输入、输出和隐藏层维度均相同，所以继续用P, X_in, X_out表示BiLSTM-MLP网络的LSTM隐藏层维度、输入维度和输出维度.此外，用Q表示MLP的第二隐层维度.对于LSTM单元，由式(8)~(10)和式(12)可知，计算每个门所需的乘法和加法运算次数均为PX_in+P².此外，计算式(11)和式(13)需要3P次乘法运算和P次加法运算.对于MLP网络，其输入为BiLSTM网络的输出，所以其输入维度为2P.每一层需要1个矩阵乘法和1个向量加法，所以MLP网络所需的乘法运算和加法运算次数均为2PQ+QX_out.因此，BiLSTM-MLP估计1个符号共需8(PX_in+P²)+ 6P+2PQ+QX_out次乘法运算和8(PX_in+P²)+2P+2PQ+QX_out次加法运算.对于1帧信号，其计算复杂度可表示为

(22)

DNN和SBGRU网络参数的设置同文献[10]和文献[12]，设置BiLSTM-MLP网络参数P=40，Q=256，X_in=4，X_out=2，代入参数值计算得到3种估计方法计算复杂度的实例化数值如表 1所示.由表可知，本文所提出的BiLSTM-MLP所需的FLOPs较SBGRU降低了96.3%，虽然较DNN高了1倍多，但BiLSTM-MLP的不同窗口之间均是相互独立的，可以并行计算不同的估计窗，而DNN由于需要输入前一个信号块的信道估计，不能同时计算不同的信号块，因此在实际应用中BiLSTM-MLP的复杂度相较DNN并不会有2倍这么高.此外，表 1中还给出了每种网络的参数数量，BiLSTM- MLP数量最少，这是因为LSTM网络每个单元参数共享，即每个时间步上神经网络的参数都相同，因此会大幅节约内存资源.
表 1(Table 1)

表 1 3种信道估计方法的计算复杂度Table 1 Computational complexity of three channel estimation methods 方法 参数数量 FLOPs DNN 218 016 5 032 960 SBGRU 157 762 291 948 800 BiLSTM-MLP 96 770 11 274 240

表 1 3种信道估计方法的计算复杂度 Table 1 Computational complexity of three channel estimation methods

3 仿真实验与分析本章主要通过仿真实验来验证BiLSTM-MLP网络在时变信道环境下的性能.首先介绍了仿真系统的设置，其次对BiLSTM-MLP网络的结构设计进行了评估，然后对BiLSTM-MLP与传统信道估计方法及其他基于深度学习的信道估计方法的MSE性能和BER性能进行了比较和分析.最后，还分析了导频密度和最大多普勒频移对BiLSTM-MLP性能的影响.
3.1 仿真设置仿真系统的主要参数如表 2所示，为了便于与文献[10]和文献[12]中的同类估计方法的性能作对比，信道参数和导频密度的选择均与之相同.
表 2(Table 2)

表 2 信道和信号参数Table 2 Channel and signal parameters 参数 参数取值 载波频率/GHz 5.2 调制方式 QPSK 采样周期/μs 4 1帧信号长度 160 信号块个数 10 1个信号块中的符号数 16 导频密度/% 50 训练时接收速度/(m·s-1) 10

表 2 信道和信号参数 Table 2 Channel and signal parameters

根据表 2所给出的信道参数，生成了1 200个信道，再根据这些信道和数据参数随机生成120 000个信号序列样本，100 000个用于训练，10 000个用于验证，10 000个用于测试.此外，为了验证不同多普勒频移环境下的性能鲁棒性，还生成了20 m/s下的测试集以及随机最大多普勒频移的测试集.
BiLSTM-MLP的网络结构参数和训练参数如表 3所示，本文选择在20 dB的信噪比下进行网络训练，在0, 5, 10, 15, 20, 25, 30 dB的信噪比下进行网络测试，优化器、学习率、批大小等超参数均按照深度学习领域的一般经验所设定.
表 3(Table 3)

表 3 网络结构与训练参数Table 3 Network structure and training parameters 参数 参数取值 BiLSTM-MLP各层维度 P=40, Q=256 窗口长度 40 批数据大小 32 优化器 Adam 损失函数 MSE 学习率 0.001 训练信噪比/dB 20 测试信噪比/dB 0, 5, 10, 15, 20, 25, 30 训练集样本数量 100 000 验证集样本数量 10 000 测试集样本数量 10 000

表 3 网络结构与训练参数 Table 3 Network structure and training parameters

3.2 BiLSTM-MLP网络结构评估在10 m/s速度环境下，通过LSTM, BiLSTM和BiLSTM-MLP三种不同网络结构的MSE性能对比(见图 5)，来验证本文所设计的网络结构的合理性.
图 5(Fig. 5)

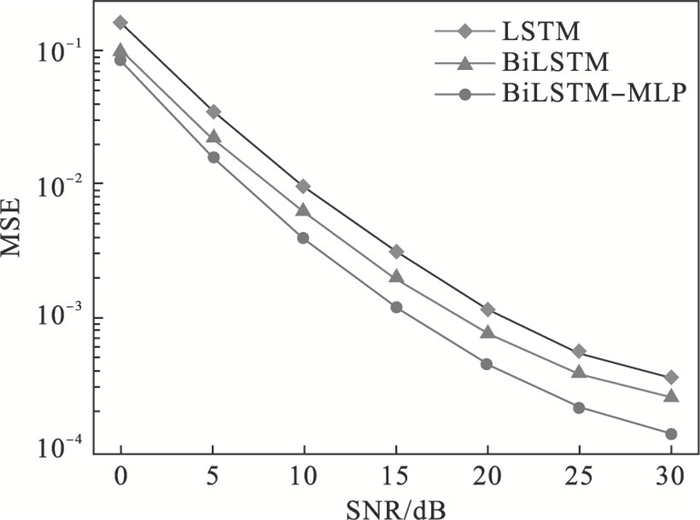图 5 不同网络结构的MSE性能对比Fig.5 MSE performance comparison of different network structures

由图 5可知，在MSE=7.5×10^-3时，BiLSTM与LSTM相比，有4 dB的SNR增益，这是因为对时变信道来说，当前时刻的信道状态与过去时刻和未来时刻的信道状态皆有关联，双向结构可以同时捕获过去和将来的信息，因此具有更好的性能.BiLSTM-MLP相比于BiLSTM有6 dB的SNR增益，这充分证明了添加的MLP网络可提高网络的去噪能力，从而提高网络的整体性能.
3.3 MSE性能图 6a和6b分别比较了10 m/s和20 m/s速度环境下，本文所设计的BiLSTM-MLP网络估计方法与LS算法、MMSE算法、DNN方法和SBGRU方法的MSE性能.
图 6(Fig. 6)

图 6 不同速度环境下几种方法的MSE性能Fig.6 MSE performance of each method in different speed environment (a)—10 m/s；(b)—20 m/s.

由图 6可知，在传统的估计方法中，LS算法在10, 20 m/s时，均表现出了很差的MSE性能，其估计精度差的主要原因在于LS算法忽略了噪声的影响.由于利用了信道的先验统计特性，MMSE算法表现出了较好的估计精度，甚至在10 m/s，0~15 dB和20 m/s，0~10 dB的低信噪比区域，MSE性能达到了最优.但是MMSE的实用性并不高，为了进行MMSE估计，需要预先给出信道的先验统计特性，在实际应用中却很难知道真实的信道模型，而且由于存在矩阵求逆运算，MMSE算法的计算复杂度极高.基于深度学习的估计方法中，基于RNN的方法的MSE性能曲线明显优于基于DNN的方法的性能曲线，在10 m/s, MSE=4×10^-3时，SBGRU和BiLSTM-MLP相比于DNN分别有10 dB和12 dB的SNR增益；在20 m/s, MSE=9.5×10^-2时，SBGRU与BiLSTM-MLP相较DNN均有14 dB的SNR增益.这充分说明相较于其他神经网络，RNN对序列数据具有更强大的处理能力.
对于两种基于RNN的信道估计方法，从10 m/s到20 m/s的速度环境下，随着多普勒频移的增加，SBGRU网络的MSE性能损失略小于BiLSTM-MLP网络.这是因为SBGRU在BiGRU网络估计窗的基础上引入了滑动的操作，即每次窗口计算后滑动1个符号，因此序列中的大多数符号被多次估计，取所有估计的平均值来给出最终结果.正如文献[12]所得到的结论，滑动操作的引入提高了SBGRU网络的性能和对多普勒频移的鲁棒性，但也为此付出了高昂的计算复杂度代价，正如2.3节所讨论的.本文所设计的BiLSTM-MLP网络虽然鲁棒性略逊于SBGRU网络，但是计算复杂度远远低于SBGRU网络，在MSE性能方面也超越了SBGRU网络.
此外，BiLSTM-MLP网络是在与文献[10]和文献[12]相同的单一速度环境下训练的，以便与其进行性能比较.实际应用中也可以将多种速度环境下生成的信道集混合在一起生成训练数据，这样训练出来的网络，多普勒频移变化对其性能的影响就会降低，鲁棒性更强.
3.4 BER性能BER性能是衡量信道估计方法对系统整体性能影响的宏观指标.图 7a和7b分别比较了10 m/s和20 m/s速度环境下，本文所设计的BiLSTM-MLP方法与LS算法、MMSE算法、DNN方法和SBGRU方法的BER性能.
图 7(Fig. 7)

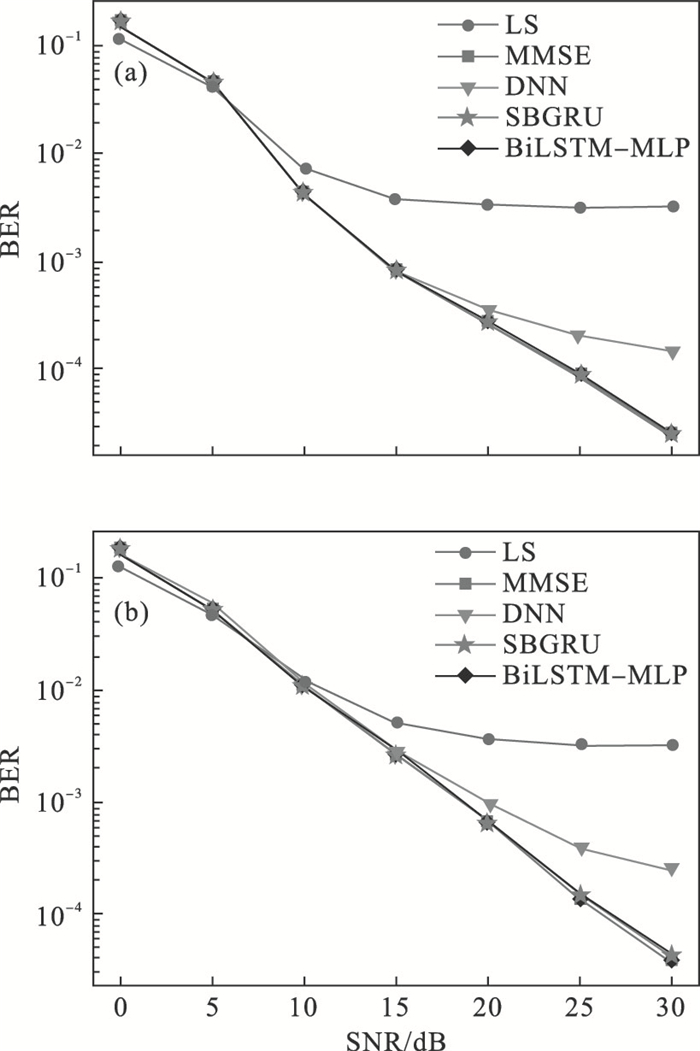图 7 不同速度环境下几种方法的BER性能Fig.7 BER performance of each method in different speed environment (a)—10 m/s；(b)—20 m/s.

从仿真结果上来看，两种速度下各估计方法的BER性能曲线变化趋势大体一致.LS的BER仍是最高的，DNN次之，MMSE, SBGRU与BiLSTM-MLP是最低的.当速度为10 m/s和20 m/s时，在高信噪比(SNR>15 dB)区域，MMSE, SBGRU, BiLSTM-MLP的BER曲线仍保持良好的下降趋势，BER性能明显优于DNN.MMSE, SBGRU以及本文所提的BiLSTM-MLP的BER曲线在整个信噪比区域都基本重合，可见它们的BER性能基本相近，但BiLSTM-MLP是以最低的复杂度达到了与它们相似的性能.此外，由于在发射机端并没有引入深度学习技术，传统的信道编码方法可以与基于深度学习的估计方法相结合，进一步提高系统的BER性能.
3.5 导频密度对性能的影响一般来说，对于一帧信号，导频越密集，信道估计性能越好.图 8比较了不同导频密度时所设计的BiLSTM-MLP网络的MSE性能，随着导频密度的降低，MSE性能确实略有下降，但并不严重.因此，BiLSTM-MLP网络具有对不同导频密度的鲁棒性.
图 8(Fig. 8)

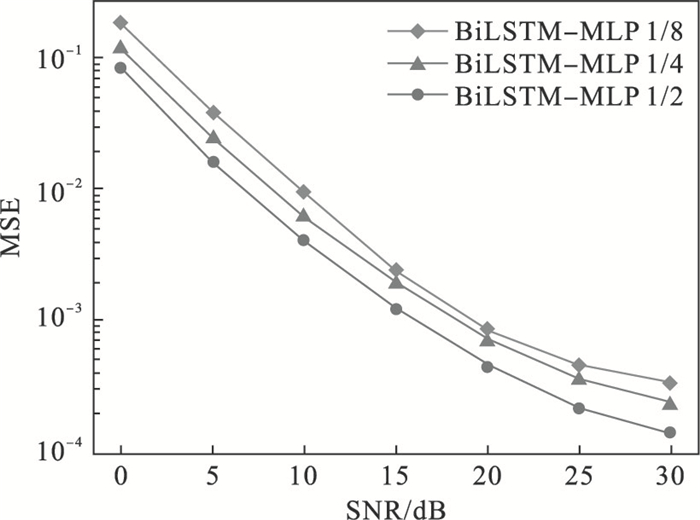图 8 导频密度对BiLSTM-MLP性能的影响Fig.8 Influence of pilot density on BiLSTM-MLP performance

3.6 最大多普勒频移对性能的影响前面所做的仿真都是在恒定最大多普勒频移f_d=173 Hz(10 m/s)和f_d=346 Hz(20 m/s)的情况下完成的，但在现实环境中，由于接收器的移动，f_d并不会恒定不变.因此，图 9比较了在三种不同形式的f_d情况下，BiLSTM-MLP网络的MSE性能.
图 9(Fig. 9)

图 9 随机最大多普勒频移对BiLSTM-MLP性能的影响Fig.9 Influence of random maximum Doppler shift on BiLSTM-MLP performance

除f_d=173 Hz固定值外，还将f_d设置为中心频率为173 Hz的0~346 Hz和0~865 Hz之间的随机变量.如图 9所示，f_d取0~346 Hz范围内的随机变量时，MSE性能基本没有下降；取0~865 Hz范围内的随机变量时，在低信噪比时MSE性能基本没有下降，在高信噪比时MSE性能有所下降，但仍可接受.因此，BiLSTM-MLP网络对于信道的随机统计特性具有鲁棒性，可适用于复杂环境.
4 结论本文系统研究了时变环境下的信道估计问题，针对传统算法和其他基于深度学习的信道估计方法性能不足或复杂度高的问题，提出一种基于LSTM的信道估计方法，通过离线训练，有效地利用了训练样本中的信道数据提升了在线估计的精度.此外，本文从计算复杂度、MSE性能和BER性能方面对比了所设计的BiLSTM-MLP方法与LS算法、MMSE算法、DNN方法和SBGRU方法的估计性能，仿真结果显示，BiLSTM-MLP方法可以以较低的复杂度实现最优的信道估计性能，并且具有对不同导频密度的鲁棒性.
参考文献

[1]	Usha S M, Mahesh H B. Least square channel estimation for image transmission with OFDM over fading channel[J]. International Journal of Computer Networks and Communications, 2020, 12(1): 1-17. DOI:10.5121/ijcnc.2020.12101
[2]	Nadeem Q U A, Kammoun A, Debbah M, et al. Asymptotic analysis of RZF over double scattering channels with MMSE estimation[J]. IEEE Transactions on Wireless Communications, 2019, 18(5): 2509-2526. DOI:10.1109/TWC.2019.2904495
[3]	薛谦. 深度学习在无线通信物理层中的应用[D]. 南京: 东南大学, 2020. (Xue Qian. Applications of deep learning in the physical layer of wireless communication[D]. Nanjing: Southeast University, 2020. )
[4]	Zhang S, Liu Y S, Gao F F, et al. Deep learning based channel extrapolation for large-scale antenna systems: opportunities, challenges and solutions[J]. IEEE Wireless Communications, 2021, 28(6): 160-167. DOI:10.1109/MWC.001.2000534
[5]	Wu B, Li K H, Yang M L, et al. A reverberation-time-aware approach to speech dereverberation based on deep neural networks[J]. IEEE/ACM Transactions on Audio, Speech and Language Processing, 2017, 25(1): 102-111. DOI:10.1109/TASLP.2016.2623559
[6]	Farsad N, Andrea G. Neural network detection of data sequences in communication systems[J]. IEEE Transactions on Signal Processing, 2018, 66(21): 5663-5678. DOI:10.1109/TSP.2018.2868322
[7]	Han S, Oh Y, Song C. A deep learning based channel estimation scheme for IEEE 802.11p systems[C]//ICC 2019-2019 IEEE International Conference on Communi-cations(ICC). Shanghai, 2019: 1-6.
[8]	Ye H, Li G Y, Juang B H. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114-117. DOI:10.1109/LWC.2017.2757490
[9]	Wang S Y, Yao R, Tsiftsis T A, et al. Signal detection in uplink time-varying OFDM systems using RNN with bidirectional LSTM[J]. IEEE Wireless Communications Letters, 2020, 9(11): 1947-1951. DOI:10.1109/LWC.2020.3009170
[10]	Ma X L, Ye H, Li Y, et al. Learning assisted estimation for time-varying channels[C]// 2018 15th International Symposium on Wireless Communication Systems. Lisbon: IEEE, 2018: 1-5.
[11]	Yang Y W, Gao F F, Ma X L, et al. Deep learning-based channel estimation for doubly selective fading channels[J]. IEEE Access, 2019, 7: 36579-36589. DOI:10.1109/ACCESS.2019.2901066
[12]	Bai Q B, Wang J T, Zhang Y, et al. Deep learning-based channel estimation algorithm over time selective fading channels[J]. IEEE Transactions on Cognitive Communications and Networking, 2020, 6(1): 125-134. DOI:10.1109/TCCN.2019.2943455
[13]	Clarke R H. A statistical theory of mobile-radio reception[J]. Bell System Technical Journal, 1968, 47(6): 957-1000. DOI:10.1002/j.1538-7305.1968.tb00069.x
[14]	Gans M J. A power-spectral theory of propagation in the mobile-radio environment[J]. IEEE Transactions on Vehicular Technology, 1972, 21(1): 27-38. DOI:10.1109/T-VT.1972.23495
[15]	Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735