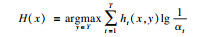, 张宇2, 于丁力2,3
, 张宇2, 于丁力2,3 1. 吉林大学 汽车仿真与控制国家重点实验室,吉林 长春 130022;
2. 吉林大学 通信工程学院,吉林 长春 130012;
3. 利物浦约翰摩尔斯大学 工程技术学院,利物浦 L33AF
收稿日期:2022-06-17
基金项目:吉林省科技厅自然科学基金资助项目(20190201099JC); 汽车仿真与控制国家重点实验室自由探索项目(ascl-zytsxm-202022)。
作者简介:李寿涛(1975-),男,吉林长春人,吉林大学教授。
摘要:针对传统帕金森患者冻结步态识别方法自适应性不佳的问题,提出一种基于变分模态分解的冻结步态识别方法.首先采用变分模态分解代替传统时频分析方法对冻结步态信号进行充分的自适应分解.其次为提高算法识别精度和识别速度,选用CART模型作为集成分类器的基分类器并进行特征降维处理.最后针对不平衡数据集和单分类器性能有限的问题,进行了数据采样-集成分类器的设计并通过贝叶斯优化对识别算法进行超参数寻优.实验结果表明,相对于AdaBoost、Tomeklinks-AdaBoost和ROS-AdaBoost集成算法,RUSBoost集成算法可以更高效地完成冻结步态识别任务.
关键词:冻结步态特征提取变分模态分解RUSBoost贝叶斯优化
Freezing of Gait Recognition Method Based on Variational Mode Decomposition
LI Shou-tao1,2, QU Ru-yi1,2

 , ZHANG Yu2, YU Ding-li2,3
, ZHANG Yu2, YU Ding-li2,3 1. State Key Laboratory of Automobile Simulation and Control, Jilin University, Changchun 130022, China;
2. School of Communication Engineering, Jilin University, Changchun 130012, China;
3. School of Engineering and Technology, Liverpool John Moores University, Liverpool L33AF, UK
Corresponding author: QU Ru-yi, E-mail: 1390214992@qq.com.
Abstract: Aiming at the problem of poor self-adaptation of the traditional freezing of gait recognition method for Parkinson's patients, the freezing of gait recognition method based on variational mode decomposition is proposed. Firstly, the variational mode decomposition is used instead of the traditional time-frequency analysis method to fully adaptively decompose the freezing of gait signal. Secondly, in order to improve the recognition accuracy and recognition speed of the algorithm, the CART model is selected as the base classifier of the ensemble classifier and the feature dimension reduction process is performed. Finally, aiming at the problem of unbalanced data set and limited performance of single classifier, the data sampling-ensemble classifier is designed and the recognition algorithm is optimized by Bayesian optimization. The experimental results show that compared with Adaboost, Tomeklinks-Adaboost, and ROS-Adaboost ensemble algorithm, RUSBoost ensemble algorithm can complete the freezing of gait recognition task more efficiently.
Key words: freezing of gaitfeature extractionvariational mode decompositionRUSBoostBayesian optimization
帕金森症(Parkinson disease, PD)是广泛流行的一种神经退行性疾病,而冻结步态(freezing of gait, FOG)是帕金森患者最常见且最具致残性的病理步态[1].从帕金森症的发病机制来看冻结步态是无法彻底治愈的[2],目前对冻结步态的治疗主要以左旋多巴胺类的药物为主[3],由于多巴胺类药物及手术对于冻结步态的治疗效果有限[4-5],因此非药物治疗就逐渐成为干预冻结步态的热门研究方向,而冻结步态识别为帕金森症的非药物治疗奠定了基础.
已有大量****开展了帕金森患者冻结步态识别的研究.Moore等[6]首次尝试了基于惯性传感器检测冻结步态,该方法可以探测出78% 的冻结步态事件.文献[7]在Moore等研究的基础上引入了新的特征指数与冻结指数,采用阈值法识别冻结步态.文献[8]通过处理安装在柄上的惯性传感器所获得的数据并利用Pearson相关系数法进行步态识别分类.Sama等[9]提出了基于加速度计的冻结步态检测算法,该算法与UPDRS-III量表的相关性证实了算法对于检测冻结步态的可行性.Slemensek等[10]提出了一种基于注意力的卷积和循环神经网络的步态识别组合检测方法.此外,Shi等[11]采用了基于卷积神经网络的方法检测冻结步态.Handojoseno等[12]提出脑电图作为一种新的技术可以有效地预测即将发生的冻结步态.然而,目前的特征识别方法仍有一些局限:基于惯性传感器的冻结步态检测方法会出现全局性能下降的情况;基于加速度计的识别方法对测量环境的要求很高,计算成本过大;基于脑电图的冻结步态预测方法非常依赖精密的专业设备.
针对以上问题,本文提出一种基于变分模态分解的帕金森冻结步态识别算法,该方法采用变分模态分解代替传统时频分析方法对冻结步态信号进行自适应分解;选择CART(classification and regression tree)模型作为集成分类器的基分类器,然后针对不平衡数据集和单分类器性能有限的情况,设计了RUSBoost集成算法并进行超参数优化,以实现冻结步态识别算法更加精确高效的目标.
1 变分模态分解理论变分模态分解(variational mode decomposition,VMD)是一种完全非递归的模态变分和信号处理方法,主要由变分问题的构建与求解两个部分组成.
变分问题的构建过程如下:
s(t)是由患者腰背部传感器采集到的加速度信号,通过变分模态分解为k个有限带宽的固有模态分量函数(bandwidth-limited inherent mode functions,BIMF)BIMFk(t),分解目标是使所有模态分量的估计带宽之和最小并且所有模态分量BIMFk(t)之和等于待分解加速度信号s(t).
首先通过希尔伯特变换求得各模态分量函数BIMFk(t)的解析信号并得到对应的单边频谱:
 | (1) |
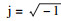
然后采用L2范数对解调之后的信号作高斯平滑处理,构造出s(t)的带约束的变分问题模型:
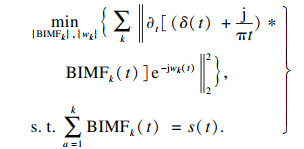 | (2) |
引入拉格朗日算子λ(t)和二次惩罚因子α,构造拉格朗日函数如下:
 | (3) |
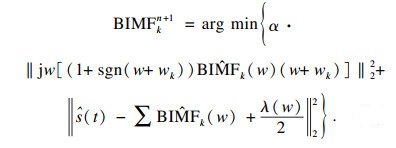 | (4) |
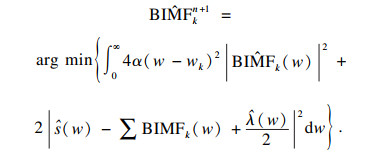 | (5) |
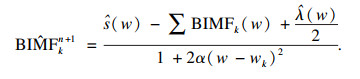 | (6) |

中心频率wk为
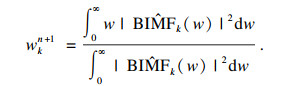 | (7) |
 | (8) |
图 1(Fig. 1)
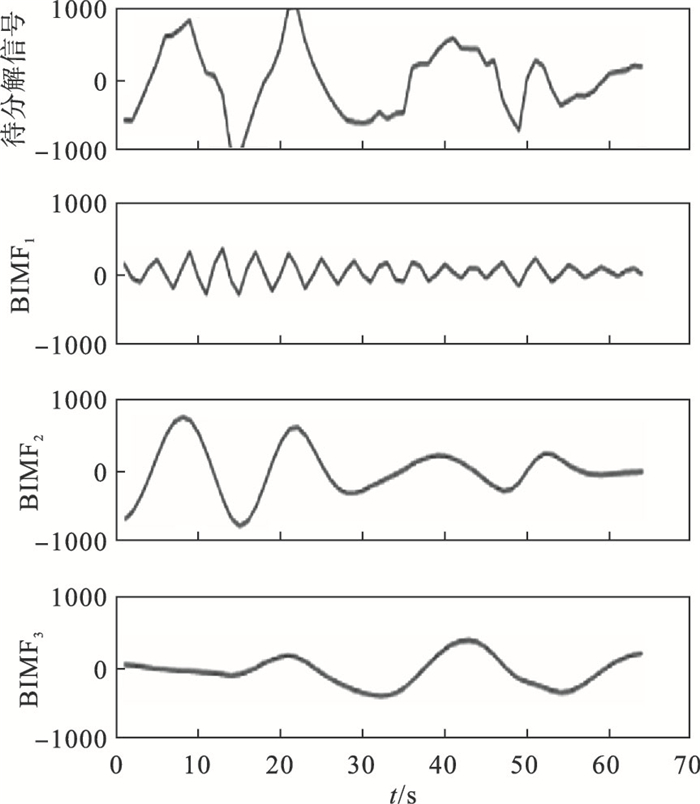 | 图 1 各BIMF时域图Fig.1 Time domain diagram of each BIMF |
图 2(Fig. 2)
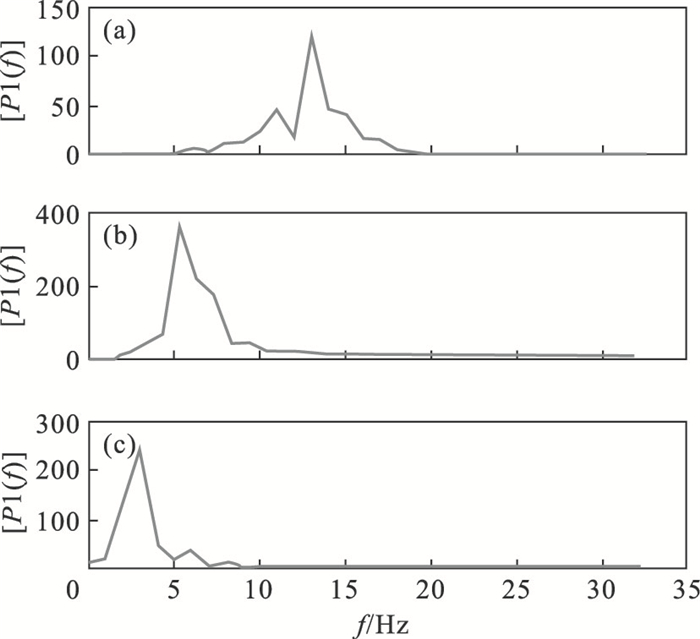 | 图 2 各BIMF频域图Fig.2 Frequency domain diagram of each BIMF (a)—BIMF1;(b)—BIMF2;(c)—BIMF3. |
2.2 基于VMD的冻结步态特征设计及处理本文使用能量熵描述步态信息的能量分布状态,可用式(9)表述:
 | (9) |
患者的加速度信号经VMD分解后,对应9个BIMF,它们的7个统计量(均值、标准差、最大值、最小值、极差、峰度和偏度)加上三轴能量熵,共66个特征值.考虑到特征冗余会影响实际应用中算法的整体性能,因此进行特征降维处理.
本文应用嵌入法进行特征降维,选择CART决策树模型作为嵌入法及后续集成分类器的基分类器模型.CART模型特征重要度为
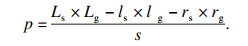 | (10) |
特征降维后选择能达到与全特征分类相似效果的重要性较高的前22个特征组成最优特征子集.实验表明,对特征集进行降维优化后,存储开销为原来的67%,特征提取阶段的时间成本压缩至原来的59%,算法训练时间缩短至原来的77%,识别速度提高至原来的1.72倍.
3 RUSBoost集成算法的设计及超参数优化3.1 基于数据采样的步态特征集平衡化由于单一的CART模型性能有限,且正负样本数量不平衡,因此,本文选用RUSBoost集成框架对CART模型进行集成.该算法是随机欠采样方法与Adaboost相结合的一种集成学习算法.
设训练集为S,xi为某一样本,yi为类别标记,基分类器为WeakerLearner, 迭代次数为T.RUSBoost算法流程见表 1.
表 1(Table 1)
| 表 1 RUSBoost算法流程 Table 1 RUSBoost algorithm process |
本文使用了Adaboost、基于欠采样和集成学习的Tomeklinks-Adaboost、RUSBoost以及基于过采样的ROS-Adaboost集成框架进行冻结步态识别实验.为排除超参数干扰,学习率均设为0.1,迭代次数为30,且均选择CART模型作为基分类器,CART模型的最大分裂数为127.各集成框架在最优特征子集上的表现如表 2所示.
表 2(Table 2)
| 表 2 各集成框架识别性能 Table 2 Recognition performance of each ensemble framework | |||||||||||||||||||||||||||||||||||||||
从实验结果看,RUSBoost集成框架在保证较高准确率的同时,提高了特异度和敏感度,且集成后的AUC值更高,有效地抑制了不平衡数据集造成的不良影响.
3.2 冻结步态识别算法的超参数优化本文使用贝叶斯优化对基于RUSBoost的集成框架进行超参数寻优.
由粗略网格搜索和简单实验发现迭代次数nc和CART模型最大分裂数mns对算法影响最大,因此将nc和mns定为优化目标.分类算法需要在提高识别效果同时减少误判,因此,需将验证集的敏感度和特异度的算术平均值Am最大化,Am表示为
 | (11) |
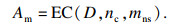 | (12) |
 | (13) |
 | (14) |
 | (15) |
 | (16) |
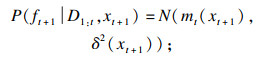 | (17) |
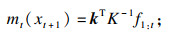 | (18) |
 | (19) |
选择EI采样函数为
 | (20) |
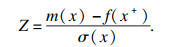 | (21) |
4 实验分析RUSBoost在训练集和验证集上的贝叶斯优化过程如图 3所示,目标函数模型估计曲面如图 4所示,目标函数模型估计等高线图见图 5,ROC曲线如图 6所示.
图 3(Fig. 3)
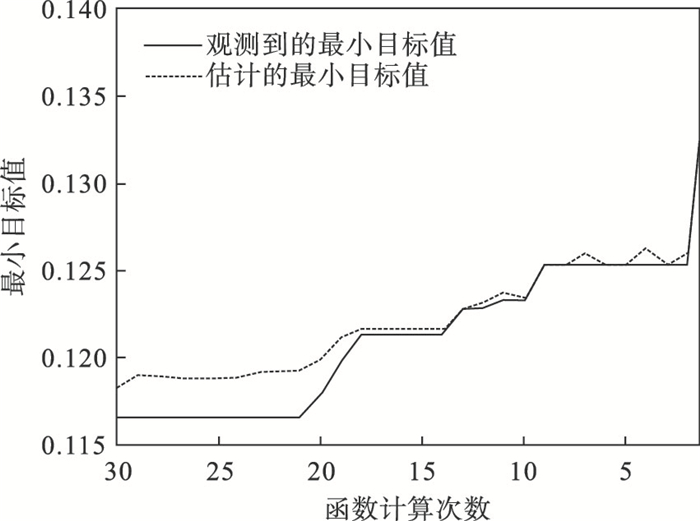 | 图 3 RUSBoost框架超参数寻优过程Fig.3 Hyperparameter optimization process of RUSBoost framework |
图 4(Fig. 4)
 | 图 4 RUSBoost目标函数模型估计曲线Fig.4 Objective function model estimation surface of RUSBoost |
图 5(Fig. 5)
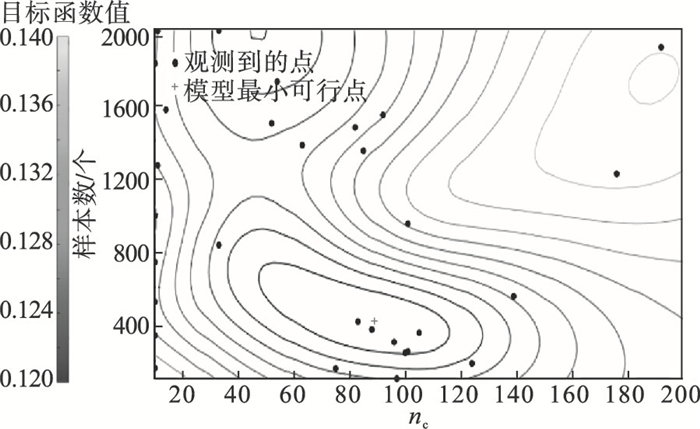 | 图 5 RUSBoost模型估计等高线Fig.5 Model estimation contour map of RUSBoost |
图 6(Fig. 6)
 | 图 6 贝叶斯优化后的ROC曲线及AUC值Fig.6 ROC curve and AUC value after Bayesian optimization |
根据贝叶斯优化的结果可以看出,当mns=413,nc=89时目标函数可以取到最小值,将这组值作为超参数再次训练RUSBoost模型并在测试集进行测试,得到RUSBoost框架准确率为91.9%,敏感度为92.3%,特异度为91.5%,Am=0.919.
5 结语本文针对帕金森患者冻结步态识别方法进行研究,首先将变分模态分解作为冻结步态信号解析工具,信号分解仿真实验证明了变分模态分解可以有效地抑制模态混叠和端点效应,得到更加精确的自适应分解结果.随后基于本文提出的特征集,选择CART模型作为集成算法的基分类器并进行特征降维,得到最优特征子集,实验证明最优特征子集在不影响算法精度的前提下能有效节约存储开销与时间成本.最后针对不平衡数据集和单分类器性能有限的情况,进行了Adaboost、Tomeklinks-Adaboost、RUSBoost和ROS-Adaboost的集成算法性能对比实验,实验结果表明RUSBoost集成算法可以更加有效地完成冻结步态识别任务,并通过贝叶斯优化对RUSBoost集成算法进行超参数寻优求得最佳识别参数.
参考文献
| [1] | Chang S J, Cajigas I, Guest J D, et al. Deep brain stimulation of the Cuneiform nucleus for levodopa-resistant freezing of gait in Parkinson's disease: study protocol for a prospective, pilot trial[J]. Pilot and Feasibility Studies, 2021, 7(1): 1-10. DOI:10.1186/s40814-020-00739-2 |
| [2] | Vitorio R, Stuart S, Mancini M, et al. Executive control of walking in people with Parkinson's disease with freezing of gait[J]. Neurorehabilitation and Neural Repair, 2020, 34(12): 1138-1149. DOI:10.1177/1545968320969940 |
| [3] | Bjorke-Monsen A L, Bjork M H, Storstein A, et al. Severe hyperhomocysteinemia in a patient with Parkinson disease[J]. Clinical Chemistry, 2022, 68(3): 396. DOI:10.1093/clinchem/hvab262 |
| [4] | Nakmode D D, Day C M, Song Y, et al. The management of Parkinson's disease: an overview of the current advancements in drug delivery systems[J]. Pharmaceutics, 2023, 15(5): 1503. DOI:10.3390/pharmaceutics15051503 |
| [5] | Woitalla D, Buhmann C, Hilker R, et al. Role of dopamine agonists in Parkinson's disease therapy[J]. Journal of Neural Transmission, 2023, 130(6): 863-873. DOI:10.1007/s00702-023-02647-0 |
| [6] | Moore S T, MacDougall H G, Ondo W G. Ambulatory monitoring of freezing of gait in Parkinson's disease[J]. Journal of neuroscience methods, 2008, 167(2): 340-348. DOI:10.1016/j.jneumeth.2007.08.023 |
| [7] | Bachlin M, Roggen D, Giladi N, et al. Deep brain stimulation effects on gait variability in Parkinson's disease[J]. Movement Disorders, 2009, 24(11): 1688-1692. DOI:10.1002/mds.22554 |
| [8] | Djuri?-Jovici? M D, Jovici? N S, Radovanovi? S M, et al. Automatic identification and classification of freezing of gait episodes in Parkinson's disease patients[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2014, 22(3): 685-694. DOI:10.1109/TNSRE.2013.2287241 |
| [9] | Sama A, Rodriguez-Martin D, Perez-Lopez C, et al. Determining the optimal features in freezing of gait detection through a single waist accelerometer in home environments[J]. Pattern Recognition Letters, 2018, 105(1): 135-143. |
| [10] | Slemensek J, Fister J, Gersak J, et al. Human gait activity recognition machine learning methods[J]. Sensors, 2023, 23(2): 745-745. DOI:10.3390/s23020745 |
| [11] | Shi B H, Tay A, Au W L, et al. Detection of freezing of gait using convolutional neural networks and data from lower limb motion sensors[J]. IEEE Transactions on Biomedical Engineering, 2022, 69(7): 2256-2267. DOI:10.1109/TBME.2022.3140258 |
| [12] | Handojoseno A M A, Naik G R, Gilat M, et al. Prediction of freezing of gait in patients with Parkinson's disease using EEG signals[J]. Studies in Health Technology and Informatics, 2018, 246: 124-131. |
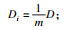
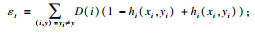
 ;
;