
 , 唐俊文, 陈锦林
, 唐俊文, 陈锦林 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2022-07-11
作者简介:赵钊(1997-), 男, 河北衡水人, 东北大学硕士研究生;
原培新(1953-), 男, 辽宁营口人, 东北大学教授。
摘要:针对SNN-HRL等传统Skill discovery类算法存在的探索困难问题, 本文基于SNN-HRL算法提出了融合多种探索策略的分层强化学习算法MES-HRL, 改进传统分层结构, 算法包括探索轨迹、学习轨迹、路径规划三层.在探索轨迹层, 训练智能体尽可能多地探索未知环境, 为后续的训练过程提供足够的环境状态信息.在学习轨迹层, 将探索轨迹层的训练结果作为“先验知识”用于该层训练, 提高训练效率.在路径规划层, 利用智能体之前获得的skill来完成路径规划任务.通过仿真对比MES-HRL与SNN-HRL算法在不同环境下的性能表现, 仿真结果显示, MES-HRL算法解决了传统算法的探索问题, 具有更出色的路径规划能力.
关键词:深度强化学习分层强化学习路径规划探索策略Skill discovery方法
Agent Path Planning Algorithm Based on Improved SNN-HRL
ZHAO Zhao, YUAN Pei-xin

 , TANG Jun-wen, CHEN Jin-lin
, TANG Jun-wen, CHEN Jin-lin School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: YUAN Pei-xin, E-mail: NEUypx@163.com.
Abstract: Aiming at the difficult exploration problems of traditional Skill discovery algorithms such as SNN-HRL(stochastic neural networks for hierarchical reinforcement learning), this paper proposes a hierarchical reinforcement learning algorithm that integrates multiple exploration strategies(MES) based on SNN-HRL algorithm. The proposed algorithm improves the traditional hierarchical structure, including three layers: exploration trajectory layer, learning trajectory layer, and path planning layer. In the exploration trajectory layer, the trained agent can explore as many unknown environments as possible to provide sufficient environmental state information for the subsequent training process. In the learning trajectory layer, the training results of the exploration trajectory layer are used as "priori knowledge" for the training to improve the training efficiency. In the path planning layer, skill that agent has learned are used to complete the path planning task. By comparing the performance of the MES-HRL and SNN-HRL algorithms in different environments, the simulation results show that MES-HRL algorithm solves the exploration problem of the traditional version of the algorithm and has better path planning capabilities.
Key words: deep reinforcement learninghierarchical reinforcement learning(HRL)path planningexploration strategySkill discovery method
随着科技的不断发展, 移动机器人被广泛用于工业、物流等各个领域, 能在各种复杂环境下进行良好的路径规划是机器人完成各种机载任务的基础前提[1].Mnih等[2]提出DQN(deep Q network)算法, 将深度学习与强化学习相结合, 使得深度强化学习在路径规划中显示出了巨大的潜力.基于强化学习的路径规划应用于复杂环境时会缺乏及时的奖励反馈,导致训练缓慢甚至训练失败.分层强化学习通过在多个时间抽象上学习动作选择策略来解决问题[1], 将一个复杂问题分解为若干个容易解决的子问题.该类算法大致分为两类:一种是基于目标的goal-reach[3-6]; 另一种是多级控制(multi-level control), 通过设计出多级控制层, 完成上层控制下层, 如常见的option, skill等[7-10].
基于信息论Skill discovery类算法采用内部奖励的方法来解决奖励稀疏问题, 该类算法一般使用最大化互信息的方法训练一系列skill来完成路径规划任务, 其训练速度和收敛稳定性远高于普通强化学习算法, 比如Florensa等[9]提出SNN-HRL算法, 考虑轨迹中每个状态S和技能Z之间的互信息, 将I(S; Z)作为reward来最大化.Finn等[10]提出DIAYDS算法在最大化I(S; Z)的同时最小化I(A; Z|S).但是此类算法也因为最大化互信息或者信息熵而导致算法不驱动甚至阻碍智能体去探索环境, 智能体倾向于已经探索过的状态而并非探索更大的状态空间.在复杂环境下, 环境探索问题使得智能体的训练变得十分困难[11].
经过上述文献调研, 针对传统Skill discovery类算法由于探索问题而导致智能体路径规划能力低的问题, 本文提出一种融合多种探索策略的分层强化学习MES-HRL(multiple exploration strategy-hierarchical reinforcement learning)算法, 相比传统分层结构增加了探索轨迹部分, 该部分融合了基于内部奖励和基于记忆的探索, 通过驱动智能体探索未知环境以获得更多的环境状态并保存相应的探索轨迹, 为后续智能体训练skill提供“先验知识”, 从而解决Skill discovery类算法的探索问题.
1 Skill discovery类算法1.1 算法基本原理在强化学习中普遍利用reward来训练智能体, reward可分为外部奖励和内部奖励.外部奖励是环境直接给予智能体的奖励, 在复杂环境下可能比较稀疏; 内部奖励是算法内部给予奖励, 需要人为引导难以获得环境奖励的智能体去处理环境问题.基于信息论的Skill discovery类算法一般采用内部奖励的方式.
内部奖励的思路一般有两种:
1) curiosity based. Dynamic model based,对Dynamic model进行预测, 预测越不准, reward越大, 越能驱动智能体对未知状态的探索[11-12].
Count based,对访问过的状态进行计数, 计数越少, reward越大, 越能驱动智能体探索未知状态[13-14].
2) empowerment based.指next state和action之间的最大互信息, 智能体对环境的控制力, 可以通过action对环境产生的影响决定[15-16].
Skill discovery类算法采用的是empowerment based方式.Empowerment的定义是基于互信息的学习, 最大化智能体执行一个动作序列和最终到达的状态之间的互信息.该类算法一般先训练一组动作序列, 并视为智能体在环境中已经学会的技能skill.用skill代表一个动作序列, 而动作序列与状态之间的互信息就转变为skill和状态之间的互信息.设skill表示为变量Z~p(z), 则状态S和skill之间的互信息表示为
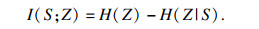 | (1) |
传统Skill discovery类算法采用Reverse形式的表达式, 式(1)分解为
 | (2) |
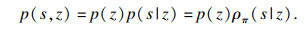 | (3) |
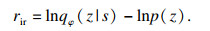 | (4) |
Reverse形式下算法奖励公式如式(5)所示, 假设z~p(z)是离散均匀分布, 即
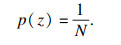 | (5) |
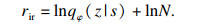 | (6) |
 | (7) |
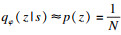
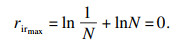 | (8) |
2 MES-HRL算法MES-HRL算法基于SNN-HRL(stochastic neural networks for hierarchical reinforcement learning)算法进行设计, 分为探索轨迹、学习轨迹、路径规划三层, 由于仿真环境为离散环境, 所以MES-HRL算法每层以Dueling DDQN(Dueling double deep Q network)算法为基础进行设计.
MES-HRL算法的训练流程如图 1所示, 智能体首先进行探索轨迹的训练, 训练的主要目的是驱动智能体尽可能多地探索环境, 为后续的路径规划工作提供足够的环境状态信息.当智能体完成探索轨迹的训练后, 将训练获得的信息作为“先验知识”用于skill的训练.最后智能体使用训练好的skill完成路径规划任务.
图 1(Fig. 1)
 | 图 1 MES-HRL算法的训练流程图Fig.1 Training flowchart of the MES-HRL algorithm |
2.1 探索轨迹强化学习的探索方法主要分为经典探索方法[12]、基于内部奖励的探索[13]和基于记忆的探索[17], 本文融合基于记忆的探索和基于内部奖励的探索来设计探索策略.探索轨迹层的主要任务是建立1个容器, 保存探索到的状态, 这个容器与普通强化学习中的优先经验回放经验池[18]类似, 保存某一状态的位置、权重W、运动轨迹、累计奖励四部分信息.具体设计方法如下:
1) 位置和权重.本文采用离散的二维栅格环境, 因此状态的位置以(X, Y)坐标形式表示和保存.为实现驱动智能体探索未知环境的目的, 使用内部奖励探索策略中的count based统计智能体访问某个状态的次数, 并以此衡量访问该状态带来的内部奖励, 次数越少智能体获得的内部奖励越大, 同时也以该次数表示权重W, 即
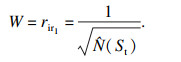 | (9) |
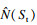
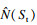
2) 运动轨迹和累计奖励.运动轨迹和累计奖励是从环境初始状态到该状态的运动轨迹和累计奖励, 出于判断运动轨迹优劣的目的, 累计奖励公式为
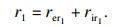 | (10) |
3) 容器更新方法.当智能体抵达某一状态时(无论是否探索过)更新其权重、运动轨迹和累计奖励.当访问到一个新状态时, 便将其相关信息保存至容器中, 如果智能体在S0(每一episode开始时的初始状态)处开始探索并探索到了新状态, 那么就将S0视为一个对于发现新状态更有价值的状态, 更新S0的权重W0, 将发现的新状态的权重Wnew按照一定比例加入到S0的权重中去, 即
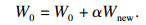 | (11) |
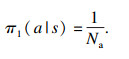 | (12) |
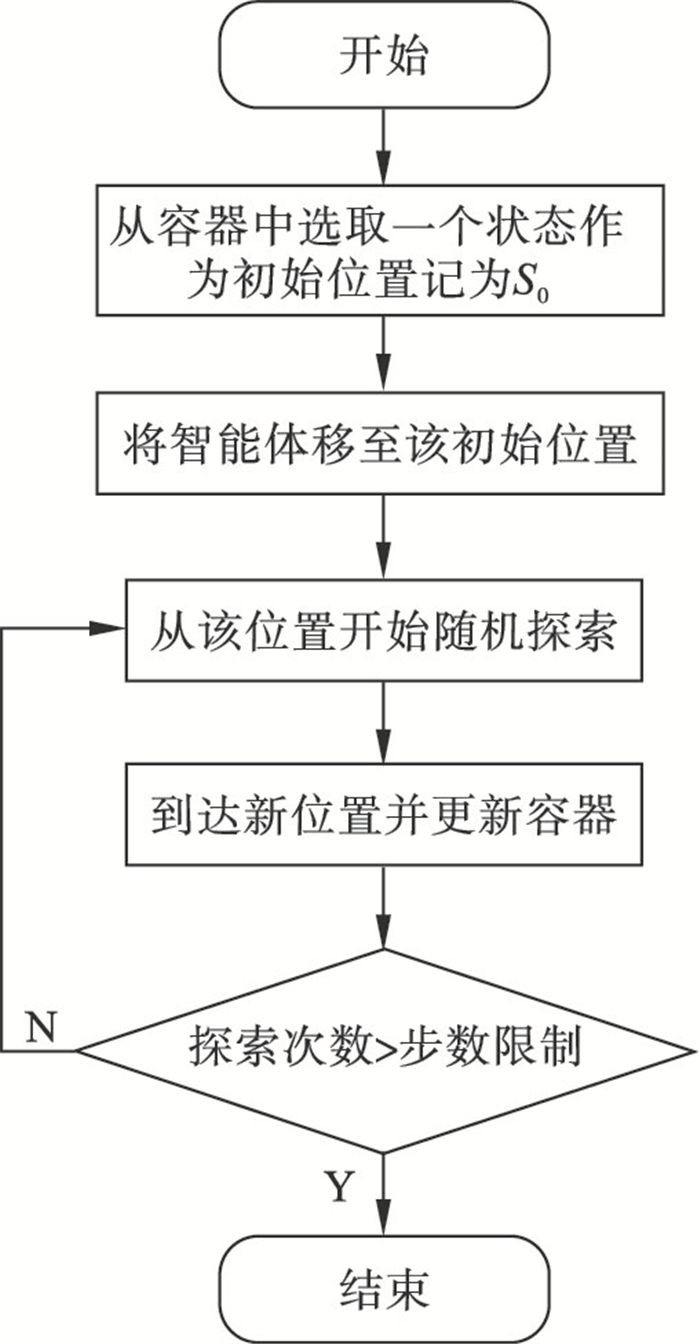 | 图 2 探索轨迹层算法流程图Fig.2 Algorithm flowchart of exploration trajectory layer |
2.2 学习轨迹智能体在该阶段学习上一阶段探索出的轨迹, 容器中保存的信息可作为“先验知识”(不是人为直接给予)用于该阶段的训练.MES-HRL算法基于信息论最大化I(S; Z)来构建目标, 选择Reverse分解方式.该阶段主要目的是训练智能体获得一些明显不同的技能skill, 即训练策略πθ(a| s, z).最大化互信息的内部奖励如式(4)所示.智能体在学习skill的过程中, SNN-HRL算法直接使用环境的最终目标, 但本阶段所使用的goal并不是环境的最终目标, 而是随机的某一状态, 因此智能体获得的外部奖励改为
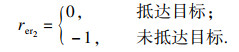 | (13) |
 | (14) |
图 3(Fig. 3)
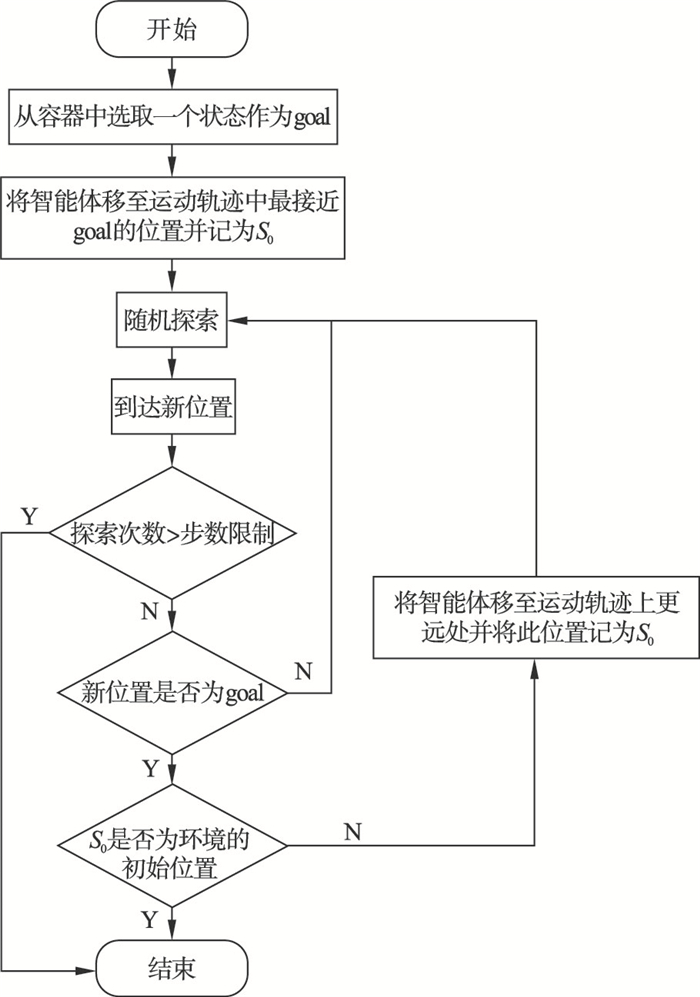 | 图 3 学习轨迹层算法流程图Fig.3 Algorithm flowchart of learning trajectory layer |
2.3 路径规划路径规划层算法与SNN-HRL算法中的路径规划部分大致相同, 经过上一阶段的训练, 智能体已经得到了一些彼此有明显不同的技能skill, 在这一阶段智能体直接接受环境的外部奖励来训练策略πφ(z|s), 其公式为
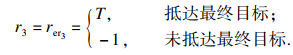 | (15) |
图 4(Fig. 4)
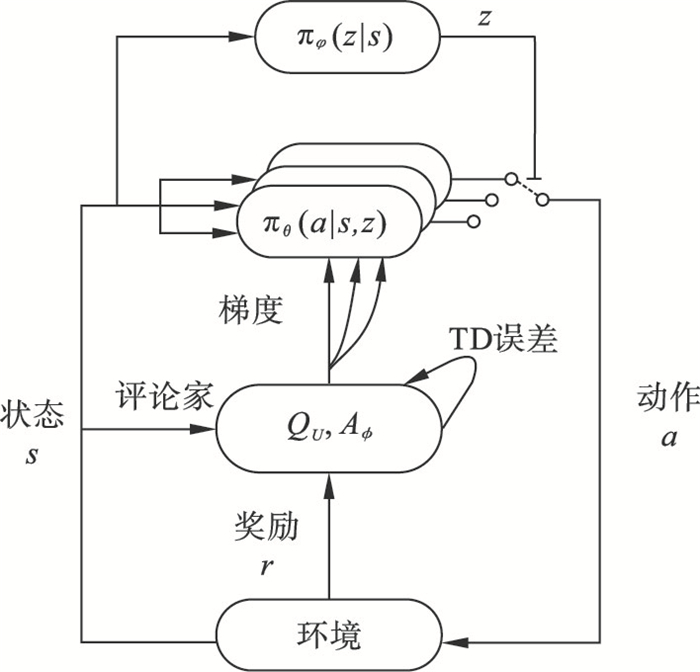 | 图 4 路径规划层算法结构图Fig.4 Algorithm structure diagram of path planning layer |
3 仿真与分析本文通过仿真验证算法性能, 使用Python编程, 在Nvidia GeForce GTX 2070 GPU和AMD Ryzen 7 5800 H CPU硬件环境下训练神经网络.MES-HRL和SNN-HRL算法每层基于Dueling DDQN算法建立.
仿真环境采用空环境、四室环境、钥匙-门环境.空环境中没有障碍物, 如图 5a所示, 三角代表智能体, 五角星代表最终目标, 该环境仅仅验证算法是否存在收敛性; 四室环境用于验证算法的全局路径规划能力, 如图 5b所示, 每个房间与相邻房间仅有一个位置可通过; 钥匙-门环境用于验证算法的逻辑推理能力, 如图 5c所示, 在该地图中, 智能体必须先取得钥匙再打开门才能到达最终目标.在以上3种地图中, 比较SNN-HRL、MES-HRL和Dueling DDQN(基础算法)3种算法的性能.
图 5(Fig. 5)
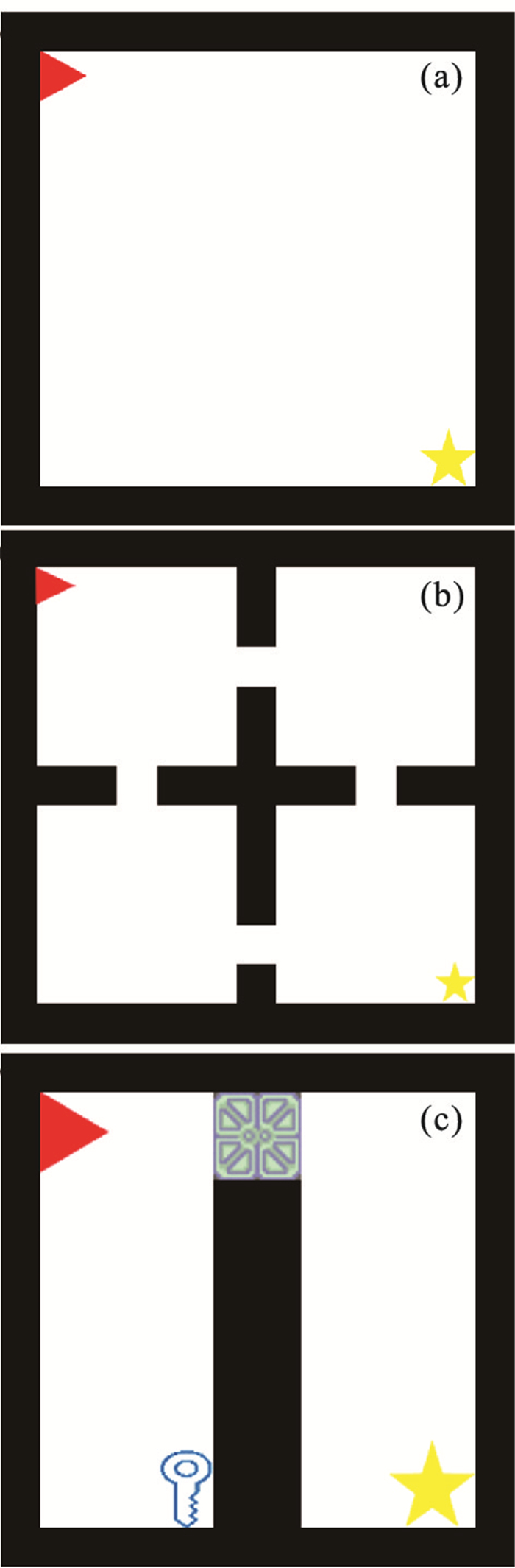 | 图 5 仿真实验环境Fig.5 Simulation experimental environment (a)—空环境;(b)—四室环境;(c)—钥匙-门环境. |
3.1 环境探索率对比实验分别在20×20空环境、15×15四室环境以及7×7钥匙-门环境中对比MES-HRL和SNN-HRL算法的环境探索率.由式(7), 式(8)可知, SNN-HRL算法是智能体为获得更多的内部奖励而导致环境探索率较低的算法, 故而影响其性能, 同时由于MES-HRL和SNN-HRL算法获得的外部奖励(见式(13))也是不同的(外部奖励不影响智能体的探索率), 所以本节实验只采用内部奖励来训练智能体获得skill.
实验结果如表 1所示, 其中的数据是当智能体完成skill的训练后统计的环境探索率.当环境越复杂时, SNN-HRL算法对环境的探索率就越低, 在空环境和四室环境环境下, SNN-HRL算法的探索率分别为95.68% 和76.19%, 此时SNN-HRL算法仍能完成路径规划任务(具体数据可见3.2节实验), 但在钥匙-门环境中的探索率仅为47.62%, 不及环境状态空间的一半, 最终没能完成路径规划任务.MES-HRL算法在3种环境下的探索率分别为99.59%,99.05% 和97.62%, 几乎完成了对整个环境的探索, 并完成了各个环境下的路径规划任务.
本节实验中, 通过对比不同环境下MES-HRL和SNN-HRL算法的环境探索率证明了MES-HRL算法解决了SNN-HRL算法存在的环境探索率低的问题.
3.2 路径规划性能对比实验分别在不同尺寸下的空环境、四室环境以及钥匙-门环境中对比SNN-HRL、MES-HRL和Dueling DDQN三种算法的性能.
3.2.1 空环境在10×10, 15×15, 20×20空环境中检验上述3种算法.结果如图 6所示.
图 6(Fig. 6)
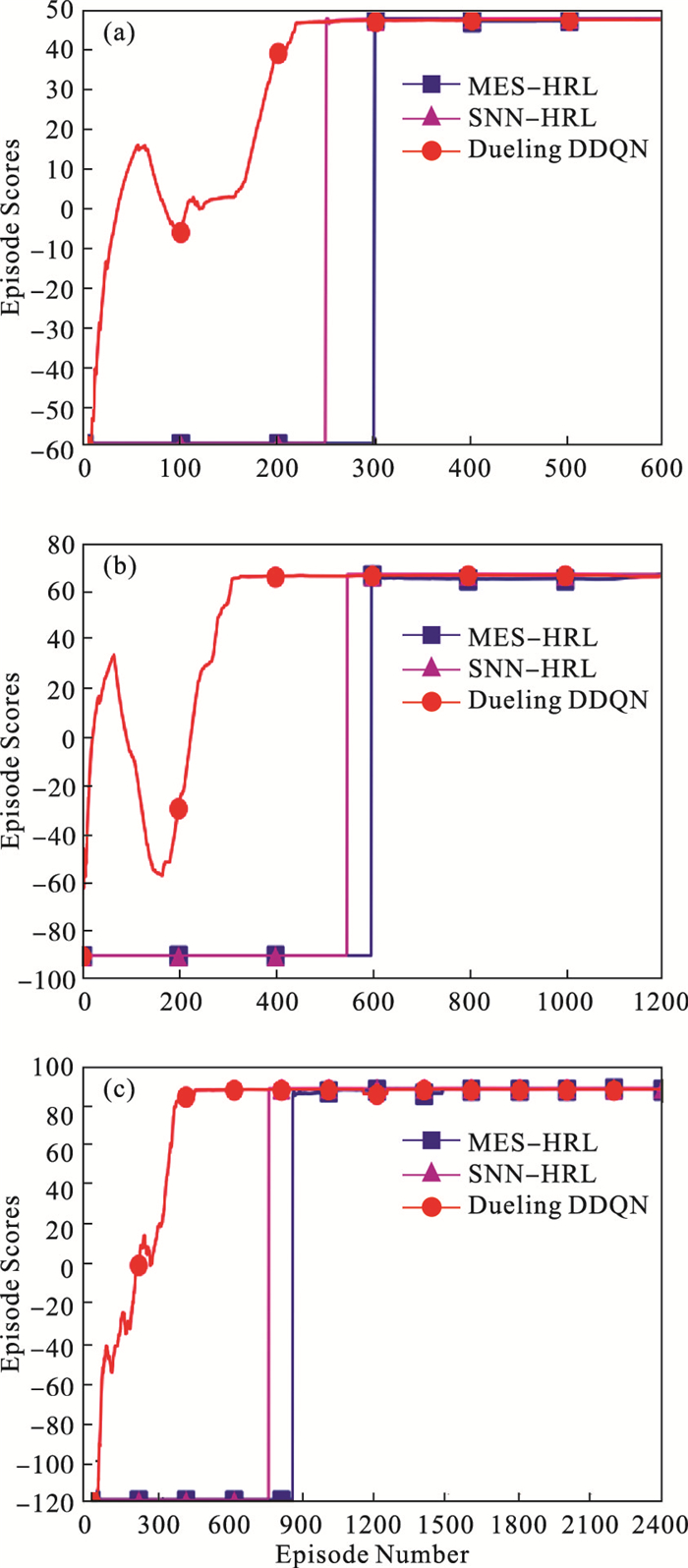 | 图 6 空环境结果图Fig.6 Result graphs of empty environment (a)—10×10;(b)—15×15;(c)—20×20. |
1) 10×10环境下的仿真结果如图 6a所示, 其中横坐标Episode Number为训练的回合数.纵坐标Episode Scores是每一episode累计获得的外部奖励.Dueling DDQN算法经过220次训练后收敛, SNN-HRL算法经过250次训练后收敛, MES-HRL算法经过300次训练收敛.
2) 15×15环境下的仿真结果如图 6b所示, 地图尺寸增大, 3种算法收敛所需的训练次数都有所增加, Dueling DDQN算法提高至350次, SNN-HRL算法提高至550次, MES-HRL算法提高至600次.
3) 20×20环境下的仿真结果如图 6c所示, 地图的尺寸进一步增大, Dueling DDQN算法的训练次数提高至450次, SNN-HRL算法提高至750次, MES-HRL算法提高至850次, 本节实验证明MES-HRL、SNN-HRL和Dueling DDQN都具备收敛性, 也表明在简单环境中, SNN-HRL、MES-HRL多层算法比Dueling DDQN需要更多次的训练.
3.2.2 四室环境在11×11, 13×13, 15×15四室环境中检验上述3种算法.结果如图 7所示.
1) 由于四室环境中加入了障碍物, 3种算法的训练次数明显多于同尺寸的空房间, 11×11环境下的仿真结果如图 7a所示, SNN-HRL算法在该环境下的路径规划的性能最好, 经过300次训练后收敛, MES-HRL算法和Dueling DDQN算法相同, 经过400次训练达到收敛.
2) 13×13环境下的仿真结果如图 7b所示, SNN-HRL算法训练次数提高至600次, MES-HRL算法提高至700次, Dueling DDQN算法提高至800次.
3) 15×15环境下的仿真结果如图 7c所示, SNN-HRL算法训练次数提高至800次, MES-HRL算法提高至1 000次, Dueling DDQN算法提高至1 300次.该结果与空环境的仿真结果不同, SNN-HRL算法与MES-HRL算法的性能都优于Dueling DDQN算法, 说明在处理四室房间这样存在一般障碍物的复杂环境时MES-HRL和SNN-HRL这类分层算法更具优势, 路径规划性能更好.同时结果中MES-HRL和SNN-HRL算法训练次数差别不大, 表明这两种算法在一般环境下具备相近的路径规划能力.
图 7(Fig. 7)
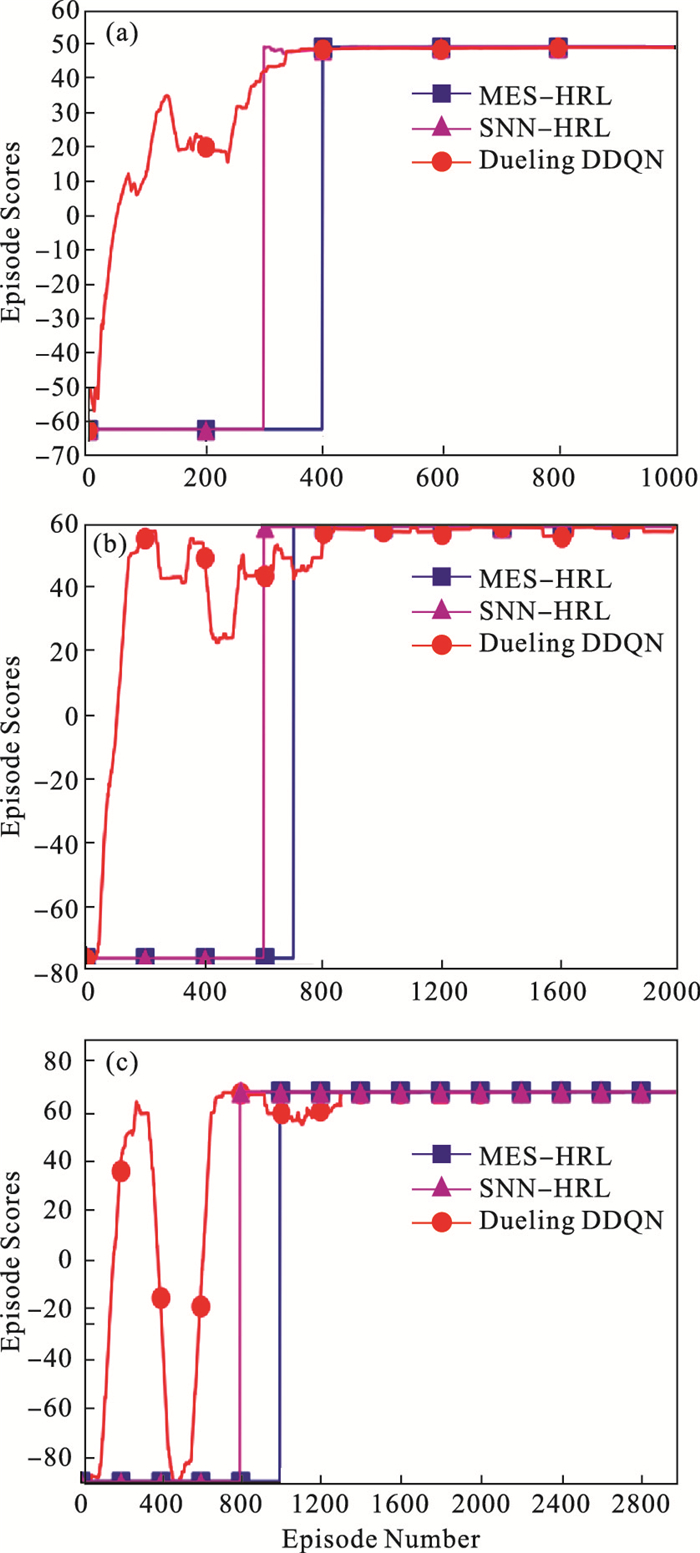 | 图 7 四室环境结果图Fig.7 Result graphs of four room environment (a)—11×11;(b)—13×13;(c)—15×15. |
3.2.3 钥匙-门环境在5×5, 6×6, 7×7钥匙-门环境中检验上述3种算法.结果如图 8所示.
图 8(Fig. 8)
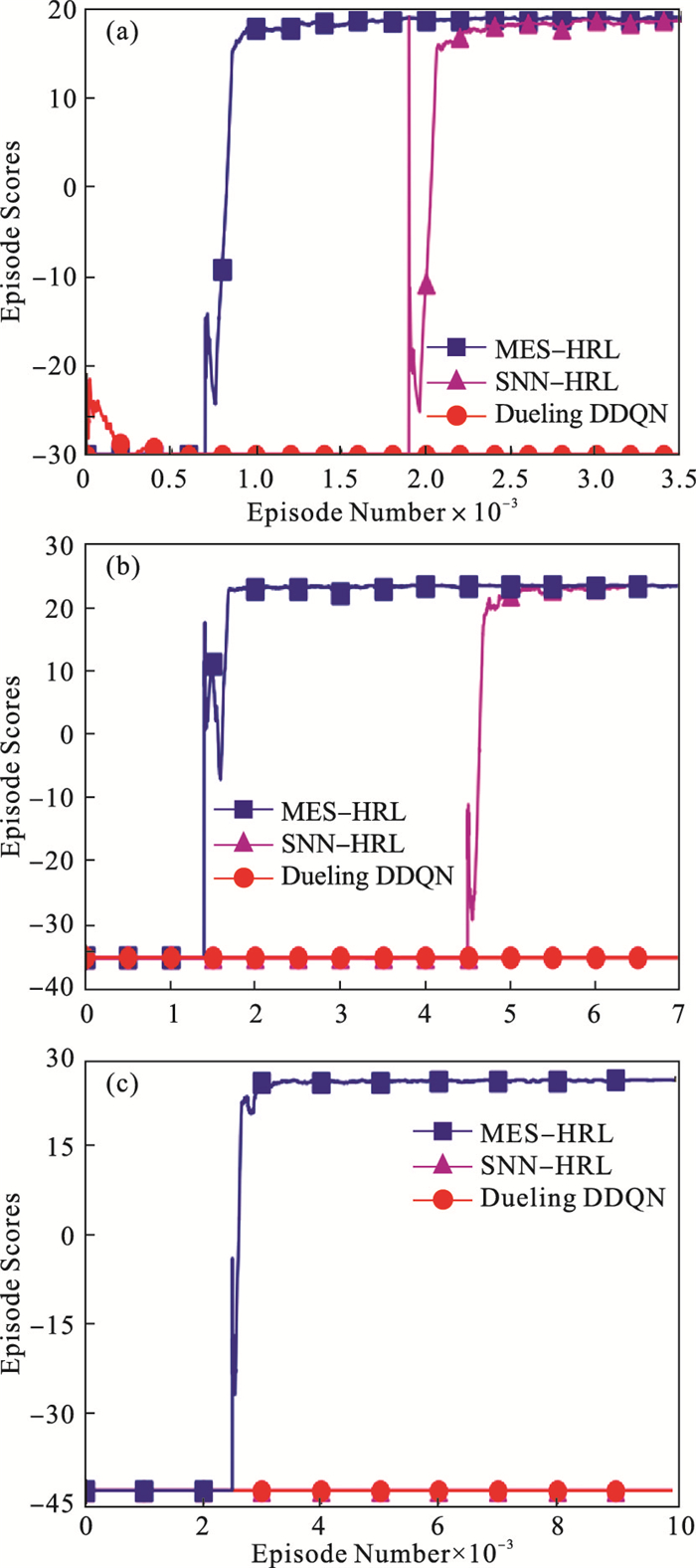 | 图 8 钥匙-门环境结果图Fig.8 Result graphs of key-door environment (a)—5×5;(b)—6×6;(c)—7×7. |
1) 5×5环境下, 3种算法有了明显差别, 如图 8a所示, MES-HRL算法经过1 500次训练后收敛, 但SNN-HRL算法经过2 600次训练后才收敛, Dueling DDQN算法在3 500次的训练过程中没有收敛.
2) 6×6环境下, SNN-HRL和MES-HRL算法的差距进一步增大, 如图 8b所示, MES-HRL算法经过2 000次训练后收敛, SNN-HRL算法经过5 500次训练后收敛.
3) 7×7环境下的仿真结果如图 8c所示, MES-HRL算法经过2 500次训练后收敛, 但SNN-HRL和Dueling DDQN算法在10 000次的训练过程中没有收敛.
本节实验表明, Dueling DDQN算法无法处理钥匙-门环境这样复杂的环境.SNN-HRL算法虽然完成了5×5和6×6尺寸下路径规划任务, 但训练次数远高于MES-HRL算法, 甚至无法完成7×7尺寸下的规划任务.由3.1节实验结果可知, 这是由于SNN-HRL算法对环境的探索率低导致智能体难以在钥匙-门环境这类复杂环境中探索到足够的状态空间来完成规划任务.而MES-HRL算法对该环境的探索率均超过97% (见表 1), 解决了探索问题, 相较于SNN-HRL算法有更好的路径规划能力, 能应对更为复杂的环境.
表 1(Table 1)
| 表 1 环境探索率 Table 1 Environmental exploration rate ? | ||||||||||||||||||||||||||||||||||||||||||||
4 结语本文提出的MES-HRL算法解决了传统Skill discovery算法存在的环境探索率低的问题, 相较于SNN-HRL算法有更好的路径规划能力, 能处理更为复杂的环境.
在仿真过程中, 主要围绕环境探索率与训练效率进行算法性能对比分析, 没有对具体的规划路径进行研究是由于当不同算法收敛时的累计外部奖励相同时, 给出的规划路径是等效的.此外, MES-HRL算法采用了基于记忆的探索方法, 这导致智能体只能在静态环境中训练, 当环境发生变化时, 智能体就需要重新进行训练.进一步的研究将针对欠缺动态环境处理能力的问题, 改进MES-HRL算法, 使其能在动态环境下进行训练.
参考文献
| [1] | 赖俊, 魏竞毅, 陈希亮. 分层强化学习综述[J]. 计算机工程与应用, 2021, 57(3): 72-79. (Lai Jun, Wei Jing-yi, Chen Xi-liang. Overview of hierarchical reinforcement learning[J]. Computer Engineering and Applications, 2021, 57(3): 72-79.) |
| [2] | Mnih V, Kavukcuoglu K, Silver D, et al. Playing atari with deep reinforcement learning[C]//Proceedings of the Workshops at the 26th Neural Information Processing Systems. Lake Tahoe: NIPS, 2013: 201-220. |
| [3] | Chen T, Shahar G, Tom Z, et al. A deep hierarchical approach to lifelong learning in minecraft[C]//Thirty-First AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2017: 1553-1561. |
| [4] | Nachum O, Gu S X, Lee H, et al. Data-efficient hierarchical reinforcement learning[J]. Advances in Neural Information Processing Systems, 2018, 31: 3307-3317. |
| [5] | Vezhnevets A S, Osindero S, Schaul T, et al. Feudal networks for hierarchical reinforcement learning[C]//Proceedings of Machine Learning Research. San Diego: PMLR, 2017: 3540-3549. |
| [6] | Harb J, Bacon P L, Klissarov M, et al. When waiting is not an option: learning options with a deliberation cost[C]//Thirty-Second AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2018: 3165-3172. |
| [7] | Konidaris G, Barto A. Skill discovery in continuous reinforcement learning domains using skill chaining[J]. Advances in Neural Information Processing Systems, 2009, 22: 1015-1023. |
| [8] | Baumli K, Warde-Farley D, Hansen S, et al. Relative variational intrinsic control[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Vancouver: AAAI, 2021: 6732-6740. |
| [9] | Florensa C, Duan Y, Abbeel P. Stochastic neural networks for hierarchical reinforcement learning[C]//Proceedings of the 5th International Conference on Learning Representations. Toulon: ICLR, 2017: 1422-1439. |
| [10] | Finn C, Abbeel P, Levine S. Model-agnostic meta-learning for fast adaptation of deep networks[C]// Proceedings of Machine Learning Research. Sydney: PMLR, 2017: 1126-1135. |
| [11] | Campos V, Trott A, Xiong C M, et al. Explore, discover and learn: unsupervised discovery of state-covering skills[C]//Proceedings of Machine Learning Research. San Diego: PMLR, 2020: 1317-1327. |
| [12] | Pathak D, Agrawal P, Efros A A, et al. Curiosity-driven exploration by self-supervised prediction[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. New York: IEEE, 2017: 488-489. |
| [13] | Bhatti A, Singh S, Garg A, et al. Modeling affect-based intrinsic rewards for exploration and learning[J]. IEEE Transactions on Cognitive and Developmental Systems, 2021, 13: 590-602. |
| [14] | Bellemare M, Srinivasan S, Ostrovski G, et al. Unifying count-based exploration and intrinsic motivation[J]. Advances in Neural Information Processing Systems, 2016, 29: 1471-1479. |
| [15] | Tang H, Houthooft R, Foote D, et al. Exploration: a study of count-based exploration for deep reinforcement learning[J]. Advances in Neural Information Processing Systems, 2017, 30: 2753-2762. |
| [16] | Mohamed S, Jimenez R D. Variational information maximisation for intrinsically motivated reinforcement learning[J]. Advances in Neural Information Processing Systems, 2015, 28: 2125-2133. |
| [17] | Gallouédec Q, Dellandréa E. Cell-free latent go-explore[C]//Proceedings of the Workshops at the 35th Neural Information Processing Systems. Virtual: NIPS, 2021: 475-487. |
| [18] | Schaul T, Quan J, Antonoglou I, et al. Prioritized experience replay[C]//Proceedings of the 4th International Conference on Learning Representations. San Juan: ICLR, 2016: 322-355. |
