

南京理工大学 自动化学院, 江苏 南京 210094
收稿日期:2022-06-29
基金项目:国家自然科学基金资助项目(62303224);江苏省研究生科研与实践创新计划项目(KYCX19_0303)。
作者简介:曹阳(1993-),男,江西赣州人,南京理工大学博士研究生;
郭健(1974-),男,江苏南通人,南京理工大学教授,博士生导师。
摘要:针对永磁同步直线电机系统中存在的模型不确定性、状态约束以及输入非线性(如非线性电磁驱动力/输入受限)问题,提出了一种基于神经网络的自适应控制器.具体来说,为了降低噪声敏感性,进一步提高跟踪精度,采用仅依赖于参考轨迹的期望信号来替代测量信号.然后,设计神经网络在线逼近未知模型和非线性函数,并通过构造连续控制的方法来处理逼近误差.此外,构造障碍李雅普诺夫函数确保系统在运行过程中状态始终满足约束条件;并且通过严格的理论分析证明了跟踪性能满足要求.最后,通过仿真实验验证了所提控制器的有效性和鲁棒性.
关键词:永磁同步直线电机模型不确定性状态约束输入非线性神经网络
Adaptive Neural Network Control for Permanent Magnet Synchronous Linear Motor with State Constraints and Input Nonlinearities
CAO Yang, GUO Jian


School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China
Corresponding author: GUO Jian, E-mail: guoj1002@njust.educn.
Abstract: An adaptive controller based on neural network is proposed for the problems of model uncertainty, state constraints and input nonlinearities(such as nonlinear electromagnetic drive force/input limitation)in permanent magnet synchronous linear motor(PMSLM). Specifically, in order to reduce the noise sensitivity and further improve the tracking accuracy, the desired signal that only depends on the reference trajectory is used to replace the measurement signal. Then, the neural network is designed to approach the unknown model and the nonlinear function online, and the approximation error is processed by constructing continuous control. In addition, an obstacle Lyapunov function is constructed to ensure that the state of the system always satisfies the constraints during the operation process; through strict theoretical analysis, it is proved that the tracking performance meets the requirements. Finally, simulation experiments verify the effectiveness and robustness of the proposed controller.
Key words: permanent magnet synchronous linear motor(PMSLM)model uncertaintystate constraintsinput nonlinearitiesneural networks
永磁同步直线电机(permanent magnet synchronous linear motor,PMSLM)相比于旋转同步电机,具有更高的推力密度和更快的动态响应,特别适用于对速度和精度要求较高的场合,广泛应用在高精密加工、轨道交通传输等现代工业领域[1-3].然而,PMSLM系统固有的不确定性对其高性能控制提出了挑战[4-6].此外,由于不可避免的硬件限制,例如,测量噪声影响可能很严重,状态受限、输入非线性(包括输入受限和非线性电磁驱动力)等,使得系统的跟踪性能严重下降,控制困难增大.
近年来,上述问题已经得到了不少关注,人们提出了一系列自适应控制策略.文献[7]将PMSLM非线性耦合系统解耦为独立的电流子系统和线速度子系统,以降低控制器的设计难度.文献[8]提出了一种基于符号误差的鲁棒积分(robust integral of the sign of the error, RISE)反馈自适应补偿方法,以适应足够光滑的有界扰动.文献[9]将摩擦力、定位力和负载突变作为电机的总扰动来估计,并将其估计值引入到反步控制律中进行补偿, 以达到消除不确定性干扰对跟踪精度的影响.文献[10]为了解决参数不确定性和测量噪声的影响,利用期望轨迹信号来估计系统未知参数.文献[11]设计了一种基于非线性高增益观测器的自适应非线性鲁棒跟踪方法, 采用高增益观测器和滤波器来削弱噪声,并且通过障碍李雅普诺夫函数来限制系统状态,使得整个动态过程的跟踪误差保持在有界的范围内.此外,对于电机系统中的输入非线性问题,文献[12]在自适应控制器中增加一个静态抗饱和控制项,能够有效保证系统的稳定.文献[13]提出了一种直流伺服电机的故障估计和容错控制方法,利用H∞框架设计鲁棒观测器,可以同时估计故障和解耦的未知输入,以应对故障的影响.为了处理参数非线性部分问题,文献[14]将非线性部分视为有界常数,然后设计自适应律对其进行估计和补偿.文献[15]提出了基于复合自适应律的自适应鲁棒控制,同时采用了输出误差与参数估计误差的相关信息构造自适应律, 获得了更好的参数估计效果.文献[16]假设摩擦力和定位力为周期性扰动,设计自适应滑模控制器改善控制性能.文献[17]将输入非线性(电磁驱动力)用三阶多项式函数来近似,开发了特定的自适应鲁棒算法,即使存在参数不确定性和未知干扰的情况,该算法也能保证系统的瞬态和稳态跟踪性能.值得注意的是,上述自适应控制的良好运行依赖于对参数的线性化要求和对未知非线性函数的精确了解.但是,很多被控对象的数学模型及环境情况难以精确描述,且不一定都能满足线性参数化要求,这就限制了现有自适应控制方法的适用范围.对于这种情况,可以利用智能算法来解决自适应控制所遇到的非线性参数不确定性甚至是函数不确定性的困难,比如神经网络和模糊逻辑系统.文献[18]设计了一种自适应神经网络控制方法来解决非线性系统中未知函数和外部干扰带来的问题,并能保证闭环系统的一致最终有界性.文献[19]设计了基于反步法的自适应神经网络控制器,克服了分数阶永磁同步电机存在的输入饱和、负载干扰和参数不确定性等问题.文献[20]基于反步法设计了自适应模糊控制器,有效地抑制了伺服系统中机械谐振的影响.文献[21]利用系统边界函数和Nussbaum函数的单调递增性质,克服了非严格反馈结构和死区输出带来的设计困难.通过设计自适应模糊控制器,保证了闭环系统所有信号的有界性和系统规定的跟踪性能.
然而,在现有的大多数基于智能算法的控制器中,由于一些近似误差相关的交叉项,很难保证系统平衡点的渐近稳定.针对这个问题,文献[22]设计了一种时变增益更新律,能在不引入符号函数情况下有效处理模糊系统中的逼近误差,从而实现精确跟踪控制,为高性能伺服系统控制设计提供了很好的借鉴.
本文针对非线性PMSLM系统,提出了一种基于神经网络的自适应控制器.该控制器可以同时处理系统的模型不确定性、状态约束和输入受限/非线性电磁驱动力等问题,设计的连续控制输入使得PMSLM系统具有较好的跟踪性能,能保证系统在运行过程中状态始终满足约束条件.此外,通过仿真实验验证了所提控制器的有效性和鲁棒性.
1 问题描述本文考虑一类具有控制输入受限和非线性电磁驱动力的PMSLM系统:
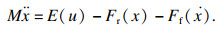 | (1) |
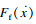
采用文献[16]中给出的定位力模型
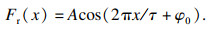 | (2) |
连续静摩擦模型表示如下[23]:
 | (3) |

非线性电磁驱动力在PMSLM系统中很常见,电机的电流-力曲线会在一定程度上表现出非线性特性[17].本文将这部分非线性考虑成执行器故障,使用以下非线性增益和偏置故障来描述.
 | (4) |
此外,出于安全考虑,一般需要对系统控制输入进行一定的限制.具体来说,实际执行器只能提供有限的控制力矩,很容易产生控制输入受限问题.为此,本文考虑输入受限问题.取最大控制输入值为umax,umax>0,δ=Es(u)-u,受限后的控制输入表示为
 | (5) |
根据上述分析,实际控制量可表示为
 | (6) |
为方便控制器设计,将式(1)中的模型改写成
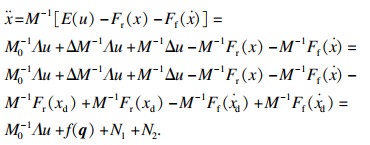 | (7) |
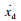
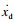


2 基于神经网络的自适应控制器设计2.1 径向基函数神经网络为了处理PMSLM系统中的未知非线性,本文利用径向基函数(radial basis function, RBP)神经网络能以任意精度逼近任何函数的特性,对PMSLM系统中的非线性函数进行自适应逼近.
RBF神经网络的输出表示为
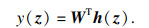 | (8) |
将高斯基函数作为神经网络隐藏层的径向基函数,式(9)是高斯基函数的一个基本表达式:
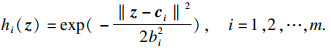 | (9) |
引理1[24]??若m选择得足够大,则连续实值函数f(z)能够被式(8)以任意精度逼近,表示为
 | (10) |
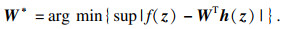 | (11) |
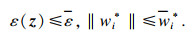 | (12) |
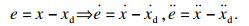 | (13) |
 | (14) |
根据式(7)和式(13)可以得到
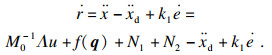 | (15) |
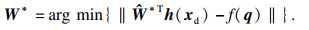 | (16) |

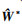
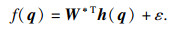 | (17) |
 | (18) |

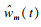
 | (19) |
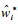

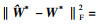
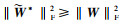
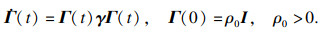 | (20) |

根据以上分析,控制器设计为
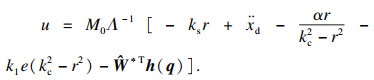 | (21) |
相关控制参数的选择基于以下约束条件:
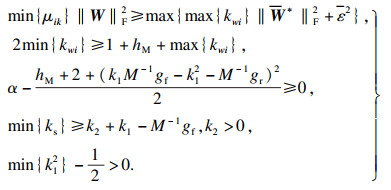 | (22) |

3 稳定性分析定理1??只要满足式(22)的增益约束和初始条件
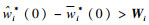
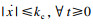
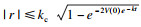
证明??根据式(13), 式(15)和式(16)可得
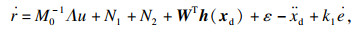 | (23) |
 | (24) |
 | (25) |

构建障碍Lyapunov函数为
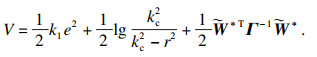 | (26) |
 | (27) |
 | (28) |
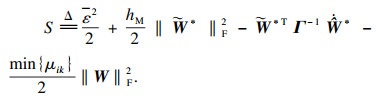 | (29) |
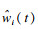
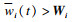
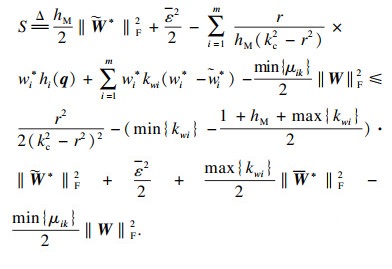 | (30) |
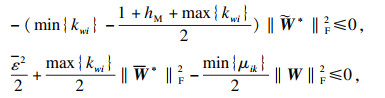 |
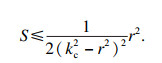 | (31) |

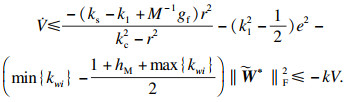 | (32) |
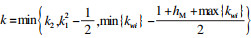
在式(32)两端同时乘以ekt并在[0, t]上求积分,则
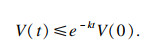 | (33) |
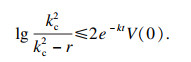 | (34) |
 | (35) |
证毕.
4 仿真验证为验证所提控制算法的可行性和有效性,对PMSLM控制系统进行仿真验证.表 1给出了PMSLM系统的基本参数.图 1给出了PMSLM控制系统总体结构框图,另外,摩擦模型的参数a1=0.09,a2=0.01,a3=0.12,c1=700,c2=15,c3=1.5;定位力模型参数A=4, φ0=0.8,umax=5,速度约束设为[-2.2, 2.2] m/s.
表 1(Table 1)
| 表 1 PMSLM基本参数 Table 1 Basic parameters of PMSLM |
图 1(Fig. 1)
 | 图 1 控制系统总体结构框图Fig.1 Overall structure diagram of control system |
为了验证所提控制器的可行性和有效性,本文对以下2种控制器进行了比较.
ANNC(adaptive neural network controller): 这是本文设计的自适应神经网络控制器,控制器参数设置如下:神经网络输入

DCARC(desired compensation adaptive robust controller): 这是基于期望补偿的自适应鲁棒控制器[10],控制参数如下:ks=2,k1=10,β=0.05.
首先将PMSLM跟踪期望轨迹设置为xd=2sin(πt/3),ANNC和DCARC两个控制器的效果如图 2所示.通过比较DCARC和ANNC的控制结果,可以看出ANNC的跟踪误差更小,控制性能更好.同时,ANNC所构造的状态受限控制律能保证速度在受限范围内,并且削弱了输入饱和现象.
图 2(Fig. 2)
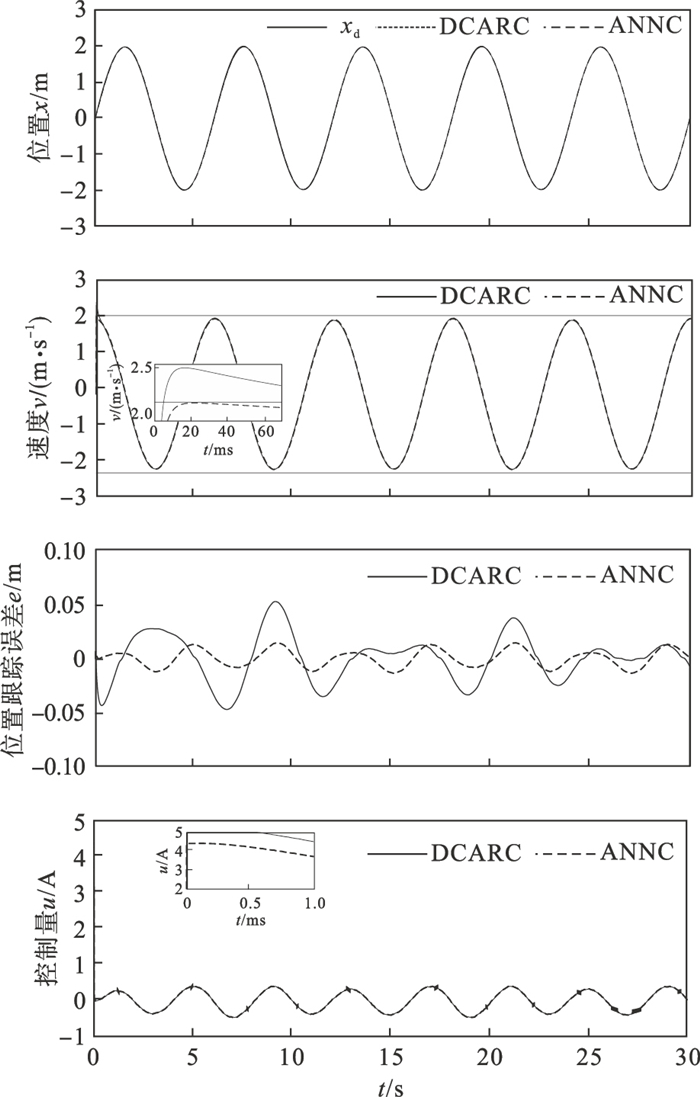 | 图 2 2个控制器的跟踪效果图Fig.2 Tracking results of two controllers |
然后,进一步测试所提的控制算法对执行机构故障的鲁棒性.
1) 整个控制过程中存在执行器故障.本组中执行器增益故障设置为κ(t)=0.7+0.3cos(t),该故障出现在初始时间,并持续作用于PMSLM.从图 3可以看出,即使系统出现执行器增益故障,所提出的ANNC仍然能够实现有效的跟踪控制,并具有良好的鲁棒性.相比之下,由于执行器增益故障,DCARC的跟踪精度不可避免地降低,最大误差达到了0.082 m,大约是ANNC最大误差的2倍.
图 3(Fig. 3)
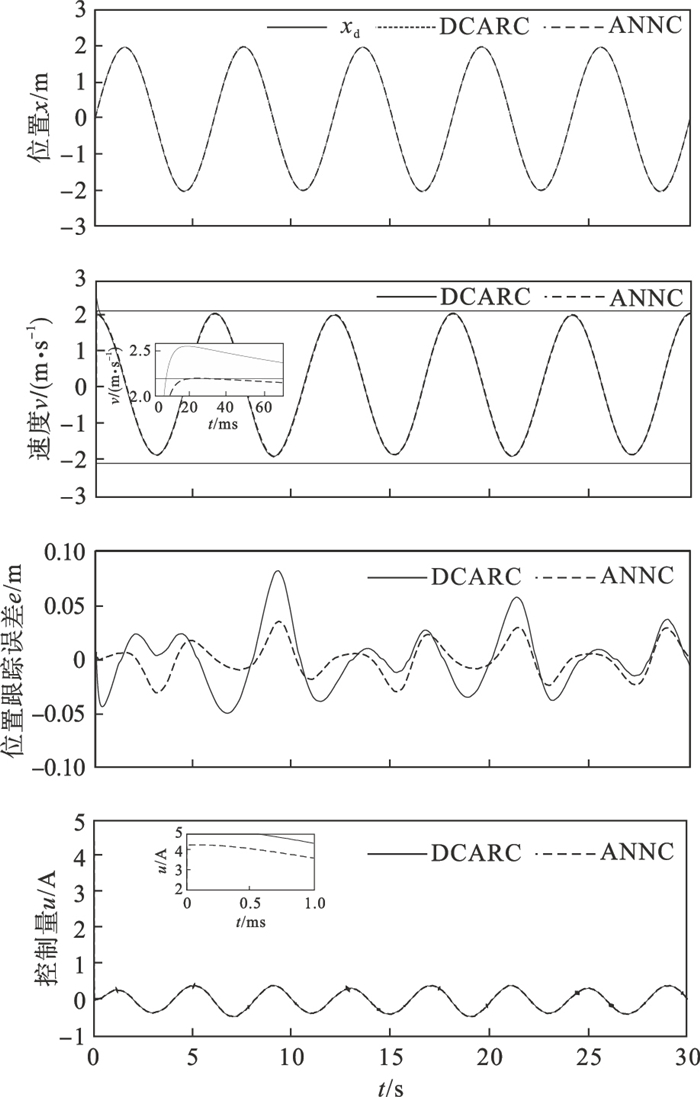 | 图 3 2个控制器在出现故障情况下的跟踪效果Fig.3 Tracking results of two controllers at faults |
2) 故障出现在具体时刻.本文在9 s时同时加入执行器增益和偏置故障,设为κ(t)=0.7+0.3cos(t)和ζ(t)=0.85sin(3t).从图 4可以看出,2个控制器的跟踪误差有所增大,但ANNC的控制效果仍然会更好.此外,ANNC通过设计增益随时间变化的更新规律,没有引入不连续的鲁棒项来处理逼近误差,可以获得连续的控制输入,避免出现抖振.
图 4(Fig. 4)
 | 图 4 故障出现在具体时刻下的控制结果Fig.4 Control results when faults occur at certain time |
最后,为了测试控制系统对外部扰动的鲁棒性能,本文分别在1,13,17 s时添加外部扰动.从图 5可以看出,由于利用较大的反馈增益来加快系统的瞬态响应速度和降低最终跟踪误差,DCARC仍然会出现饱和现象,速度也会超过限幅.此外,虽然PMSLM受到未知干扰,但所提出的ANNC仍能使位置快速回到特定轨迹,并在整个过程中保持满意的跟踪性能.
图 5(Fig. 5)
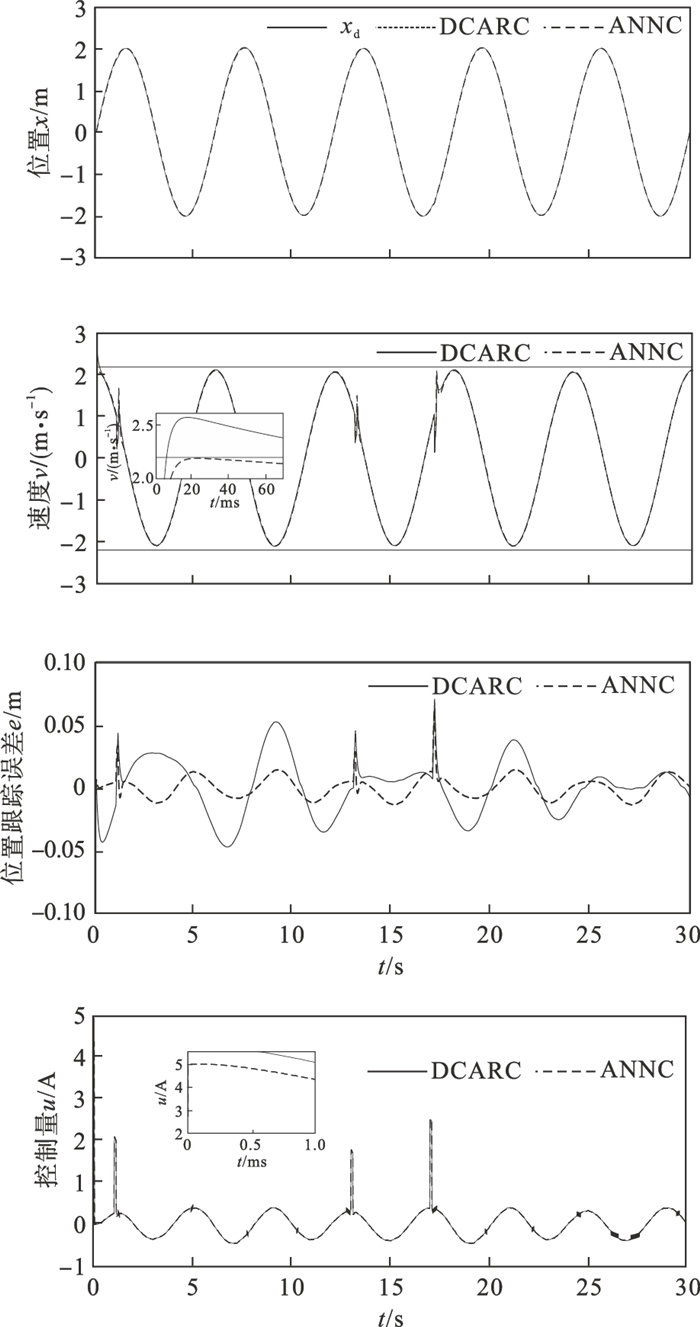 | 图 5 存在外部扰动时的控制结果Fig.5 Control results under external disturbance |
5 结语本文设计了一种自适应神经网络控制器,该控制器可以对系统动力学中的未知参数/结构进行在线逼近.在不引入符号函数情况下对逼近误差进行了适当的处理,可以获得连续的控制输入,避免了抖振的出现.同时,利用期望信号替代反馈信号来估计系统中的未知非线性函数,能够减小测量信号噪声对系统的不利影响.通过PMSLM控制系统的仿真实验,证明了所提控制器的有效性和鲁棒性.在未来的工作中,将考虑如状态时滞、输入死区等问题,然后尝试将所提出的方法扩展到两轴直线电机驱动系统.
参考文献
| [1] | Shao K, Zheng J C, Huang K, et al. Finite-time control of a linear motor positioner using adaptive recursive terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2020, 67(8): 6659-6668. DOI:10.1109/TIE.2019.2937062 |
| [2] | Du H B, Chen X P, Wen G H, et al. Discrete-time fast terminal sliding mode control for permanent magnet linear motor[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9916-9927. DOI:10.1109/TIE.2018.2815942 |
| [3] | Wang L J, Zhao J W, Yang X, et al. Robust deadbeat predictive current regulation for permanent magnet synchronous linear motor drivers with parallel parameter disturbance and load observer[J]. IEEE Transactions on Power Electronics, 2022, 37(7): 7834-7845. DOI:10.1109/TPEL.2022.3148389 |
| [4] | Sun X D, Wu M K, Yin C F, et al. Model predictive thrust force control for linear motor actuator used in active suspension[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 3063-3072. DOI:10.1109/TEC.2021.3069843 |
| [5] | Chen S Y, Chiang H H, Liu T S, et al. Precision motion control of permanent magnet linear synchronous motors using adaptive fuzzy fractional-order sliding-mode control[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(2): 741-752. DOI:10.1109/TMECH.2019.2892401 |
| [6] | Wang W, Lu Z X, Hua W, et al. Dual-level located feedforward control for five-leg two-mover permanent-magnet linear motor traction systems[J]. IEEE Transactions on Power Electronics, 2020, 35(12): 13673-13686. DOI:10.1109/TPEL.2020.2995241 |
| [7] | 张康, 王丽梅. 基于反馈线性化的永磁直线同步电机自适应动态滑模控制[J]. 电工技术学报, 2021, 36(19): 4016-4024. (Zhang Kang, Wang Li-mei. Adaptive dynamic sliding mode control of permanent magnet linear synchronous motor based on feedback linearization[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4016-4024.) |
| [8] | Yao J Y, Deng W X, Jiao Z X. RISE-based adaptive control of hydraulic systems with asymptotic tracking[J]. IEEE Transactions on Automation Science and Engineering, 2017, 14(3): 1524-1531. DOI:10.1109/TASE.2015.2434393 |
| [9] | 曹伟, 乔金杰, 孙明. 永磁直线电机扰动估计与补偿的位置反步控制[J]. 控制与决策, 2020, 35(6): 1409-1414. (Cao Wei, Qiao Jin-jie, Sun Ming. Backstepping control of disturbance estimation and compensation for permanent magnet linear motor[J]. Control and Decision, 2020, 35(6): 4016-4024.) |
| [10] | Hong Y, Yao B. A globally stable saturated desired compensation adaptive robust control for linear motor systems with comparative experiments[J]. Automatica, 2007, 43(10): 1840-1848. DOI:10.1016/j.automatica.2007.03.021 |
| [11] | 吴跃飞, 胡智琦, 马大为, 等. 具有状态约束的机电伺服系统自适应鲁棒控制[J]. 上海交通大学学报, 2014, 48(5): 707-712, 718. (Wu Yue-fei, Hu Zhi-qi, Ma Da-wei, et al. Adaptive robust control for mechatronic servo system with state constraints[J]. Journal of Shanghai Jiaotong University, 2014, 48(5): 707-712, 718.) |
| [12] | 严路, 何汉林, 江梅, 等. 基于自适应滑模抗饱和控制及其应用[J]. 华中科技大学学报(自然科学版), 2014, 42(7): 72-75. (Yan Lu, He Han-lin, Jiang Mei, et al. Anti-windup control and applications based on adaptive sliding-mode[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(7): 72-75.) |
| [13] | Fazal Q, Liaquat M, Naz N. Robust fault tolerant control of a DC motor in the presence of actuator faults[C]// The 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering(STA). Monastir: IEEE, 2015: 301-333. |
| [14] | Lu L, Yao B, Wang Q F, et al. Adaptive robust control of linear motors with dynamic friction compensation using modified LuGre model[J]. Automatica, 2009, 45(12): 2890-2896. DOI:10.1016/j.automatica.2009.09.007 |
| [15] | 张国柱, 陈杰, 李志平. 基于复合自适应律的直线电机自适应鲁棒控制[J]. 控制理论与应用, 2009, 26(8): 833-837. (Zhang Guo-zhu, Chen Jie, Li Zhi-ping. An adaptive robust control for linear motors based on composite adaptation[J]. Control Theory & Applications, 2009, 26(8): 833-837.) |
| [16] | 张康, 王丽梅. 基于周期性扰动学习的永磁直线电机自适应滑模位置控制[J]. 电机与控制学报, 2021, 25(8): 132-141. (Zhang Kang, Wang Li-mei. Adaptive sliding mode position control for permanent magnet linear motor based on periodic disturbance learning[J]. Electric Machines and Control, 2021, 25(8): 132-141.) |
| [17] | Chen Z, Yao B, Wang Q F. Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 1122-1129. |
| [18] | Yang H J, Liu J K. An adaptive RBF neural network control method for a class of nonlinear systems[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(2): 457-462. |
| [19] | Lu S, Wang X, Li Y. Adaptive neural network finite-time command filtered tracking control of fractional-order permanent magnet synchronous motor with input saturation[J]. Journal of the Franklin Institute, 2020, 357(18): 13707-13733. |
| [20] | 杜仁慧, 陶春荣, 张伟, 等. 伺服系统机械谐振抑制的自适应模糊控制方法[J]. 电机与控制学报, 2017, 21(10): 116-122. (Du Ren-hui, Tao Chun-rong, Zhang Wei, et al. Adaptive fuzzy control method for mechanical resonance suppression of servo systems[J]. Electric Machines and Control, 2017, 21(10): 116-122.) |
| [21] | Su H, Zhao X Y, Zhang W H. Prescribed performance adaptive fuzzy control for nonstrict‐feedback nonlinear systems with dead zone outputs[J]. International Journal of Adaptive Control and Signal Processing, 2021, 35(4): 567-590. |
| [22] | Yang T, Sun N, Fang Y. Adaptive fuzzy control for uncertain mechatronic systems with state estimation and input nonlinearities[J]. IEEE Transactions on Industrial Informatics, 2021, 18(3): 1770-1780. |
| [23] | Yao J Y, Jiao Z X, Ma D W. Output feedback robust control of direct current motors with nonlinear friction compensation and disturbance rejection[J]. Journal of Dynamic Systems, Measurement, and Control, 2015, 137(4): 041004. |
| [24] | Park J, Sandberg I W. Universal approximation using radial-basis-function networks[J]. Neural Computation, 1991, 3(2): 246-257. |
