成怡^1,2, 银培文¹
1. 天津工业大学 控制科学与工程学院，天津 300387;
2. 天津工业大学 天津市电气装备智能控制重点实验室, 天津 300387
收稿日期：2020-06-22
基金项目：国家自然科学基金资助项目(61973234)。
作者简介：成怡(1979-)，女，天津人，天津工业大学副教授。

摘要：零记忆非线性变换(ZMNL)方法和球不变随机过程(SIRP)是模拟复合高斯型杂波的主要方法.针对基于传统ZMNL与SIRP方法中的K与Pareto分布雷达杂波仿真中存在的形状参数只能为整数或半整数的问题，通过增加支路利用Gamma函数第二参数的可加性，提出将Gamma函数的概率密度函数(PDF)转化为二阶非线性常微分方程，并求解产生任意参数下的Gamma分布随机数，从而将复合高斯型分布杂波的形状参数扩展到一般实数.仿真实验表明：提出的方法不仅适用于非整数或非半整数形状参数值的杂波仿真，而且进一步提高了拟合度.
关键词：杂波模拟Gamma分布复合高斯分布零记忆非线性变换球不变随机过程
Improved Compound Gaussian Clutter Simulation Method
CHENG Yi^1,2, YIN Pei-wen¹
1. School of Control Science and Engineering, Tiangong University, Tianjin 300387, China;
2. Tianjin Key Laboratory of Intelligent Control of Electrical Equipment, Tiangong University, Tianjin 300387, China
Corresponding author: YIN Pei-wen, E-mail: yin754053@163.com.

Abstract: Zero memory nonlinearity(ZMNL)and spherically invariant random process(SIRP)are two mainly used methods in compound Gaussian clutter simulations. Aiming at the problem that the shape parameters in the K and Pareto distributed radar clutter simulation based on the traditional ZMNL and SIRP methods can only be integer or semi-integer, by adding branches and using the additivity of the second parameter of Gamma function, it is proposed to transform the probability density function(PDF)of the Gamma function into second-order nonlinear ordinary differential equation. Furthermore, it is solved to generate Gamma distributed random numbers under arbitrary parameters, and the shape parameters of compound Gaussian distribution clutter is extended to general real numbers. The simulation experiments show that the proposed method is not only suitable for clutter simulation with non-integer or non-semi-integer shape parameter values, but also further improves the fitting degree.
Key words: clutter simulationGamma distributioncompound Gaussian distributedzero memory nonlinearity(ZMNL)spherically invariant random process(SIRP)
雷达杂波是制约雷达目标检测和跟踪性能的主要因素之一.杂波的研究对于雷达探测和系统设计具有重要意义^[1].随着雷达研究的不断深入，以及现代战场复杂密集的电磁环境信号，使得雷达环境杂波问题日益突出^[2].因此，对杂波的模拟和特性的研究变得非常重要.目前常用的杂波统计模型有瑞利分布、对数正态分布、韦布尔分布、复合高斯分布等^[3-5].其中复合高斯分布，如K分布和Pareto分布可以较好地对高分辨雷达在低掠角情况下接收的地、海杂波进行描述，它不仅可以满足待观察环境的杂波幅值特性，还包括了脉间的相关特性，已成为杂波仿真中的一种重要统计模型.
目前，国内外诸多****对复合高斯型杂波模拟方法进行了大量的研究.文献[6]利用零记忆非线性变换(zero memory nonlinearity，ZMNL)方法产生相关K分布杂波，原理简单，但存在形状参数只能为整数或者半整数的缺陷，且当形状参数为非(半)整数时只能作近似处理，并且不能独立控制功率谱和幅度分布.文献[7]提出了基于球不变随机过程(spherically invariant random process，SIRP)的相干相关K分布杂波模拟方法.但受序列阶数和自相关函数的约束，计算量大，难以形成快速算法.文献[8-9]提出了一种新的相干相关K分布杂波建模方法，与传统SIRP与ZMNL方法相比，该方法可以使生成的杂波具有任意指定的功率谱，而且运算相对简单，但同样在形状参数为非(半)整数的情况下也作了近似计算处理.文献[10-11]利用Gamma分布的第二参数可加性，将形状参数拆分为整数部分与小数部分之和的形式，解决了形状参数需要近似处理的问题，但在小数部分中的Gamma分布随机数使用的是Beta分布与指数分布之积近似产生.虽然解决了形状参数的近似问题，但由于Beta分布在参数较小时会出现偏差，将导致最终的杂波仿真曲线与理论概率密度函数之间仍存在一定误差.
为了进一步提高复合高斯型分布杂波模拟效果，本文在现有方法基础上进一步提出一种复合高斯型分布杂波的生成方法，改进了形状参数中小数部分的计算方式.将Gamma函数的概率密度函数转化为二阶非线性常微分方程，通过求解产生任意参数下的Gamma分布随机数，不仅将复合高斯型分布杂波的形状参数扩展到一般实数，而且与理想分布曲线的拟合效果更好.
1 复合高斯型杂波模拟数学模型及方法1.1 复合高斯型杂波模拟数学模型复合高斯型杂波的概率密度函数(probability density function, PDF)可看作是纹理分量调制散斑分量的结果^[12].纹理分量是一种具有长时间相关性的缓慢变化分量，反映了海面大面积结构空间变化中后向散射的平均水平.散斑分量是一种服从瑞利分布的快速变化分量^[13-14].对于K分布杂波，其纹理分量是Gamma分布，而对于广义Pareto分布的纹理分量是逆Gamma分布，其形式如下：

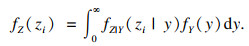(1)

其中，f_Z|Y(z_i|y)是散斑分量的PDF，服从指数分布，其表达式如下：

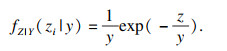(2)

纹理分量f_Y(y)的PDF视具体分布模型而定.若为K分布模型，则纹理分量服从Gamma分布^[15]，其PDF为

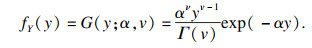(3)

式中：Γ(v)是Gamma函数；v为形状参数；α为尺度参数；G(·)是Gamma分布.
若为广义Pareto分布模型，则纹理分量f_Y(y) 服从双参数的逆Gamma分布(IG)^[16]，即1/f_Y(y) 服从Gamma分布：

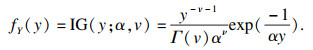(4)

因此，仿真Gamma分布是产生K分布和Pareto分布中的关键一环.
1.2 功率谱模型杂波的功率谱特性是描述雷达杂波的另一个重要参量，杂波的功率谱分布与滤波器的设计直接相关.仿真中大多采用的是高斯功率谱模型，表达式如下^[17]：

(5)

式中：S₀是杂波平均功率；f_d是多普勒频率；σ_f是功率谱的标准差，代表功率谱的展宽.
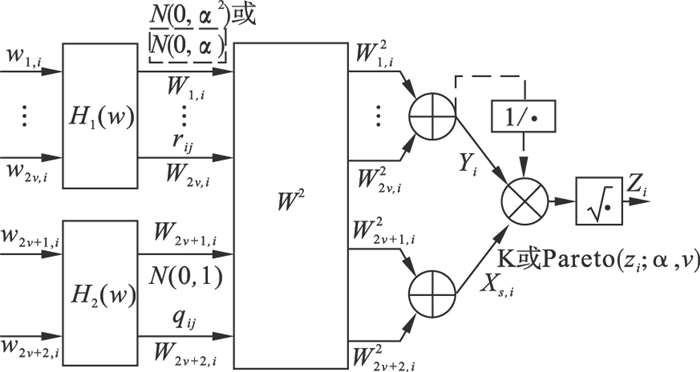
1.3 复合高斯型杂波的模拟方法复合高斯型杂波的模拟方法有ZMNL和SIRP，分别如图 1和图 2所示，其中实线部分为K分布模拟流程，虚线部分为Pareto分布模拟流程.ZMNL方法的复合高斯型杂波模拟包含2条支路，1条利用w_{1, i}，w_{2, i}，?，w_{2v, i}个独立的高斯随机序列平方和产生Gamma(逆Gamma)分布，另1条通过w_2v+1，w_2v+2两个独立的高斯随机序列平方和产生指数分布. 由此可见，通过ZMNL方法得到杂波的形状参数是整数或半整数.SIRP方法的复合高斯型杂波模拟是将序列Z_i中的每一个元素通过2个独立随机变量的乘积进行表示，即.其中Y_i是均值为零、实部虚部互相独立的复合高斯随机序列，调制变量S_i为非负的随机序列，其平方服从Gamma分布.故SIRP方法同样隐含产生Gamma分布的问题.
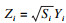
图 1(Fig. 1)

图 1 ZMNL方法复合高斯型分布杂波产生框图Fig.1 Block diagram for generation of complex Gaussian distribution clutter by ZMNL method

图 2(Fig. 2)

图 2 SIRP方法复合高斯型分布杂波产生框图Fig.2 Block diagram for generation of complex Gaussian distribution clutter by SIRP method

同时为了满足功率谱的设计要求，需要通过调整滤波器H₁和H₂来改变杂波序列的相关系数S_ij，

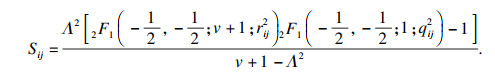(6)

其中: ₂F₁(·)是高斯超几何函数; Λ=Γ(v+3/2)Γ(3/2)/Γ(v+1)是与v有关的常数; r_ij和q_ij是Gamma过程和指数过程的相关系数.
2 改进的复合高斯型杂波模拟方法在文献[10-11]中均运用Gamma分布形状参数的可加性, 即y₁~G(y₁; v₁, 2α²)，y₂~G(y₂; v₂, 2α²)，y=y₁+y₂=G(y; v₁+v₂, 2α²).将形状参数v拆分成整数部分v₁与非整数部分v₂之和的形式.通过传统方法产生形状参数为v₁的Gamma分布随机数y₁，利用接受-拒绝法模拟Beta分布β~Beta(β; v₂, 1-v₂)，与指数分布η~Exp(η, 1)之积产生形状参数为v₂的Gamma分布随机序列y₂.文献[18]与文献[11]方法相似，只是参数设置不同，通过Beta分布随机序列β~Be(β; v₂, 2-v₂)与Gamma分布随机序列g~G(g; 2, 1)之积产生形状参数为v₂的Gamma分布随机序列y₂.
进一步分析接受-拒绝法模拟Beta分布的性能，模拟结果如图 3所示.
图 3(Fig. 3)

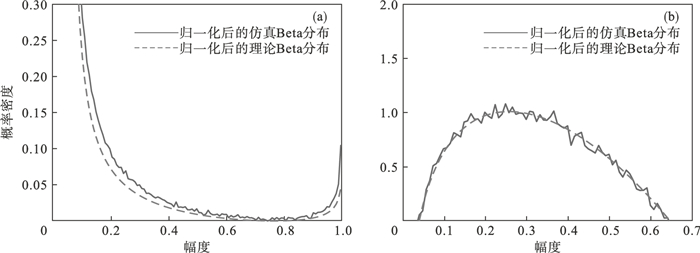图 3 模拟Beta分布与理论Beta分布PDF拟合曲线Fig.3 PDF fitting curve of simulated Beta distribution and theoretical Beta distribution (a)—参数 a=0.25, b=0.75；(b)—参数 a=1.25, b=1.75.

Beta分布的PDF为

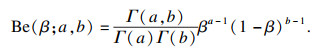(7)

其中，a>0, b>0, 0≤β≤1.
从图 3a可以看出，当a=0.25，b=0.75时，产生Beta分布随机序列的PDF与理论PDF出现偏离，这是由于当Beta分布的2个参数中的其中1个或者2个取值介于[0, 1]之间时，其PDF会随着Beta分布随机变量的取值趋于0或1而出现无穷大的情况，仿真出现偏差.而当分布参数均大于1时，在Beta分布随机数取值区间内就不会出现概率密度为无穷大的情况，模拟产生的PDF曲线与理论PDF曲线拟合较好，如图 3b所示.
针对上述问题，提出通过微分方程求解Gamma分布PDF，从而直接产生形状参数为v₂的Gamma分布，以减小由Beta分布引入而带来的杂波模拟的偏差.通过将Gamma函数的PDF转化为二阶非线性常微分方程^[19-21]，运用幂级数展开的方法产生任意参数下的Gamma分布，具体过程如下：
将Gamma函数的PDF，即式(3)转化为如下形式：

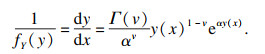(8)

式中，y是关于x的函数，x是[0, 1]均匀分布的随机数，同时再次求导，得到二阶非线性常微分方程：

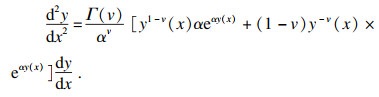(9)

将式(8)代入式(9)中化简得

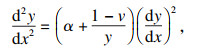(10)

等价于

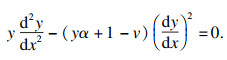(11)

令y(0)=0，当x→0时，:

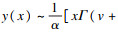
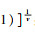
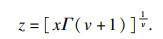(12)

将式(12)代入式(11)得

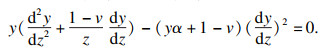(13)

其初始条件为y(0)=0，y^′(0)=1/α.
应用幂级数展开，式(13)的解为

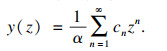(14)

将式(14)代入式(13)得

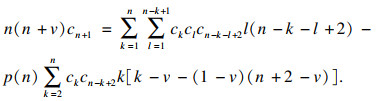(15)

其中, 当n < 2时，p(n)=0，当n≥2时，p(n)=1，可知：

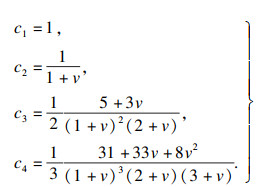(16)

最终可以求得微分方程函数的近似解为

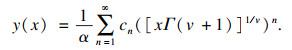(17)

通过式(17)就可模拟出在任意参数下Gamma分布，利用Gamma分布的第2参数可加性，在传统的复合高斯型杂波模拟流程框图中添加形状参数为v₂的Gamma分布支路，得到改进后的ZMNL和SIRP方法模拟复合高斯型分布杂波的流程图, 见图 4~图 5.
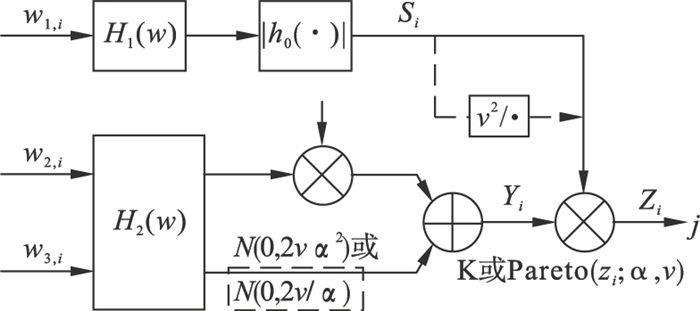
图 4(Fig. 4)

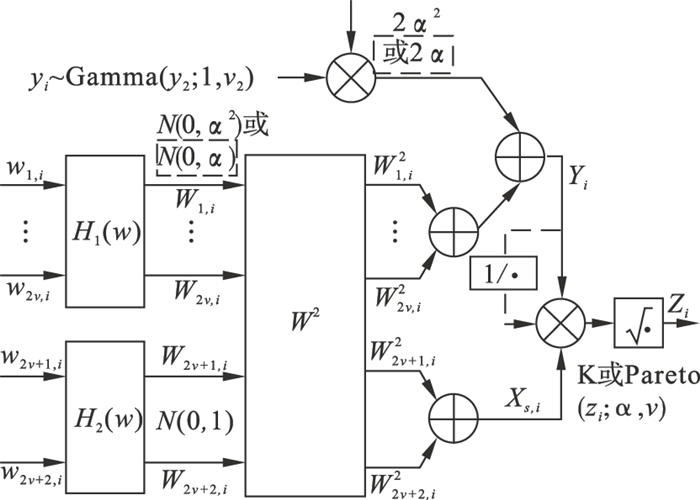图 4 改进后的ZMNL方法模拟复合高斯型分布杂波框图Fig.4 Block diagram for simulating compound Gaussian distributed clutter by improved ZMNL method

图 5(Fig. 5)

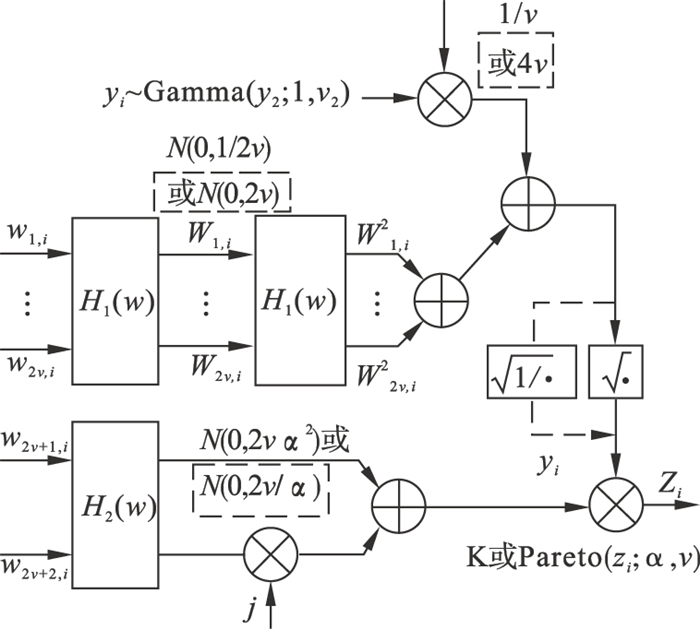图 5 改进后的SIRP方法模拟复合高斯型分布杂波框图Fig.5 Block diagram for simulating compound Gaussian distributed clutter by improved SIRP method

3 杂波模拟与检验通过文中提出的方法与文献[11]的方法进行比较，将形状参数为v₂部分的Gamma支路分别通过文献[11]的方法和文中提出的方法产生.同时设置形状参数v=0.25、尺度参数α=1，采样频率1 000 Hz，采样点数10 000，结果对比如图 6所示.从图中的局部放大曲线可以看出改进后模拟数据的概率密度曲线与理论曲线拟合效果较好.
图 6(Fig. 6)

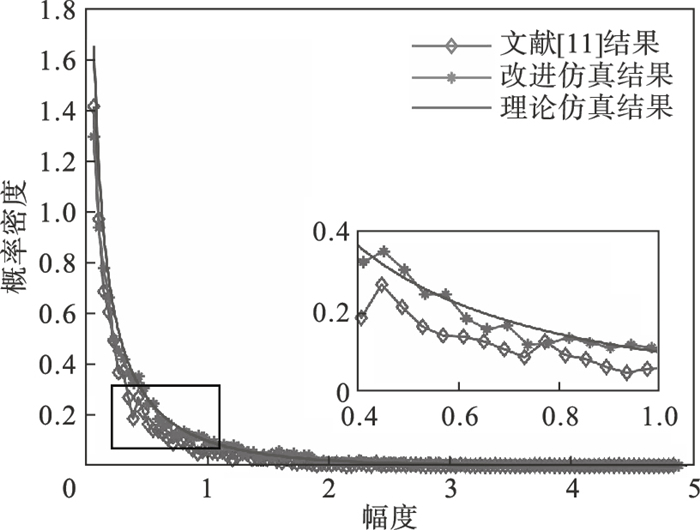图 6 改进后的Gamma杂波模型Fig.6 Improved Gamma clutter model

同时为了进一步验证所提方法性能，使用均方差检验(MSD)来测试模拟数据的拟合度.进行100次仿真实验，在每次的仿真实验中计算MSD.其中MSD的计算公式如下：

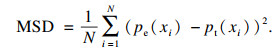(18)

式中，p_e，p_t分别为模拟的概率密度与理论概率密度.MSD越小，表明两种分布越相似.图 7为当杂波分布为Gamma分布时，不同方法的MSD结果.从图中可以看出本文提出的方法在生成Gamma分布的拟合效果在文献[11]的基础上进一步提升.
图 7(Fig. 7)

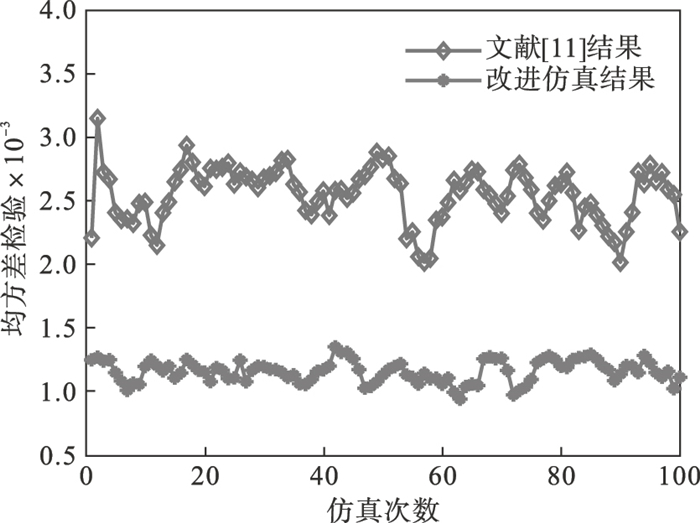图 7 MSD检验结果Fig.7 MSD inspection results

进一步验证形状参数为非整数时的效果，选择形状参数v=2.25，尺度参数α=1，频率为1 000 Hz，采样点数N=10 000，功率谱采用高斯谱，带宽σ_f=40 Hz.图 8和图 9分别为ZMNL方法仿真K分布和Pareto分布杂波的曲线对比.图 10和图 11分别为SIRP方法仿真K分布和Pareto分布杂波的曲线对比.图 8a~图 11a为传统和改进方法的幅度概率密度曲线对比，横轴为杂波幅度，纵轴为K分布或Pareto分布的幅度概率密度，其中传统方法的形状参数向下取(半)整数，即v=2.图 8b~图 11b为传统和改进方法的功率谱密度曲线对比，横轴为采样频率，纵轴为相应仿真方法的功率谱密度.观察图 8a~图 11a可以看出，不论是传统ZMNL方法或是SIRP方法模拟的复合杂波K分布或是Pareto分布的概率密度曲线与理论值有一定的偏差，相比而言，改进后的复合杂波方法，特别是当幅度值较小时，所提出的方法的拟合度都高于传统方法.比较图 8b~图 11b，可以看出新增加的支路，对复合杂波仿真的功率谱密度的影响可以忽略不计.
图 8(Fig. 8)

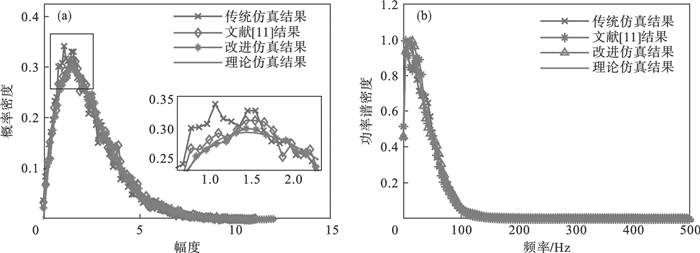图 8 ZMNL方法仿真K分布杂波Fig.8 Simulation of K-distributed clutter by ZMNL method (a)—幅度概率密度曲线；(b)—功率谱密度曲线.

图 9(Fig. 9)

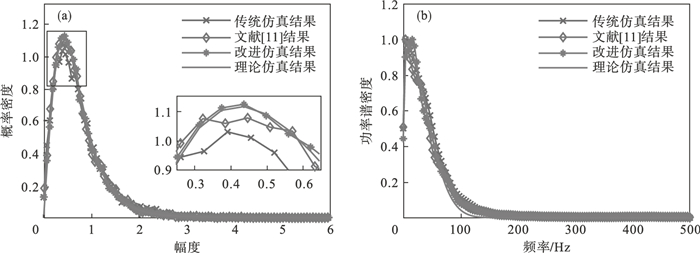图 9 ZMNL方法仿真Pareto分布杂波Fig.9 Simulation of Pareto-distributed clutter by ZMNL method (a)—幅度概率密度曲线；(b)—功率谱密度曲线.

图 10(Fig. 10)

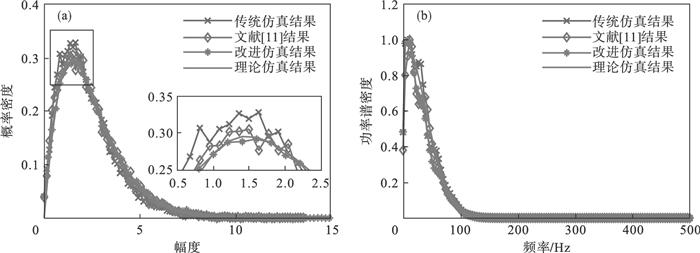图 10 SIRP方法仿真K分布杂波Fig.10 Simulation of K-distributed clutter by SIRP method (a)—幅度概率密度曲线；(b)—功率谱密度曲线.

图 11(Fig. 11)

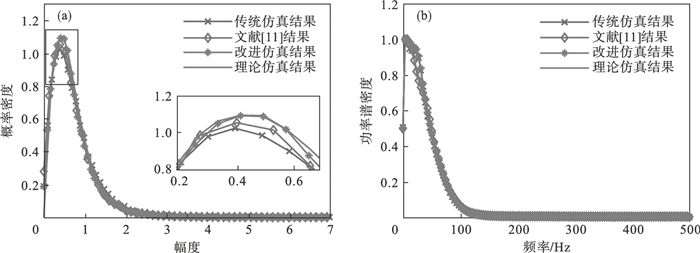图 11 SIRP方法仿真Pareto分布杂波Fig.11 Simulation of Pareto-distributed clutter by SIRP method (a)—幅度概率密度曲线；(b)—功率谱密度曲线.

4 结语本文针对传统方法在模拟K分布和Parato分布时形状参数取值存在局限的问题上，提出了将Gamma函数的概率密度函数转化为二阶非线性常微分方程，并求解产生任意参数下的Gamma分布随机数，将复合高斯分布杂波的形状参数扩展到一般实数.仿真结果表明：改进方法与现有杂波模拟方法相比，得到的复合高斯型杂波PDF仿真曲线与理论PDF曲线拟合效果更好，改善了杂波幅度特性模拟性能.
参考文献

[1]	刘宁波, 姜星宇, 丁昊. 雷达大擦地角海杂波特性与目标检测研究综述[J]. 电子与信息学报, 2021, 43(10): 2771-2780. (Liu Ning-bo, Jiang Xing-yu, Ding Hao. Summary of research on characteristic of radar sea clutter and target detection at high grazing angles[J]. Journal of Electronics & Information Technology, 2021, 43(10): 2771-2780.)
[2]	丁鹭飞, 耿富禄, 陈建春, 等. 雷达原理[M]. 6版. 北京: 电子工业出版社, 2020: 7-10. (Ding Lu-fei, Geng Fu-lu, Chen Jian-chun, et al. Radar principle[M]. 6th ed. Beijing: Publishing House of Electronics Industry, 2020: 7-10.)
[3]	杨斌, 黄默, 王长元, 等. X波段小擦地角海杂波WW分布建模[J]. 太赫兹科学与电子信息学报, 2021, 19(5): 916-921. (Yang Bin, Huang Mo, Wang Chang-yuan, et al. WW distribution modeling of X-band sea clutter with low grazing angle[J]. Journal of Terahertz Science and Electronic Information Technology, 2021, 19(5): 916-921.)
[4]	张玉石, 许心瑜, 尹雅磊, 等. L波段小擦地角海杂波幅度统计特性研究[J]. 电子与信息学报, 2014, 36(5): 1044-1048. (Zhang Yu-shi, Xu Xin-yu, Yin Ya-lei, et al. Research on amplitude statistics of L-band low grazing angle sea clutter[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1044-1048.)
[5]	Kafshgari S, Mohseni R. OFDM radar detection in Log normal clutter[C]// The 20th Telecommunications Forum(TELFOR). Belgrade: IEEE, 2012: 831-834.
[6]	Marier L J. Correlated K-distributed clutter generation for radar detection and track[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(2): 568-580. DOI:10.1109/7.381906
[7]	孙宇. 基于球不变随机过程的相干相关K分布海杂波仿真[J]. 科学技术与工程, 2009, 9(17): 5144-5147. (Sun Yu. Modeling and simulation of coherent correlated K-distribution sea clutter by SIRP[J]. Science Technology and Engineering, 2009, 9(17): 5144-5147.)
[8]	杨俊岭, 吕韶昱, 万建伟. 一种新的相干K分布模型及其在海杂波仿真中的应用[J]. 系统仿真学报, 2007, 19(2): 250-253, 260. (Yang Jun-ling, Lyu Shao-yu, Wan Jian-wei. A new coherent K-distributed model and its application in sea clutter simulation[J]. Journal of System Simulation, 2007, 19(2): 250-253, 260.)
[9]	Huang D, Zeng D Z. A new method for modeling and simulation of coherent correlated K-distributed clutter[C]// IET International Radar Conference. Guilin: IEEE, 2009: 1-9.
[10]	Conte E, Longo M, Lops M. Modelling and simulation of non-Rayleigh radar clutter[J]. IEE Proceedings F Radar and Signal Processing, 1991, 138(2): 121-130.
[11]	朱洁丽, 汤俊. 基于改进的ZMNL和SIRP的K分布杂波模拟方法[J]. 雷达学报, 2014, 3(5): 533-540. (Zhu Jie-li, Tang Jun. K-distribution clutter simulation methods based on improved ZMNL and SIRP[J]. Journal of Radars, 2014, 3(5): 533-540.)
[12]	Rosenberg L, Watts S, Greco M S. Modeling the statistics of microwave radar sea clutter[J]. IEEE Aerospace and Electronic Systems Magazine, 2019, 34(10): 44-75.
[13]	Sabrina M, Stephane K, Vincent C. Synthetic sea clutter for long integration processing[C]// The 17th European Radar Conference. Netherlands: IEEE, 2021: 13-15.
[14]	许述文, 王乐, 曾威良, 等. 逆伽马纹理复合高斯杂波参数的贝叶斯估计方法[J]. 太赫兹科学与电子信息学报, 2019, 17(4): 583-588. (Xu Shu-wen, Wang Le, Zeng Wei-liang, et al. Bayesian estimation method for compound Gaussian clutter model with inverse Gamma texture[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(4): 583-588.)
[15]	Zhou J, Chen D, Sun D W. K distribution sea clutter modeling and simulation based on ZMNL[C]// The 8th International Conference on Intelligent Computation Technology and Automation. Nanchang: IEEE, 2015: 506-509.
[16]	于涵, 水鹏朗, 施赛楠, 等. 广义Pareto分布海杂波模型参数的组合双分位点估计方法[J]. 电子与信息学报, 2019, 41(12): 2836-2843. (Yu Han, Shui Peng-lang, Shi Sai-nan, et al. Combined bipercentile parameter estimation of generalized Pareto distributed sea clutter model[J]. Journal of Electronics & Information Technology, 2019, 41(12): 2836-2843.)
[17]	陈岩, 李艳艳, 杨立波, 等. 地海杂波统计特性研究概述[J]. 空天防御, 2020, 3(4): 44-51. (Chen Yan, Li Yan-yan, Yang Li-bo, et al. An overview of statistical characteristics of ground-sea clutter[J]. Air Space Defense, 2020, 3(4): 44-51.)
[18]	Wallace N D. Computer generation of Gamma random variates with non-integral shape parameters[J]. Association for Computing Machinery, 1974, 17(12): 691-695.
[19]	Shaw W T, Luu T, Brickman N. Quantile mechanics Ⅱ: changes of variables in Monte Carlo methods and GPU optimised normal quantiles[J]. European Journal of Applied Mathematics, 2014, 25(2): 177-212.
[20]	Hilary I O, Muminu O A, Timothy A. Closed form expressions for the quantile function of the Chi square distribution using the hybrid of quantile mechanics and spline interpolation[J]. Wireless Personal Communications, 2020, 115: 2093-2112.
[21]	Hilary I O, Muminu O A, Timothy A. Approximations for the inverse cumulative distribution function of the Gamma distribution used in wireless communication[J]. Heliyon, 2020, 6(11): 240-252.