焦石岩^1,2, 廖相巍³, 闵义^1,2,3, 刘承军^1,2
1. 东北大学 多金属共生矿生态化冶金教育部重点实验室，辽宁 沈阳 110819;
2. 东北大学 冶金学院，辽宁 沈阳 110819;
3. 海洋装备用金属材料及其应用国家重点实验室，辽宁 鞍山 114021
收稿日期：2022-09-05
基金项目：国家自然科学基金资助项目(51974075)；海洋装备用金属材料及其应用国家重点实验室开放基金资助项目(SKLMEA-K202001)。
作者简介：焦石岩(1997-)，男，河北石家庄人，东北大学博士研究生;
闵义(1972-)，男，辽宁海城人，东北大学教授，博士生导师;
刘承军(1974-)，男，河南获嘉人，东北大学教授，博士生导师。

摘要：为了明晰熔渣体系中超声的空化行为，应用Rayleigh-Plesset方程模拟1 020 ℃条件下25% K₂O-30% Na₂O-45% SiO₂熔渣中空化泡的运动行为.结果表明，在空化核尺寸15 μm，声压振幅3.039 MPa的条件下，空化泡在频率25 kHz由一次振荡溃灭变为多次振荡才溃灭的瞬态空化，36 kHz变为无周期稳态空化，63 kHz变成周期稳态空化，呈现振幅降低和溃灭时间变长的特点.在空化核尺寸15 μm，频率20 kHz的条件下，空化泡在声压2.4 MPa处由稳态空化变为一次振荡溃灭的瞬态空化，17 MPa处变为2次振荡溃灭的瞬态空化，170 MPa处变为多次振荡才溃灭的瞬态空化，呈现振幅增大和溃灭时间变长的特点.在声压振幅3.039 MPa，频率20 kHz的条件下，空化泡在空化核2 μm由稳态空化变为一次振荡溃灭空化，21 μm变为多次振荡才溃灭的空化，33 μm变为非周期稳态空化，呈现振幅降低和溃灭时间变长的特点.
关键词：熔渣超声空化数值模拟
Numerical Simulation of Ultrasonic Cavitation Behavior in 25% K₂O-30% Na₂O-45% SiO₂ Slag
JIAO Shi-yan^1,2, LIAO Xiang-wei³, MIN Yi^1,2,3, LIU Cheng-jun^1,2
1. Key Laboratory for Ecological Metallurgy of Multimetallic Mineral (Ministry of Education), Northeastern University, Shenyang 110819, China;
2. School of Metallurgy, Northeastern University, Shenyang 110819, China;
3. State Key Laboratory of Metal Material for Marine Equipment and Application, Anshan 114021, China
Corresponding author: MIN Yi, E-mail: miny@mail.neu.edu.cn.

Abstract: To clarify the cavitation behavior of ultrasonic in the slag system, the Rayleigh-Plesset equation was applied to simulate the motion behavior of cavitation bubbles in the 25% K₂O-30% Na₂O-45% SiO₂ slag at 1 020 ℃. The results show that at the cavitation nucleus of 15 μm and the sound pressure of 3.039 MPa, the cavitation bubbles change from one oscillation collapse to transient cavitation with multiple oscillations before collapse at 25 kHz, to acyclic steady-state cavitation at 36 kHz, and to periodic steady-state cavitation at 63 kHz, showing an overall decrease in vibration amplitude and increase in collapse time. At cavitation nucleus of 15 μm and frequency of 20 kHz, the cavitation bubble changes from steady-state cavitation to one-oscillation collapse transient cavitation at 2.4 MPa, to two-oscillation collapse transient cavitation at 17 MPa, and to multi-oscillation collapse transient cavitation at 170 MPa, showing an overall increase in vibration amplitude and collapse time. At sound pressure of 3.039 MPa and frequency of 20 kHz, the cavitation bubble changed from periodic steady-state cavitation to one-oscillation collapse transient cavitation at 2 μm, then to multi-oscillation collapse transient cavitation at 21 μm, and finally to acyclic steady-state cavitation at 33 μm, showing an overall decrease in vibration amplitude and an increase in collapse time.
Key words: metallurgical slagultrasoundcavitationnumerical simulation
熔渣在现代钢铁冶金过程中发挥着重要功能，对于冶金质量、冶炼效率和冶金操作顺行均有重要影响^[1].熔渣冶金功能的发挥与其黏度表面张力的物理性质密切相关，欲改变熔渣的物理性质，一方面可通过改变熔渣的化学成分来实现，另一方面，鉴于冶金熔渣微观结构特征，也可通过外场调控实现.超声具有功率大、方向性好、穿透能力强的特点，在熔体中传播会引起超声空化效应.前期研究表明，在超声场作用下，硅酸盐熔渣的黏度^[2]和表面张力^[3]发生了转变，并通过微观结构解析，认为物理性质转变的原因是熔渣中结构单元的解聚，并认为是超声空化效应即空化泡溃灭时所产生的局部高温高压作用的结果^[4].但对于熔渣空化过程及影响因素并不清楚，这限制了对熔渣超声处理参数的进一步优化.
由于受到冶金熔渣的高温不透明的限制^[5]，难以对冶金熔渣中的超声空化行为进行直接实验观察，采用数值模拟方法是适合的.现阶段，国内外有关超声空化模拟主要集中于超声降解有机物^[6-7]和金属熔体细化结晶^[8-9]这两个方面，对于空化泡在冶金熔渣中的作用效果及影响因素缺乏系统的研究^[10].基于超声空化理论，本文应用Rayleigh-Plesset空化泡运动方程，探究了超声频率、声压和空化核尺寸等因素对空化泡运动行为的影响.
1 模拟方法1.1 空化泡运动方程及其解析方法超声空化是液体中微小的空化泡被超声波激活的动态过程，呈现出生长、收缩以及溃灭等特点^[11].在声波的负压阶段(即膨胀阶段)，液体受到过大的声强影响将会导致分子间的平均距离增加，当其距离超过极限时，就会产生空腔或空穴.一旦空腔形成，空化泡半径将会一直增长到负压最大的时刻.在正压阶段，这些空化泡会再次被压缩，一些空化泡会持续振荡，而另一些则会完全溃灭^[12].以此为基础，将空化行为划分成了稳态空化和瞬态空化两种类型^{[11, 13]}.稳态空化以非线性振荡为特征，可以有多个声波周期；而瞬态空化只能在大声强条件下发生，只能有一个或最多几个声波周期，随后在正压相内突然收缩以致崩溃，从而在极短的时间内和极小的空间内，产生5 000 K以上的高温和100 MPa以上的强大压力^[14].
1.1.1 空化泡运动方程空化过程实际上是空化泡壁的运动过程^[15].超声波通过冶金熔渣时，熔渣内存在的微小空化泡会受到声压拉伸压缩.为了建立超声波对空化泡壁运动的作用方程，作出了如下假设: ①空化泡运动时形状保持球型不变; ②空化泡运动时球体中心固定; ③空化泡壁仅能径向运动; ④重力效应被忽视; ⑤空化泡内部气体近似于理想气体，而熔渣为不可压缩液体.根据以上假设，对空化泡进行受力分析，依据能量守恒可以建立空化泡在超声波作用下的运动方程，即Rayleigh-Plesset方程^[16]，如式(1)所示：

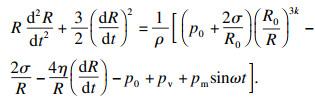(1)

式中: R是空化泡的瞬时半径，m；R₀是空化泡的初始平衡半径，m；p₀是流体静压力，Pa；p_v是熔渣蒸汽压，Pa；p_m是超声声压振幅，Pa；σ是熔渣表面张力，N/m；η是熔渣黏度，Pa · s；k是代表气体压缩规律的多变指数；ω是超声角频率；ρ为熔渣密度，kg/m³.
1.1.2 空化泡共振频率液体中并非所有空化泡均可产生显著的空化效应，超声频率与空化泡自然共振频率相等时，超声波和空化泡能量耦合才最为有效.因此，当超声波处于负压或正压一段时间后，空化泡半径增加为R=R₀+r，将其代入式(1)经化简可得

(2)

此外，对于一个初始半径为R₀的空化泡，其共振频率可由ω=2πf得到，式(2)可化简为

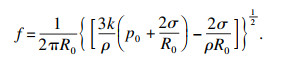(3)

式中：f为空化泡共振频率，Hz.
1.1.3 解析方法因式(1)为二阶非线性微分方程，其无法得到解析解.为了充分研究该方程中各参数对空化泡壁的影响，采用Runge-Kutta数值迭代法得出各个离散时间点所对应的空化泡半径大小^[17]，之后利用Matlab软件调用其自带ODE(ordinary differential equation) 函数，进行微分方程的编程求解.
1.2 熔渣物性参数由于超声施加设备采用高温合金制造的变幅杆和工具头，所以实验最高温度不能超过1 200 ℃，为此采用熔点为902 ℃的25% K₂O-30% Na₂O-45% SiO₂熔渣作为模拟对象.实验渣采用分析纯试剂配制，按照上述所示成分称取150 g并混合均匀后装入石墨坩埚，在1 100 ℃下进行高温预熔，保温1 h后水淬，将淬冷渣自然晾干后密封保存以供物理性质测试^[18].其中黏度、表面张力和密度分别采用旋转柱体法、拉筒法以及阿基米德法进行测定.将预熔渣放入石墨坩埚中，再将坩埚放置于炉体恒温带内，在氩气保护下以10 ℃/min的速率升温至1 020 ℃并恒温30 min后测定熔渣的表面张力、黏度和密度，如图 1所示.p_v为熔渣的饱和蒸汽压，采用FactSage软件计算^[19].熔渣的各项参数如下：t=1 020 ℃, ρ=2 288.6 kg · m^-3, σ=0.299 1 N · m^-1, η=1.924 Pa · s, p_v=0.753 Pa.
图 1(Fig. 1)

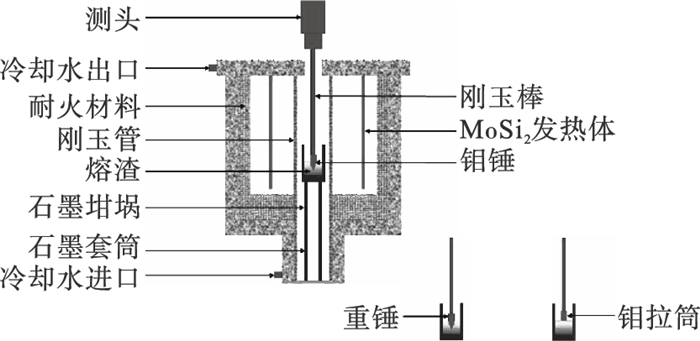图 1 熔渣物性测定系统Fig.1 Measurement system of slag physical property

2 模拟结果分析与讨论熔渣中的空化泡要产生空化效应，需超声波和空化泡能量耦合，即超声频率与空化泡共振频率相等^[20].以空化核的共振半径15 μm为基础^[21]，进而研究超声频率和超声声压对空化泡运动的影响；通过对超声波工具头振幅的测量，经计算可得到声压振幅为3.039 MPa^[22]，以此为基础研究超声频率与空化核半径对空化泡运动的影响.
2.1 超声频率的影响在1 020 ℃的冶金熔渣中，空化泡的初始半径为15 μm，声压振幅p_m为3.039 MPa的条件下，通过Matlab软件求解微分方程(1)，可获得空化泡半径与时间关系的数值模拟结果，研究发现空化泡运动状态在25，36，63 kHz处发生明显改变.因此将其划分成四段，每段取任意频率以研究超声频率对空化泡运动的影响.
图 2为不同频率下空化泡运动情况.从图中可以看出，冶金熔渣中的空化泡在0~24 kHz的超声频率下，经历1次膨胀与收缩后溃灭，空化效果显著，是瞬态空化，且10 kHz时的空化泡振动幅度比20，24 kHz时要大.随着频率的逐渐增加，在25~35 kHz时的振动周期逐渐变长，空化泡在溃灭前需要经历多次膨胀-收缩，由于25 kHz处于共振频率附近，导致其空化泡振幅突然变大，但其总体振幅随频率增大还是呈现降低的特点.在36~62 kHz时，空化泡表现为从瞬态空化向稳态空化逐步过渡，空化泡振幅变化随着频率的增加逐渐降低.当超声波频率增加到63 kHz及以上时，空化泡振幅较小，空化泡发生多次膨胀与收缩，并且直到250 μs还没溃灭.分析认为，正压区空化泡在高频率时没有足够的时间被压缩或压缩不够，来不及成长到可以产生有效空化泡的程度，因此空化泡会做振荡、增长、收缩和溃灭等一系列动力学的过程，这也是空化泡运动状态发生转变的重要原因.此外，图 3为超声频率对瞬态空化时的最大半径变化率和溃灭时间的影响.从图中可以看出，当增加超声频率时，空化泡溃灭时间先减少后增加，即在单位时间内产生的溃灭的空化泡数先增多后降低，这说明空化效率先增加后降低.因此，对熔渣施加超声时，应兼顾空化强度与空化效率，为此选择在15 kHz到24 kHz之间的超声频率对空化效应比较有利.
图 2(Fig. 2)

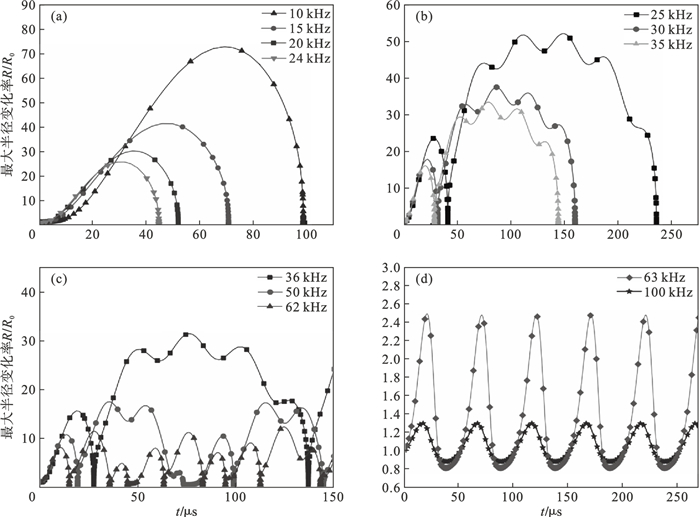图 2 不同频率下空化泡运动情况Fig.2 Motion of cavitation bubbles at different frequencies (a)—0~2 4kHz；(b)—25~35 kHz；(c)—36~62 kHz；(d)—63 kHz及以上.

图 3(Fig. 3)

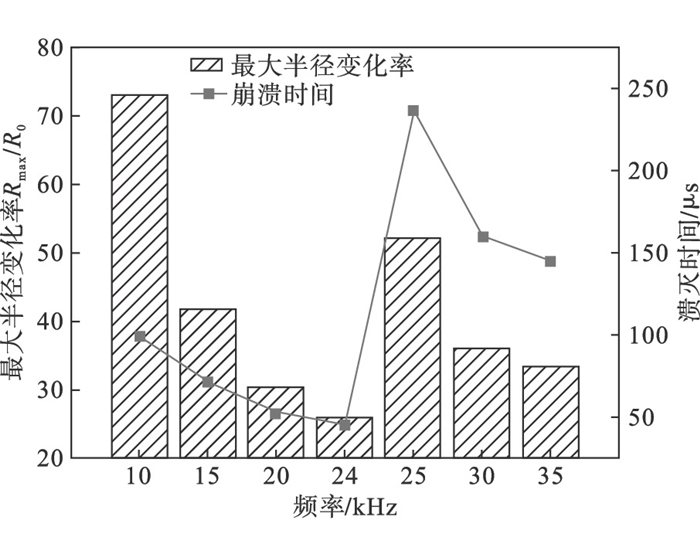图 3 超声频率对瞬态空化时的最大半径变化率Rmax/R0和崩溃时间t的影响Fig.3 Influence of ultrasonic frequency on the maximum radius change rate Rmax/R0 and collapse time t during transient cavitation

2.2 超声声压的影响在1 020 ℃的冶金熔渣中，空化泡的初始半径为15 μm，超声频率为20 kHz的条件下，通过Matlab软件求解微分方程(1)，可以获得空化泡半径与时间关系的数值模拟结果，研究发现空化泡运动状态在2.4，17，170 MPa处发生明显改变.因此将其划分成四段，每段取任意声压以研究超声声压对空化泡运动的影响.
图 4为空化泡在不同声压下的运动情况，当声压振幅在0~2.3 MPa时，冶金熔渣中的空化泡做周期性的正弦运动(即稳态过程)，表现出连续的非线性振荡.随着声压上升至2.4~16 MPa，空化泡经过一次膨胀-收缩的过程而溃灭. 在17~160 MPa时，随着声压的增大，空化泡振动幅度逐渐增大且开始经历膨胀-收缩过程才会溃灭，同时空化泡溃灭所需的时间也在增加.在170~405.2 MPa时，空化泡的溃灭周期逐渐变长，空化泡在溃灭前需要经历多次膨胀-收缩过程.分析认为，随着声压的增大，超声波负压区拉伸作用逐渐增强，空化泡半径显著增大，超声波正压区空化泡压缩作用增强，空化泡半径明显减少，势必造成空化泡溃灭时间增长，这也是导致空化泡在转折点运动状态发生改变的重要原因之一.另外，空化泡溃灭时最大温度与最大压力和超声声压有关，随着声压的升高，空化泡溃灭会变得更加剧烈，振动幅度增大.另外，由图 4中空化泡的崩溃时间也可以看出，随着声压的升高，空化泡的崩溃时间增加，这说明空化效率是逐渐降低的.分析认为，要使空化泡的半径增加，就必须采用声压较大的超声波发生器，但大声压的超声波发生器会使熔渣体系产生大量的空化泡，空化泡聚集在一起，一方面减少了熔渣成分含量，另一方面也减少了熔渣之间反应的有效接触面^[23].从上述结果可知，超声波的声压并不是越大越好，应选择适合的超声声压，进而有效缩短时间同时兼顾空化泡半径振动幅度.
图 4(Fig. 4)

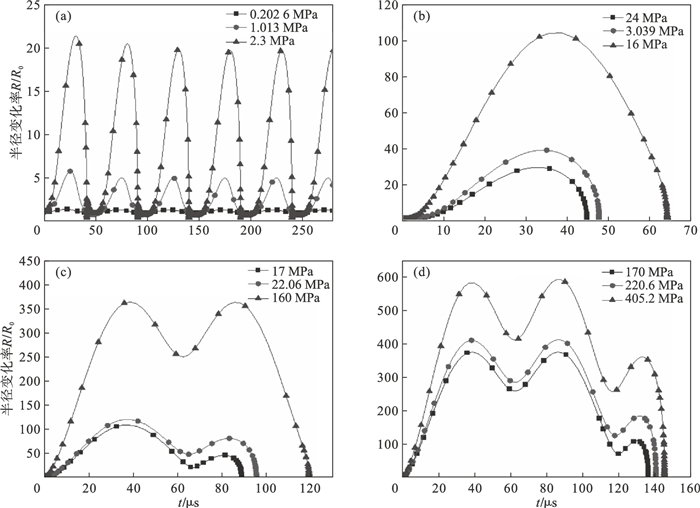图 4 不同声压对空化泡运动的影响Fig.4 Motion of cavitation bubbles under different sound pressures (a)—0~2.3 MPa; (b)—2.4~16 MPa; (c)—17~160 MPa; (d)—170~405.2 MPa.

2.3 空化核半径的影响实际液体中存在大量的气核，这些气核产生的原因有很多，如液体中分子热运动瞬时产生的汽化核子，液体中悬浮的不可溶气体形成的气核，微小的固体颗粒的缝隙中存在的不可溶性气体.由于其产生原因的不同，也导致了气核受内部蒸汽压力以及外部流场压力的大小也不同.所以，在本实验渣系中，同一时间空化核的大小也是不同的，为此需研究其半径对熔渣中空化泡的影响.
在1 020 ℃的冶金熔渣中，声压振幅p_m为3.039 MPa，超声频率f为20 kHz的条件下，通过Matlab软件求解微分方程(1)，可以得到空化核半径与时间关系的数值模拟结果，研究发现空化泡运动状态在空化核半径为2，21，33 μm时发生明显改变.因此将其划分成四段，每段取任意空化核半径以研究空化核对空化泡运动的影响.
图 5为在不同空化核半径下空化泡运动情况.在0~1 μm时，空化泡的振幅变化不大，空化泡做周期性的正弦运动(即稳态空化).当空化核半径为2~20 μm时，空化泡溃灭之前随着空化核半径增加，经历了一次膨胀与收缩，振幅在短期内变化较大，超声空化为瞬态空化.随着空化核半径的进一步增大，在21~32 μm时，空化泡振幅逐渐减小，振动周期增长，并开始经历膨胀-收缩过程才会溃灭.从33 μm开始，超声空化又将由瞬态空化变为稳态空化，使空化现象很难发生.此外，根据图 6可以看到，随空化核半径的增大，最大空化泡半径与初始平衡半径比值R_max/R₀整体呈现出逐渐减小的趋势，但是在21 μm时由于空化泡运动状态的改变导致其出现增大的情况.空化泡最大半径R_max随着空化核半径的增大呈现一直增大的现象.分析认为，随着空化核半径的增加，空化效果应该是先减少后增加最后一直减少.所以选择与共振频率相近的空化核半径对于空化效应是有利的，这对超声在冶金熔渣中的应用具有相当重要的意义.同时，通过图 6还可以看出，空化泡溃灭的时间在空化泡初始半径增大时逐渐缓慢增加，然后又迅速增加，再缓慢增加.这表明空化效率先缓慢降低，再迅速降低，再缓慢降低.因此，在对冶金熔渣应用超声时，应同时考虑空化强度和空化效率，空化核半径在15~20 μm之间，可以兼顾空化强度和空化效率.事实上，在其他条件不容易变化的条件下，为了改善超声效果，需要调节超声频率与空化核半径之间关系，使空化核半径尽可能接近或者小于共振半径.
图 5(Fig. 5)

图 5 不同空化核半径下空化泡运动情况Fig.5 Bubble motion at different cavitation nucleus sizes (a)—0~1 μm；(b)—2~20 μm；(c)—21~32 μm；(d)—33 μm及以上.

图 6(Fig. 6)

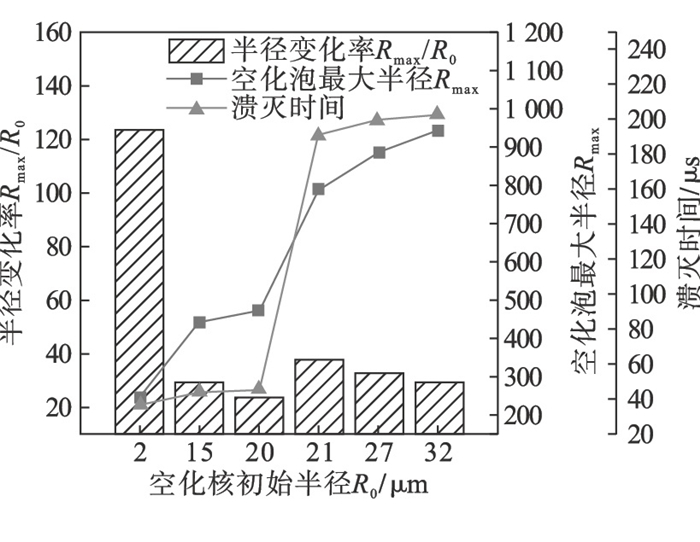图 6 空化核初始半径对瞬态空化时的最大半径变化率Rmax/R0、最大半径Rmax及溃灭时间t的影响Fig.6 Effect of initial radius of cavitation nucleus on the maximum radius change rate Rmax/R0, maximum radius Rmax and collapse time t during transient cavitation

3 结论1) 在声压振幅和空化核半径一定的情况下，由于超声频率升高导致空化泡来不及压缩从而在25，36，63 kHz处发生明显改变，由1次振荡溃灭转变为多次振荡才溃灭的瞬态空化，再转变为无周期稳态空化，最后转变成周期性稳态空化，呈现振动幅度降低和溃灭时间增大的特点，综合空化强度和空化效率，超声频率应选择15~24 kHz.
2) 在超声频率和空化核半径一定的情况下，由于声压对空化泡的拉伸作用，从而在2.4，17，170 MPa处运动状态发生明显改变，由稳态空化转变为1次振荡溃灭瞬态空化，再转变为2次振荡溃灭瞬态空化，最后转变为多次振荡才溃灭的瞬态空化，呈现振动幅度升高和溃灭时间增大的特点.综合空化强度和空化效率，声压应选择2.4~16 MPa.
3) 在超声频率和声压振幅一定的情况下，由于空化核蒸汽压及流场压力的不同，从而在空化核半径为2，21，33 μm时运动状态发生明显改变，由周期性稳态空化转变为1次振荡溃灭瞬态空化，再转变为多次振荡才溃灭的瞬态空化，最后转变为多次振荡稳态空化，虽在接近共振半径处振动幅度有所上升，但总体呈现出振动幅度降低和溃灭时间增大的特点，为提高超声效果，应尽量使空化核半径接近或者小于共振半径.
参考文献

[1]	朱立光, 王杏娟. 连铸保护渣理论与实践[M]. 北京: 冶金工业出版社, 2015: 174. (Zhu Li-guang, Wang Xing-juan. Theories and application of continuous casting mold fluxes[M]. Beijing: Metallurgical Industry Press, 2015: 174.)
[2]	Min Y, Luo J, Liu C J. Viscosity and related structure transformation of fluorine bearing silicate melt under ultrasonic field[J]. Ultrasonics Sonochemistry, 2019, 55(6): 289-296.
[3]	Min Y, Jiao S Y, Zhang R, et al. Surface tension and related ions behavior of silicate melts of the Na2O-K2O-SiO2-CaF2 system under ultrasonic irradiation[J]. ISIJ International, 2021, 61(3): 1022-1028. DOI:10.2355/isijinternational.ISIJINT-2020-557
[4]	Eskin G I, Eskin D G. Production of natural and synthesized aluminum-based composite materials with the aid of ultrasonic(cavitation)treatment of the melt[J]. Ultrasonics Sonochemistry, 2003, 10(4): 297-301.
[5]	Fox A B, Valdez M E, Gisby J, et al. Dissolution of ZrO2, Al2O3, MgO and MgAl2O4 particles in a B2O3 containing commercial fluoride-free mould slag[J]. ISIJ International, 2004, 44(5): 836-845. DOI:10.2355/isijinternational.44.836
[6]	Price G J, White A J, Clifton A A. The effect of high-intensity ultrasound on solid polymers[J]. Polymer, 1995, 36(26): 4919-4925. DOI:10.1016/0032-3861(96)81616-8
[7]	Madras G, Chattopadhyay S. Effect of solvent on the ultrasonic degradation of poly(vinyl acetate)[J]. Polymer Degradation and Stability, 2001, 71(2): 273-278. DOI:10.1016/S0141-3910(00)00174-9
[8]	Eskin G I. Broad prospects for commercial application of the ultrasonic(cavitation)melt treatment of light alloys[J]. Ultrasonics Sonochemistry, 2001, 8(3): 319-325. DOI:10.1016/S1350-4177(00)00074-2
[9]	Kang J W, Zhang X P, Wang S, et al. The comparison of ultrasonic effects in different metal melts[J]. Ultrasonics, 2015, 57: 11-17. DOI:10.1016/j.ultras.2014.10.004
[10]	Qu W X, Xie Y H, Shen Y, et al. Simulation on the effects of various factors on the motion of ultrasonic cavitation bubble[J]. Mathematical Modelling of Engineering Problems, 2017, 4(4): 173-178. DOI:10.18280/mmep.040406
[11]	应崇福. 超声学[M]. 北京: 科学出版社, 1990: 15. (Ying Chong-fu. Ultrasonics[M]. Beijing: Science Press, 1990: 15.)
[12]	Lee J H, Tey W Y, Lee K M, et al. Numerical simulation on ultrasonic cavitation due to superposition of acoustic waves[J]. Materials Science for Energy Technologies, 2020, 3: 593-600. DOI:10.1016/j.mset.2020.06.004
[13]	冯若. 超声手册[M]. 南京: 南京大学出版社, 1999: 20. (Feng Ruo. Handbook of ultrasound[M]. Nanjing: Nanjing University Press, 1999: 20.)
[14]	Chen X S, Jiao Q B, Tan X, et al. Numerical simulation of ultrasonic enhancement by acoustic streaming and thermal effect on mass transfer through a new computation model[J]. International Journal of Heat and Mass Transfer, 2021, 171: 121074. DOI:10.1016/j.ijheatmasstransfer.2021.121074
[15]	朱哲民, 龚秀芬, 杜功焕. 声学基础[M]. 上海: 上海科学技术出版社, 1981: 180. (Zhu Zhe-min, Gong Xiu-fen, Du Gong-huan. Fundamentals of acoustics[M]. Shanghai: Shanghai Science and Technology Press, 1981: 180.)
[16]	李争彩, 林书玉. 超声空化影响因素的数值模拟研究[J]. 陕西师范大学学报(自然科学版), 2008, 36(1): 38-42. (Li Zheng-cai, Lin Shu-yu. Numerical simulation of the factors influencing ultrasonic cavitation[J]. Journal of Shaanxi Normal University (Natural Science Edition), 2008, 36(1): 38-42.)
[17]	Liu L Y, Yang Y, Liu P H, et al. The influence of air content in water on ultrasonic cavitation field[J]. Ultrasonics Sonochemistry, 2014, 21(2): 566-571. DOI:10.1016/j.ultsonch.2013.10.007
[18]	许英强. 连铸保护渣技术问答[M]. 北京: 冶金工业出版社, 2013: 68. (Xu Ying-qiang. Questions and answers on slag protection technology for continuous casting[M]. Beijing: Metallurgical Industry Press, 2013: 68.)
[19]	Yu X, Pomfret R J, Coley K S. Dissolution of alumina in mold fluxes[J]. Metallurgical and Materials Transactions B, 1997, 28(2): 275-279. DOI:10.1007/s11663-997-0094-3
[20]	李杰, 陈伟庆, 何北星, 等. 超声波处理高温钢液的工具头材质研究[J]. 北京科技大学学报, 2007, 29(12): 1246-1249. (Li Jie, Chen Wei-qing, He Bei-xing, et al. Ultrasonic treatment of high-temperature steel for tool head material research[J]. Journal of University of Science and Technology Beijing, 2007, 29(12): 1246-1249.)
[21]	张鹏利. 超声空化多泡及其辐射声场的研究[D]. 西安: 陕西师范大学, 2010. (Zhang Peng-li. Study on ultrasonic cavitation multi-bubbles and their radiated sound field[D]. Xi'an: Shaanxi Normal University, 2010. )
[22]	赵世琏. 铝合金超声半连铸结晶器熔池流场数值模拟及试验研究[D]. 长沙: 中南大学, 2010. (Zhao Shi-lian. Numerical simulation and experimental study on the flow field of the melt pool of aluminum alloy ultrasonic semi-continuous crystallizer[D]. Changsha: Central South University, 2010. )
[23]	曹京京. 基于酯交换反应中超声空化的数值模拟[D]. 镇江: 江苏大学, 2013. (Cao Jing-jing. Numerical simulation of ultrasonic cavitation based on transesterification[D]. Zhenjiang: Jiangsu University, 2013. )