刘万锁, 岳向吉, 蔺增
东北大学 机械工程与自动化学院，辽宁 沈阳 110819
收稿日期：2022-06-20
基金项目：国家自然科学基金资助项目(51775096)。
作者简介：刘万锁(1989-)，男，辽宁抚顺人，东北大学博士研究生;
蔺增(1975-)，男，山东莱芜人，东北大学教授，博士生导师。

摘要：将纳维-斯托克斯(NS)方程方法与直接模拟蒙特卡罗(DSMC)方法耦合以实现过渡流态计算.相对过去欠缺反馈机制的单向耦合方法，提出以NS，DSMC速度场相互修正边界值的方法实现双向耦合方法的反馈机制，这对于非稳态研究和数值修正十分重要.结果表明，双向耦合结果与全局DSMC结果有高相似性，相对单向耦合具有更高的效率、稳定性及精度，提高耦合强度可以提升稳定性与精度.双向耦合通过采用全局NS结果边界值获得更高的子域收敛性、稳定性及精度.提出超前演算方法可以增强DSMC域的时间耦合性，为非稳态计算奠定基础.
关键词：NS/DSMC方法双向耦合过渡流超前演算PECVD
Study on Characteristics of NS/DSMC Two-Way Coupling Method Applied to Transition Flow Simulation in PECVD
LIU Wan-suo, YUE Xiang-ji, LIN Zeng
School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: LIN Zeng, E-mail: zlin@mail.neu.edu.cn.

Abstract: The Navier-Stokes(NS)method is coupled with the direct simulation Monte Carlo(DSMC) method to calculate the transition flow. The feedback mechanism of the two-way coupling method is realized by using the method of mutually modifying the boundary value of NS and DSMC, which is very important for non-steady state research and numerical correction. The results show that the two-way coupling results are highly similar to the global DSMC results, and have higher efficiency, stability, and accuracy than the one-way coupling. Improving the coupling frequency can improve stability and accuracy. The two-way coupling obtains higher subdomain convergence, stability, and accuracy by using the boundary value of global NS results. The foresight algorithm can enhance the time coupling of the DSMC domain and lay the foundation for non-steady state calculations.
Key words: NS/DSMC methodtwo-way couplingtransition flowforesight algorithmPECVD (plasma enhanced chemical vapor deposition)
半导体生产所使用的等离子体增强化学气相沉积(plasma enhanced chemical vapor deposition, PECVD)设备的工作环境是处于超洁净稀薄气体环境，处于气态和离子态的化合物随气流运动进行沉积过程，因此对于PECVD设备内流体运动特性研究可以有助于改善PECVD的产品质量.PECVD工作腔室内气体处于滑移流态和分子流态，这种情况下传统基于连续性假设的纳维-斯托克斯(Navier Stokes, NS)方程方法无法获得准确的计算结果.20世纪70年代由Bird^[1-2]提出的基于统计学的分子动力学模拟方法的直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法实现了非连续域的准确模拟.该方法采用追踪代表性粒子运动统计宏观气体运动特性，当气体稀薄程度逐步降低到滑移流、连续流时，庞大的粒子数量使得计算资源占用巨大，以至于很难实现.因此，采用NS与DSMC相结合的方法被提出，该耦合方法采用分区计算的原理，由NS模块计算滑移流和连续流，由DSMC模块计算分子流，这样既可以保证两种方法的计算精度，又能够兼顾两种方法的计算效率.NS/DSMC耦合方法在临界空间等领域早有应用，该方法的可行性得到了验证并且早已实际应用^[3-8].
通过前期****对NS/DSMC耦合方法的论述，可知****对耦合方法的基本理论和方法进行了充分的研究，但仍然有不足之处.早期的耦合方法主要采用单向耦合方法，强调数值传递的有效性，但没有考虑下游流场变化的反馈响应.这对于非稳态研究和上游数值修正很关键，因此本文提出采用双向耦合方法实现反馈机制.双向耦合方法使得各计算域的边界值能够互相修正，达到自然耦合的目的.
除耦合反馈问题外，现阶段耦合的关键技术主要集中在界面信息交换、空间界面的识别及非定常计算.其中非定常问题最难解决，由于NS与DSMC域的时间尺度差异，导致时间耦合困难，因此，目前大多采用Schwarz时间解耦式的方法，主要进行稳定解的传递并计算稳态结果，对于瞬态计算需要占用极大的资源来实现NS与DSMC域的时间尺度匹配，为此本文提出了超前演算方法来实现近似的时间耦合，这种方法也是建立在双向耦合的基础上的，可以提高结果稳定性.
1 仿真模型与数值方法流体状态可以分为连续流、滑移流、过渡流、分子流、无碰撞分子流，具体的划分界限是采用钱学森先生推荐的克努森数(Kn)来界定.Kn可以通过平均分子自由程(λ)与特征长度(l)的比值来计算，Kn=λ/l.对于复杂的环境可以采用局部Kn_GL-Q来进行精细化分，其值由平均分子自由程与基于压力梯度、速度梯度和温度梯度的特征长度比值计算，, GL代表梯度，Q代表局部通量，包括ρ，T，V(|V|=.本文采用的模型为PECVD喷淋板喷嘴模型，如图 1所示，由于结构简单所以采用全局Kn界定，几何最大直径为10 mm，喷嘴喉部直径为1 mm，结构全长40 mm，左、右腔室长度均为15 mm，喷嘴喉部长度为5 mm.经计算左腔Kn为0.01，处于滑移流态，右腔Kn为0.1，处于过渡流态.
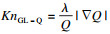
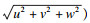
图 1(Fig. 1)

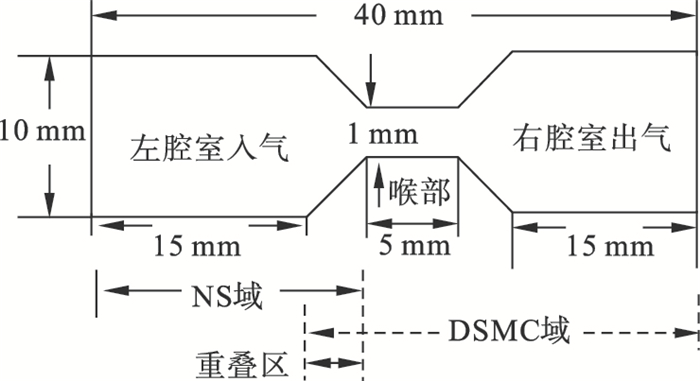图 1 喷嘴几何结构示意图Fig.1 Schematic diagram of geometric structure for nozzle

在NS域中采用左端压力入口、右端速度出口，壁面采用滑移壁面.采用隐式算法求解稳态流动，黏度模型采用k-ω方程模型，求解器为simpleFoam.在DSMC域中，求解器为dsmcFoam，采用氧原子与VHS(variable hard sphere)模型，左端速度入口，右端速度出口，壁面为Maxwell反射模型，平均每单元格代表性粒子数为20.双向NS/DSMC耦合方法采用速度场耦合与速度场反馈修正.
2 NS/DSMC耦合方法结果比对根据文献[9-11]可知，DSMC方法的计算精度是可以作为标准值来参考的，因此主要对比双向耦合方法与单向耦合方法的差异，并将两者与DSMC方法的结果进行精度比对.
图 2a为NS/DSMC耦合算法、全局NS及全局DSMC算法的计算结果.可见在耦合区x=-5~-2.5 mm，3种算法具有很高的重合度，且在x=-5 mm位置数值差异小于1%，说明该位置实现了算法的耦合^[12-14].文献[17-20]中交界单元内NS与DSMC解的差异小于5%，****认为该差异率可以确定耦合过程收敛，因此，这些近似连续区域可以实现NS与DSMC有效结果的交换.图 2中，全局NS方法的结果越接近微通道(Kn变大)，数值偏差逐步扩大，并且在喷嘴内部的流动数值偏差最为明显.全局DSMC方法基于统计学原理追踪代表性粒子的运动，其计算精度在迭代步足够的情况下具有很强的可信性^[15-16].NS/DSMC耦合方法的数据与全局DSMC方法匹配度很高，可见NS/DSMC耦合方法可以有效地反映流场运动的基本特性.如图 2b所示，通过对比单向耦合和双向耦合计算结果可见，双向耦合在NS域和DSMC域的结果能够很好地衔接，单向耦合数值在耦合区出现明显分离.说明缺乏反馈机制导致数值偏离无法修正进而造成计算误差，错误的边界造成的误差是无法消除的^[17].
图 2(Fig. 2)

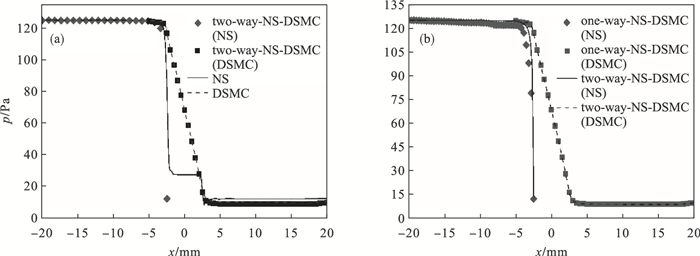图 2 耦合方法计算精度对比Fig.2 Comparison of calculation accuracy of coupling methods (a)—全局NS结果、全局DSMC结果及NS/DSMC耦合结果曲线；(b)—单向耦合与双向耦合结果曲线.

3 边界条件及耦合强度影响分析为了研究耦合强度和初始边界对于双向耦合方法在稳定性及精度方面的影响，本文进行了2种初始边界(全局DSMC结果边界与全局NS结果边界)和3种耦合强度(高、中和低，分别用high C, mid C和low C表示)的对比计算.
3.1 双向耦合的边界条件影响分析双向耦合方法具有优势，但是仍然不能完全消除边界值的影响，因此在应用双向耦合方法时对比分析了不同边界的计算结果，如图 3所示.可见，NS域采用全局DSMC结果边界后，收敛性变差、数值精度降低，直接导致DSMC域获得的耦合数值不稳定，进而造成DSMC域的数值稳定性降低，并且耦合结果偏离DSMC结果明显.相比之下，采用全局NS结果边界的耦合结果能够平稳趋近DSMC结果.说明双向耦合方法应该选择全局NS结果边界，以此提高子域的收敛性、稳定性及精度.
图 3(Fig. 3)

图 3 双向耦合方法采用全局DSMC、NS结果边界的计算结果曲线Fig.3 Curves of two-way coupling method for global DSMC and NS results boundary (a)—全局DSMC结果边界；(b)—全局NS结果边界.

3.2 双向耦合的耦合强度影响分析双向耦合计算是下游DSMC域不断向上游传递数据并修正上游NS域值的过程，可知反馈的频率(耦合强度)也同样是计算效率和精度的影响因素.如图 4a所示，双向耦合方法中，随耦合强度增加，数值精度有明显提升，NS域受耦合强度影响大于DSMC域.图 4b中可见中等耦合强度对于数值散射的抑制作用，耦合频率提高使得数值载入更加平滑，进而使得流场散射减弱.高度耦合的结果会存在额外波动(见图 4c)，可能是由于DSMC统计散射在过度耦合时，在NS域中引入了额外的扰动造成.在过度耦合强度下，NS域自身的数值波动会被DSMC域的统计散射所掩盖，进而造成持续且稳定的振荡，这会降低耦合方法的计算精度.
图 4(Fig. 4)

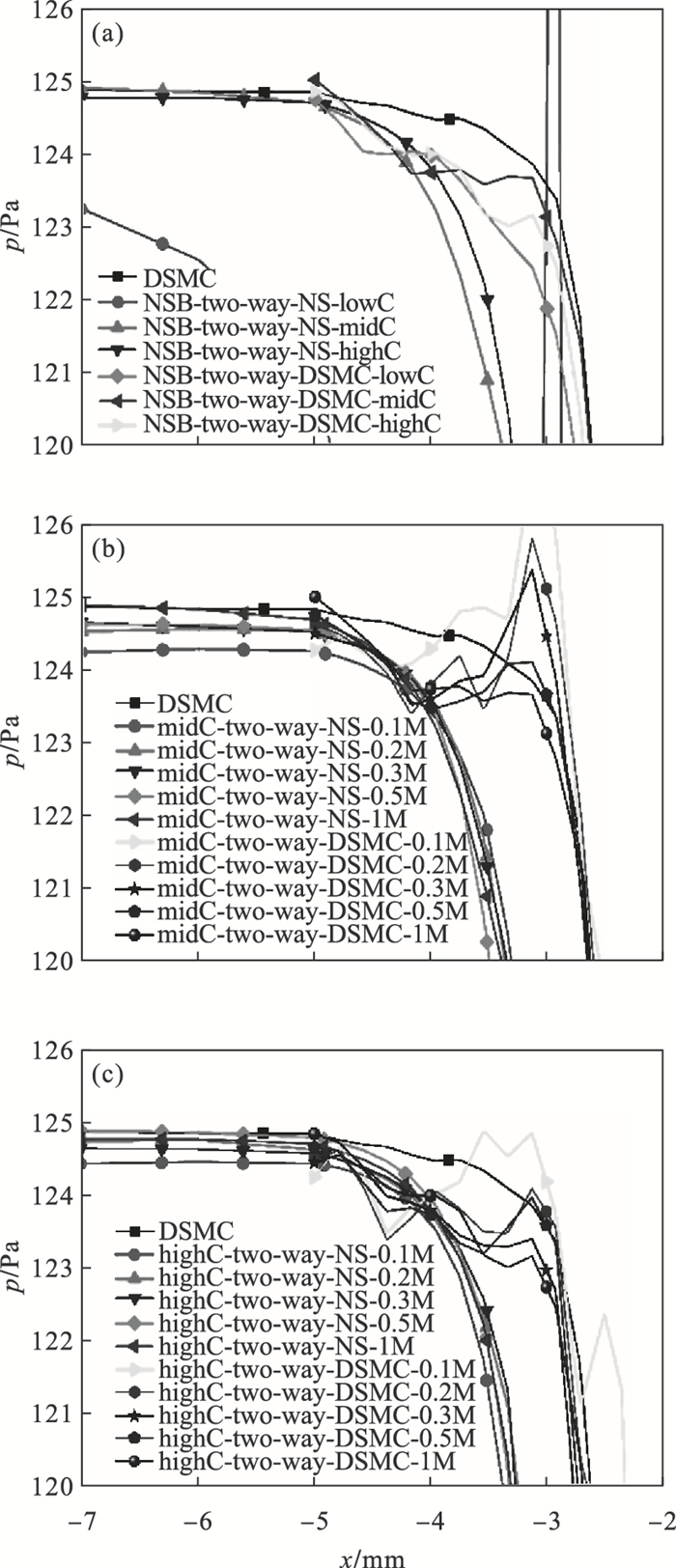图 4 3种耦合强度的计算结果曲线Fig.4 Curves of calculation results under three coupling strengths (a)—3种耦合强度经100万步计算结果曲线；(b)—中度耦合10万~100万步计算结果；(c)—高度耦合10万~100万步计算结果.

4 超前演算方法综上，NS域与DSMC域耦合并非越频繁越好.因此，本文提出超前演算计算方法，将单向耦合与双向耦合嵌套，以此实现两个目的.一是实现NS域与DSMC域耦合频率的差异化，一方面减少NS域耦合次数来降低DSMC域统计散射的影响，另一方面增加DSMC域耦合次数来减小DSMC域统计散射.二是实现NS域与DSMC域时间耦合关系的增强，突破目前以Schwarz方法为主的时间解耦的稳态计算^[18]，为非稳态计算建立时间耦合的基础.
现阶段耦合的关键问题主要集中于子域空间界面的确定、界面信息交换及非定常计算.其中界面确定是研究集中点，信息交换方法也比较完善，对于非定常计算研究几乎没有.这主要是由于NS域常规时间尺度在0.01 s量级，DSMC域常规时间尺度在1e-7 s量级.DSMC域时间尺度受物理环境限制无法改变，NS域降低时间尺度到DSMC时间量级会造成无法接受的计算量.采用超前演算方法可以有效增强DSMC域与NS域的时间耦合性，同时保证计算效率.
表 1为超前演算的计算步骤，所示为3次耦合过程，NS域计算3步，DSMC域计算15步.本文将NS域连续计算2次，但不记录第二次结果，仅将第二次结果作为DSMC域流场发展的预期值保留.之后将NS域2次连续计算结果进行线性插值.最后插值结果作为DSMC域的耦合值代入到DSMC域进行5次耦合计算.超前演算整体是双向耦合，具有反馈修正功能，但DSMC域的插值耦合则是单向耦合过程.超前演算方法中2，3步(6行、11行)与超前2，3步(5行、10行)的值并不相同，因为2，3步是经过双向耦合修正的结果，而超前2，3步是在边界条件没有修正时进行的预期计算.超前2，3步的值与单向耦合结果是一致的，因此可以保证超前2，3步值的有效性.
表 1(Table 1)

表 1 超前演算方法计算步骤Table 1 Calculation steps of foresight algorithm method 行号 NS DSMC 步骤 操作 步骤 操作 1 1步 保留结果 1步 同NS 1步 2 — — 2步 插值 3 — — 3步 插值 4 — — 4步 插值 5 超前2步 不保留结果 5步 同NS超前2步 6 2步 保留结果 6步 同NS 2步 7 — — 7步 插值 8 — — 8步 插值 9 — — 9步 插值 10 超前3步 不保留结果 10步 同NS超前3步 11 3步 保留结果 11步 同NS 3步 12 — — 12步 插值 13 — — 13步 插值 14 — — 14步 插值 15 超前4步 不保留结果 15步 同NS超前4步

表 1 超前演算方法计算步骤 Table 1 Calculation steps of foresight algorithm method

超前演算方法主要意义在于能够保持NS域时间尺度的同时增强DSMC域的时间耦合性.虽然这种经过2次近似(一次是NS域预期计算，另一次是DSMC域线性插值)的方法在结果上可能会存在较大的偏离，但是这种偏离可以通过改善NS域的计算精度和DSMC域的插值方法来控制.此外，DSMC域插值数量可以完全匹配DSMC域的计算步，但这种方法并不推荐，一方面计算量大量增加，另一方面DSMC域需要累计统计来降低散射.
5 结语通过对NS/DSMC双向耦合方法的详细研究可以轻易得出其优于单向耦合的结论，并且这种具有反馈机制的方法对于协调流场数值的作用显著.综合上述分析可知：
1) 双向耦合计算结果与DSMC结果有较高的重合度，并且相对单向耦合具有更高的计算效率、更强的稳定性以及更高的精度.
2) 应用过程中，双向耦合方法应该选择全局NS结果边界，以此提高子域的收敛性、稳定性及精度.
3) 双向耦合能够协调上下游数值，加速计算收敛速度，减小DSMC域的统计散射.这种协调性是计算稳定性的基础，通过提高耦合强度来增强协调性可以使计算稳定性提升.过度耦合会使DSMC域的统计散射影响NS域的稳定性，这种不稳定性会在耦合域中相互影响，导致耦合算法精度降低.
未来研究中还有很多工作可以进行.本文采用的双向耦合是速度的耦合与反馈，这种单数据反馈存在速度场与压力不能同步更新导致计算波动的问题，可以尝试进行速度与压力双数据反馈.对于超前演算方法可以作详细的验证，证明其对提高结果精度及时间耦合具有可行性.
参考文献

[1]	Bird G A. Molecular gas dynamics and the direct simulation of gas flows[J]. Molecular Gas Dynamics and the Direct Simulation of Gas Flows, 1994, 199: 1-9.
[2]	Bird G A. Molecular gas dynamics[J]. NASA STI/Recon Technical Report A, 1976, 76: 40225.
[3]	陈杰, 贺碧蛟, 蔡国飙. 火星环绕器羽流效应仿真研究[J]. 载人航天, 2017, 23(6): 743-750. (Chen Jie, He Bi-jiao, Cai Guo-biao. Simulation research on mars orbiter plume effect[J]. Manned Spaceflight, 2017, 23(6): 743-750. DOI:10.3969/j.issn.1674-5825.2017.06.005)
[4]	唐振宇, 贺碧蛟, 蔡国飙. 解耦NS/DSMC方法计算推力器真空羽流的边界条件研究[J]. 推进技术, 2014, 35(7): 897-904. (Tang Zhen-yu, He Bi-jiao, Cai Guo-biao. Research on boundary conditions of thruster vacuum plume calculation by decoupled NS/DSMC method[J]. Propulsion Technology, 2014, 35(7): 897-904.)
[5]	李志辉, 李中华, 杨东升, 等. 卫星姿控发动机混合物羽流场分区耦合计算研究[J]. 空气动力学学报, 2012, 30(4): 483-491. (Li Zhi-hui, Li Zhong-hua, Yang Dong-sheng, et al. Research on partition coupling calculation of mixture plume field of satellite attitude control engine[J]. Acta Aerodynamica Sinica, 2012, 30(4): 483-491. DOI:10.3969/j.issn.0258-1825.2012.04.010)
[6]	包醒东, 余西龙, 毛宏霞, 等. 基于理论解析方法的高真空羽流流动及红外辐射研究[J]. 红外与激光工程, 2020, 49(1): 0104003. (Bao Xing-dong, Yu Xi-long, Mao Hong-xia, et al. Research on high vacuum plume flow and infrared radiation based on theoretical analysis method[J]. Infrared and Laser Engineering, 2020, 49(1): 0104003.)
[7]	李中华, 李志辉, 李海燕, 等. 过渡流区NS/DSMC耦合计算研究[J]. 空气动力学学报, 2013, 31(3): 282-287. (Li Zhong-hua, Li Zhi-hui, Li Hai-yan, et al. Research on NS/DSMC coupled calculation in transitional flow region[J]. Acta Aerodynamica Sinica, 2013, 31(3): 282-287.)
[8]	李志辉, 梁杰, 李中华, 等. 跨流域空气动力学模拟方法与返回舱再入气动研究[J]. 空气动力学学报, 2018, 36(5): 826-847. (Li Zhi-hui, Liang Jie, Li Zhong-hua, et al. Cross-domain aerodynamic simulation method and reentry capsule reentry aerodynamic research[J]. Acta Aerodynamica Sinica, 2018, 36(5): 826-847.)
[9]	Yuan Z Y, Jiang Z Z, Zhao W W, et al. Analysis of gas flow over a cylinder at all Knudsen numbers based on non-newtonian constitutive models[J]. International Journal of Modern Physics B, 2020, 34(14/15/16): 2040076.
[10]	Yuan Z Y, Zhao W W, Jiang Z, et al. Modified nonlinear coupled constitutive relations model for hypersonic nonequilibrium flows[J]. Journal of Thermophysics and Heat Transfer, 2020, 34(4): 848-859.
[11]	Chen J, Zhou H. Rarefied gas effect in hypersonic shear flows[J]. Acta Mechanica Sinica, 2021, 37: 2-17.
[12]	Farber K, Farber P, Gr?bel J, et al. Development and validation of a coupled Navier-Stokes/DSMC simulation for rarefied gas flow in the production process for OLEDs[J]. Applied Mathematics and Computation, 2016, 272: 648-656.
[13]	Quarteroni A, Valli A. Domain decomposition methods for partial differential equations[M]. Oxford: Oxford University Press, 1999.
[14]	Wu J S, Lian Y Y, Cheng G, et al. Development and verification of a coupled DSMC-NS scheme using unstructured mesh[J]. Journal of Computational Physics, 2006, 219(2): 579-607.
[15]	Garcia A L, Alder B J. Generation of the Chapman-Enskog distribution[J]. Journal of Computational Physics, 1998, 140(1): 66-70.
[16]	John B, Damodaran M. Hybrid continuum-direct simulation Monte Carlo and particle-laden flow modeling in the head-disk interface gap[J]. IEEE Transactions on Magnetics, 2009, 45(11): 4929-4932.
[17]	Schwartzentruber T E, Boyd I D. A hybrid particle-continuum method applied to shock waves[J]. Journal of Computational Physics, 2006, 215(2): 402-416.
[18]	Wijesinghe H S, Hadjiconstantinou N G. Discussion of hybrid atomistic-continuum methods for multiscale hydrodynamics[J]. International Journal for Multiscale Computational Engineering, 2004, 2(2): 189-202.
[19]	Boyd I D, Chen G, Candler G V. Predicting failure of the continuum fluid equations in transitional hypersonic flows[J]. Physics of Fluids, 1995, 7(1): 210-219.
[20]	Wang W L, Boyd I D. Predicting continuum breakdown in hypersonic viscous flows[J]. Physics of Fluids, 2003, 15(1): 91-100.