
 , 陈昭, 梁力
, 陈昭, 梁力 东北大学 资源与土木工程学院,辽宁 沈阳 110819
收稿日期:2022-06-27
基金项目:中央高校基本科研业务费专项资金资助项目(N2001015)。
作者简介:李明(1980-),男,辽宁沈阳人,东北大学副教授;
梁力(1955-),男,辽宁丹东人,东北大学教授,博士生导师。
摘要:采用PHF-LSM(permeability-based hydraulic fracture-level set method)水力压裂计算模型,建立了含节理分布的岩石材料模型,将其计算结果与裂缝几何特征和诱发应力理论解对比验证模型正确性,在此基础上分析节理对水力裂缝应力阴影效应的影响.计算结果表明:基于弥散裂缝模型的PHF模型应使用等效开裂区域最外侧结点位移差作为裂缝等效开度;节理的存在会影响裂缝注水过程中水压力变化,同时会引起裂缝等效开度的增大;较大的节理入射角度与距注水点较小的节理高度会产生更大诱发应力,同时会引起最小主应力方向的改变,导致更强应力阴影效应,裂缝偏转加强.
关键词:水力压裂应力阴影PHF-LSM模型节理
Influence of Joints on Stress Shadow Effect Based on PHF-LSM Model
LI Ming

 , CHEN Zhao, LIANG Li
, CHEN Zhao, LIANG Li School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: LI Ming, E-mail: liming@mail.neu.edu.cn.
Abstract: Using PHF-LSM(permeability-based hydraulic fracture-level set method)hydraulic fracturing calculation model, a rock material model with joint distribution is established. The correctness of the model is verified by comparing the geometric characteristics of fractures and the theoretical solution of induced stress with the simulation result. On this basis, the influence of the presence of joints on the stress shadow effect of hydraulic fractures is analyzed. The simulation results indicate that: the displacement difference of the outermost node in the equivalent fracture region should be used as the equivalent fracture opening in the PHF model based on the dispersion fracture model; the existence of joints will affect the change of water pressure in the process of fracture water injection, and will increase the equivalent fractures opening; a larger joint incidence angle and a smaller joint height from the water injection point will produce greater induced stress, and change the direction of the minimum principal stress, resulting in a stronger stress shadow effect and enhanced fracture deflection.
Key words: hydraulic fracturingstress shadowPHF-LSM modeljoint
岩体的形成需要经历复杂的地质条件的作用,岩体中会存在各种结构面,如节理[1]等,这种断裂构造会对岩体的力学特性产生巨大的影响,并且在分段压裂过程中水力裂缝与节理之间产生的相互作用会引起强烈的应力场变化,称作应力阴影效应[2].这种效应会改变水力裂缝几何发展形态,因此研究节理对水力压裂应力阴影效应的影响十分必要.
应力阴影效应的研究可通过理论研究、物理实验以及数值模拟等方法.Green等[3]推导出平面应变条件下的单一裂缝应力场理论解,得到水力裂缝会对周围岩石介质产生扰动应力场;Zhao等[4]研究了存在的天然裂缝长度宽度以及与水力裂缝距离对水力压裂中套管变形的影响;Wang等[5]使用EPM(element partition method)分析不同接近角与不同地应力差下的水力裂缝与天然裂缝相互作用形态;Zhang等[6]采用BPM(bonded-particle model)分析了不同角度层理面下不同地应力差对单一水力裂缝形态的影响;Zhao等[7]研究了既有节理的摩擦力、凝聚力及不同地应力差、接近角、注入液黏度和速率对水力裂缝形态的影响;Zhang等[8]采用DDM(displacement discontinuity method)研究天然裂缝的长度、角度和分布密度对水力裂缝扩展的影响.
本文采用PHF-LSM(permeability-based hydraulic fracture-level set method)水力压裂计算模型研究水力裂缝与节理间的应力阴影效应作用,探讨在节理角度及节理与注水点距离变化下,裂缝内水压力以及裂缝等效开度的变化,及其对裂缝周围应力场的影响.
1 PHF-LSM水力压裂计算模型1.1 基本方程PHF模型[9]考虑了岩石中孔隙流体与固体骨架的耦合作用,固相开裂后使用Mohr-Coulomb破坏及强化准则描述,裂隙岩石中流体的渗透率设为平均有效应力的函数[10-11].同时将可以避免网格影响的LSM与PHF模型结合,建立不同的岩石材料有限元模型[12].控制方程如下:
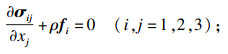 | (1) |
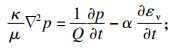 | (2) |
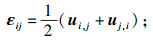 | (3) |
 | (4) |
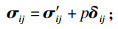 | (5) |
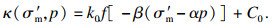 | (6) |
裂缝开裂区域的渗透系数与平均有效应力修正关系,如式(7)和式(8)所示:
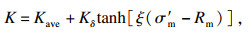 | (7) |
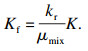 | (8) |
 | (9) |
混合黏滞系数μmix由式(10)计算:
 | (10) |
 | (11) |
 | (12) |
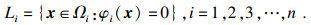 | (13) |
 | (14) |
图 1(Fig. 1)
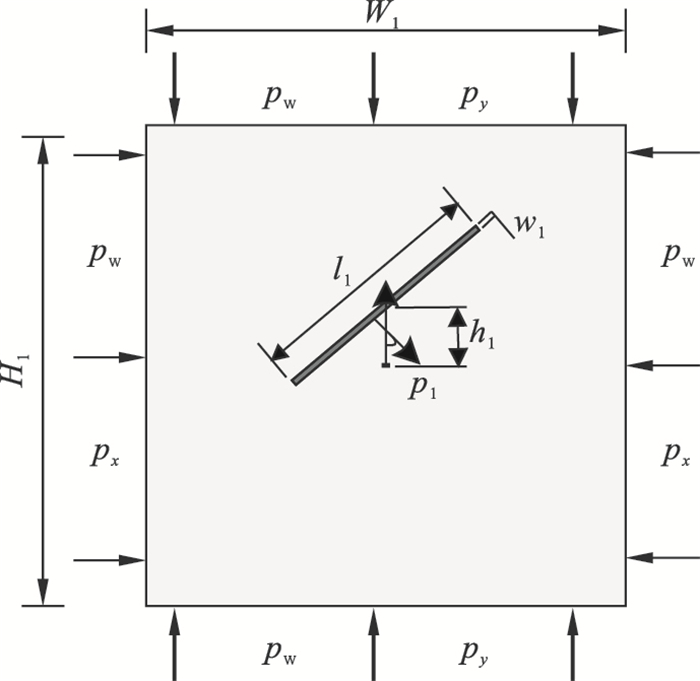 | 图 1 力学模型Fig.1 Mechanical model |
1.2 PHF-LSM模型在ABAQUS中建立通过ABAQUS软件建立PHF-LSM模型,算法流程图如图 2所示.为探讨节理对水力裂缝的影响,设置8个场变量,分别为弹性模量(E)、泊松比(υ)、抗拉强度(Rm)、渗透系数(K)、密度(ρ)、饱和度(Sw)、孔隙比(e)和混合黏滞系数(μmix).其初始值分别储存在对应的状态变量中.子程序UEXTERNALDB用于读取并初始化岩石材料参数等数据,子程序SDVINI实现LSM对不同区域进行赋值初始化并保存状态变量,最后使用子程序USDFLD依据式(7)~(11)随着有效应力的改变来修正压裂过程中的渗透系数.
图 2(Fig. 2)
 | 图 2 PHF-LSM算法流程图Fig.2 Flow chart of PHF-LSM algorithm |
1.3 岩石材料有限元模型建立根据图 1力学模型与表 1对应的材料参数,使用PHF-LSM模型建立包含节理区域的岩石有限元网格,如图 3所示.模型采用CPE8P单元进行划分,单元高宽比AR=3.0.模型共有单元83 000个,节点250 333个.模型x方向与y方向分别施加py=70 MPa和px=60 MPa初始地应力,模型水压力初始值为pw=49 MPa,节理与基岩材料参数见表 2.
表 1(Table 1)
| 表 1 力学模型参数 Table 1 Parameters of the mechanical model |
图 3(Fig. 3)
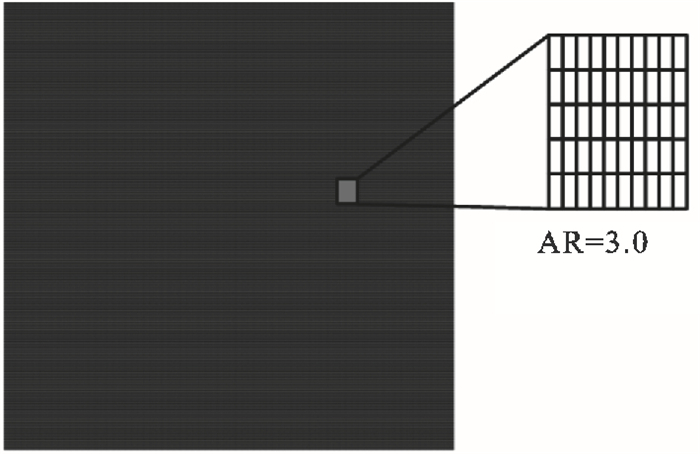 | 图 3 有限元网格Fig.3 Finite element mesh |
表 2(Table 2)
| 表 2 岩石材料属性 Table 2 Rock material properties |
1.4 岩石材料模型中的节理使用LSM在模型中建立节理区域,如图 4所示.探讨节理对水力裂缝产生的应力阴影效应的影响,在节理宽度w1范围内根据与节理中线L的不同距离对积分点赋予不同的渗透系数,建模采用线性插值,其中节理中线位置渗透系数最大,最外部渗透系数最小为基岩渗透系数.
图 4(Fig. 4)
 | 图 4 节理示意图Fig.4 Schematic diagram of joints |
2 PHF-LSM模型与理论解对比验证在图 1所示的力学模型基础上赋予表 2所列参数中基岩部分材料属性,并施加单一注水荷载qinj=0.005 62 mm/s,注水时间为1 800 s,计算并提取裂缝几何特征与诱发应力场.由于PHF模型具有弥散裂缝模型的特性,使用等效开裂区域模拟真实裂缝,其中裂缝等效开度取开裂区域最外侧结点水平方向位移差(记作wf=u+-u-),裂缝等效高度取为裂缝等效开裂区域实际高度,用2hf表示,裂缝注水扩展过程如图 5所示.
图 5(Fig. 5)
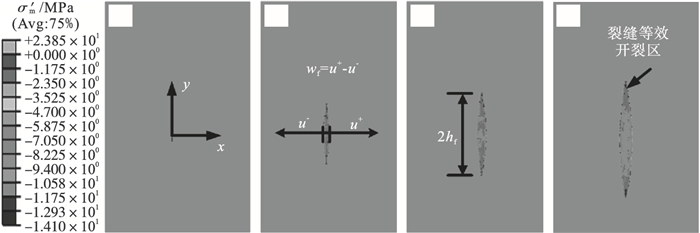 | 图 5 水力裂缝发展过程Fig.5 Development of hydraulic fracture (a)—t=65 s;(b)—t=667 s;(c)—t=1 267 s;(d)—t=3 000 s. |
采用KGD理论模型[16]计算裂缝高度2hf、开度wf和注水压力pw与时间关系,如式(15)~(17)所示:
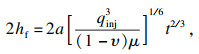 | (15) |
 | (16) |
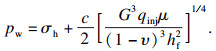 | (17) |
图 6a~6c是PHF模型水力裂缝的等效高度、等效开度与注水点水压力随注水时间变化过程和注水点应力路径变化.其中图 6a和图 6b的计算结果表明,PHF模型得到的数值解与KGD模型的理论解一致,且随着注水时间的增加裂缝的等效高度与等效开度会继续增长,但增长趋势逐渐减缓.图 6c为注水点的水压力pw随注水时间变化,其与KGD模型理论解拟合较好,但PHF模型计算的传播压力高于KGD模型理论值.
图 6(Fig. 6)
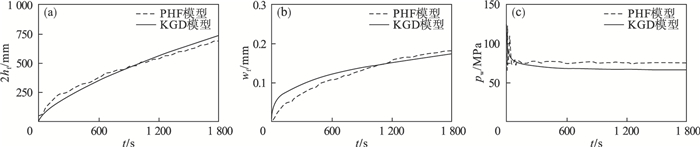 | 图 6 单一水力裂缝特征对比Fig.6 Comparison of single hydraulic fracture characteristics (a)—等效裂缝高度;(b)—等效裂缝开度;(c)—注水点位置水压力. |
对于单一裂缝发展过程中产生的诱发应力场,Sneddon等[17]基于弹性理论得到平面应变条件下垂直于裂缝方向的诱发应力理论解,如式(18)所示.
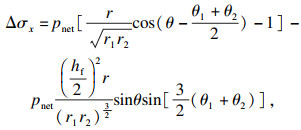 | (18) |
 | (19) |
图 7(Fig. 7)
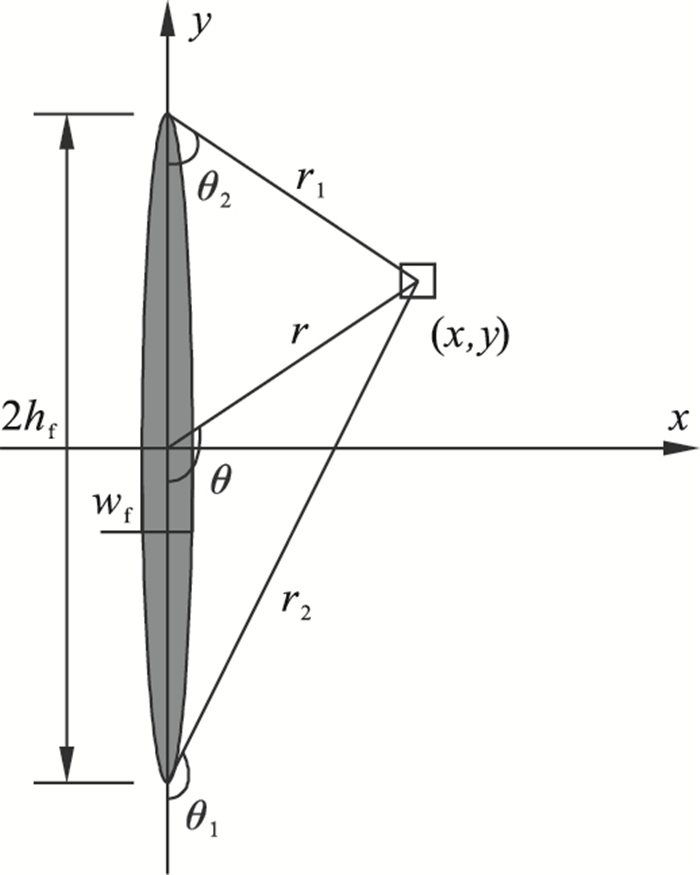 | 图 7 单裂缝坐标示意图Fig.7 Coordinates sketch of single fracture |
PHF模型计算裂缝的注水点右侧水平方向的诱发应力Δσx与裂缝内净压力pnet的比值如图 8所示,由于PHF模型基于弥散裂缝模型,模型使用σ′m<0的区域作为裂缝等效开裂区域替代真实裂缝.故在远离裂缝的位置,PHF模型计算的扰动应力数值解与理论解拟合较好.
图 8(Fig. 8)
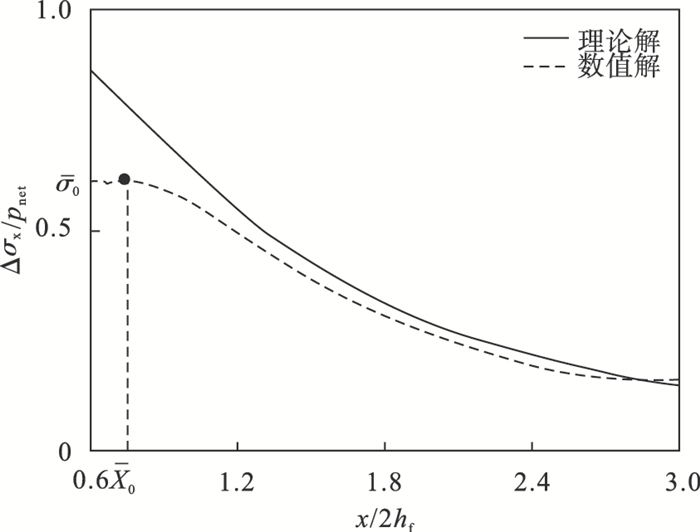 | 图 8 注水点位置垂直裂缝方向诱发应力变化(t=1 800 s)Fig.8 Induced stress along the path perpendicular to fracture starting from injection point (t=1 800 s) |
图 9是压裂完成时裂缝水平方向应力场σx与垂直方向应力场σy的分布情况.由图可知,σx在整个模型区域的影响范围与影响程度较大,且σx主要的影响范围在裂缝两侧的水平方向,并且在裂缝两侧影响较大,而σy的影响仅在裂缝邻近的位置,并且发现压裂完成后σx增加而σy降低;同时也说明应力阴影的本质影响就是导致最小水平主应力增加,引起该区域的水平应力差减小,应力发生转向,同时影响裂缝扩展及方向.
图 9(Fig. 9)
 | 图 9 PHF模型应力分布(t=1 800 s)Fig.9 Stress distribution by PHF model(t=1 800 s) (a)—σx;(b)—σy. |
3 节理几何参数的影响3.1 节理参数说明图 10为PHF模型计算得到的裂缝等效开裂区域,选取注水单元两端结点(结点间距离为la)位移差作为裂缝等效开度.当la不同时,裂缝等效开度的变化如图 11所示.当la大于开裂区域时,裂缝等效开度与KGD理论解拟合较好.该结果表明,选择等效开裂区域两端结点位移差作为裂缝等效开度是合理的.参考文献[19]尺寸比例设置节理宽度为60 mm,等效开度从图 11中可知为0.162 mm.
图 10(Fig. 10)
 | 图 10 PHF模型单元宽度选择示意Fig.10 Schematic diagram of PHF model unit width selection |
图 11(Fig. 11)
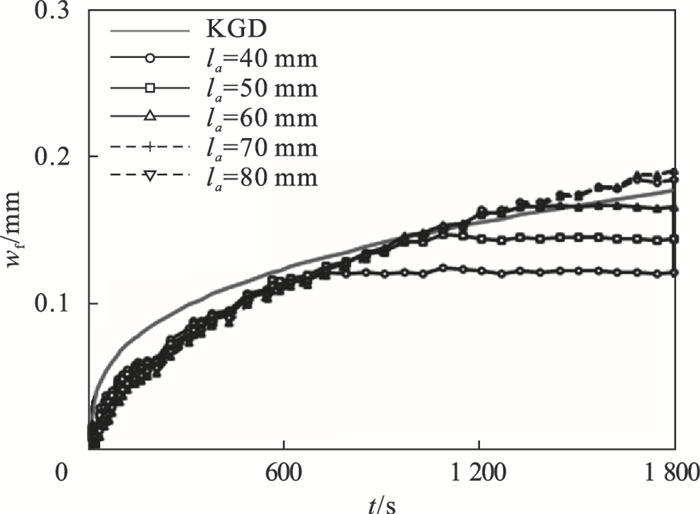 | 图 11 PHF模型单元宽度选择与等效开度关系Fig.11 Relationship between unit width selection and equivalent opening of PHF model |
3.2 节理入射角度本文考虑了节理法线方向与水力裂缝夹角θ共5种工况,即45°,50°,55°,60°和70°.在5种角度下的裂缝等效开裂区域如图 12所示.
图 12(Fig. 12)
 | 图 12 不同角度节理下的裂缝等效开裂区域Fig.12 Equivalent fracture zone under different joint angles (a)—θ=45°;(b)—θ=50°;(c)—θ=55°;(d)—θ=60°;(e)—θ=70°. |
以θ=45°的水力压裂过程为例,裂缝内水压力在142,477, 1 017 s时出现波动,对应的裂缝等效开裂区域如图 13所示.从图 14所示的水压力发展过程可以看出,当t=142 s裂缝初步扩展,此时水压力出现骤降现象,随后持续注水至t=477 s时,裂缝扩展开始受到节理的影响,水压力再次先上升后下降,当t=1 017 s时,裂缝已与节理产生相互作用,水压力下降后略微上升.
图 13(Fig. 13)
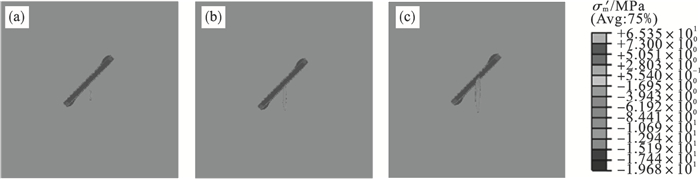 | 图 13 节理存在下的裂缝发展过程(θ=45°,hl=150 mm)Fig.13 Fracture development process with joints(θ=45°, hl=150 mm) (a)—t=142 s;(b)—t=477 s;(c)—t=1 017 s. |
图 14(Fig. 14)
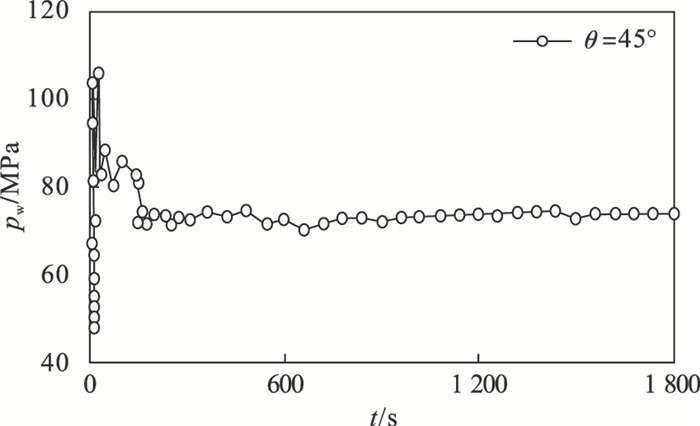 | 图 14 节理存在下的裂缝水压力(θ=45°,hl=110 mm)Fig.14 Fracture water pressure in the presence of joints(θ=45°, hl=110 mm) |
节理对裂缝等效开度的影响如图 15所示.当有节理存在时,初始裂缝等效开度增长较无节理存在时快,节理角度较大时增长会更快;当裂缝扩展直至节理附近,裂缝等效开度的增长减缓,节理角度较小时裂缝等效开度会低于无节理存在的情况,但当节理角度较大时,减缓现象不明显,裂缝等效开度一直增长;当裂缝与节理作用一段时间后,节理角度较小时裂缝等效开度的增长再次加快,角度较大时,裂缝等效开度增长幅度放缓;当压裂完成后,节理角度较大与较小情况的注水点位置处裂缝等效开度差距不大,但均大于无节理存在时的情况.
图 15(Fig. 15)
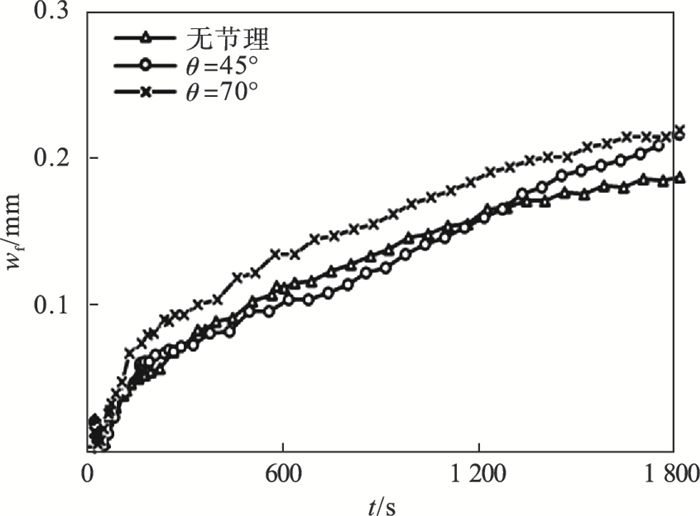 | 图 15 不同节理角度以及无节理时裂缝等效开度对比(θ=45°,θ=70°,hl=150 mm)Fig.15 Comparison of equivalent fracture opening under different joint angles and no joint (θ=45°, θ=70°, hl=150 mm) |
图 16~图 18分别为水平方向扰动峰值应力σ0、峰值位置X0和距离注水点250 mm处位置的最小主应力方向角θ受归一化节理入射角度的影响.计算结果表明:节理入射角度增加使得σ0和最小主应力增量均增大,且X0更接近裂缝,因此在较大入射角度情况下,距离裂缝更近位置受到的应力阴影效应更强;同时θ沿顺时针方向增大,裂缝弯曲程度增大,受到的应力阴影效应亦增大.
图 16(Fig. 16)
 | 图 16 节理角度对裂缝水平扰动应力峰值影响Fig.16 Influence of different joint angles on the peak value of horizontal disturbance stress of fractures |
图 17(Fig. 17)
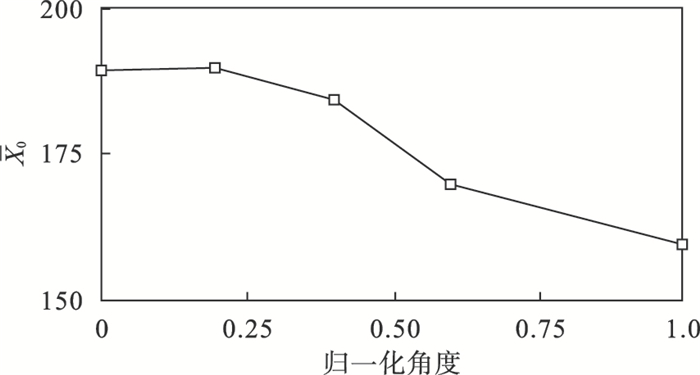 | 图 17 节理角度对裂缝水平扰动应力峰值位置影响Fig.17 Influence of different joint angles on peakvalue position of horizontal disturbance stress of fractures |
图 18(Fig. 18)
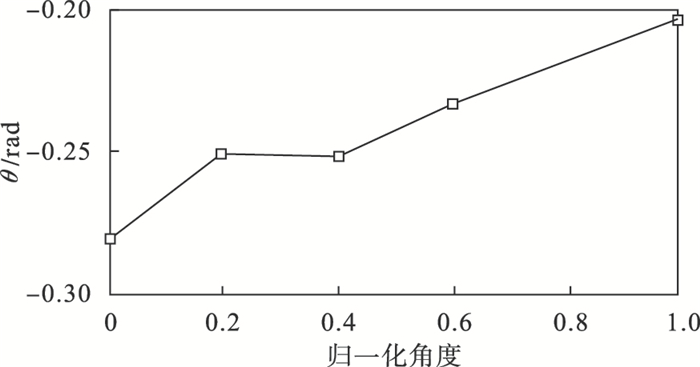 | 图 18 不同节理角度下的最小主应力方向Fig.18 Direction of minimum principal stress under different joint angles |
3.3 节理与注水点间高度当注水位置与节理之间的高度h1在110 mm到150 mm变化时,对应的裂缝等效开裂区域如图 19所示.以h1=110 mm为例,裂缝等效开裂区域和水压力发展过程分别如图 20和图 14所示,可以看出当t=80 s时,裂缝内水压力出现下降阶段,且较h1=150 mm的情况更早;当t=352 s时,裂缝接近并与节理发生相互作用,水压力下降且下降程度大于hl=150 mm的工况.
图 19(Fig. 19)
 | 图 19 不同节理高度下的裂缝等效开裂区域Fig.19 Equivalent fracturing area of fractures under different joint heights (a)—h1=110 mm;(b)—h1=120 mm;(c)—h1=130 mm;(d)—h1=140 mm;(e)—h1=150 mm. |
图 20(Fig. 20)
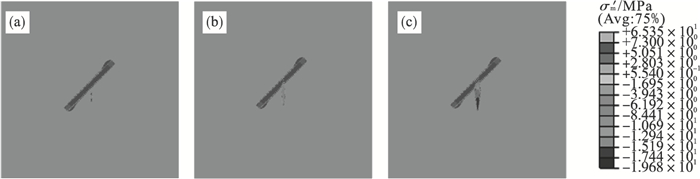 | 图 20 节理存在下的裂缝发展过程(hl=110 mm)Fig.20 Fracture development process with joints(h1=110 mm) (a)—t=80 s;(b)—t=352 s;(c)—t=995 s. |
4 结论1) PHF-LSM模型计算的裂缝等效开度选取等效开裂区域两端结点位移差为宜.
2) 节理的存在会对裂缝内水压力与等效开度的变化产生影响,较大的入射角度与距注水点较小的高度均增加注水点处的裂缝等效开度.
3) 较大入射角与距注水点高度较小的节理会使裂缝水平诱发应力增大,且峰值位置更靠近裂缝,带来的应力阴影效应更大.
4) 当节理入射角度增加或距注水点高度减小时,裂缝周围最小主应力角度沿着顺时针方向增加.
参考文献
| [1] | 杨洁, 荣冠, 程龙, 等. 节理峰值抗剪强度试验研究[J]. 岩石力学与工程学报, 2015, 34(5): 884-894. (Yang Jie, Rong Guan, Cheng Long, et al. Experimental study of peak shear strength of rock joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5): 884-894.) |
| [2] | He Q Y, Suorineni F T, Ma T H, et al. Effect of discontinuity stress shadows on hydraulic fracture re-orientation[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91: 179-194. DOI:10.1016/j.ijrmms.2016.11.021 |
| [3] | Green A E, Sneddon I N. The distribution of stress in the neighbourhood of a flat elliptical crack in an elastic solid[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1950, 46(1): 159-163. DOI:10.1017/S0305004100025585 |
| [4] | Zhao C J, Li J, Liu G H, et al. Analysis of well stress with the effect of natural fracture nearby wellbore during hydraulic fracturing in shale gas wells[J]. Journal of Petroleum Science and Engineering, 2020, 188: 106885. DOI:10.1016/j.petrol.2019.106885 |
| [5] | Wang Y J, Zhang Z N. Fully hydromechanical coupled hydraulic fracture simulation considering state transition of natural fracture[J]. Journal of Petroleum Science and Engineering, 2020, 190: 107072. DOI:10.1016/j.petrol.2020.107072 |
| [6] | Zhang Q, Zhang X P, Sun W. Hydraulic fracturing in transversely isotropic tight sandstone reservoirs: a numerical study based on bonded-particle model approach[J]. Journal of Structural Geology, 2020, 136: 104068. DOI:10.1016/j.jsg.2020.104068 |
| [7] | Zhao K K, Stean D, Kang H P, et al. Investigating the interaction of hydraulic fracture with pre-existing joints based on lattice spring modeling[J]. Computers and Geotechnics, 2020, 122: 103534. DOI:10.1016/j.compgeo.2020.103534 |
| [8] | Zhang H, Sheng J J. Numerical simulation and optimization study of the complex fracture network in naturally fractured reservoirs[J]. Journal of Petroleum Science and Engineering, 2020, 195: 107726. DOI:10.1016/j.petrol.2020.107726 |
| [9] | Rashid Y R. Ultimate strength analysis of prestressed concrete pressure vessels[J]. Nuclear Engineering and Design, 1968, 7(4): 334-344. DOI:10.1016/0029-5493(68)90066-6 |
| [10] | Li M, Guo P J, Stolle D F E, et al. Modeling method and hydraulic fracture propagation for jointed rock mass using PHF-LSM method[J]. Journal of Natural Gas Science and Engineering, 2019, 68: 102910. DOI:10.1016/j.jngse.2019.102910 |
| [11] | Li M, Guo P J, Stolle D F E, et al. Development of hydraulic fracture zone in heterogeneous material based on smeared crack method[J]. Journal of Natural Gas Science and Engineering, 2016, 35: 761-774. DOI:10.1016/j.jngse.2016.09.018 |
| [12] | Li M, Guo P J, Stolle D F E, et al. Modeling method for a rock matrix with inclusions distributed and hydraulic fracturing characteristics[J]. Journal of Petroleum Science and Engineering, 2017, 157: 409-421. DOI:10.1016/j.petrol.2017.07.017 |
| [13] | 李明, 郭培军, 李鑫, 等. 基于水平集法的非均质岩石建模及水力压裂传播特性研究[J]. 岩土力学, 2016, 37(12): 3591-3597, 3607. (Li Ming, Guo Pei-jun, Li Xin, et al. Modelling method of heterogeneous rock material based on level set method and hydraulic fracture propagation features[J]. Rock and Soil Mechanics, 2016, 37(12): 3591-3597, 3607.) |
| [14] | Li M, Guo P J, Stolle D F E, et al. Heterogeneous rock modeling method and characteristics of multistage hydraulic fracturing based on the PHF-LSM method[J]. Journal of Natural Gas Science and Engineering, 2020, 83: 103518. DOI:10.1016/j.jngse.2020.103518 |
| [15] | Li M, Guo P J, Stolle D F E, et al. Modeling hydraulic fracture in heterogeneous rock materials using permeability-based hydraulic fracture model[J]. Underground Space, 2020, 5(2): 167-183. DOI:10.1016/j.undsp.2018.12.005 |
| [16] | Wasantha P L P, Konietzky H, Xu C. Effect of in-situ stress contrast on fracture containment during single-and multi-stage hydraulic fracturing[J]. Engineering Fracture Mechanics, 2019, 205: 175-189. DOI:10.1016/j.engfracmech.2018.11.016 |
| [17] | Sneddon I N, Elliot H A. The opening of a Griffith crack under internal pressure[J]. Quarterly of Applied Mathematics, 1946, 163: 262-267. |
| [18] | Rahman M M, Rahman M K. A review of hydraulic fracture models and development of an improved pseudo-3D model for stimulating tight oil/gas sand[J]. Energy Sources, Part A: Recovery, Utilization and Environmental Effects, 2010, 32(15): 1416-1436. DOI:10.1080/15567030903060523 |
| [19] | 刘宝. 湖南省道县螃蟹木矿区锡矿普查区域地质特征[J]. 世界有色金属, 2020(19): 180-181. (Liu Bao. Regional geological characteristics of tin deposit survey in shicrab mining area, Dao County, Hunan Province[J]. World Nonferrous Metals, 2020(19): 180-181. DOI:10.3969/j.issn.1002-5065.2020.19.087) |
