刘克奇¹, 杜佃春², 赵文¹, 丁万涛³
1. 东北大学 资源与土木工程学院，辽宁 沈阳 110819;
2. 东南大学 土木工程学院，江苏 南京 211189;
3. 山东大学 齐鲁交通学院，山东 济南 250061
收稿日期：2022-07-05
基金项目：中央高校基本科研业务费专项资金资助项目(N2201017)；山东省自然科学基金资助项目(ZR2021ME135)。
作者简介：刘克奇(1991-)，男，陕西商洛人，东北大学讲师，博士;
赵文(1962-)，男，辽宁沈阳人，东北大学教授，博士生导师。

摘要：探明泥水盾构施工过程中关键掘进参数(如刀盘转速、主推进力、刀盘扭矩等)对开挖面泥浆支护效果及盾构能耗的影响规律，是保障盾构快速掘进和降低盾构机械损耗的重要前提.本研究依托济南穿黄隧道东线盾构项目掘进参数集计算各掘进环的场切深指数(FPI)和扭矩切深指数(TPI)；采用掘进比能将掘进参数集划分为优配数据集以及待优化数据集，并分别基于支持向量回归和人工神经网络方法建立了关键掘进参数的预测模型.结果表明：盾构场切深指数和扭矩切深指数可有效描述掘进地层的同一性.盾构掘进比能呈对数正态分布特征，可有效表征盾构掘进工作状态并评估盾构各项掘进参数的配置水平.同一地层中当盾构掘进能耗水平波动较大时宜采用人工神经网络预测模型对刀盘转速以及盾构主推进力进行优化.
关键词：泥水盾构掘进参数掘进比能机器学习预测模型
Machine Learning-Based Prediction and Optimization of Slurry Shield's Key Tunneling Parameters
LIU Ke-qi¹, DU Dian-chun², ZHAO Wen¹, DING Wan-tao³
1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. School of Civil Engineering, Southeast University, Nanjing 211189, China;
3. School of Qilu Transportation, Shandong University, Jinan 250061, China
Corresponding author: ZHAO Wen, E-mail: zhaowen@mail.neu.edu.cn.

Abstract: Investigating the impact of key tunneling parameters, such as cutter-head rotation speed, main thrust, and cutter-head torque, on the slurry support effect at the tunnel face and energy consumption during slurry shield construction is a crucial requirement to ensure efficient and rapid tunneling while minimizing the shield's mechanical losses. The tunneling parameters from the shield tunneling project of Jinan East Line Tunnel across Yellow River were used to calculate the field penetration index(FPI)and the torque penetration index(TPI)for each tunneling ring. The tunneling parameter set was divided into the optimal data set and the data set to be optimized using the excavation specific energy, and the prediction models of key tunneling parameters were established based on the support vector regression and artificial neural network methods respectively. The results showed that FPI and TPI can effectively describe the homogeneity of the excavated strata. The shield's excavation specific energy is log-normally distributed, which can be used to describe the shield's excavation working condition and assess the configuration level among the slurry shield's tunneling parameters. The artificial neural network prediction model is suitable for optimizing the cutter-head rotation speed and the shield's jacking force when the energy consumption level of shield tunneling fluctuates significantly in the homogeneous strata.
Key words: slurry shieldtunneling parameterexcavation specific energymachine learningprediction model
盾构施工需根据地层条件的变化实时调整掘进参数(如同步注浆量、推进力、贯入度、刀盘转速等)进而控制工作仓压力，以求在掌子面上施加有效支护力以平衡掌子面前方水土合力^[1].但因地层条件的复杂性，需实时对掘进参数作出合理且有效的控制，以求在维持开挖面稳定的同时降低盾构机能耗.根据地层参数确定目标支护力是稳定性控制的基础^[2]，而通过掘进参数的优化配置实现开挖面的有效支护是实现盾构掘进掌子面稳定性控制乃至智能掘进的关键^[3].
已有研究表明^[4]，盾构掘进参数同时受到地层条件、隧道几何参数以及盾构设计参数等众多因素的影响.为系统研究泥水盾构掘进过程中掌子面的动态平衡过程以及掘进参数优化方法，国内外****研制了一系列泥水平衡盾构模拟试验设备.Mori团队^[5]研制了?250泥水盾构试验装置，从泥水平衡盾构支护机理和掘进参数控制等方面研究了泥水盾构的掘进过程.袁大军等^[6]研制了?300泥水盾构掘进试验装置并开展了泥水盾构开挖面土体劈裂和泥浆喷发现象的研究.虽然模型试验装置能够在一定程度上还原盾构掘进过程，但是由于盾构施工过程的复杂性，依靠模型试验以及理论分析手段较难描述关键掘进参数变化规律及其优化调控方法^[7].
近年来随着机器学习与大数据技术的快速发展，一批新的研究手段在该领域表现出巨大潜力.在掘进参数预测方面，何然^[8]采用Elman-PSO耦合智能算法建立了泥水盾构掘进参数智能预测系统并实现了气仓压力预测；王传俭^[9]结合填海区复杂地层盾构工程，建立了基于Python语言的BP(back propagation)神经网络模型^[10]来预测盾构掘进参数.此外，粒子群算法^[11]、模糊逻辑理论^[12]、支持向量回归^[13]以及多元回归分析^[14]等诸多方法均在盾构掘进参数预测中表现出明显优势.在掘进参数的评估方面，Zare等^[15]基于预测掘进速度和滚刀损耗的NTNU模型，对掘进过程中时间和成本进行了评估并取得良好效果.合理的掘进参数可提高掘进效率，避免发生事故，在保障施工安全的同时最大限度降低掘进能耗^[16]和碳排放.
本研究依托济南穿黄隧道盾构工程，基于开挖面稳定性和掘进过程观测对原始掘进参数进行筛选以保证分析数据的有效性，在此基础上利用机器学习建立掘进参数的预测模型对关键掘进参数进行预测，同时依据盾构掘进能耗指标对掘进参数进行优化，以期在保证盾构安全掘进的同时降低盾构能耗.
1 工程概况济南轨道交通M2线济泺路穿黄隧道工程长3 890 m(盾构段长2 519 m)，开挖外径15.2 m，是超大直径盾构机首次穿越地上悬河.项目有深基坑、浅覆土、大直径、长距离、高水压、首次穿越地上悬河等特点，施工难度大、风险高，被誉为“万里黄河第一隧”.盾构隧道穿越地层主要为第四系上更新统(Q3)，可塑-硬塑状粉质黏土，局部夹钙质结核层、砂层，结核层呈透镜体状不均匀分布，局部富集成层，呈中密散粒状或胶结呈大块状.盾构隧道最小覆土11.2 m，最大覆土42.3 m，穿黄段覆土25~38 m，隧顶距离最大冲刷包络线约14.3~30.0 m(图 1).
图 1(Fig. 1)

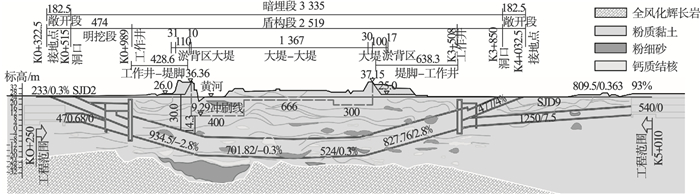图 1 济南穿黄隧道纵断面设计(单位：m)Fig.1 Longitudinal section design of Jinan Tunnel across Yellow River(unit: m)

2 盾构掘进数据预处理济南穿黄隧道东线设计全长共1 240环，收集盾构掘进过程中10个掘进参数：泥浆仓压力、刀盘转速、刀盘扭矩、刀盘主推进力、刀盘挤压力、盾构掘进速度、给料管流量与密度、出料管流量与密度.限于篇幅图 2仅展示部分参数平均值随掘进环数的变化曲线.
图 2(Fig. 2)

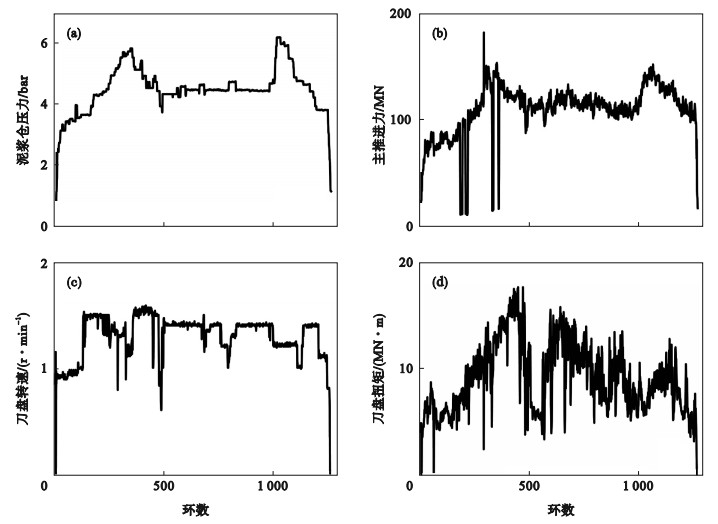图 2 济南穿黄隧道东线1 240环盾构掘进参数变化曲线Fig.2 Shield tunneling parameters for the 1 240 ring of Jinan East Line Tunnel across Yellow River (a)—泥浆仓压力；(b)—主推进力；(c)—刀盘转速；(d)—刀盘扭矩.

由于地层条件的突变导致人工操作失误或者机械故障，盾构机会产生一些异常值以及数据缺失^[17]，异常值和缺失值在数据集中都表现出不合理性，在模型构建前需对数据集进行识别并予以修正.异常值检验就是通过多种检测手段找出数据特征不同于预期效果的数据点的过程，通常异常值识别可以借助图形法(如箱线图、正态分布图)和建模法(如线性回归、聚类算法、K近邻算法)，本文使用统计学中的箱线图法^[18]进行异常值检测.
以主推进力为例说明数据预处理过程，原始数据分布见图 3a.通过上述箱线图法检测到原始数据中的异常值之后，将异常值置空，筛选之后的数据分布情况见图 3b.然后进行数据集中的空值检测，并采用移动滑窗算法^[19](sliding window algorithm，SWA)对空值进行插补，采用滑窗内所有数据的中位数来代替空值，补全之后的数据分布情况见图 3c.本研究中采用滑窗大小为30，同时对补全后的数据进行平滑处理以降低数据在小范围内的波动性，平滑处理之后的数据分布见图 3d.
图 3(Fig. 3)

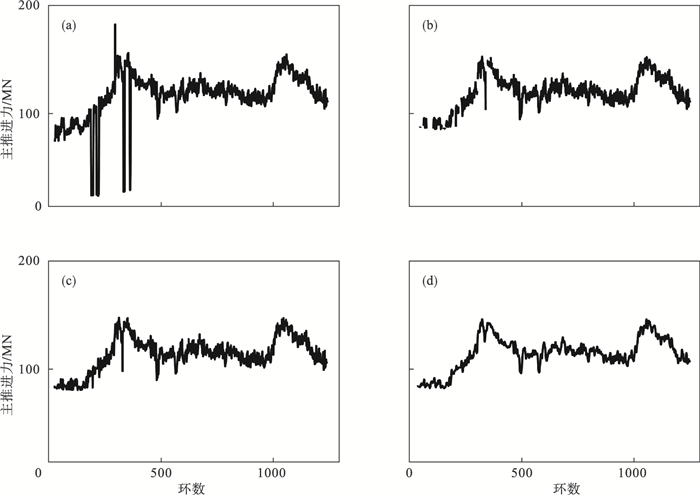图 3 原始掘进参数异常值检测及修正Fig.3 Detection and correction of outliers for the original tunneling parameter (a)—原始数据；(b)—去除异常值；(c)—数据补全；(d)—数据平滑.

3 盾构掘进能耗评估3.1 盾构掘进地层同一性判别为了在盾构掘进过程中维持掌子面的动态稳定，需要在泥浆仓内提供足够的支护压力，但是能够达到相同的泥浆仓支护效果的掘进参数组合是多种多样的.不同地层中的盾构掘进能耗差异难以避免，因此地层条件不同时对盾构掘进能耗进行比较是没有意义的.研究表明^[20]，盾构单圈切深S(即贯入度)的大小能够直观反映土层掘进的难易程度.在相同的盾构主推进力条件下单圈切深大表明刀盘前方的土质较软，更容易被切削挖掘；单圈切深小则表明土质较硬，土体难以被切削破坏.为了综合分析主推进力和单圈切深对土体掘进难易程度的反馈，采用场切深指数^[7](field penetration index，FPI)来表征土体抵抗刀具切入的能力.

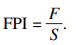(1)

式中：F代表刀盘主推进力(MN)；S为刀具单圈切深即刀盘的贯入度(mm/r)，是盾构的掘进速度v_e(mm/min)与刀盘转速ω(r/min)的比值.场切深指数(FPI)表示盾构掘进单位切深所需推进力，代表土层抵抗刀具切入的能力，具有明确的物理意义.
同理，采用扭矩切深指数(torque penetration index，TPI)来描述盾构机刀盘完成单位切深与掌子面之间的摩擦阻力矩.

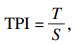(2)

式中T代表刀盘扭矩(MN·m).
采用FPI和TPI分析穿黄隧道东线盾构掘进数据见图 4.从图中可以看出，在整个掘进过程中的盾构机FPI和TPI都存在较为明显的波动性，即表明盾构机工作状态的波动性，究其原因除了地层参数的变化以外，人工操作水平的波动性也是必须考虑的重要因素之一.
图 4(Fig. 4)

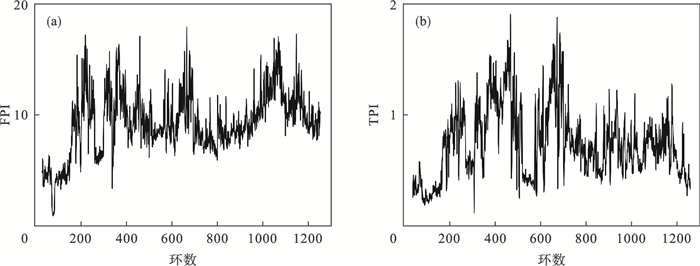图 4 FPI和TPI随掘进环数变化曲线Fig.4 FPI and TPI variation curves with the number of rings (a)—FPI；(b)—TPI.

图 5反映了FPI和TPI之间相对变化关系，可知FPI与TPI的分布大致呈现线性变化规律，这是因为较大的刀具切深往往伴随着较大的刀盘扭矩.图 5a展示的是原始数据计算结果分布情况，可知异常值的存在使得计算结果的分布范围明显超出了整体数据集合理的分布范围，且不符合FPI与TPI之间的整体变化规律.图 5b展示的是经过异常值处理以后的计算结果分布，可知本文采用的异常值处理方法能够有效地把异常值“拉回”到合理的分布区间.已有研究^[7]表明，在不同的地层中盾构掘进FPI与TPI的特征空间存在较大差异，黏性土、砂土和砂砾地层之间存在明显的界限，其中黏性土地层中盾构掘进FPI和TPI的分布范围均较小，FPI的分布范围为0~15，而TPI的分布范围为0~2.5，可知本研究中采集到的盾构掘进参数表现出较强的同一性，即属于同一类型(粉质黏土)土体中的掘进参数.
图 5(Fig. 5)

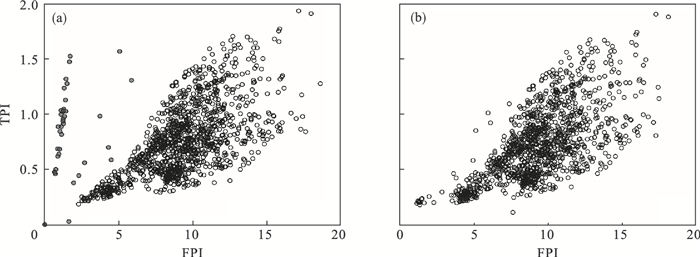图 5 盾构掘进FPI与TPI分布规律Fig.5 Distribution pattern of FPI and TPI during shield tunneling (a)—原始数据；(b)—修正数据.

3.2 盾构掘进能耗评估实际工程中盾构掘进前依据地勘资料及盾构掌子面地质状况初步计算掌子面所需的支护力，并采用试掘进的方法不断人工调整各项掘进参数.但是由于初期勘察只能粗略了解隧道沿线的地质状况，整个掘进路线上的详细地层参数未知且变化范围较大，使得掘进过程中刀盘负载多变且具有很强的非线性.不合理的掘进参数组合将会造成掌子面支护效果不佳(如支护机制不稳定、泥浆损耗过大等)以及盾构机的能耗过高.本研究采用掘进比能^[20]对收集到的1 240环有效掘进参数进行量化分析，筛选其中配置较优的掘进参数组合并进一步开展研究.定义盾构机掘进单位体积土体消耗的能量为盾构掘进比能，则掘进比能的计算公式为

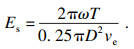(3)

式中：E_s为盾构掘进比能(kW·h/m³)；ω为刀盘转速(r/min)；D为盾构机刀盘直径(m)；v_e为盾构掘进速度(mm/min).因为刀盘转速ω和盾构掘进速度v_e之比为刀盘的贯入度S，因此式(3)可以变形为

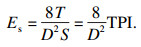(4)

可见盾构掘进比能与盾构扭矩切深指数是线性相关的，相关性系数由盾构机刀盘直径确定.
图 6展示了掘进比能随刀盘贯入度的变化曲线，从图中可以看出盾构掘进比能分布总体上随着刀盘贯入度的增大呈现负指数减小的趋势.图 6中同时展示了杨果林等^[20]基于现场数据得到的典型地层中的盾构掘进比能随刀盘贯入度的变化规律，可知典型地层中刀盘掘进比能的变化趋势与本文数据拟合变化规律基本一致.
图 6(Fig. 6)

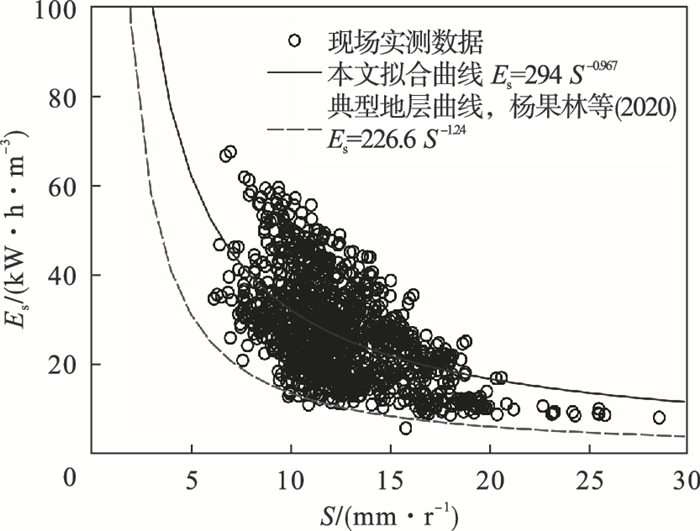图 6 掘进比能-贯入度变化曲线Fig.6 Variation curves of excavation specific energy with penetration

计算穿黄隧道东线工程盾构掘进过程中掘进比能的概率密度函数(probability density function, PDF)分布见图 7，数据集的均值为37，可知相比于正态分布，对数正态分布能够更好地描述数据集的概率密度函数分布规律.在地层条件相近的情况下，盾构掘进比能可量化评估盾构掘进参数配置的合理性，而对数正态分布能够很好地说明盾构机在不同参数组合状态下掘进比能的分布特征.在后续的研究中当盾构机的掘进比能低于均值时，认为掘进参数配置良好，反之则认为掘进参数的配置不合理.鉴于上述分析，以掘进比能的均值作为标准对盾构掘进参数组合进行筛选，选择掘进比能小于均值的掘进参数作为优配数据集并开展掘进参数预测模型的构建.
图 7(Fig. 7)

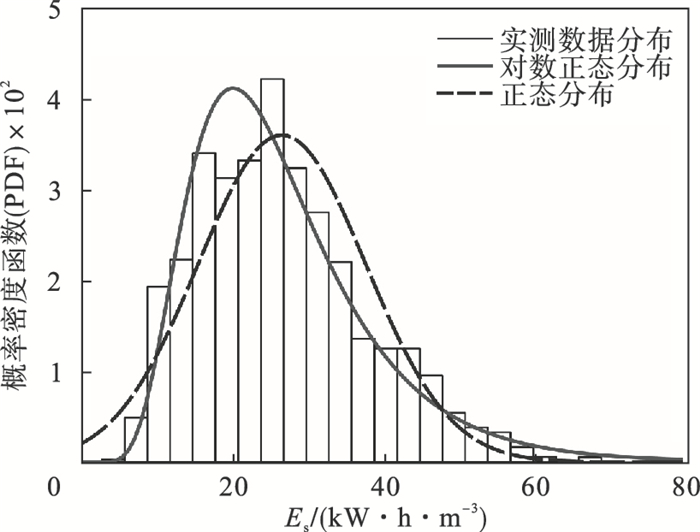图 7 掘进比能分布概率密度函数Fig.7 Probability density function of Es

4 基于机器学习的盾构掘进参数预测模型鉴于盾构掘进参数配置水平的不稳定性以及各项掘进参数间影响规律的高度非线性，建立有效的预测模型完成关键掘进参数的预测及优化，这对于盾构施工而言意义重大.依据盾构掘进比能选取济南穿黄隧道东线1 240环施工数据中的719环掘进数据建立预测模型，将盾构机刀盘主推进力、刀盘转速、刀盘扭矩3个参数作为输出参数，将泥浆仓压力、盾构掘进速度、给料管流量与密度、出料管流量与密度、刀盘挤压力7个参数作为输入参数.
4.1 数据归一化处理因原始数据集中不同特征值的单位和量级差异较大，会导致预测模型的参数计算效率低下，对数据集的单位进行归一化处理，计算公式如下:

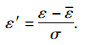(5)

式中：ε代表原始特征值；ε代表原始特征的均值；σ代表原始特征数据的标准差.
4.2 支持向量回归预测模型支持向量机(support vector machine, SVM)作为一种强大而通用的方法可以处理线性/非线性分类、回归，甚至离群点检测等问题^[21].线性SVM分类器模型通过计算决策函数W^T·x+b=w₁x₁+w₂x₂+…+w_nx_n+b来预测新的实例x所属类别.基于决策函数，预测结果如式(6)所示:

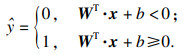(6)

式中：W为权重参数；x=[x₁, x₂, …, x_n].
相比于硬间隔线性SVM(hard margin support vector machine)，软间隔线性SVM(soft margin support vector machine)往往具有更好的泛化能力，并且可以有效地避免模型的过拟合问题，往往具有较高的应用价值，其条件极值可表示为

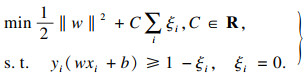(7)

式中：常数C为惩罚系数，作为一个超参数它代表决策过程是更看重决策边界的宽度，还是更希望减少错误点的数量；ξ_i是一个松弛变量，用来衡量第i个错误数据偏离决策边界的程度，上述条件极值求解的最终目的，就是要在无数个w和b中挑选最优解使得决策边界最大、错误数据最少.
支持向量回归(support vector regression, SVR)作为SVM的一个子集是回归分析的有效工具之一.SVR不是试图在2个类之间拟合最大的决策边界(SVM分类器)，而是试图在决策边界上拟合尽可能多的实例，同时限制数据在决策边界上违规^[22].核化的支持向量回归算法能够处理非线性回归问题，在众多的核函数中，高斯径向基函数(Gaussian radial basis function, GRBF)因其能将原始特征映射为无限维度而被广泛使用^[23]，其表达式为

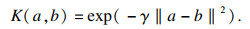(8)

式中：a, b是高斯径向基函数的2个参数；超参数γ定义了单个训练实例的影响程度，scikit learn中默认值取为数据集特征方差的倒数.
在建模过程中需要调整超参数C和γ，其中，超参数C控制着决策边界的大小与违规实例数量之间的平衡，较小的C往往代表较大的决策边界，但会伴随着更多的违规数据出现，反之亦然.与核函数相关的超参数γ代表了单个样本对超平面的影响.本研究中为了获取超参数的最优解，首先分别搜索C和γ的可能分布范围，进而采用贝叶斯优化(Bayesian optimization，BO)算法在超参数可能的分布范围内进行迭代计算.采用BO算法计算目标函数和超参数，计算结果如图 8、图 9所示.
图 8(Fig. 8)

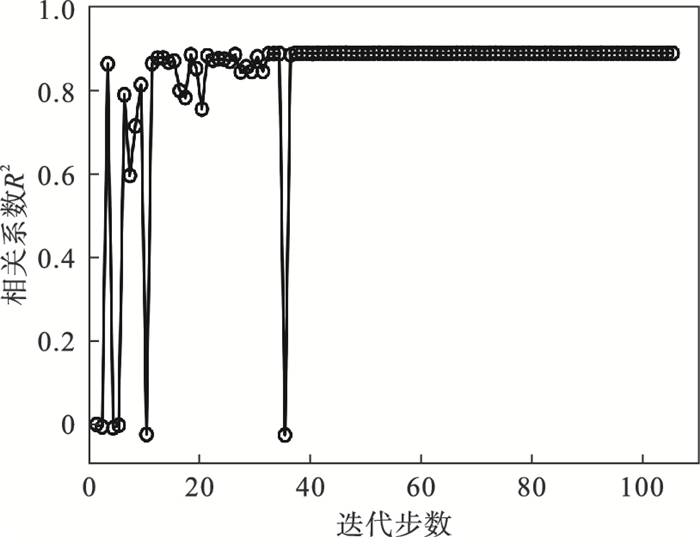图 8 BO优化目标函数变化曲线Fig.8 Variation curve of the objective function in BO optimization

图 9(Fig. 9)

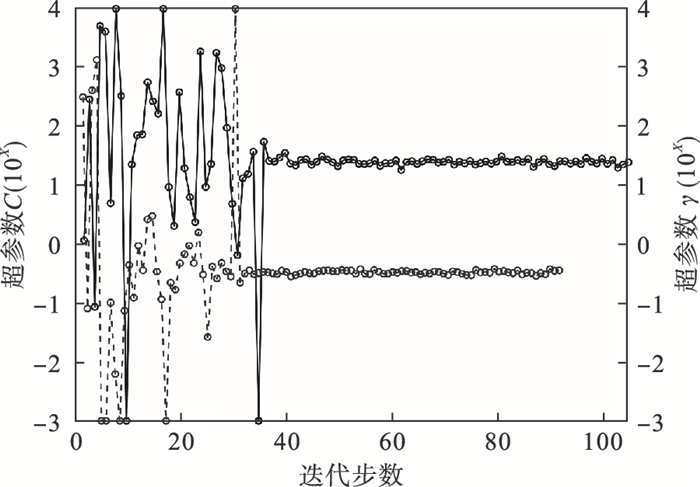图 9 BO优化超参数取值变化曲线Fig.9 Variation curves for the value of hyperparameters in BO optimization

计算结果表明，采用BO算法对超参数最优解进行搜索，当迭代步数约为40时计算结果即趋于稳定，表明该算法的计算效率较高.优化结果表明当C和γ分别为25(10^{1.398 0})和0.34(10^-0.473)时，该模型在测试集上表现最好，优化目标R²为0.900 6.
4.3 人工神经网络(ANN)预测模型人工神经网络(artificial neural network, ANN)是一种通过模拟生物神经元的功能来处理数据的强大算法^[24].ANN使用连接函数将特征与目标关联起来.神经网络有2个过程即前向传播和后向传播.在前向传播过程中，人工神经元对前一层神经元(或输入)的加权输入求和，然后使用激活函数(如ReLU函数、Sigmoid函数、tanh函数等)进行非线性运算.在得到预测目标后，利用预测目标与实际目标之间的距离，采用反向传播调整各层的权值.在后向传播过程中，采用随机梯度下降(stochastic gradient descent, SGD)、均方根传播(root mean square propagation, RMSprop)和自适应矩估计(adaptive moment estimation, Adam)等优化算法对权矩阵(W)和偏差矩阵(B)进行改进.将上述2个过程重复进行，直到预测值与实测值足够接近(通过损失函数测量)，最终确定权矩阵与偏差矩阵.神经网络的一般结构如图 10所示.第l层神经元的计算公式为式(9)~式(14).
图 10(Fig. 10)

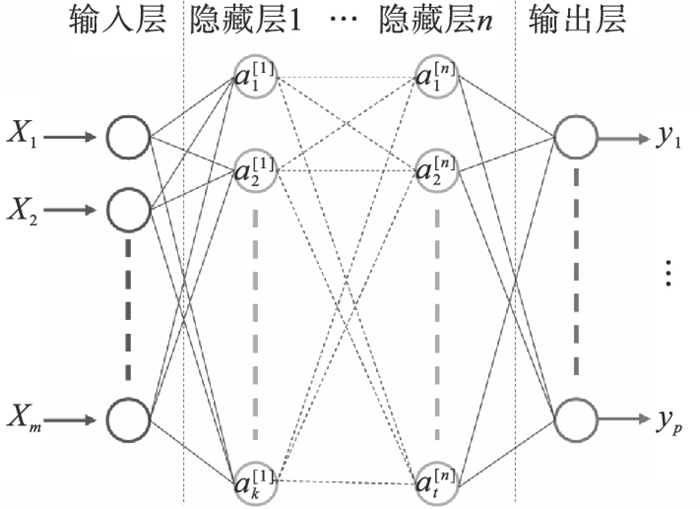图 10 人工神经网络一般结构Fig.10 General structure of an artificial neural network

前向传播：

(9)

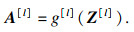(10)

后向传播:

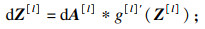(11)

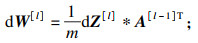(12)

(13)

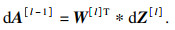(14)

式中：W^[l]，B^[l]分别代表l层的权重矩阵和偏差矩阵；Z^[l]是l层的加权和矩阵; A^[l]是l层中的激活单元，A^[l]=[a₁^[l]??a₂^[l] … a_k^[l]]；g^[l]是l层的激活函数；dZ^[l], dW^[l], dB^[l]分别是加权和矩阵Z^[l]、权重矩阵W^[l]、偏差矩阵B^[l]的导数；dA^[l-1]是l-1层激活单元的导数.
本研究采用人工神经网络(ANN)来预测盾构掘进过程中的关键参数，ANN采用Keras和Tensorflow后端实现.批尺寸(batch size)和历时数分别设置为100和1 000.采用ReLu函数作为激活函数；采用Adam优化器来改进反向传播过程中的权重.考虑到用于分析的数据集的规模较小，本研究建立了一个2层的神经网络，并将每层的神经元数量作为超参数进行优化调整.与此同时，学习率对预测模型的收敛影响显著，因此有必要将学习率作为另外一个超参数进行优化.采用BO算法研究神经元数量在2³~2¹²分布区间以及学习率在10^-4~1分布区间变化时模型的预测效果，优化的目标函数为预测结果的均方误差.通过优化分析最终确定当第一层的神经元数量为1 024个，第二层的神经元数量为2 048个，学习率为0.02时，该模型在训练集上的表现最好，均方误差为0.33.
5 盾构关键掘进参数预测与优化5.1 基于SVR模型的掘进参数预测针对前文依据掘进比能筛选出的719环“优配”数据集开展建模训练，将剩余的521环数据集作为待优化的数据集(预测集).首先采用SVR预测模型对预测集中的刀盘转速、刀盘扭矩及盾构主推进力进行预测，预测结果见图 11~图 13.
图 11(Fig. 11)

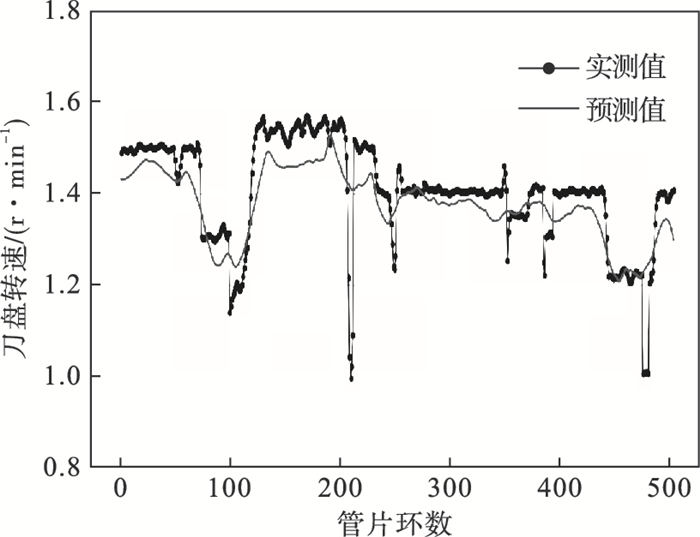图 11 刀盘转速预测值与实测值变化曲线Fig.11 Variation curves between predicted and actual values for cutter-head rotation speed

图 12(Fig. 12)

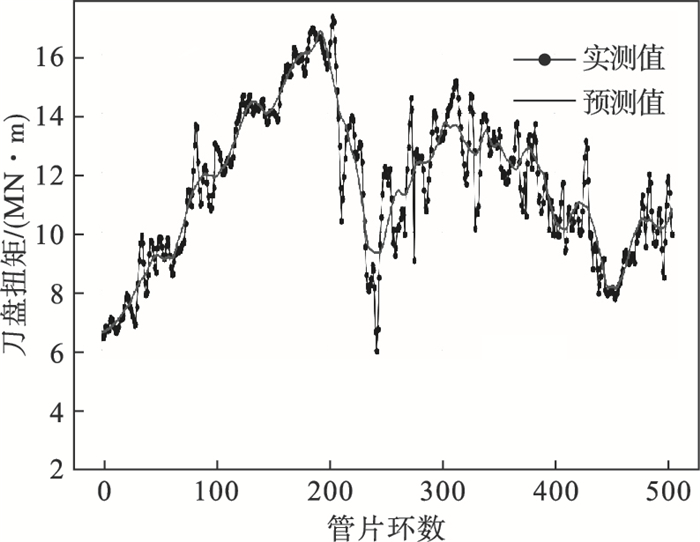图 12 刀盘扭矩预测值与实测值变化曲线Fig.12 Variation curves between predicted and actual values for cutter-head torque

图 13(Fig. 13)

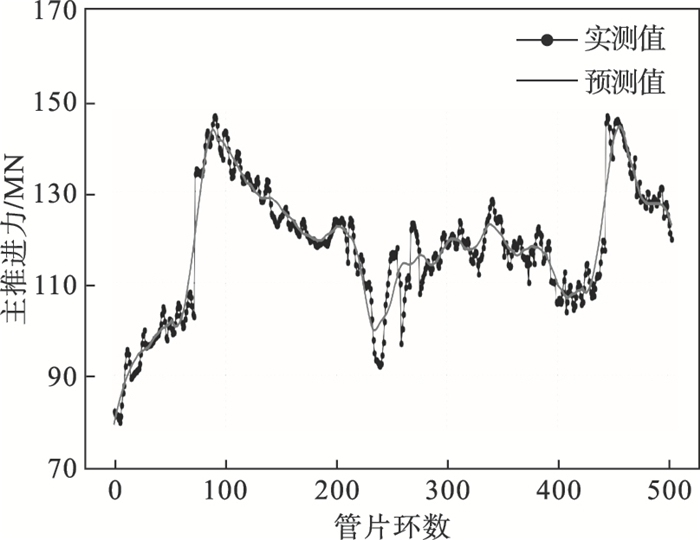图 13 盾构主推进力预测值与实测值变化曲线Fig.13 Variation curves between predicted and actual values for main thrust

由图 11可知，SVR预测模型对刀盘转速的预测结果与真实刀盘转速的变化趋势基本一致，但是部分结果仍与实测值存在较小差距，表现在刀盘转速的预测值较实测值略小，预测值决定系数为0.730 6.由图 11~图 12可知，SVR预测模型能够较好预测刀盘扭矩和盾构主推进力的变化趋势以及大小，预测值决定系数均大于0.9，意味着SVR预测模型能够准确表征盾构掘进的工作状态.
5.2 基于ANN模型的掘进参数预测采用ANN预测模型对预测数据集中的刀盘转速、刀盘扭矩以及主推进力进行预测，见图 14~图 16.由图 14可知，ANN预测模型对刀盘转速的预测基本符合实际工程中刀盘转速的分布范围，即1.0~1.6 r/min，但是刀盘转速的预测值较实测值相比略小.在预测数据集上刀盘转速的预测值决定系数为-1.121 2，均方误差为0.027 2.需要说明的是决定系数为负值表明预测值与实测值之间的误差大于实测值与其均值之间的误差，此时模型的“预测”价值并不明显.由图 14可知，预测数据集上实际刀盘转速的均值明显高于预测刀盘转速的均值，这也是预测值决定系数为负值的原因.
图 14(Fig. 14)

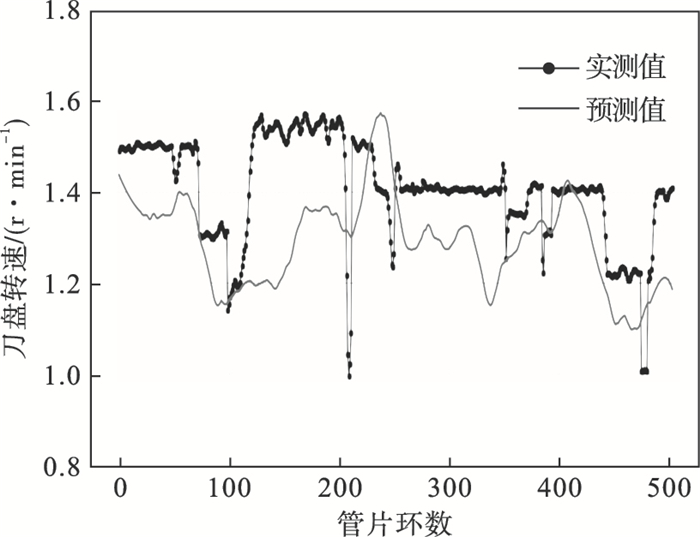图 14 刀盘转速预测值与实测值变化曲线Fig.14 Variation curves between predicted and actual values for cutter-head rotation speed

图 15(Fig. 15)

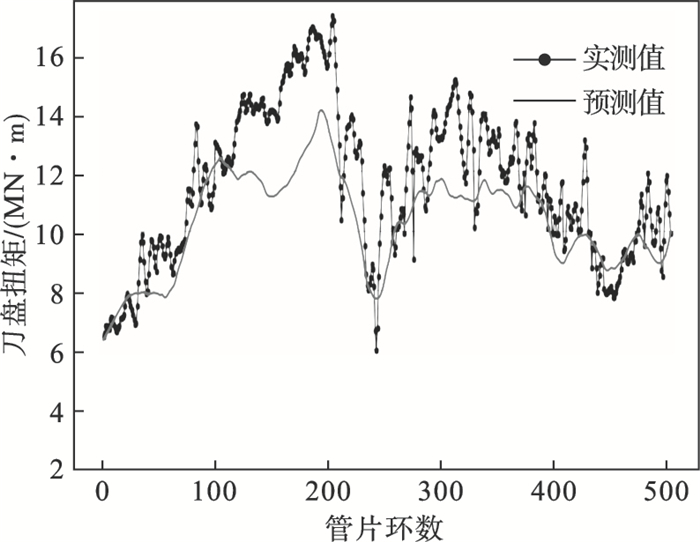图 15 刀盘扭矩预测值与实测值变化曲线Fig.15 Variation curves between predicted and actual values for cutter-head torque

图 16(Fig. 16)

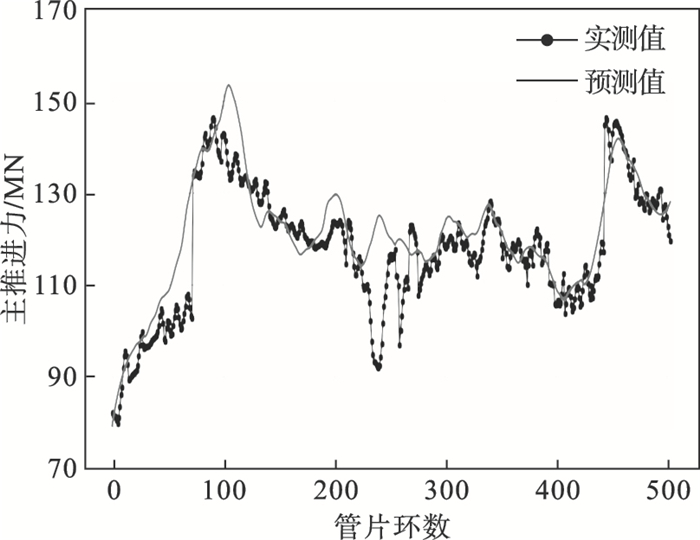图 16 盾构主推进力预测值与实测值变化曲线Fig.16 Variation curves between predicted and actual values for main thrust

图 15和图 16分别展示了预测数据集上刀盘扭矩和盾构主推进力的预测结果与实测数据的比较情况.由图 15可知，当刀盘扭矩较小时ANN预测模型能够较好预测刀盘扭矩，但是当刀盘的扭矩较大时，预测模型得到的预测值明显小于工程实际值.盾构主推进力的预测结果与实际数据间除部分开挖环(220~260环)外变化趋势基本一致.
5.3 盾构关键掘进参数优化分析在待优化数据集中，利用SVR预测模型得到的盾构关键掘进参数重新计算掘进比能，并将其预测值与实际值进行对比见图 17.实测掘进比能的平均值为36.80 kW·h·m^-3，而根据预测模型计算得到的掘进比能平均值为36.12 kW·h·m^-3，表明运用SVR预测模型得到的参数组合使得平均掘进比能降低约1.8%.综合前文SVR预测模型对掘进参数的预测效果可知，SVR预测模型整体上对掘进参数的预测效果较好，但是对于掘进能耗较高的参数集难以达到降低能耗的优化作用，因此该模型的预测功能较好，而优化功能较差.
图 17(Fig. 17)

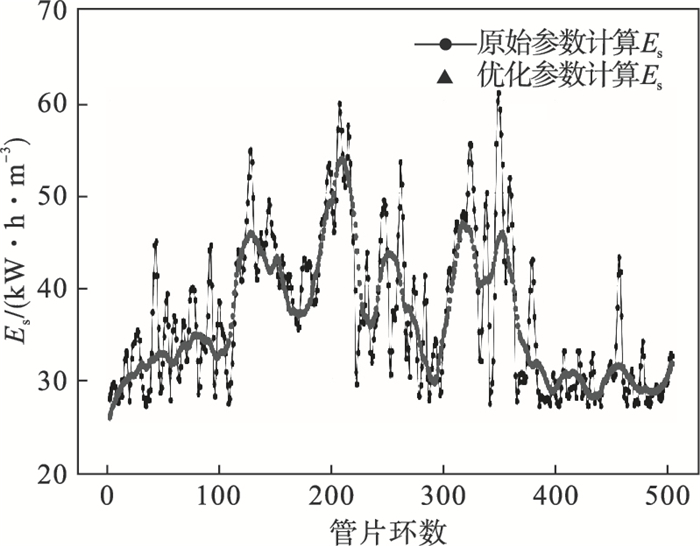图 17 基于SVR预测模型的盾构掘进比能曲线对比Fig.17 Comparison of shield tunneling specific energy based on SVR prediction model

利用ANN预测模型得到的盾构关键掘进参数重新计算盾构掘进比能，并与实测掘进参数的掘进比能进行比较，见图 18.采用ANN预测模型得到的掘进比能的平均值为30.56 kW·h·m^-3，相比于实际掘进比能降低约17%，可见ANN预测模型能够使盾构关键掘进参数之间的配置更加合理，进而显著降低盾构掘进能耗.
图 18(Fig. 18)

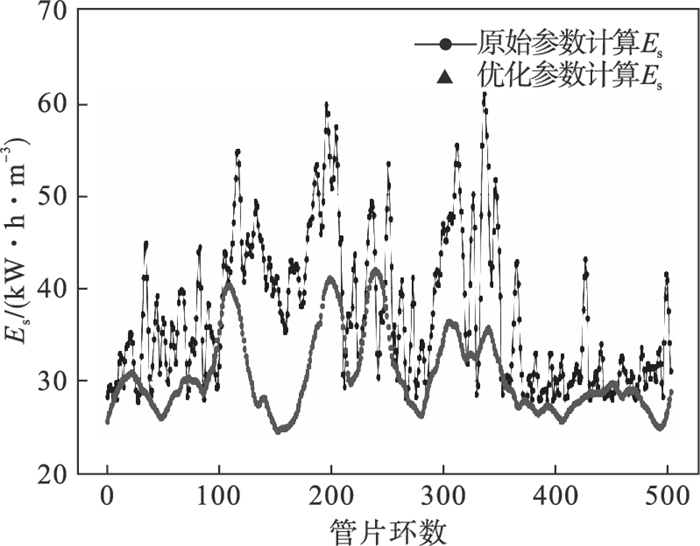图 18 基于ANN预测模型的盾构掘进比能曲线对比Fig.18 Comparison of shield tunneling specific energy based on ANN prediction model

6 结论1) 盾构掘进参数存在局部异常值，采用箱线图法对异常数据的识别效果良好，对异常值和空值进行处理后能够显著提高数据分布的合理性.依据盾构掘进的FPI和TPI可知，该工程获取的10个盾构掘进参数具有较强的地层同一性.
2) 盾构掘进过程中刀盘的贯入度小伴随较大的盾构掘进比能，表明地层的可掘性较差；反之刀盘的贯入度大伴随较小的盾构掘进比能，表明地层的可掘性较强.盾构掘进比能可以有效描述盾构掘进工作状态，且基本符合对数正态分布.
3) 支持向量回归预测模型相对于人工神经网络预测模型对盾构施工关键掘进参数的预测效果更好，但是对待优化数据集的优化效果较差.当盾构掘进能耗较高时，宜采用人工神经网络预测模型根据盾构掘进的速度要求和掌子面支护需求对刀盘的转速以及盾构主推进力进行优化，从而有效降低盾构掘进能耗.
参考文献

[1]	毛家骅. 砂土地层泥水盾构掘进泥浆动态成膜规律及开挖面稳定研究[D]. 北京: 北京交通大学, 2021. (Mao Jia-hua. Research on laws of dynamic filter cake formation and face stability during slurry shield tunnelling in sand stratum[D]. Beijing: Beijing Jiaotong University, 2021. )
[2]	刘克奇, 丁万涛, 陈瑞, 等. 盾构掌子面三维破坏模型构建与极限支护力计算[J]. 岩土力学, 2020, 41(7): 2293-2303, 2469. (Liu Ke-qi, Ding Wan-tao, Chen Rui, et al. Construction of three-dimensional failure model of shield tunnel face and calculation of the limit supporting force[J]. Rock and Soil Mechanics, 2020, 41(7): 2293-2303, 2469.)
[3]	沈翔, 袁大军, 吴俊, 等. 高水压泥水平衡盾构掘进模型试验平台的研制与应用[J]. 中国公路学报, 2020, 33(12): 164-175. (Shen Xiang, Yuan Da-jun, Wu Jun, et al. Development and application of model test platform for slurry balance shield under high water pressure[J]. China Journal of Highway and Transport, 2020, 33(12): 164-175.)
[4]	Mao J H, Yuan D J, Jin D L, et al. Influence of cutting tools on filter cake formation during slurry shield tunnelling[J]. KSCE Journal of Civil Engineering, 2021, 25(6): 2261-2274. DOI:10.1007/s12205-021-1484-9
[5]	Mori A, Kurihara K, Mori H, et al. The mechanism of the increases of the pore water pressure in sandy soils by tunnel driving with slurry type shield[J]. Journal of JSCE, 1991, 430: 115-124.
[6]	袁大军, 黄清飞, 小泉淳, 等. 水底盾构掘进泥水喷发现象研究[J]. 岩石力学与工程学报, 2007, 26(11): 2296-2301. (Yuan Da-jun, Huang Qing-fei, Koizumi Atsushi, et al. Study on slurry-water gushing during underwater shield tunnel construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2296-2301.)
[7]	邢彤, 赵阳. 盾构掘进土层识别及刀盘转速控制策略研究[J]. 浙江工业大学学报, 2010, 38(6): 649-654. (Xing Tong, Zhao Yang. Earth layer recognition during the shield machine digging and control strategy of the cutter head speed[J]. Journal of Zhejiang University of Technology, 2010, 38(6): 649-654.)
[8]	何然. 基于Elman-PSO耦合智能算法的泥水盾构参数预测控制[D]. 武汉: 华中科技大学, 2013. (He Ran. Elman-PSO based predictive control model for slurry shield tunneling in metro construction[D]. Wuhan: Huazhong University of Science and Technology, 2013. )
[9]	王传俭. 基于BP神经网络的填海区复杂地层盾构掘进参数预测与应用[J]. 城市住宅, 2019, 26(2): 129-132. (Wang Chuan-jian. Prediction and application of shield tunneling parameters for complex stratum in reclamation area based on BP neural network[J]. City & House, 2019, 26(2): 129-132.)
[10]	Cachim P, Bezuijen A. Modelling the torque with artificial neural networks on a tunnel boring machine[J]. KSCE Journal of Civil Engineering, 2019, 23(10): 4529-4537.
[11]	Yagiz S, Karahan H. Prediction of hard rock TBM penetration rate using particle swarm optimization[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(3): 427-433.
[12]	Ghasemi E, Yagiz S, Ataei M. Predicting penetration rate of hard rock tunnel boring machine using fuzzy logic[J]. Bulletin of Engineering Geology and the Environment, 2014, 73(1): 23-35.
[13]	Mahdevari S, Shahriar K, Yagiz S, et al. A support vector regression model for predicting tunnel boring machine penetration rates[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 72: 214-229.
[14]	Delisio A, Zhao J. A new model for TBM performance prediction in blocky rock conditions[J]. Tunnelling and Underground Space Technology, 2014, 43: 440-452.
[15]	Zare S, Bruland A. Applications of NTNU / SINTEF drillability indices in hard rock tunneling[J]. Rock Mechanics and Rock Engineering, 2013, 46(1): 179-187.
[16]	Zhou C, Ding L Y, Zhou Y, et al. Hybrid support vector machine optimization model for prediction of energy consumption of cutter head drives in shield tunneling[J]. Journal of Computing in Civil Engineering, 2019, 33(3): 1-17.
[17]	张勇. 基于大数据的盾构机掘进参数研究[D]. 石家庄: 石家庄铁道大学, 2019. (Zhang Yong. Study on tunneling parameters of shield machine based on big data[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2019. )
[18]	Yu X B, Li C L, Chen H, et al. Evaluate the effectiveness of multiobjective evolutionary algorithms by box plots and fuzzy TOPSIS[J]. International Journal of Computational Intelligence Systems, 2019, 12(2): 733-743.
[19]	Ganardi M, Hucke D, Lohrey M. Derandomization for sliding window algorithms with strict correctness[J]. Theory of Computing Systems, 2021, 65(3): 1-18.
[20]	杨果林, 张沛然, 陈亚军, 等. 长沙典型地层土压平衡盾构掘进参数及表现预测[J]. 中南大学学报(自然科学版), 2020, 51(8): 2069-2080. (Yang Guo-lin, Zhang Pei-ran, Chen Ya-jun, et al. Excavation parameters and performance prediction of earth pressure balance shield in typical strata of Changsha[J]. Journal of Central South University(Science and Technology), 2020, 51(8): 2069-2080.)
[21]	Géron A. Hands-on machine learning with scikit-learn, keras, and tensorFlow: concepts, tools, and techniques to build intelligent systems[M]. Sebastopol: O'Reilly Media, 2019.
[22]	Harris C R, Millman K J, van der Walt S J, et al. Array programming with NumPy[J]. Nature, 2020, 585(7825): 357-362.
[23]	Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: machine learning in Python[J]. Journal of Machine Learning Research, 2011, 12: 2825-2830.
[24]	Alnaggar M, Bhanot N. A machine learning approach for the identification of the lattice discrete particle model parameters[J]. Engineering Fracture Mechanics, 2018, 197: 160-175.