
 , 王占生2, 贾鹏蛟1
, 王占生2, 贾鹏蛟1 1. 苏州大学 轨道交通学院,江苏 苏州 215000;
2. 苏州轨道交通集团有限公司,江苏 苏州 215004
收稿日期:2022-06-21
基金项目:国家自然科学基金资助项目(52278405)。
作者简介:陈城(1993-),男,江苏盐城人,苏州大学博士研究生;
史培新(1975-), 男, 江苏溧阳人, 苏州大学教授,博士生导师。
摘要:盾构荷载作为盾构的主要性能指标,准确的荷载预测对于保证盾构安全高效工作和周边环境稳定具有重要意义.鉴于传统预测方法精度差的局限性,本研究以数据的高维度特征和时序特征为切入点,提出一种结合卷积神经网络、双向长短期记忆神经网络和注意力机制的混合模型(CNN-BiLSTM-Multiattention,CBM),对盾构荷载进行精准预测.该模型不仅可以提取数据的高维度特征和时序特征,还能突出高维度特征的重要性和关键时间节点信息.通过实验证明了相较于4种现有的模型,本文所提出的模型在3种评价指标上均优于其他模型,对推力和扭矩预测的准确率达到94.2%和96.2%.
关键词:深度学习注意力机制时序特征高维度荷载预测
Shield Load Prediction Method Based on Deep Learning with Multiattention Mechanism
CHEN Cheng1, SHI Pei-xin1

 , WANG Zhan-sheng2, JIA Peng-jiao1
, WANG Zhan-sheng2, JIA Peng-jiao1 1. School of Rail Transportation, Soochow University, Suzhou 215000, China;
2. Suzhou Rail Transit Group Co., Ltd., Suzhou 215004, China
Corresponding author: SHI Pei-xin, E-mail: pxshi@suda.edu.cn.
Abstract: Shield load is the main performance indicator of the shield, accurate load prediction is significant to ensure the safety and efficiency of the shield and the stability of the surrounding environment. Recognizing the limitations of the traditional prediction methods, this paper proposes a hybrid model(CBM), combining convolutional neural network (CNN), bi-directional long short-term memory (BiLSTM) and attention mechanism, to predict the shield load accurately based on the high-dimensional feature and time series characteristic of the data. The proposed model not only can extract the high-dimensional features and time series characteristics of the data, but also can highlight the importance of high-dimensional features and important time node information. The experiment results show that compared with the existing models, the proposed model achieves a higher prediction performance, the prediction accuracy of the thrust and torque is 94.2% and 96.2%.
Key words: deep learningattention mechanismtime series featurehigh-dimensionload prediction
近年来,中国的城市轨道交通得到大力发展,截至2021年底,全国40个城市开通运营地铁线路里程为7 300公里,还有39个城市正在建设的地铁里程达到1 222公里.盾构凭借其效率高、对环境扰动小及机械化水平高等特点被越来越多地应用到城市轨道交通建设当中[1-3].盾构荷载是盾构施工重要控制参数,荷载过小会导致盾构机难以推进和切削土体,过大则会引起掘进面前面土体发生过大的挤压变形,甚至导致刀盘被卡住或刀具崩坏而无法继续掘进[4],因此对于盾构荷载的精准预测可以帮助工程技术人员避免上述问题.
对盾构荷载的传统预测方法主要有理论分析[5-7]和数值模拟[8-9].理论分析和数值模拟方法可以预测出荷载的变化趋势,但随着工程的不断推进,预测数值往往不尽如人意,主要是由于两者在预测时都作了一定的假设或简化,且未能充分地利用监测数据里蕴含的丰富信息.与传统的预测方法不同,机器学习通过对已有的数据进行学习,挖掘历史数据内部的特征,然后对其未来的数值变化进行预测.近年来,随着人工智能的发展,机器学习技术逐渐被用到工程领域来解决回归问题,随机森林、混合粒子群优化、回归树、长短期记忆(long short term memory, LSTM)神经网络等算法被用于数据时序特征的分析,比如对轴承剩余寿命的预测[10-11]、评估TBM(tunnel boring machine)掘进的性能[12-13]、预测地表的沉降[14-15]等.在盾构荷载预测方面,Lin等[16]基于粒子群优化(particle swarm optimization, PSO)和LSTM建立盾构性能时序特征混合模型,通过深圳的工程案例验证了混合模型的预测准确性;Jin等[17]提出自适应残差长短期记忆神经网络对盾构机的扭矩进行预测,实验结果证明该模型预测有较高的准确率;Qin等[18]提出混合的深度神经网络模型对盾构扭矩进行预测,发现预测的结果优于理论分析;此外随机森林[19]、梯度提升[20]等机器学习技术也被用于盾构荷载的预测,均取得了较好的预测效果.随着隧道建设的发展,出现越来越多的盾构机直接切削既有构筑物的工程案例,在这种施工情形下,荷载大小不仅与盾构机自身的可持续工作状态有关,还与既有结构的安全使用紧密相关, 因此对于盾构荷载的准确预测显得尤为重要.现有的机器学习模型虽取得了较好的预测效果,但其主要考虑数据的时序特征,而盾构切削是多参数相互作用的过程,涉及机械参数、地质参数、隧道几何参数以及既有构筑物参数等,数据呈现高维度特征,研究数据的高维度特性有助于提升模型的预测精度.
本文以盾构机切削钢筋混凝土障碍物这一典型工程为背景,从数据高维度特性和时序特征出发,提出融合多注意力机制的深度学习算法,先对算法的基本原理和工程概况进行阐述,然后依托工程参数进行模型的构建,通过实验对本文所构建的模型的预测效果进行验证.
1 模型的基本原理本文基于卷积神经网络(convolutional neural networks, CNN)、双向长短期记忆(bi-directional LSTM,BiLSTM)神经网络和注意力(Attention)机制提出CNN-BiLSTM-Multiattention(CBM)模型.首先通过融合混合域注意力机制的卷积神经网络对数据进行高维度特征提取和突出高维度特征的重要性,再通过融合Attention机制的双向多层长短期记忆神经网络提取数据的时序特征,采用Attention机制对输出参数进行权重赋值,最后得到更新后的输出参数.具体模型结构如图 1所示.
图 1(Fig. 1)
 | 图 1 CBM模型结构Fig.1 CBM model architecture |
卷积神经网络与普通神经网络相似,神经元都由可学习的权重和偏置常量组成.卷积神经网络主要由卷积层、线性整流层、池化层和全连接层组成.卷积运算的目的是提取输入的不同特征,随着卷积层层数的增加,可以提取更复杂的特征.但面对高维度的数据,CNN算法无法突出高维度特征的重要性,而Attention机制主要是从大量信息中有选择地筛选出少量重要信息并聚焦到重要信息上,忽略大多不重要的信息[21],因此在CNN算法结构中融入Attention机制,既可以提取输入数据的不同特征,还可以突出不同特征的重要性,使得预测结果更加精确.
如图 1中的Module Ⅰ部分所示,在CNN算法结构中引入混合域机制,通过对通道域和空间域进行权重赋值,得到更新后的特征矩阵.由于引入了注意力机制,可以区分不同空间方向上数据的重要性,进一步提取数据的特征,提高预测的精度.具体方法如下:原始矩阵X′首先通过一次卷积(Ftr)操作得到矩阵U,然后将矩阵U通过最大池化操作(Fsq)分别得到3个压缩后的单位长度矩阵,分别为1×1×C, 1×1×W和1×1×H,随后经过2个全连接层(Fex(·, W)),得到权重赋值过的3个单位矩阵,先将空间域中的2个注意力矩阵进行融合,然后将通道域注意力矩阵和空间域注意力矩阵分别对原矩阵更新,最后将更新得到的2个矩阵进行融合,得到新的矩阵X,再经过全连接层等结构,将图形式的数据转换成向量形式,作为ModuleⅡ的输入.
LSTM是循环神经网络(recursive neural network, RNN)一种特殊的类型,由Hochreiter等[22]在1997年提出,并被Graves等进行了改良和推广.BiLSTM又是LSTM算法的特殊形式,其增加了反向挖掘数据信息,使得预测结果更加准确.无论是BiLSTM还是LSTM算法都是通过增加遗忘门的设计来解决RNN长序列训练导致的梯度消失和爆炸问题.它们主要是为了解决数据时序特征预测问题,但忽略了重要时间节点信息对预测结果的影响,因此考虑在BiLSTM结构中引入Attention机制,研究不同时间节点信息对预测结果的影响,以此来提高算法的预测精度.有研究表明多层LSTM结构预测效果优于单层结构[24],故算法中采用多层LSTM结构挖掘数据的时序特性.由于双向LSTM结构存在正反向,因此输出层的数值受到正反2个方向数值的影响,比如图 1中yi受到输入参数xi前后2个时间段的影响,考虑到不同时间段数据对输出层参数的影响,在输出层前增加Attention layer,可以得到更加符合实际的结果.在得到LSTM网络结构的输出后,考虑到不同时刻输出值对最后输出值的影响,再引入Attention layer,自动学习不同时刻的权重,最后得出模型的输出,结构如图 1中的ModuleⅡ所示.
2 工程案例和数据整理2.1 工程案例本文以苏州地铁2号线盾构机直接切削穿越桥梁为研究背景,盾构机需直接切削穿越14根桥桩,桥桩的直径有1 m和1.2 m,桥桩内钢筋的直径为20~22 mm.盾构切削过程中涉及到的参数较多,大致可以分为盾构机参数、隧道几何参数、地层参数、结构物参数四类.盾构机参数主要包括盾构直径、转速、推速、土仓压力、刀盘温度等;隧道几何参数主要包括隧道的埋深、直径;地层参数主要包括土的类型等;结构物参数主要包括强度、尺寸等.数据通过监测设备和地质报告获得,共计19 000项.
2.2 模型的构建盾构掘进受到时间和空间的双重影响[25],因此从时间和空间2个维度构建时空矩阵作为CNN神经网络的输入,如图 2所示.其中tn为盾构掘进的时间,Sm为盾构掘进的距离,两者对应于图 1中的空间域(H和W),组成CNN结构中的空间域.Ck为盾构切削的数据特征维度,其组成CNN结构中的通道域,盾构荷载的时空矩阵可以通过式(1)表示.时空矩阵作为CNN结构的输入层,经过混合域注意力机制处理后得到新的空间矩阵,再经过卷积、池化、展平等一系列过程,提取数据的高维度特征,得到一维阵列,作为BiLSTM的输入层,最后通过全连接层和输出层得到预测结果.
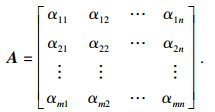 | (1) |
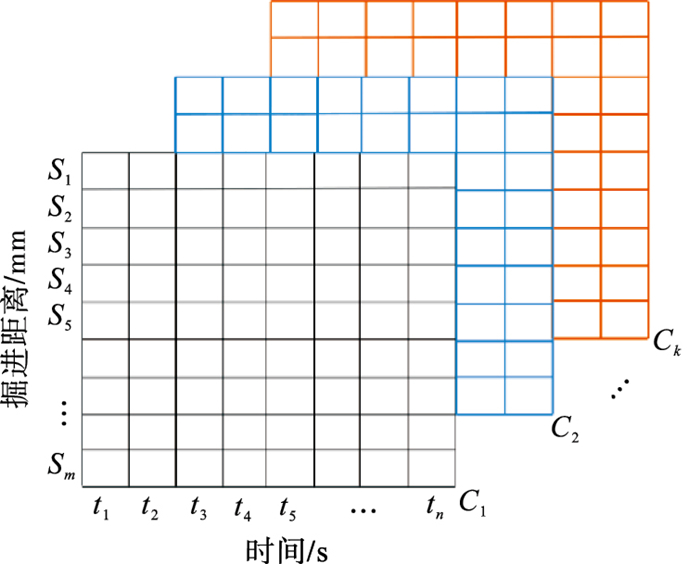 | 图 2 盾构荷载的时空矩阵Fig.2 Space-time matrix of shield load |
式中,αij代表矩阵在第i行,第j列的元素,表示盾构掘进在第i s,距离为j mm时盾构的荷载值.
模型的预测性能受到许多因素的影响,超参数的选取便是其中一个重要的因素.但是目前对于超参数的选取还没有较成熟的理论来指导[26],本文采用不断重复实验更新的办法选取超参数,最终确定的模型最优超参数如表 1所示.
表 1(Table 1)
| 表 1 最优超参数 Table 1 Optimal hyperparameters |
为方便神经网络的训练,本文采用离差标准化(max-min)对输入数据进行归一化处理.
 | (2) |
2.3 数据的划分本节先采用试错法[27](trial-and-error method)对数据集进行划分,以均方误差为评价标准,通过试错法最终确定训练子集的比例为80%,验证子集的比例为15%,测试集的比例为5%.因此将19 000项数据划分为训练数据为15 200项,验证数据2 850项,测试数据为950项.数据集的具体划分如图 3和图 4所示.
图 3(Fig. 3)
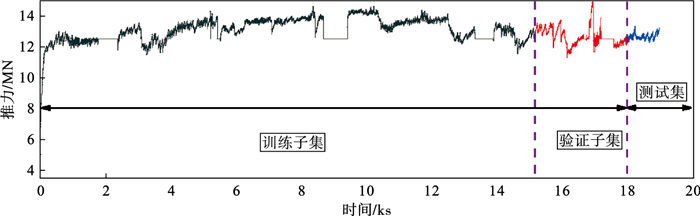 | 图 3 推力数据集划分结果Fig.3 Division result of the thrust dataset |
图 4(Fig. 4)
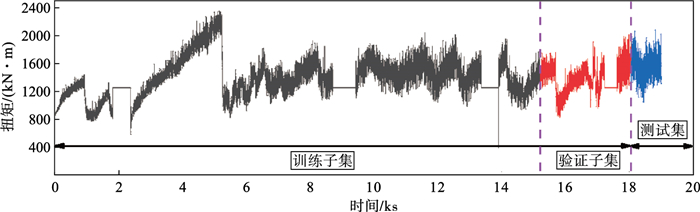 | 图 4 扭矩数据集划分结果Fig.4 Division result of the torque dataset |
2.4 模型评价指标预测的精度主要是指预测值

 | (3) |
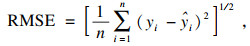 | (4) |
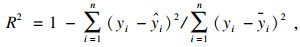 | (5) |
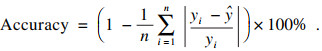 | (6) |

3 结果与讨论本章主要对本文模型的实验效果进行分析,同时为验证本文所提模型的有效性,将本文模型与CNN, BiLSTM, BiLSTM-Attention, CNN-Attention四种现有的模型进行对比实验.每次实验均在训练子集上训练模型,在验证子集上对模型效果进行分析,调整参数,最终在测试集上验证结果.
3.1 CBM模型的性能分析图 5显示了CBM模型分别在推力和扭矩数据集上的误差曲线图.从图中可以看出,随着迭代次数的增加,训练子集和验证子集上的误差值迅速下降,最终在图 5a中训练子集和验证子集的误差值分别为0.005和0.005,在图 5b中数值分别为0.003和0.005,可以发现数值较小,表明模型在训练集上具有较高的准确率;其次可以看出验证子集和训练子集之间的误差值相差较小,这表明本文所提出的模型(CBM)可以避免训练和验证过程中的过拟合问题;最后通过曲线图可以看出误差值最后趋于稳定,表明模型可以学习到数据的内部特征,掌握数据的变化规律,在训练子集和验证子集上有较好的泛化能力.
图 5(Fig. 5)
 | 图 5 训练集上的误差值Fig.5 Error values on training dataset (a)—推力的误差值;(b)—扭矩的误差值. |
3.2 现有的算法对比分析为了验证本文所提模型的优越性,本文对比分析了现有的4种模型.为了保证结果的合理性,先通过训练选取4种模型的最优超参数组合,然后将各自的预测结果与本文的模型结果进行对比.
各模型在测试集上的预测结果如表 2所示,从表中可以看出本文提出的CBM模型得到的MAE,RMSE值最小,R2值最大,表明该模型比其他4种现有模型的预测效果更优.为更直观地分析本文所提模型的优越性,绘制了CBM模型与其他模型的对比图,如图 6所示.以推力数据集为例可以看出,相比于CNN-Attention模型,CBM模型的MAE值下降99.3%,RMSE值下降99.4%,R2值提高26.9%,这是由于CBM模型中的BiLSTM结构可以充分地提取数据的时序信息,捕捉到各参数随时间的变化规律.类似地,CBM模型相比于BiLSTM-Attention模型,预测指标也得到了提升,这主要是由于增加的CNN结构可以提取数据的高维度特征,提高预测的精度.相比于CNN模型和BiLSTM模型,CBM模型预测效果的提升主要是因为融入了Attention机制,可以在模型预测过程中突出数据高维度特征的重要性和提取重要的时间节点信息.类似的结论也可以从图 6b扭矩数据集上得到.
表 2(Table 2)
| 表 2 荷载数据集的评价指标 Table 2 Evaluation metric of load dataset |
图 6(Fig. 6)
 | 图 6 不同模型预测指标对比Fig.6 Comparison of prediction indicators of the different models (a)—推力测试集;(b)—扭矩测试集. 注:CN为CNN; BIL为BiLSTM; CA为CNN-Attention; BA为BiLSTM-Attention. |
3.3 实际监测数据对比分析图 7和图 8为推力和扭矩的预测值与实际值的对比曲线,从图中可以直观地看出各模型预测曲线的变化趋势,本文所提模型的预测效果优于其他模型,与实际值误差更小,变化趋势更趋于一致.其中CNN模型的预测曲线波动性最大,和实际曲线拟合程度最低,随着时间的增加,预测效果越来越差,说明CNN模型在挖掘数据的时序特征方面较差,但是对比CNN-Attention模型可以看出,融合注意力机制之后CNN模型的预测性能得到提升.图 9绘制了各模型在推力和扭矩数据集上的预测准确率,可以发现本文提出的CBM模型对推力和扭矩的预测准确率最高,分别为94.2%和96.2%,相比于其他模型最高准确率提高了近30%,因此可以证明本文提出的CBM模型对盾构荷载的预测是可行的.
图 7(Fig. 7)
 | 图 7 不同模型的推力预测值与实际值对比Fig.7 Comparison of thrust prediction values of the different models with actual value |
图 8(Fig. 8)
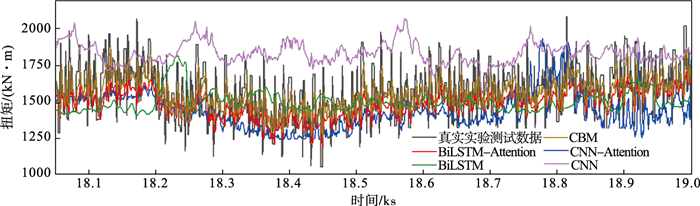 | 图 8 不同模型的扭矩预测值与实际值对比Fig.8 Comparison of torque prediction values of the different models with actual value |
图 9(Fig. 9)
 | 图 9 不同模型的准确率Fig.9 Accuracy of the different models |
4 结论1) 本文以数据的高维度特征和时序特征为切入点,提出一种结合卷积神经网络、双向长短期记忆神经网络和注意力机制的新模型(CBM)对盾构切削过程的推力和扭矩进行高精度预测.该模型可以提取数据的高维度特征和时序特征,并突出高维度特征的重要性和重要时间节点信息.
2) 本文提出的CBM模型在验证子集和训练子集之间的误差值相差较小,这表明本文所提模型(CBM)可以避免训练和验证过程中的过拟合问题;通过误差值图可以看出误差值最后趋于稳定,表明模型可以学习到数据的内部特征,在训练子集和验证子集上有较好的泛化能力.
3) 通过工程实例证明该模型的预测效果优于现有的4种模型,可以准确地预测出荷载的变化规律,实现高精度的预测.该模型不仅可应用于土木工程领域,还可为气象学、环境学、医学等领域的预测提供参考.
参考文献
| [1] | Wang L T, Yang X, Gong G F, et al. Pose and trajectory control of shield tunneling machine in complicated stratum[J]. Automation in Construction, 2018, 93: 192-199. DOI:10.1016/j.autcon.2018.05.020 |
| [2] | Huo J, Xu Z, Meng Z, et al. Coupled modeling and dynamic characteristics of TBM cutterhead system under uncertain factors[J]. Mechanical Systems and Signal Processing, 2020, 140: 106664. DOI:10.1016/j.ymssp.2020.106664 |
| [3] | Yang B, Chen S M, Sun S S, et al. Vibration suppression of tunnel boring machines using non-resonance approach[J]. Mechanical Systems and Signal Processing, 2020, 145: 106969. DOI:10.1016/j.ymssp.2020.106969 |
| [4] | 徐冲. 砂卵石地层泥水平衡盾构隧道掘进参数控制[J]. 铁道建筑, 2019, 59(2): 94-97. (Xu Chong. Control of tunnel driving parameters of slurry balance shield in sandy gravel stratum[J]. Railway Engineering, 2019, 59(2): 94-97. DOI:10.3969/j.issn.1003-1995.2019.02.23) |
| [5] | 李杰, 张斌, 付柯, 等. 基于现场掘进数据的复合地层盾构掘进性能预测方法研究[J]. 现代隧道技术, 2019, 56(4): 97-104. (Li Jie, Zhang Bin, Fu Ke, et al. Site data-based prediction of shield driving performance in compound strata[J]. Modern Tunnelling Technology, 2019, 56(4): 97-104. DOI:10.13807/j.cnki.mtt.2019.04.015) |
| [6] | Farrokh E. A study of various models used in the estimation of advance rates for hard rock TBMs[J]. Tunnelling and Underground Space Technology, 2020, 97: 103219. DOI:10.1016/j.tust.2019.103219 |
| [7] | Zhao P X, Zhuo R S, Li S G, et al. Analysis of advancing speed effect in gas safety extraction channels and pressure-relief gas extraction[J]. Fuel, 2020, 265: 116825. DOI:10.1016/j.fuel.2019.116825 |
| [8] | Hu X Y, Zhang Z X. Physical model test on the behavior of large slurry shield-driving tunnel in soft clay[J]. Journal of Shanghai Jiaotong University(Science), 2013, 18: 693-698. DOI:10.1007/s12204-013-1451-9 |
| [9] | Zheng G, Lu P, Diao Y. Advance speed-based parametric study of greenfield deformation induced by EPBM tunneling in soft ground[J]. Computers and Geotechnics, 2015, 65: 220-232. DOI:10.1016/j.compgeo.2014.12.013 |
| [10] | 王新刚, 韩凯忠, 王超, 等. 基于迁移学习的轴承剩余使用寿命预测方法[J]. 东北大学学报(自然科学版), 2021, 42(5): 665-672. (Wang Xin-gang, Han Kai-zhong, Wang Chao, et al. Bearing remaining useful life prediction method based on transfer learning[J]. Journal of Northeastern University(Natural Science), 2021, 42(5): 665-672.) |
| [11] | 申彦斌, 张小丽, 夏勇, 等. Bi-LSTM神经网络用于轴承剩余使用寿命预测研究[J]. 振动工程学报, 2021, 34(2): 411-420. (Shen Yan-bin, Zhang Xiao-li, Xia Yong, et al. Bi-LSTM neural network for remaining useful life prediction of bearings[J]. Journal of Vibration Engineering, 2021, 34(2): 411-420. DOI:10.16385/j.cnki.issn.1004-4523.2021.02.022) |
| [12] | Armaghani D J, Koopialipoor M, Marto A, et al. Application of several optimization techniques for estimating TBM advance rate in granitic rocks[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2019, 11(4): 779-789. DOI:10.1016/j.jrmge.2019.01.002 |
| [13] | Salimi A, Rostami J I, Moormann C. Application of rock mass classification systems for performance estimation of rock TBMs using regression tree and artificial intelligence algorithms[J]. Tunnelling and Underground Space Technology, 2019, 92: 103046. DOI:10.1016/j.tust.2019.103046 |
| [14] | 张钦礼, 刘奇, 赵建文. 全尾砂絮凝沉降参数预测模型研究[J]. 东北大学学报(自然科学版), 2016, 37(6): 875-879. (Zhang Qin-li, Liu Qi, Zhao Jian-wen. Study on the parameters prediction model of flocculating sedimentation of crude tailings[J]. Journal of Northeastern University(Natural Science), 2016, 37(6): 875-879. DOI:10.3969/j.issn.1005-3026.2016.06.024) |
| [15] | 王述红, 朱宝强. 山岭隧道洞口段地表沉降时序预测研究[J]. 岩土工程学报, 2021, 43(5): 813-821. (Wang Shu-hong, Zhu Bao-qiang. Time series prediction for ground settlement in portal section of mountain tunnels[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 813-821.) |
| [16] | Lin S S, Zhang N, Zhou A N, et al. Time-series prediction of shield movement performance during tunneling based on hybrid model[J]. Tunnelling and Underground Space Technology, 2022, 119: 104245. DOI:10.1016/j.tust.2021.104245 |
| [17] | Jin Y R, Qin C J, Tao J F, et al. An accurate and adaptative cutterhead torque prediction method for shield tunneling machines via adaptative residual long-short term memory network[J]. Mechanical Systems and Signal Processing, 2022, 165: 108312. DOI:10.1016/j.ymssp.2021.108312 |
| [18] | Qin C J, Shi G, Tao J F, et al. Precise cutterhead torque prediction for shield tunneling machines using a novel hybrid deep neural network[J]. Mechanical Systems and Signal Processing, 2021, 151: 107386. DOI:10.1016/j.ymssp.2020.107386 |
| [19] | Kong X X, Ling X Z, Tang L, et al. Random forest-based predictors for driving forces of earth pressure balance(EPB)shield tunnel boring machine(TBM)[J]. Tunnelling and Underground Space Technology, 2022, 122: 104373. DOI:10.1016/j.tust.2022.104373 |
| [20] | Zhang R H, Li Y Q, Goh A T C, et al. Analysis of ground surface settlement in anisotropic clays using extreme gradient boosting and random forest regression models[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2021, 13(6): 1478-1484. DOI:10.1016/j.jrmge.2021.08.001 |
| [21] | Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate[J/OL]. Computer Science, 2014: 1409.0473[2022-03-05]. https://doi.org/10.48550/arXiv.1409.0473. |
| [22] | Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [23] | Graves A, Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures[J]. Neural Networks, 2005, 18(5/6): 602-610. |
| [24] | Lu A J. From single layer networks to multilayer networks-structure dynamics and function[J]. Modern Physics, 2015, 27(4): 3-8. |
| [25] | 于广明, 雷军, 张鹏辉, 等. 盾构隧道施工引起地表沉降的"五维"空间效应探索及其展望[J]. 青岛理工大学学报, 2022, 43(2): 1-10. (Yu Guang-ming, Lei Jun, Zhang Peng-hui, et al. Exploration and prospect of "five-dimensional" space effect of ground surface settlement caused by shield tunnel construction[J]. Journal of Qingdao University of Technology, 2022, 43(2): 1-10.) |
| [26] | Zhang D M, Zhang J Z, Huang H W, et al. Machine learning-based prediction of soil compression modulus with application of 1D settlement[J]. Journal of Zhejiang University(Science A), 2020, 21(6): 430-444. DOI:10.1631/jzus.A1900515 |
| [27] | Shao H D, Jiang H K, Wang F A, et al. An enhancement deep feature fusion method for rotating machinery fault diagnosis[J]. Knowledge-Based Systems, 2017, 119: 200-220. DOI:10.1016/j.knosys.2016.12.012 |
| [28] | Zhang W G, Zhang R H, Wu C Z, et al. State-of-the-art review of soft computing applications in underground excavations[J]. Geoscience Frontiers, 2020, 11(4): 1095-1106. DOI:10.1016/j.gsf.2019.12.003 |
