
 , 王杨
, 王杨 大连理工大学 建设工程学院,辽宁 大连 116024
收稿日期:2022-06-22
基金项目:国家自然科学基金资助项目(51878113)。
作者简介:肖诗云(1973-),男,湖南澧县人,大连理工大学教授,博士生导师。
摘要:混凝土宏观率相关效应研究已经取得了十分丰富的成果,其细观结构和材料参数显著影响混凝土宏观力学性能,因此,从细观尺度研究混凝土动态性能是揭示混凝土宏观率相关效应的重要途径.本文引入应变率影响,修正界面内聚力本构模型,从细观尺度研究了不同骨料含量和骨料形状的混凝土在不同加载速率下的单轴抗拉破坏模式和力学特性.分析结果表明:随着加载速率增加,混凝土破坏裂缝分布更加均匀;混凝土抗拉强度的增量与应变率的对数呈线性关系;混凝土抗拉强度随骨料含量增加近似线性减小,但骨料形状对其影响很小.
关键词:混凝土内聚力本构模型加载速率随机骨料模型单轴受拉
Mesoscopic Uniaxial Tensile Properties of Concrete Based on Rate-Dependent Cohesive Constitutive Model
XIAO Shi-yun

 , WANG Yang
, WANG Yang School of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China
Corresponding author: XIAO Shi-yun, E-mail: shyxiao@dlut.edu.cn.
Abstract: The research on macroscopic rate-dependence of concrete has achieved very rich results, and its meso structural and material parameters significantly affect the macroscopic mechanical properties of concrete. Therefore, studying the dynamic properties of concrete at the meso-scale is an important way to reveal the macroscopic rate-dependence of concrete. In this paper, the influence of strain rate was introduced to modify the interfacial cohesion constitutive model, and the uniaxial tensile failure mode and mechanical properties of concrete with different aggregate content and shapes were studied under various loading rates from the mesoscale. The results show that the distribution of failure cracks becomes increasingly uniform with the increase of loading rate. The increment in tensile strength of concrete exhibits a linear relationship with the logarithm of strain rate. The tensile strength of concrete decreases linearly with an increase in aggregate content, while the aggregate shape has little effect on it.
Key words: concretecohesive constitutive modelloading raterandom aggregate modeluniaxial tension
混凝土是典型的率敏感材料,其在动态荷载作用下强度、变形以及破坏形式都与静态荷载作用有明显不同.混凝土率相关效应研究已经进行了一百多年,一般情况下,在宏观尺度上将混凝土假设为均质材料,引入动力放大系数来研究加载速率对混凝土力学特性的影响.由于受到试验设备的限制,混凝土动态抗拉特性的研究远远少于受压特性研究,并且绝大部分只局限于单轴抗拉特性.Bischoff等[1]总结了20世纪90年代以前混凝土动态抗拉特性研究成果,指出混凝土抗拉强度随着加载速率的增加明显增加,但这些影响受到混凝土强度、试验设备等诸多因素的影响;Malvar等[2]汇集了混凝土抗拉试验结果,绘制了文献中混凝土抗拉强度与加载速率之间的关系图.进入21世纪,随着试验设备和试验技术的发展,关于混凝土动态抗拉特性的研究更加深入了.肖诗云等[3]对混凝土进行了拉伸试验,得到了抗拉强度的增量与应变率的对数呈线性关系的结论.Yan等[4]采用哑铃型混凝土试件进行直接拉伸试验,研究预加载对混凝土动力特性的影响.宁建国等[5]对混凝土材料动态特性研究进行了总结;牛海英等[6]综述了混凝土应变率效应研究现状;李忠献等[7]对混凝土的动态本构模型进行了总结.
混凝土宏观动态特性的研究,并没有从机理上解释率相关效应,主要是因为混凝土是由水泥砂浆、骨料和界面组成的多相复合材料,其细观结构和力学特性直接影响宏观力学行为.因此,从细观尺度研究混凝土率相关效应成为了一种新的思路.自Wittmann等[8]将“细观”概念引入到混凝土材料研究以来,基于两相或三相复合材料理论,研究者提出了随机粒子模型[9]、M-H模型[10-12]、随机力学特性模型[13-14]、随机骨料模型[15-16]等混凝土细观力学模型来研究混凝土的力学特性.刘宝琛等[17]、张楚汉等[18]和单智等[19]针对细观力学试验和仿真模拟进行了总结研究.目前,对于混凝土细观动态拉伸研究相对较少.Zhou等[20-21]在高应变率下对混凝土模型进行了动态拉伸模拟,研究了惯性效应、界面过渡区和应变率对混凝土性能的影响;Zhou等[22-23]分别对混凝土进行了单轴拉伸和单轴压缩模拟,探究了压缩时接触摩擦界面和拉伸时应变率为100/s下混凝土的破坏机理;文献[24-28]探讨了应变率、尺寸效应、加载模式和细观结构不均匀特性对混凝土破坏和力学特性的影响,得到了混凝土裂纹扩展路径和破坏模式与应变率的关系.这些研究表明了混凝土动态细观力学性能与静态相比存在明显差别,但目前关于混凝土各组成成分动态性能对混凝土细观动态力学性能的影响研究十分少见,而这方面的研究对揭示混凝土宏观率相关效应具有十分重要的理论意义.
本文引入应变率影响,修正内聚力本构模型,利用ABAQUS软件和UEL子程序,采用随机骨料模型,从细观尺度对混凝土试件进行了单轴抗拉分析,研究了不同加载速率、不同骨料含量和不同骨料形状对混凝土破坏模式和力学特性的影响.
1 混凝土细观随机骨料模型本文对如图 1所示的二维混凝土试件进行了单轴抗拉分析,荷载采用位移加载方式,细观模型实体单元最大尺寸为2 mm,骨料和砂浆界面采用零厚度的内聚力单元进行模拟.
图 1(Fig. 1)
 | 图 1 单轴受拉混凝土试件Fig.1 The uniaxial tensile specimen of concrete |
1.1 骨料粒径与级配混凝土细观模型采用随机骨料模型,为简化计算,建模时将粒径在0~5 mm的细骨料简化为砂浆进行处理,将粒径在5~20 mm的粗骨料,按5 mm间隔划分为3个区间,按实体单元进行建模.骨料级配采用瓦拉文二维骨料级配公式进行计算,本文中取粗骨料含量(骨料面积占混凝土试件截面面积百分比)分别为20%,25%,30%,35%和40%的混凝土试件进行分析,3个粒径区间骨料含量如表 1所示.
表 1(Table 1)
| 表 1 各粒径区间内粗骨料含量 Table 1 Area percentage of aggregate in the range of particle size ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.2 随机骨料生成与投放本文分别采用圆形、椭圆形和多边形骨料随机骨料模型来研究骨料形状的影响.采用蒙特卡洛法进行随机骨料投放,通过Python语言对ABAQUS软件进行二次开发,一次性完成骨料投放、材料赋值等操作,避免多个软件之间互相导入带来的麻烦及不兼容等问题[29].最后设定单元的最大尺寸,采用自动网格剖分方法生成含有骨料与砂浆基质的随机骨料模型.
1.3 内聚力单元嵌入骨料和砂浆之间的界面过渡区(interfacial transition zones,ITZ)是混凝土中最薄弱的部位,对混凝土的宏观力学性能起决定性作用.界面过渡区厚度较薄,一般在20~100 μm之间,因此难以通过试验测定其力学性能.细观模拟时对界面的模拟方法主要有两种:一是设置为有厚度的实体单元进行模拟;二是设置为零厚度的Cohesive单元进行模拟.采用有厚度的实体单元进行模拟时,网格要求高,而且数量多,导致计算量巨大,因此,本文采用零厚度的内聚力单元来模拟界面.同时,在相连的2个砂浆单元之间也插入零厚度的内聚力单元,用来模拟裂缝在砂浆中的扩展.由于零厚度界面单元在软件中难以直接生成,因此,本文在自动生成的骨料砂浆有限元模型的基础上,通过Python语言后期进行嵌入.图 2给出了骨料砂浆有限元模型和后期生成的界面单元模型示意图.
图 2(Fig. 2)
 | 图 2 混凝土试件有限元模型Fig.2 Finite element model of concrete specimen (a)—骨料砂浆单元;(b)—界面内聚力单元;(c)—砂浆内聚力单元. |
2 材料特性2.1 材料本构模型混凝土细观模型中,粗骨料强度较大且一般不发生破坏,因此,本文中骨料采用线弹性本构模型;砂浆的非线性是由砂浆内部裂缝产生、扩展和融合引起的,而本文采用砂浆单元之间插入零厚度界面单元的方法模拟砂浆内部的裂缝,因此,砂浆单元也采用了线弹性本构模型进行模拟;内聚力单元是模拟混凝土非线性的重要单元,因此,内聚力单元采用非线性本构模型进行模拟.
由Xu等[30]提出的界面单元的指数型本构模型,能够较好地模拟混凝土开裂,因此被广泛采用,其控制方程如式(1)所示:
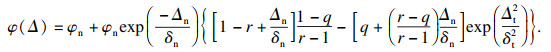 | (1) |
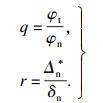 | (2) |
界面的法向和切向应力,可由断裂能对相应方向的位移求偏导得到
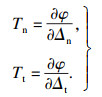 | (3) |
 | (4) |
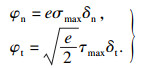 | (5) |
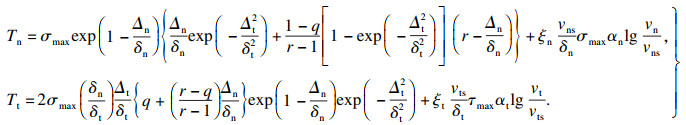 | (6) |
取0.001 mm/s为准静态加载速率,对单个界面单元分别进行不同加载速率下的法向和切向开裂模拟,归一化后应力位移曲线如图 3所示.
图 3(Fig. 3)
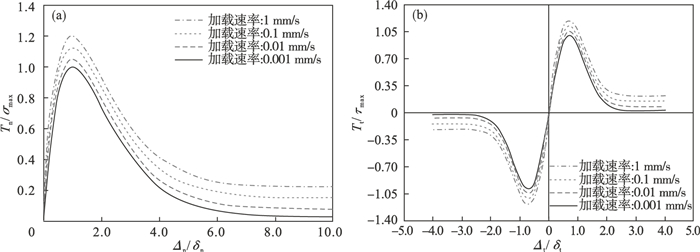 | 图 3 内聚力本构模型Fig.3 Cohesive constitutive model (a)—法向应力位移曲线;(b)—切向应力位移曲线. |
2.2 材料参数Yang等[32]取砂浆弹性模量为骨料弹性模量的1/3;ITZ界面强度较弱,一般约为砂浆基体强度的50%[23, 29, 33],本文取ITZ强度为砂浆强度的50%,黏性系数ξt,ξn均取为0.05;各个细观组分的材料参数如表 2所示.
表 2(Table 2)
| 表 2 混凝土各细观组分材料参数 Table 2 Material parameters of meso ingredients for concrete | ||||||||||||||||||||||||||||||||||||||||||||
3 混凝土模型动态受拉数值模拟Zhou等[20-21]认为骨料的形状、位置和大小会影响开裂模式.为研究不同加载速率0.001,0.01,0.1和1 mm/s(应变率为1.0×10-5~1.0×10-2 s-1)下混凝土的破坏模式和力学特性,选取5种骨料含量(20%,25%,30%,35%,40%),3种骨料形状(圆形、椭圆形、多边形)的混凝土模型进行单轴拉伸模拟,选取应变率1.0×10-5 s-1为准静态应变率.考虑到骨料的随机性会影响混凝土模型的开裂,选取10组随机骨料模型计算,然后对结果取平均值.
3.1 混凝土试件破坏模式以骨料含量为20%的混凝土试件为例,表 3给出了不同加载速率下3种骨料形状模型的最终破坏时的开裂模式.从表中可以看到,不同骨料形状的混凝土试件在相同的加载速率下,开裂模式基本类似,但是随着加载速率的变化,裂纹的分布和宽度发生较大变化.裂纹在加载速率为0.001 mm/s (对应的应变率为1.0×10-5 s-1)时,形成了1条(多边形骨料)或2条(圆形和椭圆形骨料)宏观裂缝;随着加载速率的增加,裂纹的分布更加均匀,裂纹数量增加,如加载速率增加到0.01 mm/s时,宏观裂缝增加到4条,加载速率增加到1 mm/s时,宏观裂缝增加到6条以上;同时,从图中也可以看出,宏观裂缝数量增加的同时,每条裂缝的宽度相应减小了,这与试验中观察到的现象相符[3].
表 3(Table 3)
| 表 3 不同加载速率下的模型最终开裂模式 Table 3 Final failure of specimens at different loading rates | |||||||||||||||||||||||||||||
3.2 动态拉伸应力应变曲线图 4给出了3种骨料形状的模型在4种不同加载速率下的应力应变曲线.从图中可以看出,随着加载速率的增大,3种骨料的混凝土抗拉强度和峰值位移都增加了.相比于0.001 mm/s时的准静态加载速率,加载速率为0.01,0.1,1 mm/s时,圆形骨料抗拉强度分别增加了5.84%,12.3%和18.06%,峰值位移增加了8.3%,22.2%和41.6%;椭圆形骨料的抗拉强度分别增加了6.74%,14.78%和21.06%,峰值位移分别增加了11.1%,30.5%和41.6%;多边形骨料的抗拉强度分别增加了6.3%,13.1%和18.6%,峰值位移分别增加了8.8%,23.53%和32.4%.与混凝土抗拉强度和峰值位移随着加载速率的增加而增加不同,混凝土的弹性模量在不同加载速率下基本一致,这是因为混凝土的弹性模量主要由骨料和砂浆贡献,而本文的界面模型并未考虑应变率对其弹性模量的影响.
图 4(Fig. 4)
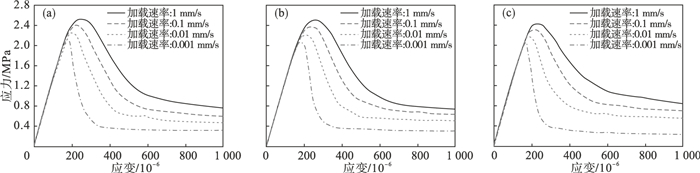 | 图 4 不同骨料形状下混凝土动态拉伸应力应变曲线Fig.4 Dynamic tensile stress-strain curves of concrete with different aggregate shapes (a)—圆形骨料;(b)—椭圆形骨料;(c)—多边形骨料. |
4 影响因素分析4.1 应变率对混凝土抗拉强度的影响以0.001 mm/s(对应的应变率为1.0×10-5s-1)为准静态加载速率,图 5给出了应变率对3种骨料混凝土动态抗拉强度的影响.从图可以看出,3种骨料的混凝土动、静抗拉强度之比与应变率的对数近似呈线性关系,拟合曲线公式如下:
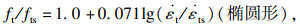 | (7) |
 | (8) |
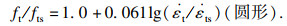 | (9) |
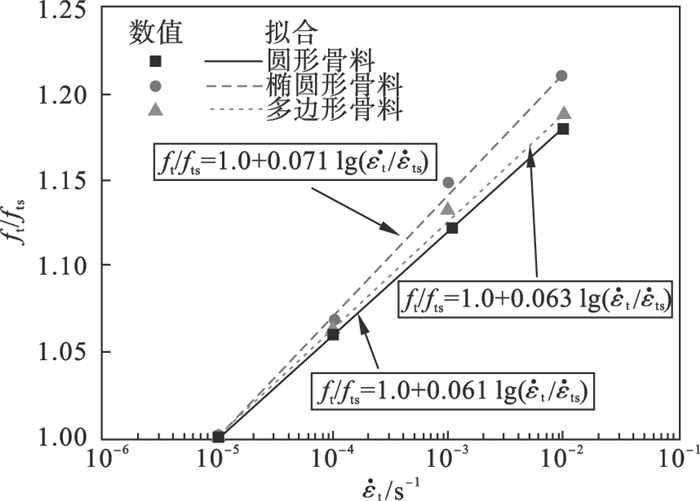 | 图 5 混凝土动态抗拉强度与应变率的关系Fig.5 The relationship between concrete strength and strain rate |
式中:ft为试件抗拉强度;fts为应变率准静态抗拉强度;
为了验证本文结果的正确性,图 6在文献[22]结果的基础上,添加了文献[3]结果以及本文3种骨料混凝土动态抗拉强度与应变率的关系,从图中可以看出,在应变率1.0×10-5 s-1至1.0×10-2 s-1范围内,本文的结果与前人试验结果较为接近.
图 6(Fig. 6)
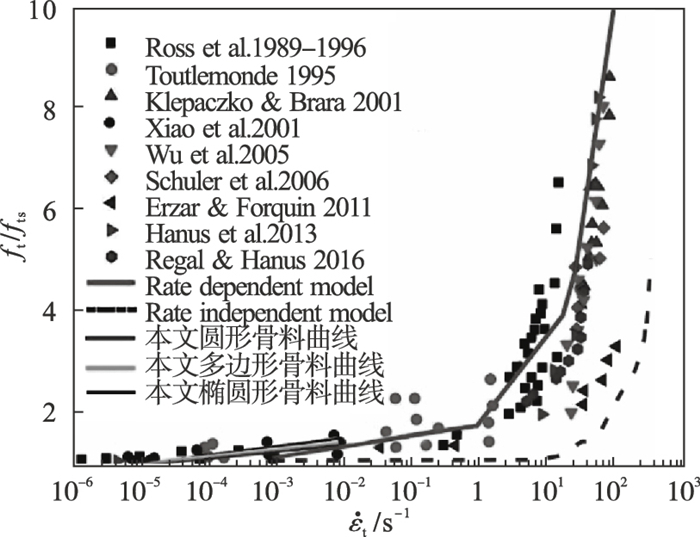 | 图 6 本文拟合结果与文献试验结果对比Fig.6 Comparison of fitting results with the experimental results |
4.2 骨料形状的影响以骨料含量为20%的混凝土试件为例,图 7给出了圆形、椭圆形和多边形骨料混凝土试件在加载速率为0.001,0.01,0.1,1 mm/s(对应的应变率分别为1.0×10-5,1.0×10-4,1.0×10-3,1.0×10-2 s-1)荷载作用下的应力应变曲线.从图中可以看出,骨料形状对混凝土应力应变曲线影响很小,特别是椭圆形骨料和圆形骨料的混凝土应力应变曲线几乎重合.
图 7(Fig. 7)
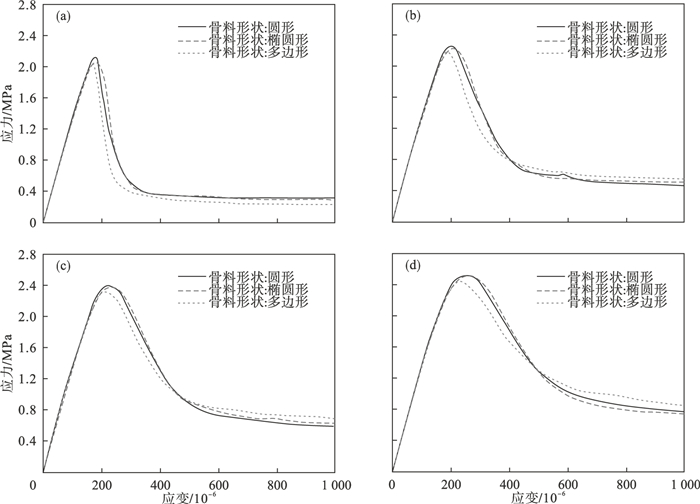 | 图 7 不同加载速率下骨料形状的影响Fig.7 Effect of aggregate shape at various loading rates (a)—加载速率0.001 mm/s;(b)—加载速率0.01 mm/s;(c)—加载速率0.1 mm/s;(d)—加载速率1 mm/s. |
4.3 骨料含量的影响以圆形骨料的混凝土试件为例,选取20%,25%,30%,35%和40%5种不同的骨料含量,研究骨料含量对混凝土力学特性的影响.图 8列出了5种不同骨料含量的混凝土试件在加载速率为1 mm/s时的破坏形态.从图中可以看出,混凝土破坏时,主裂纹沿着直径较大的粗骨料周围扩展;不同混凝土试件骨料含量虽然逐渐增加了,但直径较大粗骨料数量相差并不多,因此,骨料含量对混凝土的破坏模式影响不大.
图 8(Fig. 8)
 | 图 8 1 mm/s加载速率下圆形骨料模型不同骨料含量的破坏模式Fig.8 Failure modes of circular aggregate concrete with various aggregate contents at loading rate of 1 mm/s (a)—骨料含量20%;(b)—骨料含量25%;(c)—骨料含量30%;(d)—骨料含量35%;(e)—骨料含量40%. |
5种骨料含量的混凝土试件在不同加载速率下的应力应变曲线如图 9所示.从图 9可以看出:随着骨料含量的增加,混凝土的弹性模量略有增加,主要原因是因为骨料的弹性模量是所有细观组分中最高的,骨料含量的增加引起了混凝土弹性模量的少许增加;相同加载速率荷载作用下,混凝土峰值应力及其对应的应变都有少许降低,主要原因是随着骨料含量的增加,骨料和砂浆之间的界面单元增加,界面单元的增加削弱了混凝土试件的黏结性能,导致混凝土强度降低,同时又因为骨料增加引起了混凝土试件的刚度稍许增加,双重作用导致混凝土峰值应力对应的应变随着骨料含量的增加而减小了.
图 9(Fig. 9)
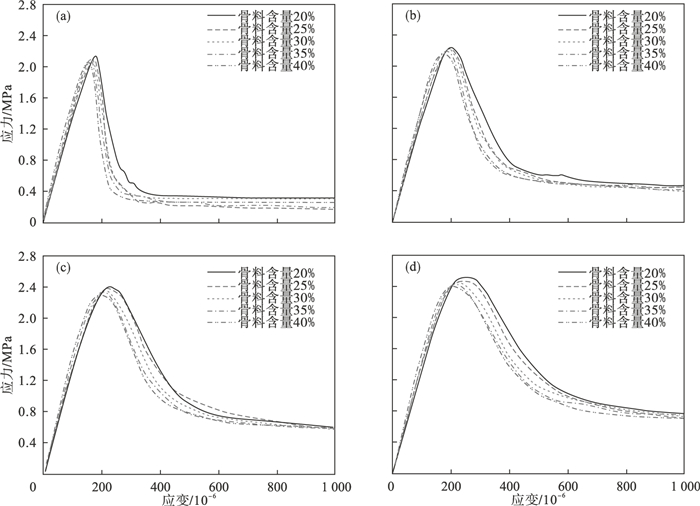 | 图 9 不同加载速率下骨料含量的影响Fig.9 Effect of aggregate content at various loading rates (a)—加载速率0.001 mm/s;(b)—加载速率0.01 mm/s;(c)—加载速率0.1 mm/s;(d)—加载速率1 mm/s. |
图 10给出了不同加载速率下的混凝土试件抗拉强度与骨料含量的关系.从图中可以看出,不同加载速率作用下,混凝土抗拉强度随着骨料含量的增加而减小,且近似呈线性关系;同时,也可看出,随着加载速率的增大,混凝土强度减小趋势更加明显;不同加载速率下的拟合公式如图 10所示.
图 10(Fig. 10)
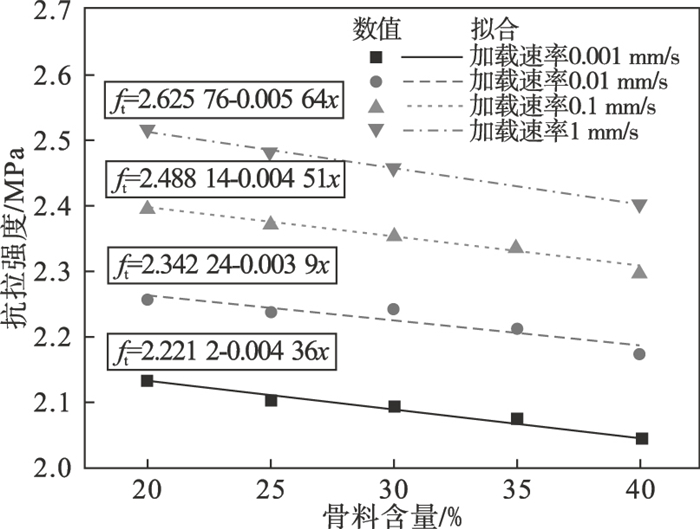 | 图 10 骨料含量对混凝土抗拉强度的影响Fig.10 Effect of aggregate content on tensile strength of concrete |
5 结论1) 裂纹在准静态加载速率下,形成了1条或2条宏观主裂缝,随着加载速率的增加,裂纹的分布更加均匀,裂纹数量增加的同时,每条裂缝的宽度相应减小了.
2) 随着加载速率的增大,3种骨料的混凝土抗拉强度和峰值位移都增加了,动态抗拉强度的增量与应变率的对数呈线性关系,但混凝土初始弹性模量保持不变.
3) 骨料形状对混凝土应力应变曲线影响很小,椭圆形骨料和圆形骨料的混凝土应力应变曲线几乎重合.
4) 骨料含量对混凝土的破坏模式影响不大,混凝土刚度随着骨料含量增加略有增加,抗拉强度随骨料含量增加近似线性减小,峰值应变随着骨料含量的增加而减小.
参考文献
| [1] | Bischoff P H, Perry S H. Impact behavior of plain concrete loaded in uniaxial compression[J]. Journal of Engineering Mechanics, 1995, 121(6): 685-693. DOI:10.1061/(ASCE)0733-9399(1995)121:6(685) |
| [2] | Malvar L J, Ross C A. Review of strain rate effects for concrete in tension[J]. ACI Materials Journal, 1998, 95(6): 735-739. |
| [3] | 肖诗云, 林皋, 王哲, 等. 应变率对混凝土抗拉特性影响[J]. 大连理工大学学报, 2001, 41(6): 721-725. (Xiao Shi-yun, Lin Gao, Wang Zhe, et al. Effects of strain rate on dynamic behavior of concrete in tension[J]. Journal of Dalian University of Technology, 2001, 41(6): 721-725.) |
| [4] | Yan D M, Liu K H, Fan L F, et al. An experimental investigation of pre-loading effects on the dynamic behaviour of concrete[J]. Magazine of Concrete Research, 2017, 69(11): 586-594. DOI:10.1680/jmacr.16.00414 |
| [5] | 宁建国, 商霖, 孙远翔. 混凝土材料动态性能的经验公式、强度理论与唯象本构模型[J]. 力学进展, 2006, 36(3): 389-405. (Ning Jian-guo, Shang Lin, Sun Yuan-xiang. The developments of dynamic constitutive behavior of concrete[J]. Advances in Mechanics, 2006, 36(3): 389-405.) |
| [6] | 牛海英, 李国一, 于林平. 混凝土应变率效应综述[J]. 大连大学学报, 2016, 37(6): 11-14. (Niu Hai-ying, Li Guo-yi, Yu Lin-ping. The state-of-the-art of concrete strain rate effect[J]. Journal of Dalian University, 2016, 37(6): 11-14.) |
| [7] | 李忠献, 刘泽锋. 混凝土动态本构模型综述[J]. 天津大学学报(自然科学与工程技术版), 2015, 48(10): 853-863. (Li Zhong-xian, Liu Ze-feng. Review of concrete dynamic constitutive model[J]. Journal of Tianjin University(Science and Technology), 2015, 48(10): 853-863.) |
| [8] | Wittmann F H, Roelfstra P E, Sadouki H. Simulation and analysis of composite structures[J]. Materials Science and Engineering, 1985, 68(2): 239-248. DOI:10.1016/0025-5416(85)90413-6 |
| [9] | Cundall P A, Strack O D L. A discrete numerrical model for granular assemblies[J]. Geotechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [10] | Mohamed A R, Hansen W. Micromechanical modeling of crack-aggregate interaction in concrete materials[J]. Cement and Concrete Composites, 1999, 21(5/6): 349-359. |
| [11] | Mohamed A R, Hansen W. Micromechanical modeling of concrete response under static loading—part 1:model development and validation[J]. ACI Materials Journal, 1999, 96(2): 196-203. |
| [12] | Mohamed A R, Hansen W. Micromechanical modeling of concrete response under static loading—part Ⅱ: model predictions for shear and compressive loading[J]. ACI Materials Journal, 1999, 96(3): 354-358. |
| [13] | Zhu W C, Tang C A. Numerical simulation on shear fracture process of concrete using mesoscopic mechanical model[J]. Construction and Building Materials, 2002, 16(8): 453-463. DOI:10.1016/S0950-0618(02)00096-X |
| [14] | Zhu W C, Teng J G, Tang C A. Mesomechanical model for concrete. part Ⅰ: model development[J]. Magazine of Concrete Research, 2004, 56(6): 313-330. DOI:10.1680/macr.2004.56.6.313 |
| [15] | Kwan A K H, Wang Z M, Chan H C. Mesoscopic study of concrete Ⅱ: nonlinear finite element analysis[J]. Computers & Structures, 1999, 70(5): 545-556. |
| [16] | Wang Z M, Kwan A K H, Chan H C. Mesoscopic study of concrete Ⅰ: generation of random aggregate structure and finite element mesh[J]. Computers & Structures, 1999, 70(5): 533-544. |
| [17] | 刘宝琛, 伍小平. 细观力学实验技术综述[J]. 实验力学, 1992, 7(1): 1-10. (Liu Bao-chen, Wu Xiao-ping. A brief review on experimental techniques of mesomechanics[J]. Journal of Experimental Mechanics, 1992, 7(1): 1-10.) |
| [18] | 张楚汉, 唐欣薇, 周元德, 等. 混凝土细观力学研究进展综述[J]. 水力发电学报, 2015, 34(12): 1-18. (Zhang Chu-han, Tang Xin-wei, Zhou Yuan-de, et al. State-of-the-art of literature review on concrete meso-scale mechanics[J]. Journal of Hydroelectric Engineering, 2015, 34(12): 1-18.) |
| [19] | 单智, 方联民, 高晶. 混凝土力学性能及其细观力学机理研究综述[J]. 混凝土, 2015, 7(7): 11-17. (Shan Zhi, Fang Lian-min, Gao Jing. Review of studies on mechanical property and micro mechanism of concrete[J]. Concrete, 2015, 7(7): 11-17.) |
| [20] | Zhou X Q, Hao H. Mesoscale modelling of concrete tensile failure mechanism at high strain rates[J]. Computers & Structures, 2008, 86(21/22): 2013-2026. |
| [21] | Zhou X Q, Hao H. Modelling of compressive behaviour of concrete-like materials at high strain rate[J]. International Journal of Solids and Structures, 2008, 45(17): 4648-4661. |
| [22] | Zhou R X, Chen H M, Lu Y. Mesoscale modelling of concrete under high strain rate tension with a rate-dependent cohesive interface approach[J]. International Journal of Impact Engineering, 2020, 139: 103500. |
| [23] | Zhou R X, Lu Y. A mesoscale interface approach to modelling fractures in concrete for material investigation[J]. Construction and Building Materials, 2018, 165: 608-620. |
| [24] | 金浏, 杨旺贤, 余文轩, 等. 骨料粒径对混凝土动态拉伸强度及尺寸效应影响分析[J]. 振动与冲击, 2020, 39(9): 24-34. (Jin Liu, Yang Wang-xian, Yu Wen-xuan, et al. Influence of aggrecate size on the dynamic tensile strength and size effect of concrete[J]. Journal of Vibration and Shock, 2020, 39(9): 24-34.) |
| [25] | 金浏, 杜修力. 加载速率对混凝土拉伸破坏行为影响的细观数值分析[J]. 工程力学, 2015, 32(8): 42-49. (Jin Liu, Du Xiu-li. Meso-scale numerical analysis of the effect of loading rate on the tensile failure behavior of concrete[J]. Engineering Mechanics, 2015, 32(8): 42-49.) |
| [26] | 金浏, 李健, 余文轩, 等. 混凝土动态双轴拉压破坏准则细观数值模拟研究[J]. 力学学报, 2022, 54(3): 800-809. (Jin Liu, Li Jian, Yu Wen-xuan, et al. Mesoscopic numerical simulation on dynamic biaxial tension-compression failure criterion of concrete[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(3): 800-809.) |
| [27] | 金浏, 余文轩, 杜修力. 应变率突增对混凝土动态拉伸破坏影响的细观模拟[J]. 振动与冲击, 2021, 40(2): 39-48. (Jin Liu, Yu Wen-xuan, Du Xiu-li. Effect of the sudden increase of strain rate on concrete dynamic tensile failure based on 3D meso-scale simulation[J]. Journal of Vibration and Shock, 2021, 40(2): 39-48.) |
| [28] | 金浏, 余文轩, 杜修力, 等. 低应变率下混凝土动态拉伸破坏尺寸效应细观模拟[J]. 工程力学, 2019, 36(8): 59-69. (Jin Liu, Yu Wen-xuan, Du Xiu-li, et al. Meso-scale simulation of size effect of dynamic tensile strength of concrete under low strain rates[J]. Engineering Mechanics, 2019, 36(8): 59-69.) |
| [29] | 李坤罡. 基于内聚力模型的混凝土细观受拉力学性能研究[D]. 大连: 大连理工大学, 2019. (Li Kun-gang. Study on meso-scale tensile mechanical properties of concrete based on cohesive zone model[D]. Dalian: Dalian University of Technology, 2019. ) |
| [30] | Xu X P, Needleman A. Void nucleation by inclusion debonding in a crystal matrix[J]. Modelling and Simulation in Materials Science and Engineering, 1993, 1(2): 111-132. |
| [31] | Gao Y F, Bower A F. A simple technique for avoiding convergence problems in finite element simulations of crack nucleation and growth on cohesive interfaces[J]. Modelling and Simulation in Materials Science and Engineering, 2004, 12(3): 453-463. |
| [32] | Yang Z J, Su X T, Chen J F, et al. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials[J]. International Journal of Solids and Structures, 2009, 46(17): 3222-3234. |
| [33] | Zhou W, Zhao C, Liu X H, et al. Mesoscopic simulation of thermo-mechanical behaviors in concrete under frost action[J]. Construction and Building Materials, 2017, 157: 117-131. |












