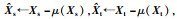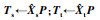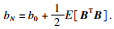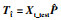, 齐天舒, 芦鹏程
, 齐天舒, 芦鹏程 东北大学秦皇岛分校 计算机与通信工程学院,河北 秦皇岛 066000
收稿日期:2022-05-29
作者简介:赵煜辉(1971-),男,河北秦皇岛人,东北大学秦皇岛分校教授。
摘要:在近红外光谱分析中,已有的标定迁移方法多基于标准样本和无参数归纳模型,普遍存在模型生存周期短、适用范围小等问题.针对此问题,提出了一种参数化对齐源域(主仪器)和目标域(从仪器)特征分布的变分推断标定自适应(variational inference calibration adaptation, VICA)方法.VICA对源域数据进行主成分分析,建立源域特征的变分回归模型.在预测时,VICA首先将目标域数据投影到源域特征子空间中,然后建立源域特征和目标域特征的分布差异函数,通过最小化该函数得到目标域的概率密度模型,实现模型迁移.实验对比表明,VICA比现有的大多数标定迁移方法的标定效果更好.
关键词:化学计量学近红外光谱领域自适应标定迁移变分推断
Research on Calibration Adaptation Method via Variational Inference for Near-Infrared Spectroscopy
ZHAO Yu-hui

 , QI Tian-shu, LU Peng-cheng
, QI Tian-shu, LU Peng-cheng School of Computer and Communication Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066000, China
Corresponding author: ZHAO Yu-hui, E-mail: 1000272@neuq.edu.cn.
Abstract: In near-infrared spectroscopy analysis, existing calibration transfer methods are mostly based on standard samples and non-parametric induction models, which generally suffer from short model lifespan, limited model applicability. To address this problem, a variational inference calibration adaptation(VICA)method is proposed, which aligns the feature distributions of the source domain(master instrument)and a target domain(slave instrument)by a parametric method. VICA performs principal component analysis on the source domain data and establishes a variational regression model for the source domain features. During prediction, VICA first projects the target domain data into the source domain feature subspace, and then establishes a distribution difference function between the source and target domain features, and obtains the probability density model of the target domain by minimizing this function, achieving model transfer. Experimental comparison results show that VICA performs better in calibration transfer than most existing methods.
Key words: chemometricsnear-infrared spectroscopydomain adaptationcalibration transfervariational inference
近红外光谱(NIRS)分析技术,是当今常用的物质定量分析和化合物结构识别方法,具有仪器设备操作简便、解析数据速率快、成本低廉、不易污染样品等优点.已应用于农业生产、化工产品生产、肉制品工业生产,以及环境监测等各个领域[1-2].近红外光谱分析的关键技术是通过统计方法与机器学习等方法对近红外光谱数据建模分析,计算其主要理化指标.当在测量仪器和测量条件并不稳定的条件下,建立的模型会产生差异.通常想到的解决方法是抛弃原有模型,进行重新建模,但建立一个稳健的模型需要大量的时间和空间成本,为解决这一问题,标定迁移的研究应运而生.标定迁移是一种能将模型复用于不同测量仪器或不同状态下采集数据的技术.其通常需要把不同特性的光谱数据投影至同一数据空间作比较,进而实现主光谱数据模型对从光谱数据模型的预测,从而节省了重复建模的开支[3].
标定迁移方法主要分为:有标样的标定迁移和标样自由的标定迁移[4].
有标样的标定迁移方法需要寻找标准样本来实现模型的迁移.标准样本是指同一物质在主、从仪器条件下分别测量的浓度或性质.标准样本的数量不必太大,但需具有良好的代表性和稳定性,以确保模型的迁移真实有效.例如,分段直接标准化(piecewise direct standardization, PDS)[5-7]通过迁移标准样本求出源域与目标域空间的转移矩阵,从而校正源域与目标域光谱的差异.基于典型相关分析的标定迁移(canonical correlation analysis calibration transfer, CCACT)方法[8]则是通过寻找使得源域光谱和目标域光谱之间关联性最大的变量,然后利用这些变量实现模型迁移.
标样自由的标定迁移方法主要有信号预处理方法和投影方法.信号预处理方法以多元散射校正(multiplicative scattering correction, MSC)[9]为例,其首先计算校准集的平均光谱作为参考光谱.然后使用线性回归的方法计算每个从光谱与参考光谱之间的斜率和偏差,从而校正主从光谱之间的差异.投影方法应用较广的有迁移成分回归(transfer component regression, TCR)[10].首先,其通过迁移成分分析(transfer component analysis, TCA)[11]将源域光谱与目标域光谱投影到一个共享再生希尔伯特空间(reproducing kernel Hilbert space, RKHS)[12]的子空间中,然后再使用普通最小二乘法求得预测的浓度.
与上述归纳为主的无参数方法不同,本文提出了一种有参数的标定自适应的方法.该方法用变分推断[13]建立源域特征与物质浓度的变分线性回归模型,并通过校正目标域特征与源域特征的分布差异,使目标域数据能够适应于源域模型.
1 理论知识1.1 变分推断对于一个含有隐变量Z的模型,直接通过最大似然估计的方法学习其后验概率p(Z|X)是一个很复杂的过程.变分推断是一种常用的通过解析的方法来近似模型的后验概率的方法,用q(Z)来近似后验概率,并使用KL散度KL(q(Z)‖p(Z|X))计算其相似度.KL散度可分解为
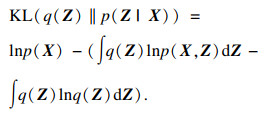 | (1) |
根据平均场理论,假设q(Z)的所有分量都相互独立,即
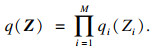 | (2) |
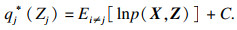 | (3) |
最后,通过坐标上升法得到p(Z|X)的最优近似q*(Z).
1.2 变分推断标定自适应方法为了实现标定自适应,本文的源域和目标域选择了不同仪器测量的光谱数据,分别以Xs和Xt代表,其光谱数据的分布是不相同的,且源域数据是有标签的,而目标域数据是无标签的.
由于光谱数据存在多重共线性,建模前需要先对数据进行降维处理,以避免高维数据所带来的维度灾难,因此使用主成分分析(principal component analysis, PCA)[14]对源域数据进行降维处理.
设P为源域数据Xs在其PCA子空间上的投影矩阵.本文将源域和目标域数据全都投影到源域PCA子空间上,得到各自特征,主仪器特征为Ts=XsP;从仪器特征为Tt=XtP.
然后构建源数据上的标定自适应模型.根据贝叶斯线性回归可知,对于一个回归问题,主仪器特征Ts与物质浓度y的回归系数B的似然函数可拆分表示为
 | (4) |
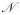
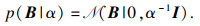 | (5) |
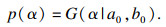 | (6) |
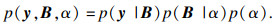 | (7) |
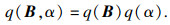 | (8) |
首先考虑α的概率分布,求对数联合概率对于B的积分且仅保留与α有函数依赖关系的项,可得
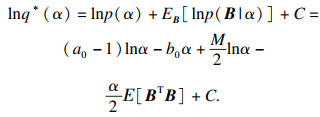 | (9) |
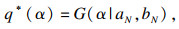 | (10) |
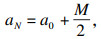 | (11) |
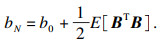 | (12) |
类似地,可以求得回归系数B上的后验概率分布的变分重估计方程:
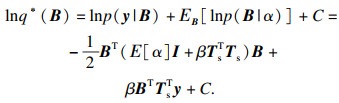 | (13) |
 | (14) |
因此,进一步可以求得式(9)和式(13)中所需的期望,其形式为
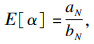 | (15) |
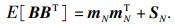 | (16) |
在变分推断的计算结束后,为使目标域和源域间的数据分布对齐,需要调整目标域到源域PCA子空间的投影矩阵.这里使用到了关联对齐法(correlation alignment, CORAL)[15],设
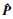

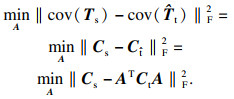 | (17) |
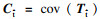


将

 | (18) |
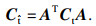 | (19) |
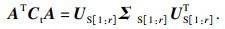 | (20) |
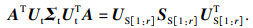 | (21) |
 | (22) |
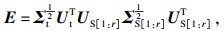 | (23) |
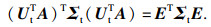 | (24) |
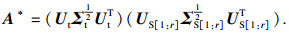 | (25) |
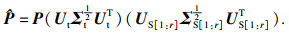 | (26) |
 | (27) |
 | (28) |

2 算法流程VICA算法见表 1.
表 1(Table 1)
| 表 1 VICA算法 Table 1 VICA algorithm |
3 实验结果分析3.1 数据集介绍本文实验用到的数据来自美国嘉吉公司的玉米数据集.该数据集由三种光谱仪对相同的80个玉米样本的观测数据所构成.每个样本有4种物质含量属性,为水分、淀粉、蛋白质、油.三种仪器型号分别为m5,mp5,mp6.光谱波长范围为1 100~2 498 nm.原始光谱的差异图如图 1所示,从图中可以看出,仪器m5与mp5,m5与mp6之间的光谱差异较大,且该差异随着波长的增加而逐渐增加,这意味着波长越长的光谱更易引入噪声.因此本文选择这两种主、从仪器的组合进行实验.
图 1(Fig. 1)
 | 图 1 玉米数据集的不同仪器之间的光谱差异Fig.1 The deviation spectrum of the corn data set between different instruments (a)—m5与mp5的光谱差异;(b)—m5与mp6的光谱差异;(c)—mp5与mp6的光谱差异. |
3.2 参数选择同一个模型的不同参数,对模型的性能影响较大.本实验中,模型的主成分数在[2, 20]中取值,通过10折交叉验证,选择均方根误差最小时的主成分数为最佳主成分个数.在做变分线性回归模型时,方差精度设置为1 000,a0和b0的初始值都为1.
在实验设置中,4种对比的迁移方法和本文方法保留相同实验设置.即主仪器模型使用相同数据集进行建模,并且潜变量的设置范围和参数优化准则均需一致.其他的具体设置为:在PDS中,最佳窗口数使用5折交叉验证在[3, 16]的搜索范围内,以2为增量选择;TCR中,TCA的子空间维度的范围为[1, 24],优化标准与文献[10]中保持一致.
3.3 模型评估实验使用均方根误差RMSE来评估模型的预测精度.其计算公式为
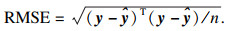 | (29) |
此外,使用RMSECV代表交叉验证的误差,使用RMSEP代表目标域的预测误差.
3.4 实验结果对比及分析根据交叉验证确定的对比模型的相应参数,利用各模型方法进行标定迁移实验.对于有标样的标定迁移方法,为使标准样本具有代表性,将实验中的标准样本个数控制在[15, 35]的范围内,以10为增量选取,以取得的RMSEP的最小值作为模型整体的RMSEP.表 2和表 3分别表示了以m5为主仪器、mp5为从仪器的RMSEP和以m5为主仪器、mp6为从仪器的RMSEP.通过表中数据对比可知,VICA方法的预测误差均小于其他4种方法.
表 2(Table 2)
| 表 2 五种方法的RMSEP(m5与mp5) Table 2 RMSEP of five methods(m5 and mp5) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3(Table 3)
| 表 3 五种方法的RMSEP(m5与mp6) Table 3 RMSEP of five methods(m5 and mp6) |
m5与mp5和m5与mp6两组实验的测量浓度与预测浓度的对比图,如图 2和图 3所示.图中直线上的点表示准确预测了测量浓度的样本.可以很直观地看到VICA在预测上取得了最好的效果.
图 2(Fig. 2)
 | 图 2 测量浓度与预测浓度对比(m5与mp5)Fig.2 Comparison of measured concentration and predicted concentration(m5 and mp5) (a)—水分;(b)—油;(c)—蛋白质;(d)—淀粉. |
图 3(Fig. 3)
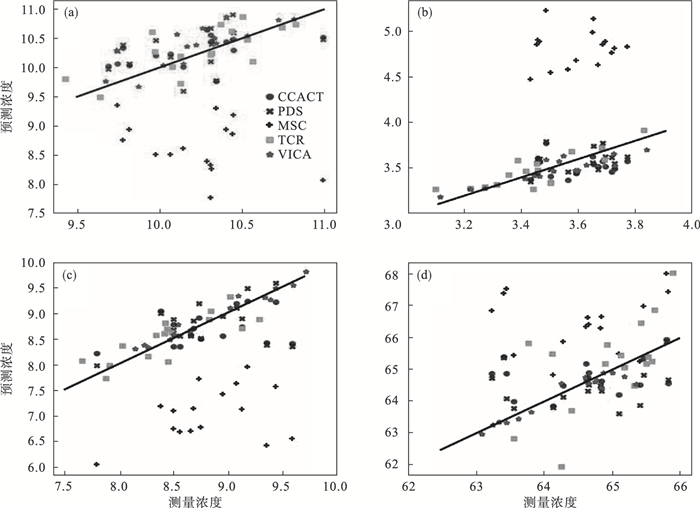 | 图 3 测量浓度与预测浓度对比(m5与mp6)Fig.3 Comparison of measured concentration and predicted concentration(m5 and mp6) (a)—水分;(b)—油;(c)—蛋白质;(d)—淀粉. |
4 结论1) 本文提出了一种参数化对齐源域数据和目标域特征分布的变分推断标定自适应方法.该方法通过建立源域特征和目标域特征的分布差异函数,快速地对齐源域与目标域的数据分布,从而使源域数据上建立的变分推断标定自适应模型可以快速扩展到多个目标域.
2) 本文提出的方法通过在训练过程中对模型参数求积分的方式,可以同时确定多个模型复杂度参数.此外,本文方法在求解回归问题上使用了变分推断的方法,通过近似推断的方式求解后验概率,节省了大量的计算代价.
3) 经实验对比,本文方法相比于PDS,CCACT,MSC和TCR这4种常用的标定迁移方法,在实验中取得了最好的预测效果.其相较于其他4种方法,还具有节省有标签数据开销、可适用性强、计算代价小的优点.
参考文献
| [1] | Aryal G H, Hunter K W, Huang L. A supramolecular red to near-infrared fluorescent probe for the detection of drugs in urine[J]. Organic & Biomolecular Chemistry, 2018, 16(40): 7425-7429. |
| [2] | Rahimpour A, Noubari H A, Kazemian M. A case-study of NIRS application for infant cerebral hemodynamic monitoring: a report of data analysis for feature extraction and infant classification into healthy and unhealthy[J]. Informatics in Medicine Unlocked, 2018, 11: 44-50. DOI:10.1016/j.imu.2018.04.001 |
| [3] | Workman J J. A review of calibration transfer practices and instrument differences in spectroscopy[J]. Applied Spectroscopy, 2018, 72(3): 340-365. DOI:10.1177/0003702817736064 |
| [4] | Weiss K, Khoshgoftaar T M, Wang D D. A survey of transfer learning[J]. Journal of Big Data, 2016, 3(1): 1-40. DOI:10.1186/s40537-015-0036-x |
| [5] | Wang Y D, Veltkamp D J, Kowalski B R. Multivariate instrument standardization[J]. Analytical Chemistry, 1991, 63(23): 530-533. |
| [6] | Wang Y D, Lysaght M J, Kowalski B R. Improvement of multivariate calibration through instrument standardization[J]. Analytical Chemistry, 1992, 64(5): 562-564. DOI:10.1021/ac00029a021 |
| [7] | Bouveresse E, Massart D L. Improvement of the piecewise direct standardisation procedure for the transfer of NIR spectra for multivariate calibration[J]. Chemometrics and Intelligent Laboratory Systems, 1996, 32(2): 201-213. DOI:10.1016/0169-7439(95)00074-7 |
| [8] | Fan W, Liang Y Z, Yuan D L, et al. Calibration model transfer for near-infrared spectra based on canonical correlation analysis[J]. Analytica Chimica Acta, 2008, 623(1): 22-29. DOI:10.1016/j.aca.2008.05.072 |
| [9] | Kramer K E, Morris R E, Rose-Pehrsson S L. Comparison of two multiplicative signal correction strategies for calibration transfer without standards[J]. Chemometrics & Intelligent Laboratory Systems, 2008, 92(1): 33-43. |
| [10] | Malli B, Birlutiu A, Natschl?ger T. Standard-free calibration transfer-an evaluation of different techniques[J]. Chemometrics & Intelligent Laboratory Systems, 2017, 161: 49-60. |
| [11] | Pan S J L, Tsang I W, Kwok J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210. DOI:10.1109/TNN.2010.2091281 |
| [12] | Fukumizu K, Bach F R, Jordan M I. Dimensionality reduction for supervised learning with reproducing kernel Hilbert spaces[J]. Journal of Machine Learning Research, 2004, 5: 73-99. |
| [13] | Blei D M, Kucukelbir A, McAuliffe J D. Variational inference: a review for statisticians[J]. Journal of the American Statistical Association, 2017, 112(518): 859-877. DOI:10.1080/01621459.2017.1285773 |
| [14] | Wold S, Esbensen K, Geladi P. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987(1/2/3): 37-52. |
| [15] | Sun B C, Feng J S, Saenko K. Correlation alignment for unsupervised domain adaptation[M]//Domain Adaptation in Computer Vision Applications. Cham: Springer, 2017: 153-171. |