
 , 陈雪萍, 赵海
, 陈雪萍, 赵海 东北大学 计算机科学与工程学院,辽宁 沈阳 110169
收稿日期:2022-05-18
基金项目:国家重点研发计划项目(2019JSJ12ZDYF01); 中央高校基本科研业务费专项资金资助项目(N2116002, 2020GFZD014)。
作者简介:柳明晗(1998-), 女, 河北唐山人, 东北大学硕士研究生;
赵海(1959-), 男, 辽宁沈阳人, 东北大学教授, 博士生导师。
摘要:传统的网络架构无法满足用户对内容缓存的需求,并且在内容交付中存在低延迟要求和高通信成本之间的冲突.为了解决这些问题,在边缘节点横向协作场景下,提出了一种基于Lyapunov优化和分支定界法的在线内容缓存与交付算法,以平衡交付时延与成本、高效的决策内容缓存与内容交付.提出的算法基于Lyapunov优化理论分解连续问题为单时隙在线优化问题,并利用分支定界算法求解.仿真实验表明,提出的算法能在有限的内容交付成本预算下实现较低的平均内容交付时延、较高的内容命中率,并且能够自适应地平衡内容交付时延与交付成本.
关键词:内容缓存内容交付边缘协作Lyapunov优化分支定界算法
Online Content Caching and Delivery Method Based on Edge Horizontal Collaboration
LIU Ming-han, CHEN Xiang-yi

 , CHEN Xue-ping, ZHAO Hai
, CHEN Xue-ping, ZHAO Hai School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: CHEN Xiang-yi, E-mail: xiangyichen3746@gmail.com.
Abstract: Traditional network architectures cannot meet user needs for content caching, and there is a conflict between low latency requirements and high communication costs in content delivery. To address these problems, an online content caching and delivery algorithm based on Lyapunov optimization and branch and bound method is proposed under the scenario of horizontal collaboration between edge nodes to balance delivery delay and cost and to make efficient decisions on content caching and content delivery. The proposed algorithm decomposes the continuous problem into a single slot online optimization problem based on Lyapunov optimization theory, and solves them using branch and bound algorithms. Simulation experiments showed that the proposed algorithm can achieve lower average content delivery delay and higher content hit rate under a limited content delivery cost budget. It can also adaptively balance content delivery delay and delivery cost.
Key words: content cachingcontent deliveryedge collaborationLyapunov optimizationbranch and bound algorithm
近年来,移动设备的数量正在飞速增长,根据思科的年度互联网报告[1],全球移动设备将从2018年的88亿增长到2023年的131亿,其中5G设备和连接将占全球移动设备和连接的10% 以上.移动设备的增长产生了巨大的网络流量,这会增加数据通信延迟,也给回程链路带来了巨大的负担.同时随着5G等新兴技术的发展,涌现了越来越多的新兴应用和智能服务,如智能交通增强和虚拟现实等[2-3],这些服务具有低时延的需求.而移动流量的飞速增长和传统网络的内容部署无法实时响应具有低时延需求的新兴服务,因此移动边缘计算(mobile edge computing,MEC)应运而生.在网络边缘,例如基站、中继站和移动设备上部署边缘服务器已被证明是一种有效的策略,它允许用户在附近的缓存节点中访问他们需要的内容[4],而不需要从云中心下载内容,减少了从云中心访问内容的延迟与带宽资源消耗.微型蜂窝网络、内容交付网络和信息中心网络,是启用缓存网络的一些示例[5].
MEC中的内容缓存问题侧重于在网络边缘缓存流行的数据内容以响应用户请求[6].现有的工作大多是研究不同内容在网络内的流行程度,依据流行度驱动缓存策略,并针对缓存的命中率做出优化设计[7-8].但受到有限的边缘服务器缓存空间和用户请求时变性等多方面影响,只依据流行度对内容进行缓存不能得到最佳的决策.还有部分工作致力于提高流行度的预测精度[9-10],而忽略了流行度和内容缓存之间的联系.此外,在现有工作中,大部分解决方案只关注内容缓存策略,而不关注内容交付到用户的过程.部分研究缓存和交付策略的工作中,内容缓存与交付是单独进行的,例如文献[11]中,使用了双重目标的方法,首先获得最佳的缓存策略,再对请求进行最佳的内容交付决策;在文献[12]中,使用多代理深度强化学习方法决策缓存替换,再根据得出的缓存替换策略做出交付内容请求,这样会得到一个次优的解决方案.
大多与内容交付相关的工作主要关注用户共享内容的成本[13-14].在用户处缓存内容可以减少通信延迟,但由于用户缓存节点的容量较小,只能缓存少部分内容,无法满足用户需求.而边缘服务器具有更大的缓存容量,并且它们之间的水平连接速度高于用户从云上内容库获取内容的速度,文献[15]中提出了横向的内容交付以提高交付的性能,较高的网络带宽能够减小交付时延,但也会导致带宽成本的提高.因此,平衡网络内的内容交付时延与成本是需要解决的关键问题.
本文考虑MEC网络中缓存节点的横向协作,提出了基于Lyapunov优化和分支定界法的在线内容缓存与交付(Lyapunov optimization and branch-and-bound-based online content caching and delivery, LBB-CCD)算法.将系统的交付成本视作队列,以在没有用户请求内容等先验信息下,实现交付成本和交付时延之间的平衡,并在长期的成本约束下实现最优的内容缓存与交付决策,最后通过理论分析了LBB-CCD算法的性能保证.
1 系统模型1.1 网络模型系统的网络模型如图 1所示,本文考虑边缘横向协作缓存与交付的网络架构.其中,用户定义为ui,i∈I={1, 2, …, U}.具有存储能力的基站定义为bj,j∈J={1, 2, …, B},基站bj具有缓存容量cj,网络中的每个基站可以为其覆盖范围内的用户提供内容.边缘服务器与基站部署在同一位置,为基站提供缓存内容的能力,在图 1中标识为内容服务器.每个基站都可以在其存储容量限制内缓存内容,定义为f∈Φ={1, 2, …, F},内容f的大小为sf.由于云中心具有较强的计算存储能力,所有的内容都可以在云中心上的内容服务器里检索到.考虑基站间横向协作的有线通信具有异构的网络带宽,定义基站bj和基站bj′之间的通信带宽为wjj′∈W.本文将时隙离散为t∈T={0, 1, …, τ-1},由于内容请求的随机性,在每个时隙中,用户以一定概率生成内容请求.
图 1(Fig. 1)
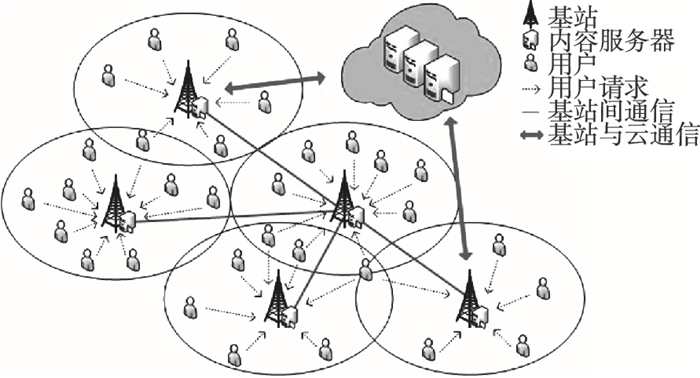 | 图 1 内容缓存和交付的网络模型Fig.1 Network model of content caching and delivery |
由于边缘服务器的缓存能力有限,用户请求的内容无法全部在邻近基站处获取,因此考虑边缘服务器之间的横向协作,以更好地对用户的请求进行及时地响应.为此,本文构建横向协作中包含有线通信和无线通信两部分的通信模型.
定义用户ui的位置pi(t)=(xi(t), yi(t)),固定基站bj的位置pj=(xj, yj).如果用户ui在基站bj的覆盖范围内,则由基站bj向用户ui交付内容的传输速率rijB可以计算为
 | (1) |
1.2 决策模型本文研究了基于边缘横向协作的边缘内容缓存与交付决策问题,以最小化内容交付时延.定义时隙t内的内容缓存决策为xjf(t)∈{0, 1}.具体地,如果基站bj在时隙t缓存了内容f,则xjf(t)=1,否则xjf(t)=0.内容交付决策定义为yji(t)∈{0, 1},如果基站bj在时隙t对用户ui请求的内容进行交付,则yji(t)=1,否则yji(t)=0.如果用户ui请求的内容不能在边缘交付,则由云中心进行交付,即ycloudi(t)=1.
定义用户ui在时隙t发出对内容qi(t)∈Φ的请求,请求本身的大小为siq,若用户ui在时隙t不发出请求,则qi(t)=0.交付用户ui请求内容的无线部分请求传输与内容下载时延di, jw(t)计算为
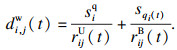 | (2) |
对于基站间的横向协作,在基站bj对用户ui请求的内容进行交付的路径中,基站间进行边缘协作交付内容的有线部分请求传输与内容下载时延di, jl(t)计算为
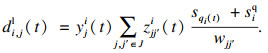 | (3) |
由于路由决策不是问题的直接决策,而是依赖于交付决策的.对于得出的交付决策,将基站和用户分别视为源节点和目的节点,使用Dijkstra算法选取权重最小的路径作为路由决策.
由式(2),式(3),对用户ui请求的内容进行交付的总时延计算为
 | (4) |
对于用户ui请求的内容qi(t),根据内容大小sqi(t)在基站bj缓存容量cj的占比来考虑其在基站中的检索成本,定义用户ui在基站bj检索其请求内容的检索成本ψi, js(t)为
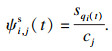 | (5) |
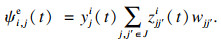 | (6) |
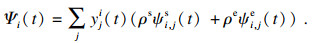 | (7) |
由式(7),系统的总交付成本可以表示为
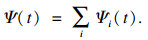 | (8) |
1.3 问题定制对于时隙t的内容缓存决策xjf(t)与内容交付决策yji(t)需要满足以下约束:
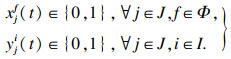 | (9) |
 | (10) |
 | (11) |
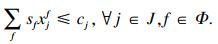 | (12) |
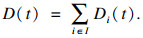 | (13) |
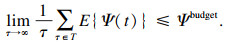 | (14) |
因此,长期成本预算下的长期用户交付时延优化问题可以表述如下:
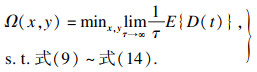 | (15) |
2 LBB-CCD算法为了解决前文提出的问题,利用目标结合成本的Lyapunov漂移[16]重新定义问题优化目标,将连续优化问题分解为多个单时隙在线优化问题并通过分支定界法求解.本文提出了LBB-CCD算法,以联合获得最优的内容缓存和内容交付决策.
2.1 基于Lyapunov优化的在线内容缓存与交付为了控制长期的内容交付成本,网络运营商需要为网络内的所有基站构建并维护一个内容交付成本的虚拟队列Q(t),它表示时隙t所有基站的内容交付成本超出预算的部分,在时隙t+1成本队列更新如下:
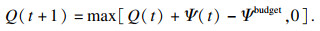 | (16) |
在任意时隙t,二次李雅普诺夫函数定义如下:
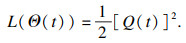 | (17) |
由于用户请求的随机性,本文将单时隙Lyapunov漂移定义为相邻时隙二次Lyapunov函数差的条件期望,即
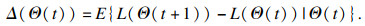 | (18) |
对于长期成本预算的约束,内容交付的成本队列Q(t)的长期平均期望满足式(19)时,
 | (19) |
为了优化交付时延的同时保证交付成本队列的稳定,使用参数V来控制调整网络中的交付成本与时延,将时隙t的优化目标定义如下:
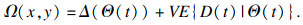 | (20) |
 | (21) |

根据机会性最小化条件期望的框架,可以在没有期望的情况下最小化目标上限[16],由此,单时隙优化问题可以重新定义为
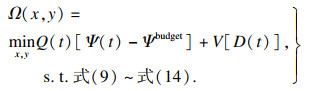 | (22) |
算法1描述了使用LBB-CCD算法求解问题的伪代码.其中算法1的4~27行对应于求解单时隙问题的分支定界算法.
对于决策变量X={xif}B×F和Y={yij}B×U,分支定界法首先将所有的二元变量在根问题(RP)处放宽为0到1的连续变量(算法1第4行).如果得到的决策变量满足两个条件:①|
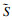
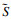
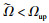
在根问题(RP)处,如果问题不可行或得到了整数解,进行剪枝可以加快分支定界的运行(算法1第6~10,11~16行).
如果在根问题(RP)处,得到的解不满足完整性约束,则继续进行分支,将宽松的决策变量之一(即xif或yij)固定为左侧分支的“0”和右侧分支的“1”,得到左右两个子问题(SP_L和SP_R)(算法1第19~20行),并在下一次循环中作为当前的根问题(算法1第23行).
为了保证接近最优解的存在,设置最优性容差η为非负值(算法1第22行).具体来说,当目标在界限内收紧并且上限和下限之间的差异小于最优性容差时,得到的解是最优的,表示如下:
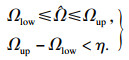 | (23) |
输入:内容交付预算成本Ψbudget,完整性阈值ε,最优性阈值η.
输出:时隙t+1的内容交付成本队列Q(t+1).
1.初始化: Q(0)=0
2.for each time slot t∈{0, 1, …, τ-1} do
3.????获得用户请求qi(t), 内容交付成本的虚拟队列Q(t)
4.????初始化: 下限Ωlow=0, 上限Ωup=+∞, 活动节点数Nactive=1, Z={X, Y}∈[0, 1]
5.????更新活动节点数Nactive←Nactive-1
6.????if root problem(RP)is feasible then
7.????????求解问题(RP)得到解
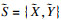
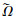
8.????else
9.????????????剪枝
10.????end if
11.????if |
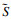
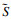
12.????if
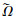
13.????得到最优解
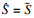

14.????Ωup←
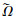
15.????end if
16.????????剪枝
17.????else
18.????Ωlow←
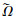
19.????选择未进行分支的决策变量ρ∈Z分支得到两个子问题(SP_L和SP_R), Nactive←Nactive+2
20.????更新约束ρ←1 or ρ←0
21.????end if
22.????if Nactive≠0 and Ωup-Ωlow>η then
23.????设置子问题(SP)为新的根问题(RP), 转向算法第5行
24.????else
25.????获得最优解
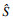

26.????end if
27.??根据Q(t+1)的定义更新内容交付成本的虚拟队列
28. end for
对用于求解单时隙问题的分支定界法,最优解在根问题处得到时,算法1的复杂度最低,但当子问题在分支定界树的左右节点上处于活动状态时,复杂度会变得很高.使用随机过程近似分支过程在深度优先搜索策略下可以得出分支定界法具有多项式复杂度O(n3 ln(n))[19],本问题模型中n=B(F+U)是决策变量数,则算法1的总体复杂度为O(τB3 max(F, U)3ln(B max(F, U))).
3 性能分析在本节中,使用最优容差[20]和随机网络优化[16]分析了LBB-CCD算法的良好性能.
首先分析了单时隙问题下算法解的最优性,在最优容差η下,单时隙问题式(22)在有限步数内收敛.
定理1??分支定界法在最优容差η下会在有限步数内收敛.并且,对任意η>0存在步数μη∈N,使得
 | (24) |
证明??假设对于第d个目标值
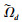
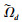
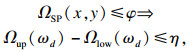 |
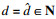
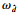
 |
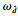


同时,由分支定界法的步骤,有
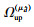
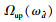
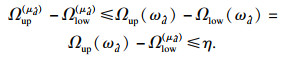 | (25) |
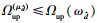
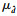
接下来,考虑在

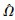


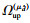

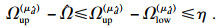 |

利用分支定界得到的最优容差η,将单时隙问题进行扩展,得到LBB-CCD算法的最优性保证.
定理2??LBB-CCD算法返回的方案与最优解之间的差距可以表示为
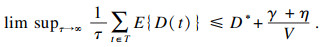 | (26) |
4 性能评估为了评估LBB-CCD算法的性能,本文通过仿真实验评估内容交付成本约束下的内容缓存与交付性能.
4.1 仿真设置在仿真实验中,部署了16台固定的具有缓存能力的基站,并在基站的覆盖范围内随机部署用户.假设每个用户在一个时隙中至少处于一个基站的覆盖范围内.基站的存储容量设置为在5~10 GB内均匀分布.仿真实验中构建了80个内容,内容大小在100~1 000 Mb内均匀分布.用参数(-0.95,0.5)的MZipf分布[21-22]设置内容流行度,用户根据内容的流行度发出对内容的请求.对于在云中心上交付的时延和成本,考虑设置合适的大于边缘交付的值.另外,对于总成本的两部分在实验中首先进行一致性处理,以减小数值原因对算法产生的影响.
其他重要的仿真参数如表 1所示.为了评估本文提出的LBB-CCD算法的性能,将其与现有算法进行了比较.
表 1(Table 1)
| 表 1 仿真参数 Table 1 Simulation parameters |
本文考虑两种内容缓存算法:按内容流行度优先部署内容(PC)[23]和在边缘基站随机部署内容(RC).两种内容交付算法:低时延优先交付(DPD)和低成本优先交付(CPD).对于交付方式,另外考虑权衡成本与时延进行贪心交付的算法(LGD).结合以上缓存与交付方案得到5种对比算法.
4.2 仿真结果为了评估LBB-CCD算法的性能,本文选择了多个性能指标,包括内容命中率和内容交付时延.此外,本文还研究了控制参数V对性能指标的影响.
1) 内容命中率:内容命中率是评估基站内容缓存的重要指标,在时隙t所有用户请求的内容在边缘的命中率为
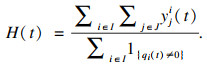 |
图 2(Fig. 2)
 | 图 2 不同条件下的内容命中率Fig.2 Content hit rate under different conditions (a)—用户数;(b)—成本预算. |
图 2表明考虑内容流行度的命中率要高于在边缘随机缓存内容,但本文提出的LBB-CCD算法的内容命中率是最优的.这是由于LBB-CCD算法考虑了基站间的横向协作,当用户请求的内容不能在邻近基站获取时,可以通过横向协作在其他拥有内容的基站处获取,这让更多用户请求的内容可以在边缘命中,并且通过对内容交付成本队列的控制,可以在有限的成本下命中更多用户请求的内容.
2) 内容平均交付时延:交付时延是评估用户内容请求交付的重要指标,本文考虑每Mb内容的平均交付时延.图 3显示了具有不同成本预算和用户数的内容平均交付时延.从图 3a中可以发现,在不同的用户数下,LBB-CCD算法的平均交付时延都优于对比算法,随着用户数的增加,受到网络内带宽成本的限制,平均交付时延逐渐增加.通过图 3b可以发现,在不同的带宽成本预算下,LBB-CCD算法的平均交付时延也是最优的,随着成本预算的增加,平均交付时延逐渐降低.从图 3中还可以观察到,虽然两种采用DPD的算法考虑低时延优先,但低时延带来的高带宽成本导致了内容命中率的降低,也导致总的平均时延较低.
图 3(Fig. 3)
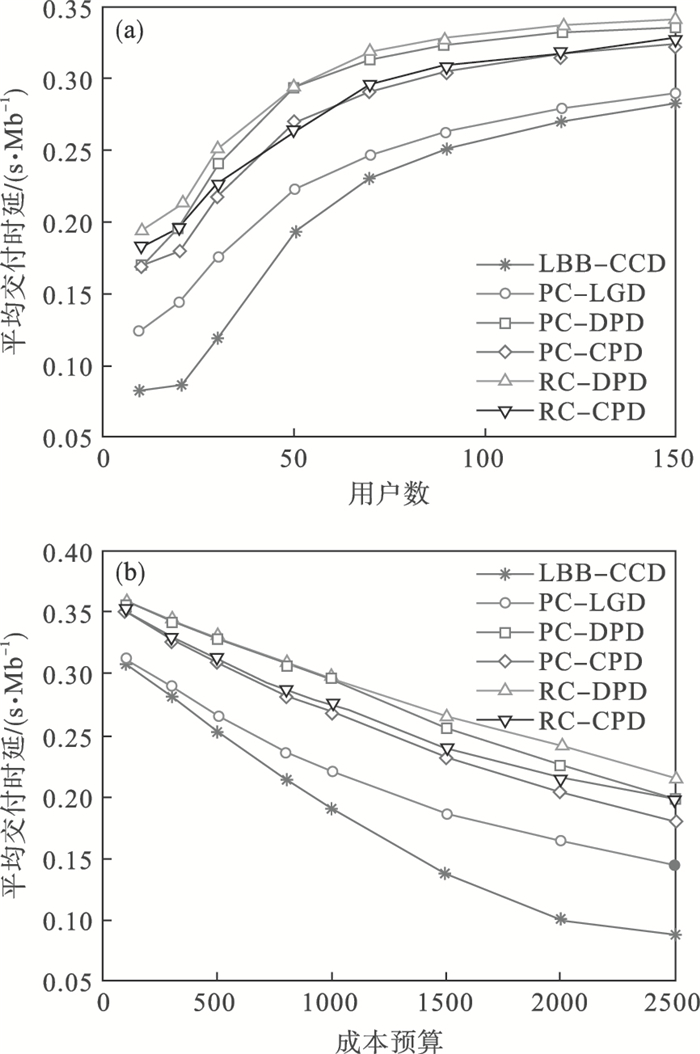 | 图 3 不同条件下的内容平均交付时延Fig.3 Average content delivery delay under different conditions (a)—用户数;(b)—成本预算. |
图 4表示了用户请求在基站部分交付的平均交付时延.在基站交付部分,DPD算法表现出了相较于CPD算法的优势,而本文提出的LBB-CCD算法能在时延上逼近PC-DPD算法.这是由于考虑基站间的横向协作扩大了交付用户请求内容的范围,并且联合内容缓存与内容的交付决策能够依据用户请求在边缘缓存更合适的内容,这使得更多用户请求的内容可以在边缘命中.同时LBB-CCD算法在边缘权衡内容的交付时延与成本,不仅能够使用户整体的平均交付时延最优,用户边缘部分的平均交付时延也具有与PC-DPD算法相当的性能.
图 4(Fig. 4)
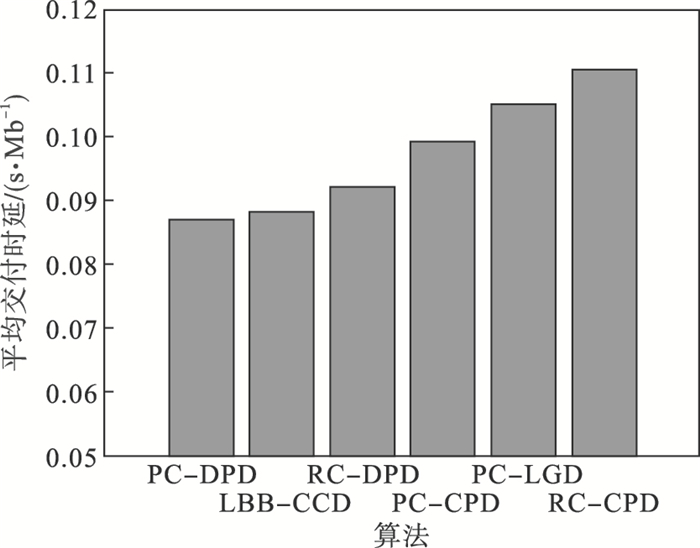 | 图 4 基站部分交付的内容平均交付时延Fig.4 Average delivery delay of the content delivered by the base station part |
3) 控制参数:网络运营商可以通过控制参数V控制MEC网络.图 5给出了不同V值下的平均交付时延与内容交付成本以及队列积压在时隙t下的收敛曲线.从图 5可以看到,内容平均交付时延与内容交付成本以及队列积压都随着时隙的增加逐渐趋于稳定,系统收敛时间也随着V值的增加而增加.这说明LBB-CCD算法保证了队列的稳定,进而控制内容交付成本的增长,保证了内容交付成本与交付时延的收敛.
图 5(Fig. 5)
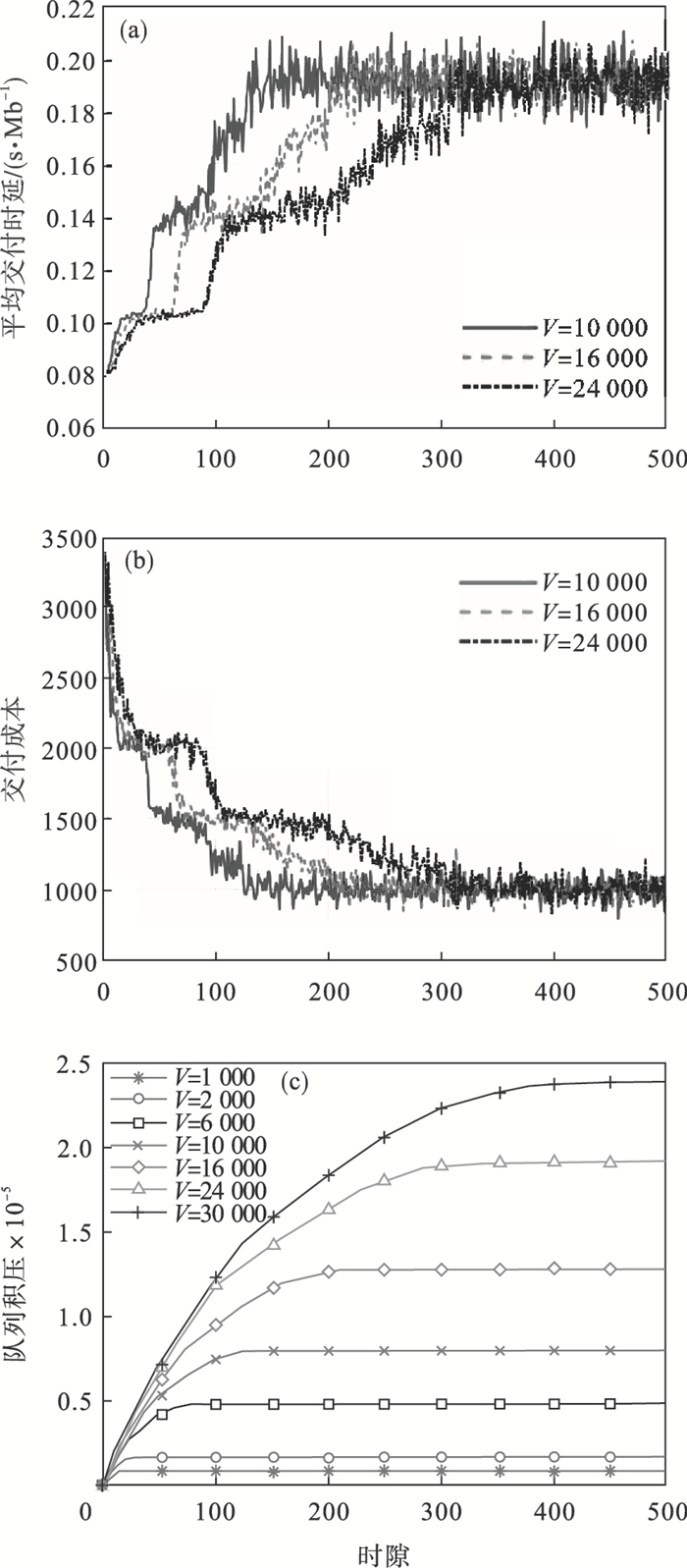 | 图 5 各指标时隙收敛图Fig.5 Convergence over time of each indicator (a)—平均交付时延;(b)—交付成本;(c)—队列积压. |
不同V值下的内容命中率与平均交付时延如图 6所示.随着V值的增加,内容平均交付时延和内容命中率都逐渐趋于稳定,因此选取较高的V值可以实现网络的最优控制.根据内容供应商的不同需求,LBB-CCD算法可以通过控制参数V,自适应调整内容交付成本.
图 6(Fig. 6)
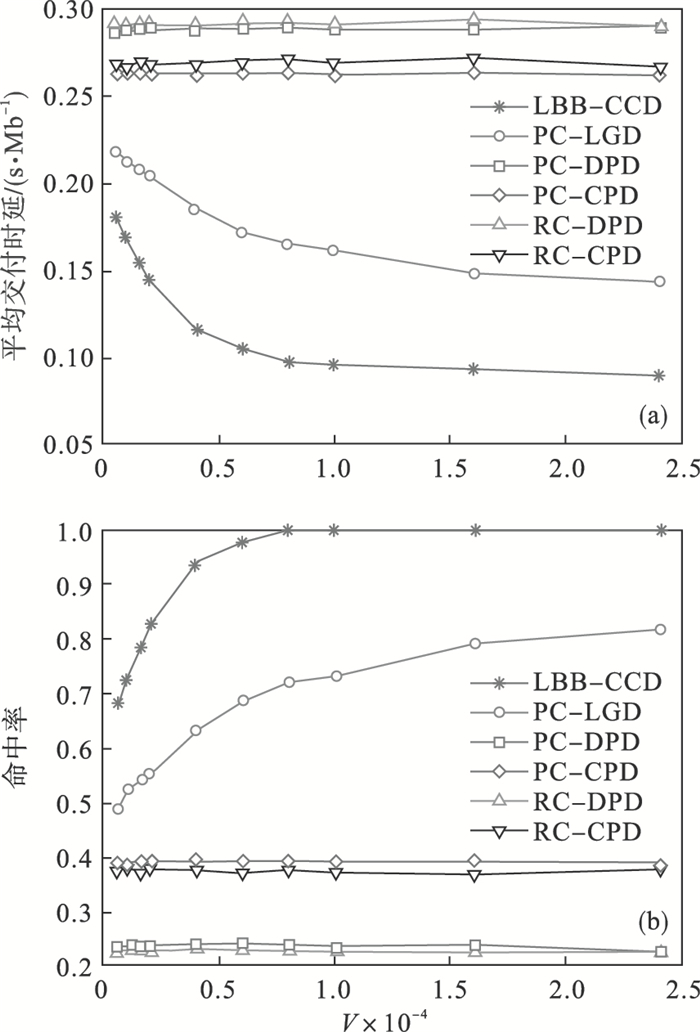 | 图 6 不同V值下的内容平均交付时延和内容命中率Fig.6 Average content delivery delay and content hit rate under different values of V (a)—平均交付时延;(b)—命中率. |
5 结语本文研究了联合内容缓存与内容交付的问题,在边缘横向协作的场景下,基于Lyapunov优化理论和分支定界法提出LBB-CCD算法,完成了在内容交付成本的限制下对内容缓存与交付的在线优化.并通过仿真实验,从内容平均交付时延和内容命中率等方面对算法的性能进行了评估,结果表明了本文提出的算法能在有限成本预算下实现较低的时延以及较高的命中率,达成优于对比算法的性能,并且能够自适应平衡内容交付时延与交付成本.
参考文献
| [1] | Cisco. Cisco annual internet report(2018—2023)white paper [EB/OL]. (2022-03-10)[2022-03-30] https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html. |
| [2] | Muhammad A, Sorkhoh I, Qu L, et al. Delay-sensitive multi-source multicast resource optimization in NFV-enabled networks: a column generation approach[J]. IEEE Transactions on Network and Service Management, 2021, 18(1): 286-300. DOI:10.1109/TNSM.2021.3049718 |
| [3] | Sun Y P, Chen Z Y, Tao M X, et al. Communications, caching, and computing for mobile virtual reality: modeling and tradeoff[J]. IEEE Transactions on Communications, 2019, 67(11): 7573-7586. DOI:10.1109/TCOMM.2019.2920594 |
| [4] | Liu D, Chen B Q, Yang C Y, et al. Caching at the wireless edge: design aspects, challenges, and future directions[J]. IEEE Communications Magazine, 2016, 54(9): 22-28. DOI:10.1109/MCOM.2016.7565183 |
| [5] | Chu W B, Yu Z W, Lui J C S, et al. Jointly optimizing throughput and content delivery cost over lossy cache networks[J]. IEEE Transactions on Communications, 2021, 69(6): 3846-3863. DOI:10.1109/TCOMM.2021.3061685 |
| [6] | Malik A, Kim J, Kim K S, et al. A personalized preference learning framework for caching in mobile networks[J]. IEEE Transactions on Mobile Computing, 2021, 20(6): 2124-2139. DOI:10.1109/TMC.2020.2975786 |
| [7] | Chen Q, Wang W, Yu F R, et al. Content caching oriented popularity prediction: a weighted clustering approach[J]. IEEE Transactions on Wireless Communications, 2021, 20(1): 623-636. DOI:10.1109/TWC.2020.3027596 |
| [8] | Jiang W, Feng G, Qin S. Optimal cooperative content caching and delivery policy for heterogeneous cellular networks[J]. IEEE Transactions on Mobile Computing, 2017, 16(5): 1382-1393. DOI:10.1109/TMC.2016.2597851 |
| [9] | Saputra Y M, Hoang D T, Nguyen D N, et al. A novel mobile edge network architecture with joint caching-delivering and horizontal cooperation[J]. IEEE Transactions on Mobile Computing, 2021, 20(1): 19-31. DOI:10.1109/TMC.2019.2938510 |
| [10] | Garg N, Sellathurai M, Bhatia V, et al. Online content popularity prediction and learning in wireless edge caching[J]. IEEE Transactions on Communications, 2020, 68(2): 1087-1100. DOI:10.1109/TCOMM.2019.2956041 |
| [11] | Shanmugam K, Golrezaei N, Dimakis A G, et al. FemtoCaching: wireless content delivery through distributed caching helpers[J]. IEEE Transactions on Information Theory, 2013, 59(12): 8402-8413. DOI:10.1109/TIT.2013.2281606 |
| [12] | Chang J L, Zhang N F, Tao M X, et al. Federated multi-agent reinforcement learning for collaborative edge caching in content delivery networks[C] // 2022 14th International Conference on Wireless Communications and Signal Processing. Nanjing, 2022: 166-170. |
| [13] | Asheralieva A, Niyato D. Combining contract theory and Lyapunov optimization for content sharing with edge caching and device-to-device communications[J]. IEEE/ACM Transactions on Networking, 2020, 28(3): 1213-1226. DOI:10.1109/TNET.2020.2978117 |
| [14] | Kumar S, Misra S. Enabling multi-source device-to-device content delivery in cellular networks[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10853-10863. DOI:10.1109/TVT.2021.3106059 |
| [15] | Qu Z H, Ye B L, Tang B, et al. Cooperative caching for multiple bitrate videos in small cell edges[J]. IEEE Transactions on Mobile Computing, 2020, 19(2): 288-299. DOI:10.1109/TMC.2019.2893917 |
| [16] | Neely M J. Stochastic network optimization with application to communication and queueing systems[M]. San Rafael: Morgan & Claypool Publishers, 2010. |
| [17] | Vielma J P. Mixed integer linear programming formulation techniques[J]. SIAM Review, 2015, 57(1): 3-57. DOI:10.1137/130915303 |
| [18] | Chen X Y, Bi Y G, Chen X P, et al. Dynamic service migration and request routing for microservice in multi-cell mobile edge computing[J]. IEEE Internet of Things Journal, 2022, 9(15): 13126-13143. DOI:10.1109/JIOT.2022.3140183 |
| [19] | Smith D R. Random trees and the analysis of branch and bound procedures[J]. Journal of the ACM, 1984, 31(1): 163-188. DOI:10.1145/2422.322422 |
| [20] | Fowkes J M, Gould N I M, Farmer C L. A branch and bound algorithm for the global optimization of Hessian Lipschitz continuous functions[J]. Journal of Global Optimization, 2013, 56: 1791-1815. DOI:10.1007/s10898-012-9937-9 |
| [21] | Hefeeda M, Saleh O. Traffic modeling and proportional partial caching for peer-to-peer systems[J]. IEEE/ACM Transactions on Networking, 2008, 16(6): 1447-1460. DOI:10.1109/TNET.2008.918081 |
| [22] | Wang X F, Li R B, Wang C Y, et al. Attention-weighted federated deep reinforcement learning for device-to-device assisted heterogeneous collaborative edge caching[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(1): 154-169. DOI:10.1109/JSAC.2020.3036946 |
| [23] | Hassine N B, Milocco R, Minet P. ARMA based popularity prediction for caching in content delivery networks[C] // 2017 Wireless Days. Porto, 2017: 113-120. |
