
 , 张剑宇, 张石
, 张剑宇, 张石 东北大学 计算机科学与工程学院,辽宁 沈阳 110169
收稿日期:2022-06-06
基金项目:辽宁省教育厅高等学校基本科研项目(LJKZ0011)。
作者简介:佘黎煌(1980-),男,福建莆田人,东北大学讲师,博士;
张石(1963-),男,辽宁抚顺人,东北大学教授,博士生导师。
摘要:为了提高混合信号的波达方向(direction of arrival, DOA)估计精度并降低其阵列孔径损失,提出一种基于斜投影算子的高精度DOA估计算法.所提算法将混合信号中独立信号与相干信号分两个阶段进行估计,首先利用ESPRIT(estimating signal parameter via rotational invariance techniques)算法处理阵元接收数据的协方差矩阵,得到混合信号中独立信号的DOA估计值;而后利用斜投影算子去除混合信号中独立信号的信息,得到新的协方差矩阵;利用新得到的协方差矩阵的信号子空间进行去相干处理;最后结合ESPRIT算法计算得到相干信号的DOA估计值.仿真结果表明,相较传统的混合信号DOA估计算法,所提算法在低信噪比情况下以及信号入射间隔较小的情况下有较高精度,有效地降低了阵列孔径的损失.在不同的采样快拍数下,本文算法也表现出更强的鲁棒性.
关键词:混合信号波达方向估计斜投影算子信号子空间ESPRIT算法
DOA Estimation Algorithm of Mixed Signals Based on Oblique Projection Operator
SHE Li-huang

 , ZHANG Jian-yu, ZHANG Shi
, ZHANG Jian-yu, ZHANG Shi School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: SHE Li-huang, E-mail: shelihuang@ise.neu.edu.cn.
Abstract: In order to improve the DOA estimation accuracy of mixed signals and reduce array aperture loss, a high-precision DOA estimation algorithm based on oblique projection operator is proposed. The proposed algorithm estimates the independent and coherent signals of the mixed signals in two stages. Firstly, the covariance matrix of the data received by the array element is processed by the estimating signal parameter via rotational invariance techniques(ESPRIT), and the DOA estimates of the independent signals in the mixed signals are calculated. Then, the algorithm uses the oblique projection operator to remove the independent signal information in the mixed signals to obtain a new covariance matrix. The signal subspace of the newly obtained covariance matrix is used for decoherence processing. Finally, the ESPRIT algorithm is used to calculate the DOA estimates of the coherent signals. Simulation results show that the proposed algorithm has higher accuracy than traditional mixed signal DOA estimation algorithms in the case of low signal-to-noise ratio and small signal incidence interval, and effectively reduces array aperture loss. Under the condition of different sampling snapshot numbers, the proposed algorithm also shows stronger robustness.
Key words: mixed signalsDOA(direction of arrival) estimationoblique projection operatorsignal subspaceESPRIT algorithm
阵列信号处理是信号处理的一个重要分支,它在水声信号探测、地震勘测和医疗等领域获得了广泛应用和迅速发展.而波达方向(direction of arrival, DOA)估计是阵列信号处理的一个主要研究方向[1-2].由于通信环境中的同频干扰以及多径传输的存在,导致入射到阵列的信号中往往会混杂有相干信号.混合信号中的相干信号会使传统的高分辨率算法性能急剧下降,制约了子空间类算法[3]的发展.因此对混合信号DOA估计的研究具有重要的研究价值与实际意义.
混合信号中的相干信号会导致子空间类算法中协方差矩阵秩的亏损,从而导致子空间类算法的失效.解相干的经典方法主要有两类:一类是降维处理,比如前后向空间平滑算法[4],通过划分子阵的方式来恢复协方差矩阵的秩[5],有良好的解相干性能,但存在阵列孔径损失和在低信噪比情况下解相干性能降低等问题;另一类则是不进行降维处理,通过重构Toeplitz矩阵来实现解相干[6],虽然不会损失阵列孔径,但会增加计算复杂度并且性能降低.针对前后向空间平滑算法无法充分利用协方差矩阵信息的问题,文献[7]提出了改进的空间平滑算法,不仅利用了单个子阵的协方差矩阵,而且利用了不同子阵列的交叉协方差矩阵,但仍存在对噪声的鲁棒性低,在低信噪比情况下对小间隔的入射信号估计误差较大等问题.文献[8]对此作出改进,提出了ESS-SS算法,该算法在全相干信号的情况下表现出非常优异的性能,但在混合信号的情况下并无明显改进.文献[9]中针对混合信号提出了一种两阶段的DOA估计算法,首先估计混合信号中的独立信号,然后利用空间差分的方法去除混合信号中独立信号的信息,最后通过空间平滑算法来得到相干信号方位角.该算法在低信噪比时对独立信号估计较为准确,提高了阵列孔径,但空间差分法会导致相干信号信息的不完整,并且该算法在小信号间隔下表现一般.本文提出一种两阶段的DOA估计算法,首先利用ESPRIT算法[3]估计混合信号中的独立信号信息,而后利用斜投影算子构造仅包含相干信号信息的协方差矩阵,最后利用新构造的协方差矩阵的信号子空间进行去相干处理,从而得到相干信号的DOA估计信息.仿真结果证明本文所提算法在低信噪比、小快拍数以及入射角度间隔较小时波达方向估计有更加优越的性能.
1 混合信源信号模型假设存在M个满足远场条件的各向同性的阵元组成的均匀线阵模型.同时有K个独立信号与相干信号组成的远场窄带混合信号作用在均匀线阵上,入射角度为θk(k=1, 2, …, K).均匀线阵的阵元间隔为入射目标信号的半波长,即d=λ/2.以第一个阵元为参考阵元,可以得到阵列的方向向量为
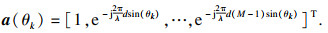 | (1) |
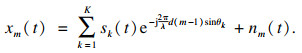 | (2) |
假设K个信号中包含Ku个独立信号和Kc个相干信号,而Kc个相干信号分为L组,每组相干信号相互独立,数目设置为Pk(k=1, …, L).由以上的假设可以得到均匀线阵在t时刻接收到的数据矢量为
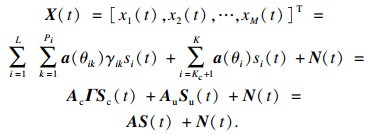 | (3) |
通过式(3)可以得到理想观测数据的协方差矩为
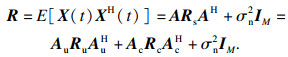 | (4) |
2 本文方法描述2.1 ESPRIT算法解决非相干信号的DOA估计,ESPRIT算法可以达到高分辨率估计的效果.假设信号模型中K个入射信号均为独立信号,将前M-1个阵元组成第1个子阵,后M-1个阵元组成第2个子阵,X1表示第1个子阵接收到的来波信号,X2表示第2个子阵接收到的来波信号,将阵列的流型矩阵分块:
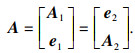 | (5) |
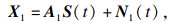 | (6) |
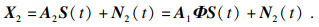 | (7) |
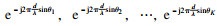
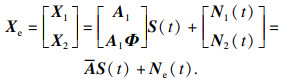 | (8) |
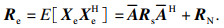 | (9) |
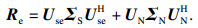 | (10) |
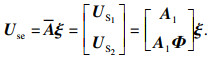 | (11) |
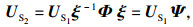 | (12) |
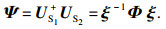 | (13) |
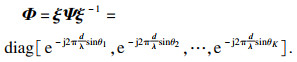 | (14) |
2.2 斜投影算子在DOA估计中,斜投影算子可以提取期望信号,滤除干扰信号的影响[10-11].从文献[10]中得知斜投影算子的定义, 对于线性子空间H与零空间Q,斜投影算子EH/Q是一个非正交投影,可表示为
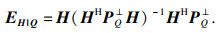 | (15) |
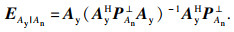 | (16) |
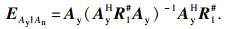 | (17) |
2.3 基于斜投影的混合信号DOA估计算法ESPRIT算法是一种极具代表性的子空间分解类算法,对于不相关信号的估计具有极佳的性能.但混合信号中的相干信号会造成矩阵秩的亏损,从而导致此算法失效[12].ESPRIT算法虽然无法直接用于估计混合信号中的所有信号,但是可以首先用于估计混合信号中的独立信号[13-14].因此,为了解决混合信号的DOA估计问题,本文提出了一种基于斜投影算子的DOA分段估计算法.算法分为两个阶段,第一阶段是对独立信号的角度估计,第二阶段是对相干信号的角度估计.
2.3.1 独立信号的波达方向估计以第1节中的混合信号模型为研究基础,第一阶段首先是对混合信号中的Ku个独立信号进行估计.对协方差矩阵R进行特征值分解,得到
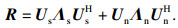 | (18) |
根据ESPRIT算法的原理可知,存在唯一非奇异矩阵Ξ使得Us=AΞ,将Us分割成(M-1)×K的两个重叠的子阵:
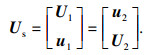 | (19) |
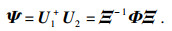 | (20) |
在实际的测向环境中,由于噪声、快拍数据不理想等因素的影响,不相关信号的特征值不会严格等于1.此时,选取Ku个模值最接近1的特征值.
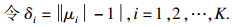 | (21) |
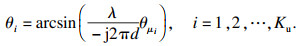 | (22) |
 | (23) |
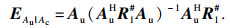 | (24) |
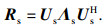 | (25) |
 | (26) |
 | (27) |
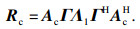 | (28) |
将Rc进行特征分解,得到
 | (29) |
将Usc纵向依次划分为N个重叠的P(P>L)行L列的子矩阵,N与P满足N+P-1=M,则第i(i=1, 2, …, N)个子矩阵由Usc的第i行到第i+P-1行构成,假设其为Vi,定义Vii=ViΛcViH,利用Vii构造新的协方差矩阵来恢复原协方差矩阵Rc的秩:
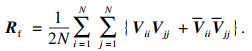 | (30) |
1) 根据式(4)构造数据观测矩阵的协方差矩阵R,并对R进行特征分解,得到信号子空间Us;
2) 根据式(19)将信号子空间分块,并利用式(20)计算Ψ并对其进行特征分解;
3) 选取Ψ特征值的模值最接近1的Ku个特征值,根据式(22)计算得到独立信号的DOA估计值;
4) 根据式(1)和式(23)计算独立信号的流型矩阵;
5) 根据式(24)计算斜投影算子并根据式(26)计算得到去除独立信号信息的协方差矩阵Rc;
6) 通过式(30)对Rc进行去相干处理,得到秩恢复的协方差矩阵Rf;
7) 将Rf进行特征分解,利用ESPRIT算法得到混合信号中相干信号的DOA估计角度.
3 实验验证与比较针对提出的基于斜投影算子的混合信源的DOA分段估计算法的性能进行测试.为了验证本文算法的各项性能,仿真实验中对比了文献[7]中的ISS算法、文献[8]中的ESS-SS算法以及文献[9]中的基于空间差分技术的DOA估计算法.其中,ISS算法与ESS-SS算法为空间平滑算法的改进算法,直接对全部的混合信号进行DOA估计.文献[9]中算法与本文算法同为两阶段的DOA估计算法,将独立信号与相干信号分别进行DOA估计.
3.1 验证算法的有效性为了验证本文算法的有效性,以成功检测概率为指标.成功检测概率即全部蒙特卡洛实验中成功估计入射信号的概率,通过DOA估计成功的实验次数与全部的实验次数之比得到.
实验1??阵列设置为8阵元的均匀线阵,阵元间距为信号半波长,假设有3个入射信号,其中前2个信号为一组相干信号,分别为-15°和5°,两个相干目标信号对应的衰减系数设置为[1,0.9],第3个信号为独立信号,设为50°.采样快拍数为500,信噪比以3 dB为间隔从-15 dB增加到15 dB,进行500次蒙特卡洛实验.
由图 1可知,4种算法对混合信号源DOA估计的成功概率均随信噪比的增加而增大,在信噪比大于0 dB时,4种算法均能有效地对混合信号源进行DOA估计.
图 1(Fig. 1)
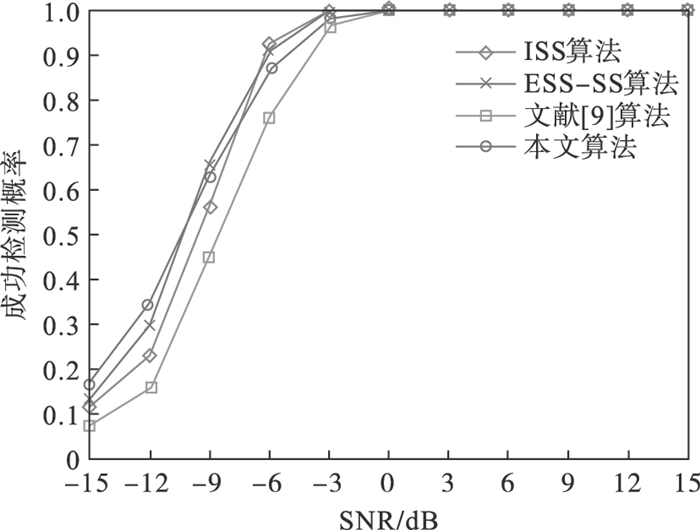 | 图 1 不同信噪比环境下4种算法的成功检测概率Fig.1 Successful estimation probability of the four algorithms under different SNR environments |
3.2 本文算法的精度实验为了验证本文算法的DOA估计精度,以估计角度的均方根误差(RMSE)作为衡量算法准确性的标准.
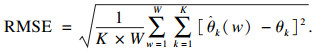 | (31) |
下面将在不同的入射信源个数、不同的信噪比以及不同的快拍数条件下分别实验.
实验2??阵列设置为8阵元的均匀线阵,阵元间距为信号半波长;假设入射信号源为3个,前2个入射信号是相干的,设为10°和15°,对应的衰减系数设置为[1,0.9],第3个入射信号为独立信号,设为50°.采样快拍数为500,信噪比以3 dB的间隔从-15 dB增加到15 dB,分别进行500次蒙特卡洛实验计算估计角度的均方根误差.
由图 2可知,在入射角度相隔较小的条件下,4种算法的均方根误差均随信噪比的增加呈下降趋势,在信噪比低于-3 dB时,本文算法的均方根误差明显低于其他3种算法.同时,本文算法更加接近算法的无偏估计量下界(CRB)[15],相较其他算法拥有更高的DOA估计精度.
图 2(Fig. 2)
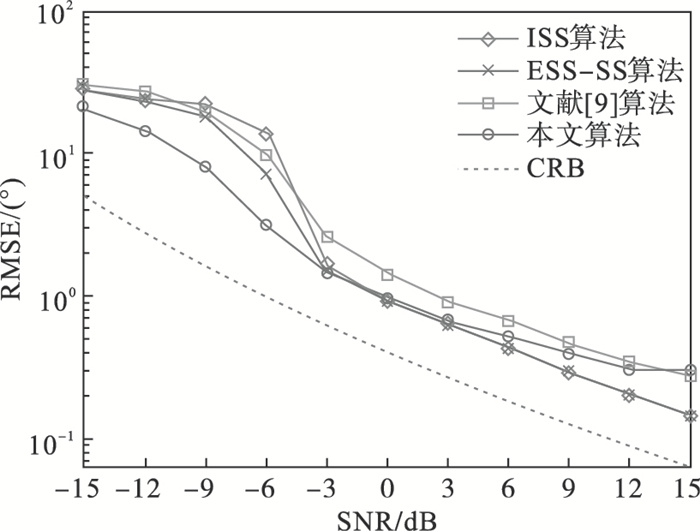 | 图 2 不同信噪比环境下4种算法DOA估计精度对比(实验2)Fig.2 Comparison of DOA estimation accuracy of the four algorithms under different SNR environments(No.2 experiment) |
实验3??阵列模型以及入射信源角度同实验2,信噪比固定为0 dB不变,采样快拍数以50为间隔从100增加至600,每种快拍数条件下进行500次蒙特卡洛实验,计算估计角度的均方根误差,实验结果如图 3所示.
图 3(Fig. 3)
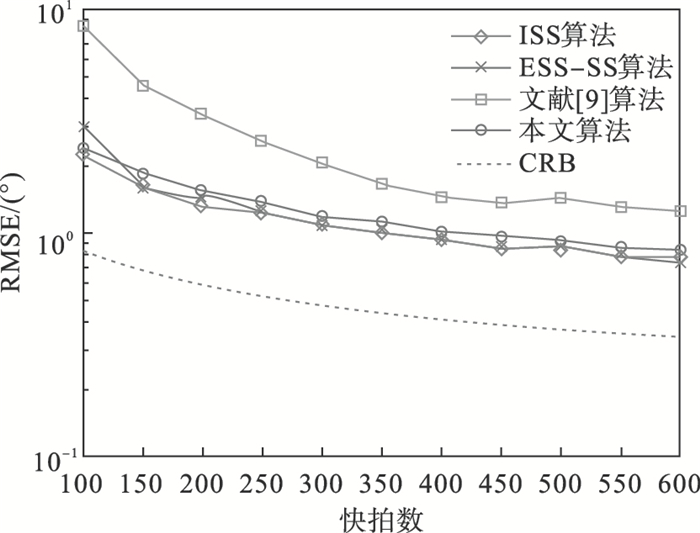 | 图 3 4种算法的均方根误差与快拍数之间的关系Fig.3 Relationship between RMSE of the four algorithms and the number of snapshots |
由图 3可知,在其他条件固定时,4种算法的DOA估计精度总体会随着快拍数的增加而提高.在快拍数较小时,文献[9]中算法DOA估计精度较低.而本文提出的算法与ISS算法以及ESS-SS算法的曲线随快拍数的变化相对较为平稳并且更加接近无偏估计量下界CRB,拥有更高的DOA估计精度及更强的鲁棒性.
实验4??阵列设置为9个阵元的均匀线阵,阵元间距为信号半波长.入射信源的数量增加为6个.混合信源中独立信源的数量设为2个,入射角度分别为-10°和60°,相干信源设为两组,第1组为-60°和-40°,衰减系数设置为[1,0.9],第2组为20°和50°,衰减系数设置为[1,0.8].采样数及信噪比变化同实验1,进行500次蒙特卡洛实验来计算估计角度的均方根误差,实验结果如图 4所示.
图 4(Fig. 4)
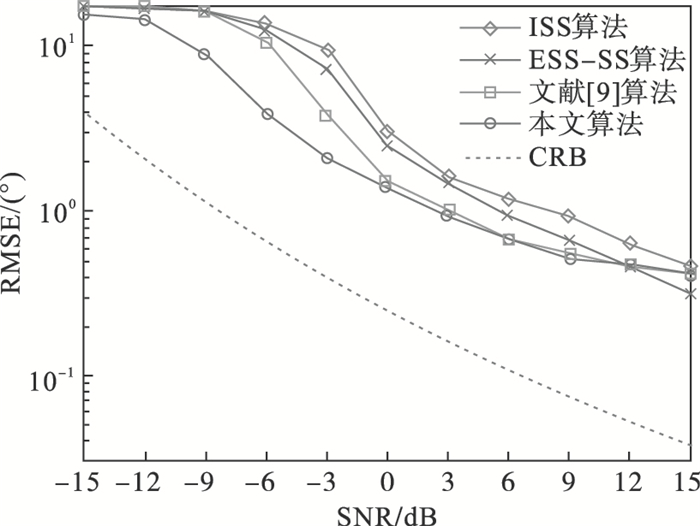 | 图 4 不同信噪比环境下4种算法DOA估计精度对比(实验4)Fig.4 Comparison of DOA estimation accuracy of the four algorithms under different SNR environments(No.4 experiment) |
由图 4可知,在存在多个独立信源与多组相干信源时,随着信噪比的增加,4种算法的精度均得到了有效提升.在信噪比低于-6 dB时,其余的3种算法失效,在信噪比较高的条件下4种算法均能得到有效的估计角度.本文算法的精度在不同的信噪比环境下较其他3种算法均有明显的提升.
实验5??均匀线阵设置同实验4.继续增加入射信源的数量,总信源数设置为8个.混合信源中独立信源设为3个,入射角度分别为-10°,40°和60°.相干信号源设置为两组,第1组包含3个相干信源,分别为-10°,-40°和-60°,衰减系数设置为[1,0.93,0.84],第2组包含2个相干信源,分别为20°和50°,衰减系数设置为[1,0.9].采样快拍数固定为500,信噪比变化同实验3,进行500次蒙特卡洛实验.
由图 5可知,在信源数目增加到8个时,ISS算法和ESS-SS算法已经失效,而本文算法与文献[9]中算法仍有较为良好的估计效果并且本文算法的最终结果更优.前两种算法是对混合信源的所有信号直接估计,并且因为划分子阵而导致阵列孔径变小,所以可估计的总信源数相对较少.本文所提算法与文献[9]中算法为分段式DOA估计,相较传统的DOA估计算法可以突破阵列规模的限制从而估计更多的入射角度.在本实验中,来自独立信号源中的-10°与第1组相干信号源中的-10°被成功地检测出来,这是因为独立信源与相干信源是分两个步骤进行估计的,这也是本文所提算法的优势.
图 5(Fig. 5)
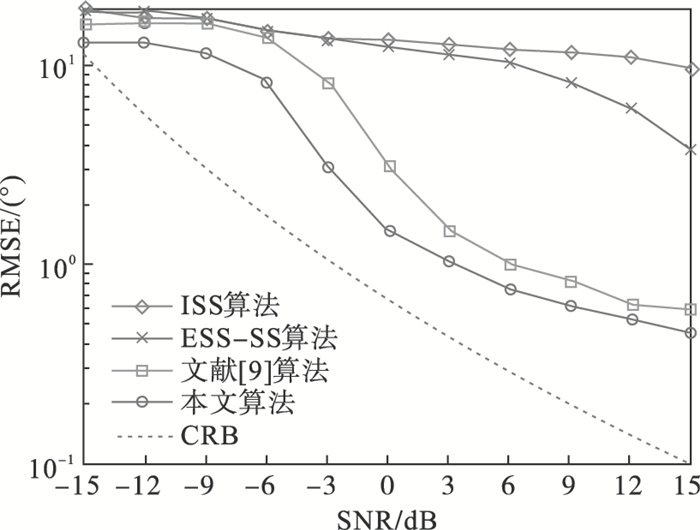 | 图 5 不同信噪比环境下4种算法DOA估计精度对比(实验5)Fig.5 Comparison of DOA estimation accuracy of the four algorithms under different SNR environments(No.5 experiment) |
4 结论针对混合信号的DOA估计中精度损失与阵列孔径损失的问题,本文提出了一种基于斜投影算子的高精度DOA分段估计算法.本文算法将混合信号的DOA估计分为两个阶段,第一阶段是对独立信号的估计,通过ESPRIT算法完成,第二阶段则是对相干信号的估计.在第二阶段中,首先利用斜投影算子去除独立信号的信息,得到仅包含相干信号信息的协方差矩阵,而后利用新得到的协方差矩阵的信号子空间进行去相干处理,最后结合ESPRIT算法估计相干信号的波达方向.仿真实验结果表明,相较传统算法,本文提出的算法有效地提升了阵列的孔径,能够有效地区分小间隔的入射信号,在快拍数少以及信噪比较低的情况下仍有较好的DOA估计性能.
参考文献
| [1] | Jaafer Z, Goli S, Elameer A S. Best performance analysis of DOA estimation algorithms[C]//2018 1st Annual International Conference on Information and Sciences(AiCIS). Fallujah, 2018: 235-239. |
| [2] | Jiang X Q, Qian S S. DOA estimation of coherent signals based on modified MUSIC algorithm[C]//2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology(ICCASIT). Changsha, 2021: 918-921. |
| [3] | Roy R, Paulraj A, Kailath T. Estimation of signal parameters via rotational invariance techniques—ESRRIT[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995. DOI:10.1109/29.32276 |
| [4] | Pillai S U, Kwon B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8-15. DOI:10.1109/29.17496 |
| [5] | Karmous N, El Hassan M O, Choubeni F. An improved ESPRIT algorithm for DOA estimation of coherent signals[C]//2018 International Conference on Smart Communications and Networking(SmartNets). Yasmine Hammamet, 2018: 1-4. |
| [6] | Zhang W, Han Y, Jin M, et al. An improved ESPRIT-like algorithm for coherent signals DOA estimation[J]. IEEE Communications Letters, 2020, 24(2): 339-343. DOI:10.1109/LCOMM.2019.2953851 |
| [7] | Dong M, Zhang S H, Wu X D, et al. A high resolution spatial smoothing algorithm[C]//2007 International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications. Hangzhou, 2007: 1031-1034. |
| [8] | Pan J J, Sun M, Wang Y D, et al. An enhanced spatial smoothing technique with ESPRIT algorithm for direction of arrival estimation in coherent scenarios[J]. IEEE Transactions on Signal Processing, 2020, 68: 3635-3643. DOI:10.1109/TSP.2020.2994514 |
| [9] | Shi H P, Leng W, Wang A G, et al. DOA estimation for mixed uncorrelated and coherent sources in multipath environment[J]. International Journal of Antennas and Propagation, 2015, 2015: 1-8. |
| [10] | Xu X, Ye Z, Peng J. Method of direction-of-arrival estimation for uncorrelated, partially correlated and coherent sources[J]. IET Microwaves, Antennas & Propagation, 2007, 1(4): 949-954. |
| [11] | Zuo W L, Xin J M, Zheng N N, et al. Subspace-based near-field source localization in unknown spatially nonuniform noise environment[J]. IEEE Transactions on Signal Processing, 2020, 68: 4713-4726. DOI:10.1109/TSP.2020.3013419 |
| [12] | 张石, 许方晗, 佘黎煌, 等. 基于重构噪声子空间的相干信号DOA估计[J]. 东北大学学报(自然科学版), 2021, 42(12): 1696-1700. (Zhang Shi, Xu Fang-han, She Li-haung, et al. DOA estimation of coherent signals based on reconstruct noise subspace[J]. Journal of Northeastern University(Natural Science), 2021, 42(12): 1696-1700. DOI:10.12068/j.issn.1005-3026.2021.12.004) |
| [13] | Gan L, Luo X Y. Direction-of-arrival estimation for uncorrelated and coherent signals in the presence of multipath propagation[J]. IET Microwaves Antennas & Propagation, 2013, 7(9): 746-753. |
| [14] | 胡盈绮, 邓科, 殷勤业. 采用前向空间平滑分组的混合信号波达方向估计算法[J]. 西安交通大学学报, 2020, 54(9): 164-172. (Hu Ying-qi, Deng Ke, Yin Qin-ye. Direction of arrival estimation method for mixed signals by forward spatial smooth grouping[J]. Journal of Xi'an Jiaotong University, 2020, 54(9): 164-172.) |
| [15] | Stoica P, Larsson E G, Gershman A B. The stochastic CRB for array processing: a textbook derivation[J]. IEEE Signal Processing Letters, 2001, 8(5): 148-150. DOI:10.1109/97.917699 |
